Effects of Fines Migration on Low-Salinity Waterflooding: Analytical Modelling

Abstract

We discuss the governing system for oil–water flow with varying water composition. The model accounts for wettability alteration, which affects the relative permeability, and for salinity-variation-induced fines migration, which reduces the relative permeability of water. The overall ionic strength represents the aqueous phase composition in the model. One-dimensional displacement of oil by high-salinity water followed by low-salinity-slug injection and high-salinity water chase drive allows for exact analytical solution. The solution is derived using the splitting method. The analytical model obtained analyses the effects of wettability alteration and fines migration on oil recovery as two distinct physical mechanisms. For typical reservoir conditions, the significant effects of both mechanisms are observed.

1 Introduction

Injection of low-salinity (LS) or “smart” water into oilfields for recovery enhancement has several advantages, such as low cost relative to other enhanced oil recovery (EOR) techniques, often readily available injectant, negligible environmental impact, and straightforward field implementation. Planning and designing a waterflood having an alternative composition includes study of numerous physical mechanisms of incremental recovery; the degree of freedom for possible injection compositions highly exceeds those for “normal” flooding (Agbalaka et al. 2009; Austad et al. 2010; Sheng 2014; Brady et al. 2015; Khorsandi et al. 2016). The injected water composition strongly affects the success of “smart” waterflooding and is extremely sensitive to numerous factors, such as formation water and crude composition, and mineral content of the rock (Tang and Morrow 1999; RezaeiDoust et al. 2009; Morrow and Buckley 2011; Fogden et al. 2011). Therefore, decision-making on low-salinity waterflooding must include a multi-variant sensitivity study with reliable laboratory-based mathematical modelling. The need for numerous multi-variant simulations motivates the search for an analytical model.

Multiple physics effects in two-phase flow with varying salinity and the consequent EOR mechanisms are presently not well understood (Sheng 2014). Therefore, in the current work, we use a so-called mechanistic model for one-dimensional low-salinity waterflooding (Qiao et al. 2015, 2016; Khorsandi et al. 2016), which is similar to the model for “multi-component polymer flooding” (Braginskaya and Entov 1980; Pope 1980; Lake et al. 2014; Barenblatt et al. 1989; Dahl et al. 1992). The one-component “lumped” model, presented by Jerauld et al. (2008) and used in the current paper, groups all salts in one pseudo-component, referring to salinity as the “ionic strength”. The multi-component models for low-salinity waterflooding include monovalent and divalent anions with active-mass-law kinetics of chemical reactions and adsorption on clay sites, and cations in brine (Omekeh et al. 2013; Dang et al. 2013; Nghiem et al. 2015; Qiao et al. 2015, 2016; Khorsandi et al. 2016). The models also account for dissolution of calcite cement in the brine, and sorption of some oleic components on the rock surface (Al Shalabi et al. 2014a, b; Alexeev et al. 2015).

Planning and design of low-salinity waterflooding includes fines management (Civan 2007, 2010, 2011; Fogden 2012). Often the injected water salinity is chosen to avoid fines mobilisation and migration in order to limit the consequent formation damage, although this is not always possible (Scheuerman and Bergersen 1990; Pingo-Almada et al. 2013). Moreover, the fines-induced reduction in permeability decelerates the injected water, which enhances sweep efficiency (Zeinijahromi et al. 2013). The effective management of fines migration with varying injected water composition requires mathematical modelling. The equations for two-phase flow with fines migration have been presented for homogeneous reservoirs in large-scale approximations (Yuan and Shapiro 2011; Zeinijahromi et al. 2013). Their averaging in layer-cake formations yields pseudo-relative permeability equations (Lemon et al. 2011). However, to our knowledge, basic equations in the literature for low-salinity waterflooding do not account simultaneously for wettability alteration and for fines mobilisation, migration, and straining.

In large-scale approximation, one-dimensional solutions of continuous injection depend on one group x / t, i.e. are self-similar (Pope 1980; Polyanin and Zaitsev 2012; Lake et al. 2014). However, the solutions for sequential injection of high-salinity (HS) and LS slugs with HS chase drive are non-self-similar. The corresponding interactions of saturation and concentration waves have been investigated in Barenblatt et al. (1989), Entov and Zazovskii (1989) and Bedrikovetsky (1993). Analytical solutions have not been obtained for oil displacement by HS water followed by LS water slug and HS chase drive.

In the present work, we present a mathematical model, in which a two-phase immiscible flow model that uses the “lumped” salt concentration in water, is merged with the model of fines mobilisation, migration, and aqueous phase permeability impairment. For the case where the initial concentration of attached fines is below its maximum, we propose the extrapolation of the maximum retained function into the area where particle mobilisation does not occur, in order to avoid different systems of equations in two (x, t)-domains. The one-dimensional (1D) problem of “normal” waterflooding followed by the injection of LS water slug and HS chase drive allows for exact solution. We obtained it by the splitting method, using the Lagrangian coordinate instead of time in the system of governing equations. The exact solution provides explicit formulae for concentration and saturation profiles, front velocities, breakthrough concentration, and the recovery factor. The solution encompasses both cases of secondary and tertiary recovery. The analytical model allows for sensitivity analysis of how the incremental oil recovery is affected by two independent physical factors: contact angle alteration and fines migration.

The structure of the paper is as follows. Section 2 derives the governing equations for two-phase flow with varying salinity and fines migration in large-scale approximation. Section 3 derives an exact solution corresponding to injection of HS and LS water slugs followed by HS chase drive. Section 4 contains the results of analytical modelling and analysis of incremental oil recovery with LS waterflooding applications. Section 5 discusses applications and limitations of the derived analytical model. Section 6 concludes the paper.

2 Governing Equations

Sections 2.1 and 2.2 introduce a maximum retention function in single-phase and two-phase environments, respectively. The maximum retention function is a mathematical model for fines detachment. Section 2.3 derives the basic equations for two-phase flow with varying salinity and induced fines mobilisation and straining. Section 2.4 presents the formulation of 1D waterflooding using low-salinity water slugs with high-salinity chase drive.

2.1 Particle Detachment During Single-Phase Flow

In this section, we discuss fine particle mobilisation, migration, and straining during a single-phase flow in porous media. Figure 1 shows a particle on a rough surface of the rock or internal cake in a single-phase environment. The drag $F_{\mathrm{d}}$, lift $F_{\mathrm{l}}$, electrostatic force $F_{\mathrm{e}}$, and gravitational force $F_{\mathrm{g}}$ exert the particle subject to water flow in porous space.

Fig. 1

Schematic for torque balance exerted on the particle at the moment of mobilisation: a lever arm is defined by the mutual particle-rock deformation and b the particle starts rotating around the asperity

The mechanical equilibrium of particles on the rock surface is determined by the torque balance for drag, lift, electrostatic, and gravitational forces, i.e. the total torque is equal to zero (Khilar and Fogler 1998; Bradford et al. 2006, 2011):

$$\begin{aligned} F_{\mathrm{d}} l_{\mathrm{d}} +F_{\mathrm{l}} l_{\mathrm{e}} =({F_{\mathrm{e}} +F_g})l_{\mathrm{e}}. \end{aligned}$$

(1)

Here $l_{\mathrm{d}}$ and $l_{\mathrm{e}}$ are the lever arms for tangential and normal forces, respectively. The tangential lever arm for a solid particle can be assumed to equal the particle radius, and the normal lever arm is determined by the Hertz theory of the contact area between the deformable particle and surface. Depending on the Young modulus and the Poisson ratio for rock and particle matters, the lever arm ratio $l_{\mathrm{e}}/l_{\mathrm{d}}$ varies in the interval 100–1000. In principle, the particle could revolve around an asperity on the rough rock surface (Fig. 1b). However, the available laboratory data on particle dislodgment are in close agreement with the Hertz theory (Kalantariasl et al. 2014, 2015).

Consider a mono-layer of multiple-size particles on the rock surface. The torque balance (1) determines whether a given particle is mobilised or remains attached to the surface. The forces in Eq. (1) depend on the carrier fluid velocity, ionic strength, temperature, effective stress, and other parameters affecting the forces (Bedrikovetsky et al. 2011, 2012). Therefore, this equation determines the amount of attached fines. This dependency is called the critical retention function. Under constant flow velocity, temperature, and effective stress, the attached concentration is a function of salinity only.

For fixed injection rate and pore size, all forces in Eq. (1) depend on salinity and particle radius. This allows expressing the ratio between particle radius versus salinity at which the particle is mobilised: $r_{\mathrm{s}}=r_{\mathrm{s}}(\gamma )$, where ${\gamma }$ represents salinity. The obtained dependency is monotonically increasing. Thus, the particles are mobilised in order of decreasing their radii during flow with decreasing salinity. Therefore, the maximum retention function is equal to the accumulated size distribution of particles attached to the rock surface:

$$\begin{aligned} \sigma _{\mathrm{cr}} (\gamma )=\sigma _{\mathrm{a}0} \int \limits _0^{r_{\mathrm{s}} (\gamma )} {{\varSigma } (r)\mathrm{d}r}, \end{aligned}$$

(2)

where ${\varSigma } (r_{\mathrm{s}})$ is the concentration distribution of attached particles over radii and $\sigma _{\mathrm{a}0}$ is the overall initial concentration of attached fine particles. The detailed derivations are given by You et al. (2015).

Further in the text, the critical retention function for one-phase flow is denoted as

$$\begin{aligned} \sigma _{\mathrm{a}} =\sigma _{\mathrm{cr}} (\gamma ), \end{aligned}$$

(3)

where $\gamma$ is the salinity, and the flow velocity, temperature, and effective stress are assumed to be constant.

The plots of maximum retention function $\sigma =\sigma _{\mathrm{cr}}({\gamma })$ for a mono-layer of fines particles are given in Fig. 2a; black, red and blue curves correspond to velocities $u=10^{-4},\,1.5\times 10^{-4}$ and $2\times 10^{-4}\,\hbox {m}/\hbox {s}$, respectively. The maximum retention function defined by Eq. (3), is calculated for mono-layers of multi-sized particles in a cylindrical capillary. It is assumed that in the sandstone rock, the kaolinite fines are attached to the grain surfaces. The typical values of physical properties are as follows: salinity is equal to seawater salinity ${\gamma }_{\mathrm{I}} =28{,}000$ ppm of NaCl, Hamaker constant $A_{132}= 9.5561\times 10^{-21}\,\hbox {J}$, and electrostatic potentials for quartz-brine and kaolinite brine are −19.1 and −10.7 mV, respectively. For salinity equal to ${\gamma }_{J} =1500$ ppm of NaCl and Hamaker constant $A_{132}=9.5938\times 10^{-21}\,\hbox {J}$, electrostatic potentials for quartz–brine and kaolinite brine are −34.9 and −23.0 mV, respectively. For either salinity, mean particle size $r_{\mathrm{s}}=3\,{\upmu }\hbox {m}$, drag factor $\omega =60$, and formation damage coefficient $\beta =1000$ (Khilar and Fogler 1998; Israelachvili 2011). The permeability is $k=8\times 10^{-13 }\,\hbox {m}^{2}$ and the porosity is $\phi =0.2$; so the mean pore radius as calculated by the formula $r_{\mathrm{p}}=5(k/\phi )^{1/2}$ equals $10^{-5}\,\hbox { m}$ (Barenblatt et al. 1989). Flow velocity is $1.5\times 10^{-4}\,\hbox {m}/\hbox {s}$. The injected and initial points are located on the red maximum retention curve (Fig. 2a).

Fig. 2

In large-scale approximation, strained concentration ${\sigma }_{\mathrm{s}}$ is determined by the maximum retention function ${\sigma }_{\mathrm{cr}}\,(\gamma )$; here, concentrations ${\sigma }_{\mathrm{s}}$ and ${\sigma }_{\mathrm{cr}}\,(\gamma )$ are approximated by the vanishing function into the domain $\sigma <\sigma _{\mathrm{cr}}\,(\gamma )$, where no particles are mobilised: a maximum retention curves for different flow velocities and b extrapolation of the maximum retention curve into the “under-saturated” area ${\gamma }<{\gamma }_{\mathrm{cr}}$ of no fines release

The higher the velocity, the larger the drag and lift forces and the lower the maximum retention concentration.

The maximum retention function can also be calculated for the case of poly-layers of mono-size particles on the cylindrical pore wall. The salinity decrease yields a decrease in electrostatic force and normal lever arm, thereby decreasing the right hand side of Eq. (1). The corresponding decrease in drag $F_{\mathrm{d}}$ is achieved via the particle’s dislodging, cake thickness decrease, and decrease in the interstitial velocity in the pore. The detailed derivations are presented in Bedrikovetsky et al. (2011).

In the general case of arbitrary pore space geometry, particle size, and shape distributions, the maximum retention function is a phenomenological function of the model.

The above two models for theoretical prediction of the maximum retention function have been validated by laboratory experiments (Zeinijahromi et al. 2013; You et al. 2015).

The typical form of the maximum retention function $\sigma ={\sigma }_{\mathrm{cr}}({\gamma })$ is given in Fig. 2b. For the points below the maximum retention curve, the attaching torque of electrostatic and gravitational forces exceeds those for the detaching drag and lift forces. The initial point corresponds to the “under-saturated” state, i.e. the fine particle mobilisation can begin only after the salinity has decreased from ${\gamma }_{\mathrm{I}}$ to ${\gamma }_{\mathrm{cr}}$. Therefore, along the path, the horizontal line depicts no fines release, and the curve indicates the release of an amount of fines denoted as ${\sigma }_{\mathrm{s}}$. The critical salinity is determined as a minimum salinity where the fines are released:

$$\begin{aligned} \sigma _{\mathrm{cr}} ({\gamma _{\mathrm{cr}}})=\sigma _{\mathrm{a}0}. \end{aligned}$$

(4)

Therefore, salinity variation from ${\gamma }_{\mathrm{I}}$ to ${\gamma }_{\mathrm{cr}}$ does not cause any particle mobilisation. Salinity decrease from ${\gamma }_{\mathrm{cr}}$ to ${\gamma }$ yields release of fine particles that corresponds to decrease in the attached particle concentration by ${\sigma }_{\mathrm{a}0}-{\sigma }_{\mathrm{cr}}({\gamma })$.

In order to avoid two systems of equations, with and without fines release, we approximate the maximum retention function for ${\gamma }<{\gamma }_{\mathrm{I}}$ by a curve that crosses point I and passes negligibly below the horizontal line ${\sigma } ={\sigma }_{\mathrm{a}0}$ (Fig. 2b). It provides negligible fines detachment for ${\gamma }>{\gamma }_{\mathrm{cr}}$; the fines release occurs at any salinity below the initial salinity and allows using the mathematical model for flow with fines release (3) for the overall interval of salinities.

2.2 The Model for Particle Detachment During Two-Phase Flow

Following Zeinijahromi et al. (2013, (2016), this section discusses fine particle mobilisation under two-phase flow in porous media. Figure 3 shows the attached and strained fine particles, which are retained in the rock (with concentrations ${\sigma }_{\mathrm{a}}$ and ${\sigma }_{\mathrm{s}}$, respectively). Figure 3 also shows the fractions of the overall solid-liquid interface accessible to water $A_{\mathrm{w}}$ and oil $A_{\mathrm{o}}$, which is one of the schemas for oil and water distribution in mixed-wet rocks (Salathiel 1973; Kovscek et al. 1993; Kim and Kovscek 2013). The higher the water saturation and the lower the contact angle, the greater the accessible-to-water surface fraction $A_{\mathrm{w}}(s,\gamma )$. Consequently, the surface fraction $A_{\mathrm{o}}$ is a monotonically decreasing function of s and a monotonically increasing function of the contact angle $\theta$. The contact angle is a salinity function: $\theta =\theta (\gamma )$.

The overall specific rock–liquid surface comprises that accessible to water and that accessible to oil:

$$\begin{aligned} A_{\mathrm{w}} ({s,\gamma })+A_\mathrm{o} ({s,\gamma })=1. \end{aligned}$$

(5)

Sarkar and Sharma (1990) and Sharma and Filoco (2000) investigated the permeability reduction resulting from the injection of low-salinity water. The permeability damage in the presence of residual oil was observed to be significantly lower than in a single-phase flow. This is attributed to incomplete accessibility of mobile water to the rock surface under saturation of rock by water and oil. The formation damage in the presence of polar residual oil was found to be lower than that under the non-polar oil. The rock is fully wet with water in the non-polar-oil case, whereas the rock is partly wet in the case of polar oil. Thus, the rock surface accessible for mobile water is higher for the case of non-polar oil, implying that low-salinity water detaches more particles.

Berg et al. (2010), Cense et al. (2011), Fogden (2012) and Mahani et al. (2015a, (2015b) found a decrease in the contact angle during the salinity decrease, with further detachment of oil from the clay surface and expansion of the water-accessible clay surface. Fogden et al. (2011) observed kaolinite release by the low-salinity water flux after residual oil removal.

The poly-molecular water film covering the oil-wet rock minerals is not included into the area $A_{\mathrm{w}}$; the film is located in the area $A_{\mathrm{o}}$ (Mahani et al. 2015a, b). Area $A_{\mathrm{w}}$ corresponds only to mobile water, which can remove the attached particles. We neglect the salt diffusion through the poly-molecular water film covering the oil-wet rock minerals. Thus, the amount of fines attached to area $A_{\mathrm{o}}$ is not affected by salinity, but that on the $A_{\mathrm{w}}$-surface depends on salinity (Schembre and Kovscek 2005; Schembre et al. 2006; Zeinijahromi et al. 2013, 2016).

Fig. 3

Schematic for porosity, phase saturations, and particle concentrations in porous space: the fine particles are attached to the rock surface $(\sigma _{\mathrm{a}})$ and strained in thin pores $({\sigma }_{\mathrm{s}})$

Fig. 4

The attached particles can be detached from the rock surface accessible to water $A_{\mathrm{w}}$ by the injected water; fines attached to the surface $A_{\mathrm{o}}$ remain immobile

Figures 3 and 4 show oil films covering clay surface in the area invaded by the injected water; the corresponding saturation is equal to $s-s_{\mathrm{wi}}$ and water-accessible surface is $A_{\mathrm{w}}(s, \gamma )-A_{\mathrm{w}}(s_{\mathrm{wi}},\, \gamma )$. Oil is not present in the $s_{\mathrm{wi}}$th fraction of the pore space. Here we discuss water injection into the reservoir with connate water saturation $s_{\mathrm{wi}}$.

The model also assumes that the drag acting on a particle from the flowing oil is not sufficient to mobilise it.

From the above statements on the fines state in porous media, saturated by two-phase fluid, it follows that the overall attached fine particle concentration in the rock encompasses the particles attached to the rock surface

• (1) saturated by the connate water $A_{\mathrm{w}}(s_{\mathrm{I}},\,\gamma )$;

• (2) accessible to water, where oil is released by low-salinity water $b({\gamma })\{A_{\mathrm{w}}(s,\, \gamma )-A_{\mathrm{w}}(s_{\mathrm{I}},\, \gamma )\}$;

• (3) accessible to water, where oil is not released $[1-b({\gamma })]\{A_{\mathrm{w}}(s,\, \gamma )-A_{\mathrm{w}}(s_{\mathrm{I}},\, \gamma )\}$; and

• (4) accessible to oil $A_{\mathrm{o}}(s,\, {\gamma })$.

Here b is the fraction of the clay surface from which the attached oil is removed. In the case of clay particles (kaolinite, illite, etc.), the dependency $b({\gamma })$ defines the fraction of the surface where the varying-salinity water removes the residual oil due to wettability altering.

The fines attached to the rock surface related to connate water, or accessible to water and released from the attached oil (types 1 and 2), can be mobilised by drag’s being exerted on particles from the carrier water. The decrease in salinity weakens the attractive electrostatic particle-grain forces, which means that maximum retention is a monotonically increasing function of salinity (Khilar and Fogler 1998; Israelachvili 2011).

For the case of instant fines release, the attached concentration is equal to the maximum retention function of the rock ${\sigma }_{\mathrm{cr}}(s,\,\gamma )$ and is the total of four concentrations of the above-mentioned particles:

$$\begin{aligned} \sigma _{\mathrm{a}}= & {} \sigma _{\mathrm{cr}} ({s,\gamma })=\sigma _{\mathrm{cr}} (\gamma )A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma })+\sigma _{\mathrm{cr}} (\gamma )b(\gamma )\left[ {A_{\mathrm{w}}({s,\gamma })-A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma })} \right] \nonumber \\&+\,\sigma _{\mathrm{a}0} [ {1-b(\gamma )}]\left[ {A_{\mathrm{w}} ({s,\gamma })-A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma })}\right] +\sigma _{\mathrm{a}0} [{1-A_{\mathrm{w}} ({s,\gamma })}], \end{aligned}$$

(6)

where the function ${\sigma }_{\mathrm{cr}}({\gamma })$ corresponds to single-phase water flow through the rock.

Only types 1 and 4 are present in the rock under connate water saturation. Substituting $s=s_{\mathrm{I}}$ in Eq. (6) yields the expression for initial amount of attached particles in the rock:

$$\begin{aligned} \sigma _{\mathrm{a}} =\sigma _{\mathrm{cr}} ({s_{\mathrm{I}},\gamma _{\mathrm{I}}})=\sigma _{\mathrm{cr}} ({\gamma _{\mathrm{I}}})A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma _{\mathrm{I}}})+\sigma _{\mathrm{a}0} \left[ {1-A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma _{\mathrm{I}}})} \right] . \end{aligned}$$

(7)

The assumption of instant capture of the released fines leads to

$$\begin{aligned} \sigma _{\mathrm{s}}= & {} \sigma _{\mathrm{cr}} ({s_{\mathrm{I}},\gamma _{\mathrm{I}}})-\sigma _{\mathrm{cr}} ({s,\gamma }) \nonumber \\= & {} \left[ {\sigma _{\mathrm{cr}} ({\gamma _{\mathrm{I}}})-\sigma _{\mathrm{cr}} (\gamma )} \right] A_{\mathrm{w}}({s_{\mathrm{I}},\gamma })+\left[ {\sigma _{\mathrm{a}0} -\sigma _{\mathrm{cr}} (\gamma )} \right] b(\gamma )\left[ {A_{\mathrm{w}} ({s,\gamma })-A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma })} \right] . \end{aligned}$$

(8)

Using the extrapolated maximum retention curve (Fig. 2b) allows deriving the “saturated” state of the initial fines, i.e.

$$\begin{aligned} \sigma _{\mathrm{a}0} =\sigma _{\mathrm{cr}} ({\gamma _{\mathrm{I}}}). \end{aligned}$$

(9)

The expression (8) for strained concentration (9) becomes

$$\begin{aligned} \sigma _{\mathrm{s}} =\left[ {\sigma _{\mathrm{a}0} -\sigma _{\mathrm{cr}} (\gamma )} \right] \left\{ {A_{\mathrm{w}} ({s_{\mathrm{I}},\gamma })+b(\gamma )\left( {A_{\mathrm{w}} ({s,\gamma })-A_{\mathrm{w}} ({s_{\mathrm{I}} ,\gamma })} \right) } \right\} . \end{aligned}$$

(10)

Now we introduce the rock surface fraction $A_{\mathrm{s}}$ from which the fines can be detached:

$$\begin{aligned} A_{\mathrm{s}} (s,\gamma )=\left\{ \begin{array}{ll} A_{\mathrm{w}} (s_{\mathrm{I}},\gamma ), &{}\quad s<s_{\mathrm{I}} \\ A_{\mathrm{w}} (s_{\mathrm{I}},\gamma )+b(\gamma )\left( A_{\mathrm{w}}(s,\gamma )-A_{\mathrm{w}} (s_{\mathrm{I}},\gamma ) \right) , &{}\quad s>s_{\mathrm{I}} \end{array} \right. . \end{aligned}$$

(11)

Figure 5 shows the water-accessible area $A_{\mathrm{w}}(s,\gamma )$ and the particle detachment area $A_{\mathrm{s}}(s,\gamma )$ for the formation and injected water salinities.

The expression (10) for strained concentration (8) can be simplified to

$$\begin{aligned} \sigma _{\mathrm{s}} =\left[ {\sigma _{\mathrm{a}0} -\sigma _{\mathrm{cr}} (\gamma )} \right] A_{\mathrm{s}} (s,\gamma ). \end{aligned}$$

(12)

In particular, the amount of strained particles during the overall displacement period is

$$\begin{aligned} \sigma _{\mathrm{s}} =\left[ {\sigma _{\mathrm{a}0} -\sigma _{\mathrm{cr}} ({\gamma _J})} \right] A_{\mathrm{s}} \left( {1-s_{\mathrm{or}},\gamma _J} \right) . \end{aligned}$$

(13)

For the case of water-wet particles (silica, lousy sand, feldspar), the attached concentration is a total of the particles on the rock surface accessible to water, and the attached particles on the accessible-to-oil surface (Yuan and Shapiro 2011; Zeinijahromi et al. 2013, 2016):

$$\begin{aligned} \sigma _{\mathrm{a}} =\sigma _{\mathrm{cr}} ({s,\gamma })=\sigma _{\mathrm{cr}} (\gamma )A_{\mathrm{w}} ({s,\gamma })+\sigma _{\mathrm{a}0}({1-A_{\mathrm{w}} ({s,\gamma })}). \end{aligned}$$

(14)

2.3 Model Assumptions and Governing System

Let us discuss the governing equations for oil displacement by low-salinity water that account for particle detachment and straining, causing damage to the aqueous phase.

We assume the conditions of large-scale approximation, where dissipative fluxes (capillary pressure and dispersion) are negligible compared with the advective fluxes of phases and components, and the relaxation times of non-equilibrium processes (kinetics of wettability alternation and fines release and straining) are negligible compared with the injection of one pore volume (Bedrikovetsky 1993). The conditions of large-scale approximation assume that the following dimensionless groups vanish for large L:

$$\begin{aligned} \frac{\sigma _{\mathrm{wo}} ({\gamma _{\mathrm{I}}})\,\cos \theta ({\gamma _{\mathrm{I}}})\,\sqrt{k\phi }}{\,\mu _\mathrm{o} uL},\quad \frac{\alpha _{L} }{L}, {\Lambda } L,\quad \frac{u\tau _\theta }{\phi L},\quad \frac{u\tau _\sigma }{\phi L} \ll 1, \end{aligned}$$

(15)

where ${\sigma }_{\mathrm{wo}}$ is the interfacial tension between oil and water, $\mu _{\mathrm{o}}$ is the oil viscosity, L is the reservoir (core) length, $\alpha _{{L}}$ is the rock dispersivity, ${\varLambda }$ is the filtration coefficient, $\tau _{\theta }$ is the relaxation time of the contact angle alteration, and $\tau _{\sigma }$ is the delay in fine particles release.

Fig. 5

The functions that determine the rock surface fraction of the clay detachment: a plots of the water-accessible area $A_{\mathrm{w}}\,(s,\gamma )$ (solid curves) and the particle detachment area $A_{\mathrm{s}}\,(s,\gamma )$ (dashed curves) and b the fraction of clay area $b(\gamma )$ released from the attached residual oil by low-salinity water

To be more specific, the large-scale conditions (15) mean that the viscous pressure drop highly exceeds capillary pressure. So, the capillary pressure is negligible compared with oil or water pressure. Salt dispersion is negligible compared with the advective mass transfer of the salt component by the carrier aqueous phase. The free-run length of particle is significantly smaller than the core length.

The delay in establishing the salinity-dependent contact angle is negligible compared with the residence time in the core (reservoir). Also, salt diffuses from the particle-rock contact space to the bulk solution in the pore centre, which means that the attached concentration takes values of the maximum retention function with some delay (Mahani et al. 2015a, b). In large-scale approximation, it is assumed that the delay is negligible compared to the time of injection of one pore volume, implying that the dependency (10) is established instantly.

Therefore, instant straining of the released fine particles occurs, and there are no suspended particles. Straining concentration in Eq. (10) is the difference between the initial and current values of the maximum retention function. Concentration of strained particles ${\sigma }_{\mathrm{s}}$ in Fig. 2b is the difference between the initial and current values of the maximum retention function for a single-phase flow.

The overall molar concentration of cations is represented by the equivalent sodium ion concentration (so-called ionic strength ${\gamma }$). Two phases are assumed to be immiscible and incompressible (Fig. 3). Variation in small sodium concentration does not change the aqueous phase density and viscosity. Other assumptions of the model are that relative phase permeabilities depend on the contact angle; the equilibrium contact angle depends on salinity; and porosity is constant. It is also assumed that small fines concentrations yield significant permeability decline but do not affect water viscosity or density (Muecke 1979; Khilar and Fogler 1998).

A fraction of attached particles is mobilised into the suspension with the following straining in thin pore throats (Figs. 3, 4). The attached fines coat the grain surfaces and pore walls. As a consequence, the particle detachment by the drag force negligibly increases porosity and permeability. The significant permeability reduction by a small number of suspended mobilised particles is explained by the clay fines’ being thin, large plates of kaolinite and shells of chlorite, accompanied by long illite fines, where a small-volume fine particle can strain even a large pore throat (Muecke 1979; Lever and Dawe 1984; Sarkar and Sharma 1990). So, the straining of low-concentration fines suspension can alter the pore structure. Therefore, fines mobilisation is assumed not to change water viscosity, but the water relative permeability and capillary pressure are strained concentration dependent. Fines are strained by the rock fraction where the aqueous suspension flows. Therefore, relative permeability of water depends on the strained fine concentration, and oil relative permeability is independent of the concentration of strained fines. The mobilised fine particles are assumed to be water-wet and transported by the aqueous phase (Muecke 1979; Yuan and Shapiro 2011).

Mass balance equations for incompressible immiscible water and oil phases (Lake et al. 2014) are

$$\begin{aligned} \phi \,\frac{\partial s}{\partial t}+\frac{\partial u_{\mathrm{w}} }{\partial x}=0,\quad \phi \,\frac{\partial \,(1 - s)}{\partial t}+\frac{\partial \,u_\mathrm{o}}{\partial x}=0. \end{aligned}$$

(16)

Here $u_{\mathrm{w}}$ and $u_{\mathrm{o}}$ are velocities of water and oil, respectively.

The modifying Darcy’s law with equal phase pressures depicts momentum balances for aqueous and oil phases:

$$\begin{aligned} u_{\mathrm{w}} =-\,\frac{k k_{\mathrm{rw}} (s,\gamma ,\sigma _{\mathrm{s}})}{\mu _{\mathrm{w}} }\,\frac{\partial p}{\partial x},\quad u_\mathrm{o} =-\,\frac{k k_{\mathrm{ro}} (s,\gamma )}{\mu _\mathrm{o}}\,\frac{\partial p}{\partial x}, \end{aligned}$$

(17)

where p is the pressure, and $k_{\mathrm{rw}}$ and $k_{\mathrm{ro}}$ are relative permeabilities for water and oil, respectively.

The salinity dependency of the relative permeability in Eq. (17) depicts the effect of wettability variation with salinity.

For a single-phase flow, straining of porous media by particles yields the permeability decrease as

$$\begin{aligned} k({\sigma _{\mathrm{s}}})=\frac{k(0)}{1+\beta \sigma _s}, \end{aligned}$$

(18)

where k(0) is the initial permeability and $\beta$ is the empirical formation damage coefficient. This expression is obtained from the zero- and first-order terms in Taylor’s series for the function $k(0)/k({\sigma }_{\mathrm{s}})$. For fines transported by water, we apply the same expression for water relative permeability. Thus, the formation damage to the aqueous phase due to straining of the released fines is

$$\begin{aligned} k_{\mathrm{rw}} ({s,\gamma ,\sigma _{\mathrm{s}}})=\frac{{k}'_{\mathrm{rw}} ({s,\gamma })}{1+\beta \sigma _{\mathrm{s}}}, \end{aligned}$$

(19)

i.e. the effect of attached particles on relative permeability for water is negligible (Civan 2007, 2010). Here, $k_{\mathrm{rw}}^{/}(s,\gamma )$ is relative permeability for water for fines-free flow.

In the mass conservation law for salt, we account for advective transport of salt by the carrier aqueous phase only:

$$\begin{aligned} \phi \frac{\partial \gamma s}{\partial t}+\frac{\partial \gamma u_{\mathrm{w}}}{\partial x}=0. \end{aligned}$$

(20)

It is follows from the above assumptions, the mobilised particles are instantly strained, i.e. Eqs. (10, 11) determine the amount of strained fines.

For the reservoir part where the critical salinity is exceeded, the reservoir fines remain attached $(\gamma >\gamma _{\mathrm{cr}},{\sigma }_{\mathrm{s}}=0)$ and the model comprises the Buckley–Leverett equations with changing salinity (16, 17) without fines migration, i.e. $\sigma _{\mathrm{s}}=0$ and ${\sigma }_{\mathrm{a}}={\sigma }_{\mathrm{a}0}$. Extrapolation of the maximum retention function in the semi-interval $[{\gamma }<{\gamma }_{\mathrm{I}}]$ allows using the governing system for the overall interval of salinity variation $[{\gamma }_{J},{\gamma }_{\mathrm{I}}]$.

Adding Eq. (16) results in conservation of the total flux of two incompressible phases:

$$\begin{aligned} u\,(t)=\,u_{\mathrm{w}} \,+\,u_\mathrm{o}. \end{aligned}$$

(21)

Calculation of the total flux u by adding Eq. (17) yields

$$\begin{aligned} u=-k\left( {\frac{k_{\mathrm{rw}} (s,\gamma ,\sigma _{\mathrm{s}})}{\mu _{\mathrm{w}} }+\frac{k_{\mathrm{ro}} (s,\gamma )}{\mu _\mathrm{o}}} \right) \frac{\partial p}{\partial x}. \end{aligned}$$

(22)

Expressing the pressure gradient from Eq. (22) and substituting it into the first Eq. (17) results in the following expression for water flux:

$$\begin{aligned} u_{\mathrm{w}} =fu,\,f(s,\gamma ,\sigma _{\mathrm{s}})=\frac{\frac{k_{\mathrm{rw}} (s,\gamma ,\sigma _{\mathrm{s}})}{\mu _{\mathrm{w}}}}{\frac{k_{\mathrm{rw}} (s,\gamma ,\sigma _{\mathrm{s}})}{\mu _{\mathrm{w}} }+\frac{k_{\mathrm{ro}} (s,\gamma )}{\mu _\mathrm{o}}}. \end{aligned}$$

(23)

where f is the fractional flow function.

2.4 Dimensionless Equations

The following dimensionless coordinates and parameters will apply to the system of dimensional equations (16–20):

$$\begin{aligned} x_\mathrm{D} =\frac{x}{L},\quad t_\mathrm{D} =\frac{1}{\phi L}\mathop {\int }\limits _0^t u(\tau )\mathrm{d}\tau ,\quad S_{\mathrm{a}} =\frac{\sigma _{\mathrm{a}} }{\sigma _{\mathrm{a}0}},\quad S_{\mathrm{s}} =\frac{\sigma _{\mathrm{s}}}{\sigma _{\mathrm{a}0}},\quad P=\frac{kp}{\mu _\mathrm{o} uL}. \end{aligned}$$

(24)

Substituting the dimensionless parameters (24) along with expression (23) into the governing system (16, 20, 22) yields (Zeinijahromi et al. 2013; Hussain et al. 2013):

$$\begin{aligned}&\frac{\partial s}{\partial t_\mathrm{D}}+\frac{\partial f(s,\gamma )}{\partial x_\mathrm{D}}\,=0 \end{aligned}$$

(25)

$$\begin{aligned}&S_{\mathrm{s}} =\left( {S_{\mathrm{a}0} -S_{\mathrm{cr}} (\gamma )} \right) A_{\mathrm{s}} ({s,\gamma }),\quad f(s,\gamma )=f\left( {s,\gamma ,S_{\mathrm{s}} (\gamma )} \right) \end{aligned}$$

(26)

$$\begin{aligned}&\frac{\partial \gamma s}{\partial t_\mathrm{D}}+\frac{\partial \gamma f(s,\gamma )}{\partial x_\mathrm{D}}\,=0 \end{aligned}$$

(27)

$$\begin{aligned}&1=-\lambda ({s,\gamma })\frac{\partial P}{\partial x_\mathrm{D}}, \quad \lambda ({s,\gamma })=\frac{k_{\mathrm{rw}} (s,\gamma ,S_{\mathrm{s}})\mu _\mathrm{o}}{\mu _{\mathrm{w}}}+k_{\mathrm{ro}} (s,\gamma ). \end{aligned}$$

(28)

The governing system (25–27) is a $2\times 2$ hyperbolic system of quasi-linear equations for two variables s and $\gamma$ (Courant and Friedrichs 1976). Equation (28) separates from system (25–27), i.e. pressure distribution calculation follows the solution of system (25–27).

The initial conditions correspond to reservoir saturation and salinity of formation water before the injection:

$$\begin{aligned} t_\mathrm{D} =0: s=s_{\mathrm{I}}, \gamma =\gamma _{\mathrm{I}}. \end{aligned}$$

(29)

Points I in Figs. 6a, 8a, and 11a correspond to initial conditions (29).

Entrance boundary conditions for continuous low-salinity water injection are a fixed fraction of injected water and injected salt concentration:

$$\begin{aligned} x_\mathrm{D} =0: f(s_J,\gamma _J)=1, \quad \gamma =\gamma _J. \end{aligned}$$

(30)

Points $s_{J}^{L}$ in Figs. 6a, 8a, and 11a correspond to boundary conditions (30) for the case of low-salinity water injection. The inlet points $s^{H}_{J}$ in those figures correspond to high-salinity waterflooding.

For formation water injection followed by the injection of low-salinity-water slug with high-salinity drive, the volume of injected formation water ${\varOmega }_\mathrm{H}$ is used to dimensionalise coordinates x and t in Eq. (24); the dimensionless coordinate of the core outlet (production well row) becomes $\phi L/ {\varOmega }_\mathrm{H}$. The inlet boundary conditions are

$$\begin{aligned} x_\mathrm{D} =0: f(s_J,\gamma _J)=1,\quad \gamma =\left\{ {{\begin{array}{cl} \gamma _{\mathrm{I}}&{} \quad 0<t_\mathrm{D}<1 \\ \gamma _{J}&{} \quad 1<t_\mathrm{D}<t_{\mathrm{s}} \\ \gamma _{\mathrm{I}}&{} \quad t_{\mathrm{s}}<t_\mathrm{D} <\infty \\ \end{array}}} \right. . \end{aligned}$$

(31)

Fig. 6

Analytical model and graphical solution for continuous low-salinity water injection: a solutions for formation water injection $(s_{J}^{H}\rightarrow 6\rightarrow I)$, medium salinity $(s_{J}^{L}\rightarrow 4\rightarrow 5\longrightarrow 6\rightarrow I)$, and low-salinity flooding $(s_{J}^{L}\longrightarrow 2\rightarrow 3 \rightarrow I)$ using the fractional flow curves, b saturation profiles for three displacement cases and c water-cut history for the three cases of displacement

Fig. 7

Mapping using the stream-function $\varphi (x_{\mathrm{D}},t_{\mathrm{D}})$: a initial and boundary conditions and front velocity at the plane $(x_{\mathrm{D}},t_{\mathrm{D}})$; b mapped initial and boundary conditions and front velocity at the plane $(x_{\mathrm{D}},\varphi )$ and c graphical presentation of Lagrangian speed V and Eulerian speed D at the (s, f)-plane

Fig. 8

Graphical solution for 1D displacement of oil by formation water followed by LS slug and HS water chase drive: a fractional flow curves and typical saturations corresponding to points $2,3,{\ldots },6$; b zoom near to residual oil saturation; c lifting of the solution for the auxiliary problem in the (U, F)-plane and d zoom near to injection points $s_{J}$

Fig. 9

Solution for injection of HS and LS slugs followed by HS water chase drive in $(x_{\mathrm{D}},\varphi )$ coordinates: a solution of the auxiliary system and b solution of the lifting equation

Fig. 10

Analytical model for 1D injection problem of HS and LS slugs followed by HS water drive in $(x_{\mathrm{D}},t_{\mathrm{D}})$ coordinates: a trajectories of saturation and concentration waves in the $(x_{\mathrm{D}},t_{\mathrm{D}})$-plane along with typical zones I, II, ${\ldots },$ XII; b saturation profiles at four different times and c salinity profiles at three different times

Fig. 11

Fractional flow curves for injection of formation water and low-salinity water: green curve corresponds to injection of formation water; red curve encompasses effects of both wettability alternation and induced fines migration; black curve presents the case of fines-free and wettability-affected low-salinity flood; blue curve corresponds to no wettability alteration and fines mobilisation with straining during low-salinity waterflood

Fig. 12

Comparison of four cases of oil displacement by formation of HS water (green), by LS water accounting for wettability alteration effect only (black), by LS water accounting for fines migration effect only (blue), and by LS water accounting for both effects (red): a water-cut history, b recovery factor versus PVI and c pressure drop across the reservoir

Fig. 13

The effect of formation water volume injected before LS water slug on the recovery factor: oil displacement by formation HS water (green); injection of 0.1, 0.3, and 1.0 PV of HS water before LS water injection (red, blue, and brown, respectively); continuous LS flood (black)

Point $s_{J}^{H}$ in Fig. 8a corresponds to boundary condition (31) during high-salinity water injection. The inlet point changes up to the value $s_{J}^{L}$ for $t_{\mathrm{D}}>1$.

Here for the sake of simplicity, it is assumed that the compositions of formation and high-salinity injected waters are identical. In this case, no ion exchange, wettability alteration, or fines mobilisation occur after high-salinity waterflooding. This case is suitable for comparison between low-salinity-water injection and “normal” waterflooding.

3 Analytical Models for Low-Salinity Waterflood with Fines Migration

This section presents exact solutions for fines-assisted LS waterflooding given the large-scale approximation, Eqs. (25–27). The splitting procedure is used for the exact integration (“Appendix 1”). Secondary recovery corresponds to continuous injection of LS water yielding an $x_{\mathrm{D}}/t_{\mathrm{D}}$-dependent self-similar solution (Sect. 3.1). Tertiary recovery by LS water slug injection with high-salinity chase drive follows “normal” waterflooding; the solution is non-self-similar (Sect. 3.2).

3.1 Self-Similar Solutions for Continuous Injection of Low-Salinity Water

The solutions of the continuous injection problem (29, 30) for system (25–27) are well known (Pope 1980; Jerauld et al. 2008; Lake et al. 2014). The solutions $s(x_{\mathrm{D}},t_{\mathrm{D}}),\, \gamma (x_{\mathrm{D}},t_{\mathrm{D}})$ are self-similar and depend on the group $x_{\mathrm{D}}/t_{\mathrm{D}}$. Figure 6a presents the graphical solution. Points 6, 2, and 4 are tangent points of straight lines I–6, 0–2, and 0–4, respectively, to the fractional flow curves ${\gamma }={\gamma }_{\mathrm{I}}$ and ${\gamma }={\gamma }_{J}$. The corresponding slopes are the speeds of the jumps, where the points ahead and behind the jumps are located on those straight lines I–6, 0–2, and 0–4.

Following Courant and Friedrichs (1976), we denote rarefaction waves linking points A and B by A–B. We denote a shock from point A to point B as $A\rightarrow B$, i.e. points $A^{-}$ and $B^{+}$ corresponds to states behind and ahead of shocks, respectively. The solution corresponds to the path in the (s, f)-plane consisting of a rarefaction wave from the saturation $s_{J}^{L}$ to point 2, ${\gamma }$-jump from 2 to 3, and s-jump from 3 to $s_{\mathrm{I}}$:

$$\begin{aligned} s_J^L -2\rightarrow 3\rightarrow I \end{aligned}$$

(32)

for the case where point 3 is located below point 6 $(s_{3}<s_{6})$.

Figure 6b shows the saturation profiles for injection of formation water (green curve), low-salinity water (blue curve), and medium-salinity water (red curve). The salinity profile is a step-function, given by a ${\gamma }$-jump from ${\gamma }_{J}$ to ${\gamma }_{\mathrm{I}}$ with velocity $D_{2}$. Water-cut history is shown in Fig. 6c. The graphic analytical technique for the solution is available from Lake et al. (2014) and Bedrikovetsky (1993).

Figure 6a shows the fractional flow curve (in red) where the intersection point 5 is located above point 6 $(s_{3}>s_{6})$. The corresponding path is

$$\begin{aligned} s_J^L -4\rightarrow 5-6\rightarrow I. \end{aligned}$$

(33)

Table 1 Exact solution for 1D oil displacement by formation water and low-salinity slug in the ($x_{\mathrm{D}}$, $\varphi$)-domain

Table 2 Exact solution for 1D oil displacement by formation water and low-salinity slug in the (x, t)-domain

Figure 6b, c shows profiles of saturation and water-cut history for normal waterflooding (green curves), intermediate-salinity waterflooding (red curves), and low-salinity waterflooding (blue curves). Blue and red fractional flow curves correspond to the cases with the same residual oil saturation. It follows from the curve shapes that for 1D continuous water injection, low-salinity waterflooding results in a later breakthrough than with formation water injection; it also decreases water-cut during production of an oil–water bank and for a short period after the breakthrough of the injected water. It also results in lower oil residual at the later stage of waterflooding. Oil production with intermediate-salinity water injection coincides with normal flooding from the beginning of injection to beyond the water breakthrough. Afterwards, normal waterflooding exhibits higher water-cut and higher residual oil.

3.2 Non-self-similar Solutions for Displacement of Oil by Formation Water Followed by Low-Salinity Water Slug

In this section, we derive an exact solution for the displacement of oil by HS water followed by injection of LS water slug with HS water chase drive. The splitting derivations as applied to the problem (25–27) are presented in “Appendix 1”. The method uses the stream-function (Lagrangian coordinate) $\varphi (x_{\mathrm{D}},t_{\mathrm{D}})$ as an independent variable in the governing system (25–27), instead of using time $t_{\mathrm{D}}$ (Eq. 55). Figure 7 shows the corresponding mapping K, which transforms mass balance for water, given by Eq. (25), into conservation law Eq. (58). The graphical solution of the slug problem (63) is presented in the plane of fractional flow curves (s, f) in Fig. 8a, b and is presented in the plane of flux and density (U, G) of conservation law (58) in Fig. 8c, d. The corresponding characteristics and front trajectories are presented in planes $(x_{\mathrm{D}},\varphi )$ and $(x_{\mathrm{D}},t_{\mathrm{D}})$ (Figs. 9, 10). The figures show different flow zones; the exact formulae for salinity and saturation in each zone are presented in Tables 1 and 2.

In contrast to the continuous injection discussed in the previous section, the solution of the large-scale system (25–27) subject to boundary conditions (31) is non-self-similar. Decays of three Riemann discontinuities occur. The solution of the Riemann problem in origins of planes $(x_{\mathrm{D}},\varphi )$ and $(x_{\mathrm{D}},t_{\mathrm{D}})$ corresponds to oil displacement by HS water: $s_{J}^{H}$—$6\rightarrow I$. We show the corresponding path in blue in Fig. 8a, c. In points (0, 1) of the planes $(x_{\mathrm{D}},\varphi )$ and $(x_{\mathrm{D}},t_{\mathrm{D}})$ occur displacement of HS water by LS water under residual oil saturation with the following Riemann solution: $s_{J}^{L}$—$5\rightarrow s_{J}^{H}$. The corresponding path is shown in red in Fig. 8a, c. Displacement of LS water by HS water under residual oil saturation occur in points $(0,t_{\mathrm{s}})$ of planes $(x_{\mathrm{D}},\varphi )$ and $(x_{\mathrm{D}},t_{\mathrm{D}})$; the corresponding solution consists of $\gamma$-jump $s_{J}^{L} \rightarrow s_{J}^{L}$. The path is shown in green in Fig. 8b, d.

Auxiliary problem The auxiliary equation (60) shows that in different domains of the $(x_{\mathrm{D}},\varphi )$-plane, salinity depends on Lagrangian coordinate $\varphi$ only. The solution of Eq. (60) subject to initial and boundary conditions (62) and (63) is

$$\begin{aligned} \gamma \left( \frac{\varphi }{x_\mathrm{D}}\right) =\left\{ {{\begin{array}{ll} \gamma _{\mathrm{I}}, &{} \quad -s_{\mathrm{I}}<\frac{\varphi }{x_\mathrm{D}}<0 \\ \gamma _{\mathrm{I}}, &{} \quad 0<x_\mathrm{D}<\infty , 0<\varphi<1 \\ \gamma _J, &{} \quad 0<x_\mathrm{D}<\infty ,1<\varphi<t_{\mathrm{s}} \\ \gamma _{\mathrm{I}}, &{} \quad 0<x_\mathrm{D}<\infty ,t_{\mathrm{s}}<\varphi <\infty \\ \end{array}}} \right. . \end{aligned}$$

(34)

Figure 9a presents three zones with constant salinities ${\gamma }_{\mathrm{I}}$ and ${\gamma }_{J}$.

Lifting procedure The lifting problem is solved by investigating how a simple s-wave interacts with s- and ${\gamma }$-shocks. The method and nomenclature follow Courant and Friedrichs (1976) and Bedrikovetsky (1993).

According to the initial and boundary conditions (62, 63), the decay of discontinuity from $(s_{J}^{H},1)$ to I occurs in the origin of the plane $(x_{\mathrm{D}},\varphi )$. The corresponding points are shown in Fig. 8. The Riemann solution is given by the sequence of rarefaction wave and the shock, $(s_{J}^{H})-6\rightarrow I$, where point 6 is a tangent of the straight line I–6 and the curve $\gamma =\gamma _{\mathrm{I}}$. Saturation in zone I in Fig. 9b is equal to $s_{J}^{H}$. The rarefaction wave $s_{J}^{H}$-6 propagates from the origin in zone II. The characteristic lines transport the values from $s_{J}^{H}$ to $s_{4}$ until the shock trajectory $\varphi =1$, where the jump ${\gamma }_{J} \rightarrow {\gamma }_{\mathrm{I}}$ occurs. It follows from (65) that density G is continuous where speed V tends to infinity, $[G]=0$. Therefore, the G-values above and below axis $\varphi =1$ are equal. In particular, $G_{4}=G_{2}$. The above determines the values of saturation above the axis $\varphi =1$:

$$\begin{aligned} \frac{\varphi }{x_\mathrm{D}}= & {} {G}'_U \left( {U^{+}\left( {x_\mathrm{D},\varphi } \right) ,\gamma _{\mathrm{I}}} \right) \end{aligned}$$

(35)

$$\begin{aligned} G\left( {U^{+}\left( {x_\mathrm{D},\varphi } \right) ,\gamma _{\mathrm{I}}} \right)= & {} G\left( {U^{-}\left( {x_\mathrm{D},\varphi } \right) ,\gamma _J} \right) . \end{aligned}$$

(36)

The corresponding points above the “front” $\varphi =1$ vary from 5 to 2.

The saturation values above axis $\varphi =1$ propagate into zone VI in a simple s-wave:

$$\begin{aligned} \frac{{\varphi }'-1}{{x}'_\mathrm{D} -x_\mathrm{D}}={G}'_U \left( {U\left( {{x}'_\mathrm{D} ,{\varphi }'} \right) ,\gamma _J} \right) , U\left( {{x}'_\mathrm{D},{\varphi }'} \right) =U^{-}\left( {x_\mathrm{D},1} \right) . \end{aligned}$$

(37)

i.e. $\gamma =\gamma _{J}$ in this zone, and flux U is constant along the characteristic lines in solution (37).

Saturation above axis $\varphi =1$ reaches value $s_{2}$ at point M in Fig. 9b:

$$\begin{aligned} G({x_M,1})=G_2, \end{aligned}$$

(38)

where $\gamma$-jump $2\rightarrow 4$ occurs. Point 2 is held above the line $\varphi$=1, where $x>x_{M}$. $G_{2}$ is the maximum value along the curve $\gamma =\gamma _{J}$. The rarefaction wave spreads the values above $G_{4}$ below the point M. Therefore, the transition ${\gamma }_{J}\rightarrow {\gamma }_{\mathrm{I}}$ cannot be performed for $G^{+}>G_{4}$. For this case, the decay configuration is $2\rightarrow 3\rightarrow s^{+}$ (Fig. 8a, c). Point 3 is held below line $\varphi =1$, where $x>x_{M}$. As a result, zone VII has constant saturation $s_{3}$.

Trajectory $\varphi =\varphi _{L2}(x_{\mathrm{D}})$ separates the portion of rarefaction wave 4–6 that appears in zone II, from constant state 3 that appears in zone VII. The trajectory is defined by the condition on characteristic line

$$\begin{aligned} \frac{\varphi }{x_{L2} (\varphi )}={G}'_U \left( {U^{-}\left( {x_{L2} (\varphi )} \right) ,\gamma _{\mathrm{I}}} \right) , \end{aligned}$$

(39)

and the Hugoniot–Rankine condition that corresponds to conservation law (58):

$$\begin{aligned} \frac{\mathrm{d}\varphi _{L2}}{\mathrm{d}x_\mathrm{D}}=\frac{G\left( {U^{-}\left( {\varphi _{L2} \left( {x_\mathrm{D}} \right) } \right) ,\gamma _{\mathrm{I}}} \right) -G_3}{U^{-}\left( {\varphi _{L2} \left( {x_\mathrm{D}} \right) } \right) -U_3}. \end{aligned}$$

(40)

Here $\varphi =\varphi _{L2}(x_{\mathrm{D}})$ is the inverse function to $x_{\mathrm{D}}=x_{L2}(\varphi )$.

Integrating Eq. (58) along the contour $\omega \,{:}\,(0, 0)\rightarrow (x_{M},\, \varphi _{M}) \rightarrow (x_{L2},\, \varphi _{L2}) \rightarrow (0,0)$, and applying Green’s theorem yields

$$\begin{aligned} \int \int _{\Omega } {\left( {\frac{\partial G}{\partial \varphi }+\frac{\partial U}{\partial x_\mathrm{D}}} \right) } \mathrm{d}x_\mathrm{D} \mathrm{d}\varphi= & {} \oint U\mathrm{d}\varphi -G\mathrm{d}x_\mathrm{D} =\int \limits _{\left( {0,0} \right) }^{\left( {x_M ,1} \right) } {U\mathrm{d}\varphi -G\mathrm{d}x_\mathrm{D}} \nonumber \\&+\,\int \limits _{\left( {x_M,1}\right) }^{\left( {x_{L2} (\varphi ),\varphi } \right) } +\int \limits _{\left( {x_{L2}(\varphi ),\varphi } \right) }^{\left( {0,0} \right) } =0 \nonumber \\ \omega= & {} \partial {\Omega } \end{aligned}$$

(41)

resulting in the first integral for ordinary differential equation (40), defining the trajectory $x=x_{L2}(\varphi )$:

$$\begin{aligned} x_{L2} (\varphi )= & {} \frac{\left( {G_4 -G_3} \right) \left( {\frac{1}{V_4}} \right) -U_4 +U_3}{\Delta _3 \left( {U,\hbox {G}} \right) } \nonumber \\ \Delta _3 \left( {U,\hbox {G}} \right)= & {} \left( {G\left( \frac{\varphi }{x_{\mathrm{D}}}\right) -G_3} \right) +{G}'_U \left( {U\left( \frac{\varphi }{x_{\mathrm{D}}} \right) ,\gamma _{\mathrm{I}}} \right) \left( U_3 -U\left( \frac{\varphi }{x_{\mathrm{D}}} \right) \right) . \end{aligned}$$

(42)

The intersection between the front trajectory $\varphi =\varphi _{L2}(x_{\mathrm{D}})$ and straight line $\varphi =-s_{\mathrm{I}}x_{\mathrm{D}}$ corresponds to point 6 behind the shock. It gives the intersection moment $\varphi =\varphi _{E}$. Point E in Fig. 9b corresponds to the intersection. The jump $3\rightarrow I$ appears after the intersection.

The boundary value of saturation $s_{J}^{L}$ appears for $\varphi >1$ due to change in salinity. The corresponding rarefaction $s_{J}^{L}$ -5 connects the points along the curve ${\gamma }={\gamma }_{J}$ in Fig. 9b (zones IV and V). Saturation is constant and equal to $s_{5}$ in zone V.

The salinity jump ${\gamma }_{J}\rightarrow {\gamma }_{\mathrm{I}}$ occurs along the front $\varphi =t_{\mathrm{s}}$. Saturation ${\gamma }$-jumps occur along this shock, with conservation of density $G(U,\,\gamma )$. The saturation values behind this shock are determined from the continuity of the density $G(U,\,\gamma )$, analogous to Eq. (38). The saturation values above axis $\varphi =t_{\mathrm{s}}$ propagate in zones VIII to XI along the characteristic lines in simple waves, analogous to Eqs. (35–37). The corresponding formulae are presented in Table 1. Finally, the lifting solution for $s(x_{\mathrm{D}},\varphi )$ is obtained for the overall domain $x_{\mathrm{D}}>0,\, -s_{\mathrm{I}}<\varphi /x_{\mathrm{D}}<\infty$.

Table 3 Recovery factor calculations during sequential injection of formation- and low-salinity water

Inverse transformation $K^{-1}$ Calculating $t_{\mathrm{D}}$ $(x_{\mathrm{D}},\varphi )$ for each point of the domain by formula (66) maps the solution of the auxiliary and lifting problems into variables $(x_{\mathrm{D}},t_{\mathrm{D}})$. Each point of zones I to IX in the plane $(x_{\mathrm{D}},\varphi )$ can be connected with the origin via the sequence of characteristics, because the solution in those zones is given by simple s-waves. Because saturation is constant along those characteristics, integrating (66) along the sequences of characteristics yields straight-line images in plane $(x_{\mathrm{D}},t_{\mathrm{D}})$. The mapping $K^{-1}$ transforms zones with constant (U, G) in plane $(x_{\mathrm{D}},\varphi )$ into zones with constant (s, f) in plane $(x_{\mathrm{D}},t_{\mathrm{D}})$.

The formulae in Table 2 are obtained from those in Table 1 by integrating (66). The points $(x_{\mathrm{D}},t_{\mathrm{D}})$ and $(x_{\mathrm{D}}^{/},t_{\mathrm{D}}^{/})$ in zone VI of Table 2 are located on the same characteristic line, as are points $(x_{\mathrm{D}},t_{\mathrm{D}})$ and $(x_{\mathrm{D}}^{//},t_{\mathrm{D}}^{//})$ in zone IX and $(x_{\mathrm{D}},t_{\mathrm{D}})$ and $(x_{\mathrm{D}}^{///},t_{\mathrm{D}}^{///})$ in zone XI.

The lifting solution contains four fronts: $\varphi =-s_{\mathrm{I}}x_{\mathrm{D}}$ and $x_{\mathrm{D}}=x_{L1}(\varphi )$ along axis $\varphi =1, x_{\mathrm{D}}=x_{L2}(\varphi )$, and $\varphi =t_{\mathrm{s}}$. Applying the inverse mapping (66) to the front $x_{\mathrm{D}}=x_{L1}(\varphi )$ causes it to be mapped into the following trajectory $x_{L1}(t_{\mathrm{D}})$, determined parametrically:

$$\begin{aligned} x_{_{L1}} ({t_\mathrm{D}})=\frac{\partial f\left( {s^{+},\gamma _{\mathrm{I}}} \right) }{\partial s}t_\mathrm{D},\quad t_\mathrm{D} =\frac{1}{\Delta _0 \left( {s^{+},\gamma _{\mathrm{I}}} \right) }, \quad s^{+}=s^{+}\left( {x_{_{L1}} ({t_\mathrm{D}})} \right) , \end{aligned}$$

(43)

where

$$\begin{aligned} \Delta _0 ({s,\gamma })=f({s,\gamma })-s{f}'_{\mathrm{s}} ({s,\gamma }). \end{aligned}$$

(44)

Figure 7c shows how to calculate trajectory (43) geometrically. In Fig. 8a, $A0={\varDelta }_{0}(s^{+},\,\gamma _{\mathrm{I}})$ and $B0={\varDelta }_{0}(s^{+} ,\,\gamma _{\mathrm{I}})/f_{\mathrm{s}}^{/}(s^{+},\,\gamma _{\mathrm{I}})$. This allows for graphical expression of the dependency $x_{L1}=x_{L1}(t_{\mathrm{D}})$: point A is determined by $A0=1/t_{\mathrm{D}}$ for any arbitrary $t_{\mathrm{D}}$; point B is determined by tangent line $A-s^{+}$ to fractional flow curve ${\gamma }={\gamma }_{\mathrm{I}}$; and the front coordinate $x_{L1}$ is determined by $B0=1/x_{L1}(t_{\mathrm{D}})$. The images of fronts $x_{L2}(\varphi )$ for $x_{M}<x_{\mathrm{D}}<x_{E}$ and $\varphi =t_{\mathrm{s}}$ are given by analogous formulae and presented in Table 2. The images of fronts $\varphi =-s_{\mathrm{I}}x_{\mathrm{D}}, \varphi =1$ for $0<x_{\mathrm{D}}<x_{N}$ and $x_{\mathrm{D}}>x_{M}$, and $\varphi =t_{\mathrm{s}}$ for $0<x_{\mathrm{D}}<x_{R}$ are straight lines.

Substitution of flux continuity condition on shocks (67) into Eq. (55) shows that there is no mass flux through ${\gamma }$-shocks. Therefore, the trajectories of ${\gamma }$-shocks in the $(x_{\mathrm{D}}, \varphi )$-plane are given by the lines $\varphi$ = const (Fig. 9a). Varying saturation in simple s-waves results in curvilinear ${\gamma }$-shock trajectories. The trajectory of the ${\gamma }$-shock with ${\gamma }^{-}=\gamma _{J}$ and ${\gamma }^{+} =\gamma _{\mathrm{I}}$, initiated at the moment $t_{\mathrm{D}}=1$, propagates with constant speed along straight line 1—N; at $t_{\mathrm{D}}>t_{N}$ the ${\gamma }$-shock moves sequentially along the curve $x_{L1}$ and the straight line with the jump $2\rightarrow 3$; the ${\gamma }$-shock speed stabilizes at the moment $t_{\mathrm{D}}=t_{M}$ (Fig. 10a). Constant saturation values $s_{J}^{H}$ and $s_{5}$ maintain behind and ahead of the shock 1—N, respectively. The points ahead of the shock $x_{L1}$ vary from $s_{J}^{H}$ to 4 during time interval [$t_{N},t_{M}$]; the corresponding points behind the front vary from 5 to 2. The s-shock propagates $x_{L2}$ propagates during time interval [$t_{M},t_{E}$] ahead of the $\gamma$-shock; the points ahead of the shock $x_{L2}$ vary 4 to 6; point 3 maintains behind the front. From the moment $t_{E}$ on, the jump $3\rightarrow I$ occurs along the concentration front, which coincides with the first shock in the solution for continuous LS water injection given by Eq. (30).

At the moment $t_{\mathrm{s}},\, {\gamma }$-shock with ${\upgamma }^{-}={\upgamma }_{\mathrm{I}}$ and ${\upgamma }^{+}={\upgamma }_{J}$ appears due to beginning of the HS chase drive injection. The trajectory of the ${\gamma }$-shock propagates with constant speed along straight line $t_{\mathrm{s}}$—R; at $t_{\mathrm{D}}>t_{R}$ the ${\gamma }$-shock moves sequentially along the curve $x_{\mathrm{H}1}$, the straight line PT, and the curve $x_{\mathrm{H}2}$. Constant saturation values $\hbox {s}_{\mathrm{J}}^{{L}}$ maintain behind and ahead of the shock $t_{\mathrm{s}}$—R. The points ahead of the shock $x_{\mathrm{H}1}$ vary from $s^{L}_J$ to 5 during time interval [$t_{R},t_{P}$]; the corresponding points behind the front vary from $s_{J}^{L}$ to $s_{J}^{H}$. During time interval [$t_{P},t_{T}$], the values ahead and behind the shock are 5 and $s_{J}^{H}$. The points ahead of the shock $x_{\mathrm{H}2}$ vary from 5 to 2 during time period [$t_{T},\, \infty$); the corresponding points behind the front vary from $s_{J}^{H}$ to 4.

When time tends to infinity, saturation in the low-salinity slug tends to ${s}_{2}$. The salt flux through the front and rear front of the slug are equal zero. Therefore, the amount of injected salt is equal to that remained in the slug when time tends to infinity, i.e. $t_{\mathrm{s}}$—$1=s_{2}B$. This determines the limit of the slug size B.

Flow-zone structure Figure 10 presents the trajectories of saturation and concentration shocks in the $(x_{\mathrm{D}},t_{\mathrm{D}})$-plane. The displacement zone consists of the following reference patterns:

• 0 Unperturbed zone of initial water saturation $s_{\mathrm{I}}$;

• I Zone with residual immobile oil and injected formation water $s_{J}^{H}$;

• II Zone of oil flow together with injected formation water, saturation changes from $s_{J}^{H}$ to $s_{6}$ at the displacement front;

• III Zone with residual immobile oil and injected LS water $s_{J}^{L}$;

• IV Zone with low-mobility oil and injected LS water, which takes the place of zone I during the displacement;

• V Oil–LS water bank with saturation $s_{5}$;

• VI Zone of oil flow together with injected LS water, saturation changes from $s_{5}$ to $s_{2};$

• VII Oil–LS water bank with saturation $s_{3}$;

• VIII Zone of immobile oil with saturation $s_{J}^{L}$;

• IX Zone of immobile oil with saturation varying from $s_{J}^{L}$ to $s_{J}^{H}$;

• X Zone of immobile oil with saturation $s_{J}^{H}$;

• XI Zone with injected HS water, saturation changes from $s_{J}^{H}$ to $s_{4}$, which take the place of zone VII during the displacement.

Figure 10b, c presents the profiles of salinity and saturation at four moments. Horizontal lines $t_{k}=\hbox {const}, \, k=1,{\ldots },4$ in the $(x_{\mathrm{D}},t_{\mathrm{D}})$ plane correspond to the profiles at those moments. Those lines $t_{k}$ = const pass through different zones. The corresponding points of the intersection with fronts that separate different zones are shown in Fig. 10b, c. The profile $t_{1}$ is taken during HS waterflood and corresponds to the Buckley–Leverett solution (Lake et al. 2014). The oil–water bank with reduced water-cut $f(s_{3},\,\gamma _{\mathrm{I}})$ follows the HS flood profile at moment $t_{2}$; the water-cut behind the bank is also below the water-cut for the HS flood. At moment $t_{3}$, the reduced water-cut is exhibited in zones IX and VIII. If compared with the HS flood, the lower residual oil is exhibited in zones VIII and IX. At the moment $t_{4}$, both profiles are continuous.

3.3 Pressure Drop Calculations

In this section, we calculate pressure drop across the reservoir (core) during 1D continuous LS waterflood given by formula (30). Expressing the pressure gradient from Eq. (28) and integrating over $x_{\mathrm{D}}$ across the reservoir before the breakthrough $t_{\mathrm{D}}<1/D_{3}$ yields

$$\begin{aligned} \Delta P(t_\mathrm{D})= & {} t_\mathrm{D} \int \limits _{1-s_{\mathrm{or}} ({\gamma _J})}^{s_2} {\frac{{f}''\left( {s,\gamma _J} \right) ds}{\lambda \left( {s,\gamma _J} \right) }} +t_\mathrm{D} \left( {D_3 -D_2}\right) \frac{1}{\lambda \left( {s_3,\gamma _{\mathrm{I}}} \right) } \nonumber \\&+\,(1-t_\mathrm{D} D_3)\frac{1}{\lambda \left( {s_{\mathrm{I}},\gamma _{\mathrm{I}}} \right) }. \end{aligned}$$

(45)

It follows from Eq. (45) that the pressure drop grows linearly with PVI before the water breakthrough.

The pressure drop expression during the production of the oil–water bank $(1/D_{3}<t_{\mathrm{D}}<1/D_{2})$ contains the integral on the right side of Eq. (45); the second term becomes $t_{\mathrm{D}}$-dependent and linear with respect to $t_{\mathrm{D}}$, and the third term disappears. Thus, the pressure drop grows linearly with PVI during oil–water bank production.

After the salinity-front breakthrough $(t_{\mathrm{D}} >1/D_{3})$, the second and third terms on the right side of Eq. (45) disappear, and the lower limit in the integral become s-dependent, where $1/t_{\mathrm{D}}=f^{/}(s,\, {\gamma }_{J})$.

3.4 Recovery Factor Calculations

Implicit formulae for the solution of the HS flood followed by LS slug injection and HS chase drive, presented in Table 2, allow for explicit calculation of the recovery factor

$$\begin{aligned} RF(t_\mathrm{D})=\frac{\left\langle s \right\rangle \left( {t_\mathrm{D}} \right) -s_{\mathrm{I}}}{1-s_{\mathrm{I}}}. \end{aligned}$$

(46)

To derive the formula for average water saturation $\langle s\rangle (t_{\mathrm{D}})$, the pore volume $\phi L$ is used to dimensionalise coordinate x and time t in Eq. (24). Point (1, $t_{\mathrm{D}}$) can be linked with either of axes via the sequence of characteristic lines

$$\begin{aligned} \Delta x_{D_{k}} =f_s^/ \left( {s_k,\gamma _k} \right) \Delta t_{D_{k}},\quad \sum _{k=1}^n {\Delta t_{D_{k}}} =t_\mathrm{D},\quad \sum _{k=1}^n {\Delta x_{D_{k}}} =1,\quad k=1,2,\ldots ,n. \end{aligned}$$

(47)

where ${\varDelta } x_{Dk}$ and ${\varDelta } t_{Dk}$ correspond to different segments in this sequence, and the saturation values along the segments are $s_{k},\, k=1,2,{\ldots },n$. Equation (25) can be integrated by the domain bounded by the contour $(0, 0)\rightarrow (0, t_{\mathrm{D}})\rightarrow (1,\, t_{\mathrm{D}})\rightarrow (1-{\varDelta } x_{Dn},\, t_{\mathrm{D}}-{\varDelta } t_{Dn})\rightarrow (1-{\varDelta } x_{Dn}-{\varDelta } x_{Dn-1},\, t_{\mathrm{D}}-{\varDelta } t_{Dn}-{\varDelta } t_{Dn-1})\rightarrow {\cdots }\rightarrow (1-{\varDelta } x_{D1},\, t_{\mathrm{D}}- {\varDelta } t_{D1})\rightarrow (0, 0)$. Following Green’s theorem, the mass integral is equal to the integral of mass flux form $f\mathrm{d}t_{\mathrm{D}}-s\mathrm{d}x_{\mathrm{D}}$ along this contour. The integral over the side $(0,t_{\mathrm{D}})\rightarrow (1,t_{\mathrm{D}})$ is equal to -$\langle s\rangle (t_{\mathrm{D}})$. The integral over the interval $(0,0)\rightarrow (0,t_{\mathrm{D}})$ is equal to $t_{\mathrm{D}}$. The equality of the overall integral to zero implies

$$\begin{aligned} t_\mathrm{D} -\left\langle s \right\rangle \left( {t_\mathrm{D}} \right) =\sum _{k=1}^n {\int \limits _{\left( x_{D_{k}},t_{D_{k}} \right) }^{\left( x_{D_{k+1}},t_{D_{k+1}} \right) } {f\mathrm{d}t_\mathrm{D} -s\mathrm{d}x_\mathrm{D}}} =\sum _{k=1}^n {f_k \Delta t_{D_{k}} -s_k \Delta x_{D_{k}}}. \end{aligned}$$

(48)

Substituting Eq. (35) into Eq. (48) yields

$$\begin{aligned} \left\langle s \right\rangle \left( {t_\mathrm{D}} \right)= & {} \sum _{k=1}^n {\left( {1-f_k} \right) \Delta t_{D_{k}} +s_k \Delta x_{D_{k}} =} \sum _{k=1}^n {\left( {1-f_k} \right) \Delta t_{D_{k}} +s_k \Delta x_{D_{k}}} \nonumber \\= & {} \sum _{k=1}^n {\left( {s_k +\frac{1-f_k}{f_s^/ \left( {s_k,\gamma _k} \right) }} \right) \Delta x_{D_{k}}} \end{aligned}$$

(49)

which can be rewritten as

$$\begin{aligned} \left\langle s \right\rangle \left( {t_\mathrm{D}} \right) =\sum _{k=1}^n {\left\langle {s_k} \right\rangle \Delta x_{D_{k}}},\quad \left\langle {s_k} \right\rangle =s_k +\frac{1-f_k}{f_s^{/} \left( {s_k ,\gamma _k} \right) }. \end{aligned}$$

(50)

Consider a point $(s_{k},\, f(s_{k},\, {\gamma }_{k}))$ in Fig. 8a, which is located at the fractional flow curve ${\gamma }={\gamma }_{k}$. The abscissa of the intersection between the tangent line to the fractional flow curve at the point $(s_{k},f(s_{k},{\gamma }_{k}))$ and axis $f=1$ is equal to $\langle s_{k}\rangle$. This allows for graphical calculation of the average saturation (generalisation of Welge’s method).

Average saturation (50) can be substituted into formula (46) for recovery factor calculation.

4 Results

This section compares the waterflood cases of injection of formation and LS water. The effects of LS water on relative permeability and on fines mobilisation and straining are treated together in the mathematical model (25–28). However, alteration of wettability and residual oil, and fines straining with water-permeability reduction, are independent physical mechanisms. The effect of LS is expressed in Eq. (17) by the ${\gamma }$-dependency of relative permeability: salinity decrease causes the decline in water relative permeability and in residual oil saturation, and causes a mild increase in the relative permeability for oil. The above mechanisms yield the reduction in fractional flow for water and the increase in fractional flow for oil, thereby enhancing oil recovery.

As explained at the beginning of Sect. 2.1, fine particle mobilisation is triggered by weakening of electrostatic particle-grain attraction, which decreases as the salinity decreases. Fines mobilisation and migration are followed by particle straining in thin pore throats. Because we discuss the case where the particles are transported by water, the result is a decline in relative permeability for water, shown in Eq. (19). The main effect of induced fines migration is the reduction in relative permeability of water and deceleration of the aqueous phase. However, sweep on the micro-scale can increase, thereby reducing residual oil saturation.

Those effects reduce the fractional flow function for water and cause consequent oil recovery enhancement.

A separate effect of salinity on relative permeability, where the fines are not mobilised, corresponds to $\beta =0$ in Eq. (19). A separate effect of fines-induced formation damage, where the contact angle remains constant with salinity decrease, corresponds to salinity-independent relative permeability of water $k^{/}_{\mathrm{rw}}$ in Eq. (19). The effects of fractional flow reduction on 1D displacement of oil have been described at the end of Sect. 3.1.

Relative phase permeability is given by Corey’s formulae

$$\begin{aligned} k_{\mathrm{ro}} (s,\gamma )= & {} k_{\mathrm{rowi}} (\gamma )\left( {\frac{1-s_{\mathrm{or}} (\gamma )-s}{1-s_{\mathrm{or}} (\gamma )-s_{wi} (\gamma )}} \right) ^{n_\mathrm{o} (\gamma )}, \nonumber \\ k_{\mathrm{rw}} (s,\gamma ,S_s)= & {} {k_{\mathrm{rwor}} (\gamma )\left( {\frac{s-s_{wi} (\gamma )}{1-s_{\mathrm{or}} (\gamma )-s_{wi} (\gamma )}} \right) ^{n_{\mathrm{w}} (\gamma )}}\Bigg /{\left( {1+\beta S_{\mathrm{s}}} \right) } \end{aligned}$$

(51)

where the values of endpoint saturations and relative permeability are presented in Table 3 for injected and reservoir salinities. The data correspond to LS waterflood in field A from the North Sea (Kowollik 2015). The salinity dependences of all Corey parameters in Eq. (51) are linear (Seccombe et al. 2008; Lager et al. 2007, 2008, 2011). Table 3 presents the corresponding Corey parameters for injected and reservoir salinities. In particular, application of LS water causes $s_{\mathrm{or}}$-reduction by 0.1, but the residual oil saturation reduction due to fines straining and the induced diversion of water into unswept domains can be ignored.

For calculation of water-accessible area $A_{\mathrm{w}}(s,{\gamma })$, we assume the simplified rock geometry to be a bundle of parallel cylindrical capillaries. Wetting water fills the small capillaries. The saturation is defined by distribution of volumes of the cylinders, and the area is defined by their surfaces:

$$\begin{aligned} s=\frac{\int \limits _0^{r(s)} {r^{2}g(r)\mathrm{d}r} }{\int \limits _0^\infty {r^{2}g(r)\mathrm{d}r}},\quad A_{\mathrm{w}} (s)=\frac{\int \limits _0^{r(s)} {rg(r)\mathrm{d}r} }{\int \limits _0^\infty {rg(r)\mathrm{d}r}} \end{aligned}$$

(52)

The functions of the area where the fines are detached $A_{\mathrm{s}}(s,{\gamma })$ and fraction of clay area released from attached oil $b({\gamma })$ are estimated from permeability data for HS and LS waters under two-phase flow. Sarkar and Sharma (1990) measured the permeability decline after the injection of LS water with and without the presence of residual oil. Two cores were cut from the same Berea block. Switching from HS to fresh water yielded permeability decline from 65.43 to 0.093 mD (test 1). Equation (18) allows calculating the product $\beta \sigma _{\mathrm{s}}=713.3$. For two-phase displacement, the permeability decreased from 31.45 mD for “dry” core, to 0.193 mD in the presence of residual oil, allowing calculating the product $\beta A_{\mathrm{s}}(1-s_{\mathrm{or}} ,\gamma _{J}){\sigma }_{\mathrm{s}}=146$ (test 5-1 from Sarkar and Sharma 1990). Assuming the same maximum retention function in two sister cores, we calculate the ratio $A_{\mathrm{s}}(1-s_{\mathrm{or}}({\gamma }_{J}), \gamma _{J})=0.21$. The corresponding value of the fraction of clay area released from attached oil $b({\gamma }_{J})=0.08$.

Average pore radius has been calculated from core permeability and porosity using the formula $r_{\mathrm{p}}=5(k/\phi )^{1/2}$ (Barenblatt et al. 1989). For $k=8\times 10^{-13}\,\hbox { m}^{2}$ and $\phi =0.20$, we obtain $r_{\mathrm{p}}=10^{-5}\,\hbox {m}$. The water-accessible area $A_{\mathrm{w}}(s,{\gamma })$ is calculated from Eq. (52). The bundle-of-parallel-capillaries model does not capture the effect of contact angle on $A_{\mathrm{w}}$. Lognormal distribution for pore radii with mean $r_{\mathrm{p}}=10^{-5}$ m and variance coefficient $C_{v}=0.15$ have been used for calculation of $A_{\mathrm{w}}$ by Eq. (52). This variance coefficient is typical for sandstone (Jensen et al. 2007).

The above data for $A_{\mathrm{w}}$, $A_{\mathrm{s}}$, and $b ({\gamma })$ have been used to calculate relative permeability for water using Eq. (19).

For another core from test 4 by Sarkar and Sharma (1990), the obtained values are: $A_{\mathrm{s}}(1-s_{\mathrm{or}}({\gamma }_{J}), \gamma _{J})=0.17$, and $b({\gamma }_{J})=0.05$.

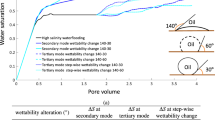
Fractional flow curves for HS and the three above-mentioned LS cases are shown in Fig. 11. Water-cut and recovery factors as calculated from the analytical model (25–27), subject to initial and boundary conditions (29, 30) and using formulae (46) for the recovery factor, are presented in Fig. 12a, b. That the blue fractional flow curve is above the black curve means that the impact of fines-induced formation damage is lower than that of wettability alteration. Because fines straining does not alter the residual oil saturation, the blue curve in Fig. 12b tends towards the green curve at large times. Wettability variation does alter the residual oil, such that the black and red curves converge at large times. Compared with HS flood, LS flood yields 0.3 incremental oil after 1 PVI, due to both effects. Separately, the wettability alteration and fines migration effects after 1 PVI bring 0.18 and 0.11 of incremental oil, respectively.

The effects of wettability alteration and fines migration, induced by LS water injection on the pressure drop across the core (reservoir) are presented in Fig. 12c. Compared with formation water injection (HS), alteration of wettability and some decrease in relative permeability for water causes increase in the maximum pressure drop 1.2 times. Comparing with the injection of formation water (HS), the permeability damage for water induced by fines mobilisation and straining (FM-LS) yields a 4.5-fold increase in the maximum pressure drop. Both effects (LS) results in 4.3 times increase in maximum pressure drop.

The results of recovery factor calculations for different volumes of HS water injected before the LS water are given in Fig. 13. The trajectories of concentration and saturation fronts in plane $(x_{\mathrm{D}},t_{\mathrm{D}})$ are shown in Fig. 10a. Here, time and the linear coordinate are dimensionalised using the volume ${\varOmega }_\mathrm{H}$ of HS water injected, i.e. $x_{\mathrm{D}}\rightarrow \phi x_{\mathrm{D}}/ {\varOmega }_\mathrm{H},\, t_{\mathrm{D}}\rightarrow ut_{\mathrm{D}}/{\varOmega }_\mathrm{H}$. The dimensionless moment of switching from HS to LS is constant and equal to unity, but the dimensionless coordinate of the production line $x_{\mathrm{D}}=\phi L/{\varOmega }_\mathrm{H}$ depends on the volume ${\varOmega }_\mathrm{H}$. With the increase in the volume ${\varOmega }_\mathrm{H}$ of injected HS water, the solution in the $(x_{\mathrm{D}},\, t_{\mathrm{D}})$-plane is intact, but the line of production wells $x_{\mathrm{D}}=\phi L/{\varOmega }_\mathrm{H}$ shifts to the left.

Figure 10a shows that for a small volume ${\varOmega }_\mathrm{H}$ of injected HS water, $x_{F}<\phi L/{\varOmega }_\mathrm{H}$, the bank of formation water and oil having composition 3 arrives at the production row after water breakthrough; the injected LS water arrives after the bank production with water-cut 2 (Fig. 6a), which will monotonically rise, i.e. the solution asymptotically approaches that for continuous injection of LS water. For larger HS volumes, the arrival time, the water-cut at the arrival, and its further growth coincide with that of continuous HS waterflood; the water-cut decrease occurs after the arrival of the LS water front. For sufficiently large HS volume such that $\phi L/{\varOmega }_\mathrm{H}$ is equal to the maximum coordinate of zone I, the production coincides with HS flood exactly until the 100 % water-cut. LS water arrives at that moment, and water-cut falls up to point 5, with further increase during oil production with LS water.

Figure 13 presents the recovery curves for different volumes of HS water injected before the LS waterflood. The higher the injected HS volume, the lower the recovery. High HS volumes tend towards recovery at HS water injection. At low volumes of injected HS water, the recovery tends to that of continuous LS flood from the very beginning.

Table 3 presents calculations for a specific contribution of wettability alteration and fines migration and for oil recovery. For both effects, compared with “normal” 1D waterflooding, injection of water with salinity with typical conditions results in the increase of the water-less production period from 0.25 to 0.34, decrease of water-cut from 0.82 to 0.41 before the salinity front breakthrough, and increase of recovery factor after 1 PVI from 0.36 to 0.66.

For only the wettability alteration effect (the case of zero formation damage coefficient), compared with “normal” 1D waterflooding, injection of LS water results in increase of the water-less production period from 0.25 to 0.3, decrease of water-cut from 0.82 to 0.52 before the salinity front breakthrough, and increase of recovery factor after 1 PVI from 0.36 to 0.54.

Comparing the effect of fines migration only (water relative permeability in the numerator in Eq. (19)), independent of salinity, against “normal” 1D waterflooding, injection of LS water results in increase of the water-less production period from 0.25 to 0.28, decrease of water-cut from 0.82 to 0.59 before the salinity front breakthrough, and increase in the recovery factor after 1 PVI from 0.36 to 0.47.

5 Discussion

Impact of wettability alteration and fines migration on LS waterflood The distinguished physical effects of LS waterflood are wettability alteration and fines-migration-induced formation damage, both triggered by the difference between salinities of formation and of injected waters. In order to compare LS and “normal” waterflooding, we discuss waterflood by formation water, where no salinity alteration occurs. So, the term “high-salinity” in this paper assumes equality of connate and injected HS waters.

Wettability alteration results in the decrease in $s_{\mathrm{or}}$ and $k_{\mathrm{rw}}$ (Omekeh et al. 2013; Dang et al. 2013; Nghiem et al. 2015), leading to displacement coefficient enhancement, as is the case for chemical EOR (Lake et al. 2014). Fines-migration-induced formation damage for water yields the redirection of injected water into un-swept zones, leading to sweep enhancement, as is with mobility control EOR.

The explicit analytical formulae for sequential injection of HS slug, LS slug, and HS drive that are presented in Tables 2 and 3 can be implemented in Excel or MATLAB and used for sensitivity study and LS EOR screening.

The 1D analytical modelling presented in Sect. 4 shows that for typical values of wettability alteration and induced formation damage by application of LS water, either effect can greatly increase incremental oil recovery compared with HS water. For example, for typical conditions of secondary LS waterflood (Table 3), the incremental recovery after 1 PVI due to collective effects of wettability alteration and fines migration is 0.3, but for each effect separately the incremental recovery is 0.18 and 0.11, respectively. For tertiary LS slug injection with wettability alteration effect only, the incremental recovery after 1.5 PVI is 0.2, 0.18, and 0.05, with secondary injection of 0.1, 0.3, and 1.0 PVI of HS water, respectively.

Wettability alteration and fines migration affect also 2D LS waterflooding. The wettability alteration reduces residual oil and causes more complete oil displacement from the swept areas. The induced fines migration and consequent permeability damage in the swept area decrease water flux and divert it into unswept zones, enhancing sweep efficiency. The 2D effects of increased sweep with LS water injection have been discussed in detail by Lemon et al. (2011) and Zeinijahromi et al. (2013). The derived analytical model can be used for 3D reservoir simulation in stream-line models (Blunt et al. 1996; Crane and Blunt 1999; Oladyshkin and Panfilov 2007).

Roles of dissipative and non-equilibrium effects Large-scale approximation for displacement of oil by varying salinity water with wettability alteration and fines mobilisation, migration, and straining is assumed in the current paper and expressed by inequalities (15), i.e. the dissipative effects of capillary pressure, dispersion of components, kinetics of the contact angle alteration, and kinetics of fines detachment and straining are disregarded. Yet, those effects must be considered with interpretation of the coreflood data. The capillary pressure effect smoothers the saturation shocks, but other effects of dispersivity and non-equilibrium smooth the concentration shocks.

Thickness of smoothed zones for the saturation-concentration shocks is determined from the travelling wave solutions (Duijn and Knabner 1992; Duijn et al. 1997). A travelling wave converges to each shock, with the dissipative dimensionless groups (15) tending to zero. The condition that the shock thickness is significantly smaller than the core length results in a more precise estimate of large-scale approximation than the vanishing conditions for small dimensionless groups (15) (Bedrikovetsky 1993).

In large-scale approximation, relative phase permeability can be determined from HS and LS corefloods using the generalised Weldge-JBN method (Jerauld et al. 2008; Zeinijahromi et al. 2016). If large-scale approximation conditions (15) are not fulfilled for the coreflood test, the solution depends on unknown dissipative and non-equilibrium terms. This increases the uncertainty in determining the relative phase permeability from coreflood data (Hussain et al. 2013). The above advantages foster reaching the conditions of large-scale approximation by selecting proper velocity, oil viscosity, core length, etc. in laboratory tests.

Recently obtained semi-analytical and exact solutions for two-phase multi-component systems with dissipation and non-equilibrium (Schmid and Geiger 2013; Geiger et al. 2012; Borazjani et al. 2016) simplify the solution of the inverse problem for the general system, but do not eliminate the uncertainty.

More complex mathematical models Different behaviour of oil-wet, mixed-wet, and water-wet fines during LS waterflooding has been reported by Sarkar and Sharma (1990) and Tang and Morrow (1999), etc. Here, we discuss initially oil-wet fine particles, like those of kaolinite or illite. Residual oil coats the oil-wet particles, so there is no direct contact between the particles and water. However, arrival of LS water alters wettability, resulting in the oil sweep from the rock surface and exposing it to the injected water (Berg et al. 2010; Cense et al. 2011; Mahani et al. 2015a). From this moment forward, particle equilibrium on the rock surface is determined by torque balance of drag and electrostatic forces. The electrostatic particle-rock attraction decreases with salinity decrease, resulting in particle mobilisation. Therefore, particle detachment occurs when oil is already immobile, supporting the assumption of the current model that fines are transported by water only.

However, a more detailed model that accounts for non-equilibrium effects should reflect transport of mixed-wet and partial-wet fines by the capillary oil–water menisci. Basic equations for movement of oil–water interface, developed by Shapiro (2015, (2016), can be used to describe transport of mixed-wet fines by the oil–water interface.

The current paper discussed two EOR mechanisms of LS waterflooding: the wettability and interfacial tension alterations resulting in change to the relative permeability, and the induced formation damage to the aqueous phase through mobilising and straining of the natural reservoir fines. However, numerous other EOR mechanisms are currently under investigation. More sophisticated multi-component ionic exchange models reflect the effect of different cations on rock surface and wettability alteration during their adsorption on clay sites (Omekeh et al. 2013; Nesterov et al. 2015). Sheng (2014) and Qiao et al. (2015, (2016) reviewed the mechanisms of fines migration, mineral dissolution, increased pH effect, and reduced interfacial tension, saponification, multicomponent ion exchange, wettability alteration, etc. Morrow and Buckley (2011) cited osmotic pressure as an important factor leading to incremental oil recovery. Sandengen and Arntzen (2013) described in detail how osmosis could operate. These works noted that the mechanisms for LS waterflooding are not yet well understood, and their modelling is a subject of forthcoming research.

The model (25–28) uses the maximum retention function for two-phase flow (Zeinijahromi et al. 2013). In particular, the model uses the dependency $A_{\mathrm{w}}(s,{\gamma })$ for the area of water-accessible rock surface, whose pore geometry is approximated as a bundle of parallel cylindrical capillaries. Using the triangular pores would introduce contact angle dependency of the area $A_{\mathrm{w}}(s,\theta$) (Patzek and Kristensen 2001). The percolation or network model can incorporate the geometric grid properties of the porous space (Blunt 2001). The single-phase maximum retention model for fines detachment has been validated by comparison with numerous laboratory studies (Zeinijahromi et al. 2013; You et al. 2015); validation of the two-phase model still needs to be performed.

Exact analytical solutions for LS slug problems The exact solution (35–50) is obtained using the mapping where the Lagrangian coordinate $\varphi$ substitutes for time $t_{\mathrm{D}}$. The same technique can be used for a multi-component ion-exchange system for the cases of Henry’s and Langmuir’s sorption. The mapping splits the general $(n+1)\times$ ($n+1$) system with unknowns $(s,\gamma _{1} {\ldots }\gamma _{n})$ into the auxiliary $n\times n$ system with unknowns $({\gamma }_{1} \ldots \gamma _{n})$ and the lifting equation that determines the saturation distribution $s(x,\varphi )$ (“Appendix 1”). The auxiliary system is equivalent to a set of single-phase solute-transport equations in coordinates $(x_{\mathrm{D}},t_{\mathrm{D}}- x_{\mathrm{D}})$ and includes the adsorption isotherms; the solution is independent of viscosities and relative permeabilities of oil and water. For the case of Henry’s sorption, the concentration fronts in plane $(x_{\mathrm{D}},\varphi )$ are straight lines (Fig. 9a). The auxiliary solution can be revealed from laboratory corefloods or reservoir data by plotting the concentrations and fractional flow in the produced fluid, versus the produced water volume $\varphi (1,t_{\mathrm{D}})$.

The exact solution (35–50) significantly differs from the front-tracking method (Holden and Risebro 2013), where the rarefaction s-wave is approximated by the sequence of s-shocks; the front-tracking solution converges to the exact solution with jumps [s] in approximated shocks tending to zero.

6 Conclusions

Derivation of the exact solution for the 1D LS slug problem that accounts for wettability alteration and fines migration, and recovery prediction by the analytical modelling, allows drawing the following conclusions:

• 1. In large-scale approximation, the excess of the attached particle concentration over the maximum retention value instantly transferees to strained concentration, yielding instant permeability damage for the aqueous phase. The governing equations are equivalent to the fractional flow model of oil displacement by chemical solution.

  Extrapolation of the maximum retention function for the salinity values that are above the critical salinity allows using the same system of governing equations in the domains with and without fines migration.

• 2. A well-known analytical EOR model describes a lumped-salt LS waterflooding and accounts for both wettability alteration and induced fines migration.

• 3. Continuous LS waterflooding results in later breakthrough than does formation water injection; the former decreases water-cut during production of the oil–water bank and during a short period after the breakthrough of the injected water. It also lowers oil residual at later stages of waterflooding.

• 4. With injection of intermediate-salinity water, the breakthrough moment and water-cut sometime after the breakthrough coincide with formation waterflooding. Afterwards, water-cut at the intermediate-salinity water is lower, as is the residual oil.

• 5. The 1D problem for oil displacement by formation water with further injection of LS slug and HS chase drive allows for exact solution. The saturation and salinity front trajectories are described by implicit formulae.

  The trajectory formulae are linear with respect to time $t_{\mathrm{D}}$ and coordinate $x_{\mathrm{D}}$. The nonlinear terms ${\varDelta }$ are equal to the water volume flowing via the corresponding characteristic line. The terms ${\varDelta }$ allow for a simple geometric interpretation at the fractional-flow-curve plane, yielding a graphical solution for front trajectories.

• 6. For short-term formation water injection before LS waterflooding, the solution asymptotically tends to that for oil displacement by LS water. For long-term formation water injection, the solution tends to that for oil displacement by LS water under with high initial water saturation.

Appendix 1: Splitting Method for Equations of Two-Phase Multi-component Mass Transfer in Porous Media

Following Wagner (1987), Pires et al. (2004, (2006) and Polyanin and Zaitsev (2012), here we briefly present the splitting procedure for hyperbolic system (25–27). Let us assume that the solution of the system $s(x_{\mathrm{D}},t_{\mathrm{D}})$ and ${\gamma }(x_{\mathrm{D}},t_{\mathrm{D}})$ is already known, f and introduce the stream-function $\varphi (x_{\mathrm{D}},t_{\mathrm{D}})$:

$$\begin{aligned} \varphi \left( {x_\mathrm{D},t_\mathrm{D}} \right) =\int \limits _{\left( {0,0} \right) }^{\left( {x_\mathrm{D},t_\mathrm{D}} \right) } {f\mathrm{d}t_\mathrm{D} -s\mathrm{d}x_\mathrm{D}} \end{aligned}$$

(53)

It follows from the conservation law (25) that unknowns s and f are the partial derivatives of the stream-function

$$\begin{aligned} s=-\frac{\partial \varphi }{\partial x_\mathrm{D}},\quad f=\frac{\partial \varphi }{\partial t_\mathrm{D}} \end{aligned}$$

(54)

and the stream-function $\varphi (x_{\mathrm{D}},t_{\mathrm{D}})$ is independent of the integration path that links point $(x_{\mathrm{D}},t_{\mathrm{D}})$ with the origin (0, 0) (Bear 2013; Courant and Friedrichs 1976). The equality of the second mixed derivatives of the stream-function yields the conservation law (25).

From Eq. (53), it follows that the corresponding differential form of the flux has the following shape (Cartan 2006):

$$\begin{aligned} \mathrm{d}\varphi =f\mathrm{d}t_\mathrm{D} -s\mathrm{d}x_\mathrm{D} \end{aligned}$$

(55)

and the lines of constant stream-function are stream-lines of the flow

$$\begin{aligned} \frac{\mathrm{d}x_\mathrm{D}}{\mathrm{d}t_\mathrm{D}}=\frac{f}{s}. \end{aligned}$$

(56)

The volumetric flux between any two stream-lines is given by the difference of their stream-function values. In particular, the difference $\varphi (x_{\mathrm{D}},t_{\mathrm{D}})-\varphi (x_{\mathrm{D}},0)$ is the volume of water that flows via the cross section $x_{\mathrm{D}}$ = constant during time $t_{\mathrm{D}}$.

Differential $\mathrm{d}t_{\mathrm{D}}$ can be expressed from Eq. (55) as

$$\begin{aligned} \mathrm{d}t_\mathrm{D} =\frac{\mathrm{d}\varphi }{f}+\frac{s\mathrm{d}x_\mathrm{D}}{f}. \end{aligned}$$

(57)

The equality of second mixed derivatives of function $t_{\mathrm{D}}=t_{\mathrm{D}}$ $(x_{\mathrm{D}},\varphi )$ in Eq. (57) yields

$$\begin{aligned}&\frac{\partial G({U,\gamma })}{\partial \varphi }+\frac{\partial U}{\partial x_\mathrm{D}}=0, \nonumber \\&\quad U=\frac{1}{f({s,\gamma })},\quad G({U,\gamma })=-\frac{s}{f({s,\gamma })}. \end{aligned}$$

(58)

Equation (58) is the result of the Eq. (25) transform to coordinates $(x_{\mathrm{D}},\varphi )$.

Applying Green’s theorem over any arbitrary domain $\varpi$ with continuous boundary to Eq. (27) and accounting for Eq. (55)

$$\begin{aligned} 0= & {} \oint \limits _{\partial \varpi } {({\gamma f})\mathrm{d}t_\mathrm{D}} -({\gamma s})\mathrm{d}x_\mathrm{D} =\oint \limits _{\partial \varpi } {\gamma \left( {f\mathrm{d}t_\mathrm{D} -s\mathrm{d}x_\mathrm{D}} \right) } =\oint \limits _{\partial \varpi } {\gamma \mathrm{d}\varphi } \nonumber \\= & {} \int \!\!\!\int \limits _\varpi {\frac{\partial \gamma }{\partial x_\mathrm{D}}\mathrm{d}x_\mathrm{D} \mathrm{d}\varphi }, \end{aligned}$$

(59)

yields the transformation of Eq. (27) to $(x_{\mathrm{D}},\varphi )$-coordinates

$$\begin{aligned} \frac{\partial \gamma }{\partial x_\mathrm{D}}=0. \end{aligned}$$

(60)

So, the original system (25–27) in $(x_{\mathrm{D}},\varphi )$-coordinates has the form (58, 60). Equations (58) and (60) are called the lifting and auxiliary equations, respectively.

Figure 7a, b shows the mapping $K\,{:}\,(x_{\mathrm{D}},t_{\mathrm{D}})\, \rightarrow \,(x_{\mathrm{D}},\varphi )$ along with the images of the initial condition axis $t_{\mathrm{D}}=0$ and the boundary condition axis $x_{\mathrm{D}}=0$. The images depend on initial and boundary data.

System (58, 60) can be formally obtained by the change of variables $(x_{\mathrm{D}},t_{\mathrm{D}}) \rightarrow (x_{\mathrm{D}},\varphi )$ in the system (25,27), but the calculations are more cumbersome than those given by Eqs. (57) and (59). Equation (60) can be derived directly from mass conservation for salt in coordinates $(x_{\mathrm{D}},\varphi )$.

Inlet boundary condition for continuous injection (30) in coordinates $(x_{\mathrm{D}},\, \varphi )$ becomes

$$\begin{aligned} x_\mathrm{D} =0: U=1, \gamma =\gamma _J. \end{aligned}$$

(61)

Initial condition (29) in coordinates $(x_{\mathrm{D}},\, \varphi )$ take the form

$$\begin{aligned} \varphi =-s_{\mathrm{I}} x_\mathrm{D}:\gamma =\gamma _{\mathrm{I}}, U\rightarrow \infty . \end{aligned}$$

(62)

The inlet boundary condition for formation water injection followed by the injection of LS water (31) in coordinates $(x_{\mathrm{D}},\varphi )$ becomes

$$\begin{aligned} x_\mathrm{D} =0: \gamma =\left\{ {{\begin{array}{l} {\gamma _{\mathrm{I}},} \\ {\gamma _J,} \\ {\gamma _{\mathrm{I}},} \\ \end{array}}{\begin{array}{l} {0<\varphi<1} \\ {1<\varphi<t_{\mathrm{s}}} \\ {t_{\mathrm{s}}<\varphi <\infty } \\ \end{array}}} \right. . \end{aligned}$$

(63)

The elementary hyperbolic waves for the $2\times 2$ conservation law system (58, 60) include one rarefaction s-wave and s- and ${\gamma }$-jumps. The salinity is constant in the rarefaction wave; the explicit formula is given by Eq. (35).

Substituting a trajectory $\varphi (x_{\mathrm{D}})$ and $t_{\mathrm{D}}(x_{\mathrm{D}})$ into the flux (55) and taking the corresponding derivatives shows that speeds of rarefaction and shock waves in planes $(x_{\mathrm{D}},\varphi )$ and $(x_{\mathrm{D}},t_{\mathrm{D}})$ (V and D, respectively) are related as

$$\begin{aligned} \frac{1}{V}=\frac{f}{D}-s. \end{aligned}$$

(64)

The geometric interpretation of Eulerian and Lagrangian speeds D and V, respectively, are shown in Fig. 7c.

We introduce a shock [A] of a physical value A that is equal to the difference between A-value ahead and behind the shock: $[A]=A^{+}-A^{-}$. The Hugoniot–Rankine conditions of flux continuity on the discontinuities for the two conservation laws (58) and (60) are (Courant and Friedrichs 1976)

$$\begin{aligned} \left[ U \right] =V\left[ G \right] , \left[ \gamma \right] =0. \end{aligned}$$

(65)

Those shocks are called s-shocks. They correspond to jump along the curve ${\gamma }$ = constant in planes (s, f) or (U, G) (Fig. 8a, c, respectively).

It follows from the auxiliary equation (58) that shocks with salinity and saturation discontinuities can occur across the axis $\varphi =0$ that corresponds to infinite velocity V. Equation  (65) shows that $[G]=0$, i.e. density G must be continuous. The salinity jump can take any arbitrary value. Therefore, the ratio s / f must be continuous also. Those discontinuities are called ${\gamma }$-shocks.

Equation (60) for unknown ${\gamma }$ separates from Eq. (58). Thus, Eq. (58) is solved with respect to unknown $s(x_{\mathrm{D}},\varphi )$ for known ${\gamma }(x_{\mathrm{D}},\, \varphi )$ using the method of characteristics (Figs. 8, 9, 10). Equation (58), subject to the boundary and initial conditions (61, 62), is the so-called the lifting problem. It follows from Eq. (58) that the solutions for initial-boundary problems with piecewise constant ${\gamma }$-values contain those values only. Figure 8a shows the form of density curves $G=G(U, \gamma )$ for ${\gamma }$-values ${\gamma }_{\mathrm{I}}$ and ${\gamma }_{J}$ appearing in initial and boundary conditions (62) and (63). Finally, the transformation of solution $s(x_{\mathrm{D}},\varphi ),\, \gamma \,(x_{\mathrm{D}},\varphi )$ to coordinates $(x_{\mathrm{D}},t_{\mathrm{D}})$ is performed by the inverse mapping $K^{-1}$ (Fig. 7a, b), i.e. by calculation of $t_{\mathrm{D}}= t_{\mathrm{D}}(x_{\mathrm{D}},\varphi )$ from Eq. (55):

$$\begin{aligned} t_\mathrm{D} \left( {x_\mathrm{D},\varphi } \right) =\int \limits ^{\left( {x_\mathrm{D},\varphi } \right) } {\frac{\mathrm{d}\varphi }{f}+\frac{s\mathrm{d}x_\mathrm{D}}{f}}, \end{aligned}$$

(66)

where any arbitrary point $(x_{\mathrm{D}},\varphi )$ is connected to the point with $\varphi =0$ or $x_{\mathrm{D}}=0$ by a sequence of the characteristic lines.

The mass balance conditions on $\gamma$-shocks at the $(x_{\mathrm{D}},t_{\mathrm{D}})$ plane follow from (64) and (65):

$$\begin{aligned} D=\frac{f\left( {s^{-},\gamma ^{-}} \right) }{s^{-}}=\frac{f\left( {s^{+},\gamma ^{+}} \right) }{s^{+}}. \end{aligned}$$

(67)

Example

Solutions for continuous injections in coordinates $(x_{\mathrm{D}},t_{\mathrm{D}})$ are self-similar and depend on the group $x_{\mathrm{D}}/t_{\mathrm{D}}$. The corresponding solutions in the $(x_{\mathrm{D}},\varphi )$-plane are also self-similar and depend on the group $\varphi /x_{\mathrm{D}}$. The solution ${\gamma }(x_{\mathrm{D}},\varphi )$ for continuous injection (61) is achieved by a single infinite-speed jump along the axis $\varphi =0$. The solution $s(\varphi /x_{\mathrm{D}})$ corresponds to rarefaction wave $J-2$, jump $2\rightarrow 3$, and jump $3\rightarrow I$ in Fig. 8c. The solution $s(x_{\mathrm{D}}/t_{\mathrm{D}}),\, \gamma (x_{\mathrm{D}}/t_{\mathrm{D}})$ corresponds to rarefaction wave $J-2$, jump $2\rightarrow 3$, and jump $3\rightarrow I$ in Figs. 6a and 8a. The solution is presented in Sect. 3.1.