1 Introduction

Analysis of coupling the flow and chemical reactions between liquid and porous medium is an area of interest for many scientific, industrial, and engineering processes. Injection of water is a conventional technique for recovering oil from reservoirs. A considerable research is currently focused around injection of the chemistry-optimized water by tuning the salinity and ionic composition in order to increase the recovery (Zhang et al. 2007; Alotaibi and Nasr-El-Din 2009; Austad et al. 2011). This process (often called “smart water injection”) may involve a large number of physico-chemical mechanisms like chemical reactions, mass transfer between phases, and change of transport properties. Dissolution and precipitation are the two important processes affecting brine chemistry as they can significantly modify the physical and chemical properties of porous media (Lasaga 1984; Singurindy and Berkowitz 2003; Bedrikovetsky et al. 2009a, b; Carageorgos et al. 2010). Experimental data (Pu et al. 2010; Houston et al. 2006) support the fact that mineral dissolution takes place during smart water floods and therefore its effect should be quantified. Another mechanism of smart water flooding mentioned in many studies is crude oil/brine/rock interactions that alter the wettability state of the rock and hence the relative permeability curves (Jerauld et al. 2008; Omekeh et al. 2012). Other mechanisms are also mentioned in the literature (see overview in Tang and Morrow (1999), Zahid et al. (2011, 2012)).

Similar studies (Aharonov et al. 1997) have previously been carried out under the assumption that the fluid was incompressible. Compressibility of the oil–brine–rock system might, however, be of importance. The density of the brine depends on its composition and pressure. The compositional compressibility may be stronger than pressure compressibility. The dissolution may occur under condition of the volume disbalance (the individual volumes of dissolved species will be different from those in the solid state). Dissolution of a mineral is accompanied by a volume change, and a corresponding pressure adjustment. These changes are probably small, but they may play some role in a confined space. Thus, an equation of state for brine is required, which can be taken from the correlation data available for the specific ion content of the brine (Spivey et al. 2004; Lam et al. 2008). To the best of our knowledge, this is the main difference of our work with the available commercial simulators like TOUGH2 (Pruess et al. 1999) where the additivity of the individual volumes in solution is assumed. It has turned out that this non-additivity represents a problem for numerical simulations. Only a fully implicit scheme seems to be capable for accounting for this effect in the full scale.

In this paper, a 1D numerical model for two-phase compressible flows with chemical reactions is presented. An example of such a process is an injection of a weak acid or carbonated water in a reservoir. The model incorporates description of macroscale transport on the basis of a generalized Darcy law and general non-equilibrium kinetics. It may be used to study a wide range of chemical water–rock interactions, including dissolution, precipitation, adsorption, and multicomponent ion exchange. Incorporation of a particular type of interaction may require a relation between flow/reservoir properties and chemical species concentrations. A key feature of the model is its capacity to account for the strong coupling between the fluid flow and mineral reactions that cannot be analyzed separately.

The paper is organized as follows. In the first section, we formulate a set of partial differential equations and boundary conditions describing reactive two-phase flow of compressible fluids through porous media. In the second section, the numerical method is outlined. In the third section, sample simulations are presented. We analyze reservoir properties: porosity and permeability, together with composition of produced water, pressure distribution, and displacement profiles. Different scenarios for fast and slow reaction rates are studied. It is demonstrated that the model is capable of describing an effect similar to wormholing: formation of zones with anomalous high porosity and permeability closer to inlet, if the reactions are sufficiently fast. The volumetric non-additivity is found not to play any significant role in a single-dimensional case: it only slightly affects the velocity of the displacement front. Multidimensional simulations are probably required for better account of this effect.

2 Theory

The following description is similar to that by Aharonov et al. (1997). An important difference is that we consider a two-phase flow of compressible fluids. The approach is based on the macroscopic approximation of mechanics of continuous medium. Solid phase, i.e., matrix of porous material, and the two fluid phases, water and oil, are assumed to occupy the same elementary volume. Each phase contains a number of components which cause physico-chemical interactions between phases. Chemical interactions are expected to influence both flow and reservoir parameters, such as porosity, absolute permeability, residual oil saturation, and/or relative permeability curves.

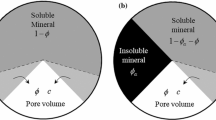
The chemical species will be denoted by \(X_i\). For each species, the phase should be specified. The phases under consideration are water, oil, and solid, which will be denoted with index \(\alpha =w,o,s\) correspondingly. The general description is presented for a system containing \(M\) mineral species in the solid that undergo dissolution or precipitation, \(n_\mathrm{aq} \) components in water and a single oil component. We use index \(m=m_1 ,\ldots ,m_M \) to refer to mineral species and index \(i=1,\ldots ,n_\mathrm{aq}\) to refer to aqueous components.

2.1 Mineral Dissolution and Precipitation Reactions

We study non-equilibrium mineral dissolution and precipitation reactions that take place on the interface between the water and mineral surface. According to classification introduced by Rubin (1983), these reactions are referred as “insufficiently fast” heterogeneous surface reactions. The general form of dissolution/precipitation reactions is represented by

$$\begin{aligned} X_m \rightleftarrows \sum \limits _{i=1}^{n_\mathrm{aq}}{\nu _{im} X_i},\quad m=m_1,\ldots ,m_M , \end{aligned}$$
(1)

The changes of moles of aqueous species \(X_i\) are related to the reaction rate via the matrix of the stoichiometric coefficients \(\nu _{im}\):

$$\begin{aligned} \mathrm{d}_t C_i =r_i =\sum \limits _{m=m_1 }^{m_M } {\nu _{im} \dot{r}_m},\quad i=1,\ldots ,n_\mathrm{aq}. \end{aligned}$$
(2)

The rate law for mineral dissolution and precipitation reaction is given by Omekeh et al. (2012):

$$\begin{aligned} -\mathrm{d}_t C_m =\dot{r}_m =\hat{{A}}_m \left( {\tilde{k}_m^+ \prod \limits _{i=1}^{n_\mathrm{aq} } {({c}'_i )^{|(\nu _{im} |-\nu _{im} )/2}} -\tilde{k}_m^- \prod \limits _{i=1}^{n_\mathrm{aq} } {({c}'_i )^{(\nu _{im} +|\nu _{im} |)/2}} } \right) , \end{aligned}$$
(3)

where \(\hat{{A}}_m \) is the reactive specific surface for mineral reaction \(m\), \(\tilde{k}_m^+ \) and \(\tilde{k}_m^- \) include rate constants and activity coefficients, \(C_m \), and \(C_i \) are the global molar concentrations (per bulk volume) and \({c}'_i \) are aqueous component concentrations divided by some reference concentrations \(c_i^\mathrm{ref} \) . It can be verified that Eq. (3) produces conventional results: the product of concentrations of species consumed together with the mineral (negative \(\nu _{im} )\) is used to calculate the forward reaction rate, and product of concentrations of species that are produced on dissolution is used to calculate the backward reaction rate.

2.2 Material Balance Equations

The material balance equations for a system containing \(M\) minerals undergoing dissolution/precipitation and \(n_\mathrm{aq} \) aqueous species excluding diffusion/dispersion effects are the following:

$$\begin{aligned}&\displaystyle \frac{\mathrm{d}C_m }{\mathrm{d}t}=-\dot{r}_m ,\quad m=m_1 ,\ldots ,m_M , \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \frac{\partial \left( {\phi sc_i } \right) }{\partial t}+\nabla \cdot \left( {c_i \mathbf{u}_w } \right) =r_i ,\quad i=1,\ldots ,n_\mathrm{aq} , \end{aligned}$$
(5)
$$\begin{aligned}&\displaystyle \frac{\partial \left( {\phi s\rho _w } \right) }{\partial t}+\nabla \cdot \left( {\rho _w \mathbf{u}_w } \right) =\sum \limits _{i=1}^{n_\mathrm{aq} } {M_i r_i } , \end{aligned}$$
(6)
$$\begin{aligned}&\displaystyle \frac{\partial \left( {\phi (1-s)\rho _o } \right) }{\partial t}+\nabla \cdot \left( {\rho _o \mathbf{u}_o } \right) =0, \end{aligned}$$
(7)
$$\begin{aligned}&\displaystyle \frac{\mathrm{d}\left( {(1-\phi )\rho _s } \right) }{\mathrm{d}t}=-\sum \limits _{m=m_1 }^{m_M } {M_m \dot{r}_m }, \end{aligned}$$
(8)

where \(c_i =C_i /(\phi s)\) are the molar concentrations of aqueous species, \(\phi \) is the porosity, \(\rho _b \) and \(\rho _o \) are the brine and oil densities, respectively, and \(M_i \) is the molar mass of component. Vectors \(\mathbf{u}_w \) and \(\mathbf{u}_o \) are superficial velocities for water and oil in \(\hbox {m s}^{-1}\).

Equations (4) and (5) describe the material balances for species. Equations (6)–(8) constitute the material balances for phases.

2.3 Fluid Properties

Equations of state for the fluid phases are required to close the system of material balance equations. The model of weakly compressible fluid for water phase is modified by introducing additional dependence of density of the composition of water.

Dissolution of external species in water may affect its density. Moreover, the individual molar volumes of these species may change, leading to the forced expansion/contraction of aqueous phase. Variation of the aqueous phase density due to change in composition is commonly much larger compared with compressibility due to pressure change. Thus, certain pressure effects may arise to adjust for the change in density caused by physical–chemical interactions between the rock and aqueous phase. A problem of constituting the equation of state for brines was discussed in (Spivey et al. 2004), where the data for modeling densities of electrolyte solutions are provided. In accordance with this data, we introduce a linearized equation of state for brine in the following form:

$$\begin{aligned} \rho _w (P,\bar{{c}})=\rho _w^0 \left( {1+\hat{{c}}_{P,w} (P-P^{0})+\sum \limits _{i=1}^{n_\mathrm{aq} } {\hat{{c}}_{wc, i} (c_i -c_i^0 )} } \right) , \end{aligned}$$
(9)

with constant compressibilities \(\hat{{c}}_{P,w} \), \(\hat{{c}}_{wc,i} \) with regard to pressure and composition correspondingly, and \(P^{0}\) and \(c_i^0 \) represent the chosen reference state. Simple investigation of the non-additive mixing showed that for small concentrations of solute, compressibility due to change in composition of brine can be successfully calculated by

$$\begin{aligned} \hat{{c}}_{wc, i} =1-(1+\gamma _m )\rho _w /\rho _m , \end{aligned}$$
(10)

where coefficient \(\gamma _m \) is the relative change in molar volume on the dissolution of mineral \(m\). Our study of the correlations data showed that typical absolute value of the coefficient \(\gamma _m \) can be in a range from 0 to almost one. See the appendix for details.

The equation of state for oil is chosen to account for pressure compressibility:

$$\begin{aligned} \rho _o (P)=\rho _o^0 \left( {1+\hat{{c}}_{P, o} (P-P^{0})} \right) . \end{aligned}$$
(11)

2.4 Rock Properties

The properties of the rock, such as porosity, permeability, and specific surface, are to be related to reservoir pressure and mineral content. If the reservoir pressure has a significant effect on the state of the rock, then an appropriate geomechanical model should be included in the reactive transport (Settari and Mourits 1998). Most of the models use the pressure-dependent compressibility of rock to approximate the geomechanical effects on porosity and permeability. The water-weakening of the rock may also result in fracturing. The question of appropriate geomechanical model is to be considered for each type for the rock separately and is beyond the scope of this article. In this paper, we only consider variation of porosity and permeability due to chemical reactions with the fluid and the corresponding transformation of the rock.

With the assumption that pressure does not affect the state of the rock, one can relate the porosity to the amount of mineral species present:

$$\begin{aligned} \phi (\bar{{C}})=\phi ^{0}-\sum \limits _{m=m_1 }^M {\rho _m^{-1} M_m \left( C_m -C_m^0 \right) .} \end{aligned}$$
(12)

Equation (12) is the closure relation for porosity which allows eliminating material balance Eq. (8) for the solid phase. If the initial porosity field \(\phi ^{0}\) is given, then the porosity at each time can be calculated if solution for global concentrations of mineral components is known.

Reactive surface \(\hat{{A}}_m \) is another important parameter in the calculation of the rate of mineral dissolution and precipitation. The following equation is used to calculate the reactive surface are with the change of moles of minerals:

$$\begin{aligned} \hat{{A}}_m =\hat{{A}}_m^0 \times \left( C_m /C_m^0 \right) . \end{aligned}$$
(13)

The relation between the absolute permeability \(k\) and the microgeometry of porous space is important for modeling nonlinear processes involved in the study. Permeability is commonly assumed to be a power law function of the porosity and specific surface \(\hat{{A}}\) in \(\hbox {m}^{2}\,\hbox {m}^{-3}\). In our study, we use the conventional Kozeny’s equation, which is successfully applied to predict permeability of chalks (Alam et al. 2011):

$$\begin{aligned} k=c_K \frac{1}{(\hat{{A}})^{2}}\frac{\phi ^{3}}{(1-\phi )^{2}}, \end{aligned}$$
(14)

where \(c_K \) is Kozeny’s constant. The specific surface \(\hat{{A}}\) is, in general, a complex function that depends on the porosity \(\phi \), pore-size distribution, and whether a mineral is dissolving or depositing. However, due to the lack of general models on this kind of dependence, the specific surface \(\hat{{A}}\) is approximated as constant.

We also assume that while the rock is getting dissolved, the total amount of residual oil does not change. But this automatically implies the variation of the residual oil saturation \(s_\mathrm{or} \). One can deduce therefore that

$$\begin{aligned} s_\mathrm{or} =s_{\mathrm{or}}^0 \times \left( \phi ^{0}/\phi \right) . \end{aligned}$$
(15)

Therefore, the residual oil saturation decreases on dissolution and increases during precipitation process, whereas the total mass of the trapped oil per bulk volume \(\phi s_\mathrm{or} \rho _o \) always remains the same.

2.5 Momentum Balances

The generalized Darcy law relates a driving pressure \(P_\alpha \) and the fluxes of the fluids.

$$\begin{aligned} u_\alpha =-\frac{kk_{r\alpha } }{\mu _\alpha }\frac{\partial P_\alpha }{\partial x},\quad \alpha =w,o, \end{aligned}$$
(16)

where \(\mu _\alpha \) is the phase viscosity and \(k_{r\alpha } \) is the phase relative permeability.

Models for relative permeabilities may include dependence on brine salinity, composition, or amount of adsorbed aqueous species (Omekeh et al. 2012). In our work, the relative permeabilities are defined by the conventional Corey approximation (Brooks and Corey 1964):

$$\begin{aligned}&\displaystyle k_{rw} =k_\mathrm{rwor} \left( {\frac{s-s_\mathrm{wi} }{1-s_\mathrm{wi} -s_\mathrm{or} }} \right) ^{a_w } \end{aligned}$$
(17)
$$\begin{aligned}&\displaystyle k_{ro} =k_\mathrm{rowi} \left( {\frac{1-s-s_\mathrm{or} }{1-s_\mathrm{wi} -s_\mathrm{or} }} \right) ^{a_o}. \end{aligned}$$
(18)

Since the relative permeabilities depend on residual saturations, varying according to Eq. (15), the relative permeabilities vary correspondingly.

We do not account for the capillary pressure difference, assuming that it can be neglected. This is usually a reasonable assumption if the size of a system is large enough (Bedrikovetsky 1993). Therefore, the net velocity simplifies to

$$\begin{aligned}&\displaystyle U=\sum _{\alpha =w,o} {u_\alpha } =-k\sum _{\alpha =w,o} {\frac{k_{r\alpha } }{\mu _\alpha }\frac{\partial P}{\partial x}} \end{aligned}$$
(19)
$$\begin{aligned}&\displaystyle u_\alpha =F_\alpha U,\quad \alpha =w,o \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle F\equiv F_w =1-F_o =\frac{k_{rw} /\mu _w }{k_{rw} /\mu _w +k_{ro} /\mu _o}. \end{aligned}$$
(21)

Here \(F_\alpha \) are the fractional flow functions which describe the fraction of fluid \(\alpha \) in the flow.

2.6 Boundary and Initial Conditions

As discussed above, the porosity is excluded from the set of independent variables. Thus, the total number of unknowns is \(M+n_\mathrm{aq} +2\), including \(M\) mineral component, \(n_\mathrm{aq} \) aqueous components, saturation \(s\), and pressure \(P\).

In order to close the system of material balance Eqs. (4)–(7), we need to supplement the initial and boundary conditions. We require \(M\) initial conditions for the mineral components, \(n_\mathrm{aq}\) initial and boundary conditions for aqueous components, initial and boundary condition for saturation, and initial and two boundary conditions for pressure.

Initially, the porous media are filled with oil and irreducible formation water. The mineral content in the rock is also to be specified. Thus, initial data are given by

$$\begin{aligned}&\displaystyle s(0,x)=s_\mathrm{wi}, \end{aligned}$$
(22)
$$\begin{aligned}&\displaystyle c_i (0,x)=c_i^{FW} ,\quad i=1,\ldots ,n_\mathrm{aq}, \end{aligned}$$
(23)
$$\begin{aligned}&\displaystyle C_m (0,x)=C_m^0 ,\quad m=m_1 ,\ldots ,m_M. \end{aligned}$$
(24)

Initial pressure distribution is obtained as a result of the solution of stationary filtration problem

$$\begin{aligned} P(0,x)=P_\mathrm{init} (x). \end{aligned}$$
(25)

We apply mixed boundary conditions: a constant flux boundary condition at the inlet together with fixed composition of the injection water and constant pressure at the outlet. Thus, the boundary condition for pressure at the inlet is specified by the constancy of the net velocity \(U\) at the inlet, and boundary condition for saturation is specified by setting the fractional flow function at the inlet to be unity which corresponds to water injection.

  • Boundary conditions at the inlet:

    $$\begin{aligned}&\displaystyle U(t,0)=U^{0} \end{aligned}$$
    (26)
    $$\begin{aligned}&\displaystyle F(t,0)=1 \end{aligned}$$
    (27)
    $$\begin{aligned}&\displaystyle c_i (t,0)=c_i^{INJ} ,\quad i=1,\ldots ,n_\mathrm{aq}. \end{aligned}$$
    (28)

  • Boundary conditions at the outlet:

    $$\begin{aligned} P(t,L)=P^{0}. \end{aligned}$$
    (29)

Equations (2), (3) for rates of reactions, (9) and (11) for fluid densities, (12) for porosity, (13) for reactive surface, (14) for absolute permeability, (15) for residual oil saturation, and (19)–(21) for the superficial velocities of fluids are to be substituted in Eqs. (4)–(7). The resultant system together with initial conditions (22)–(25) and boundary conditions (26)–(29) forms the closed system.

2.7 Bringing the Equations to a Dimensionless Form

In order to obtain a dimensionless form of the system (4)–(7), we introduce the characteristic length of the core\(L\), characteristic pressure drop \(\Delta P\), and linear velocity \(U^{0}=k^{0}k_\mathrm{rwor} \Delta P/(\mu _w L)\), corresponding to the velocity of one phase flow of water through the porous matrix. We define the dimensionless variables as follows:

$$\begin{aligned} X&= x/L, \end{aligned}$$
(30)
$$\begin{aligned} {\phi }'&= \phi /\phi ^{0}, \end{aligned}$$
(31)
$$\begin{aligned} {p}'&= p/\Delta P, \end{aligned}$$
(32)
$$\begin{aligned} u&= U/U^{0}, \end{aligned}$$
(33)
$$\begin{aligned} T&= \frac{U^{0}}{L\phi }t. \end{aligned}$$
(34)
$$\begin{aligned} k^{\prime }&= k/k^{0} \end{aligned}$$
(35)
$$\begin{aligned} {\rho }'_\alpha&= \rho _\alpha /\rho _\alpha ^0 \end{aligned}$$
(36)
$$\begin{aligned} {c}'_i&= c_i /c_i^\mathrm{ref} \end{aligned}$$
(37)
$$\begin{aligned} {\mu }'_\alpha&= \mu _\alpha /\mu _w \end{aligned}$$
(38)
$$\begin{aligned} {C}'_m&= C_m /C_m^0 \end{aligned}$$
(39)

The reference values for the molality of aqueous components are usually taken to be 1 mol/kg(\(\hbox {H}_{2}\hbox {O}\)) which is approximately the same as \(c^\mathrm{ref} =\) 1 mol/l which we use for all the \(c_i^\mathrm{ref} \) values in our case.

The reaction rate is calculated according to Eq. (3). We define the reference rate as follows:

$$\begin{aligned} \dot{r}_m^\mathrm{ref} =\hat{{A}}_m^0 \tilde{k}_m^+. \end{aligned}$$
(40)

Thus, the dimensionless rate is calculated as

$$\begin{aligned} {r}'_m =r_m /r_m^\mathrm{ref} =\left( {\prod \limits _{i=1}^{n_\mathrm{aq} } {({c}'_i )^{|(\nu _{im} |-\nu _{im} )/2}} -\frac{\tilde{k}_m^- }{\tilde{k}_m^+ }\prod \limits _{i=1}^{n_\mathrm{aq} } {({c}'_i )^{(\nu _{im} +|\nu _{im} |)/2}} } \right) . \end{aligned}$$
(41)

The dimensionless time \(T\) is measured in multiples of pore volumes injected, determined with regard to the initial pore volume (IPVI) (recalling that pore volume may change with dissolution/precipitation).

The control parameters for the problem are the Damköhler numbers for each mineral reaction defined as

$$\begin{aligned} \beta _m =\frac{Lk_m M_m \hat{{A}}_m^0 }{\rho _w^0 U^{0}}. \end{aligned}$$
(42)

There are some differences in the literature on the way one define the Damköhler (e.g. Aharonov et al. 1997). However, the introduce value has a similar physical meaning: it compares the characteristic times of the convective flow and of the chemical equilibration. This ratio is useful to determine whether the advection rates or reaction rates determine the distribution of aqueous components in the system. For very small Damköhler numbers \(\beta \ll 1\), advection occurs much faster than reaction, and thus, the distribution of components is very similar with the distribution of inert tracer in water. At very high Damköhler numbers \(\beta \gg 1\) the reaction in almost instantaneous, the equilibrium concentrations are achieved before the flux redistributes the components. The intermediate values of Damköhler number are of particular interest as they represent the real system behavior. Note also that for intermediate values of \(\beta \), the reaction terms in the right- hand side of the material balance equation for water cannot be neglected.

The resulting dimensionless system of equations to be solved assumes the form:

$$\begin{aligned}&\displaystyle d_T {C}'_m =-\beta _m \times \frac{\rho _w^0 \phi ^{0}}{M_m C_m^0 }{C}'_m {r}'_m ,\quad m=m_1 ,\ldots ,m_M \end{aligned}$$
(43)
$$\begin{aligned}&\displaystyle \partial _T \left( {{\phi }'s{c}'_i } \right) +\partial _X \left( {{c}'_i Fu} \right) =\sum \limits _{m=m_1 }^{m_m } {\beta _m \times \nu _{im} \frac{\rho _w^0 }{c_i^\mathrm{ref} M_m }{C}'_m {r}'_m } ,\quad i=1,\ldots ,n_\mathrm{aq} \end{aligned}$$
(44)
$$\begin{aligned}&\displaystyle \partial _T \left( {{\phi }'s{\rho }'_w } \right) +\partial _X \left( {{\rho }'_w Fu} \right) =\sum \limits _{m=m_1 }^{m_m } {\beta _m \times {C}'_m {r}'_m } \end{aligned}$$
(45)
$$\begin{aligned}&\displaystyle \partial _T \left( {\phi (1-s){\rho }'_o } \right) +\partial _X \left( {{\rho }'_o (1-F)u} \right) =0 \end{aligned}$$
(46)
$$\begin{aligned}&\displaystyle u=-{k}'\sum \limits _{\alpha =w,o} {\frac{k_{r\alpha } }{{\mu }'_\alpha }\times } \partial _X {p}'. \end{aligned}$$
(47)

The initial and boundary conditions for the problem (43)–(47) are obtained directly applying transformation (30)–(39):

  • Initial conditions:

    $$\begin{aligned} \begin{aligned}&{{p}'(0,X)=P_\mathrm{init} (LX)/\Delta P,} \quad {{C}'_m (0,X)=1,\quad m=m_1 ,\ldots ,m_M ,} \\&{s(0,X)=s_\mathrm{wi} ,} \quad {c}'_i (0,X)=c_i^{FW} /c^\mathrm{ref} ,\quad i=1,\ldots ,n_\mathrm{aq} . \end{aligned} \end{aligned}$$
    (48)

  • Boundary conditions:

    $$\begin{aligned} \begin{aligned}&{u(T,0)=1,\quad } {F(T,0)=1,\quad } {p{\prime }(T,1)=P^{0}/\Delta P,}\\&{c}'_i (T,0)=c_i^{INJ} /c^\mathrm{ref} ,\quad i=1,\ldots ,n_\mathrm{aq} . \end{aligned} \end{aligned}$$
    (49)

3 Description of the Numerical Model

3.1 Spatial Discretization

The governing system of Eqs. (43)–(46) is based on the conservation laws. Hence, it is convenient to choose the finite volume method (FVM) for its spatial discretization. The physical domain \(\Omega \) is represented by a collection of small control volumes \(\Omega _i \), so that the solution on an element is approximated by the cell average at its center. The flux term in FVMs is reduced to a surface integral by application of Gauss’ divergence theorem and thus evaluated at the boundaries of the elements. The flux between the two neighboring elements is calculated by the two-point flux approximation (TPFA), which is a low-order approximation but is sufficient for the problems studied on orthogonal grids.

3.2 Temporal Discretization

Initially, our approach was based on the usage of the fully explicit method (FEM). Masses of phases and components were updated at the first step, and the subsequent step was to calculate the pressure and saturation using the constraint that the sum of all phase volumetric fractions should be equal to one. However, this approach demanded an extremely small time step, in order to avoid large changes in pressure. We also tried several other ways of discretization, making the different variables or their combinations implicit. However, only the fully implicit scheme seems to really work and produce stable results. This method is computationally costly per unit step. However, due to better stability, it allows for significantly larger time stepping, making time integration more efficient. We believe that the conventionally used operator splitting method allowing to split the integration of the equations in two steps is not applicable because of the dependence of density on both pressure and component mass fractions.

In general a semi-discrete model representing (43)–(46) can be formulated as

$$\begin{aligned} \frac{\mathrm{d}\mathbf{m}(\mathbf{X})}{\mathrm{d}T}=\mathbf{f}(\mathbf{X},T), \end{aligned}$$
(50)

where \(\mathbf{X}=\{{p}'_k ,s_k ,{\bar{{C}}}'_k ,{\bar{{c}}}'_k \}\) and index \(k\) is used to denote \(k\)th finite volume element.

Rewriting discretized form of (50), one can obtain

$$\begin{aligned} \mathbf{g}(\mathbf{X}^{n+1})\equiv \mathbf{m}(\mathbf{X}^{n+1})-\mathbf{m}(\mathbf{X}^{n})-\Delta T\cdot \mathbf{f}(\mathbf{X}^{n+1},T)=0, \end{aligned}$$
(51)

which is an implicit problem formulation. The solution is obtained by application of the iterative Newton-Raphson method:

$$\begin{aligned} \mathbf{X}^{{n}'+1}=\mathbf{X}^{{n}'}-\mathbf{J}^{-1}\cdot \mathbf{g}(\mathbf{X}^{{n}'}), \end{aligned}$$
(52)

until condition for convergence \(|\mathbf{X}^{{n}'+1}-\mathbf{X}^{{n}'}| <\varepsilon _\mathrm{tol} \) is not fulfilled. It requires only a few steps to converge to a reasonable accuracy as we are provided with a good initial guess, which is a solution at the previous time step.

In the last equation, J is the Jacobian defined via

$$\begin{aligned} \mathbf{J}=\frac{\partial \mathbf{g}(\mathbf{X})}{\partial \mathbf{X}}. \end{aligned}$$
(53)

Calculation of the Jacobian J is performed numerically.

4 Simulation Results

The theory presented was used to establish a numerical simulation of waterflooding with mineral dissolution. In our simulation, we studied the dissolution of a single mineral component (\(M=1\)), and \(n_\mathrm{aq} =2\). The two aqueous components represent the active solute \(S\) in the water that was causing the dissolution, and a complex \(C\) which is a combined excess of dissolution reaction so that stoichiometry of the reaction can be represented by

$$\begin{aligned} X_M +X_S \rightleftarrows X_C. \end{aligned}$$
(54)

Thus, the matrix of stoichiometric coefficients for aqueous species is then given by

$$\begin{aligned} \varvec{\nu }=\left[ {{\begin{array}{cc} {-1;}&{} 1 \\ \end{array} }} \right] . \end{aligned}$$
(55)

The following data were used for particular simulations. For the relative permeability curves given by Eqs. (17) and (18), we use \(k_\mathrm{rwor} =0.8\), \(k_\mathrm{rowi} =0.5\), \(\mu _w =1 \hbox {cP}\), \(\mu _o =3 \hbox {cP}\), \(\alpha _w =2\), \(\alpha _o =1.5\), \(s_\mathrm{wi} =0.2\), and \(s_\mathrm{or}^0 =0.3\). The distance between inlet and outlet \(L\) = 100 m, characteristic linear velocity \(U^{0}\)= 10\(^{-6}\) m/s, permeability 100 mD, characteristic pressure drop \(\Delta P\) = 1 MPa, and the pressure at the effluent \(P^{0}\) = 0.1 MPa. Initial porosity \(\phi ^{0}=0.2\) with the maximum porosity \(\phi _{\max } =0.3\) calculated for \({C}'_M =0\), which correspond to the volumetric fraction of dissolvable mineral to be 12.5 % of the initial reservoir rock.

The simulations were performed with 300 finite volume cells. The number of time steps to inject one IPVI is 800. All the simulations were stopped at \(T=5 \hbox {IPVI}\). We tested our model for a number of control parameters: \(\beta =0.01,\;0.03,\;0.1,\;1.0,\;10.0\); \(\gamma =0,\;\pm 0.25,\;\pm 0.4\); \(\hat{{c}}_{P\alpha } =0.5\times 10^{-10},0.5\times 10^{-8}\).

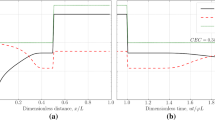
Rock dissolution affects mainly porosity, absolute permeability and, hence, pressure drop over the region of dissolution. Varying the Damköhler number \(\beta \), we were able to observe different scenarios of reservoir evolution. Porosity and permeability variation with time are presented in Fig. 1 for slow reactions and in Fig. 2 for fast reactions. The main difference between the two scenarios is that for slow reactions and low \(\beta \), the chemical equilibration length is larger than the system size, and thus the dissolution will span the whole system, Fig. 1. Meanwhile, for fast reactions and high \(\beta \), the reaction is localized in a narrow region of dissolution with formation of the dissolution front (Fig. 2). Qualitative behavior of porosity and permeability is very similar for the two cases; the main difference is in the magnitude of variation.

Fig. 1
figure 1

Evolution of reservoir properties under slow dissolution: a porosity and b permeability profiles at the injection times \(T\): 1 0.5 IPVI; 2 2.5 IPVI; 3 5 IPVI

Full size image
Fig. 2
figure 2

Evolution of reservoir properties under fast dissolution: a porosity and b permeability profiles at at the injection times \(T\): 1 0.5 IPVI; 2 2.5 IPVI; 3 5 IPVI

Full size image

The pressure distribution is visualized in Fig. 3. The pressure drop is visibly altered behind the dissolution front. No additional effects on pressure due to volumetric non-additivity of dissolution process were noticed. For a homogeneous reservoir at late time stages, the pressure distribution is almost linear. For slow reaction rates (depicted by dashed lines), the pressure distribution is represented by a convex smooth curve, in correspondence with gradually varying permeability of the rock. For fast reaction rates depicted by solid lines, pressure distribution is nearly piecewise-linear, corresponding to heterogeneity of reservoir permeability on the different sides of the dissolution front.

Fig. 3
figure 3

Evolution of pressure in case of fast (solid) and slow (dashed) reactions: pressure profiles at the injection times \(T\): 1 1 IPVI; 2 2.5 IPVI; 3 5 IPVI

Full size image

The behavior of porosity, permeability, and pressure for high reaction rates is shown in Figs. 2 and 3, may be interpreted as formation of wormholes close to the inlet. However, the indication of this process, based solely on porosity and permeability variation, is indirect. A more detailed study of wormhole formation would require three-dimensional simulations.

Dissolution also affects saturation profiles in the reservoir rock. The most noticeable effect is an increase in water saturation close to the inlet caused by the fact that dissolution provides additional porous space for the injected fluid. Fig. 4 illustrates that residual oil saturation \(s_\mathrm{or}\) changes during the dissolution. This, however, does not imply any increment in the recovery, as residual saturation is a volumetric factor which changes solely due to an increase in pore volume, while the overall volume and mass of the trapped oil remain the same.

Fig. 4
figure 4

Comparison of displacement profiles for fast (solid) and slow (dashed) reactions: saturation profiles at the injection times \(T\): 1 0.15 IPVI; 2 0.3 IPVI; 3 1 IPVI; 4 2.5 IPVI; 5 5 IPVI

Full size image

The displacement fronts propagate with slightly different rates in the cases of fast or slow dissolution. This effect is very small and occurs due to volumetric non-additivity (see Fig. 5). In the case of negative volumetric effect (\(\gamma <0)\), the combined volume of water + dissolved species is smaller than the combined volume of water + original mineral. Hence, dissolution creates additional volume for the brine to occupy and requires injecting more fluid in order to compensate for this additional volume. This results in a lower displacement front velocity. In the opposite case (\(\gamma >0)\), the velocity of the displacement front slightly increases.

Fig. 5
figure 5

Comparison of displacement profiles for cases with positive (solid) and negative (dashed) volumetric effects: saturation profiles at the injection times \(T\) : 1 0.15 IPVI; 2 0.3 IPVI; 3 1 IPVI; 4 2.5 IPVI; 5 5 IPVI

Full size image

Composition of the produced brine is shown in Fig. 6. At low values of \(\beta \), the active component in the brine penetrates rapidly the whole length of the sample, and for large \(\beta \), the active component is not able to penetrate far from the inlet until complete dissolution; from Fig. 6a, one can see that with increasing Damköhler number, we produce much less active solute at the effluent, and thus, almost everything we inject is consumed during the dissolution.

Fig. 6
figure 6

Composition of produced brine: a solute and b complex mass fractions for different Damkohler numbers \(\beta \): 0.01 (solid); 0.03 (dashed); 0.1 (dash-dotted)

Full size image

5 Conclusions

A numerical 1D model for two-phase multicomponent flows in porous media accounting for non-equilibrium dissolution and pressure-compositional compressibility of the fluids has been developed. Study of density disbalance in the course of rock dissolution indicates that the effect may be rather large (the disbalance ratio \(\gamma \) is negative and is down to \(-0.8\)). The governing continuum-scale equations are solved using a fully implicit scheme. The governing equations are strongly coupled and need to be solved simultaneously, which excludes a possibility for application of explicit or time-splitting methods. Only the fully implicit scheme is capable of solving such a system.

The results of numerical modeling provide qualitative description of the effect of mineral dissolution on waterflooding. Volumetric non-additivity affects the displacement process. The effect is that the displacement front velocity is slightly changed. We can see an increase in the front velocity in case of the positive volumetric effect (volume of mineral on dissolution increases) and decrease in the velocity for the negative volumetric effect. The change of mineral volume on dissolution does not affect the pressure in the system but affects the local pressure gradient. If the reaction rates are sufficiently high, the variation of permeability and porosity close to the injection point resembles wormhole formation. Stronger effects are expected to be observed in the multidimensional flows, which are a subject to a separate study.