1 Introduction

Progress over the last decade in miniaturization of various technological devices such as pumps, turbines, mixers and heat pipes, which are generally referred to as micro-flow devices, has led to the new discipline of microfluidics. Such micro-devices have revolutionized complex systems for medical diagnosis and surgery, chemical analysis, biotechnology and electronic cooling (Lee and Vafai 1999b; Vafai and Zhu 1999; Vafai and Khaled 2005; Khaled and Vafai 2011; Mirzaei and Dehghan 2013; Dehghan et al. 2015a; Mahmoudi 2015).

The flow regimes and modelling of flow in micro-systems are classified using the Knudsen number \((Kn = l / D_{h})\) defined as the ratio of the molecular mean-free-path \((l)\) to a characteristic macroscopic length scale, i.e., the hydraulic diameter \((D_{h})\). It allows having a measure of the validity of the continuum model. The Navier–Stokes equations assume the continuum flow work well with the no-slip conditions at \(Kn < 0.001\). The continuum assumption is still valid when \(0.001 < Kn < 0.1\), while a finite slip should be considered at the boundary of the flow domain (Hooman 2007, 2008a; Hooman and Ejlali 2010; Mirzaei and Dehghan 2013). The regime of flow with \(0.001 < Kn < 0.1\) is called slip flow regime. At higher Knudsen numbers, the Navier–stokes equation is not applicable and the kinetic theory must be applied (Dehghan and Basirat Tabrizi 2012, 2014). This article focuses on the slip flow regime in a channel filled with a porous material. Fluid flow in most of micro-devices can be regarded as a continuum flow between parallel plates. Hence, it makes good engineering sense to understand the hydrothermal behaviour of these micro-systems. Modelling of flow and transport phenomena in such micro-devices is different from the macro-scale systems mainly due to the inclusion of velocity slip and temperature jump in micro-systems (Tunc and Bayazitoglu 2002; Mirzaei and Dehghan 2013). In this limit, numerous studies were dedicated to investigate the important phenomena in micro-scale such as velocity slip, temperature jump and temperature-dependent properties of the fluid in the micro-channel heat sink (e.g., Hooman 2007, 2008a; Hooman and Ejlali 2010; Mirzaei and Dehghan 2013). Moreover, a simplified way of analysis of micro-channel heat sinks has been introduced by Koh and Colony (1986). They used the Darcy’s law of motion and an averaging procedure (based on the theory of porous media) to find the temperature field equation at the local thermal equilibrium (LTE) condition together with the no-jump condition. Kim and Kim (1999) and Kim (2004) used the Darcy-Brinkman model for the fluid motion in a porous medium and investigated the effects of channel height in micro-channel heat sinks based on the porous media approach. Deng et al. (2010) studied the conjugate heat transfer (conduction in the bottom-side of a micro-channel heat sink and the forced convection inside channels) by modifying the model proposed by Kim and Kim (1999). Thus, the conventional porous medium model for micro-channel heat sinks was extended to the substrate, and an analytical solution was derived for hydrodynamically and thermal fully developed flow in the micro-channel (Deng et al. 2010). The normalized temperatures obtained in their work were compared with those obtained from three-dimensional numerical simulation and the previous porous medium model. Deng et al. (2010) found that the discrepancy between the numerical simulation and the porous medium model increases with an increase in the channel height.

In parallel with the micro-channel heat sink development, it is now well demonstrated that using porous materials improves the heat transfer characteristics of such micro-devices (e.g., Hooman 2008b, 2009; Shokouhmand et al. 2010; Hashemi et al. 2011; Buonomo et al. 2014). However, filling a micro-channel with a porous material pushes the porous media theory into a new regime in which the velocity slip and temperature jump at the walls play a key role in the hydraulic and thermal performance of such micro-systems.

In principle, there are two methods of modelling heat transfer in the porous medium: LTE and local thermal non-equilibrium (LTNE) models (Lee and Vafai 1999a; Jiang et al. 1999; Yang and Vafai 2011a, b; Mahmoudi and Maerefat 2011; Imani et al. 2013; Mahmoudi and Karimi 2014). LTE assumes that no temperature difference exists between the two solid and fluid phases within the porous medium by using one-equation model for the balance of thermal energy and thus greatly facilitates the heat transfer analysis (Rashidi et al. 2014; Valipour et al. 2014; Bovand et al. 2015). However, in some real applications of porous media, temperature differences between the two phases are not negligible and thus the LTE model is not valid. In such cases, the local thermal non-equilibrium (LTNE) model based on the two-equation model for the fluid and solid phases is applicable. Under LTE condition, free convection heat transfer in micro-channel filled with a porous medium was investigated by Haddad et al. (2005) for the first time. Haddad et al. (2005) considered gaseous flow in a vertical open-ended parallel-plate micro-channel filled with porous media in the slip flow regime. It was found that the heat transfer rate decreases as the Knudsen number or Forchheimer number increases (Haddad et al. 2005). In another study, Haddad et al. (2006) investigated numerically the problem of forced convection inside a micro-channel. Haddad et al. (2006) found that the rate of heat transfer increases as the Darcy number increases and it decreases when the Knudsen number increases. In addition, they showed that compared with the other working parameters, the sensitivity of the Nusselt number to the Forchheimer number is not noticeable (Haddad et al. 2006). Haddad et al. (2007) extended their study in numerical modelling of thermal behaviour of flow in a micro-channel, by considering LTNE condition in the porous region. Their study showed that with the increase in Darcy number, the skin friction increases, whereas increasing the Forchheimer number or Knudsen number decreases the skin friction. Furthermore, they showed that the rate of heat transfer decreases as the Knudsen number, Forchheimer number or fluid to solid effective conductivity ratio increases (Haddad et al. 2007).

For the first time in the slip flow regime, Nield and Kuznetsov (2006) obtained an analytical solution for the forced convection flow in a parallel-plate channel and a circular duct occupied by a porous medium saturated with a rarefied gas. They extended their analysis for developing flows in the slip regime inside a channel filled with a porous material at constant wall heat flux boundary condition (Kuznetsov and Nield 2009). Fully developed forced convection in a rectangular micro-channel filled with or without a porous medium under LTE condition was investigated analytically by Hooman (2008a, 2009) in the range of \(10^{-3} < Kn < 10^{-1}\). Using the Brinkman flow model with the inclusion of slip velocity and the temperature jump, he obtained expressions for the local and average velocity and temperature profiles, the friction factor, the slip coefficient and the Nusselt number (Hooman 2008a).

Thermally developing forced convection in circular micro-channel and nano-channel filled with porous media was investigated numerically by Shokouhmand et al. (2010) using Darcy-Brinkman-Forchheimer flow model, slip boundary condition and LTE model between the solid and fluid phases at large Knudsen numbers. They considered variation in Kn number along the channel due to the pressure gradient and commented that such variation leads to considerable effects on the Nusselt and temperature distribution across the channel cross section. Hashemi et al. (2011) analytically studied the flow and heat transfer in a micro-annulus at the LTE condition in the presence of finite slip and jump conditions. They showed that the Nusselt number decreases as the Knudsen number and annulus aspect ratio (ratio of the inner radius to the outer radius) increase. Recently, Buonomo et al. (2014) investigated the forced convection heat transfer in micro-channels filled with porous media for rarefied gaseous slip flows between two parallel plates under LTNE condition. In their study for high Biot numbers, the difference between the Nusselt numbers obtained under LTNE condition with those of LTE condition was negligible.

In the above-mentioned studies, the effect of radiative heat transfer on the temperature field and Nusselt number in the porous medium has been assumed to be negligible. However, in a review by Viskanta (2009) it was pointed out that foam-like open-cellular porous materials like ceramics and metals are strongly attenuating and have a large radiation extinction coefficient. Viskanta (2009) also reported that the radiative heat transfer in such materials even of small thickness can be treated as an effective diffusion process. The diffusion-like modelling of radiation heat transfer was introduced by Rosseland in 1936 (Rosseland 1936; Siegel and Howell 1993). The Rosseland model is used in optically thick materials. In other words, this model is accompanied by errors in regions very close to the boundaries (Siegel and Howell 1993). Zhao et al. (2004, 2008) and Tseng et al. (2011) recently verified the applicability of the Rosseland model experimentally. Based on this model and in the macro-scale heat transfer where the no-slip velocity and no-jump temperature are valid, Nield and Kuznetsov (2010) investigated numerically the problem of the combined convective–radiative process in a channel occupied by a saturated cellular porous medium under LTE condition. They highlighted the role of radiative heat transfer in such porous–fluid system. Thus, as pointed out by Viskanta (2009), the radiative heat transfer in their study was treated as a diffusion process and the radiative conductivity was assumed to be a function of the temperature. Nield and Kuznetsov (2010) reported that the Nusselt number increases due to a variable conductivity arising from the radiative heat transfer. Andreozzi et al. (2012) showed effects of porosity and pore-scale diameter on the radiative conductivity of the Rosseland model. Leroy et al. (2013) studied a macroscopic model based on the thermal non-equilibrium condition, by coupling the radiation with the other heat transfer modes. They emphasized that their coupled upscaling procedure could be applied to different combinations of opaque, transparent or semi-transparent phases. Very recently, in macro-scale heat transfer, Mahmoudi (2014) numerically investigated the effects of thermal radiation from the solid phase on the temperature differential and the rate of heat transfer in a pipe partially filled with a porous material using discrete ordinate method to compute the radiative heat flux. Mahmoudi (2014) showed that the thermal radiation leads the system towards the LTE condition. In addition, he revealed that ignoring the effect of thermal radiation in the porous region leads to a substantial error in prediction of the solid and fluid temperature fields. Wang et al. (2014) studied two commonly used methods for irradiative transfer problems in porous media, namely P1 approximation and Rosseland approximation, and showed that these two models give almost the same results. Dehghan et al. (2015b) investigated semi-analytically (based on the homotopy perturbation method) and numerically (based on the finite difference method) the combined radiation–convection heat transfer inside a solar heat exchanger filled with metal foams. They discussed on the applicability of the semi-analytical method in such complicated nonlinear problems and presented the advantages and limitations of these methods. Dehghan et al. (2015c) analytically solved the problem of forced convection inside a channel filled with a porous medium with a linearly temperature-dependent thermal conductivity (arising from the variable property of the medium or moderate radiative heat transfer). They concluded a linear increase in the Nusselt number.

In high-temperature thermal systems, the convection and radiation modes of heat transfer are both important. The purpose for this technique is to use porous media to enhance combined convective–radiative transfer in order to save remarkable energy or to keep heat from releasing, from high temperature areas for combustion requirements in industrial furnaces, combustors and porous radiant burners. This is also the case for application in macro-systems as well as in micro-systems, whenever the medium is under the influence of radiation heat transfer or works at a high temperature, for example in micro-reactors, micro-nuclear engines, micro-combustors, and micro-heat-pipes (Lin and Pisano 1991; Badran et al. 1993; Duncan and Peterson 1994; Tso and Mahulikar 2000; Kockmann 2008; Rad and Aghanajafi 2009). Although the effect of thermal radiation on the hydrothermal characteristics of porous–fluid systems in macro-scales has been studied, no study so far has considered the combined problem of convection-condition-radiation in micro-channels filled with a porous material, and the present work aims at filling this gap. To fulfil this objective, the effects of velocity slip and temperature jump on the overall thermal behaviour of the porous medium are investigated in a fluid-saturated cellular porous medium. The problem is relevant to cellular porous materials (foams) formed from plastics, ceramics and metals, which are characterized by high porosity and large radiation extinction coefficient. It is worthwhile to mention that for rarefied gaseous flow like air at the low vacuum condition (1–30 kPa), the mean-free-path ranges from \(10^{-7}\) to \(10^{-4}\hbox { m}\) (Jennings 1988; Harley et al. 1995). Consequently, the Knudsen number for such flows in conventional macro-channels falls within the range of 0.001–0.1, and therefore, the slip flow regime applies. Thus, the result of the present work can be applied to both the gaseous flow inside the micro-scale channels and the rarefied gaseous flow inside the conventional macro-channels.

2 Mathematical Modelling

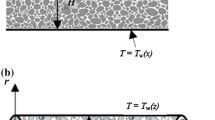
The problem is formulated as a combined conductive–convective–radiative problem. The solution procedure is built upon the recent work of Nield and Kuznetsov (2010), while in micro-channel, that includes the effects of velocity slip and temperature jump. A schematic diagram of the physical model is shown in Fig. 1. The dimension of the channel in the normal direction to the plane of view is large enough to ensure the two dimensionality of the problem. The height of the channel is \(2H\). The channel walls are subjected to a constant heat flux \(q_w^{\prime \prime }\). The viscous heat generation is ignored, and there is no internal heat production. Radiative heat transfer is considered in the porous medium and is modelled by a diffusion process (Zhao et al. 2008; Viskanta 2009; Nield and Kuznetsov 2010; Dehghan et al. 2015b). Therefore, the combined conduction–radiation heat transfer in the porous material is treated as an effective conduction process. Radiative conductivity is assumed to be temperature dependent, while other thermo-physical properties of the porous material and the fluid phase are assumed to be constant. The porosity of the porous medium is considered to be uniform and constant. A steady, laminar and incompressible flow is considered, and the flow is assumed to be hydrodynamically and thermally fully developed.

Fig. 1
figure 1

Schematic diagram of the problem

Full size image

According to the above-mentioned assumptions and knowing that for a fully developed flow the velocity is \(u^{*}(y^{*})\), the momentum equation in the porous medium is modelled using Darcy-Brinkman equation as following (Nield and Bejan 2006; Dehghan et al. 2014b; Mahmoudi et al. 2014):

$$\begin{aligned} \mu _{\hbox {eff}} \frac{d^{2}u^{*}}{\hbox {dy}^{*2}}-\frac{\mu }{K}u^*+G=0, \end{aligned}$$
(1)

where variables with asterisk \(({}^{*})\) denote dimensional variables. \(y^{*}\) is the perpendicular axis to the flow direction. \(u^{*}\) is the fluid velocity, \(\rho \) is the fluid density and \(\mu \) is the fluid viscosity. \(G\) is the negative of the applied pressure gradient in the flow direction \((x^{*})\). Permeability of the medium is denoted by \(K\), and \(\mu _{\hbox {eff}}\) is the effective viscosity of the porous medium equal to \(\mu /\phi \), where \(\phi \) is the porosity of the porous medium (Alazmi and Vafai 2002). The Forchheimer term in the momentum equation has been neglected, since it has minor effects on the normalized velocity and on the thermal field as well (Nield and Bejan 2006; Dehghan et al. 2014a, b). Dehghan et al. (2014a, b) using a perturbation analysis showed that the normalized velocity is independent of the Forchheimer effect by the order of , where \(s\) denotes the porous medium shape parameter given by Eq. (8). The porous medium shape parameter has a high value in practical porous media (Dehghan et al. 2014a, b). \(s\sim 1\) represents semi-clear fluid flows (highly rarefied porous media) while \(s\rightarrow \infty \, (s>O(10^{2}))\) denotes the Darcy regime.

For energy equation, it is assumed that the LTE holds between the solid and fluid phases in the porous medium (Mohammad 2003; Nield and Kuznetsov 2006; Nield and Kuznetsov 2009). Also, Mahmoudi (2014) showed that thermal radiation leads the temperature field in the porous region towards the LTE condition. For mini-porous media, Jiang et al. (2006) experimentally verified that the interfacial convective heat transfer coefficient between the solid and fluid phases is high. Furthermore, the specific area (area per volume) increases by decreasing the mean diameter of elements (Nield and Bejan 2006; Yang and Vafai 2010, 2011a, b; Ouyang et al. 2013; Dehghan et al. 2014a, b). Dehghan et al. (2014a, b) showed that the temperature difference between the fluid and solid phases is inversely proportional to the product of the interfacial convective heat transfer coefficient and the specific area. Consequently, the temperature difference between the fluid and solid phases for a microporous medium is small and hence the LTE model holds. Recently, Buonomo et al. (2014) concluded that at high Biot numbers, which translate to strong convective heat exchange between the solid and fluid phases, the LTE condition holds between the two phases. Interestingly, in their study, it was found that the non-dimensionalized temperature difference between the solid and fluid phases is not a function of the temperature jump coefficient. However, in their study, the temperature jump and velocity slip coefficients were considered on the wall surfaces and not on the porous matrix. Their work was based on the assumption that the volumetric heat transfer coefficient, \(h_{sf}\), is constant and independent of the local velocity, velocity slip and temperature jump at the solid–fluid interface. That is why in their results, changing the temperature jump coefficient had no noticeable effect on the temperature difference of the two phases. As a result, it is still possible that velocity slip and temperature jump have a large effect on \(h_{sf}\) and the solid–fluid temperature difference in a micro-porous medium with a large Kn. Thus, it is expected that the interphase convection heat transfer coefficient decreases in the slip flow regime because of the temperature jump phenomenon occurring at the interface of solid and fluid of the porous medium. Consequently, the Biot number in the slip flow regime is lower than its analogue in the no-slip regime. The influence of the Knudsen number on the inter-phase heat transfer between the fluid and solid phases was discussed in a discussion between Al-Nimr and Haddad (2007) and Nield and Kuznetsov (2007). Al-Nimr and Haddad (2007) argued since the Knudsen number based on the permeability of the medium is considerable, the convective inter-phase heat transfer coefficient is smaller than the one of the no-slip regime. Consequently, the LTNE model is more appropriate for the flow in micro-channels. In the present work, we try to study the hydrothermal behaviour of a microporous medium with the inclusion of thermal radiation. Thus, for simplicity based on the assumption of Kuznetsov and Nield (2009), effects of the inter-phase heat transfer on the overall thermal behaviour of the porous material are ignored in this work. The present study is a pioneering study investigating the overall thermal behaviour of a porous material under the influence of the radiation heat transfer in the slip flow regime. To summarize, the one-equation model is used for the energy balance of the porous medium similar to the study of Nield and Kuznetsov (2006), Kuznetsov and Nield (2009), and Nield and Kuznetsov (2010):

$$\begin{aligned} \rho c_p u^{*}\frac{\partial T}{\partial x^{*}}=\frac{\partial }{\partial y^{*}}\left( {k\frac{\partial T}{\partial y^{*}}} \right) . \end{aligned}$$
(2)

In the present work, the radiative heat transfer is modelled as a diffusion process using an effective conductivity introduced by Eq. (8) (Viskanta 2009; Nield and Kuznetsov 2010). This effective conductivity enters the energy equation in both axial and transverse directions. However, as pointed out by Bejan (2004) in a conduction–convection problem, the axial conduction can be neglected compared to the transverse one when the order of Peclet number is higher than 1, i.e., \(O\)(Pe) \(> 1\). Since for air it holds that \(O\)(Pr) \(\sim 1\), consequently the Reynolds number based on the hydraulic diameter of the channel should be an order greater than unity (\(O\)(Re) \(> 10\)) to surely ignore the axial conduction. \(T\) is temperature, \(c_{p}\) is the specific heat of the fluid phase and \(k\) is the effective thermal conductivity of the porous material given by (Nield and Bejan 2006):

$$\begin{aligned} k=\varphi k_f +\left( {1-\varphi } \right) k_s, \end{aligned}$$
(3)

where \(k_{s}\) and \(k_{f}\) are the conductivity of the solid and fluid phases of the porous medium, respectively.

Due to the symmetry of the problem, only the upper half of the channel is considered. Thus, at \(y^{*} = 0\) the symmetry boundary condition is imposed which assumes that the gradients of the axial velocity and temperature in \(y^{*}\) direction are zero,

$$\begin{aligned} \begin{array}{l} \frac{{\begin{array}{l} \hbox {d}u^{*} \\ \end{array}}}{\hbox {d}y^{*}}=0, \\ {\frac{\hbox {d}T}{\hbox {d}y^{*}}=0.} \\ \end{array} \quad \hbox { at }y^{*} = 0 \end{aligned}$$
(4a)

Velocity slip and temperature jump conditions are imposed at the channel wall \((y^{*} = H)\) reads (White 2006; Nield and Kuznetsov 2006; Nield and Kuznetsov 2009):

$$\begin{aligned} u= & {} -\alpha ^{*}\frac{\hbox {d}u^{*}}{\hbox {d}y^{*}} \quad \hbox { at }y^{*}\,=H,\end{aligned}$$
(4b)
$$\begin{aligned} T-T_w= & {} -\beta ^{*}\frac{\hbox {d}T}{\hbox {d}y^{*}} \quad \hbox { at }y^{*}\,=H. \end{aligned}$$
(4c)

In Eqs. (4b and 4c), \(\alpha ^{*}\) and \(\beta ^{*}\) are the velocity slip and temperature jump coefficients, respectively, as follows (Harley et al. 1995; White 2006):

$$\begin{aligned} \alpha ^{*}= & {} \left( {\frac{2}{F}-1} \right) l,\end{aligned}$$
(5a)
$$\begin{aligned} \beta ^{*}= & {} \left( {\frac{2}{F_T }-1} \right) \left( {\frac{2\gamma }{\gamma +1}\frac{kl}{\mu c_p }} \right) _f, \end{aligned}$$
(5b)

where \(F\) is the momentum accommodation coefficient, \(F_{T}\) is the thermal accommodation coefficient and \(\gamma \) is the specific-heat ratio of the working fluid. The momentum accommodation coefficient shows the ratio of the diffuse collisions to the perfect (specular) collisions at the wall. In other words, it represents the tangential momentum loss on the wall and has a value between 0 and 1. The thermal momentum accommodation has been proposed based on a similar approach to the momentum accommodation coefficient and almost is equal to unity (Harley et al. 1995; White 2006).

The radiative heat transfer is treated as a diffusion process by introducing the radiative conductivity in cellular porous materials and metal foams (Zhao et al. 2008; Viskanta 2009; Nield and Kuznetsov 2010). The radiative conductivity varying with the temperature can be analytically predicted based on the characteristics of porous media or can be experimentally measured (Zhao et al. 2008). The total heat flux can be written in the following form:

$$\begin{aligned} q_w^{\prime \prime } =-\left( {k_c +k_r } \right) \frac{\partial T}{\partial y^{*}}=-k\frac{\partial T}{\partial y^{*}}, \end{aligned}$$
(6)

where \(k_c,\, k_r\) and \(k\) are the conductive (molecular), radiative and effective conductivities, respectively. The radiative conductivity \(k_{r}\) and the effective conductivity are approximated by (Nield and Kuznetsov 2010):

$$\begin{aligned} k_r= & {} \frac{16\sigma T^{3}}{3\beta _{R}},\end{aligned}$$
(7a)
$$\begin{aligned} k= & {} k_c +\frac{16\sigma T^{3}}{3\beta _{R}}, \end{aligned}$$
(7b)

where, \(\beta _R\) is the Rosseland mean extinction coefficient and \(\sigma \) is the Stefan-Boltzmann constant. To reduce the number of variables included in the formulated problem, a normalization process is introduced. We define the following dimensionless variables to non-dimensionalize the governing equations and boundary conditions (Dehghan et al. 2014b):

$$\begin{aligned} y= & {} \frac{y^{*}}{H},\quad u=\frac{\mu u^{*}}{GH^{2}}, \quad M=\frac{\mu _{\hbox {eff}} }{\mu },\quad Da=\frac{K}{H^{2}},\quad \alpha =\frac{\alpha ^{*}}{H}=\left( {\frac{2}{F}-1} \right) Kn,\end{aligned}$$
(8a)
$$\begin{aligned} s= & {} \frac{1}{\sqrt{DaM}}=\sqrt{\frac{\varphi }{Da}}, \end{aligned}$$
(8b)

where \(M\) is the viscosity ratio, \(s\) is the porous medium shape parameter, \(\alpha \) is the dimensionless slip coefficient and Da is the Darcy number. Dimensionless forms of the momentum equation (Eq. 1) and the corresponding boundary conditions are:

$$\begin{aligned} \frac{d^{2}u}{\hbox {d}y^{2}}-s^{2}u+\frac{1}{M}=0, \end{aligned}$$
(9)
$$\begin{aligned} \frac{du}{\hbox {d}y}= & {} 0 \quad \hbox { at }y= 0,\end{aligned}$$
(10a)
$$\begin{aligned} u= & {} -\alpha \frac{du}{\hbox {d}y} \quad \hbox { at } y= 1. \end{aligned}$$
(10b)

In the above equations, \(y\) is the dimensionless axis perpendicular to the flow direction and \(u\) is the dimensionless velocity. Using boundary conditions (10a) and (10b) and solving the ordinary differential Eq. (10a) and (10b), the velocity in the fully developed region is obtained (Nield and Kuznetsov 2006):

$$\begin{aligned} u=Da\left( {1-\frac{\cosh (sy)}{[1+\alpha s\tanh (s)]\cosh (s)}} \right) . \end{aligned}$$
(11)

The energy Eq. (2) is non-dimensionalized using the following definitions (Dehghan et al. 2014b):

$$\begin{aligned} \theta= & {} \frac{T-T_w }{T_m -T_w },\end{aligned}$$
(12)
$$\begin{aligned} T_m= & {} \frac{1}{Hu_m }\int _0^H {u^{*}T\hbox {d}y^{*}}, \end{aligned}$$
(13)

where \(\theta \) and \(T_{m}\) are the dimensionless temperature and the bulk mean temperature, respectively. Writing the first law of thermodynamics over a differential control volume containing the channel leads to (Dehghan et al. 2014b, 2015b):

$$\begin{aligned} \frac{\partial T}{\partial x^{*}}=\frac{q_w^{\prime \prime } }{\rho c_p u^{*}_m H}, \end{aligned}$$
(14)

where \(u^{*}_m \) is the mean velocity given by:

$$\begin{aligned} u^{*}_m =\frac{1}{H}\int _0^H {u^{*}\hbox {d}y^{*}}. \end{aligned}$$
(15)

Substituting Eq. (14) into Eq. (2) gives:

(16)

where is the normalized velocity written as:

(17)

For \(\alpha = 0\) (in the case of \(Kn = 0\)), Eq. (21) simplifies to

(18)

which is the velocity profile for the Brinkman model in the no-slip flow regime. Similar to Buonomo et al. (2014), by combining Eqs. (8), (11) and (17), and knowing that \(f_K =G\sqrt{K}/(\rho u_m^{*2} )\), it can be shown:

$$\begin{aligned} f_K =\frac{1}{\hbox {Re}_K }\frac{1}{1-\frac{\tanh (s)}{s[1+\alpha s\tanh (s)]}}, \end{aligned}$$
(19)

where \(f_K \) is the friction factor and \(\hbox {Re}_K =\rho u^{*}\sqrt{K}/\mu \) is the modified Reynolds number based on the permeability of the porous medium.

To write the effective conductivity Eq. (7b) in a dimensionless form, it is convenient to take the wall temperature \(T_{w}\) as a reference temperature and expand the temperature \((T)\) about this value as following (Nield and Kuznetsov 2010):

$$\begin{aligned}&\displaystyle T^3 =T_w^3 +3T_w^2 \left( {T-T_w} \right) +3T_w \left( {T-T_w} \right) ^{2}+\left( {T-T_w} \right) ^{3},\end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle k = k_0 \left[ {1+\left( {3\lambda T_r } \right) \theta +\left( {3\lambda T_r^{2}} \right) \theta ^{2}+\left( {\lambda T_r^{3}} \right) \theta ^{3}} \right] ,\end{aligned}$$
(21)
$$\begin{aligned}&\displaystyle \lambda = \frac{1}{1+\left( {{3\beta _R k_c }/{16\sigma T_w^3 }} \right) },\quad T_r =\frac{T_m -T_w }{T_w },\quad k_0 =k_c +\frac{16\sigma T_w^3 }{3\beta _R }, \end{aligned}$$
(22)

where \(T_{r}\) is referred as the temperature variation parameter and \(\lambda \) is the radiation parameter ranges from 0.5 to 1 (Nield and Kuznetsov 2010). Combining Eqs. (8a), (12), (16) and (21), and knowing that \(Nu=\frac{q_w{\prime \prime } \left( {4H} \right) }{k_0 \left( {T_w -T_m } \right) }\) and \(\beta =\frac{\beta ^{*}}{H}\) result in:

(23)
$$\begin{aligned} \left. {\frac{d\theta }{\hbox {d}y}} \right| _{y=0} =0,\quad \theta \left( 1 \right) =-\beta \left. {\frac{d\theta }{\hbox {d}y}} \right| _{y=1}, \end{aligned}$$
(24)

where Nu is the Nusselt number based on the hydraulic diameter of the channel and \(\beta \) is the dimensionless jump coefficient. Eq. (23) has two unknowns, Nu and \(\theta \). In order to find them, an additional equation is required. This equation is found based on the given definitions of dimensionless temperature (12), the bulk mean temperature (13) and the normalized velocity (17) as follows:

(25)

In order to obtain the Nusselt number, we need to solve Eq. (23) along with the boundary conditions (24) and the compatibility equation (25). Eq. (23) is a differential equation classified as a highly nonlinear equation of the third order that cannot be solved analytically and needs to be solved numerically.

3 Numerical Simulation

To find the Nusselt number, an explicit finite difference scheme with the second order of precision (Dehghan and Basirat Tabrizi 2012; Dehghan et al. 2013; Dehghan and Basirat Tabrizi 2014; Dehghan et al. 2014a, 2015b) has been used to solve Eq. (23). A non-uniform structured grid has been adopted (Mahmoudi and Karimi 2014; Dehghan et al. 2014a, 2015b; Rashidi et al. 2015).

According to Fig. 2, the first and second orders of differentiation have been discretized as following (Dehghan and Basirat Tabrizi 2012, 2014):

$$\begin{aligned}&\displaystyle \left( {\frac{d\theta }{\hbox {d}y}} \right) _i =\frac{\theta _{i+1} +\left( {ddy^{2}-1} \right) \theta _i -ddy^{2}\times \theta _{i-1} }{\left( {ddy+1} \right) \Delta y_i }+O\left( {\Delta y_i^2 } \right) ,\end{aligned}$$
(26)
$$\begin{aligned}&\displaystyle \frac{d}{\hbox {d}y}\left( {\nu \frac{d\theta }{\hbox {d}y}} \right) _i =\frac{\left( {\frac{\nu _i +\nu _{i+1} }{2}} \right) \left( {\frac{\theta _{i+1} -\theta _i }{\Delta y_i }} \right) +\left( {\frac{\nu _i +\nu _{i-1} }{2}} \right) \left( {\frac{\theta _i -\theta _{i-1} }{\Delta y_{i-1} }} \right) }{0.5\left( {\Delta y_i +\Delta y_{i-1} } \right) }+O\left( {\Delta y_i^2 } \right) \nonumber \\&\displaystyle =\frac{\left( {\nu _i +\nu _{i+1} } \right) \left( {\frac{\theta _{i+1} -\theta _i }{\Delta y_i }} \right) +\left( {\nu _i +\nu _{i-1} } \right) \left( {\frac{\theta _i -\theta _{i-1} }{\Delta y_{i-1} }} \right) }{\left( {\Delta y_i +\Delta y_{i-1} } \right) }+O\left( {\Delta y_i^2 } \right) . \end{aligned}$$
(27)

\(ddy\) is the expansion factor of the grid step-size, \(\nu \) is an arbitrary dependent parameter and \(\Delta y_i \) is the step-size of the \(i^{\mathrm{th}}\) node:

$$\begin{aligned} \Delta y_i= & {} y_{i+1} -y_i, \end{aligned}$$
(28a)
$$\begin{aligned} ddy= & {} \frac{\Delta y_i }{\Delta y_{i-1} }. \end{aligned}$$
(28b)
Fig. 2
figure 2

Schematic diagram of the computational domain

Full size image

To achieve higher accuracy and stability in the numerical simulation, the under-relaxation technique has been adopted (Dehghan et al. 2014a). For stable cases (i.e., small values of \(\lambda \)), an over-relaxation has been applied to decrease the time of convergence. The nonlinear terms have been linearized as following (Hooman 2008c; Dehghan et al. 2014a, 2015b):

$$\begin{aligned} \left( {\theta _i^n } \right) ^{2}=\theta _i^{n-1} \theta _i^n, \end{aligned}$$
(29)

where \(i\) shows steps in \(y\)-direction and \(n\) shows the number of iterations. The half of the channel has been assumed as the numerical simulation domain with 201 grid-points and a grid step-size decrease factor (ddy) of 0.99. Since the domain is dimensionless and normalized, the computational domain is \(y\in [0,1]\). The maximum difference between the Nusselt numbers obtained for 401 grid-points and those of 201 grid-points is below \(10^{-4}\). Thus, the results presented here are obtained using 201 grid-points.

In order to find the Nusselt number, at first a value for the Nusselt number is guessed. Then, Eq. (23), along with the boundary conditions (24) by incorporating the normalized velocity distribution Eq. (17), is solved to find the dimensionless temperature \((\theta )\). The maximum dimensionless temperature difference between the two successive iterations below \(10^{-7}\) has been adopted for the convergence criterion. After convergence and finding the dimensionless temperature, the compatibility condition (25) is used to correct the dimensionless temperature found. Then, the Nusselt number is obtained based on the new dimensionless temperature according to the Nusselt number definition:

$$\begin{aligned} Nu_{new} =\frac{q_w^{\prime \prime } \left( {4H} \right) }{k_0 \left( {T_w -T_m } \right) }=-4\left. {\frac{d\theta _{new} }{\hbox {d}y}} \right| _{y=1}. \end{aligned}$$
(30)

This value of the Nusselt number is put into Eq. (23), and the process continues until the difference between two successive Nusselt numbers is below \(10^{-7}\).

4 Results and Discussion

In this section, effects of temperature variation parameter (\(T_{r})\), radiation parameter \((\lambda )\), velocity slip coefficient \((\alpha )\), and temperature jump coefficient \((\beta )\) for different porous medium shape parameters \((s)\) on the Nusselt number are presented. Furthermore, effects of working parameters on the dimensionless temperature are discussed at the end of this section. The porous medium shape parameter \((s)\) represents the characteristics of the porous medium structure and incorporates both the Darcy number and the porosity of the medium (see Eq. 8b). To find a criterion showing the importance of radiation heat transfer, one can write based on Eq. (7b):

$$\begin{aligned} k=k_m \left( 1+\frac{16\sigma T^3 }{3\beta _R k_m }\right) \end{aligned}$$
(31)

If the order of magnitude of the term “\(16\sigma T^3 /3\beta _R k_m\)” is not negligible \((O(16\sigma T^3 /3\beta _R k_m )>10^{-1})\), the radiation heat transfer cannot be ignored. For example, \(16\sigma T^3 /3\beta _R k_m =1.35\) at the temperature of 1000 K for a ceramic foam called 7.5 % 65 PPI (pores per inch) SiC foam in the study of Tseng et al. (2011) with \(k_{m} = 1.317\) (W/mK) and \(\beta _{R} = 170\) (1/m). The results of this study are presented for three different \(s\) values: \(s = 1\) (semi-clear fluid), \(s = 100\) (semi-Darcian flow) and \(s = 10\) (the intermediate value). The different cases considered here based on the varying working parameters are shown in Table 1.

Table 1 Different cases considered to investigate the effect of velocity slip and temperature jump
Full size table

4.1 Validation

For the validation purpose, the numerical Nusselt numbers obtained in the absence of radiative heat transfer are compared to those of the analytical results of Nield and Kuznetsov (2010) for a hyper-porous medium saturated with a rarefied gas in the slip flow regime. A comparison with the two asymptotic cases is shown in Fig. 3. It shows an excellent agreement between the numerical results and the analytical solution in the two limiting cases (\(s = 1\) and \(s = 100\)). It should be noted that the Nusselt numbers obtained by Nield and Kuznetsov (2006, 2010) are based on the channel height \((2H)\), whereas in the present study, the channel hydraulic diameter \((4H)\) has been adopted in the definition of Nusselt number. Thus, the Nusselt numbers obtained by Nield and Kuznetsov (2006, 2010) are half of those obtained in the present study.

Fig. 3
figure 3

Comparison of the present fully developed Nusselt number versus temperature jump coefficient \(\beta \) with different velocity slip coefficients \(\alpha \) in the absence of radiative heat transfer, with the analytical solution of Nield and Kuznetsov (2006) (case 0); a \(s = 1\) and b \(s = 100\)

Full size image

4.2 Effect of Velocity Slip and Temperature Jump

In this part, the case of combined conduction–convection–radiation in the presence of finite velocity slip and temperature jump is investigated. For further validation, the results of Nield and Kuznetsov (2010) for the case of combined convection–conduction–radiation in the no-slip regime \((\alpha = \beta = 0)\) are also shown in Figs. 4, 5, 6, 7.

Fig. 4
figure 4

Effects of velocity slip and temperature jump on the Nusselt number in the presence of radiation for case 1 (\(T_{r} = -0.5\) and \(\lambda = 0.5\)); a \(s = 1\), b \(s = 10\), and c \(s = 100\)

Full size image
Fig. 5
figure 5

Effects of velocity slip and temperature jump on the Nusselt number in the presence of radiation for case 2 \((T_{r} = 0.5\) and \(\lambda = 0.5\)); a \(s = 1\), b \(s= 10\), and c \(s= 100\)

Full size image
Fig. 6
figure 6

Effects of velocity slip and temperature jump on the Nusselt number in the presence of radiation for case 3 \((T_{r} = -0.5\) and \(\lambda = 1)\); a \(s = 1\), b \(s = 10\), and c \(s = 100\)

Full size image
Fig. 7
figure 7

Effects of velocity slip and temperature jump on the Nusselt number in the presence of radiation for case 4 (\(T_{r} = 0.5\) and \(\lambda = 1\)); a \(s = 1\), b \(s= 10\), and c \(s = 100\)

Full size image

Figure 4 represents the effect of velocity slip coefficient \((\alpha )\) and temperature jump coefficient \((\beta )\) on the Nusselt number obtained for case 1 \((T_{r} = -0.5\) and \(\lambda = 0.5)\) and different porous medium shape parameters \((s)\). The figure shows that for all \(s\) considered here, the results obtained in the present work for \(\alpha = \beta = 0\) are in good agreement with those of Nield and Kuznetsov (2010). Furthermore, Fig. 4 shows that as \(\alpha \) is fixed, the Nusselt number increases with increased \(\beta \) for all porous medium shape parameters, since the temperature jump acts as a thermal resistance and impedes the heat transfer from the wall into the porous medium. Figure 4a shows that for low \(\beta \), the value of the Nusselt number increases as \(\alpha \) increases, since an increase in the velocity slip leads to a more uniform velocity profile over the flow cross section. Accordingly, the fluid parcels move faster in near-wall regions, and hence, the heat transferring ability increases. However, the Nusselt number is independent of the velocity slip coefficient for high values of \(\beta \). This happens since the temperature jump becomes the dominant thermal resistance (in comparison with the resistance of combined conduction–convection–radiation) and plays the most important role in the heat transfer rate at high jump coefficients.

As \(s\) increases, Fig. 4b shows that the dependency of Nusselt number on \(\alpha \) decreases. In addition, comparing Fig. 4a, b reveals that as \(s\) increases, the value of the Nusselt number slightly increases for a fixed \(\beta \) or \(\alpha \). For instance, when \(\beta \rightarrow 1\) the Nusselt number obtained for \(s = 10\) is almost 10 % higher than that obtained for \(s = 1\). For high porous medium shape parameters, Fig. 4c shows that for a fixed \(\beta \), the Nusselt number is independent of the velocity slip coefficient \((\alpha )\). It happens since the velocity distribution is almost uniform across the channel height for high values of \(s\), and thus, the velocity profile does not change with the change of \(\alpha \) for \(\alpha = \beta = 0\) (Hooman 2008c; Dehghan et al. 2014a, b). Consequently, the Nusselt number remains unchanged with the variation in \(\alpha \).

Figure 5 is produced for the case 2 \((T_{r} = -0.5\) and \(\lambda = 0.5\)) in Table (1) and different porous medium shape parameters \((s)\). From to Fig. 4, it is seen that when \(T_{r} = -0.5\), the magnitude of the Nusselt number is approximately doubled. According to Eq. (21), a positive value of \(T_{r}\) results in a higher effective conductivity of the medium \((k_{c}+k_{r})\) which enhances the heat transfer rate and increases the Nusselt number (Mirzaei and Dehghan 2013). It is seen that similar to Fig. 4, for a fixed \(\alpha \) and all porous medium shape parameters \((s)\), an increase in \(\beta \) decreases the Nusselt number. For low values of \(\beta \) and when compared with the results presented in Fig. 4, it is seen that for \(T_{r} = -0.5\), a steep decrease in the Nusselt number is observed with an increase in \(\beta \). Fig. 5a shows that similar to Fig. 4a, as \(\alpha \) increases, the magnitude of the Nusselt number increases. However, comparing Figs. 4 and  5 reveals that for \(T_{r} = -0.5\), the effect of \(\alpha \) on the Nusselt number decreases. For \(s = 10\), Fig. 5b shows that the variation in the Nusselt number with respect to \(\alpha \) is negligible. For a high porous medium shape parameter \((s = 100)\), the velocity slip coefficient has no effect on the Nusselt number.

Figure 6 is obtained using the radiation parameters of case 3 with \(T_{r} = -0.5\) and \(\lambda = 1\), which compared to case 1 has a higher \(\lambda \). Interestingly, the figure shows that for all porous medium shape parameters, and \(\beta > 0.25\), the Nusselt number remains almost unchanged with the increase in \(\beta \). For example, in Fig. 6a, the difference between the Nu number obtained for \(\beta = 0.5\) and \(\beta = 1\) is about 15 %. Furthermore, a comparison between Figs. 4 and 6 shows that the Nusselt number decreases with increased \(\lambda \) for negative values of \(T_{r}\). When \(T_{r}\) is negative, an increase in \(\lambda \) results in a lower effective thermal conductivity of the medium based on Eq. (21). Consequently, the reduction in the Nusselt number can be interpreted (Mirzaei and Dehghan 2013).

Figure 7 shows the variation in Nu number versus \(\beta \) obtained for case 4 with \(T_{r} = 0.5\) and \(\lambda = 1\). Again, similar to Fig. 5, it is seen that for positive \(T_{r}\) and \(\beta < 0.25\), the Nu number dramatically decreases as the jump coefficient increases. Furthermore, in this limit and comparing to other cases (Figs. 4 to 6) it is seen that the Nusselt number for case 4 yields the maximum value. The dimensionless temperature is normalized and its order of magnitude does not change with working parameters. according to Eq. (21) for a positive \(T_{r}\), an increase in \(\lambda \) leads to an increase in the effective thermal conductivity of the porous medium. Consequently, the rate of heat transfer and Nu number increase (Mirzaei and Dehghan 2013).

From Figs. 3,  4,  5,  6, 7, one can clearly observe that the effects of porous medium shape parameter \((s)\) on the Nusselt number decrease when the jump coefficient \((\beta )\) increases. For \(\alpha = \beta = 0\), we see that for all cases studied here, the Nusselt number obtained for \(s = 100\) is about 40 % higher than that obtained for \(s = 1\), while for \(\alpha = \beta = 1\), the increase in the Nusselt number for the case of \(s = 100\) is found to be about 2 % higher than that obtained for \(s = 1\), except case 3 (Fig. 6) where the increase in the Nusselt number form \(s = 1\) to \(s = 100\) is about 30 %. For high values of \(\beta \), the thermal resistance due to the temperature jump dominates, and the Nusselt number will not be effectively increased by the increase in \(s\), which decreases the thermal resistance due to the convection. Thus, in the slip regime, inserting a porous medium into a flow passage cannot effectively enhance the heat transfer ability in the absence of radiation (case 0), while increase the friction factor \((f_{K})\) and the required pumping power (see Eq. 19). Also, at high temperature jump coefficients, the porous medium cannot effectively enhance the heat transfer rate in the presence of radiation heat transfer, except for case 3. This case 3 has a distinguished characteristic, which is the minimum effective thermal conductivity among other cases. Also, case 3 is accompanied by the minimum reduction in the Nusselt number with respect to the temperature jump coefficient \((\beta )\) among other cases. It shows that when \(\beta \) could not play a key role, the role of the porous medium insertion would become more important in the heat transfer rate.

To see effects of radiation parameters (\(\lambda \) and \(T_{r}\)) as well as the slip and jump coefficients, \(\alpha \) and \(\beta \), on the dimensionless temperature distribution \((\theta )\), Figs. 8 and 9 are produced. Figure 8 shows that for high porous medium shape parameters, increasing the temperature variation parameter \((T_{r})\) tends to make a more uniform dimensionless temperature distribution and to increase the absolute value of the slope of the dimensionless temperature profile at the wall, which represents a higher Nu number (see Eq. 30). From Fig. 9, it can be seen that a higher value of porous medium shape parameter \((s)\) has a higher value of the dimensionless temperature at the middle plane \((y = 0)\) because of a decrease in the absolute value of \((T_{m}-T_{w})\) (Dehghan et al. 2014a, b). Also, the difference between profiles of different values of \(s\) is negligible at high values of jump coefficient \((\beta )\), the same as what has been seen for the Nusselt number.

Fig. 8
figure 8

Effects of the temperature variation parameter (Tr) on the dimensionless temperature profile along the channel height for \(\hbox {s} = 100,\, \uplambda = 0.5,\, \upalpha = 0\) and \(\upbeta = 0\)

Full size image
Fig. 9
figure 9

Effects of the porous medium shape parameter \((s)\) on dimensionless temperature profile along the channel height in the slip regime for \(T_{r} = 0.5\) and \(\lambda = 0.5\)

Full size image

5 Conclusion

In this work, a numerical study investigating the effects of the thermal radiation on the forced convection heat transfer through cellular porous media bounded by a micro-scale channel has been presented in the slip flow regime. The problem has been modelled as a combined conductive–convective–radiative problem in which the radiative heat transfer is treated as a diffusion process. A constant heat flux has been imposed at the channel walls in the presence of a finite velocity slip and a temperature jump. The Darcy-Brinkman equation along with a temperature-dependent conductivity has been used to model the heat and fluid flows through the porous medium. The major findings of this study can be summarized as follows:

  • The Nusselt number increases by increasing the radiation parameters due to inclusion of the radiation conductivity (via modelling the radiation heat transfer as a diffusion process), which results in a higher effective conductivity of the porous medium and a higher overall Nusselt number as well.

  • In the no-slip regime, as the porous medium shape parameter \((s)\) increases, the flow will be more uniform over the cross-sectional area and thus the Nusselt number increases.

  • The dependency of the Nusselt number to the velocity slip decreases when the porous medium shape parameter increases.

  • The temperature jump coefficient has more influence on the Nusselt number compared to the velocity slip coefficient.

  • At high temperature jump conditions, the dominant thermal resistance relates to the temperature jump phenomenon. In addition, a high value of jump coefficient controls the heat transfer rate (Nu) of the medium regardless of the radiation parameters or the porous medium characteristics \((s)\).

  • Finally, insertion of a porous material inside a channel in the presence of a temperature jump (occurring in slip flow regime) does not enhance significantly the heat transfer rate, while increases the pumping power required compared to the clear fluid flow.