Perturbation Analysis of the Local Thermal Non-equilibrium Condition in a Fluid-Saturated Porous Medium Bounded by an Iso-thermal Channel

Abstract

This study focuses analytically on the local thermal non-equilibrium (LTNE) effects in the developed region of forced convection in a saturated porous medium bounded by isothermal parallel-plates. The flow in the channel is described by the Brinkman–Forchheimer-extended Darcy equation and the LTNE effects are accounted by utilizing the two-equation model. Profiles describing the velocity field obtained by perturbation techniques are used to find the temperature distributions by the successive approximation method. A fundamental relation for the temperature difference between the fluid and solid phases (the LTNE intensity) is established based on a perturbation analysis. It is found that the LTNE intensity ($\Delta \textit{NE}$) is proportional to the product of the normalized velocity and the dimensionless temperature at LTE condition. Also, it depends on the conductivity ratio, Da number, and the porosity of the medium. The intensity of LTNE condition ($\Delta \textit{NE}$) is maximum at the middle of the channel and decreases smoothly to zero by moving to the wall. Finally, the established relation for the intensity of LTNE condition is simple and fundamental for estimating the importance of LTNE condition and validation of numerical simulation results.

1 Introduction

In recent years, the study of local thermal non-equilibrium (LTNE) has been more important due to its engineering applications such as electronic-cooling systems, heat pipes, nuclear reactors, drying technology, and multiphase catalytic reactors. There are several industrial applications where the high local speed of the fluid in a porous medium, high heat flux, or high boundary temperature compared to the fluid temperature, and chemical reactions lead to a significant degree of LTNE condition. An example is the thermal storage of solar energy conversion system, where a heated fluid flows from the solar collectors into a porous bed and energy is recovered by reversing the flow in the bed (White and Korpela 1979; Spiga and Spiga 1981; Nield and Kuznetsov 1999; Alazmi and Vafai 2002).

Analytical study of Schumann (1929) was a step forward in dealing with the local thermal non-equilibrium phenomenon. After him, many other researchers investigated analytically the LTNE phenomenon, but all of them used the Darcy model for the flow field. Kuznetsov (1996, 1997a) studied analytically the LTNE effects in Cartesian frame work for the 2-D and 3-D convection in saturated porous beds based on the Darcy’s law (uniform velocity across the medium). Nield (1998) analyzed the LTNE situation in both conduction and convection in saturated porous channels. He assumed the Darcy’s law to clarify situations in which the LTNE could be important. Kuznetsov (1997b) concentrated on the study of thermal non-equilibrium effects in a channel filled with a fluid-saturated porous medium based on a perturbation analysis. He used the results of previous studies (Vafai and Kim 1989, 1995; Nield et al. 1996) for the flow field and a two-energy-equation model for the temperature field. It was the first time that the LTNE phenomenon was treated analytically based on the Brinkman–Forchheimer-extended Darcy model. Kuznetsov (1997b) proposed a simplified equation for measuring the LTNE intensity at constant heat flux condition imposed to a porous-saturated channel. Later, Nield and Kuznetsov (1999) studied analytically the conjugate problem of LNTE condition in a saturated porous channel with including the thermal resistance of the channel wall based on the Darcy model. Alazmi and Vafai (2002) investigated the heat transfer in a fluid saturated porous medium under the local thermal non-equilibrium condition numerically. The geometry in their study was flow between parallel-plates and the thermal boundary condition was constant heat flux at the wall.

Forced convection in a channel filled with a porous medium, consisting of two layers with the same porosity and permeability but with different solid conductivity, and saturated by a single fluid, was analyzed at the LTNE condition by Nield and Kuznetsov (2001). They used the Darcy’s law and found that the effect of local thermal nonequilibrium is significant when the solid conductivity in each layer is greater than the fluid conductivity. After that, Nield et al. (2002) applied the classical Graetz methodology to study the effect of LTNE on the developing forced convection in a parallel-plate channel filled by a saturated porous medium. Hooman and Merrikh (2006) studied the flow and heat transfer in fluid-saturated porous ducts analytically based on the Fourier series. They proposed analytical expression for Nusselt number and temperature field for the case of constant heat flux thermal boundary condition. Hooman (2008) proposed expressions for the velocity and temperature distributions for the flow between infinite parallel-plates under a constant heat flux imposed at the walls based on perturbation techniques in two limiting cases, large and small Darcy numbers. Hung and Tso (2009) investigated the heat transfer in a fluid-saturated porous channel under a constant heat flux condition. They proposed a closed-form solution for the temperature field including the frictional heating effects. All of the mentioned works in the present paragraph were on the basis of the local thermal equilibrium assumption. Results of them can be used as a start point to study of LTNE condition in future studies similar to this work.

Mahmoudi and Maerefat (2011) investigated analytically the forced convection through a channel partially filled with a porous medium under the constant heat flux at the walls. They assumed thermally developed condition and the local thermal non-equilibrium model to obtain the exact solutions of both fluid and solid temperature fields for flow inside the porous region as well as for flow in the clear region. Khandelwal and Bera (2012) studied the influence of thermal non-equilibrium state on the fully developed mixed convection in a vertical channel filled with a porous medium. They showed that an increase in the inter-phase heat transfer coefficient decreases the amount of LTNE. Qu et al. (2012) proposed an analytical solution using modified Bessel functions for fully developed forced convective heat transfer in an annulus partially filled with a metallic foam. The inner surface attached with the annular metallic foam layer was exposed to a constant heat flux while the outer one was adiabatic. In the porous medium region, the Brinkman–Darcy equation was used to describe the fluid flow and the thermal non-equilibrium model was employed to establish the heat transfer equations.

Most of analytical studies have used constant heat flux for the thermal boundary condition, because it simplifies the energy equation. There are few investigations that have assumed iso-thermal boundary condition, like Nield and Kuznetsov (1999) and Nield and Kuznetsov (2004). But, they consider basic models, especially the Darcy model. Also, a number of attempts for studying the iso-thermal boundary condition assumed a simplifier assumption which questions the fact of the fully developed condition. They neglected the axial change of temperature at fully developed region and added a viscous dissipation term to balance the energy equation (Mahmud and Fraser 2005a, b; Hooman and Gurgenci 2007). On the other hand, the Nu number is the ratio of convected heat to the conducted heat by the medium. So, if the axial temperature variation (the convective term in the energy balance equation) be neglected, the Nu number would become meaningless.

In this study, a fluid-saturated porous medium bounded by two iso-thermal infinite parallel-plates has been investigated based on the perturbation technique. The flow field has been modeled using the Brinkman–Forchheimer-extended Darcy equation. The situation of local thermal non-equilibrium has been assumed for the temperature. The energy equation has been solved by the successive approximation method. A simple expression representing the intensity of the local thermal non-equilibrium condition has been proposed based on the scale analysis and perturbation technique. To our knowledge, such a simple equation representing the intensity of the LTNE condition subjected to the iso-thermal boundary condition has been rarely proposed in previous works.

2 Mathematical Modeling

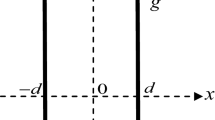
The schematic diagram of the problem is shown in Fig. 1. The following assumptions are invoked in the formulation of the model:

Fig. 1

Schematic diagram of the porous-saturated channel

• The flow in the porous media is incompressible.

• The steady-state fully developed forced convection is desired.

• The natural convection and the radiation heat transfer are neglected.

• The medium is assumed to have constant, isotropic, and homogenous characteristics and properties (permeability, porosity, viscosity, and conductivity).

• The walls are kept at a constant temperature.

• Walls are impermeable parallel-plates which have infinite dimension perpendicular to the plane of view. As a result, the problem could be treated as a two-dimensional transfer of heat and flow.

• It is allowed that the temperature of solid and fluid phases be different (LTNE condition).

According to the stated assumptions, the governing equations can be presented as following (Kuznetsov 1997a, b; Nield and Bejan 2006; Hooman 2008):

$$\begin{aligned} \mu _\mathrm{eff} \frac{d^{2}u^{*}}{dy^*{^{2}}}-\frac{\mu }{K}u^{*}-\frac{C_\mathrm{F} \rho u^{*}{^{2}}}{\sqrt{K}}+G=0 \end{aligned}$$

(1)

Equation (1) is the momentum equation (the Brinkman–Forchheimer-extended Darcy equation) where $y^*$ is the perpendicular axis to the flow direction, $u^{*}$ is the fluid velocity, $\mu$ is the fluid viscosity, $K$ is the permeability of the medium, $\rho$ is the fluid density, $C_\mathrm{F}$ is the inertial coefficient, $G$ is the negative of the applied pressure gradient in the flow direction ($x^*)$, and $\mu _\mathrm{eff}$ is the effective viscosity which is equal to $\mu /\phi$ (Kuznetsov 1997a, b; Vafai and Kim 1989). $\phi$ is the porosity of the medium.

The steady state energy equations of the solid and fluid phases are (Kuznetsov 1997a, b; Nield and Bejan 2006):

$$\begin{aligned}&\rho c_p u^{*}\frac{\partial T_\mathrm{f} }{\partial x^*}=k_{\mathrm{f,eff}} \frac{\partial ^{2}T_\mathrm{f} }{\partial y^*{^{2}}}+h_{\mathrm{sf}} a_{\mathrm{sf}} \left( {T_\mathrm{s} -T_\mathrm{f} } \right) \end{aligned}$$

(2)

$$\begin{aligned}&0=k_{\mathrm{s,eff}} \frac{\partial ^{2}T_\mathrm{s} }{\partial y^*{^{2}}}-h_{\mathrm{sf}} a_{\mathrm{sf}} \left( {T_\mathrm{s} -T_\mathrm{f} } \right) \end{aligned}$$

(3)

Equations (2) and (3) are the energy equations for the fluid and solid phases, respectively. In Eqs. (2) and (3) it is assumed that the axial heat conduction is negligible. In these equations the subscripts “s” and “f” denote solid and fluid phases, respectively. $T$ is temperature, $c_{p}$ is the specific heat of the fluid phase, $k_{\mathrm{s,eff}}$ and $k_{\mathrm{f,eff}}$ are effective thermal conductivities of the solid and fluid phases given by:

$$\begin{aligned} k_{\mathrm{s,eff}}&= \left( {\hbox {1}-\phi } \right) k_\mathrm{s}\end{aligned}$$

(4)

$$\begin{aligned} k_{\mathrm{f,eff}}&= \phi k_\mathrm{f} \end{aligned}$$

(5)

$h_{\mathrm{sf}}$ and $a_{\mathrm{sf}}$ are the fluid–solid heat transfer coefficient and specific surface area (surface per unit volume) given by (Alazmi and Vafai 2002; Nield and Bejan 2006):

$$\begin{aligned}&\displaystyle a_{\mathrm{sf}} ={6\left( {1-\phi } \right) }\big /{d_\mathrm{p} }\end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle h_{\mathrm{sf}} =\frac{k_\mathrm{f} }{d_\mathrm{p} }\left[ {2+1.1 {Pr ^{1/3}} \left( {\frac{\rho u^{*}d_\mathrm{p} }{\mu }} \right) ^{0.6}} \right] \end{aligned}$$

(7)

$d_{\mathrm{p}}$ is particle diameter and Pr is the Prandtl number. Equations (1–3) are subjected to the no-slip and no-jump boundary conditions. Also, the symmetry is imposed by the geometry of the problem. Consequently, the boundary conditions of Eqs. (1–3) are as following:

$$\begin{aligned}&\left. {\frac{\mathrm{d}u^{*}}{\mathrm{d}y^*}} \right| _{y^*=0} =0,\quad u^{*}\left( {y^*=H} \right) =0\end{aligned}$$

(8)

$$\begin{aligned}&\begin{array}{l} \frac{\partial T_\mathrm{f} }{\partial y^*}=\frac{\partial T_\mathrm{s} }{\partial y^*}=\hbox {0}\quad \hbox {at }\quad y^*=0 \\ T_\mathrm{f} =T_\mathrm{s} =T_\mathrm{w}\quad \hbox {\, at }\quad y^*=H \\ \end{array} \end{aligned}$$

(9)

3 Analysis and Solution

Dimensionless form of the momentum Eq. (1) and the boundary conditions (8) are:

$$\begin{aligned}&\frac{\mathrm{d}^{2}u}{\mathrm{d}y^{2}}-s^{2}u-Fsu^{2}+\frac{1}{M}=0\end{aligned}$$

(10)

$$\begin{aligned}&\left. {\frac{\mathrm{d}u}{\mathrm{d}y}} \right| _{y=0} =0,\quad \hbox { }u\left( {y=1} \right) =0 \end{aligned}$$

(11)

where $y$ is non-dimensional axis perpendicular to the flow direction, $u$ is non-dimensional velocity, $M$ is viscosity ratio, and $s$ is the porous media shape parameter and they are defined as:

$$\begin{aligned}&y=\frac{y^*}{H},\quad u=\frac{\mu u^{*}}{GH^{2}},\quad \hbox { }M=\frac{\mu _{\mathrm{eff}} }{\mu }\quad Da=\frac{K}{H^{2}},\hbox { F}=\frac{C_\mathrm{F} \rho GH^{3}}{\mu _{\mathrm{eff}} \mu }\end{aligned}$$

(12)

$$\begin{aligned}&s=\frac{1}{\sqrt{DaM}}=\sqrt{\frac{\upphi }{Da}} \end{aligned}$$

(13)

here, Da and $F$ are the Darcy and Forchheimer numbers, respectively. The normalized velocity ($\mathop {u}\limits ^{{\frown }}$) is defined as:

$$\begin{aligned} \mathop {u}\limits ^{{\frown }} =\frac{u^{*}}{u^{*}_\mathrm{m} } \end{aligned}$$

(14)

$u^*_{\mathrm{m}}$ is the mean velocity and is given by:

$$\begin{aligned} u^{*}_\mathrm{m} =\frac{1}{H}\int \limits _0^H {u^{*} \mathrm{d}y^*} \end{aligned}$$

(15)

According to Hooman (2008) the velocity field of the present problem can be obtained using the perturbation technique in two limiting cases: small and large values of the porous media shape parameter $(s)$. The normalized velocity for the case of $s<1$ using the asymptotic expansion method is (Hooman 2008):

$$\begin{aligned} \mathop {u}\limits ^{{\frown }} =\frac{3}{2}\left( {1-y^{2}} \right) +\frac{Fs}{280M}\left( {7y^{6}-35y^{4}+33y^{2}-5} \right) +O\left( {s^{2}} \right) ;\quad s<1 \end{aligned}$$

(16)

For $s>1$ the momentum Eq. (10) is a singular perturbation differential equation having two boundary layers at each boundary (Nayfeh 1981). This type of equation should be solved by the method of multiple scales or the method of matched asymptotic expansions. In a brief view, the solution procedure could be stated as following:

The method of multiple scales needs at least three scales: $y_{0} = y$, $y_{1} = s(1 - \hbox {y})$, and $y_{2}$ = sy. The method of matched asymptotic expansion needs defining two inner layers at each boundary and one outer layer far from the boundaries. But, Eq. (10) and its boundary conditions (11) are an especial case in which the boundary condition could be ensured at $y$=0 by the outer solution. So, it can be solved with only one inner layer at $y=1$. The stretched coordinate at $y=1$ is: $y_{1} = \hbox {s}(1 - \hbox {y})$. After some mathematical operations, one could show that the solution of momentum Eq. (10) subjected to the boundary conditions (11) would be as:

$$\begin{aligned} \mathop {u}\limits ^{{\frown }} =\frac{1-\exp \left\{ {s\left( {y-1} \right) } \right\} }{1-1/s+{\exp \left( {-s} \right) }/s}+O\left( {\frac{1}{s^{3}}} \right) ;\quad s>1 \end{aligned}$$

(17)

At this point, the velocity field of the problem has been defined by Eqs. (16) and (17). For the temperature field, analysis will be started with Eq. (3). Using the scale analysis and noting that the product of $h_\mathrm{sf} \, a_\mathrm{sf}$ is a large value, one could show the following result from Eq. (3) (Kuznetsov 1997a, b):

$$\begin{aligned} T_\mathrm{s} =T_\mathrm{f} +O\left( {\varepsilon =\frac{1}{h_{\mathrm{sf}} a_{\mathrm{sf}} }} \right) \end{aligned}$$

(18)

where $\varepsilon$ is a small value. Combining Eqs. (3) and (18) yields:

$$\begin{aligned} \left( {T_\mathrm{s} -T_\mathrm{f} } \right) =\frac{1}{h_{\mathrm{sf}} a_{\mathrm{sf}} }\frac{k_{\mathrm{s,eff}} }{k_\mathrm{m} }k_\mathrm{m} \frac{\partial ^{2}T_\mathrm{f} }{\partial y^*{^{2}}}+O\left( \varepsilon \right) \end{aligned}$$

(19)

$k_{\mathrm{m}}$ is the effective thermal conductivity of the medium and equals to $k_{\mathrm{s,eff}} + k_{\mathrm{f,eff}}$. To define the temperature difference (or the intensity of LTNE condition), the value of ${\partial ^{2}T_\mathrm{f} }/{\partial y^*{^{2}}}$ should be defined. From Eqs. (2), (3), and (18) it can be shown that:

$$\begin{aligned} \rho c_p u^{*}\frac{\partial T_\mathrm{f} }{\partial x*}=k_\mathrm{m} \frac{\partial ^{2}T_\mathrm{f} }{\partial y^*{^{2}}}+O\left( \varepsilon \right) \!. \end{aligned}$$

(20)

So, the solution reduces to solving a fluid-saturated porous medium under the LTE condition subjected to isothermal boundary condition. To solve Eq. (20), some definitions are given as following:

$$\begin{aligned} \theta&= \frac{T-T_\mathrm{w} }{T_\mathrm{m} -T_\mathrm{w} }\end{aligned}$$

(21)

$$\begin{aligned} T_\mathrm{m}&= \frac{1}{Hu_\mathrm{m} }\int \limits _0^H {u^{*}Tdy^*} \end{aligned}$$

(22)

where $\theta$ and $T_{\mathrm{m}}$ are dimensionless temperature and the bulk mean temperature, respectively. Combining Eqs. (21) and (22) results in:

$$\begin{aligned} \frac{\partial T_\mathrm{f} }{\partial x*}=\theta _\mathrm{f} \frac{\mathrm{d}T_\mathrm{m} }{\mathrm{d}x*}+O(\varepsilon ). \end{aligned}$$

(23)

Writing the first law of thermodynamics over a differential control volume containing the channel and using Eq. (23), one can obtain:

$$\begin{aligned} \frac{\partial T_\mathrm{f} }{\partial x^*}=\theta _\mathrm{f} \frac{q^{\prime \prime }_\mathrm{w} \left( {x^*} \right) }{\rho c_p u_\mathrm{m} H}+O(\varepsilon ), \end{aligned}$$

(24)

$q^{\prime \prime }_\mathrm{w} ({x^*})$ is the heat flux at section $x^*$ of the channel which is a function of $x^*$. Combining Eqs. (19), (20), and (24) yields:

$$\begin{aligned} \left( {T_\mathrm{s} -T_\mathrm{f} } \right) =\frac{1}{h_{\mathrm{sf}} a_{\mathrm{sf}} }\frac{k_{\mathrm{s,eff}} }{k_\mathrm{m} }\mathop {u}\limits ^{{\frown }} \theta _\mathrm{f} \frac{q_\mathrm{w} \left( {x^*} \right) }{H}+O\left( \varepsilon \right) \end{aligned}$$

(25)

Dividing Eq. (25) by ($T_{\mathrm{m}} - T_{\mathrm{w}})$, using the Nusselt number definition, and rearranging the Eq. (25) give:

$$\begin{aligned} \Delta {\textit{N}E}=\frac{k_{\mathrm{s,eff}} }{k_\mathrm{m} }\mathop {u}\limits ^{{\frown }}\theta _\mathrm{f} +O(\varepsilon ) \end{aligned}$$

(26)

$\Delta \textit{NE}$ is a complex representing the intensity of LTNE condition and is equal to:

$$\begin{aligned} \Delta {\textit{N}E}=\left| {\frac{\left( {\theta _\mathrm{s} -\theta _\mathrm{f} } \right) h_{\mathrm{sf}} a_{\mathrm{sf}} 4H^{2}}{k_\mathrm{m} Nu}} \right| \end{aligned}$$

(27)

Nu in Eq. (27) is the Nusselt number based on the hydraulic diameter:

$$\begin{aligned} {\textit{N}u}=\frac{q^{\prime \prime }_\mathrm{w} \left( {x^*} \right) \times 4H}{\left( {T_\mathrm{w} -T_\mathrm{m} } \right) k_\mathrm{m} }. \end{aligned}$$

(28)

Equation (26) only needs the normalized velocity ($\mathop {u}\limits ^{{\frown }})$ and non-dimensional temperature ($\theta$) distributions in a porous medium under the assumption of LTE condition. The normalized velocity distribution is given by Eqs. (16) and (17). The non-dimensional temperature distribution under LTE condition could be estimated by the successive approximation method. At first, Eq. (20) should be non-dimensionalized as following:

$$\begin{aligned} -\frac{Nu\!\mathop {u}\limits ^{{\frown }}}{4}\theta _\mathrm{f} =\frac{\mathrm{d}^{2}\theta _\mathrm{f} }{\mathrm{d}y^{2}}. \end{aligned}$$

(29)

And the non-dimensional boundary conditions would be as:

$$\begin{aligned} \left. {\frac{\mathrm{d}\theta _\mathrm{f} }{\mathrm{d}y}} \right| _{y=0} =0,\quad \theta _\mathrm{f} (1)=0. \end{aligned}$$

(30)

For the sake of brevity, the subscript “f” will be dropped. At the first step, a profile for $\theta (y)$ should be guessed. In this study, a flat profile ($\theta (y)$ = 1) is used for the first step. This profile is substituted to the LHS of Eq. (29) and then is integrated two times. Equation (30) will be used to define the constants of the integrals. The perturbation integration method should be used in integrating and the dominant terms should be held. Then, from the definition of the Nu number, the Nusselt number of the step could be evaluated:

$$\begin{aligned} Nu=-4\left. {\frac{\mathrm{d}\theta }{\mathrm{d}y}} \right| _{y=1.} \end{aligned}$$

(31)

The new profile should be substituted into the LHS of Eq. (29) and the process could be repeated until the difference of the Nu of the nth-step and available Nu numbers of other researchers falls below a coast-profit determined percentage. In this study, this percentage is adopted 5 %. The dominant terms of obtained temperature distribution ($\theta (y))$ for $s<$1 after four steps will be as:

$$\begin{aligned}&\theta \left( y \right) =Nu^{3}\{-1.23\times 10^{-5}y^{10}+9.02\times 10^{-5}y^{8}-5.00\times 10^{-4}y^{6}+1.574\times 10^{-3}y^{4} \nonumber \\&-3.952\times 10^{-3}y^{2}+2.800\times 10^{-3}+\frac{sF}{M}\left( -1.12\times 10^{-5}y^{10}+1.92\times 10^{-4}y^{8}\right. \nonumber \\&\left. -\hbox {5.84}\times 10^{-4}y^{6}+\hbox {6.35}\times 10^{-4}y^{4}{-2.22}\times 10^{-5}y^{2}{-2.105}\times 10^{-4}\right) \}+\hbox {O}\left( {s}^{2}\right) . \end{aligned}$$

(32)

The Nusselt number at this step is 7.90 as $s \rightarrow \,0$. The Nusselt number of the numerical simulation is 7.54 (Kaviany 1985). So, the non-dimensional difference is 4.8 %. Nu number of the next step is 7.78 and is 3.2 % rough. The Nu number at this step is:

$$\begin{aligned} \textit{Nu}=7.78\left( {1+0.029s} \right) ,\quad s<1 \end{aligned}$$

(33)

Equation (33) has been used to draw the non-dimensional temperature profile and to evaluate the $\Delta \textit{NE}$. For the case of $s>1$, after seven steps the dominant terms of non-dimensional temperature profile would be as:

$$\begin{aligned}&\theta \left( y \right) =\left( \frac{Nu}{1-1/s+{\exp ({-s})}/s}\right) ^{6}\left( 0.01261\mathrm{y}^{8} -0.2673\mathrm{y}^6+3.2943\mathrm{y}^{4} \right. \nonumber \\&\left. -16.755\mathrm{y}^{2}+13.676\right) \times 10^{-7}+\left( \frac{Nu}{1-1/s+{\exp \left( {-s} \right) }/s}\right) ^{5}\left( -25.92\times \left( \frac{1}{s}\right) ^{2} \right. \nonumber \\&\left. +41.37\left( \frac{1}{{s}}\right) ^{2}\hbox {y}^{2}-8.477\left( \frac{1}{{s}}\right) ^{2} \hbox {y}^{4}\right) \times 10^{-6}+\mathrm{O}\left( \frac{1}{{s}}\right) ^{3} \end{aligned}$$

(34)

The Nusselt number at this step is 10.24 as $s \rightarrow$ $\infty$ and the numerical simulation based Nusselt number is 9.87 (Kaviany 1985). So, the non-dimensional difference is 3.7 %:

$$\begin{aligned} \textit{Nu}=10.24\left( {1-{1.2}/s} \right) ,\quad s>1 \end{aligned}$$

(35)

In a brief view, an equation proposing the importance of LTNE condition has been obtained based on the analytical approach. Equation (26) is a simple and general relation that can be used for the estimation of LTNE condition and for numerical simulation validations. The obtained results based on Eqs. (26) and (32–35) will be presented in the next section.

4 Results and Discussions

At first, the obtained non-dimensional temperature distributions are compared with numerical results of Kaviany (1985). Results of Eqs. (32) and (34) are plotted in Fig. 2. It can be seen that the results of successive approximation method (Eqs. 32 and 34) are in good agreement with the numerical results of Kaviany (1985) in both cases ($s<1$ and $s>1$).

Fig. 2

Non-dimensional temperature distribution

After investigating the accuracy of obtained non-dimensional temperature profile, the results of LTNE condition based on Eq. (26) are discussed. Figure 3 shows effects of porosity on the intensity of LTNE condition. From Fig. 3a, b, it can be seen that the intensity of LTNE condition ($\Delta \textit{NE}$) reaches its maximum value at the middle of the channel and decreases smoothly to zero by moving to the wall. Also, the intensity of LTNE condition decreases with increasing the porosity ($\phi )$. At higher porosities, the occupying solid phase has less thermal inertia and would follow the fluid phase stronger (Mirzaei and Dehghan 2013). This trend can be seen for all Da numbers in Fig. 4. Another matter is that there is local thermal equilibrium (LTE) at the boundary. This was expected because of the thermal boundary condition at the channel wall. Also, the value of $\Delta \textit{NE}$ reaches zero smoothly. This happens because in Eq. (26) both $\mathop {u}\limits ^{{\frown }}$ and $\theta$ are zero at the wall ($y=1$). So, $\Delta \textit{NE}$ has a root of order two at the wall.

Fig. 3

Effects of porosity on the intensity of LTNE condition: a Da $=$ 0.01, b Da $=$ 0.0001

Fig. 4

Effects of Da number on the intensity of LTNE condition; a $\upphi =0.4$, b $\upphi =0.8$

In Figs. 3 and 4 the conductivity ratio ($k={k_\mathrm{f}}/{k_\mathrm{s}})$ is equal to one. To see effects of the conductivity ratio, Figs. 5 and 6 are plotted. The intensity of LTNE condition decreases by increasing the conductivity ratio ($k$). It is not surprising since the ability of fluid in the heat transfer increases in comparison with the solid phase. As a result, the solid phase would obey the fluid phase closer and vice versa. Another matter than can be obtained from Figs. 5 and 6 is that although the intensity of LTNE condition decreases at higher porosities, but the difference between different conductivity ratios increases. For example, at $\upphi =0.2$ the profile of $k=0.2$ is about two times greater than the profile of $k=5$, but at ${\upphi }=0.8$ the profile of $k=0.2$ is about 10 times greater than the profile of $k=5$ at the middle of the channel ($y=0$).

The other is that the intensity of LTNE condition ($\Delta \textit{NE}$) is higher at higher Da numbers at the middle of the channel as it can be seen in Fig. 6. But by moving to the wall, the lower $Da$ number would have higher values of $\Delta \textit{NE}$. This occurs because of the redistribution of velocity field by the Da number. The Da number has a little influence on the temperature field in comparison with its influence on the velocity field. At low Da numbers (high $s$ values), the velocity profile is more uniform. Also, increasing the porosity decreases this difference between profiles of different Da numbers.

Fig. 5

Effects of conductivity ratio ($k$) on the intensity of LTNE condition at Da $=$0.01: a $\upphi =0.2$ and b $\upphi =0.8$

Fig. 6

Effects of conductivity ratio ($k$) and Da number on the intensity of LTNE condition: a $\upphi =0.2$ and b $\upphi =0.8$

5 Conclusion

The situation of local thermal non-equilibrium (LTNE) in a saturated porous medium bounded by isothermal parallel plates in a fully developed region has been discussed. The velocity and the temperature fields have been found using the perturbation techniques and the successive approximation method, respectively. The profile for the non-dimensional temperature distribution has been proposed at two limiting values of porous media shape parameter: small and large $s$. Other major results of this study are highlighted as following:

• A fundamental relation for the temperature difference between the fluid and solid phases (the thermal nonequilibrium intensity) has been established based on a perturbation analysis.

• It is found that the LTNE intensity ($\Delta$ NE) is proportional to the product of the normalized velocity and the non-dimensional temperature at LTE condition. Also, it depends on the conductivity ratio and porosity of the medium.

• The maximum intensity of LTNE condition occurs at the middle of the channel where the normalized velocity and the non-dimensional temperature have their maximum values.

• There is LTE condition at the walls because of the no-slip and no-jump conditions at the walls of channel.

• Increasing the conductivity ratio ($k={k_\mathrm{f}}/{k_\mathrm{s}})$ and porosity of the medium results in decreasing $\Delta \textit{NE}$.

• The trend is similar for all Da numbers. Also, the Da number has the least effects on the $\Delta \textit{NE}$ in comparison with the effects of porosity and conductivity ratio.

• Finally, the proposed relation for the intensity of LTNE condition (Eq. 26) is simple and fundamental for estimating the importance of LTNE condition and validation of numerical simulation results.