Coupled Upscaling Approaches For Conduction, Convection, and Radiation in Porous Media: Theoretical Developments

Abstract

This study deals with macroscopic modeling of heat transfer in porous media subjected to high temperature. The derivation of the macroscopic model, based on thermal non-equilibrium, includes coupling of radiation with the other heat transfer modes. In order to account for non-Beerian homogenized phases, the radiation model is based on the generalized radiation transfer equation and, under some conditions, on the radiative Fourier law. The originality of the present upscaling procedure lies in the application of the volume averaging method to local energy conservation equations in which radiation transfer is included. This coupled homogenization mainly raises three challenges. First, the physical natures of the coupled heat transfer modes are different. We have to deal with the coexistence of both the material system (where heat conduction and/or convection take place) and the non-material radiation field composed of photons. This radiation field is homogenized using a statistical approach leading to the definition of radiation properties characterized by statistical functions continuously defined in the whole volume of the porous medium. The second difficulty concerns the different scales involved in the upscaling procedure. Scale separation, required by the volume averaging method, must be compatible with the characteristic length scale of the statistical approach. The third challenge lies in radiation emission modeling, which depends on the temperature of the material system. For a semi-transparent phase, this temperature is obtained by averaging the local-scale temperature using a radiation intrinsic average while a radiation interface average is used for an opaque phase. This coupled upscaling procedure is applied to different combinations of opaque, transparent, or semi-transparent phases. The resulting macroscopic models involve several effective transport properties which are obtained by solving closure problems derived from the local-scale physics.

1 Introduction

This study concerns the derivation of a macroscopic model for heat transfer in porous media at high temperatures. The originality of this theoretical analysis lies in the coupling of upscaling approaches in order to account for both radiation and diffusion/convection. The present homogenization process, based on local thermal non-equilibrium, consists in applying the volume averaging method (Whitaker 1999) to the local energy conservation equations where homogenized radiation heat transfer is included at the local scale (i.e., at scale equal to or smaller than the pore size). So far, homogenization procedures for radiation and diffusion/convection in porous media have been separately performed.

Homogenization of heat transfer in porous media in the absence of radiation has often been studied using the volume averaging method both in the context of local thermal equilibrium or local thermal non-equilibrium (Carbonell and Whitaker 1984; Moyne 1997; Quintard and Whitaker 1993a; Quintard et al. 1997; Quintard and Whitaker 2000). In the first case, upscaling energy conservation leads to the averaged one-equation model while the thermal non-equilibrium situation naturally gives rise to a two-equation model whose coupling between phases is described by interfacial exchange terms and effective transport properties. These latter are obtained by solving associated local closure problems and dispersion effects when convection is considered. Constant homogeneous and/or heterogeneous thermal sources have also been included (Whitaker 1998; Quintard et al. 2000) leading to an additionnal distribution coefficient for the heterogeneous thermal source. As shown in the next sections, including radiation actually leads to similar models, but in that case, the homogeneous and/or heterogeneous thermal sources are not constant.

Radiation in porous media has been the subject of a specific attention during the last decades and a first actual challenge consists in characterizing the homogenized porous media in terms of the averaged radiative properties. Most of the time, these properties are obtained using a parameter identification technique (Baillis and Sacadura 2000). The emission and scattering coefficients of the porous medium are identified from experimental data, assuming that the homogenized radiative transfer can be modeled using a classical radiation transfer equation (RTE). The radiative characterization of the porous medium can now be based on a direct statistical homogenization; the microstructure of the solid matrix is then often taken into account from X- and $\gamma$-ray tomography data. The homogenized semi-transparent phase is accurately characterized from the chord distribution functions of the medium (Torquato and Lu 1993). This method was first developed by Tancrez and Taine (2004) and extensively used and further developed in numerous studies (Zeghondy et al. 2006b; Petrasch et al. 2007; Bellet et al. 2009; Haussener et al. 2009, 2010a; b,Taine et al. 2010; Chahlafi et al. 2012). A detailed review is provided by Taine and Iacona (Taine and Iacona 2012) for statistically isotropic media. These statistical homogenization approaches can be applied to any microscopic morphology (isotropic or not) and, contrary to identification methods, are not limited to homogenized medium assumingly obeying Beer’s laws (i.e., absorption, extinction, and scattering have an exponential behavior).

An alternative method based on spatial averaging has been introduced by Consalvi et al. (2002) in order to derive a homogenized RTE for multiphase systems. This methodology has been improved by averaging in each phase giving rise to the conventional RTE. This model takes into account exchange of radiation between phases (Gusarov 2008). A similar approach has been used by (Lipiński et al. 2010a; Lipiński et al. 2010b) and by Petrasch (2011) for semi-transparent two-phase media.

The coupled homogenization procedure proposed in the present study mainly raises three difficulties. The first one is related to the different physical nature of radiation, which refers to a non-material field composed of photons, and conduction/convection, which take place in the material system. The radiation field is homogenized, in a rather general case, using a statistical approach leading to the definition of radiation properties characterized by continuous statistical functions defined in the whole system (cumulated extinction distribution function, cumulated absorption probability, and cumulated scattering probability). In this general case, the homogenized phases are not Beerian and the radiation model is based on the Generalized Radiative Transfer Equation (GRTE) (Taine et al. 2010; Taine and Iacona 2012) and on the radiative Fourier law under some validity conditions (Gomart and Taine 2011).

The second difficulty concerns the compatibility between the characteristic length scale of the statistical approach and the length scale constraints imposed by the volume averaging method. The third challenge lies in modeling of emission, which depends on the temperature of the material system. For a semi-transparent phase, this temperature is obtained by averaging the local-scale temperature using a radiation intrinsic averaging operator; for an opaque phase, a radiation interface average is used.

The present analysis only considers transfer phenomena in the core of the porous medium. Indeed, macroscopic modeling at the interface between a homogeneous and a porous medium is beyond its scope. The paper is organized as follows: first, the challenges we are facing in this coupled upscaling procedure are presented in Sect. 2. Then, a generalized statistical radiation model is briefly described and applied for different combinations of opaque, transparent, and semi-transparent phases (Sect. 3). Sect. 4 is dedicated to the coupled upscaling procedure, giving rise to the macroscopic governing equations and the closure problems associated with the effective transfer properties. Finally, Sect. 5 presents the results of numerical calculations of effective properties.

2 Challenges of Coupling

The porous medium under consideration is composed of a rigid solid matrix (index $s$) assumed to be statistically isotropic and uniform, saturated by a fluid (index $f$), the two phases composing the material system. The fluid (gas at ambient pressure) is motionless or not and the solid phase is subjected to high temperature. As previously mentioned, the present analysis aims at deriving a macroscopic model for non-equilibrium heat transfer including radiation. The originality of the present upscaling procedure lies in the fact that the volume averaging method (Whitaker 1999) is applied to local conservation equations where the radiative transfer is taken into account after a statistical homogenization. In this context, we are facing a number of challenges.

One of the difficulties in upscaling these coupled transfer phenomena lies in their different physical natures. Indeed, in the problem under consideration, we have to deal with the coexistence of both the material system, where heat conduction and convection take place, and the non-material radiation field, composed of photons. This radiation field is homogenized using a statistical approach leading to the definition of the associated radiative properties. Note that these $\gamma$-phase radiative properties are continuously defined over the whole volume of the medium with a spatial resolution smaller than the pore size. It is important to recall that in the statistical approach, the different phases are not spatially separated, their existence being defined by a presence probability through the $\gamma$-phase volume fraction $\varPi _\gamma$. On the other hand, diffusion and convection in the pores are described by a discrete representation where conservation equations for each phase are coupled by fluid-solid interfacial boundary conditions. The derivation of an equivalent (continuous) macroscopic description taking into account this duality represents one of the major issues of the present analysis.

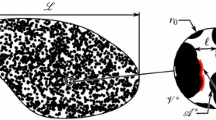
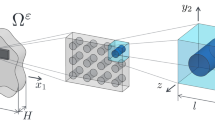
The second difficulty concerns the different scales involved in the upscaling procedure. Indeed, the volume averaging method is developed using an averaging volume $\fancyscript{V}^\mathrm{m}$ (Fig. 1) whose size $r^\mathrm{m}$ is assumed to satisfy scale separation given by the length scale constraints

$$\begin{aligned} l_f\ll r^\mathrm{m} \ll L \end{aligned}$$

(1)

where $l_f$ and $L$ are the local and the macroscopic characteristic length scales, respectively. Obviously, these scales have to be compatible with the characteristic length scale of the radiation statistical approach.

Fig. 1

Averaging volumes

Finally, the third challenge lies in the modeling of radiation emission which depends, at local thermodynamic equilibrium, on a temperature $\varTheta _\gamma$ compatible with the statistical definition of the $\gamma$-phase used in the radiation modeling. For a semi-transparent phase, $\varTheta _\gamma$ is obtained by averaging the local temperature $T_\gamma$ using the radiative intrinsic average operator (Fig. 1)

$$\begin{aligned} \varTheta _\gamma = \langle {T_\gamma }\rangle ^{\mathrm{R}\gamma } = \frac{1}{\fancyscript{V}^\mathrm{R}_\gamma } \int _{\fancyscript{V}^\mathrm{R}_\gamma } T_\gamma \,\mathrm{d}\fancyscript{V}, \end{aligned}$$

(2)

where $\fancyscript{V}^\mathrm{R}$ is the radiative averaging volume, included in $\fancyscript{V}^\mathrm{m}$ (Fig. 1), while $\fancyscript{V}^\mathrm{R}_\gamma$ is the part of $\fancyscript{V}^\mathrm{R}$ occupied by the $\gamma$-phase in the material system. The characteristic length scale for $\varTheta _\gamma$ is $r^\mathrm{R}$ (radius of $\fancyscript{V}^\mathrm{R}$); its values are discussed in Sect. 4.

For opaque walls, the homogenized wall temperature $\varTheta _w$ is defined, using the radiative interface average, by

$$\begin{aligned} \varTheta _w= \langle {T_w}\rangle ^{\fancyscript{A}^\mathrm{R}} = \frac{1}{\fancyscript{A}^\mathrm{R}} \int _{\fancyscript{A}^\mathrm{R}} T_w\, \mathrm{d}\fancyscript{A} \end{aligned}$$

(3)

where $\fancyscript{A}^\mathrm{R}$ is the part of the fluid-solid interface $\fancyscript{A}^\mathrm{m}$ included in $\fancyscript{V}^\mathrm{R}$, and $T_w$ is the interface temperature.

3 Homogenization of the Radiation Field

For the sake of simplicity, the medium is assumed to be statistically isotropic, uniform and geometrical optics laws are assumed to be valid at any scale. Therefore, if $l_f$ represents the pore size, the radiation wavelength $\lambda$ must satisfy

$$\begin{aligned} \lambda \ll l_f. \end{aligned}$$

(4)

Diffraction phenomena are then negligible.

The radiation statistical model which is coupled to the material system model in Sect. 4 has been given by Taine and Iacona (2012) and detailed by Tancrez and Taine (2004) and Taine et al. (2010). It is only briefly summarized here.

3.1 Principles of the Radiation Model

Any non-opaque $\gamma$-phase of the porous medium is fully characterized by effective radiative properties after homogenization.

If radiation extinction within a homogenized phase is characterized by an exponential law (case of a Beerian medium), these properties are extinction, scattering, or absorption coefficients ($\beta _\gamma , \sigma _\gamma$, or $\kappa _\gamma$, respectively), and a phase function $p_\gamma$. All of these quantities are, in our model, determined using the Radiative Distribution Function Identification method (RDFI) (Tancrez and Taine 2004). Coupled classical Radiative Transfer Equations (RTEs) associated with the different non-opaque phases allow the radiative intensity fields $I_{\gamma ,\nu } \left( \mathbf{{r}}, \mathbf{{u}} \right)$ in all these phases to be computed.

In many cases, however, extinction within a homogenized phase is not characterized by an exponential law: the medium is then non-Beerian. It is commonly the case of statistically anisotropic porous media or even of some statistically isotropic (e.g., foams of intermediate porosity). Such homogenized phases are completely characterized, in our approach (Taine et al. 2010), by an extinction cumulated distribution function ($G^\mathrm{ext}_\gamma$), an absorption or a scattering cumulated probability ($P^\mathrm{sc}_\gamma$ or $P^\mathrm{a}_\gamma$, respectively), and a phase function ($p_\gamma$). These quantities have been determined using the methods defined in previous studies (Tancrez and Taine 2004; Zeghondy et al. 2006a; Petrasch et al. 2007; Haussener et al. 2009; Haussener et al. 2010b; Taine et al. 2010; Taine and Iacona 2012). In that case, coupled Generalized Radiative Transfer Equations (GRTEs) associated with the different non-opaque phases also allow the radiative intensity fields $I_{\gamma ,\nu } \left( \mathbf{{r}}, \mathbf{{u}} \right)$ to be computed. As a GRTE is directly expressed as a function of $G^\mathrm{ext}_\gamma , P^\mathrm{sc}_\gamma$, and $p_\gamma$, a numerical Monte Carlo transfer model, based on cumulative distribution functions, does not require more computing time than in the case of a classical RTE (Taine et al. 2010).

The coupling method in the present paper can be applied to both Beerian and non-Beerian homogenized phases, by following the same procedure. Within any homogenized non-opaque phase $\gamma$ (fluid or solid), the radiative energy generation rate per unit volume of the medium $P^\mathrm{R}_\gamma$ is given, at a point $M(\mathbf{{r}})$, by

$$\begin{aligned} \fancyscript{P}^\mathrm{R}_\gamma \left( \mathbf{{r}} \right) = -{\varvec{\nabla }\, \cdot \,}\mathbf{{q}}_\gamma ^\mathrm{R}, \end{aligned}$$

(5)

where $\mathbf{{q}}^\mathrm{R}_\gamma$ is the radiative flux vector. This flux is a function of the radiative intensity field $I_{\gamma ,\nu }$ in the $\gamma$-phase such that

$$\begin{aligned} \mathbf{{q}}_\gamma ^\mathrm{R} \left( \mathbf{{r}} \right) = \int _0^\infty \left( \int _{4 \,\pi } \mathbf{{u}} \ I_{\gamma ,\nu } \left( \mathbf{{r}}, \mathbf{{u}} \right) \, \mathrm{d}\varOmega \right) \mathrm{d}\nu , \end{aligned}$$

(6)

where $\nu$ is the frequency and $\mathbf{{u}}$ is the current unit vector.

The coupled transfer model is iterative. At iteration $n,{\fancyscript{P}_\gamma ^\mathrm{R}}^{(n)}$ and, if necessary, the radiative flux ${\mathbf{{q}}_\gamma ^\mathrm{R}}^{(n)} \left( \mathbf{{r}} \right) \cdot \mathbf{{n}}$ at an opaque wall are computed from the temperature fields issued, at iteration $n-1$, from the energy balance equations of the phases and their boundary conditions. At iteration $n$, ${P_\gamma ^\mathrm{R}}^{(n)}$ is then a source term of the $\gamma$-phase energy balance equation and ${\mathbf{{q}}_\gamma ^\mathrm{R}}^{(n)} \left( \mathbf{{r}} \right) \cdot \mathbf{{n}}$ is a contribution to the boundary condition at any possible opaque interface. This scheme is applied in Sect. 4.

In practice, a radiative Fourier law, also called diffusion approximation, can very often be applied to homogenized phases of a porous medium. Gomart and Taine (2011) have shown that this law is valid around a point $M(\mathbf{{r}})$ if two conditions are satisfied: (a) The point $M(\mathbf{{r}})$ does not belong to a radiative boundary layer of the whole porous medium, i.e., is located at least at a distance greater than $l_b^\mathrm{R} = 5 / \kappa ^\mathrm{eff}_\gamma$ from any boundary of the porous medium; $\kappa ^\mathrm{eff}_\gamma$ is an effective absorption coefficient which accounts for multiple scattering. This first criterion ensures that the medium is optically thick in all directions. (b) The temperature field $\varTheta _\gamma (M)$ satisfies the second criterion

$$\begin{aligned} \frac{1}{\varTheta _\gamma } \frac{\mathrm{d}\varTheta _\gamma }{\mathrm{d}x} < \eta \, \kappa _\gamma ^\mathrm{eff}, \end{aligned}$$

(7)

where $\eta$ depends on the desired accuracy on the result (Gomart and Taine 2011). Eq. (7) has to be satisfied at any scale $\mathrm{d}x$, starting from the finest one at which $\varTheta _\gamma$ is defined. High temperature variations or discontinuities, for instance due to a flame front within the medium, therefore, prevent the radiative Fourier law from being used in the whole medium.

The radiative Fourier law is a function of the temperature gradients within possibly coupled non-opaque phase. In the Beerian case, a perturbation technique of the RTE allows the radiative conductivity tensors to be expressed, from the refractive index $n_\gamma$, the extinction and scattering coefficients, $\beta _\gamma$ and $\sigma _\gamma$, and the scattering asymmetry parameter $g_\gamma$ of the phases (Taine et al. 2010; Taine and Iacona 2012). This development is similar to the introduction of the classical thermal conductivity by a perturbation of the Boltzman equation in the continuous medium approach. For non-Beerian homogenized phases, generalized extinction and scattering coefficients at equilibrium, $B_\gamma$ and $\Sigma _\gamma$, replace the classical extinction and absorption coefficients (Taine et al. 2010; Taine and Iacona 2012; Chahlafi et al. 2012). The perturbation development is carried out up to the first order, i.e.,

$$\begin{aligned} \fancyscript{P}^\mathrm{R}_\gamma = {\fancyscript{P}^\mathrm{R}_\gamma }^{(0)} + {\fancyscript{P}^\mathrm{R}_\gamma }^{(1)} \end{aligned}$$

(8)

where ${\fancyscript{P}^\mathrm{R}_\gamma }^{(i)}$ is the $i$-th perturbation order. The zeroth-order term ${\fancyscript{P}^\mathrm{R}_\gamma }^{(0)}$ represents the radiative exchanges within an elementary volume $\mathrm{d}\fancyscript{V}$ where each phase is assumed isothermal. It vanishes if only one of the two phases is absorbing. The first-order term ${\fancyscript{P}^\mathrm{R}_\gamma }^{(1)}$ is associated with exchanges between $\mathrm{d}\fancyscript{V}$ and adjacent volumes $\mathrm{d}\fancyscript{V}^{\prime }$.

At this point, it is worth discussing the spatial resolution of the radiation model. On the one hand, the spatial resolution of the radiative properties of extinction, absorption, and scattering are mainly limited by the spatial scale $l_t$ of the description of the medium, that is often the spatial resolution of an X- or $\gamma$-ray tomography. If the medium is analytically defined, geometrical information is available at any scale and $l_t$ is only limited by the resolution of the computational model. These limitations are generally much smaller than the pore size.

On the other hand, radiation emission is based, at local thermodynamic equilibrium of matter, on the spatial resolution of the temperature field $\varTheta _\gamma$, which depends in practice on the matter modeling, as discussed in Sect. 4. This spatial limitation is generally more restrictive and strongly depends on the couple of phases involved: opaque/transparent (O/T), semi-transparent/semi-transparent (ST/ST), semi-transparent/transparent (ST/T), or opaque/semi-transparent (O/ST). The first three cases are pesented in the next section. The last O/ST case, more complex, is not addressed by this paper (see for instance (Chahlafi et al. 2012)).

3.2 Considered Couples of Phases

Porous media with an opaque solid phase and a transparent fluid one (O/T) are encountered in many applications involving gases (Baillis and Sacadura 2000; Tancrez and Taine 2004; Haussener et al. 2010b; Petrasch et al. 2007). Indeed, gases are generally considered optically transparent at the local scale and radiation transfer only occurs between the walls of the opaque solid matrix. The only homogenized propagation phase $w$ is then characterized by a presence probability within the porous medium, i.e., porosity. It accounts for the statistical wall distribution in a given volume of the porous medium.

The radiative energy generation rate per unit volume ${\fancyscript{P}^\mathrm{R}_w}$ in the propagation phase is determined using Eqs. (5) and (6). Since the propagation phase is in fact, transparent, it is physically more relevant to consider a radiative isotropic homogenized flux $\varphi ^\mathrm{R}_w$ at the fluid-solid interface, given by

$$\begin{aligned} \varphi ^\mathrm{R}_w= \frac{\fancyscript{P}^\mathrm{R}_w}{A}, \end{aligned}$$

(9)

where $A$ stands for the interfacial area per unit volume of the porous medium. Computations of $\varphi ^\mathrm{R}_w$ can be carried out from a RTE (or a GRTE) applied to the homogenized phase.

If the validity conditions of the Fourier law defined in Sect. 3.1 are satisfied, ${\fancyscript{P}^\mathrm{R}_w}^{(0)}$ is zero, since the fluid phase is transparent. An isotropic radiative conductivity $k_w^\mathrm{R}$ is introduced at the first perturbation order and $\varphi _w^\mathrm{R}$ becomes

$$\begin{aligned} \varphi ^\mathrm{R}_w= \frac{1}{A} {\varvec{\nabla }\, \cdot \,}\left[ k^\mathrm{R}_w\left( \varTheta _w\right) {\varvec{\nabla }}\varTheta _w\right] , \end{aligned}$$

(10)

where the radiative conductivity $k_w^\mathrm{R}$ is a scalar, as the homogenized phase is statistically isotropic; $k_w^\mathrm{R}$ simply writes, if the homogenized phase is non-Beerian and gray (Taine et al. 2010),

$$\begin{aligned} k^\mathrm{R}_w\left( \varTheta _w\right) = \frac{16 \pi }{3} \frac{\varPi _f}{B_w- \Sigma _wg_w} \, \sigma \, \varTheta _w^3, \end{aligned}$$

(11)

where $\sigma$ is the Stefan-Boltzmann constant and $\varPi _f$ the volume fraction of the fluid phase. If the medium is Beerian, $B_w$ and $\Sigma _w$ are replaced by $\beta _w$ and $\sigma _w$, respectively. A generalization to a non-gray medium is given by Taine et al. (2010).

When both the solid and fluid phases are semi-transparent (ST/ST), two GRTEs (or RTEs) are coupled (Zeghondy et al. 2006a; Taine and Iacona 2012). The obtained coupled intensity fields allow the radiative energy generation rate per unit volume given by Eq. (5) to be determined in each phase.

When the validity conditions of the Fourier law, given in Sect. 3.1, are satisfied, the perturbation zeroth-order contribution to the radiative energy generation rate per unit volume is given, for gray phases for simplicity, by

$$\begin{aligned} {\fancyscript{P}_f^\mathrm{R}}^{(0)} = -{\fancyscript{P}_s^\mathrm{R}}^{(0)} = \frac{ \varPi _f\, n_f^2 \, K_f\, K_s\, \Sigma _{{ fs}}}{ K_{f} K_{s} + K_{f} \Sigma _{{{ sf}}} + K_{s} \Sigma _{{{ fs}}} } \, \sigma \left( \varTheta _s^4 -\varTheta _f^4 \right) , \end{aligned}$$

(12)

where $\varTheta _f$ and $\varTheta _s$ are the homogenized temperatures given by Eq. (2). $\Sigma _{{ sf}}$ is the partial scattering coefficient associated with radiation that is scattered from the homogenized phase $s$ to the homogenized phase $f$ (transmitted at the local scale from the $s$ phase to the $f$ phase). Eq. (12) represents the power exchanged between the phases within an elementary volume $\mathrm{d}V$ of the porous medium.

The first-order contributions account for radiative exchanges between $\mathrm{d}V$ and the adjacent volume elements, within the same phase and between the two phases, i.e.,

$$\begin{aligned} {\fancyscript{P}^\mathrm{R}_\gamma }^{(1)} = {\varvec{\nabla }\, \cdot \,}\left( k_{\gamma f}^\mathrm{R} {\varvec{\nabla }}\varTheta _f+ k_{\gamma s}^\mathrm{R} {\varvec{\nabla }}\varTheta _s\right) \gamma = f,s. \end{aligned}$$

(13)

The partial conductivities $k_{\gamma f}^\mathrm{R}$ and $k_{\gamma s}^\mathrm{R}$ are numerically determined using a procedure similar to the approach of Chahlafi et al. (2012). It is worth noticing that the zeroth-order term is generally dominant (Chahlafi et al. 2012).

A porous medium with a transparent fluid phase and an opaque solid one (O/T) has often been considered in previous studies (Baillis and Sacadura 2000; Zeghondy et al. 2006a; Haussener et al. 2009). The associated model is deduced from the ST/ST case by considering that the homogenized fluid phase does not emit or absorb, but only scatters radiation (Taine and Iacona 2012). The GRTE (or RTE) for the solid phase remains unchanged. When the validity conditions of the Fourier law given in Sect. 3.1 are satisfied, ${\fancyscript{P}^\mathrm{R}_f}^{(0)}, {\fancyscript{P}^\mathrm{R}_s}^{(0)}$, and ${\fancyscript{P}^\mathrm{R}_f}^{(1)}$ are zero, since emission and absorption only occur within the solid phase. Therefore, the only contribution is

$$\begin{aligned} {\fancyscript{P}^\mathrm{R}_s}^{(1)} = {\varvec{\nabla }\, \cdot \,}\left( k^\mathrm{R}_s{\varvec{\nabla }}\varTheta _s\right) . \end{aligned}$$

(14)

In Eq. (14), the value of $k^\mathrm{R}_s$ is strongly influenced by the scattering properties associated with the transparent fluid phase, especially at high porosity.

4 Macroscopic Modeling

This section is dedicated to the coupling of the radiative transfer model with an upscaling model for energy transport in matter based on the volume averaging method (Whitaker 1999). As previously mentioned, this upscaling method requires the scale separation given by Eq. (1). More accurately, the use of the spatial averaging theorems and the simplifications associated with the spatial decomposition in the averaging procedure leads to the following form of the length-scale constraints (Whitaker 1999)

$$\begin{aligned} l_f, l_s&\ll r^\mathrm{m}, \end{aligned}$$

(15)

$$\begin{aligned} \left( r^\mathrm{m}\right) ^2&\ll L^2, \end{aligned}$$

(16)

where the characteristic length scales of the fluid $l_f$ and solid $l_s$ phases within the averaging volume are generally assumed to be of the same order of magnitude. Let us recall that these length-scale constraints have been written assuming that conduction and convection within phases at the pore scale are based on the continuum approach (the mean free path smaller than $l_f, l_s$).

For conciseness, the volume averaging procedure is not detailed in the present section where only the main steps are described and where our attention is focused on the radiation contribution in the derivation of the macroscopic model. Details regarding the volume averaging method applied to heat transfer with thermal non equilibrium are provided by Quintard and Whitaker (1993a) and Quintard and Whitaker (2000). Let us just recall that this upscaling method consists in applying the averaging operator

$$\begin{aligned} \langle {\varPsi _\gamma }\rangle ^\mathrm{m} = \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{V}_\gamma ^\mathrm{m}} \varPsi _\gamma \, \mathrm{d}\fancyscript{V}, \end{aligned}$$

(17)

to the different terms of the local conservation equations. In Eq. (17), $\langle {\varPsi _\gamma }\rangle ^\mathrm{m}$ is the superficial average of the generic quantity $\varPsi _\gamma$ in the $\gamma$-phase. The introduction of the intrinsic average

$$\begin{aligned} \langle {\varPsi _\gamma }\rangle ^{\mathrm{m}\gamma } = \frac{1}{\fancyscript{V}^\mathrm{m}_\gamma } \int _{\fancyscript{V}_\gamma ^\mathrm{m}} \varPsi _\gamma \, \mathrm{d}\fancyscript{V} \end{aligned}$$

(18)

is also required. The intrinsic and superficial averages are related by

$$\begin{aligned} \langle {\varPsi _\gamma }\rangle ^\mathrm{m} = \varPi _\gamma \langle {\varPsi _\gamma }\rangle ^{\mathrm{m}\gamma } \end{aligned}$$

(19)

where $\varPi _\gamma$ is the volume fraction of the $\gamma$-phase. The volume averaging method requires the application of the following averaging theorems:

$$\begin{aligned} \langle {\nabla \varPsi _\gamma }\rangle ^\mathrm{m}&= \nabla \langle {\varPsi _\gamma }\rangle ^\mathrm{m} + \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\varPsi _\gamma \ \mathrm{d}\fancyscript{A},\end{aligned}$$

(20)

$$\begin{aligned} \langle {\nabla \cdot \mathbf{{A_\gamma }}}\rangle ^\mathrm{m}&= \nabla \cdot \langle {\mathbf{{A_\gamma }}}\rangle ^\mathrm{m} + \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot \mathbf{{A_\gamma }} \ \mathrm{d}\fancyscript{A},\end{aligned}$$

(21)

$$\begin{aligned} \left\langle {\frac{\partial \varPsi _\gamma }{\partial t}}^\mathrm{m}\right\rangle&= \frac{\partial \langle {\varPsi _\gamma }\rangle ^\mathrm{m} }{\partial t} - \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot \mathbf{{w}}_{{ fs}}\varPsi _\gamma \ \mathrm{d}\fancyscript{A}, \end{aligned}$$

(22)

where $\mathbf{{A}}_\gamma$ is a generic vector quantity and $\mathbf{{w}}_{{ fs}}$ is the velocity of the fluid-solid interface. Furthermore, this upscaling method requires at different levels the introduction of the spatial decomposition (Gray 1975)

$$\begin{aligned} \varPsi _\gamma = \langle {\varPsi _\gamma }\rangle ^{\mathrm{m} \gamma } + \widetilde{\varPsi }_\gamma \end{aligned}$$

(23)

where $\widetilde{\varPsi }_\gamma$ represents the deviation of $\varPsi _\gamma$ in the $\gamma$-phase. In order to include radiative transfer in this averaging procedure, it is first necessary to verify the compatibility of these length scale constraints with the local spatial resolution used for the radiation model at the local scale. As mentioned before, this compatibility is obtained when the tomography resolution $l_t$ of the local structure of the porous medium satisfies

$$\begin{aligned} l_t \ll l_f. \end{aligned}$$

(24)

It is worth mentioning that the homogenized temperature $\varTheta _{\gamma }$, given by Eq. (2) or (3), has a resolution of the order of magnitude of the size $r^\mathrm{R}$ of the radiative averaging volume $\fancyscript{V}^\mathrm{R}$. $r^\mathrm{R}$ has to be chosen as small as possible to guarantee the best tracking of the variations of $\varTheta _\gamma$; its minimal size is the one which guarantees the inclusion of a representative element (regarding radiation) of the $\gamma$-phase in $\fancyscript{V}^\mathrm{R}$. In macroscopic 1D configurations, $\varTheta _\gamma$ is constant over planes; in macroscopic 2D configurations, it is constant over lines. In these two cases, $r^\mathrm{R}$ is, therefore, close to $l_t$. In macroscopic 3D configurations, the $\varTheta _\gamma$ field does not feature any spatial invariance and $r^\mathrm{R}$ is close to $l_f$. In the following sections, the coupled upscaling procedure is applied for different combinations of opaque, transparent, or semi-transparent phases.

4.1 The Opaque/Transparent (O/T) Case

The local equations for energy conservation for the fluid and the solid phases are, respectively,

$$\begin{aligned} \left( \rho _fc_{p f} \right) \left( \frac{\partial T_f}{\partial t} + \mathbf{{v}}_f\cdot {\varvec{\nabla }}T_f\right)&= {\varvec{\nabla }\, \cdot \,}\left( k_f{\varvec{\nabla }}T_f\right) \quad \quad \quad \text{ within } \,\fancyscript{V}^\mathrm{m}_f,\end{aligned}$$

(25)

$$\begin{aligned} \left( \rho _sc_{p s} \right) \frac{\partial T_s}{\partial t}&= {\varvec{\nabla }\, \cdot \,}\left( k_s{\varvec{\nabla }}T_s\right) \quad \quad \quad \text{ within } \,\fancyscript{V}^\mathrm{m}_s. \end{aligned}$$

(26)

These equations are associated with the boundary conditions at the fluid-solid interface $\fancyscript{A}^\mathrm{m}$

$$\begin{aligned} T_f&= T_s\quad \quad \qquad \qquad \qquad \ \text{ at } \,\fancyscript{A}^\mathrm{m},\end{aligned}$$

(27)

$$\begin{aligned} - \mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}T_f+ \varphi ^\mathrm{R}_w&= - \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}T_s\quad \quad \quad \text{ at } \,\fancyscript{A}^\mathrm{m}, \end{aligned}$$

(28)

where $\mathbf{{n}}_{{ fs}}$ is the interfacial normal vector oriented from the fluid phase to the solid phase, and $\varphi ^\mathrm{R}_w$ is a homogenized isotropic radiative flux. If the validity conditions of Fourier’s law are satisfied, $\varphi ^\mathrm{R}_w$ is given by Eq. (10). Otherwise, it is obtained from Eqs. (5), (6), and (9) by using the GRTE (Taine et al. 2010). Let us recall that $\varphi ^\mathrm{R}_w$ strongly depends on the temperature $\varTheta _w$ through the emission source term (Taine and Iacona 2012). If the macroscopic system does not feature any invariance, the three-dimensional spatial variations of $\varTheta _w$ are accurately represented by considering $\fancyscript{V}^\mathrm{R}$ as small as possible, but large enough to include a fluid/solid interface element. This is generally satisfied if ${r}^\mathrm{R}$ is of the same order of magnitude as $l_\gamma$ ($\gamma = f,s$). It is worth noticing that the definition of the $\varTheta _w$ field makes the resolution of the energy conservation numerical and iterative.

Assuming that the scale separation given by Eqs. (15) and (16) is satisfied, the application of the averaging theorems to Eqs. (25) and (26) leads to the non-closed averaged conservation equations for both the fluid and solid phases

$$\begin{aligned}&\varPi _f\left( \rho _fc_{pf} \right) \frac{\partial \langle {T_f}\rangle ^{\mathrm{m}f}}{\partial t} + \varPi _f\left( \rho _fc_{pf} \right) \langle {\mathbf{{v}}_f}\rangle ^{\mathrm{m}f} \cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \left( \rho _fc_{pf} \right) {\varvec{\nabla }\, \cdot \,}\langle {{\mathbf{{\widetilde{v}}}_f}{\widetilde{T}_{f}}^\mathrm{m}}\rangle \nonumber \\&\quad =\varPi _f{\varvec{\nabla }\, \cdot \,}\left( k_f{\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\widetilde{T}_f \ \mathrm{d}\fancyscript{A} \right) + \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\widetilde{T}_f \ \mathrm{d}\fancyscript{A},\qquad \quad \end{aligned}$$

(29)

$$\begin{aligned}&\qquad \quad \varPi _s\left( \rho _sc_{ps} \right) \frac{\partial \langle {T_s}\rangle ^{\mathrm{m}s}}{\partial t} = \varPi _s{\varvec{\nabla }\, \cdot \,}\left( k_s{\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + {\varvec{\nabla }\, \cdot \,}\left( \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\widetilde{T}_s \ \mathrm{d}\fancyscript{A} \right) \nonumber \\&\quad \quad \quad + \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}\widetilde{T}_s \ \mathrm{d}\fancyscript{A}. \end{aligned}$$

(30)

At this stage, note that Eqs. (29) and (30) are identical to those provided in the absence of radiation (Quintard et al. 1997; Quintard and Whitaker 2000).

In order to derive a closed form of these equations, the deviations of the temperature fields $\widetilde{T}_\gamma$ ($\gamma = l,s$) have to be written in terms of intrinsic averaged quantities. This is achieved by the derivation of associated closure problems, the first step consisting in deriving deviation problems.

4.1.1 Deviation Problems

The deviation equations are obtained by subtracting the non-closed macroscopic equations (Eqs. (29) and (30)), divided by the porosity $\varPi _f$, from the local equations (Eqs. (25) and (26)) in which the spatial decomposition (Eq. (23)) is introduced. Under the quasi-stationary assumption (Whitaker 1999), the temperature deviation equation for the fluid phase takes the form

$$\begin{aligned}&\left( \rho _fc_{p f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}\widetilde{T}_f+ \left( \rho _fc_{p f} \right) \mathbf{{\widetilde{v}}}_f\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f}\nonumber \\&\quad = k_f{\varvec{\nabla }}^2 \widetilde{T}_f- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\widetilde{T}_f \ \mathrm{d}\fancyscript{A} \quad \quad \text{ within } \, \fancyscript{V}^\mathrm{m}_f. \end{aligned}$$

(31)

Similarly, the temperature deviation equation for the solid phase is

$$\begin{aligned} 0 = k_s{\varvec{\nabla }}^2 \widetilde{T}_s- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}\widetilde{T}_s \ \mathrm{d}\fancyscript{A} \quad \quad \quad \text{ within } \, \fancyscript{V}^\mathrm{m}_s. \end{aligned}$$

(32)

Use of the spatial decomposition (23) in boundary condition (27) leads to

$$\begin{aligned} \widetilde{T}_f= \widetilde{T}_s+ \left( \langle {T_s}\rangle ^{\mathrm{m}s} - \langle {T_f}\rangle ^{\mathrm{m}f} \right) \quad \quad \quad \text{ at } \, \fancyscript{A}^\mathrm{m}. \end{aligned}$$

(33)

As intensity, radiative source terms or other radiative quantities associated with the energy generation rate, $\varphi _w^\mathrm{R}$ is continuously defined over the volume of the whole medium. It can be decomposed under the form

$$\begin{aligned} \varphi _w^\mathrm{R} = \langle {\varphi _w^\mathrm{R}}\rangle ^\mathrm{m} + \widetilde{\varphi }_w^\mathrm{R}. \end{aligned}$$

(34)

Under these circumstances, the deviation form of the boundary condition given by Eq. (28) becomes

$$\begin{aligned}&-\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\widetilde{T}_f+ \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\widetilde{T}_s+ \widetilde{\varphi }^\mathrm{R}_w\nonumber \\&\quad = \mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} - \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \quad \quad \text{ at } \, \fancyscript{A}^\mathrm{m} \end{aligned}$$

(35)

where $\widetilde{\varphi }^\mathrm{R}_w$ has the same spatial resolution as $\varTheta _w$.

4.1.2 Closure

At this stage, we need to express the radiative flux deviation $\widetilde{\varphi }^\mathrm{R}_w$ as a function of $\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$. Let us assume that

$$\begin{aligned} \widetilde{\varphi }^\mathrm{R}_w= \alpha \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \end{aligned}$$

(36)

where $\alpha$ is not a closure variable since it implicitly depends on $\varTheta _w$, itself resulting from the local temperature $T_f$ and $T_s$.

Note that the treatment required for $\varphi ^\mathrm{R}_w$ is actually similar to closure associated with problems involving heterogeneous reactions (Wood et al. 2000; Valdés-Parada et al. 2006). The introduction of Eq. (36) into the boundary condition (35) yields

$$\begin{aligned}&-\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\widetilde{T}_f+ \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\widetilde{T}_s\nonumber \\&\quad =\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} - ( 1 + \alpha ) \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \quad \quad \text{ at } \,\fancyscript{A}^\mathrm{m}. \end{aligned}$$

(37)

Therefore, the deviation problem, where Eq. (35) has been replaced by Eq. (37), suggests to write the deviation temperature fields under the form

$$\begin{aligned} \widetilde{T}_f&= \mathbf{{b}}_{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \mathbf{{b}}_{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} + s_f\left( \langle {T_s}\rangle ^{\mathrm{m}s} - \langle {T_f}\rangle ^{\mathrm{m}f} \right) +r_f\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}, \end{aligned}$$

(38)

$$\begin{aligned} \widetilde{T}_s&= \mathbf{{b}}_{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \mathbf{{b}}_{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s}- s_s\left( \langle {T_f}\rangle ^{\mathrm{m}f} - \langle {T_s}\rangle ^{\mathrm{m}s} \right) + r_s\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}, \end{aligned}$$

(39)

where $\mathbf{{b}}_{{ ff}}, \mathbf{{b}}_{{ fs}}, s_f$, and $r_f$ are the closure variables associated with the fluid phase and $\mathbf{{b}}_{{ sf}}, \mathbf{{b}}_{{ ss}}, s_s$, and $r_s$ those associated with the solid phase. This decomposition is close to the one proposed for a constant interfacial source term (Quintard and Whitaker 2000). In the present case, the closure variables $r_f$ and $r_s$ are associated with the non-constant radiative source.

The introduction of expressions (38) and (39) into the deviation problem provides four closure problems associated with the closure variables $\mathbf{{b}}_{\gamma _1,\gamma _2}, s_\gamma$, and $r_\gamma$, the first three being presented by Quintard et al. (1997) with the same symbols (see Sect. 3 of this reference). For conciseness, we only consider here the derivation of the closure problem associated with the radiative closure variables $r_f$ and $r_s$. This latter takes the following form:

Problem IV

$$\begin{aligned}&\left( \rho _fc_{p_f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}r_f= k_f{\varvec{\nabla }}^2 r_f- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_f \ \mathrm{d}\fancyscript{A}&\text{ within } \, \fancyscript{V}^\mathrm{m}_f\end{aligned}$$

(40a)

$$\begin{aligned}&0 = k_s{\varvec{\nabla }}^2 r_s- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}r_s \ \mathrm{d}\fancyscript{A}&\text{ within } \, \fancyscript{V}^\mathrm{m}_s\end{aligned}$$

(40b)

$$\begin{aligned}&r_f= r_s&\text{ at } \,\fancyscript{A}^\mathrm{m}\end{aligned}$$

(40c)

$$\begin{aligned}&\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}r_f= \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}r_s+ 1 + \alpha&\text{ at } \,\fancyscript{A}^\mathrm{m}\end{aligned}$$

(40d)

$$\begin{aligned}&r_f(\mathbf{{r}} + l_i ) = r_f( \mathbf{{r}} )&\text{ for } \,i = 1,2,3\end{aligned}$$

(40e)

$$\begin{aligned}&r_s( \mathbf{{r}} + l_i ) = r_s( \mathbf{{r}})&\text{ for } \,i = 1,2,3\end{aligned}$$

(40f)

$$\begin{aligned}&\langle {r_f}\rangle ^{\mathrm{m}f} = 0\end{aligned}$$

(40g)

$$\begin{aligned}&\langle {r_s}\rangle ^{\mathrm{m}s} = 0 \end{aligned}$$

(40h)

The validity of the periodic boundary conditions (40e) and (40f) has already been discussed by Quintard and Whitaker (1993b, 1994): They are valid for periodic unit cells and for disordered media where the scale separation constraint is satisfied.

The solution of closure problem IV is the original point of the method. It is important to note that this closure problem depends on $\alpha$, itself depending on the local temperature fields $T_f$ and $T_s$. Consequently, the solution of closure problem IV depends on the solution of the macroscopic conservation equations (see the following section). Therefore, the resolution of the coupled problem requires to follow an iterative sequence (see Fig. 2):

Fig. 2

Flowchart of the iterative sequence

• 1. Closure problems I, II, and III are solved.

• 2. Closure problem IV is solved for initialization. Since this step is performed with $\alpha = 0$, the solution does not depend on the macroscopic fields.

• 3. Effective properties are computed from the solutions of closure problems I–IV. The macroscopic radiation flux field $\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$ is initialized using a macroscopic approximate calculation.

• 4. Closed macroscopic energy equations (64) and (69) (see the following section) are solved.

• 5. Local temperature fields $T_f\left( \mathbf{{r}} \right)$ and $T_s\left( \mathbf{{r}} \right)$ are computed in a volume $\fancyscript{V} \left( \mathbf{{x}} \right)$, centered at $\mathbf{{x}}$. The decomposition $T_\gamma (\mathbf{r} ) = \langle {T_\gamma }\rangle ^{\mathrm{m}\gamma } ( \mathbf{r} ) + \widetilde{T}_\gamma ( \mathbf{r} )$ and Eqs. (38) and (39) can be used. $\fancyscript{V} \left( \mathbf{{x}} \right)$ must be optically thick and can be bigger than the averaging volume $\fancyscript{V}^\mathrm{m} \left( \mathbf{{x}} \right)$. $\varTheta _w$ is then computed over $\fancyscript{V} \left( \mathbf{{x}} \right)$.

• 6. Radiative transfer is computed, using the appriopriate method (GRTE, degenerated GRTE, and radiative Fourier law). This yields the $\varphi ^\mathrm{R}_w$ field, its average $\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$ and the $\alpha$ field.

• 7. Closure problem IV is solved using the new value of the $\alpha$ field.

• 8. Effective properties are computed from the solutions of closure problems I–IV.

Steps 4 to 8 are repeated until convergence of $r_f, r_s$ and $\varphi ^\mathrm{m}_w$ is reached.

4.1.3 Closed Form

The averaged equations are closed by introducing closure relations (38) and (39) into Eqs. (29) and (30). For the fluid phase, this yields

$$\begin{aligned}&\varPi _f\left( \rho _fc_{p f} \right) \frac{\partial \langle {T_f}\rangle ^{\mathrm{m}f}}{\partial t} + \varPi _f\left( \rho _fc_{p f} \right) \langle {\mathbf{{v}}_f}\rangle ^{\mathrm{m}f} \cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \!-\! \mathbf{{u}}_{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \!-\! \mathbf{{u}}_{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s}\nonumber \\&\quad = {\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + A \, h \left( \langle {T_s}\rangle ^{\mathrm{m}s} - \langle {T_f}\rangle ^{\mathrm{m}f} \right) \nonumber \\&\quad \quad + A \, \xi _f\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}, + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_f\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \right) \end{aligned}$$

(41)

where

$$\begin{aligned} A \, \xi _f&= \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_f \ \mathrm{d}\fancyscript{A},\end{aligned}$$

(42)

$$\begin{aligned} A\,\mathbf{{p}}_f&= \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}r_f \ \mathrm{d}\fancyscript{A} - \rho _fc_{p f} \langle {\widetilde{v}_fr_f}\rangle ^\mathrm{m}, \end{aligned}$$

(43)

are the effective transport properties associated with radiation heat transfer. The other transport properties are more classical and their expressions are given by Quintard et al. (1997) (see Sect. 3 of this reference). Similarly, the closed form of the macroscopic transport equation for the solid phase is given by

$$\begin{aligned}&\varPi _s\left( \rho _sc_{p s} \right) \frac{\partial \langle {T_s}\rangle ^{\mathrm{m}s}}{\partial t} - \mathbf{{u}}_{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{u}}_{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s}\nonumber \\&\quad = {\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + A \, h \left( \langle {T_f}\rangle ^{\mathrm{m}f} - \langle {T_s}\rangle ^{\mathrm{m}s} \right) \nonumber \\&\quad \quad + A \, \xi _s\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}. + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_s\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \right) \end{aligned}$$

(44)

Therefore, the effective transport properties associated with radiation are such that

$$\begin{aligned} A \,\xi _s&= \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}r_s \ \mathrm{d}\fancyscript{A},\end{aligned}$$

(45)

$$\begin{aligned} A \, \mathbf{{p}}_s&= \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}r_s \ \mathrm{d}\fancyscript{A}. \end{aligned}$$

(46)

The fourth term in Eqs. (41) and (44) (associated with $\xi _\gamma$) stands for the spatial distribution of the macroscopic volumetric source term due to the radiative flux. In expressions (42) and (45), the scalars $\xi _\gamma$ ($\gamma = f, s$) are analogous to the distribution coefficient introduced by Quintard and Whitaker (2000). A major difference, due to the presence of a non-zero $\alpha$ coefficient in boundary condition (37), is that $\xi _f+ \xi _s$ does not equal 1:

$$\begin{aligned} A \left( \xi _f+ \xi _s\right)&= \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\left( r_f- r_s\right) \ \mathrm{d}\fancyscript{A} \nonumber \\&= \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} 1 + \alpha \ \mathrm{d}\fancyscript{A} \nonumber \\&= A + \frac{1}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \alpha \ \mathrm{d}\fancyscript{A}. \end{aligned}$$

(47)

$\int _{\fancyscript{A}^\mathrm{m}} \alpha \ \mathrm{d}\fancyscript{A}$ will be zero only if the $\alpha$ is symmetric over the averaging volume.

The fifth term on the right-hand side of Eqs. (41) and (44) (associated with $\mathbf{{p}}_\gamma$) represents a macroscopic contribution due to the heterogeneities of the average radiative flux at the fluid/solid interface. It includes coupling effects at the local scale between diffusion, convection (through dispersion), and radiation as well as tortuosity effects. The expressions of the vectors $\mathbf{{p}}_\gamma$ are similar with those of the diffusion-dispersion tensors $\mathbb K _{\gamma _1 \gamma _2}$. The associated macroscopic terms include diffusive and tortuous effects; however, they cannot be interpreted as macroscopic diffusive contributions.

Let us remark that if $\widetilde{\varphi }^\mathrm{R}_w$ is negligible compared to $\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}, \alpha$ becomes negligible compared to $1$ and problem IV degenerates into a form identical to the one presented by Quintard and Whitaker (2000).

4.2 The Semi-Transparent/Semi-Transparent (ST/ST) Case

Let us consider the case where both phases are semi-transparent. Although less common than the O/T case, this case is interesting because of the symmetry between the phases involved.

The radiative energy generation rate is introduced as a volumetric source term in both the fluid and solid local governing equations, yielding, respectively,

$$\begin{aligned} \left( \rho _fc_{p f} \right) \left( \frac{\partial T_f}{\partial t} + \mathbf{{v}}_f\cdot {\varvec{\nabla }}T_f\right)&= {\varvec{\nabla }\, \cdot \,}\left( k_f{\varvec{\nabla }}T_f\right) + P^\mathrm{R}_f\quad \text{ within } \,\fancyscript{V}^\mathrm{m}_f,\end{aligned}$$

(48)

$$\begin{aligned} \left( \rho _sc_{p s} \right) \frac{\partial T_s}{\partial t}&= {\varvec{\nabla }\, \cdot \,}\left( k_s{\varvec{\nabla }}T_s\right) + P^\mathrm{R}_s\quad \text{ within } \,\fancyscript{V}^\mathrm{m}_s, \end{aligned}$$

(49)

where $P^\mathrm{R}_\gamma$ ($\gamma = f, s$) is the energy generation rate provided by the GRTE (denoted $\fancyscript{P}^\mathrm{R}_\gamma$) and divided by phase volume fraction $\varPi _\gamma$. The associated boundary conditions are

$$\begin{aligned} T_f&= T_s\quad \qquad \qquad \qquad \ \text{ at } \,\fancyscript{A}^\mathrm{m},\end{aligned}$$

(50)

$$\begin{aligned} - \mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}T_f&= - \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}T_s\quad \quad \text{ at } \,\fancyscript{A}^\mathrm{m}. \end{aligned}$$

(51)

The application of the averaging theorems on Eqs. (48) and (49) gives rise to the following two non-closed averaged equations

$$\begin{aligned}&\varPi _f\left( \rho _fc_{pf} \right) \frac{\partial \langle {T_f}\rangle ^{\mathrm{m}f}}{\partial t} + \varPi _f\left( \rho _fc_{pf} \right) \langle {\mathbf{{v}}_f}\rangle ^{\mathrm{m}f} \cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \left( \rho _fc_{pf} \right) {\varvec{\nabla }\, \cdot \,}\langle {\widetilde{\mathbf{{v}}}_f\widetilde{T}_f}\rangle \nonumber \\&\quad = \varPi _f{\varvec{\nabla }\, \cdot \,}\left( k_f{\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\widetilde{T}_f \ \mathrm{d}\fancyscript{A} \right) \nonumber \\&\quad \quad +\frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\widetilde{T}_f \ \mathrm{d}\fancyscript{A}+ \varPi _f\langle {P_f^\mathrm{R}}\rangle ^{\mathrm{m}f},\end{aligned}$$

(52)

$$\begin{aligned}&\varPi _s\left( \rho _sc_{ps} \right) \frac{\partial \langle {T_s}\rangle ^{\mathrm{m}s}}{\partial t}=\varPi _s{\varvec{\nabla }\, \cdot \,}\left( k_s{\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + {\varvec{\nabla }\, \cdot \,}\left( \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\widetilde{T}_s \ \mathrm{d}\fancyscript{A} \right) \nonumber \\&\quad +\frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}\widetilde{T}_s \ \mathrm{d}\fancyscript{A}+\varPi _s\langle {P_s^\mathrm{R}}\rangle ^{\mathrm{m}s}, \end{aligned}$$

(53)

where the last terms, $\varPi _f\langle {P_f^\mathrm{R}}\rangle ^{\mathrm{m}f}$ and $\varPi _s\langle {P_s^\mathrm{R}}\rangle ^{\mathrm{m}s}$, are the upscaled energy generation rate in the respective phases.

4.2.1 Deviation Problem

The deviation problem is obtained as in Sect. 4.1.1. For the fluid phase, the deviation equation takes the form

$$\begin{aligned} \left( \rho _fc_{p f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}\widetilde{T}_f&+ \left( \rho _fc_{p f} \right) \widetilde{\mathbf{{v}}}_f\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f}\nonumber \\&= k_f{\varvec{\nabla }}^2 \widetilde{T}_f- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\widetilde{T}_f \ \mathrm{d}\fancyscript{A} + \widetilde{P}^ \mathrm{R}_f\quad \quad \quad \text{ within } \,\fancyscript{V}^\mathrm{m}_f, \end{aligned}$$

(54)

while for the solid phase, we have

$$\begin{aligned} 0 = k_s{\varvec{\nabla }}^2 \widetilde{T}_s- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}\widetilde{T}_s \ \mathrm{d}\fancyscript{A} + \widetilde{P}^\mathrm{R}_s\quad \quad \quad \text{ within } \,\fancyscript{V}^\mathrm{m}_s. \end{aligned}$$

(55)

Use of the spatial decomposition in the boundary conditions (51) and (50) leads to an equation identical to Eq. (33), and to the boundary condition

$$\begin{aligned} - \mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\widetilde{T}_f+ \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\widetilde{T}_s= \mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \quad \quad \text{ at } \, \fancyscript{A}^\mathrm{m}. \end{aligned}$$

(56)

4.2.2 Closure

As in the O/T case, the deviation terms need to be expressed as functions of the macroscopic source terms. Following the approach adopted in Sect. 4.1.2, $\widetilde{P}^\mathrm{R}_\gamma$ ($\gamma = f, s$) is expressed as a function of $\langle {P^\mathrm{R}_\gamma }\rangle ^{\mathrm{m}\gamma }$ such that

$$\begin{aligned} \widetilde{P}^\mathrm{R}_\gamma = \alpha _\gamma \langle {P^\mathrm{R}_\gamma }\rangle ^{\mathrm{m}\gamma }. \end{aligned}$$

(57)

This expression is introduced in Eqs. (54) and (55) to obtain

$$\begin{aligned} \left( \rho _fc_{p f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}\widetilde{T}_f&+ \left( \rho _fc_{p f} \right) \widetilde{\mathbf{{v}}}_f\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f}\nonumber \\&= k_f{\varvec{\nabla }}^2 \widetilde{T}_f- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}\widetilde{T}_f \ \mathrm{d}\fancyscript{A} + \alpha _f\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} \quad \text{ within } \,\fancyscript{V}^\mathrm{m}_f\qquad \quad \end{aligned}$$

(58)

and

$$\begin{aligned} 0 = k_s{\varvec{\nabla }}^2 \widetilde{T}_s- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}\widetilde{T}_s \ \mathrm{d}\fancyscript{A} + \alpha _s\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s} \text{ within } \,\fancyscript{V}^\mathrm{m}_s\end{aligned}$$

(59)

Here, the deviation problem involves the two additional source terms $\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f}$ and $\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s}$. This suggests the following form for the temperature deviations

$$\begin{aligned} \widetilde{T}_f&= \mathbf{{b}}_{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \mathbf{{b}}_{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} + s_f\left( \langle {T_s}\rangle ^{\mathrm{m}s} - \langle {T_f}\rangle ^{\mathrm{m}f} \right) \nonumber \\&\quad + r_{{ ff}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} + r_{{ fs}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s}, \end{aligned}$$

(60)

$$\begin{aligned} \widetilde{T}_s&= \mathbf{{b}}_{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} + \mathbf{{b}}_{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} - s_s\left( \langle {T_f}\rangle ^{\mathrm{m}f} - \langle {T_s}\rangle ^{\mathrm{m}s} \right) \nonumber \\&\quad + r_{{ sf}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} + r_{{ ss}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s}. \end{aligned}$$

(61)

The introduction of expressions (60) and (61) in the deviation problem leads to five closure problems. Those associated with the first three closure variables are identical to problems I, II, and III already derived in Sect. 4.1.2. Closure problems IV and V for variables $r_{{ ff}}, r_{{ fs}}, r_{{ sf}}$, and $r_{{ ss}}$ are provided below.

Problem IV

$$\begin{aligned}&\left( \rho _fc_{p_f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}r_{{ ff}}= k_f{\varvec{\nabla }}^2 r_{{ ff}}- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ ff}} \ \mathrm{d}\fancyscript{A}+ \alpha _f&\text{ within } \,\fancyscript{V}^\mathrm{m}_f\end{aligned}$$

(62a)

$$\begin{aligned}&0 = k_s{\varvec{\nabla }}^2 r_{{ sf}}- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}r_{{ sf}} \ \mathrm{d}\fancyscript{A}&\text{ within } \,\fancyscript{V}^\mathrm{m}_s\end{aligned}$$

(62b)

$$\begin{aligned}&r_{{ ff}}= r_{{ sf}}&\text{ at } \,\fancyscript{A}^\mathrm{m}\end{aligned}$$

(62c)

$$\begin{aligned}&\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}r_{{ ff}}= \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}r_{{ sf}}&\fancyscript{A}^\mathrm{m}\end{aligned}$$

(62d)

$$\begin{aligned}&r_{{ ff}}( \mathbf{{r}} + l_i ) = r_{{ ff}}( \mathbf{{r}} )&\text{ for } \,i = 1,2,3\end{aligned}$$

(62e)

$$\begin{aligned}&r_{{ sf}}( \mathbf{{r}} + l_i ) = r_{{ sf}}( \mathbf{{r}} )&\text{ for } \,i = 1,2,3\end{aligned}$$

(62f)

$$\begin{aligned}&\langle {r_{{ ff}}}\rangle ^{\mathrm{m}f} = 0\end{aligned}$$

(62g)

$$\begin{aligned}&\langle {r_{{ sf}}}\rangle ^{\mathrm{m}s} = 0 \end{aligned}$$

(62h)

Problem V

$$\begin{aligned}&\left( \rho _fc_{p_f} \right) \mathbf{{v}}_f\cdot {\varvec{\nabla }}r_{{ fs}}= k_f{\varvec{\nabla }}^2 r_f- \frac{k_f}{\fancyscript{V}^\mathrm{m}_f} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ fs}} \ \mathrm{d}\fancyscript{A}&\text{ within } \, \fancyscript{V}^\mathrm{m}_f\end{aligned}$$

(63a)

$$\begin{aligned}&0 = k_s{\varvec{\nabla }}^2 r_{{ ss}}- \frac{k_s}{\fancyscript{V}^\mathrm{m}_s} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}\cdot {\varvec{\nabla }}r_{{ ss}} \ \mathrm{d}\fancyscript{A} + \alpha _s&\text{ within } \,\fancyscript{V}^\mathrm{m}_s\end{aligned}$$

(63b)

$$\begin{aligned}&r_{{ fs}}= r_{{ ss}}&\text{ at } \,\fancyscript{A}^\mathrm{m}\end{aligned}$$

(63c)

$$\begin{aligned}&\mathbf{{n}}_{{ fs}}\cdot k_f{\varvec{\nabla }}r_{{ fs}}= \mathbf{{n}}_{{ fs}}\cdot k_s{\varvec{\nabla }}r_{{ ss}}&\text{ at } \,\fancyscript{A}^\mathrm{m}\end{aligned}$$

(63d)

$$\begin{aligned}&r_{{ fs}}( \mathbf{{r}} + l_i ) = r_f( \mathbf{{r}} )&\text{ for } \,i = 1,2,3\end{aligned}$$

(63e)

$$\begin{aligned}&r_{{ ss}}( \mathbf{{r}} + l_i ) = r_s( \mathbf{{r}} )&\text{ for }\,i = 1,2,3\end{aligned}$$

(63f)

$$\begin{aligned}&\langle {r_{{ fs}}}\rangle ^{\mathrm{m}f} = 0\end{aligned}$$

(63g)

$$\begin{aligned}&\langle {r_{{ ss}}}\rangle ^{\mathrm{m}s} = 0 \end{aligned}$$

(63h)

Comments made in the previous section also apply for these closure problems. The resolution sequence is the same as in the O/T case (see Sect. 4.1.2).

4.2.3 Closed Form

The averaged equations are closed by introducing the closure relations (60) and (61) into Eqs. (52) and (53). The closed form for the fluid phase is

$$\begin{aligned}&\varPi _f\left( \rho _fc_{p f} \right) \frac{\partial \langle {T_f}\rangle ^{\mathrm{m}f}}{\partial t}\!+\! \varPi _f\left( \rho _fc_{p f} \right) \langle {\mathbf{{v}}_f}\rangle ^{\mathrm{m}f} \cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{u}}_{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{u}}_{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s}\nonumber \\&\quad ={\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ ff}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ fs}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + A \, h \left( \langle {T_s}\rangle ^{\mathrm{m}s} - \langle {T_f}\rangle ^{\mathrm{m}f} \right) \nonumber \\&\quad \quad + \varPi _f\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} - \xi _{{ sf}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} + \xi _{{ fs}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s}\nonumber \\&\quad \quad + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_{{ ff}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_{{ fs}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s} \right) \end{aligned}$$

(64)

where the effective properties associated with radiation transfer are given by

$$\begin{aligned} \xi _{{ sf}}&= - \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ ff}} \ \mathrm{d}\fancyscript{A} = \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ sf}} \ \mathrm{d}\fancyscript{A},\end{aligned}$$

(65)

$$\begin{aligned} \xi _{{ fs}}&= \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ fs}} \ \mathrm{d}\fancyscript{A} = - \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}\cdot {\varvec{\nabla }}r_{{ ss}} \ \mathrm{d}\fancyscript{A}, \end{aligned}$$

(66)

$$\begin{aligned} A \, \mathbf{{p}}_{{ ff}}&= \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}r_{{ ff}} \ \mathrm{d}\fancyscript{A} - \left( \rho _fc_{p f} \right) \langle {\widetilde{\mathbf{{v}}}_fr_{{ ff}}}\rangle ^\mathrm{m}, \end{aligned}$$

(67)

$$\begin{aligned} A \, \mathbf{{p}}_{{ fs}}&= \frac{k_f}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ fs}}r_{{ fs}} \ \mathrm{d}\fancyscript{A} - \left( \rho _fc_{p f} \right) \langle {\widetilde{\mathbf{{v}}}_fr_{{ fs}}}\rangle ^\mathrm{m}, \end{aligned}$$

(68)

Similarly, we have, for the solid phase,

$$\begin{aligned}&\varPi _s\left( \rho _sc_{p s} \right) \frac{\partial \langle {T_s}\rangle ^{\mathrm{m}s}}{\partial t} - \mathbf{{u}}_{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} - \mathbf{{u}}_{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s}\nonumber \\&={\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ sf}}\cdot {\varvec{\nabla }}\langle {T_f}\rangle ^{\mathrm{m}f} \right) +{\varvec{\nabla }\, \cdot \,}\left( \mathbb K _{{ ss}}\cdot {\varvec{\nabla }}\langle {T_s}\rangle ^{\mathrm{m}s} \right) + A \, h \left( \langle {T_f}\rangle ^{\mathrm{m}f} - \langle {T_s}\rangle ^{\mathrm{m}s} \right) \nonumber \\&\quad + \varPi _s\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s} + \xi _{{ sf}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} - \xi _{{ fs}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s}\nonumber \\&\quad + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_{{ sf}}\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f} \right) + {\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_{{ ss}}\langle {P^\mathrm{R}_s}\rangle ^{\mathrm{m}s} \right) \end{aligned}$$

(69)

where the additional effective transport properties associated with radiation are

$$\begin{aligned} A \, \mathbf{{p}}_{{ sf}}&= \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}r_{{ sf}} \ \mathrm{d}\fancyscript{A}, \end{aligned}$$

(70)

$$\begin{aligned} A \, \mathbf{{p}}_{{ ss}}&= \frac{k_s}{\fancyscript{V}^\mathrm{m}} \int _{\fancyscript{A}^\mathrm{m}} \mathbf{{n}}_{{ sf}}r_{{ ss}} \ \mathrm{d}\fancyscript{A}. \end{aligned}$$

(71)

The last five terms on the right-hand side of Eqs. (64) and (69) are macroscopic radiative source terms. The first one represents the phase repartition of the radiative energy generation rate. Provided that the conditions of an optically thick medium are satisfied, and according to Eq. (8), this radiative source can be decomposed into zeroth- and first-order contributions. The zeroth order corresponds to the radiative exchange between phases due to radiation (Eq. (12)) while the first-order contribution stands for a diffusive inter-phase interaction (Eq. (13)) originating from radiation. The second and the third terms represent the macroscopic phase exchange where the scalars $\xi _{\gamma _1 \gamma _2}$ distribute a part of the macroscopic radiative energy generation rate from a phase to the other. It is interesting to note that because of its nature, the expressions for $\xi _{\gamma _1 \gamma _2}$ given by Eqs (64) and (69) are similar to the expression of the heat transfer coefficient $h$ provided by Quintard et al. (1997) (see Sect. 3 of this reference). The same observation can be made for the last two terms where the vectors $\mathbf{{p}}_{\gamma _1 \gamma _2}$ contain contributions associated with both the tortuosity of the porous microstructure and the dispersion contribution (for the fluid phase). The other transport properties associated with the classical diffusion/convection modes are given by Quintard et al. (1997).

4.3 The Semi-Transparent/Transparent (ST/T) Case

In this configuration, more common than the previous ST/ST case, the solid phase is semi-transparent while the fluid one is transparent. The ST/T case is a particular case of the ST/ST configuration. The major difference lies in the zero value of the radiative energy generation rate $P^\mathrm{R}_f$ and its average $\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f}$. The closure variables $r_{{ ff}}$ and $r_{{ fs}}$ are consequently removed from the closure relations (60) and (61). The reduction of the number of closure variables leads to the removal of closure problem IV (Eqs. (40a)). Closure problem V remains unchanged.

The macroscopic closed form is made of Eqs. (64) and (69) in which every term associated with $\langle {P^\mathrm{R}_f}\rangle ^{\mathrm{m}f}$ is removed. The expressions of the effective properties involved remain unchanged.

5 Numerical Determination of the Averaged Properties

This section concerns the determination of the effective transport properties associated with radiation in the closed form of the macroscopic equations for the opaque/transparent (O/T) case (Eqs. (64) and (69)). A simple case, in which $\alpha = 0$, is considered. It corresponds to a case in which the deviation field $\widetilde{\varphi }^\mathrm{R}_w$ of the radiation flux is negligible. This corresponds to steps 1 and 2 of the iterative sequence mentioned in Sect. 4.1.3. The associated closure problems are solved in unit cells where the solid phase is composed of cylinders arranged in an equilateral triangle array (see Fig. 3). Numerical calculations are performed using the COMSOL Multipysics software package, for different values of the conductivity ratio $k_s/ k_f$ and of the cell Péclet nummber defined by

$$\begin{aligned} \mathrm{Pe}= \frac{\rho _fc_{p f} \langle {\mathbf{v}_f}\rangle ^f l_f}{k_f} \end{aligned}$$

(72)

The validation of the numerical solutions of the closure problems has been performed by comparing the solutions of closure problems I-III with the data provided by Quintard et al. (1997) for inline and staggered arrays of cylinders, with a porosity $\varPi _f= {0.38}$. For conciseness, only the longitudinal thermal dispersion coefficient is represented in Fig. 4 but all the averaged properties have been compared. As expected, a diffusion regime is observed at small values of the Péclet number, while an asymptotic dispersive regime is found at large Péclet number. The influence of the conductivity ratio is also in quantitative agreement with the results presented by Quintard et al. (1997): changes are significant only for ${0.1} \le k_s/k_f\le 10$. Very good agreement with the data provided by Quintard et al. (1997) is found for the other dispersion-diffusion coefficients and for the volumetric heat transfer coefficient. Discrepencies have been observed in the results for the pseudo-convective vectors $\mathbf{{u}}_{\gamma _1, \gamma _2}$; however, since no additional reference data have been published, the interpretation of these discrepencies remains unsure.

Fig. 3

Geometry of the equilateral array of cylinders

Fig. 4

Longitudinal thermal dispersion tensor for inline (left) and staggered array of cylinders (right). $\varPi _f= {0.38}$

As shown in Sect. 4.1.3, the closed form of the macroscopic conservation equations for an opaque/transparent configuration (Eqs. (41) and (44)) involves the additional averaged properties $\xi , \mathbf{{p}}_f$, and $\mathbf{{p}}_s$, associated with radiation effects, which depend on the closure variables $r_f$ and $r_s$ associated with closure problem IV.

The distribution coefficient $\xi$ and on the vectors $\mathbf{{p}}_\gamma$ are represented in Figs.  and 6, respectively, for a porosity $\varPi _f= {0.80}$. Only the relevant conductivity ratios are considered: $k_s/ k_f< 1$ can only occur if the fluid is a liquid, which cannot be considered as transparent. $\xi$ hardly depends on the Péclet number while it is very sensitive to the conductivity ratio. These results are consistent with those obtained by Quintard and Whitaker (2000) for a generic uniform heterogeneous source term.

Fig. 5

Distribution coefficient. $\varPi _f= {0.80}$

Fig. 6

Radiative flux average coefficient for the fluid (left) and the solid (right) phases. $\varPi _f= {0.80}$

Figure 6 shows that the order of magnitude of the radiative coefficient $A \mathbf{{p}}_s$ is much smaller than its counterpart in the fluid phase $A \mathbf{{p}}_f$. An estimate of the associated terms in the macroscopic energy equations can be established based on the values presented in Figs.  and 6. In the considered case, we have:

$$\begin{aligned} \frac{{\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_s\, \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \right) }{ A \, \left( 1 - \xi \right) \, \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} } = \fancyscript{O}\left( A \, \mathbf{{p}}_s\ \frac{l_f}{L} \frac{1}{1 - \xi } \right) . \end{aligned}$$

(73)

where $l_f$ is the typical pore size and $L$ is the size of the macroscopic system. This estimate is based on the following assumption:

$$\begin{aligned} A = \fancyscript{O}\left( \frac{1}{l_f} \right) . \end{aligned}$$

(74)

The scale separation constaint also requires that

$$\begin{aligned} \frac{l_f}{L} \ll 1. \end{aligned}$$

(75)

In the conditions considered, we have

$$\begin{aligned} 1 - \xi = \fancyscript{O}\left( 1 \right) . \end{aligned}$$

(76)

Since the values of $A \, \mathbf{{p}}_s$, are smaller than e-2, ${\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_s\, \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \right)$ will always be negligible compared to the radiative source term in the solid phase $A \left( 1 - \xi \right) \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$. Since estimating the value of $\langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$ is difficult, comparing ${\varvec{\nabla }\, \cdot \,}\left( A \, \mathbf{{p}}_f\, \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m} \right)$ with terms in its macroscopic equation other than the radiative source term $A \xi \langle {\varphi ^\mathrm{R}_w}\rangle ^\mathrm{m}$ (which should be small in most cases due to the small value of $\xi$) cannot be done without additional information.

6 Conclusion

In this paper, a coupled upscaling analysis has been developed in order to derive a macroscopic model for heat transfer, including radiation, in porous media subjected to high temperature. The averaging procedure, based on local thermal non-equilibrium, has been performed by applying a volume averaging method to the local energy conservation equations accounting for radiation. A specific statistical homogenization has been performed for radiation, leading to the radiative properties characterized by statistical continuous functions defined in the whole system. When non-Beerian phases are considered, the radiation model is based on the Generalized Radiative Transfer Equation (GRTE) and in some cases on the radiative Fourier law.

The main results regarding the present analysis can be summed up as follows. First, coupled upscaling was achieved in spite of the non-material nature of the radiative heat transfer. The length scale constraints imposed by the volume averaging method were found to be compatible with the characteristic length scale of the radiative statistical approach. Finally, the radiation emission modeling depends on the temperature field of the material system which must be compatible with the statistical definition of the phase for radiation. Indeed, for a semi-transparent phase, this temperature is obtained by averaging the local temperature using the radiative intrinsic average while a radiative interface average is used for an opaque phase.

For the three solid/fluid configurations considered (opaque/transparent, semi-transparent/semi-transparent, and semi-transparent/transparent), macroscopic thermal non-equilibrium models have been obtained and associated closure problems for the determination of the effective transfer properties have been derived. For each phase, additional macroscopic terms due to radiation have been found. The two additional terms found in the most common case (O/T) represent a diffusive flux and a spatial distribution of the macroscopic volumetric source term, both due to the radiative flux at the fluid/solid interface. For the symmetrical ST/ST case, the five additional macroscopic terms (only two for the ST/T case) stand for the volumetric phase repartition and the exchange between phases due to the radiative energy generation rate. The closure problems for the related closure variables have been derived. Some of these variables contain contributions associated with both the tortuosity of the porous microstructure and the dispersion contribution (for the fluid phase). Their numerical determination on realistic structures and the calculation of the macroscopic terms due to radiation in a simplified configuration will be the subject of a specific study.

As a conclusion, it is interesting to note that the coupled upscaling procedure for heat transfer in porous media including radiation gives rise to technical characteristics similar to those encountered during the averaging procedure of homogeneous or heterogeneous reactive transport. In both cases, one of the main difficulties is due to the fact that interfacial and volumetric source terms depend on the local fields (temperature or concentration for instance). This challenge could be addressed by developing a downscaling procedure in order to obtain the local fields from the resolution of the macroscopic problem.