Vibration Effect on the Nonlinear Regimes of Thermal Convection in a Two-Layer System of Fluid and Saturated Porous Medium

Abstract

The effect of high-frequency vibrations on the nonlinear regimes of thermal convection in a two-layer system composed of a horizontal pure fluid layer and fluid-saturated porous layer heated from below is studied in the framework of the average approach. For large porous layer thicknesses it has been found, that at low vibration intensities the evolution of convective regimes with the growth of the Rayleigh number proceeds as follows: stationary regime—oscillatory regime—stationary regime. At high vibration intensities the stationary convective regimes take place at any values of the supercriticality used in the calculations. At close values of the fluid layer and porous layer thicknesses the interaction between the short-wave and long-wave instability modes is investigated. It has been found that at high vibration intensities the ambiguity of the stationary solutions is observed in a certain range of supercriticalities.

1 Introduction

The paper is concerned with the effect of vertical high-frequency vibrations on the onset and evolution of convection in a two-layer system of a pure fluid and saturated porous medium heated from below and subject to the field of gravity. Such systems are frequently encountered in various natural and industrial processes. For example, during crystal growth from the melt in terrestrial conditions a two-phase mushy zone with properties similar to the properties of porous medium saturated with the fluid is formed between the melt and solidification front. Convection in the melt and in the mushy zone affects the structure of the crystal.

A linear problem on the equilibrium stability of a two-layer system involving a horizontal pure fluid layer and fluid-saturated porous layer in a static gravity field was considered in Lyubimov and Muratov (1977), Chen and Chen (1988, 2001). It was found, that the neutral curves of equilibrium stability are bimodal over some range of parameters (the ratio of layer thicknesses, permeability of the porous medium, the thermal conductivity ratio, etc.). When the fluid moves through a porous medium it becomes resistant to the porous matrix. Therefore in the systems with a rather thick fluid layer a convective flow is initiated just in this layer. In this case the instability is caused by the evolution of short-wave perturbations. And vice versa, in the case of thick porous layers most dangerous are the long-wave perturbations, which spread through both layers. At intermediate values of the layer thickness ratio, one can observe a competition between the short-wave and long-wave perturbations corresponding to the minima of bimodal neutral curves.

The structure of the convective flow and heat transfer in a two-layer system composed of a horizontal pure fluid layer and fluid-saturated porous layer in a static gravity field were investigated numerically and experimentally in Chen and Chen (1992, 1989) for different values of supercriticality. The calculations carried out in Chen and Chen (1992) up to the twentyfold supercriticality showed that a stationary regime of convection was maintained over the entire examined range of parameters. It was found, that a sharp growth of the Nusselt number with the growth of the supercriticality, occurring at small values of the ratio of fluid layer to porous layer thicknesses, is replaced by a moderate increase of the heat flux with a growth of the heat intensity at a certain critical value of the thickness ratio. The obtained data are in a good agreement with the experimental results (Chen and Chen 1989).

The interaction between the short-wave and long-wave instability modes at small supercriticalities was studied in Lyubimov et al. (2002, 2004). The focus of these papers was a three-layer system consisting of two saturated porous layers separated by a pure fluid layer in a static gravity field. It was found that at small values of the supercriticality the long-wave vortex loses its stability and breaks down into a few short-wave vortices located in the fluid layer.

The analysis of the nature of the convection excitation and supercritical convective regimes in a two-layer system of a horizontal pure fluid layer and a fluid-saturated porous layer heated from below in a static gravity field was carried out in Kolchanova et al. (2013). It was found, that in the case when the thickness of the fluid layer is small compared to the thickness of the porous layer and the long-wave mode of convection is predominate, the stationary regime of convection loses its stability at some value of the supercriticality and is replaced by the oscillatory regime, which is again replaced by the stationary regime with a further increase of the supercriticality In addition, the paper investigates the interaction between the short-wave and long-wave instability modes near the threshold of the convection and the evolution of the convection up to the fivefold supercriticality at comparable thicknesses of the fluid and porous layers.

In recent years, various theoretical and experimental studies have supported the idea that vibrations can be used as one of the ways to control the behavior of hydrodynamical systems. The effect of vibrations of finite frequency and amplitude on linear stability of a conductive state of saturated horizontal porous layer subjected to vertical temperature gradient was studied in Govender (2004, 2005a, b, c), weakly-non-linear analysis was carried out in Govender (2005d). It is found that the increase of frequency results in the rapid stabilization of convection below the transition point from the synchronous to subharmonic convection and in the slow destabilization of convection above the transition point.

The effect of high-frequency vibrations on the onset of convection in a fluid-saturated horizontal porous layer was studied in Zenkovskaya and Rogovenko (1999) in the framework of average approach accounting for the viscosity in the equations for pulsations. It has been found, that vertical vibrations stabilize conductive state, moreover the effect of absolute stabilization can be achieved.

In Bardan and Mojtabi (2000) the effect of high-frequency vertical vibrations on linear stability of Lapwood convection in a rectangular cavity was studied analytically and numerically in the framework of the same approach as in Zenkovskaya and Rogovenko (1999). The stabilizing effect of vibrations was demonstrated.

Vibration effect on the onset of Soret-driven convection in binary-fluid-saturated porous medium was investigated in Charrier-Mojtabi et al. (2004, 2007), Elhajjar et al. (2009).

The onset of convection in a system of superposed horizontal layers of pure fluid and fluid-saturated porous medium subjected to the gravity field and vertical high-frequency vibrations was studied in Lyubimov et al. (2004) for the case of thin fluid layer, in the framework of average approach. The authors succeeded to reduce the problem of convection in a two-layer system to the problem of convection in a single porous layer and the presence of a fluid layer was taken into account by effective boundary conditions at the upper boundary of porous layer. The neutral curves were found to be unimodal which well corresponds to the above discussion. It was shown, that with the growth of the vibration intensity the threshold of the conductive state instability rises and the wavelength of most dangerous perturbations increases. In the limit case of zero liquid layer thickness the results obtained for the porous layer with rigid boundaries are reproduced.

In Lyubimov et al. (2008), the same problem was considered for a two-layer system with fluid layer of arbitrary thickness. It has been shown, that in this case, as well as in the absence of vibrations, in some parameter range the neutral curves are bimodal. Vibrations make stabilizing effect on both modes, besides, stabilization effect on the short-wave perturbations located in the fluid layer is much greater than that on the long-wave perturbations spreading all over the system. This result is explained by a different relative role of inertial effects in the fluid and porous layers. For thin fluid layers the lower instability mode is related to the perturbations which cover the entire system and most of the perturbation energy falls in the porous layer. In this case vibrational stabilization is rather weak. In opposite case of thick fluid layers, the flow is mainly concentrated in this layer, it penetrates only slightly into the porous layer and is strongly stabilized by vibrations. Note that, due to the smallness of the hydraulic resistance in the fluid layer, thick fluid layers go over to asymptotic behavior fairly rapidly.

The nonlinear regimes of convection in a two-layer system of a horizontal pure fluid layer and a fluid-saturated porous layer heated from below in the gravity field and subjected to vertical high-frequency vibrations were not investigated.

2 Governing Equations and Boundary Conditions

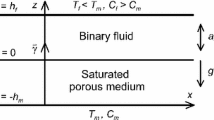
Consider a two-layer system composed of a horizontal pure fluid layer and a porous layer saturated by the same fluid (Fig. 1). The upper and lower rigid boundaries of the system are kept at different constant temperatures. The system is subject to the gravity field and vertical vibrations with the frequency $\omega$ and amplitude $a$. We restrict the discussion to a two-dimensional case, i.e., the horizontal layers are assumed to be homogeneous along the $z$-axis.

Fig. 1

System configuration

The flow in the nonuniformly heated fluid layer is described by the equations of thermal buoyancy convection in the Boussinesq approximation (Gershuni and Zhukhovitskii 1972). The natural convective filtration of the fluid in the saturated porous medium is described by equations written in the Darcy-Boussinesq approximation (Nield and Bejan 2013).

The equations are written in the reference frame of the layer oscillating boundaries and for the fluid layer are given as

$$\begin{aligned}&\displaystyle \frac{\partial {{\varvec{v}}}}{\partial t} + ( {{\varvec{v}}} \varvec{\nabla } ) {{\varvec{v}}} = -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} p + \nu _\mathrm{f}\nabla ^2 {{\varvec{v}}} + \beta _\mathrm{T} T ( g - a \omega ^2 \cos \omega t ) {{\varvec{j}}}, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle \frac{\partial T}{\partial t} + ( {{\varvec{v}}}{\varvec{\nabla }} ) T = \chi _\mathrm{f} \nabla ^2 T, \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{v}}} = 0, \end{aligned}$$

(3)

and for the porous layer are

$$\begin{aligned}&\displaystyle \frac{1}{m}\frac{\partial {{\varvec{u}}}}{\partial t} = -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} \pi - \frac{\nu _\mathrm{f}}{K} {{\varvec{u}}} + \beta _\mathrm{T} \vartheta ( g - a \omega ^2 \cos \omega t ) {{\varvec{j}}},\end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta }{\partial t} + ( {{\varvec{u}}} {\varvec{\nabla }} ) \vartheta = \chi _\mathrm{eff} \nabla ^2 \vartheta ,\end{aligned}$$

(5)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{u}}} = 0. \end{aligned}$$

(6)

Here, ${{\varvec{v}}}$ is the convective flow velocity in the fluid layer, ${{\varvec{u}}}$ is the velocity of the convective filtration in the porous medium; $p$, $\pi$ are the pressures in the fluid and porous medium layers excluding the hydrostatic additive; $T$, $\vartheta$ are the temperature deviations from the average values in the fluid and porous layers; $\rho _\mathrm{f}$, $\nu _\mathrm{f}$ are the density and the kinematic viscosity of the fluid; $\beta _T$ is the thermal expansion coefficient; $g$ is the acceleration of gravity; $m$ is the porosity, $K$ is the permeability of the porous medium; $b$ is the ratio of the porous medium heat capacity to that of the fluid per unit volume, $\chi _\mathrm{f}$, $\chi _\mathrm{m}$ are the thermal diffusivities of the fluid and the porous medium, $\chi _\mathrm{eff}$ is the effective thermal diffusivity defined by the ratio of the thermal conductivity of the fluid-saturated porous medium to the fluid heat capacity per unit volume, $\chi _\mathrm{eff} = b \chi _\mathrm{m}$, ${{\varvec{j}}}$ is the unit vector of the vertical axis. Indices f and m stand for the fluid and porous medium, respectively.

The no-slip condition is imposed at the upper rigid boundary of the two-layer system and the impermeability condition at the lower boundary; the constant different temperatures are maintained at both boundaries:

$$\begin{aligned} y&= h_\mathrm{f}: \quad v_x = v_y = 0,\quad T = - \varTheta _\mathrm{f}, \nonumber \\ y&= -h_\mathrm{m}: \quad u_y = 0,\quad \vartheta = \varTheta _\mathrm{m}. \end{aligned}$$

(7)

The interface between the fluid and porous layer is assumed to meet the following conditions: the continuity of vertical velocity component, the jump of the tangential velocity component, the continuity of the temperature and heat flux and the balance of normal stresses

$$\begin{aligned} y = 0: \quad v_y&= u_y, \quad v_x = 0, \quad T = \vartheta ,\end{aligned}$$

(8)

$$\begin{aligned} \kappa _f \frac{\partial T}{\partial y}&= \kappa _\mathrm{m} \frac{\partial \vartheta }{\partial y}, \quad p = \pi . \end{aligned}$$

(9)

The application of the boundary condition $v_x = 0$ is justified by the fact that the velocities of the convective filtration in the porous medium are generally small because of small characteristic values of the porous medium permeability $K$ (Lyubimov and Muratov 1977). In this case the condition of the normal stress balance reduces to the pressure balance at the interface between the layers (Lyubimov and Muratov 1977; Kolchanova et al. 2013).

According to the theory of thermal vibrational convection in the pure fluid (Gershuni and Lyubimov 1998) and in the saturated porous medium (Zenkovskaya and Rogovenko 1999; Bardan and Mojtabi 2000; Lyubimov et al. 2004, 2008), we represent the velocity, temperature, and pressure fields in the fluid and porous layers as a sum of average and pulsation components:

$$\begin{aligned} {{\varvec{v}}}&= {{\varvec{v}}}_a + {{\varvec{v}}}_\mathrm{p}, \quad T = T_a + T_\mathrm{p}, \quad p = p_a + p_\mathrm{p},\end{aligned}$$

(10)

$$\begin{aligned} {{\varvec{u}}}&= {{\varvec{u}}}_a + {{\varvec{u}}}_\mathrm{p}, \quad \vartheta = \vartheta _a + \vartheta _\mathrm{p}, \quad \pi = \pi _a + \pi _\mathrm{p}. \end{aligned}$$

(11)

We consider the case of vertical vibrations. The vibration frequency is assumed to be so high that the thicknesses of the viscous and thermal boundary layers near the rigid boundaries and near the interface are small compared to the thickness of the layers $L$: $(\nu _\mathrm{f} / \omega )^{1/2} = \delta _v \ll L, (\chi _\mathrm{f} / \omega )^{1/2} = \delta _T \ll L$ or $\omega L^2 / \nu _\mathrm{f} \gg 1, \omega L^2 / \chi _\mathrm{f} \gg 1$.

At the same time, it is supposed that the sound wavelength at this frequency of vibrations is large compared to the thickness of the layers. This imposes the upper limit on the frequency: if the condition $\omega \ll c / L$ ($c$ is the sound velocity) is fulfilled, one can neglect the effect of the fluid compressibility. Thus, the range of frequencies to be considered is $\nu _\mathrm{f} / L^2 \ll \omega \ll c / L$. For example, for water ($\nu _\mathrm{f} = 0.01$ cm${}^2/$ s) at $L = 1$ cm the range of examined frequencies is $10^{-2} \ll \omega \ll 10^5$ s${}^{-1}$ or $10^{-3} \ll \omega / 2 \pi \ll 10^4$ Hz.

The amplitude of vibrations is assumed to be so small that the nonlinear term $( {{\varvec{v}}}_\mathrm{p} {\varvec{\nabla }} ) {{\varvec{v}}}_\mathrm{p}$ can be neglected as opposed to the acceleration $\partial {{\varvec{v}}}_\mathrm{p} / \partial t$ in the momentum equation for pulsations. In view of the fact that the pulsating component of the velocity is defined by the relationship $v_\mathrm{p} \sim a \omega \beta _\mathrm{T} \vartheta$ (where $\vartheta$ is the temperature difference at the boundaries of the fluid layer), this condition leads to the following limit on the amplitude of vibrations: $a \ll L / \beta _\mathrm{T} \vartheta$. Since the Boussinesq parameter $\beta _\mathrm{T} \vartheta$ is generally small, the vibration amplitude and the thickness of the fluid layer may have the same order of magnitude (Gershuni and Lyubimov 1998).

We also neglect the buoyancy force in the static gravity field in the equations for pulsations assuming that $\frac{g \beta _\mathrm{T} \vartheta }{{\omega ^2 L}} \ll 1$ , i.e., the ratio $\frac{g}{a \omega ^2}$ of the gravitational acceleration to the vibrational one multiplied by $\frac{a \beta _\mathrm{T} \vartheta }{L}$ should be small which is satisfied due to our assumption of small vibration amplitude.

The assumptions described above makes it possible to neglect the viscous and nonlinear terms in the equations for pulsations in the fluid layer. However, we cannot neglect the viscous term in the equation for pulsations in the saturated porous medium because of the small characteristic values of the porous medium permeability $K$ (Zenkovskaya and Rogovenko 1999; Bardan and Mojtabi 2000; Lyubimov et al. 2004, 2008). In this case, the ratio $\nu _\mathrm{f} m / K \omega$ of the viscous term to acceleration can be small only if $\omega \gg \nu _\mathrm{f} m / K$ (where $K^{1/2}$ is the pore size). For the layer of sand saturated by water and having thickness $L = 1$ cm, permeability $K = 10^{-6}$ cm${}^2$ and porosity $m = 0.25$ we get $2.5 \times 10^3 \ll \omega \ll 10^5$ s${}^{-1}$ or $2.5 \times 10^2 \ll \omega / 2 \pi \ll 10^4$ Hz. Thus, for moderately high vibration frequencies it is necessary to take into account the viscous term in the equation for pulsations in the porous layer.

The nonlinear terms in the equations for pulsations in the porous layer can be neglected because of the small amplitude of vibrations ($a \ll m L/ \beta _\mathrm{T} \theta$), where $\theta$ is the temperature difference at the boundaries of the porous layer).

Taking into account the assumptions made above, we obtain the following system of equations for pulsations in the fluid layer:

$$\begin{aligned}&\displaystyle \frac{\partial {{\varvec{v}}}_\mathrm{p}}{\partial t} = -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} p_\mathrm{p} - a \omega ^2 \beta _\mathrm{T} T_a {{\varvec{j}}} \cos \omega t,\end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \frac{\partial T_\mathrm{p}}{\partial t} = -({{\varvec{v}}}_\mathrm{p} {\varvec{\nabla }}) T_a, \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{v}}}_\mathrm{p} = 0, \end{aligned}$$

(14)

and in the porous layer:

$$\begin{aligned}&\displaystyle \frac{1}{m} \frac{\partial {{\varvec{u}}}_\mathrm{p}}{\partial t} = -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} \pi _\mathrm{p} - \frac{\nu _\mathrm{f}}{K} {{\varvec{u}}}_\mathrm{p} - a \omega ^2 \beta _\mathrm{T} \vartheta _a {{\varvec{j}}} \cos \omega t, \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta _\mathrm{p}}{\partial t} = -( {{\varvec{u}}}_\mathrm{p} {\varvec{\nabla }} ) \vartheta _a, \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{u}}}_\mathrm{p} = 0. \end{aligned}$$

(17)

We will search for the solution of equations (12)–(17) given by

$$\begin{aligned} {{\varvec{v}}}_\mathrm{p}&= \mathfrak {R}\left( {{\varvec{V}}}_\mathrm{p} \mathrm {e}^{i\omega t} \right) , \;\; p_\mathrm{p} = \mathfrak {R}\left( P_\mathrm{p} \mathrm {e}^{i\omega t} \right) ,\\ {{\varvec{u}}}_\mathrm{p}&= \mathfrak {R}\left( {{\varvec{W}}}_\mathrm{p} \mathrm {e}^{i\omega t} \right) , \;\; \pi _\mathrm{p} = \mathfrak {R}\left( \varPi _\mathrm{p} \mathrm {e}^{i\omega t}\right) . \end{aligned}$$

Using these formulas and integrating the Eqs. (13) and (16) we obtain the following explicit expressions for temperature pulsations in the fluid and porous layers:

$$\begin{aligned} T_\mathrm{p} = \frac{1}{\omega }\mathfrak {R}\left( i\left( {{{{{\varvec{V}}}}_\mathrm{p}}{\varvec{\nabla }} } \right) {T_a} \mathrm {e}^{i\omega t} \right) , \quad \vartheta _\mathrm{p} = \frac{1}{\omega b} \mathfrak {R}\left( i\left( {{\varvec{W}}}_\mathrm{p}{\varvec{\nabla }} \right) \vartheta _a \mathrm {e}^{i\omega t} \right) . \end{aligned}$$

(18)

The equations for amplitudes of the pulsating components of velocity and pressure in the fluid and porous layers can be written as

$$\begin{aligned}&\displaystyle i\omega {{\varvec{V}}}_\mathrm{p} = -\frac{1}{\rho _\mathrm{f}} {\varvec{\nabla }} P_\mathrm{p} - a \omega ^2 \beta _\mathrm{T} T_a {{\varvec{j}}},\end{aligned}$$

(19)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{V}}}_\mathrm{p} = 0,\end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle \frac{i\omega }{m} {{\varvec{W}}}_\mathrm{p} = -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} \varPi _\mathrm{p} - \frac{\nu _\mathrm{f}}{K} {{\varvec{W}}}_\mathrm{p} - a \omega ^2 \beta _\mathrm{T} \vartheta _a {{\varvec{j}}}, \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{W}}}_\mathrm{p} = 0. \end{aligned}$$

(22)

Averaging Eqs. (12)–(17) over the fast time (the period of vibrations) and applying the relations

$$\begin{aligned} \overline{T_\mathrm{p} \cos \omega t} = \frac{1}{2\omega } \mathfrak {R}( i ( {{\varvec{V}}}_\mathrm{p}{\varvec{\nabla }} ) T_a ), \quad \overline{\vartheta _\mathrm{p} \cos \omega t} = \frac{1}{2\omega b} \mathfrak {R}(i ( {{\varvec{W}}}_\mathrm{p}{\varvec{\nabla }} ) \vartheta _a), \end{aligned}$$

we obtain the following equations for average components of the velocity, temperature and pressure fields in the fluid layer:

$$\begin{aligned} \frac{\partial {{\varvec{v}}}_a}{\partial t} + \left( {{\varvec{v}}}_a {\varvec{\nabla }} \right) {{\varvec{v}}}_a&= -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} p_a + \nu _\mathrm{f}\nabla ^2 {{\varvec{v}}}_a + g \beta _\mathrm{T} T_a {{\varvec{j}}} \nonumber \\&- \frac{a\omega }{2} \beta _\mathrm{T} {{\varvec{j}}} \mathfrak {R}\left( i\left( {{\varvec{V}}}_\mathrm{p} {\varvec{\nabla }} \right) T_a \right) , \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle \frac{\partial T_a}{\partial t} + \left( {{\varvec{v}}}_a {\varvec{\nabla }} \right) T_a = \chi _\mathrm{f} \nabla ^2 T_a, \end{aligned}$$

(24)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{v}}}_a = 0, \end{aligned}$$

(25)

and in the porous layer:

$$\begin{aligned}&\displaystyle -\frac{1}{\rho _\mathrm{f}}{\varvec{\nabla }} \pi _a - \frac{\nu _\mathrm{f}}{K} {{\varvec{u}}}_a + g \beta _\mathrm{T} \vartheta _a {{\varvec{j}}} - \frac{a\omega }{2b} \beta _\mathrm{T} {{\varvec{j}}} \mathfrak {R}\left( i\left( {{\varvec{W}}}_\mathrm{p} {\varvec{\nabla }} \right) \vartheta _a \right) = 0,\end{aligned}$$

(26)

$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta _a}{\partial t} + \left( {{\varvec{u}}}_a {\varvec{\nabla }} \right) \vartheta _a = \chi _\mathrm{eff} \nabla ^2 \vartheta _a,\end{aligned}$$

(27)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{u}}}_a = 0. \end{aligned}$$

(28)

Boundary conditions (7) and (8) should be completed by the conditions for velocity and pressure pulsations at the rigid boundaries:

$$\begin{aligned} y&= h_\mathrm{f}: \quad {{\varvec{V}}}_\mathrm{p} \cdot {{\varvec{j}}} = 0, \nonumber \\ y&= -h_\mathrm{m}: \quad {{\varvec{W}}}_\mathrm{p} \cdot {{\varvec{j}}} = 0, \end{aligned}$$

(29)

and at the interface between the layers:

$$\begin{aligned} y = 0: \quad {{\varvec{V}}}_\mathrm{p} \cdot {{\varvec{j}}} = {{\varvec{W}}}_\mathrm{p} \cdot {{\varvec{j}}}, \quad P_\mathrm{p} = \varPi _\mathrm{p}. \end{aligned}$$

(30)

Note that the term $(1 / m) \partial {{\varvec{u}}}_a / \partial t$ in Eq. (24) for the average flow in the porous medium can be neglected due to small characteristic values of convective filtration velocities. However, the term $(1 / m) \partial {{\varvec{u}}}_\mathrm{p} / \partial t$ in Eq. (15) for pulsations cannot be neglected since it is proportional to the vibration frequency $\omega \gg 1$ (Zenkovskaya and Rogovenko 1999; Bardan and Mojtabi 2000; Lyubimov et al. 2004, 2008). The necessity to take into account the time-derivative in the momentum equation for porous medium was pointed out earlier by Vadasz and Straughan (Vadasz 1998; Straughan 2001) in their studies of the stability of the rotating porous layer where it was found that if the time-derivative is left in the momentum equation, then the convection may arise in oscillatory way.

The main goal of the present paper is to study the effect of vibrations on the non-linear regimes of convection in the two-layer system of superposed pure fluid layer and fluid-saturated porous layer. That is why we choose the same scales as in Kolchanova et al. (2013) where the same problem was studied for the case when vibrations are absent, i.e., for the length, time, average components of the temperature, velocity and pressure and amplitudes of the pulsating components of the velocity and pressure we use the quantities

$$\begin{aligned}&\displaystyle \left[ x,y,z\right] = h_\mathrm{f} \equiv L, \;\; \left[ t\right] = \frac{L^2}{\chi _\mathrm{f}}, \;\; \left[ T_a\right] = \left[ \vartheta _a\right] = A_\mathrm{f} L, \\&\displaystyle \left[ {{\varvec{v}}}_a\right] = \left[ {{\varvec{u}}}_a\right] = \frac{\chi _\mathrm{f}}{L}, \;\; \left[ p_a\right] = \left[ \pi _a\right] = \frac{\eta _\mathrm{f} \chi _\mathrm{f}}{K}, \\&\displaystyle \left[ {{\varvec{V}}}_\mathrm{p}\right] = \left[ {{\varvec{W}}}_\mathrm{p}\right] = \frac{a\omega ^2 \beta _\mathrm{T} A_\mathrm{f} L K}{\nu _\mathrm{f}}, \;\; \left[ P_\mathrm{p}\right] = \left[ \varPi _\mathrm{p}\right] = a \omega ^2 \rho _\mathrm{f} A_\mathrm{f} L^2 \beta _\mathrm{T}. \end{aligned}$$

The dimensionless equations for thermal vibrational convection in the fluid layer can be written as

$$\begin{aligned} \frac{1}{\mathrm {Pr}_\mathrm{f}} \left( \frac{\partial {{\varvec{v}}}_a}{\partial t} + ( {{\varvec{v}}}_a {\varvec{\nabla }} ) {{\varvec{v}}}_a \right)&= - {\varvec{\nabla }} p_a + \nabla ^2 {{\varvec{v}}}_a + {R}_\mathrm{f} T_a {{\varvec{j}}} \nonumber \\&-\,{R}_\mathrm{fv} {{\varvec{j}}} \mathfrak {R}( i ( {{\varvec{V}}}_\mathrm{p} {\varvec{\nabla }} ) T_a ), \end{aligned}$$

(31)

$$\begin{aligned}&\displaystyle \frac{\partial T_a}{\partial t} + ({{\varvec{v}}}_a {\varvec{\nabla }}) T_a = \nabla ^2 T_a,\end{aligned}$$

(32)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{v}}}_a = 0,\end{aligned}$$

(33)

$$\begin{aligned}&\displaystyle i \varOmega _\mathrm{f} {{\varvec{V}}}_\mathrm{p} = -{\varvec{\nabla }} P_\mathrm{p} - T_a {{\varvec{j}}}, \end{aligned}$$

(34)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{V}}}_\mathrm{p} = 0, \end{aligned}$$

(35)

and in the porous layer:

$$\begin{aligned}&\displaystyle -\varepsilon _\mathrm{f} {\varvec{\nabla }} \pi _a - {{\varvec{u}}}_a + \varepsilon _\mathrm{f} {R}_\mathrm{f} \vartheta _a {{\varvec{j}}} - \frac{\varepsilon _\mathrm{f}}{b} {R}_\mathrm{fv} {{\varvec{j}}} \mathfrak {R}( i( {{\varvec{W}}}_\mathrm{p} {\varvec{\nabla }} ) \vartheta _a ) = 0,\end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta _a}{\partial t} + ( {{\varvec{u}}}_a {\varvec{\nabla }} ) \vartheta _a = \kappa \nabla ^2 \vartheta _a,\end{aligned}$$

(37)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{u}}}_a = 0,\end{aligned}$$

(38)

$$\begin{aligned}&\displaystyle \frac{i \varOmega _\mathrm{f}}{m} {{\varvec{W}}}_\mathrm{p} = -{\varvec{\nabla }} \varPi _\mathrm{p} -\frac{1}{\varepsilon _\mathrm{f}} {{\varvec{W}}}_\mathrm{p} - \vartheta _a {{\varvec{j}}},\end{aligned}$$

(39)

$$\begin{aligned}&\displaystyle {\varvec{\nabla }} \cdot {{\varvec{W}}}_\mathrm{p} = 0, \end{aligned}$$

(40)

with the following boundary conditions at the upper and lower boundaries of the system:

$$\begin{aligned} y&= 1: \quad {{\varvec{v}}}_a = 0, \;\; T_a = -1, \;\; {{\varvec{V}}}_\mathrm{p} \cdot {{\varvec{j}}} = 0, \nonumber \\ y&= -h: \quad {{\varvec{u}}}\cdot {{\varvec{j}}} = 0, \;\; \vartheta _a = \frac{h}{\kappa }, \;\; {{\varvec{W}}}_\mathrm{p} \cdot {{\varvec{j}}} = 0, \end{aligned}$$

(41)

and at the interface between the layers:

$$\begin{aligned} y = 0: \quad {{\varvec{v}}}_a \cdot {{\varvec{j}}}&= {{\varvec{u}}}_a \cdot {{\varvec{j}}}, \quad v_{ax} = 0, \quad p_a = \pi _a, \nonumber \\ T_a&= \vartheta _a, \quad \frac{\partial T_a}{\partial y} = \kappa \frac{\partial \vartheta _a}{\partial y}, \quad {{\varvec{V}}}_\mathrm{p} \cdot {{\varvec{j}}} = {{\varvec{W}}}_\mathrm{p} \cdot {{\varvec{j}}}, \quad P_\mathrm{p} = \varPi _\mathrm{p}, \end{aligned}$$

(42)

The system of Eqs. (31)–(40) and the boundary conditions (41), (42) contain the following dimensionless parameters: the ratio of porous layer thickness to that of the fluid layer $h = h_\mathrm{m} / h_\mathrm{f}$, the effective permeability of porous medium $\varepsilon _f = K / L^2$ ($\varepsilon _\mathrm{f} =h^2 Da$ where $Da$ is the Darcy number), the Prandtl number $\mathrm {Pr}_\mathrm{f} = \nu _\mathrm{f} / \chi _\mathrm{f}$, the Rayleigh number for homogeneous fluid ${R}_\mathrm{f} = \frac{g \beta _\mathrm{T} A_\mathrm{f} L^4}{\nu _\mathrm{f} \chi _\mathrm{f}}$, the vibrational Rayleigh number for homogeneous fluid ${R}_\mathrm{fv} = \frac{(a \omega A_\mathrm{f} \beta _\mathrm{T} L^3)^2 \omega }{2 \nu _\mathrm{f}^2 \chi _\mathrm{f}}$, the dimensionless frequency of vibrations $\varOmega _\mathrm{f} = \omega L^2 / \nu _\mathrm{f}$, the ratio of thermal conductivity of the porous medium saturated by the fluid to that of the fluid $\kappa = \kappa _\mathrm{m} / \kappa _\mathrm{f}$.

Let us introduce the stream functions for the average and pulsating components of the velocity field in the fluid and porous layers and the vorticity of the flow in the pure fluid layer

$$\begin{aligned} v_{ax}&= \frac{\partial \psi }{\partial y}, \;\; v_{ay} = -\frac{\partial \psi }{\partial x}, \;\; u_{ax} = \frac{\partial \varphi }{\partial y}, \;\; u_{ay} = -\frac{\partial \varphi }{\partial x}, \;\; {{\varvec{J}}} = {\varvec{\nabla }} \times {{\varvec{v}}}_a, \\ V_{\mathrm{p}x}&= \frac{\partial \varPsi }{\partial y}, \;\; V_{\mathrm{p}y} = -\frac{\partial \varPsi }{\partial x}, \;\; W_{\mathrm{p}x} = \frac{\partial \varPhi }{\partial y}, \;\; W_{\mathrm{p}y} = -\frac{\partial \varPhi }{\partial x}. \end{aligned}$$

A complete system of equations for average components and pulsation amplitudes written in terms of the stream functions and vorticity in the fluid layer is

$$\begin{aligned}&\frac{1}{\mathrm {Pr}_\mathrm{f}} \left( \frac{\partial J_z}{\partial t} + \left( \frac{\partial \psi }{\partial y}\frac{\partial J_z}{\partial x} \right. \right. - \left. \left. \frac{\partial \psi }{\partial x}\frac{\partial J_z}{\partial y} \right) \right) \nonumber \\&\quad = \nabla ^2 J_z + {R}_\mathrm{f} \frac{\partial T_a}{\partial x}- {R}_\mathrm{fv} \mathfrak {R}\left( i \frac{\partial }{\partial x} \left( \frac{\partial \varPsi }{\partial y}\frac{\partial T_a}{\partial x} - \frac{\partial \varPsi }{\partial x}\frac{\partial T_a}{\partial y} \right) \right) , \end{aligned}$$

(43)

$$\begin{aligned}&\displaystyle \frac{\partial T_a}{\partial t} + \left( \frac{\partial \psi }{\partial y}\frac{\partial T_a}{\partial x} \right. - \left. \frac{\partial \psi }{\partial x}\frac{\partial T_a}{\partial y} \right) = \nabla ^2 T_a, \end{aligned}$$

(44)

$$\begin{aligned}&\displaystyle J_z = -\nabla ^2 \psi ,\end{aligned}$$

(45)

$$\begin{aligned}&\displaystyle i \varOmega _\mathrm{f} \nabla ^2 \varPsi = \frac{\partial T_a}{\partial x}, \end{aligned}$$

(46)

and in the porous layer:

$$\begin{aligned}&\displaystyle \nabla ^2 \varphi + \varepsilon _\mathrm{f} {R}_\mathrm{f} \frac{\partial \vartheta _a}{\partial x} - \frac{\varepsilon _\mathrm{f}}{b}{R}_\mathrm{fv} \mathfrak {R}\left( i\frac{\partial }{\partial x}\left( \frac{\partial \varPhi }{\partial y}\frac{\partial \vartheta _a}{\partial x} - \frac{\partial \varPhi }{\partial x}\frac{\partial \vartheta _a}{\partial y} \right) \right) = 0, \end{aligned}$$

(47)

$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta _a}{\partial t} + \left( \frac{\partial \varphi }{\partial y}\frac{\partial \vartheta _a}{\partial x} - \frac{\partial \varphi }{\partial x}\frac{\partial \vartheta _a}{\partial y} \right) = \kappa \nabla ^2 \vartheta _a, \end{aligned}$$

(48)

$$\begin{aligned}&\displaystyle \frac{i \varOmega _\mathrm{f}}{m}\nabla ^2 \varPhi = - \frac{1}{\varepsilon _\mathrm{f}}\nabla ^2 \varPhi + \frac{\partial \vartheta _a}{\partial x}, \end{aligned}$$

(49)

with the boundary conditions:

$$\begin{aligned} y = 1: \quad \psi&= 0, \;\; T_a = -1, \;\; \varPsi = 0, \nonumber \\ y = -h: \quad \varphi&= 0, \;\; \vartheta _a = \frac{h}{\kappa }, \;\; \varPhi = 0,\end{aligned}$$

(50)

$$\begin{aligned} y = 0: \quad \psi&= \varphi , \;\; \frac{\partial \psi }{\partial y} = 0, \;\; \varepsilon _\mathrm{f} \frac{\partial ^3 \psi }{\partial y^3} + \frac{\partial \varphi }{\partial y} = 0, \nonumber \\ T_a&= \vartheta _a, \;\; \frac{\partial T_a}{\partial y} = \kappa \frac{\partial \vartheta _a}{\partial y}, \nonumber \\ \varPsi&= \varPhi , \;\; \frac{\partial \varPsi }{\partial y} = \frac{\partial \varPhi }{\partial y} \left( \frac{1}{m} - \frac{i}{\varepsilon _\mathrm{f} \varOmega _\mathrm{f}} \right) . \end{aligned}$$

(51)

Here the condition of the normal stress balance $p_a = \pi _a$ at the interface between the fluid and porous layers (at $y = 0$) for average fields is written in terms of the stream functions. This condition is derived using the horizontal projections of the momentum equations for fluid (31) and for porous medium (36). Then, taking into account the smallness of the Darcy parameter $\varepsilon _f$ and inertial terms compared to the viscous term and the force of resistance of the porous matrix to the fluid motion, we obtain the condition

$$\begin{aligned} \varepsilon _\mathrm{f} \frac{\partial ^2 v_x}{\partial y^2} + u_x = 0 \end{aligned}$$

rather than the pressure continuity condition. When written in terms of the stream functions this condition is given as

$$\begin{aligned} \varepsilon _\mathrm{f} \frac{\partial ^3 \psi }{\partial y^3} + \frac{\partial \varphi }{\partial y} = 0. \end{aligned}$$

Similarly, the condition of the normal stress continuity at the layer–layer interface for amplitudes of the pulsating components $P_\mathrm{p}$ and $\varPi _\mathrm{p}$ can be written in terms of the stream functions as

$$\begin{aligned} \frac{\partial \varPsi }{\partial y} = \frac{\partial \varPhi }{\partial y}\left( \frac{1}{m} - \frac{i}{\varepsilon _\mathrm{f}\varOmega _\mathrm{f}} \right) . \end{aligned}$$

3 Method of Numerical Solution

The numerical solution to the problem (43)–(51) was obtained by the finite-difference method. The calculations were performed following the explicit finite-difference scheme, in which the central differences are used to approximate the spatial derivatives.

The Poisson equation (45) was solved by the method of successive over-relaxation.

According to the data of the linear stability analysis (Lyubimov et al. 2008), the horizontal dimension of the computational domain was chosen to be equal to the wave length $l = 2\pi / k$ of most dangerous perturbations. At the vertical boundaries of the computational domain, $x = \pm l / 2$ all functions satisfy the periodical condition $f(-l/2, y, t) = f(l/2, y, t)$.

4 Numerical Results

The calculations were performed at fixed values of the parameters $\kappa$, $b$, $\mathrm {Pr}_\mathrm{f}$, $\varepsilon _\mathrm{f}$, $\varOmega _\mathrm{f}$ and $m$: $\kappa =1$, $b = 1$, $\mathrm {Pr}_\mathrm{f} = 6.7$, $\varepsilon _\mathrm{f} = 10^{-3}$, $\varOmega _\mathrm{f} = 10$ and $m = 0.25$.

Two cases differing by the ratio of porous to fluid layer thicknesses were considered: (1) the case of thick porous layer ($h = 8$), when according to the linear stability analysis (Lyubimov et al. 2008) the long-wave perturbations are realized in both layers; (2) the case of comparable layer thicknesses ($h = 3$), when the critical Rayleigh numbers determining the thresholds of equilibrium instability with respect to the long-wave and short-wave perturbations are similar.

According to the linear stability theory (Lyubimov et al. 2008), the effect of vibration is stronger for the short-wave perturbations located in the fluid layer than for long-wave perturbations occurring in both layers since the inertial effects in the porous medium are weak compared to the pure fluid layer (typical values of the effective permeability $\varepsilon _\mathrm{f}$ are usually small) (Lyubimov et al. 2008). This result is confirmed by Fig. 2a and b, which show the neutral curves of the conductive state stability in the two-layer system for two values of thickness ratio $h = 3$ and $h = 8$ and different values of the vibrational Rayleigh number.

It is known that in most situations, vertical high-frequency vibrations make stabilizing effect on pure fluids up to the absolute stabilization (see, Gershuni and Lyubimov 1998). The same result was found in Zenkovskaya and Rogovenko (1999); Bardan and Mojtabi (2000); Lyubimov et al. (2004) for saturated porous media. In Fig. 3 we plotted the dependence of minimal critical Rayleigh number on the vibrational parameter $\eta = (2 \mathrm {Pr} \varOmega _\mathrm{f} {R}_\mathrm{fv} / R_\mathrm{f}^2)^{1/2}$ which does not contain the temperature gradient (it equals to the ratio of the vibrational to gravitational accelerations) for the short-wave instability mode. As one can see, there is strong stabilization of this instability mode by vibrations. Note, however, that for the parameter values under consideration, the long-wave minimum of the neutral curve lies lower than the short-wave one, i.e., the long-wave instability mode is more dangerous. As it is seen from Fig. 2a and b, the effect of vibrations on the long-wave instability mode is much weaker than that on the short-wave mode. As mentioned above, this is related to the fact that the inertial effects in the porous medium are weaker due to the very small values of the effective permeability $\varepsilon _f$. The smallness of the vibration effect on the long-wave instability mode can be also explained in terms of the vibrational Rayleigh numbers: the ratio of the vibrational Rayleigh number in porous medium ${R}_\mathrm{pv}= \frac{{(a\omega A_\mathrm{m} \beta _\mathrm{T} KL)^2 \omega }}{{2b\nu ^2 \chi _\mathrm{eff} }}$ to that in the pure fluid ${R}_\mathrm{fv} = \frac{(a\omega A_\mathrm{f} \beta _\mathrm{T} L^3)^2 \omega }{2 \nu _\mathrm{f}^2 \chi _\mathrm{f}}$ is of the order of ${\varepsilon _\mathrm{f}}^2$, i.e., in our case it is of the order of $10^{-6}$ (if both ${R}_\mathrm{fv}$ and ${R}_\mathrm{pv}$ are defined using the same length scale). Thus, to achieve essential stabilization of the long-wave instability mode (and thus, for the parameter values under consideration, essential stabilization in total) we should apply vibrations of much larger intensity.

Fig. 2

Neutral curves of the conductive state stability for various values of the vibrational Rayleigh number ${R}_\mathrm{fv}$: 1 - ${R}_\mathrm{fv} = 0$, 2 - ${R}_\mathrm{fv} = 1,000$, 3 - ${R}_\mathrm{fv} = 5,000$, 4 - ${R}_\mathrm{fv} = 10,000$, a $h = 3$, b $h = 8$

Fig. 3

Minimal critical Rayleigh number versus vibrational parameter $\eta$

Let us discuss the results of the investigation of nonlinear regimes and the nature of convection excitation in the examined two-layer system in the presence of high-frequency vibrations for two values of the thickness ratio $h$: $h = 3$ and $h = 8$.

4.1 Thick Porous Layer ($h = 8$). Implementation of Long-Wave Perturbations

In Fig. 4a and b, the maximum modules of the stream function are plotted versus the thermal Rayleigh number at various values of the vibrational Rayleigh number ${R}_\mathrm{fv}$ for short-wave and long-wave modes of stationary solutions corresponding to the neutral curve minima at $h = 8$ (Fig. 2b). The calculations were carried out for square cavity using the uniform mesh with ($h_x = h_y = H$). The long-wave branch was obtained at $H = 0.1$ and the short-wave one – at $H = 0.04$. The main criterion for the generation of these meshes is maintenance of the optimal balance between the computation time and accuracy of results.

Following Fig. 4, the convection is excited via direct bifurcation both in the presence and in the absence of vibrations, and at small supercriticalities the flow intensity increases with ${R}_\mathrm{f}$ according to the square root law for both instability modes. Vibrations do not have a marked effect on the threshold of the conductive state stability with respect to long-wave perturbations (Fig. 4a), in contrast to the case of short-wave perturbations, which are strongly stabilized by vibrations (Fig. 4b). Thus, the nonlinear calculations confirm the results obtained with the use of the linear stability analysis (Fig. 2).

Fig. 4

The maximum module of the stream function versus thermal Rayleigh number at $h = 8$ and various values of the vibrational Rayleigh number ${R}_\mathrm{fv}$: a long-wave mode of instability (with wave length $l = 16$), b short-wave mode of instability (with wave length $l = 3$)

As it was shown in Kolchanova et al. (2013), in the absence of vibrations, with increasing supercriticality up to a certain value, the large-scale stationary flow becomes unstable and is replaced by the oscillatory regime. At even higher values of supercriticality the flow again transfers to a stationary regime, which however has a different structure (the black solid curve at Fig. 4a). Figure 5a shows variation of the maximum module of the stream function in the absence and in the presence of vibrations for ${R}_\mathrm{fv} = 200$. It can be seen that vibrations lead to a decrease in the range of ${R}_\mathrm{f}$ in which a stationary solution does not exist. The calculations carried out at different values of the vibrational Rayleigh number show that at ${R}_\mathrm{fv} = 330$ the indicated range completely disappears (Fig. 5b) and stable stationary convective regimes are observed at all values of ${R}_\mathrm{f}$. According to the obtained estimates, the supercriticality range, corresponding to the oscillatory regime of the convection, completely disappears at the vibrational acceleration $a \omega ^2 = (2 \mathrm {Pr} \varOmega _\mathrm{f} {R}_\mathrm{fv} / R_\mathrm{f}^2)^{1/2} g \approx 0.34g$.

Fig. 5

Long-wave mode of stationary solutions: a dependences of maximum module of the stream function on the thermal Rayleigh number at two different values of the vibrational Rayleigh number ${R}_\mathrm{fv}$: ${R}_\mathrm{fv} = 0$ (solid line), ${R}_\mathrm{fv} = 200$ (dashed line). b the dependence of the thermal Rayleigh number determining the lower and upper limits of the oscillatory regime existence on the vibrational Rayleigh number

Let us compare the change of the flow structure during oscillations in the absence or in the presence of vibrations at the same intensity of heating (${R}_\mathrm{f} = 600$). Figures 6 and 7 present the oscillation modes of the maximum module of the stream function at ${R}_\mathrm{fv} = 0$ (in the absence of vibrations) and at ${R}_\mathrm{fv} = 200$. The Fourier spectra of the oscillations in the absence and in the presence of vibrations are shown in Fig. 8. It can be seen, that with the growth of the vibrational Rayleigh number the amplitude of oscillations decreases (see Figs. 6a, 7a) and the period of oscillations increases (see Figs. 6b, 7b). In this case, the spectrum of oscillations is shifted toward the low-frequency range (Fig. 8b).

Fig. 6

The long-wave mode of stationary solutions at ${R}_\mathrm{f} = 600$ (after the loss of stability of stationary solutions) in the absence of vibrations: a the dependence of the maximum module of the stream function on time, b the dependence of the maximum module of the stream function on time within the 1.5th of the oscillation period determined by the minimum frequency

Fig. 7

The long-wave mode of stationary solutions at ${R}_\mathrm{f} = 600$ and ${R}_\mathrm{fv} = 200$ (after the loss of stability of stationary solutions): a the dependence of the maximum module of the stream function on time, b the dependence of the maximum module of the stream function on time within the 1.5th of the oscillation period determined by the minimum frequency

Fig. 8

Fourier spectra of oscillations of the maximum module of the stream function for the long-wave instability mode at ${R}_\mathrm{f} = 600$ (after the loss of stability of the stationary solution): a in the absence of vibrations, b in the presence of vibrations (${R}_\mathrm{fv} = 200$)

A rearrangement of the flow structure with a change of the thermal Rayleigh number is illustrated in Fig. 9, which presents the stream function fields for ${R}_\mathrm{fv} = 200$ at the instants of time corresponding to dots in Fig. 7b. As it was shown in Kolchanova et al. (2013), in the absence of vibrations a large-scale vortex occupying both layers coexists with the vortices located in the fluid layer. During oscillations one of the additional vortices gradually increases in size. This growth proceeds in an orderly fashion until the vortex is separated and reconnected to the adjacent additional vortex formed in the region of the upstream flow. Then the process is repeated. In the presence of vibrations a qualitative change in the flow structure during oscillations occurs in the same way as in the case of the static gravity field: a moderate growth of one of the additional vortices (Fig. 9a, b) is followed by its separation and reconnection to the adjacent additional vortex (Fig. 9c–e). The main difference from the vibration-free case is that in the presence of vibrations the growth of one of the additional vortices takes more time (points 1 and 2 in Figs. 6b, 7b) and the number of reconnections of additional vortices during one period determined by the minimum oscillation frequency is much less (see curve maxima in Figs. 6b, 7b).

Fig. 9

The stream function for long-wave instability mode at ${R}_\mathrm{f} = 600$ and ${R}_\mathrm{fv} = 200$ (after the loss of stability of the stationary solution stability) at various time intervals within the 1.5th of the oscillation period determined by the minimum frequency at points indicated in Fig. 7b: a $t = 240.1$ (point 1), b $t = 273.2$ (point 2), c $t = 276.2$ (point 3), d $t = 278.1$ (point 4), e $t = 278.9$ (point 5), f $t = 286.8$ (point 6). The streamlines are spaced at the same intervals equal to $0.2$

We compared the structure of convective flows at finite supercriticalities for two values of ${R}_\mathrm{fv}$: ${R}_\mathrm{fv} = 0$ ($a \omega ^2 = 0$) and ${R}_\mathrm{fv} = 5,000$ ($a \omega ^2 = (2 \mathrm {Pr} \varOmega _\mathrm{f} {R}_\mathrm{fv} / R_\mathrm{f}^2)^{1/2} g \approx 0.87g$, where ${R}_\mathrm{f} = 880$). Figure 10 shows the streamlines for the long-wave instability mode at ${R}_\mathrm{f} = 880$ in the absence and in the presence of vibrations with ${R}_\mathrm{fv} = 5,000$, respectively. As is seen from Fig. 10a, in the absence of vibrations, apart from the main large-scale vortex occurring in both layers there are two additional vortices formed in the fluid layer in the downstream region. In the presence of vibrations and at the value of the Rayleigh number (${R}_\mathrm{f} = 880$) identical to that used in the vibration-free case, additional vortices in the fluid layer do not arise (Fig. 10b).

Fig. 10

The structures of the stationary flow for the long-wave instability mode at $h = 8$ and ${R}_\mathrm{f} = 880$ for two values of the vibrational Rayleigh number ${R}_\mathrm{fv}$: a ${R}_\mathrm{fv} = 0$, b ${R}_\mathrm{fv} = 5,000$. The streamlines are spaced at the same intervals equal to 0.4

For the short-wave instability mode in the considered range of parameters the flow structure (Fig. 11) and the maximum value of the stream function (Fig. 4b) obtained at the thermal Rayleigh number ${R}_\mathrm{f} = 4,500$, widely deviating from the threshold value, do not actually depend on the vibration intensity. This is explained by the fact that with increasing supercriticality the perturbations begin to penetrate into the porous layer where the inertial effects are less pronounced than in the pure fluid layer (Fig. 11). However, near the threshold an increase in the vibrational Rayleigh number ${R}_\mathrm{fv}$ results in a significant difference in the values of the stream functions (Fig. 4b), which is related to the occurrence and original localization of the convective flow in the fluid layer.

Fig. 11

The structures of the stationary flow for the long-wave instability mode at $h = 8$ and ${R}_\mathrm{f} = 4,500$ for two values of the vibrational Rayleigh number ${R}_\mathrm{fv}$: a ${R}_\mathrm{fv} = 0$, b ${R}_\mathrm{fv} = 5,000$. The streamlines are spaced at the same intervals equal to 0.2

4.2 The Interaction of the Long-Wave and Short-Wave Instability Modes

Let us analyze and compare the stationary solutions in the case of close threshold values of the thermal Rayleigh number for short-wave and long-wave instability modes at $h = 3$ (see Fig. 2a) and various intensities of vibrations. Figure 12 shows the dependence of the maximum module of the stream function on the thermal Rayleigh number at different values of the vibrational Rayleigh number ${R}_\mathrm{fv}$ (the size of the computational domain is defined by the size of the long-wave vortex with the wave number $k \approx \pi /4.5$ corresponding to the minimum of the neutral curve 1 in Fig. 2a at ${R}_\mathrm{fv} = 0$).

As it is shown in Kolchanova et al. (2013), in the absence of vibrations, the long-wave vortex emerging near the threshold loses its stability with increase of supercriticality and breaks down into a few short-wave vortices located in the fluid layer; with a further increase of ${R}_\mathrm{f}$ the intensity of the steady motion in this layer grows in accordance with the square root law (see a part of the curve 1 at large supercriticalities in Fig. 12a). A transition mode corresponds to the arc-shaped part of curve 1 in Fig. 12 (the part of the curve at low supercriticalities). In the absence of vibrations the size of the region of transition modes increases with the growth of ${R}_\mathrm{fv}$ (see curve 2 and 5 in Fig. 12a). This is attributed to the fact that the short-wave perturbations are strongly stabilized by vibrations in contrast to the long-wave perturbations, for which the effect of vibrations is considerably weaker (see curves 2–4 in Fig. 2a).

Fig. 12

The interaction between the long-wave and short-wave modes of stationary solutions at $h = 3$. The dependence of the maximum absolute stream function on the thermal Rayleigh number: a at various values of the vibrational Rayleigh number ${R}_\mathrm{fv}$ (1 - ${R}_\mathrm{fv} = 0$, 2 - ${R}_\mathrm{fv} = 500$, 3 - ${R}_\mathrm{fv} = 1,000$, 4 - ${R}_\mathrm{fv} = 2,200$, 5 - ${R}_\mathrm{fv} = 3,000$, 6 - ${R}_\mathrm{fv} = 5,000$), b at ${R}_\mathrm{fv} = 3,000$

Fig. 13

The structures of the stationary flow near the onset of convection in the case of the interaction between the long-wave and short-wave instability modes at $h = 3$, ${R}_\mathrm{fv} = 3,000$ and different values of the thermal Rayleigh number at points indicated in Fig. 12b: a ${R}_\mathrm{f} = 1,330$ (point 1), b ${R}_\mathrm{f} = 1,360$ (point 2), c $\mathrm {R}_f = 1,390$ (point 3), d ${R}_\mathrm{f} = 1,410$ (point 4), e ${R}_\mathrm{f} = 1,390$ (point 5), f ${R}_f = 1,410$ (point 6), g ${R}_\mathrm{f} = 1,450$ (point 7), h ${R}_\mathrm{f} = 1,466$ (point 8). The streamlines are spaced at the same intervals equal to 0.03

At sufficiently high intensities of vibrations (${R}_\mathrm{fv} > 1,000$) there is an abrupt transition to another branch of the steady flows (curves 4, 5, 6 in Fig. 12a). In the absence of vibrations (curve 1) this transition is not observed. The calculations made in the case of inverse change in the thermal Rayleigh number from large to small values, reveals a hysteresis effect: over some range of ${R}_\mathrm{f}$ the solution is ambiguous.

Figure 13 illustrates the rearrangement of the steady-state flow structure caused by variation of the thermal Rayleigh number at a fixed value of the vibrational Rayleigh number ${R}_\mathrm{fv} = 3,000$ (the figure shows the flow structure at the points indicated by dots in Fig. 12b). As it is readily seen, the main long-wave vortex occurs near the threshold (Fig. 13a, point 1 in Fig. 12b). With the growth of the Rayleigh number the center of this vortex is shifted to the interface between the upward flows (Fig. 13b, point 2 in Fig. 12b). With a further increase of the Rayleigh number the main vortex is supplemented by a number of small vortices arising in the fluid layer and rotating in the same direction as the main vortex (Fig. 13c, the point 3 in Fig. 12b). As supercriticality grows further, the number of additional vortices in the fluid layer increases and there appear a number of vortices rotating in the opposite direction relative to the main large-scale vortex. (Fig. 13d, point 4 in Fig. 12b). In the range of Rayleigh number values $1384 < {R}_\mathrm{f} < 1420$ the stationary solution is ambiguous. Thus, at ${R}_\mathrm{f} = 1390$ there are two stable regimes of convection, the intensity of which is determined by the value of the maximum module of the stream function at points 3 and 5 in Fig. 12b. The structure of flows in a fluid layer for these two regimes is shown Fig. 14 on a larger scale. It is seen that a gradual increase of ${R}_\mathrm{f}$ leads to the onset of convective regime characterized by co-existence of the main large-scale vortex and additional vortices located in a fluid layer and rotating in the same direction as the main one (Fig. 14a). And in the case of gradual decrease of ${R}_\mathrm{f}$ or when the initial supercriticality is set equal to a high value, the regimes of convection are excited in a finite-amplitude manner and involve the formation of additional vortices in the fluid layer rotating in the opposite direction relative to the direction of the main vortex (Fig. 14b). In this case, the flow in the fluid layer is more intensive than in the case of a gradual increase of ${R}_\mathrm{f}$. In the range of the Rayleigh number values ${R}_\mathrm{f} > 1,420$ there is the stationary solution, for which the intensity of additional vortices increases with the increase of supercriticality (Fig. 13g, point 7 in Fig. 12b), and the main large-scale vortex loses its stability and breaks into several short-wave vortices (Fig. 13h, point 8 in Fig. 12b).

Fig. 14

The structures of the stationary flow in the fluid layer for case of the interaction between the long-wave and short-wave instability modes at $h = 3$, ${R}_\mathrm{fv} = 3,000$, ${R}_\mathrm{f} = 1,390$ at points marked in Fig. 12b: a point 3, b point 5. The contour values for streamlines are of the same interval equal to 0.08. Solid lines correspond to positive values of the stream function, dashed lines – to negative values of the stream function

5 Conclusion

We have investigated the onset and nonlinear regimes of convection in a two-layer system composed of horizontal pure fluid layer and fluid-saturated porous layer subjected to the gravity field and high-frequency vibrations.

Previous investigations of linear stability of a conductive state of superposed horizontal pure fluid layer and saturated porous layer have shown that in some range of the ratios of porous layer to fluid layer thicknesses $h$ the neutral curves of the conductive state instability are bimodal: there exist long-wave instability mode when perturbations cover both layers and short-wave instability mode when perturbations develop in the fluid layer. We have performed the calculations for two values of $h$: for comparable layer thicknesses $h = 3$ when the critical Rayleigh numbers determining the thresholds of the conductive state instability with respect to the long-wave and short-wave perturbations are close and for $h = 8$ (thick porous layer) when the long-wave perturbations are more dangerous.

High-frequency vertical vibrations exert stabilizing effect on both instability modes, besides, the effect of vibrations on the short-wave perturbations located in the fluid layer is much stronger than on the long-wave perturbations occurring in both layers since the inertial effects in the porous medium are weak compared to the pure fluid layer (typical values of the effective permeability $\varepsilon _f$ are small).

Investigation of the convection excitation type has shown that in both cases convection is excited via direct bifurcation.

The study of nonlinear regimes of convection in the absence of vibrations have shown that in the case, when the thickness of the fluid layer is small compared to the thickness of the porous layer ($h = 8$) and a long-wave mode of convection predominates, with the growth of supercriticality the steady-state regime losses its stability and is replaced by oscillatory regime. With further growth of supercriticality the oscillatory regime in its turn becomes unstable and is replaced again by steady-state regime. The transition to the oscillatory regime, in our opinion, is related to the stability loss of the conductive state in a fluid layer: additional vortices generated as a result of this instability are located in the fluid layer. The instability is of the oscillatory nature; during oscillations the reconnection of additional vortices is observed. With further growth of the Rayleigh number the large-scale vortices covering porous and fluid layers and additional vortices formed in the fluid layer merge and a steady-state regime of convection is re-established.

Vertical vibrations usually stabilize the conductive state of the fluid heated from below. In the examined situation, they also have a stabilizing effect: they prevent the occurrence of the additional vortices in the fluid layer and thus increase the threshold of the oscillatory regime of convection. As it follows from the calculations, vibrations also reduce the Rayleigh number, at which the oscillatory convective regime is again replaced by the stationary regime. Thus, vibrations reduce the range of parameters responsible for the oscillatory regime, so that at sufficiently high vibration intensity and at any values of the supercriticality the steady-state regime of convection takes place.

For comparable thicknesses of the fluid and porous layers ($h = 3$) we have investigated the interaction between the short-wave and long-wave instability modes near the threshold of convection and the development of convection with a nearly five-fold increase in the supercriticality. In this case in the absence of vibrations with the supercriticality growth the large-scale vortex occurring near the threshold of the conductive state instability and spreading through both layers is splitted into several short-wave vortices located in the fluid layer. Under the action of vibrations the rearrangement of the structure flow with the growth of supercriticality generally follows the same scenario as in the absence of vibrations. However, at sufficiently large values of vibration intensity the solution becomes nonunique in some range of the Rayleigh numbers, and a change in the supercriticality leads to hysteresis. In this case, if the initial supercriticality is assigned high value, the arising flow structure involves the main large-scale vortices and a few additional vortices generated in the fluid layer in the direction opposite to the direction of the large-scale vortices.

The work was made under financial support of Russian Scientific Foundation (grant N 14-21-00090).