1 Introduction

The present work is devoted to studying the onset and development of convection in a system of two horizontal layers of a pure fluid layer and porous medium saturated by the same fluid in a static gravitational field. The convective flows in the fluid and porous layers are widely distributed in various natural and technological processes, which explains a keen interest of researchers in such flows. Thermocirculation of water in lakes and coastal areas, currents in geysers and hot springs, groundwater flows are known to be due to convection. In industry, this problem is commonly encountered while dealing with granulated insulation materials, heat exchangers for nuclear reactors, crystallization, and reservoir water circulation processes.

The onset of convection in a two-layer system consisting of the fluid layer and porous medium saturated by the same fluid in a static gravity field was first investigated by Nield (1977) under the conditions of the free upper and solid lower boundaries and a constant heat flux at both boundaries. The problem was solved in the framework of the Darcy model using the Beavers–Joseph boundary condition specified at the interface between the fluid and porous layers (Beavers and Joseph 1967) to take into account the jump in the tangential velocities at the interface. The analytical formula for the critical Rayleigh number determining the stability boundary for the equilibrium state of the system is derived. The critical wave number is supposed to be zero due to thermally insulated boundaries.

The stability of mechanical equilibrium in a three-layer system consisting of a porous layer sandwiched between two fluid layers of equal thickness was studied in Nield (1983) and Pillatsis et al. (1987). Nield (1983) considered the case when the top and bottom boundaries of the system were assumed solid. Pillatsis et al. (1987) described the system with free upper and lower boundaries, at which a constant heat flux was set, similarly as Nield (1977) did. The stability diagrams for various Darcy numbers and layer thickness ratios were obtained. It was shown that in the case of solid boundaries the stability threshold is larger than in the case of free boundaries.

To our knowledge, the stability of equilibrium in a two-layer system of a fluid and porous medium saturated by the same fluid in the case when the upper and lower solid boundaries were isothermal was first investigated by Sun (1973). A convective fluid flow in porous medium was described by the Darcy model using the Beavers–Joseph boundary condition at the interface between the fluid and porous layers. It was found that a decrease in the fluid layer thickness leads to a growth of the critical porous Rayleigh number. The obtained data was confirmed by the experimental results, which were also provided by Sun (1973). The authors focused only on the case of large-scale perturbations extending through the bulk of the fluid and porous layers.

The bimodal nature of the neutral curves for the system of horizontal layers of the fluid and porous medium saturated by the fluid was first discovered by Lyubimov and Muratov (1977). They investigated a three-layer system, consisting of a fluid layer sandwiched between the two porous layers. Different constant temperatures were imposed at the top and bottom solid boundaries. Treatment of the problem was based on the Darcy model with the boundary condition of zero tangential fluid velocity at the interface between layers. It was found that in the case of large fluid layer thicknesses, the neutral curves were unimodal and the short-wave perturbations generally located in the fluid layer were most dangerous. With decreasing relative thickness of the fluid layer, the neutral curves became bimodal. The reconstruction of neutral curves for variable permeability of the porous medium was also studied. The stability diagram on the plane of parameters (layer thickness ratio and permeability of the porous medium) involving the region of bimodal neutral curves was obtained.

The bimodal nature of neutral curves was later found by Chen and Chen (1988) while solving the linear stability problem for a two-layer system of the fluid and porous medium saturated by the same fluid. They described the fluid motion in a porous medium in the framework of the Darcy model using the Beavers–Joseph boundary condition at the interface between the fluid and porous layers. The stability of the system equilibrium was investigated at various values of the Darcy number, the ratio of the fluid to porous layer thicknesses and the ratio of the fluid to porous medium thermal conductivities. The critical value of the thickness ratio, at which the nature of the most dangerous perturbations changed and a transition from the long-wave to the short-wave perturbations occurred, was defined.

Various methods for description of the convective fluid motion in porous medium and boundary conditions at the interface between the fluid and porous layers were compared in the papers by Hirata et al. (2006, 2007a, b) in the context of the linear stability problem for the equilibrium stability in a two-layer system of a fluid and porous medium saturated by the fluid in the static gravity field. Hirata et al. (2006, 2007a) studied the linear stability problem using the following approaches: (1) one-domain approach, in which the convective fluid flow was described by a single equation for both media and the medium properties were assumed dependent on the coordinates; (2) two-domain approach, in which the fluid flow in the porous layer was described by the Darcy model using the Beavers–Joseph boundary condition at the interface between the layers; (3) two-domain approach, in which the fluid flow in the porous medium was described by the Brinkman model allowing for viscous diffusion of the momentum and using the tangential stress continuity condition at the interface between the layers. Hirata et al. (2007b) applied a two-domain approach, in which the Brinkman model was used to describe the convective fluid filtration in porous medium. However, instead of the boundary condition of tangential stress continuity they used the stress jump boundary conditions for tangential stresses offered by Ochoa-Tapia and Whitaker (1995a), (1995b). According to numerical simulations Hirata et al. (2007b), the value of the coefficient determining the tangential stress jump at the interface between the layers strongly affects the position of neutrals curves for small wave lengths and virtually has no effect on the stability boundary of equilibrium with respect to the long-wave perturbations.

Numerical calculations for the heat flux rate and supercritical convective flow structures in a two-layer system of the fluid and porous medium saturated by the fluid in the static gravity field were carried out by Chen and Chen (1992). In this work, the fluid flow in the porous layer was described by the Darcy equation supplemented by the Brinkman term for viscous diffusion of the momentum and Forchheimer term for the inertial effects manifesting themselves at high velocities of the convective fluid flow in the porous medium. The calculations were conducted up to the twentyfold supercriticality. The steady-state convection was observed over the entire range of the examined parameters. It was found that with increasing ratio of the fluid layer thickness to that of the porous layer the nature of the Nusselt number dependence on the supercriticality changes: a sharp increase in the heat flux with the growth of supercriticality occurred at small values of the thickness ratio and a moderate growth of the heat flux was observed at the thickness ratio exceeding some critical value. The obtained values of the heat flux at the thickness ratios of 0.1 and 0.2 were in good agreement with the experimental data (Chen and Chen 1989). The competition between the long-wave and short-wave modes of convection near the threshold of the equilibrium stability was not analyzed.

Papers by Lyubimov et al. (2002, 2004) were devoted to the question of convection mode competition in a three-layer system consisting of two porous layers separated by a pure fluid layer in the static gravity field for the case of small supercriticalities. The fluid motion was described by the Darcy model using the boundary condition of zero tangential fluid velocity at the interface between the layers. The authors used the layer thickness ratio, at which the minimal critical Grashof numbers of the short-wave and long-wave instabilities have close values. It has been found that already at low supercriticalities, the long-wave convection becomes unstable with respect to the short-wave perturbations. With the growth of supercriticality, the large-scale vortex, extending through the fluid layer and both porous layers, was replaced by a few small vortexes located in the fluid layer. A transition regime, which is a superposition of the long-wave and short-wave modes of instability, was investigated by Lyubimov et al. (2004). Here, the authors also derived a relationship between the maximum stream function and the Grashof number for various wave numbers. The calculations showed that with increasing supercriticality the intensity of the steady-state solutions near the threshold grows according to the square-root law.

In this paper, we explore the supercritical convective regimes and the nature of convection excitation in a two-layer system consisting of a fluid layer and porous medium saturated by the same fluid in the static gravity field. Here, our main concern is with studying the competition between the long-wave and short-wave convective modes near the threshold of the equilibrium stability and the nonlinear development of long-wave and short-wave modes. In Sect. 2, we discuss the problem formulation and governing equations with the boundary conditions, Sect. 3 is concerned with the numerical method of the problem solution, and in Sect. 4, the results of the study are presented. In Sect. 5, we discuss the main interesting results of this paper.

2 Problem Statement. Governing Equations and Boundary Conditions

Consider the problem of the onset of convection and its nonlinear regimes in a two-layer system containing a horizontal pure fluid layer of thickness \({h_\mathrm{f}}\) and an underlying porous layer of thickness \({h_\mathrm{m}},\) saturated by the fluid in the static gravity field (Fig. 1). The top and the bottom boundaries of the system are solid planes at different constant temperatures. We restrict our discussion to a plane problem, which implies that the layers are uniform along the z-axis.

Fig. 1
figure 1

System configuration

Full size image

The convective flow in the fluid layer is described by the free thermal convection equations in the Boussinesq approximation, and in the porous layer saturated by the fluid, it is described by the free convective filtration equation in the Darcy–Boussinesq approximation. Thus, the equations for the velocity, temperature, and pressure fields in the fluid layer are written as

$$\begin{aligned} \frac{\partial v}{\partial t} + (v\nabla )v = - \frac{1}{\rho }\nabla {p_\mathrm{f}} + \nu \Delta v + g\beta T{{\gamma }} \end{aligned}$$
(1)
$$\begin{aligned} \frac{{\partial T}}{{\partial t}} + (v\nabla )T = {\chi _\mathrm{f}}\Delta T \end{aligned}$$
(2)
$$\begin{aligned} \text{ div}\,v = 0 \end{aligned}$$
(3)

and in the porous layer

$$\begin{aligned} \frac{1}{m}\frac{{\partial u}}{{\partial t}} + \frac{1}{{{m^2}}}(u\nabla )u = - \frac{1}{\rho }\nabla {p_\mathrm{m}}-\frac{\nu }{K}u + g\beta \vartheta {\gamma } \end{aligned}$$
(4)
$$\begin{aligned} b\frac{{\partial \vartheta }}{{\partial t}} + (u\nabla )\vartheta = {\chi _\mathrm{eff}}\Delta \vartheta \end{aligned}$$
(5)
$$\begin{aligned} {\text{ div}}\,u = 0. \end{aligned}$$
(6)

Here v is the convective flow velocity in the fluid layer, u is the convective filtration velocity in the porous medium, \({p_\mathrm{f}}, {p_\mathrm{m}}\) are the pressures in the fluid and porous layers without hydrostatic pressure, \(T, \vartheta \) are the deviation of temperature in the fluid and porous layers from its mean value, \(\rho , \nu \) are the fluid density and kinematic viscosity, \(\beta \) is the thermal expansion coefficient, g is the acceleration of gravity, m is the porosity, K is the permeability of the porous medium, b is the ratio of the porous medium heat capacity to that of the fluid per unit volume, \({\chi _\mathrm{f}}, {\chi _\mathrm{m}}\) are the thermal diffusivities of the fluid and porous medium, \({\chi _\mathrm{eff}}\) is the effective thermal diffusivity (the ratio of the porous medium thermal conductivity to the fluid heat capacity per unit volume), \({\chi _\mathrm{eff}} = b{\chi _\mathrm{m}}, \gamma \) is the vertical axis unit vector. Indexes: f is the fluid, m is the porous medium.

Since the convective filtration velocities in the porous medium are generally small, the terms \(\frac{1}{m}\frac{{\partial u}}{{\partial t}}, \frac{1}{{{m^2}}}(u\nabla )u\) in the left-side part of the momentum equation for the porous layer (4) can be considered negligible in comparison with the drag force. Further, the equations will be written without regard to these two terms.

The system of Eqs. (1)–(6) is supplemented with the following boundary conditions. The no-slip condition is fulfilled at the top boundary of the two-layer system, the impermeability condition is fulfilled at the bottom boundary, and both boundaries are assumed to have different constant temperatures

$$\begin{aligned} y&= {h_\mathrm{f}}{:}\; v_x = v_y = 0, \quad T = - {\Theta _\mathrm{f}}, \\ \nonumber y&= -h_\mathrm{m}{:}\; u_y = 0, \quad \vartheta ={\Theta _\mathrm{m}}. \end{aligned}$$
(7)

The boundary conditions at the interface between the fluid and porous layers are the continuity of the vertical velocity component, the jump in the tangential fluid velocity component and the balance of the normal stresses

$$\begin{aligned} y = 0{:}\; v_y = u_y, \quad v_x = 0, \quad T = \vartheta , \\ \nonumber {\kappa _\mathrm{f}} \frac{{\partial T}}{{\partial y}} = {\kappa _\mathrm{m}} \frac{{\partial \vartheta }}{{\partial y}}, \quad {p_\mathrm{f}} = {p_\mathrm{m}}. \end{aligned}$$
(8)

Let us clarify the last boundary condition. In the case of relatively small permeability of the porous medium, the viscous momentum diffusion is usually neglected (Darcy–Boussinesq approximation), so that in the general form the balance of normal stresses can be written as

$$\begin{aligned} p_\mathrm{f}-2\nu \rho \frac{\partial v_y}{\partial y} = p_\mathrm{m}. \end{aligned}$$
(9)

The derivative \(\partial v_y/\partial y\) is equal to zero because of the zero jump in the tangential component of the fluid velocity at the interface and the continuity equation.

Nondimensionalization of the equations with respect to the fluid layer parameters is performed by introducing the length, time, temperature, velocity, and pressure scales \([r] = {h_\mathrm{f}} = L, [t] = {L^2}/{\chi _\mathrm{f}}, [T] = [\vartheta ] = {A_\mathrm{f}}L, [v] = [u] = {\chi _\mathrm{f}}/L, [p_\mathrm{f}] = [p_\mathrm{m}] = \rho \nu {\chi _\mathrm{f}}/{L^2}.\)

The obtained system of non-dimensional equations for the fluid layer is written as

$$\begin{aligned} \frac{1}{{Pr}}\frac{\partial v}{{\partial t}} + \frac{1}{{Pr}}(v\nabla )v = -\nabla p_\mathrm{f} + \Delta v + RaT{\gamma } \end{aligned}$$
(10)
$$\begin{aligned} \frac{{\partial T}}{{\partial t}} + (v\nabla )T = \Delta T \end{aligned}$$
(11)
$$\begin{aligned} {\text{ div}}\,v= 0 \end{aligned}$$
(12)

and for the porous layer

$$\begin{aligned}&\displaystyle -{\varepsilon _\mathrm{f}}\nabla p_\mathrm{m}-u + {\varepsilon _\mathrm{f}} Ra\vartheta \gamma = 0\end{aligned}$$
(13)
$$\begin{aligned}&\displaystyle b\frac{\partial \vartheta }{\partial t} + (u\nabla )\vartheta = \kappa \Delta \vartheta \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle {\text{ div}}\,u = 0 \end{aligned}$$
(15)

with the boundary conditions

$$\begin{aligned} y&= 1{:}\;v_x = v_y = 0, \quad T = - 1, \nonumber \\ y&= - h{:}\;u_y = 0, \quad \vartheta = h/\kappa .\\ \nonumber y&= 0{:}\;v_y = u_y, \quad v_x =0,\quad T = \vartheta ,\\&\qquad \frac{\partial T}{\partial y} = \kappa \frac{\partial \vartheta }{\partial y}, \quad {p_\mathrm{f}} = {p_\mathrm{m}}. \nonumber \end{aligned}$$
(16)

Here, as it follows from the heat flux continuity condition, \(\kappa _\mathrm{f}A_\mathrm{f} = \kappa _\mathrm{m}A_\mathrm{m}\) or \(\kappa = \kappa _\mathrm{m}/\kappa _\mathrm{f} = A_\mathrm{f}/A_\mathrm{m},\) where \(\kappa _\mathrm{f}, \kappa _\mathrm{m}\) are the thermal conductivities of the fluid layer and porous medium saturated by the fluid, \(A_\mathrm{f}, A_\mathrm{m}\) are the vertical equilibrium temperature gradients in the fluid and porous layers. The problem includes the following non-dimensional parameters

$$\begin{aligned} \varepsilon _\mathrm{f} = \frac{K}{L^2}, \quad Pr = \frac{\nu }{\chi _\mathrm{f}}, \quad Ra = \frac{{g\beta A_\mathrm{f}{L^4}}}{\nu \chi _\mathrm{f}}, \quad \kappa = \frac{\kappa _\mathrm{m}}{\kappa _\mathrm{f}}, \quad b = \frac{{(\rho c_\mathrm{p})}_\mathrm{m}}{{(\rho c_\mathrm{p})}_\mathrm{f}}, \quad h = \frac{h_\mathrm{m}}{h_\mathrm{f}}. \end{aligned}$$

Introduce the stream functions for flows in the fluid and porous layers and the vorticity of the flow in the fluid layer

$$\begin{aligned} v_x = \frac{\partial \psi }{\partial y}, \quad v_y = - \frac{\partial \psi }{\partial x}, \quad u_x = \frac{\partial \varphi }{\partial y}, \quad u_y = - \frac{\partial \varphi }{\partial x}, \quad \Omega = \text{ rot}\,v. \end{aligned}$$

The system of equations in terms of the stream functions and vorticity for the fluid layer is

$$\begin{aligned} \frac{\partial \Omega }{\partial t} + \frac{\partial \psi }{\partial y}\frac{\partial \Omega }{\partial x} - \frac{\partial \psi }{\partial x}\frac{{\partial \Omega }}{{\partial y}} = Pr \left( {\Delta \Omega + Ra\frac{{\partial T}}{{\partial x}}} \right) \end{aligned}$$
(17)
$$\begin{aligned} \frac{{\partial T}}{{\partial t}} + \frac{{\partial \psi }}{{\partial y}}\frac{{\partial T}}{{\partial x}} - \frac{{\partial \psi }}{{\partial x}}\frac{{\partial T}}{{\partial y}} = \Delta T \end{aligned}$$
(18)
$$\begin{aligned} \Omega = - \Delta \psi \end{aligned}$$
(19)

and for the porous layer

$$\begin{aligned}&\displaystyle \Delta \varphi + {\varepsilon _\mathrm{f}}Ra\frac{{\partial \vartheta }}{{\partial x}}=0\end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle b\frac{{\partial \vartheta }}{{\partial t}} + \frac{{\partial \varphi }}{{\partial y}}\frac{{\partial \vartheta }}{{\partial x}} - \frac{{\partial \varphi }}{{\partial x}}\frac{{\partial \vartheta }}{{\partial y}} = \kappa \Delta \vartheta . \end{aligned}$$
(21)

Let us discuss the boundary condition of the normal stress continuity at the interface between the fluid and porous layers at \(y = 0{:}\; {p_\mathrm{f}} = {p_\mathrm{m}}.\) Using the horizontal projections of the momentum equations for the fluid and porous layers (10) and (13) and taking into account the smallness of the Darcy number \(\varepsilon _\mathrm{f}\) and the inertial terms compared to the viscous term and the drag force of the porous matrix we get the normal stress continuity condition defined as

$$\begin{aligned} \varepsilon _\mathrm{f}\frac{{\partial ^2}{v_x}}{\partial {y^2}} + u_x = 0, \end{aligned}$$

or in terms of the stream functions

$$\begin{aligned} {\varepsilon _\mathrm{f}}\frac{{{\partial ^3}\psi }}{{\partial {y^3}}} + \frac{{\partial \varphi }}{{\partial y}} = 0. \end{aligned}$$

Thus, the boundary conditions in terms of the stream functions take the following form:

$$\begin{aligned} y&= 1{:}\;\psi = 0, \quad T = - 1, \nonumber \\ y&= - h{:}\;\varphi = 0, \quad \vartheta = h/\kappa .\\ \nonumber y&= 0{:}\;\psi = \varphi , \quad \frac{{\partial \psi }}{{\partial y}} = 0, \quad T = \vartheta , \\ \nonumber&\qquad \frac{{\partial T}}{{\partial y}} = \kappa \frac{{\partial \vartheta }}{{\partial y}},\quad {\varepsilon _\mathrm{f}}\frac{{{\partial ^3}\psi }}{{\partial {y^3}}} + \frac{{\partial \varphi }}{{\partial y}} = 0. \end{aligned}$$
(22)

3 Numerical Method

The problem (17)–(22) was solved numerically by the finite-difference method. Numerical calculations were based on the explicit finite-difference scheme. All spatial derivatives were approximated by the central differences. Poissons equation (19) was solved by the method of successive over-relaxation. Computations were carried out for the grid cells, the horizontal size of which was equal to the most dangerous perturbation wavelength \(\lambda \), according to the data of the linear stability analysis. The periodicity condition \(f(-\lambda /2,y,t) = f(\lambda /2,y,t)\) was imposed at the side boundaries of the computational domain \(x = \pm \lambda /2\) for all functions. The program was tested by comparing the numerical results with the available data obtained for the case of pure fluid convection in a heated from below horizontal porous layer saturated by the fluid under gravity conditions. The main calculations were conducted at fixed values of parameters \(\kappa , b, Pr, {\varepsilon _\mathrm{f}}\!\!: \kappa = 1, b = 1, Pr = 6.7, {\varepsilon _\mathrm{f}} = {10^{- 3}}.\)

4 Numerical Results

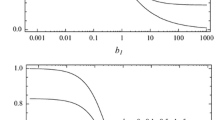
It is known (Lyubimov and Muratov 1977; Chen and Chen 1988) that at some values of parameters the neutral curves of the linear mechanical equilibrium stability in a heated from below two-layer system of a pure fluid layer and porous medium saturated by the fluid are bimodal. Figure 2 shows the equilibrium–stability neutral curves at \(\kappa = 1, b = 1, Pr = 6.7, {\varepsilon _\mathrm{f}} = {10^{-3}}\) and various ratios of the porous layer to the fluid layer thicknesses h. As it is seen from the graph, at small thickness ratios the neutral curve has one minimum (curve 5) and the short-wave perturbations, occurring in the fluid layer and poorly penetrating the porous medium, are most dangerous (since the fluid moving in a porous medium experiences the resistance of porous matrix, the perturbations begin to penetrate the porous medium only at large porous layer thickness). With increasing porous layer thickness, the critical Rayleigh number and the critical wave number corresponding to the short-wave minimum are nearly constant (short-wave perturbations are located in the fluid layer and the fluid layer thickness is set to be unit, i.e., it is one and the same for all h). However, the neutral curve gets one more minimum at small wave numbers (see curve 4). With a further increase in h, the minimum falls below the short-wave value and the long-wave perturbations become most dangerous (see curves 3, 4, and 5).

Fig. 2
figure 2

Equilibrium–stability neutral curves at various thickness ratios: \(1 - h = 8, 2 - h = 5, 3 - h = 3, 4 - h = 2.5, 5 - h = 2\)

Full size image

Figure 3 shows the transformation of the neutral curves with the change of \({\varepsilon _\mathrm{f}}\) and \(h\) for \(\kappa = 1.43.\) The range of the bimodal neutral curves existence is located between the curves 1 and 3. Besides, in the range between the curves 1 and 2, the long-wave minimum is lower than the short-wave one and in the range between the curves 2 and 3, the short-wave minimum is lower. Curve 2 corresponds to the case of close values of critical Rayleigh number.

Fig. 3
figure 3

Diagram \({\varepsilon _\mathrm{f}}-h;\) the range of the bimodal neutral curves existence is located between the curves 1 and 3 (the shaded region stands for most dangerous short-wave perturbations)

Full size image

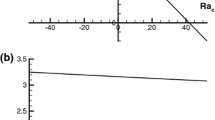
To study the effect of the boundary conditions at the interface on the results of linear stability analysis we have performed the calculations using the Beavers–Joseph condition at various values of the constant \({\alpha _\mathrm{BJ}}\) instead of the condition of zero tangential component of the fluid velocity. These calculations show that the short-wave perturbations localized in the clear liquid layer are more affected by the boundary conditions type and the effect of the boundary conditions on the long-wave perturbations developing in both layers is rather weak (see Fig. 4).

Fig. 4
figure 4

Equilibrium–stability neutral curves at various types of boundary conditions

Full size image

The numerical results obtained by solving the nonlinear problem at various thickness ratios are presented in Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, and 17.

Fig. 5
figure 5

The long-wave (\(\lambda = 16,\) curve 1) and short-wave (\(\lambda = 3,\) curve 2) instability modes. a The dependence of the maximum absolute stream function on the Rayleigh number. b The dependence of the Nusselt number on the Rayleigh number

Full size image
Fig. 6
figure 6

The stream function for the long-wave mode of steady-state solutions at \(Ra = 536\) (near the point of stability loss of a steady-state solution). The contour values for streamlines are of the same interval equal to 0.2

Full size image
Fig. 7
figure 7

The long-wave mode of steady-state solutions at \(Ra = 540\) (immediately after the loss of steady-state solution stability). a The dependence of the maximum absolute stream function on time. b The dependence of the maximum absolute stream function on time within 1.5th of the oscillation period determined by the minimum frequency

Full size image
Fig. 8
figure 8

The Fourier spectrum of maximum absolute stream function oscillations for the long-wave mode of steady-state solutions at \(Ra = 540\) (immediately after the loss of steady-state solution stability)

Full size image
Fig. 9
figure 9

Stream functions for the long-wave mode of steady-state solutions at \(Ra = 540\) (immediately after the loss of steady-state solution stability) and various time intervals within 1.5th of the oscillation period determined by the minimum frequency, at points presented in Fig. 6b: a \(t = 503.0\) (point 1), b \(t = 504.2\) (point 2), c \(t = 506.6\) (point 3), d \(t = 509.6\) (point 4). The contour values for streamlines are of the same interval equal to 0.2

Full size image
Fig. 10
figure 10

The long-wave mode of steady-state solutions at \(Ra = 600\) (after the loss of steady-state solution stability). a The dependence of the maximum absolute stream function on time. b The dependence of the maximum absolute stream function on time within the 1.5th of oscillation period determined by the minimum frequency

Full size image
Fig. 11
figure 11

The Fourier spectrum of the maximum absolute stream function oscillations for the long-wave mode of steady-state solutions at \(Ra = 600\) (after the loss of steady-state solution stability)

Full size image
Fig. 12
figure 12

Stream functions for the long-wave mode of steady-state solutions at \(Ra = 600\) (after the loss of steady-state solution stability) and various time intervals within 1.5th of oscillation period determined by the minimum frequency, at points presented in Fig.10b: a \(t = 202.0\) (point 1), b \(t = 212.0\) (point 2), c \(t = 214.0\) (point 3), d \(t = 215.0\) (point 4), e \(t = 216.5\) (point 5), f \(t = 217.0\) (point 6). The contour values for streamlines are of the same interval equal to 0.2

Full size image
Fig. 13
figure 13

The stream function for the long-wave mode of steady-state solutions at \(Ra = 750\). The contour values for streamlines are of the same interval equal to 0.2

Full size image
Fig. 14
figure 14

The dependence of the maximum absolute stream function on the Rayleigh number for the long-wave instability mode at various types of boundary conditions

Full size image
Fig. 15
figure 15

Stream functions for the short-wave mode of steady-state solutions at various Rayleigh numbers: a \(Ra = 1{,}500\), b \(Ra = 2{,}500\), c \(Ra = 3{,}500\), d \(Ra = 4{,}500.\) The contour values for streamlines are of the same interval equal to 0.2

Full size image
Fig. 16
figure 16

The dependence of the maximum absolute stream function on the Rayleigh number: a for finite supercriticalities, b near the threshold

Full size image
Fig. 17
figure 17

Steady-state flow structures near the threshold in the case of the competition between the long-wave and short-wave convective modes at \(h = 3\) and various Rayleigh numbers: a \(Ra = 1,320\), b \(Ra = 1,321\), c \(Ra = 1,322\), d \(Ra = 1,324\), e \(Ra = 1,326\), f \(Ra = 1,328\), g \(Ra = 1,330\), h \(Ra = 1,331\), i \(Ra = 1,332\). The contour values for streamlines are of the same interval equal to 0.005

Full size image

Figure 5a shows the dependence of the maximum absolute stream function \(\Psi \) on the Rayleigh number and Fig. 5b represents the dependence of the Nusselt number on the Rayleigh number in the case when the ratio of the porous layer thickness to the fluid layer thickness is equal to 8. In this case, the lowest instability level is related with the long-wave perturbations. The results were obtained on the uniform grid with square cells \(({h_x} = {h_y} = H).\) The long-wave branch is obtained at \(H = 0.1\) and the short-wave branch—at \(H = 0.04.\) The selection of the computational grid was based on test computations performed on various grids under the requirement of the optimal relation between the computational time and accuracy. It is readily seen from Fig. 5a that soft excitation of convection is observed for both the long-wave and short-wave instability modes and the intensity of motion grows with increasing supercriticality according to the square-root law. Moreover, the long-wave mode grows much faster than the short-wave mode.

Let us analyze the behavior of solutions at finite supercriticalities. First, we will consider the solutions for the long-wave instability mode. The structure of the steady-state flow for this mode at \(Ra = 536\) is shown in Fig. 6. As it is seen from the graph, the steady-state flow has the structure of large-scale convective rolls occupying both layers and involving small additional vortexes of opposite direction formed in the fluid layer at the interface between the rolls in the downstream region.

At the Rayleigh number of about 538, the steady-state solution given in Fig. 6 becomes unstable and is replaced by the oscillatory regime. Figure 7a, b shows the types of oscillations that occur after the loss of stability of the steady-state regime at \(Ra = 540\).

The Fourier spectrum and the data on the rearrangement of the flow structure during oscillations at \(Ra = 540\) are illustrated in Figs. 8 and 9 (the time moments for depicted flow structures are denoted by dots in Fig. 7b). As is evident from the figure, the spectrum includes a set of high and low frequencies. The basic oscillations in the spectrum are determined by the high frequency and a change in the amplitude of these oscillations corresponds to the low frequency (Fig. 7b). During oscillations a reconnection of additional vortexes takes place. The intensity of one of the vortexes gradually decreases (Fig. 9a, b) and it reconnects with another vortex, the intensity of which starts to grow (Fig. 9c). Then process is repeated (Fig. 9d).

The oscillation of the maximum absolute stream function at \(Ra = 600\) is illustrated in Fig. 10a, b. It can be readily seen that the oscillation amplitude rises as the Rayleigh number increases. The oscillation spectrum is shifted toward the region of lower frequencies (Fig. 11).

Figure 12 shows rearrangement of the fluid flow structure at time intervals marked by dots in Fig. 10b. The intensity of one of the vortexes located in the fluid layer starts to grow (Fig. 12a, b) then it is separated from the basic large-scale roll and reconnects with another vortex formed in the fluid (Fig. 12c–f). After this, the process is repeated.

According to computations, the fluid flow again becomes stationary at \(Ra = 750\). Moreover, in the fluid layer near the interface between the rolls in the downstream domain a small additional vortex of the same direction as the basic one is formed in each basic vortex extending through both layers (Fig. 13).

Numerical simulations of the nonlinear convective regimes using the Beavers–Joseph condition at various values of the constant \({\alpha _\mathrm{BJ}}\) show that the increase of \({\alpha _\mathrm{BJ}}\) results in the decrease of the Rayleigh number range where the oscillatory regime takes place (see Fig. 14). Note that the results obtained for \({\alpha _\mathrm{BJ}} = 0.78\) are in a good agreement with the results obtained with the condition of zero tangential component of the fluid velocity at the interface.

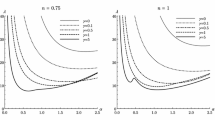
Figure 15 presents the numerical data on the changes in the fluid flow structure with a growth of the Rayleigh number for the short-wave instability mode. The calculations show that for this instability mode the steady-state solution exists for the whole range of the Rayleigh numbers examined here, and the oscillatory regime does not occur. As you can see from Fig. 15, with increasing Rayleigh number the fluid flow starts to penetrate the porous layer and at sufficiently great Ra a large-scale vortex is formed inside the two-layer system.

The formation of the large-scale vortex is accompanied by a change in the slope of curve 2 (Fig. 5a) showing the dependence of the maximum absolute stream function for the short-wave mode of steady-state solutions on the Rayleigh number and also by a change in the slope of curve 2 (Fig. 5b) illustrating the Nusselt number as a function of the Rayleigh number for this instability mode.

Now, we consider the behavior of solutions for the layer thickness ratio, at which the values of the threshold Rayleigh numbers for the short-wave and long-wave instability modes are close. Preliminary calculations show that the long-wave vortex is unstable and even at low supercriticalities falls into small short-wave vortexes located in the fluid layer. Therefore, we consider the case when the threshold of the equilibrium stability with respect to the long-wave perturbations is slightly below the stability threshold with respect to the short-wave perturbations.

Figure 16a shows the dependence of the maximum absolute stream function on the Rayleigh number in the case when the ratio of the porous layer thickness to the fluid layer thickness is equal to 3 [the dimensions of the computational domain correspond to the size of the long-wave vortex with the wave number \(k = \pi /4.5\) associated with the minimum critical Rayleigh number for neutral perturbations (see Fig. 2)]. The part of the curve describing this dependence at Rayleigh numbers near the instability threshold is shown in Fig. 16b.

Figure 17 illustrates the rearrangement of the fluid flow structure with the growth of Rayleigh number. The flow structure shown in this figure corresponds to the values of the Rayleigh number marked by triangles in Fig. 16b. As one can see from the figure, the formation of a large-scale long-wave vortex occupying both layers occurs when the Rayleigh number reaches its threshold value. An increase in the supercriticality leads to the appearance of additional short-wave vortexes in the fluid layer. With a further growth of the Rayleigh number the long-wave vortex losses its stability and breaks down into a few small short-wave vortexes located in the fluid layer.

5 Conclusions

We have studied the convection excitation in a two-layer system composed of the horizontal fluid and porous layers under the gravity conditions. We consider two cases of the layer thickness ratio: (1) \(h = 8\) when the long-wave perturbations are most dangerous, according to the linear stability theory; (2) \(h = 3\) when according to the linear stability theory, the critical Rayleigh numbers determining thresholds of the equilibrium stability with respect to the long-wave and short-wave perturbations take close values. The calculations show that in both cases the convection is softly generated.

In the case of the predominant long-wave convective mode \((h = 8),\) when perturbations take the form of large-scale rolls occupying the bulk of both layers, a steady-state convective regime is first to appear. Then the regime losses its stability and gives place to an oscillatory regime at \(Ra = 538\). The basic vortexes covering both layers are nearly stagnant. All changes occur mainly in the fluid layer where small additional vortexes of the opposite direction and time-dependent intensity appear at the interface between the rolls in the downstream domain. The types of oscillations for the maximum absolute stream function in the computational domain and Fourier spectra of oscillations at various Rayleigh numbers have been found. It has been shown that at the Rayleigh number equal to about 750, the oscillatory regime is again replaced by the steady-state convective regime. The numerical data of the fluid flow restructuring for the short-wave instability mode has also been obtained for \(h = 8\). The computations show that the steady-state vortexes located in the fluid layer are formed at small supercriticalities and with increasing the Rayleigh number the fluid flow begins to penetrate the porous medium. The oscillatory regime for the short-wave instability mode is not discovered.

For the layer thickness \(h = 3,\) the exploration of the long-wave and short-wave mode competition shows that even at small supercriticalities the long-wave vortex becomes unstable and breaks down into small-scale short-wave vortexes located in the fluid layer. The obtained data is qualitatively confirmed by the results presented in papers (Lyubimov et al. 2002, 2004), in which the authors numerically investigated the problem of the convection excitation in a three-layer system consisting of a fluid layer confined between two porous layers saturated by the fluid.