Analytical Modeling of Flow Behavior for Wormholes in Naturally Fractured–Vuggy Porous Media

Abstract

Acidizing technology has been widely applied when developing naturally fractured–vuggy reservoirs. So testing and evaluating acidizing wells’ pressure behavior become necessary for further improving the wells’ performance. Analyzing transient pressure data can estimate some key reservoir parameters. Generally speaking, carbonate minerals are usually composed of dolomite and calcite which are easy to be dissolved by hydrochloric acid which is often used to react with the rock to create a high conductivity channel, namely wormhole. Pressure transient behavior in fractured–vuggy reservoirs has been studied for many years; however, the models of acidizing wells with wormholes were not reported in previous studies. This article presented an analytical model for wormholes in naturally fractured–vuggy carbonate reservoirs, and wormholes solutions were obtained through point sink integral method. The results were validated accurately by comparing with previous results and numerical simulation. Then in this paper, type curves were established to recognize the flow characteristics, and flow was divided into six flow regimes comprehensively. The calculative results showed that the characteristics of type curves were influenced by inter-porosity flow factor, wormhole number, fluids capacitance coefficient. We also showed that the pressure behavior was affected by the angles between wormholes, and the pressure depletion increased as the angle decreased, because the wormholes were closer, their interaction became stronger. At the end, a reservoir example was showed to demonstrate the methodology of new type curve analysis.

1 Introduction

Characterizing vuggy fractured rock has gained an increasing worldwide attention because many fractured vuggy reservoirs have been found by many countries such as Canada and China (Kossack and Curpine 2001; Rivas-Gomez et al. 2001; Camacho-Velázquez et al. 2005; Wu et al. 2006, 2007); however, complex pore systems in fractured–vuggy reservoirs are posing significant research challenges (Noushabadi 2011; Popov et al. 2009; Rzonca 2008; Guo et al. 2012).

Generally speaking, fractured–vuggy porous media are composed of matrix, fractures, and vugs systems and have varying properties such as porosity, permeability, and fluid transport behaviors (Liu et al. 2003; Mai and Kantzas 2007; Guo et al. 2012). Recently, many scholars have made some efforts to simulate the fluids flow and transport behaviors in fractured–vuggy reservoirs through numerical simulation and analytical methods (Arana et al. 2009; Akram et al. 2010; Cobett et al. 2010; Djatmiko and Hansamuit 2010; Gulbransen et al. 2010; Leveinen 2000; Guo et al. 2012; Wu et al. 2006, 2007; Yao et al. 2010). Arana et al. (2009) presented a very practical and simple technique to numerically simulate the multiphase flow in multi-porosity naturally fractured reservoirs. Akram et al. (2010) modeled the dynamic behavior of a fissured dual-carbonate reservoir with discrete fracture network, and the results showed the dynamic features of the reservoir and demonstrated how the simulation model was calibrated using all variable information, particularly, the pressure buildup. Cobett et al. (2010) studied the numerical well test modeling of fractured carbonate rocks, and showed that numerical well testing had its limitations, especially when simulating disperse vugs. Djatmiko and Hansamuit (2010) presented some techniques to identify vugs in a real pressure buildup data, and their technique could be used to quantify vugs from well testing when analytical dual porosity or triple porosity model was unable to handle all matrix-to-fracture inter-porosity flow due to reservoir heterogeneity. Gulbransen et al. (2010) developed a multi-scale mixed finite-element (MsMFE) method for detailed modeling of vuggy and naturally fractured reservoirs. Guo et al. (2012) established a test analysis model of a horizontal well, and triple porosity and dual permeability flow behavior were modeled; their results showed that type curves were dominated by external boundary conditions as well as the permeability ratio of fracture system to the sum of fracture and matrix systems. Wu et al. (2007) proposed an analytical approach for pressure transient test analysis in naturally fractured–vuggy reservoirs, and analytical solutions were obtained. Finally, actual well test data from a fractured–vuggy reservoir in Western China were analyzed by using their model.

During oil and gas development, the near well zone is often damaged by well drilling and completion, fines migration, and other operations, which hinders the hydrocarbons flow into the well. In this case, the near well zone needs to be treated to improve fluids flow ability (Liu et al. 2013). Carbonate minerals are usually composed of dolomite and calcite which are easy to be dissolved by hydrochloric acid (Fredd 2000), which is often used to react with the rock to create a high conductivity channel, namely wormhole, so that hydrocarbons can bypass the damaged zone, called as carbonate acidizing. At present, carbonate acidizing has been widely implemented into fractured–vuggy reservoirs. Therefore, wormhole propagation problems have been studied by many researchers (Sollman et al. 1990; Gdanski 1999; Hung and Sepehrnoori 1989; Jia et al. 2013; Yuan 1999; Huang et al. 1999; Fredd 2000; Wang and Chen 2004; Tremblay 2005; Istchenko and Gates 2011, 2012; Liu et al. 2013), and most of above papers studied the mechanism of wormhole forming. Their results showed that acid selectively flowed into the big pores to create wormhole structures, which could be divided into five main types of dissolution structures: 1. Face dissolution. 2. Conical wormholes. 3. Dominant wormholes. 4. Ramified wormholes. 5. Uniform dissolution. The transition from dissolution structure 1–5 is commonly observed as acid injection rate increases (Fredd 2000).

Wormholes were not considered into the above models presented by those authors (Arana et al. 2009; Akram et al. 2010; Cobett et al. 2010; Djatmiko and Hansamuit 2010; Gulbransen et al. 2010; Leveinen 2000; Guo et al. 2012; Wu et al. 2006, 2007; Yao et al. 2010). Most of the authors studied the pressure transient behaviors of only vertical wells or horizontal wells. At present, there is no analytical model or numerical model presented on the wormholes in naturally fractured–vuggy porous media. In this paper, a wormhole seepage model for fractured–vuggy carbonate reservoirs was investigated for the first time. The rest of the article was structured as follows: Sect. 2 will introduce physical assumptions on physical properties in naturally fractured–vuggy reservoirs which were conceptualized as multiple-continuum medium, consisting of highly permeable fractures, low-permeability rock matrix, vugs, and multi-branched wormholes with high conductivity. Section 3 established the mathematical model, and the point source solution was obtained by using Laplace transformation. Then, multi-branched wormholes solutions were presented through using point sink integral method. Section 4 established type curves and analyzed the flow characteristics, and showed the effect of some key parameters on type curves. Finally, a case example was matched with type curves.

2 Physical Modeling

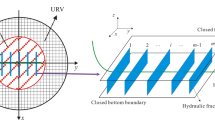
Fractured–vuggy carbonate reservoirs with multi-branched wormholes are naturally structured by matrix system, fractures system, vugs system. (See Fig. 1a–c). Figure 2 shows the physical modeling scheme of fractured–vuggy carbonate medium. As shown in Fig. 2, four types of systems are relatively independent. Similar to the conventional double-porosity model (Warren and Root 1963), fractures are considered as main pathways of global flow, connected with multi-branched wormholes, and ultimately fluids flowed from multi-branched wormholes into the wellbore.

Fig. 1

Schematic diagram: a fractured–vuggy carbonate reservoirs with multi-branched wormholes. b The system of matrix, fractures, vugs. c Wormholes

Fig. 2

Physical modeling scheme of fractured–vuggy carbonate medium

The fracture–vug–matrix–wormhole system can be conceptualized as consisting of (1) fractures, (2) vugs, (3) matrix, (4) and wormholes. With those conceptualizations above, the assumptions of physical model are as follows:

• (1) Sugar cube fractures as seen in classical multiple porosity media models are used in this article (Warren and Root 1963; Wu et al. 2006, 2007); the shape of matrix blocks and vugs varied with different shapes with different geometric shape factors $\alpha _\mathrm{fv}, \alpha _\mathrm{fm}$, and $\alpha _\mathrm{vm}$ (Wu et al. 2007; Cobett et al. 2010).

• (2) All rock properties (including matrix, natural fractures, vugs), such as permeability and porosity, are constant. Fluids compressibility and viscosity are assumed to be constant. The formation thickness is constant.

• (3) Wormholes are conceptualized as vertical plates extending from the top to the bottom of the domain in vertical direction ($z$ axis). In horizontal direction ($x-y$ plate), each wormhole looks like a line which has a length $x_\mathrm{f}$.

• (4) The external boundary of the reservoir in the radial direction ($r$ axis direction) is infinite. The top boundary of the reservoir is closed or impermeable, and the bottom boundary of the reservoir is also closed or impermeable.

• (5) Isothermal and Darcy flow are assumed.

• (6) The total production of multi-branched wormholes is equal to total production Q.

• (7) The well is considered into a point sink at changing rate $q(t)$.

• (8) At the starting time of production, the pressure is uniformly distributed and is equal to the initial pressure $(p_\mathrm{i})$.

3 Mathematical Modeling

3.1 The Governing Equations

To obtain wormhole pressure solution, point source model should be first established. It is well known that fluids flow only occurs in the natural fracture system in naturally fractured–vuggy porous media. Now to establish fracture equation, we consider a unit volume. Eq. (1) shows the results. The first term in the right of governing equation represents change of the mass flow flux under unit time in the unit volume. The first term in the left of governing equation represents the difference between mass flow in and mass flow out in the unit volume. The second term in the left of governing equation represents inter-porosity flow volume from the matrix into the fractures. The third term in the left of governing equation represents inter-porosity flow volume from the vugs into the fractures (Liu et al. 2003; Wu et al. 2006, 2007):

$$\begin{aligned} \frac{k_\mathrm{f} }{\mu }\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial p_\mathrm{f} }{\partial r}} \right) -\phi _\mathrm{m} c_\mathrm{m} m \frac{\partial p_\mathrm{m} }{\partial t}-\phi _\mathrm{v} c_\mathrm{v} \frac{\partial p_\mathrm{v} }{\partial t}=\phi _\mathrm{f} c_\mathrm{f} \frac{\partial p_\mathrm{f} }{\partial t}. \end{aligned}$$

(1)

When vugs are regarded as unit volume, the total change of mass flow flux in unit volume of the vugs is the sum of inter-porosity outflow volume from vugs into the fractures, and inter-porosity outflow volume from the vugs into the matrix, which could be seen from the direction of the arrow in Fig. 3,

$$\begin{aligned} \phi _\mathrm{v} c_\mathrm{v} \frac{\partial p_\mathrm{v} }{\partial t}=\frac{\alpha _\mathrm{fv} k_\mathrm{v} }{\mu }(p_\mathrm{f} -p_\mathrm{v} )+\frac{\alpha _\mathrm{vm} k_\mathrm{m} }{\mu }(p_\mathrm{m} -p_\mathrm{v} ). \end{aligned}$$

(2)

Fig. 3

Wellbore multiple wormholes model

Similarly, when matrix is regarded as the unit volume, the total change of mass flow flux in unit body of the matrix is the sum of inter-porosity outflow volume from matrix into the fractures, and inter-porosity inflow volume from the vugs into the matrix,.

$$\begin{aligned} \phi _\mathrm{m} c_\mathrm{m} \frac{\partial p_\mathrm{m} }{\partial t}=\frac{\alpha _\mathrm{fm} k_\mathrm{m} }{\mu }(p_\mathrm{f} -p_\mathrm{m} )+\frac{\alpha _\mathrm{vm} k_\mathrm{m} }{\mu }(p_\mathrm{v} -p_\mathrm{m} ). \end{aligned}$$

(3)

The initial condition is

$$\begin{aligned} p_\mathrm{f} (r,0)=p_\mathrm{v} (r,0)=p_\mathrm{m} (r,0)=p_\mathrm{i}. \end{aligned}$$

(4)

Outer boundary at constant pressure for infinite system can be expressed as

$$\begin{aligned} p_\mathrm{f} (r\rightarrow \infty ,t)=p_\mathrm{v} (r\rightarrow \infty ,t)=p_\mathrm{m} (r\rightarrow \infty ,t)=p_\mathrm{i}. \end{aligned}$$

(5)

In this paper, inner boundary condition of point source which is different from that given by Wu et al. (2007) can be decided by a changing flow rate, $q(t)$, imposed to the wellbore. It can be given as

$$\begin{aligned} \frac{2\pi r_\mathrm{w} k_\mathrm{f} h}{\mu }\frac{\partial p_\mathrm{f} }{\partial r}(r_\mathrm{w} \rightarrow 0,t)=q(t). \end{aligned}$$

(6)

Equations (1)–(6) can be redefined by using dimensionless quantities which are listed in Table 1. The dimensionless equations are defined as following:

$$\begin{aligned}&\displaystyle \omega _\mathrm{f} \frac{\partial p_\mathrm{Df} }{\partial t_\mathrm{D} }-\frac{1}{r_\mathrm{D} }\frac{\partial }{\partial r_\mathrm{D} }\left( {r_\mathrm{D} \frac{\partial p_\mathrm{Df} }{\partial r_\mathrm{D} }} \right) -\lambda _\mathrm{fv} (p_\mathrm{Dv} -p_\mathrm{Df} )-\lambda _\mathrm{fm} (p_\mathrm{Dm} -p_\mathrm{Df} )=0.\end{aligned}$$

(7)

$$\begin{aligned}&\displaystyle \omega _\mathrm{v} \frac{\partial p_\mathrm{Dv} }{\partial t_\mathrm{D} }+\lambda _\mathrm{fv} (p_\mathrm{Dv} -p_\mathrm{Df} )+\lambda _\mathrm{vm} (p_\mathrm{Dv} -p_\mathrm{Dm} )=0.\end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle \omega _\mathrm{m} \frac{\partial p_\mathrm{Dm} }{\partial t_\mathrm{D} }+\lambda _\mathrm{fm} (p_\mathrm{Dm} -p_\mathrm{Df} )-\lambda _\mathrm{vm} (p_\mathrm{Dv} -p_\mathrm{Dm} )=0. \end{aligned}$$

(9)

Table 1 Dimensionless variables

Initial condition is

$$\begin{aligned} p_\mathrm{Df} (r_\mathrm{D} ,0)=p_\mathrm{Dv} (r_\mathrm{D} ,0)=p_\mathrm{Dm} (r_\mathrm{D} ,0)=0. \end{aligned}$$

(10)

Outer boundary condition is

$$\begin{aligned} p_\mathrm{Df} (r_\mathrm{D} \rightarrow \infty ,t_\mathrm{D} )=0. \end{aligned}$$

(11)

Inner boundary condition is

$$\begin{aligned} -r_\mathrm{D} \frac{\partial p_\mathrm{Df} }{\partial r_\mathrm{D} }_{r_\mathrm{D} \rightarrow 0} =q_\mathrm{D} (t_\mathrm{D} ). \end{aligned}$$

(12)

3.2 The Point Source Solution in Laplace Space

The Laplace transform is based on $t_\mathrm{D}$ and functions as follows

$$\begin{aligned} \tilde{p}_\mathrm{D} (r_\mathrm{D} ,s)=\int _0^\infty {p_\mathrm{D} (r_\mathrm{D} ,t_\mathrm{D} )e^{-st_\mathrm{D} }dt_\mathrm{D} }. \end{aligned}$$

(13)

Applying the Laplace transformation to Eqs. (7)–(12), we have

$$\begin{aligned}&\displaystyle \omega _\mathrm{f} s\tilde{p}_\mathrm{Df} -\frac{1}{r_\mathrm{D} }\frac{\partial }{\partial r_\mathrm{D} }\left( {r_\mathrm{D} \frac{\partial \tilde{p}_\mathrm{Df} }{\partial r_\mathrm{D} }} \right) -\lambda _\mathrm{fv} (\tilde{p}_\mathrm{Dv} -\tilde{p}_\mathrm{Df} )-\lambda _\mathrm{fm} (\tilde{p}_\mathrm{Dm} -\tilde{p}_\mathrm{Df} )=0.\end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \omega _\mathrm{v} s\tilde{p}_\mathrm{Dv} +\lambda _\mathrm{fv} (\tilde{p}_\mathrm{Dv} -\tilde{p}_\mathrm{Df} )+\lambda _\mathrm{vm} (\tilde{p}_\mathrm{Dv} -\tilde{p}_\mathrm{Dm} )=0.\end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle \omega _\mathrm{m} s\tilde{p}_\mathrm{Dm} +\lambda _\mathrm{fm} (\tilde{p}_\mathrm{Dm} -\tilde{p}_\mathrm{Df} )-\lambda _\mathrm{vm} (\tilde{p}_\mathrm{Dv} -\tilde{p}_\mathrm{Dm} )=0 \end{aligned}$$

(16)

Outer boundary condition is

$$\begin{aligned} \tilde{p}_\mathrm{Df} (r_D \rightarrow \infty ,s)=0. \end{aligned}$$

(17)

Inner boundary condition is

$$\begin{aligned} -r_D \frac{\partial \tilde{p}_\mathrm{Df} }{\partial r_\mathrm{D} }_{r_\mathrm{D} \rightarrow 0} =\tilde{q}_\mathrm{D} (s). \end{aligned}$$

(18)

Substituting the vug and matrix equations of (15) and (16) into the fracture equation (14), we can obtain

$$\begin{aligned} \frac{1}{r_\mathrm{D} }\frac{\partial }{\partial r_\mathrm{D} }\left( {r_\mathrm{D} \frac{\partial \tilde{p}_\mathrm{Df} }{\partial r_\mathrm{D} }} \right) -sg(s)\tilde{p}_\mathrm{Df} =0, \end{aligned}$$

(19)

where

$$\begin{aligned} g(s)=w_\mathrm{f} +\frac{(\lambda _\mathrm{fv} +\lambda _\mathrm{fm} )s+\frac{1-\omega _\mathrm{f} }{\omega _\mathrm{v} \omega _\mathrm{m}}\left[ {\lambda _\mathrm{fv} \lambda _\mathrm{fm} +(\lambda _\mathrm{fv} +\lambda _\mathrm{fm} )\lambda _\mathrm{vm} } \right] }{s^{2}+\left[ {\frac{\lambda _\mathrm{fv} }{\omega _\mathrm{v} }+\frac{\lambda _\mathrm{fm} }{\omega _\mathrm{m} }+\left( {\frac{1}{\omega _\mathrm{v} }+\frac{1}{\omega _\mathrm{m} }} \right) \lambda _\mathrm{vm} } \right] s+\frac{\lambda _\mathrm{fv} \lambda _\mathrm{fm} +(\lambda _\mathrm{fv} +\lambda _\mathrm{fm} )\lambda _\mathrm{vm} }{\omega _\mathrm{v} \omega _\mathrm{m} }}. \end{aligned}$$

(20)

The general solution of Eqs. (17)–(19) could be expressed as

$$\begin{aligned} \tilde{p}_\mathrm{Df} =\tilde{q}_\mathrm{D} (s)K_0 (R_\mathrm{D} \sqrt{sg(s)}). \end{aligned}$$

(21)

Equation (21) represents a point source solution in Laplace space.

3.3 Multi-branched Wormholes Solution

The points $(r,\theta )$ and $(r{^{\prime }},\theta {^{\prime }})$ represent the any position and source position in the reservoir, respectively. And $R$ represents the distance from any point to source position. Therefore, as is known, the following relationships can be given in the polar coordinates:

$$\begin{aligned} R=\sqrt{r^{2}+r{^\prime 2}-2r{^ \prime }r(\cos \theta \cos \theta {^ \prime }+\sin \theta \sin \theta {^ \prime })}. \end{aligned}$$

(22)

Equation (22) can be re-written as following by defining the dimensionless variables $r_\mathrm{D} =r/x_\mathrm{f}$ and $\beta =r{^ \prime }/x_\mathrm{f}$

$$\begin{aligned} R_\mathrm{D} =\sqrt{r_\mathrm{D}^2 +\beta ^{2}-2r_\mathrm{D }\beta \cos (\theta -\theta {^\prime })}. \end{aligned}$$

(23)

Using point sink integral method, for a single wormhole solution in polar coordinates,

Equation (21) can become

$$\begin{aligned} \tilde{p}_\mathrm{Df} (R_\mathrm{D} ,s)=\int _0^1 {\tilde{q}_\mathrm{Df} } (\beta ,s)K_0 \left( R_\mathrm{D} \sqrt{sg(s)}\right) d\beta . \end{aligned}$$

(24)

As shown in Fig. 3, near wellbore, multiple wormholes are composed of a finite number, $N$, of wormholes with the same length, $x_\mathrm{f}$. The dendritic wormholes are assumed to be vertical and to extend from the top to the bottom of the formation of thickness $h$, and the wormholes have infinite conductivity. The well is located at the center and the radius of the well is $r_\mathrm{w}$.

Consider $N$ multiple wormholes as shown in Fig. 3. With the solution given in Eq. (24) for a single wormhole and the method of superposition, the following expression in the Laplace space to compute the dimensionless pressure at any point of the reservoir due to the production of $N$ wormholes can be obtained

$$\begin{aligned} \tilde{p}_\mathrm{Df} (R_\mathrm{D} ,s)=\sum _{k=1}^n {\int _0^1 {\tilde{q}_{\mathrm{Df}k} } (\beta ,s)\Omega _k (R_{\mathrm{D}k} ,s)d\beta }, \end{aligned}$$

(25a)

where

$$\begin{aligned} \Omega _k (R_{\mathrm{D}k} ,s)=K_0 \left( R_{\mathrm{D}k} \sqrt{sg(s)}\right) , \end{aligned}$$

(25b)

and

$$\begin{aligned} R_{\mathrm{D}k} =\sqrt{r_\mathrm{D}^2 +\beta ^{2}-2r_\mathrm{D} \beta \cos (\theta -\theta _{\mathrm{fk}} )}, \end{aligned}$$

(25c)

where $(r_\mathrm{D} ,\theta )$ and $(\beta ,\theta _{\mathrm{fk}})$ are the polar coordinates in the reservoir and along the $k$th wormhole, respectively.

If uniform flux distribution along the wormholes, Eq. (25) for the $j$th wormhole at $\theta =\theta _{\mathrm{f}j}$ can be evaluated as

$$\begin{aligned} \tilde{p}_{\mathrm{Df}j} (R_{\mathrm{D}jk} ,s)=\sum _{k=1}^n {\tilde{q}_{\mathrm{Df}k} \int _0^1 {\Omega _{jk} (R_{\mathrm{D}jk} ,s)} d\beta }, \end{aligned}$$

(26a)

With

$$\begin{aligned} R_{\mathrm{D}jk} =\sqrt{r_\mathrm{D}^2 +\beta ^{2}-2r_\mathrm{D} \beta \cos (\theta _{\mathrm{f}j} -\theta _{\mathrm{f}k} )}. \end{aligned}$$

(26b)

Integrating Eq. (26a) along the $j$th wormhole approximates the infinite conductivity wellbore condition, Eq. (26a) can be written as

$$\begin{aligned} \tilde{p}_{\mathrm{Df}j} (R_{\mathrm{D}jk} ,s)=\sum _{k=1}^n {\int _0^1 {\int _0^1 {\tilde{q}_{\mathrm{Df}k} \Omega _{jk} (R_{\mathrm{D}jk} ,s)} } d\beta } dr_\mathrm{D}. \end{aligned}$$

(27)

The integral of the flux along the wormholes should be equal to the total well flow rate, and thus we have

Flux equation

$$\begin{aligned} \sum _{k=1}^n {\tilde{q}_{\mathrm{Df}k} =\frac{1}{s}}, \end{aligned}$$

(28)

Writing Eq. (27) for each wormhole, requiring the pressure at each wormhole be equal to the wellbore pressure $\tilde{p}_\mathrm{Dw} (s)$, will produce $n+1$ equations with $n+1$ unknowns. These equations can be obtained in a matrix form as

$$\begin{aligned} \left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\delta _{11} }&{} {\delta _{12} }&{} .&{} {\delta _{1n} }&{} {-1} \\ {\delta _{21} }&{} {\delta _{22} }&{} .&{} {\delta _{2n} }&{} {-1} \\ .&{} .&{} .&{} .&{} . \\ {\delta _{n1} }&{} {\delta _{n2} }&{} .&{} {\delta _{nn} }&{} {-1} \\ 1&{} 1&{} .&{} 1&{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\tilde{q}_\mathrm{Df1} } \\ {\tilde{q}_\mathrm{Df2} } \\ . \\ {\tilde{q}_\mathrm{Dfn} } \\ {\tilde{p}_\mathrm{Dw} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ {\frac{1}{s}} \\ \end{array} }} \right] \end{aligned}$$

(29)

where

$$\begin{aligned} \delta _{jk} =\int _0^1 {\int _0^1 {\Omega _{jk} d\beta \mathrm{d}r_\mathrm{D} } } \end{aligned}$$

(30)

The solution for the matrix system given in Eq. (29) yields wellbore pressure. The Laplace space solution can be numerically inverted by using the Stehfest algorithm (Stehfest 1970).

4 Results and Discussions

4.1 Validation of the Presented Solution

Figure 4 compares the results from this work and those computed data with commercial soft Eclipse with four wormholes. The input parameters are listed in Table 3 and g(s) in Eq. (24) is set to be 1. Eclipse uses the numerical solution for four wormholes. The comparison suggests that the results from this work are highly consistent with the results from commercial soft. Thus far, the eight wormholes model is hard to simulate by using Eclipse. There we could not validate more wormhole number through numerical simulation.

Fig. 4

Validation for numerical simulation

As early as Kuchuk and Brigham (1979), Kuchuk and Brigham studied the analytical solutions for two wings of fracture at the angle of 180$^{\circ }$ in homogeneous reservoirs. To compare our solution with theirs, we must select a special case in our model. First, the solution of two branched-wormholes at the angle of 180$^{\circ }$ is used. Second, let the variable $g(s)$ be equal to 1 and thus our model could be simplified as the solution of homogeneous reservoirs. As shown in Fig. 5, our results obtained in this paper are consistent with the results in the literature, which verifies that the results of this paper should be correct.

Fig. 5

The solution for two branched-wormholes at the angle of 180 degrees used to compare with that in the literature

4.2 Flow Characteristics

The transient transport characteristics are graphically showed by type curves, which can be used to analyze transient pressure so as to recognize the flow characteristics of fluids in fractured–vuggy reservoirs. In addition, by Type curves matching, some reservoir property parameters, such as permeability, skin factor, oil in place, reservoir drainage area, can be obtained. (Wang et al. 2013; Nie et al. 2012).

On the pressure derivative curves of Fig. 6, the first V-shaped segment represents the inter-porosity flow from vugs to fractures, and the second V-shaped segment represents the inter-porosity flow from matrix to fractures and from vugs to matrix. It’s possible that both the first V-shaped and the second V-shaped segments emerge in linear flow period (as shown in Fig. 6a), or both of them emerge in the radial flow period (as shown in Fig. 6b), or one of them emerges in linear flow period and the other one emerges in the radial flow period (as shown in Fig. 6c). Therefore, according to the emergence of two V-shaped segments mentioned above, the following three cases are analyzed in detail and the used data is listed in Table 2:

Fig. 6

Flow regimes can be divided into the following three cases: a two V-shaped segments are both occurring in the linear flow regime. b Two V-shaped segments are both occurring in the radial flow regime. c One of two V-shaped segments is occurring in the linear flow regime and the other is occurring in the radial flow regime

Case I (See Fig. 6a):

Two V-shaped segments are both appearing in the linear flow regime.

• (i) Linear flow regime shows a 0.5 slope straight line on the pressure derivative curve.

• (ii) Inter-porosity flow regime (a) is a regime of supplement from vug system to the fracture system. Inter-porosity flow of vugs system to fracture system takes place first because the fracture permeability is better than the matrix permeability. The derivative curve shows the first V-shaped segment.

• (iii) Transition flow regime (a) shows 0.5 slope straight line on the pressure derivative curve.

• (iv) Inter-porosity flow regime (b) represents the inter-porosity flow regime of matrix system to fracture system and vug system to matrix system. The pressure derivative curve also shows the second V-shaped segment. This V-shaped segment is controlled by two physical processes: one is inter-porosity flow from matrix system to fracture system, another one is inter-porosity flow from vug system to matrix system.

• (v) Transition flow regime (b) also shows a 0.5 slope straight line on the pressure derivative curve.

• (vi) The radial flow regime shows a zero slope straight line on the pressure derivative curve. In this regime, inter-porosity flows have already finished and the pressure between matrix, fracture, and vug systems have gone up to a state of dynamic balance.

Case II (See Fig. 6b):

Table 2 The data used in Fig. 6

Two V-shaped segments are both appearing in the radial flow regime.

• (i) Linear flow regime is that the pressure derivative curve shows a 0.5 slope straight line. There is no supplement in this regime.

• (ii) Transition flow regime (a) shows zero slope straight line on the pressure derivative curve.

• (iii) Inter-porosity flow regime (a) is a regime of supplement from vug system to the fracture system. Because fluids in the fractures are rich enough, this regime is found later.

• (iv) Transition flow regime (b) also shows zero slope straight line on the pressure derivative curve.

• (v) Inter-porosity flow regime (b) represents the inter-porosity flow regime of matrix system to fracture system and vug system to matrix system.

• (vi) The radial flow regime shows a zero slope straight line on the pressure derivative curve.

Case III (See Fig. 6c):

One of two V-shaped segments is appearing in the linear flow region and the other is appearing in the radial flow regime.

• (i) Linear flow regime is that the pressure derivative curve shows a 0.5 slope straight line. This regime is similar to Regime 1 of Case 1.

• (ii) Inter-porosity flow regime (a) is a regime of supplement from vug system to the fracture system. This regime is similar to regime 2 of case 1.

• (iii) Transition flow regime (a) shows 0.5 slope straight line on the pressure derivative curve.

• (iv) Transition flow regime (b) also shows zero slope straight line on the pressure derivative curve.

• (v) Inter-porosity flow regime (b) represents the inter-porosity flow regime of matrix system to fractures system and vugs system to matrix system.

• (vi) The radial flow regime shows a zero slope straight line on the pressure derivative curve.

The type curve shapes are affected by a number of parameters including, inter-porosity flow factor, wormhole number, fluid capacitance coefficient et al. In addition, both linear flow regime and radial flow regime are inherent features of fluids flow in porous media. However, double V-shaped derivative curves are typical of fluids flow in fractured–vuggy carbonate reservoirs. The first V-shaped segment is due to the occurrence of inter-porosity flow between vug system and fracture system, and the second V-shaped segment is owing to the occurrence of inter-porosity flow between vug system and matrix system, and inter-porosity flow between matrix system and fracture system.

4.3 Parameter Influence

Figures 7, 8, 9, 10, 11 show the influence of parameters (wormhole number $N$, vugs capacitance coefficient $\omega _\mathrm{v}$, fractures capacitance coefficient $\omega _\mathrm{f}$, inter-porosity flow coefficient between vugs and fractures $\lambda _\mathrm{fv}$, and inter-porosity flow coefficient between matrix and fractures $\lambda _\mathrm{fm} )$ on pressure and pressure derivative curves and the same data are listed in Table 3. The ranges of parameters are presented in Table 4.

Fig. 7

The influence of wormhole number $N$ on type curves: a pressure curves. b Pressure derivative curves

Fig. 8

The influence of vugs capacitance coefficient $\omega _\mathrm{v}$ on type curves: a pressure curves. b Pressure derivative curves

Fig. 9

The influence of fractures capacitance coefficient $\omega _\mathrm{f}$ on type curves: a pressure curves. b Pressure derivative curves

Fig. 10

The influence of inter-porosity flow coefficient $\lambda _\mathrm{fv}$ on type curves: a pressure curves. b Pressure derivative curves

Fig. 11

The influence of inter-porosity flow coefficient $\lambda _\mathrm{fm}$ on type curves: a pressure curves. b Pressure derivative curves

Figure 7 shows the effects of the wormhole number $N$ on pressure and pressure derivative curves. The value of wormhole number $N$ is fixed as 1, 2, 4, and 8, respectively, and the angle of any two wormholes is same (e.g., four branched wormholes, $90^{\circ }$). The wormhole number represents total conductivity near well zone, and a big wormhole number means a high total conductivity. According to the definition of the dimensionless pressure, a bigger dimensionless pressure will mean bigger pressure depletion. As shown in Fig. 7a, the dimensionless pressure will cut down as the wormhole number increases and this means a bigger wormhole number will obtain smaller pressure depletion. During the process of carbonate acidizing, forming more wormholes can help reduce pressure depletion to improve well production. In addition, the dimensionless pressure increases like a ladder as the dimensionless time becomes long, which are inherent flow characteristics in fractured–vuggy reservoirs. The pressure derivative curves can reflect fluids flow behavior in porous media (for example, linear flow showing 0.5 slope straight line and radial flow showing 0 slope straight line in derivative curves). Figure 7b shows the effects of wormhole number $N$ on pressure derivative curves. We can see that the curves for different wormhole number are nearly parallel in linear flow regime and inter-porosity flow between vug system and fracture system (the first V-shaped segment); however, the curves are normalized as the dimensionless time increases and the more the wormhole number, the more soon the curves become normalized. Due to the same lined angle for any two wormholes, changing of starting and ending time of flow regime is not obvious, but the difference can be found when any two wormholes are forming at different lined angles. This point will be discussed in the following section.

Table 3 The data used in Figs. 7, 8, 9, 10, 11, 12

Table 4 The ranges of each sensitivity variable

The fluid capacitance coefficient of the vug system $\omega _\mathrm{v}$ represents the relative capacity of fluid stored in a vug system. According to the definitions of fluid capacitance coefficients of vugs, matrix, fractures, $\omega _\mathrm{v}, \omega _\mathrm{m}, \omega _\mathrm{f}$ listed in Table 1, they are related such that $\omega _f +\omega _m +\omega _\mathrm{v} =1$. Figure 8 shows the effects of vugs capacitance coefficient $\omega _\mathrm{v}$ on pressure and pressure derivative curves. When $\omega _\mathrm{f}$ is fixed as 0.0005 and $\omega _\mathrm{v}$ is set as 0.008, 0.04, and 0.1, respectively, thus $\omega _\mathrm{m}$ will be automatically set as 0.9915, 0.9595, and 0.8995, respectively. The effect of $\omega _\mathrm{v}$ on pressure curves is shown in Fig. 8a, from which it can be found that we can see there are two flat segments showing zero slope and the smaller the $\omega _\mathrm{v}$ value is, the shorter the first flat segment is. Besides, a bigger $\omega _\mathrm{v}$ will lead to smaller pressure depletion. Figure 8b shows how $\omega _\mathrm{v}$ affects flow characteristics. The first V-shaped segment reflects supplement from vugs to fractures, and the second V-shape represents the supplement between vugs and matrix, between matrix and fractures (See Figs. 10 and 11). As $\omega _\mathrm{v}$ increases, the first V-shape on the left deepens, and the second V-shape on the right deepens, which indicates that the supplement of the matrix to fractures will reduce when the vugs have fluids in abundance.

The fluid capacitance coefficient of the fracture system $\omega _\mathrm{f}$ displays the relative capacity of fluid stored in a fracture system. The effects of $\omega _\mathrm{f}$ on pressure curves are illustrated in Fig. 9. When $\omega _\mathrm{v}$ is fixed as 0.04 and $\omega _\mathrm{f}$ is set as 0.00002, 0.0001, and 0.0005, respectively, thus $\omega _\mathrm{m}$ will be automatically set as 0.95998, 0.9599, and 0.9595, respectively. We can see from Fig. 9a that the effects of $\omega _\mathrm{f}$ on pressure curves are concentrated in the early time. As $\omega _\mathrm{f}$ increases, the pressure depletion reduces and the first horizontal segment which represents the supplement segment from vugs becomes shorter. Figure 9b shows the effects of $\omega _\mathrm{f}$ on pressure derivative curves. As $\omega _\mathrm{f}$ increases, the linear flow regime becomes longer and the first V-shaped segment rapidly becomes swallow, which means the supplement from vugs will be decreased owing to rich fluids stored in the fractures.

The inner-porosity flow coefficient between a vug system and a fracture system $\lambda _\mathrm{fv}$ represents the starting time of inter-porosity of the vug system to the fracture system. Figure 10 shows the type curves characteristics are affected by $\lambda _\mathrm{fv}$ values, which are set as 30, 300, and 3000, respectively. As shown in Fig. 10a, the first horizontal segment on the pressure curve uplifts and the linear flow segment extends upward as $\lambda _\mathrm{fv}$ decreases, which implies that a smaller $\lambda _\mathrm{fv}$ value will cause bigger pressure depletion. The corresponding pressure derivative curves in Fig. 10b also show the linear flow segment extends upward as $\lambda _\mathrm{fv}$ decreases; however, the size of the first V-shape segment is not changing with increasing $\lambda _\mathrm{fv}$ value, indicating that only the starting time of supplement from vugs to fractures is influenced by $\lambda _\mathrm{fv}$ value but the energy of supplement is not affected by it.

The inner-porosity flow coefficient of a matrix system to a fracture system $\lambda _\mathrm{fm}$ represents the starting time of inter-porosity of the matrix system to the fracture system. Figure 11 shows the type curves characteristics affected by $\lambda _\mathrm{fm}$ value, which are set as 0.1, 1, and 10, respectively. As shown in Fig. 11a, the second horizontal segment on the pressure curve uplifts as $\lambda _\mathrm{fm}$ decreases. The corresponding pressure derivative curves in Fig. 11b also shows the size of the second V-shaped segment is not changing with increasing $\lambda _\mathrm{fm}$ value, indicating that only the starting time of supplement from matrix to fractures is influenced by $\lambda _\mathrm{fm}$ value but the energy of supplement is not affected by it.

In a word, the energy is decided by the capacitance coefficients $\omega _\mathrm{v}, \omega _\mathrm{m}, \omega _\mathrm{f}$, but inter-porosity flow coefficients $\lambda _\mathrm{fv}$ and $\lambda _\mathrm{fm}$ only affect the starting time of supplement between vugs and fractures, and between matrix and fractures.

4.4 The Effect of Angle of Wormholes on Type Curves

In Fig. 12, the pressure responses for two asymmetric wormholes are presented. One of the wormholes is in the direction of the $x$ axis and the other one makes an angle $\eta$ with the $x$ direction. As shown in Fig. 12a, the pressure is affected by the angles and as the angle decreases, the pressure depletion increases, because as the wormholes are closer, their interaction becomes stronger. When the angle of the wormholes is bigger than $90^{\circ }$, the pressure curves coincide with each other and the pressure behavior is nearly not affected by the angle. Figure 12b shows that in the early time and for the angle between the wormholes bigger than $1^{\circ }$, the pressure derivative exhibits linear flow, and the duration of the linear flow is a function of the angle. As the angle decreases, duration of the linear flow ends earlier. When the angle of the wormholes is bigger than $90^{\circ }$, the pressure derivative curves coincide with each other and the flow characteristic is nearly not affected by the angle. Finally, the late time behavior illustrates that the derivatives are not influenced by the angle and can be analyzed in conventional method.

Fig. 12

The pressure is affected by the angles $\eta$: a pressure curves. b Pressure derivative curves

4.5 Case Example

Pressure transient data from acidizing Well A in Tahe oil field which is a naturally fractured vuggy reservoir in western China are used to make matching by using type curves. Figure 13 presents the buildup data that are used to match by using wormholes model proposed in this article. The buildup data are so good that two V-shaped segments are observed, representing inter-porosity flow from vugs to fractures and from matrix to fractures. As shown in Fig. 13, model results reasonably match both measured pressure and pressure derivative data from Well A. The corresponding results are presented in Table 5. The wormholes number is equal to eight, which implies that the level of carbonate acidizing is okay.

Fig. 13

Type curves are used to match the data in naturally fractured vuggy reservoirs

Table 5 Type curves used to match field-case example

5 Conclusions

• (1) Based on a multiple-continuum-medium concept, a wormhole model is presented to analyze flow behavior through fractured–vuggy rock. The proposed multiple-continuum model is a natural extension of the classic double-porosity model. Analytical solutions are obtained through point sink integral and Laplace transformation methods.

• (2) The solution of two branched-wormholes at the angle of 180 degrees is used to compare with previous results in the literature. The presented results in this paper are consistent with the results in the literature, which validates the accuracy of the solution in this paper.

• (3) Flow characteristics are proposed in this article, which can be divided into three cases discussed according to the time of occurrence of the first V-shaped segment and the second V-shaped segment. Each case is comprehensively sub-divided into six regimes.

• (4) The influence of parameters (wormhole number $N$, vugs capacitance coefficient $\omega _\mathrm{v}$, fractures capacitance coefficient $\omega _\mathrm{f}$, inter-porosity flow coefficient between vugs and fractures $\lambda _\mathrm{fv}$, and inter-porosity flow coefficient between matrix and fractures $\lambda _\mathrm{fm}$) on pressure and pressure derivative curves are discussed in detail.

• (5) The pressure responses for four asymmetric wormholes are presented, and the results show that the pressure is affected by the angles and as the angle decreases, the pressure depletion increases because as the wormholes are closer, their interaction becomes stronger and starts to affect the pressure responses. In the process of the development, to reduce pressure depletion, wormholes should be uniformly distributed.