Introduction

In the past decades, many tight gas reservoirs with ultra-low permeability have been discovered and developed around the world. It has been proved in practice that horizontal well combined with volume fracturing technology is considered as an effective way to develop tight gas reservoirs. Massive hydraulic fracturing creates several main hydraulic fractures as well as an induced fracture network around them (Clarkson 2013). The fracture network is usually called stimulated reservoir volume (SRV), in which the reservoir properties are very different from those of unstimulated reservoir volume (URV) (Mayerhofer et al. 2010).

Compared with the conventional models of the multi-stage fractured horizontal (MSFH) wells without SRV (Wang and Yi 2018; Ren and Guo 2018a, b), the models of the MSFH wells with SRV are much more complex. Recently, various models have been established to study the performance of the MSFH wells with SRV. Ozkan et al. (2011) used the tri-linear flow model to investigate the transient pressure for the MSFH well with SRV. Some scholars improved the flow model proposed by Ozkan et al. (2011) to incorporate multiple mechanisms (Apaydin et al. 2012; Tian et al. 2014) or to consider more linear-flow regions (Stalgorova and Mattar 2012; Yuan et al. 2015). However, the tri-linear flow model and its improved versions cannot describe some flow characteristics of the MSFH well with SRV (e.g., the radial flow and the hydraulic-fracture interference). Zhao et al. (2014) employed the point-source function method to establish the flow model of the MSFH well considering the impact of the SRV and studied the performance of the MSFH well. Zeng et al. (2015) and Xu et al. (2015a) established flow models of the MSFH well with SRV in a shale gas reservoir including multiple mechanisms such as desorption, diffusive flow and stress sensitivity. Xu et al. (2015b) proposed a dual-porosity composite model of the MSFH well with elliptical SRV in tight reservoirs. Wei et al. (2016) presented a numerical composite model of the MSFH well with elliptical SRV region for each hydraulic fracture and studied the characteristic of the Blasingame’s type curves of the MSFH well. Guo et al. (2016) extended the previous model (Xu et al. 2015a) to establish a more comprehensive model of an MSFH well in a shale gas reservoir, which can consider the impact of the presence of the SRV, fracture conductivity and multiple transport mechanisms. Ren and Guo (2017) proposed a composite model of the MSFH well with SRV taking into account the impact of the quadratic gradient term. Chen et al. (2018) established an arbitrary composite model of the MSFH well with SRV based on boundary element method and investigated the effect of the shape and size of the SRV on the pressure response and production performance. However, as far as we know, previous models for the MSFH well with SRV are established by incorporating the classical Darcy law, which cannot capture the anomalous diffusion in fractured reservoirs (Raghavan and Chen 2013a, 2015) and may lead to errors in the prediction of the transient pressure and transient rate for the MSFH well with SRV. It has been found that the fractional Darcy law, which is the generalized form of the classical Darcy law, can be used to describe the anomalous diffusion and is more suitable for the fractured reservoirs. In recent years, some seepage models for various wells in fractured reservoirs have been established by incorporating the fractional Darcy law into the governing equations, such as vertical wells (Raghavan 2012a; Razminia et al. 2014), fractured vertical wells (Raghavan 2012b; Raghavan and Chen 2013a), horizontal wells (Raghavan and Chen 2015), MSFH wells (Raghavan and Chen 2013b, 2017; Ren and Guo 2015), and so on. However, there is no work to study the model of the MSFH well with SRV by incorporating the fractional Darcy law. Therefore, the existing models of the MSFH well with SRV have some limitations in interpreting and forecasting the transient pressure and transient rate.

In this paper, we introduce the fractional Darcy law to develop the model of the MSFH well with SRV in tight gas reservoirs. The proposed model can take into account the effect of the anomalous diffusion in fractured rocks, and thus it has a wider application compared to the previous models.

Physical model

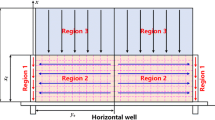
The physical model is shown in Fig. 1 and based on the assumptions as follows:

Fig. 1
figure 1

Schematic of an MSFH well in a composite system

Full size image
  1. 1.

    The tight gas formation is viewed as a composite system including the inner and outer regions. Both the regions are dual-porosity medium systems with different physical properties of reservoir rocks. The inner and outer regions denote the SRV and URV, respectively.

  2. 2.

    Gas flow in the porous medium obeys the fractional Darcy law, and the interporosity flow between the matrix and fracture systems follows the pseudo-steady model proposed by Warren and Root (1963).

  3. 3.

    An MSFH well is located in the SRV region and produces at a constant rate or a constant bottomhole pressure. Each infinite-conductivity hydraulic fracture perpendicularly intersects with the horizontal wellbore and completely penetrates the reservoir.

Mathematical model

Point source model

Owing to the disordered distribution of natural and induced hydraulic fractures in the tight gas formation, gas flow in the porous medium usually obeys the fractional Darcy law (Raghavan and Chen 2015), which can be written in radial cylindrical coordinate as follows:

$$\upsilon \left( {r,t} \right)= - \frac{{{k_{{\varvec{\upbeta}}}}}}{\mu }\frac{{{\partial ^{1 - \beta }}}}{{\partial {t^{1 - \beta }}}}\frac{{\partial p\left( {r,t} \right)}}{{\partial r}},$$
(1)

where \(\beta\) is anomalous diffusion exponent in the range of \(\beta \leq 1\), the definition of the fractional derivative \({{{\partial ^\beta }f\left( t \right)} \mathord{\left/ {\vphantom {{{\partial ^\beta }f\left( t \right)} {\partial {t^\beta }}}} \right. \kern-0pt} {\partial {t^\beta }}}\) can refer to the literature (Caputo 1967; Xu and Meng 2016; Zuo et al. 2017), which is defined as

$$\frac{{{\partial ^\beta }f\left( t \right)}}{{\partial {t^\beta }}}=\frac{1}{{\Gamma \left( {1 - \beta } \right)}}\int_{0}^{t} {{{\left( {t - t^{\prime}} \right)}^{ - \beta }}\frac{{\partial f\left( {t^{\prime}} \right)}}{{\partial t^{\prime}}}{\text{d}}t^{\prime}} ,$$
(2)

where \(\Gamma \left( x \right)\) is the Gamma function defined by

$$\Gamma \left( x \right)=\int_{0}^{\infty } {{e^{ - z}}{z^{x - 1}}{\text{d}}z} .$$
(3)

The expressions with fractional derivative such as Eq. (1) lead to fractional differential equations which have been widely applied in various fields (Zhang et al. 2014, 2017; Feng and Meng 2017; Obembe et al. 2017; Zhang 2017; Li and Wang 2018; Shen et al. 2018).

It is noted that when \(\beta\) is set as one, Eq. (1) becomes the conventional Darcy law:

$$\upsilon \left( {r,t} \right)= - \frac{k}{\mu }\frac{{\partial p\left( {r,t} \right)}}{{\partial r}}.$$
(4)

Compared with the conventional Darcy law, the fractional Darcy law has a much wider field of application and is more suitable for unconventional reservoirs, especially for fractured reservoirs with complex fracture network.

In the following, the point source model in the composite system will be established by introducing the fractional Darcy law.

For inner region (i.e., SRV region) \(\left( {0 \leq r \leq {r_{\text{f}}}} \right).\)

On the basis of the mass-conservation law, the continuity equation for the fracture system can be given as

$$\frac{1}{r}\frac{{\partial \left( {r{\rho _{1{\text{f}}}}{\upsilon _{1{\text{f}}}}} \right)}}{{\partial r}}+\frac{{\partial \left( {{\rho _{1{\text{f}}}}{\phi _{1{\text{f}}}}} \right)}}{{\partial t}} - {q_{{\text{1m}}}}=0.$$
(5)

According to the assumption of the pseudo-steady flow (Warren and Root 1963), the continuity equation for the matrix system can be expressed by

$$\frac{{\partial \left( {{\rho _{1{\text{m}}}}{\phi _{1{\text{m}}}}} \right)}}{{\partial t}}+{q_{{\text{1m}}}}=0,$$
(6)

where \({q_{{\text{1m}}}}\) in Eqs. (5) and (6) is the matrix-fracture interporosity flow rate, which is given as Warren and Root (1963)

$${q_{{\text{1m}}}}=\frac{{{\alpha _1}{k_{1{\text{m}}}}}}{\mu }\left( {{\rho _{1{\text{m}}}}{p_{1{\text{m}}}} - {\rho _{1{\text{f}}}}{p_{1{\text{f}}}}} \right).$$
(7)

The fractional Darcy law for the SRV region is

$${\upsilon _{1{\text{f}}}}= - \frac{{{k_{{{1\varvec{\upbeta}}}}}}}{\mu }\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial {t^{1 - {\beta _1}}}}}\frac{{\partial {p_{1{\text{f}}}}}}{{\partial r}}.$$
(8)

The real-gas state equations for the matrix and fracture systems in the SRV region are, respectively, written as

$${\rho _{1{\text{m}}}}=\frac{{{p_{1{\text{m}}}}M}}{{ZRT}},$$
(9)
$${\rho _{1{\text{f}}}}=\frac{{{p_{1{\text{f}}}}M}}{{ZRT}}.$$
(10)

The gas compressibility and rock compressibility in the SRV region are, respectively, given as

$${c_\phi }_{{{\text{1}}j}}=\frac{1}{{{\phi _{{\text{1}}j}}}}\frac{{\partial {\phi _{{\text{1}}j}}}}{{\partial {p_{{\text{1}}j}}}},\left( {j={\text{m}},{\text{f}}} \right),$$
(11)
$${c_{{{\varvec{\uprho}1}}j}}=\frac{1}{{{\rho _{{\text{1}}j}}}}\frac{{\partial {\rho _{{\text{1}}j}}}}{{\partial {p_{{\text{1}}j}}}},\left( {j={\text{m}},{\text{f}}} \right).$$
(12)

Substituting Eqs. (8)–(12) into Eqs. (5)–(7), respectively, yields that

$$\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial {t^{1 - {\beta _1}}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{{k_{1{{\varvec{\upbeta}}}}}}}{\mu }\frac{{{p_{1{\text{f}}}}M}}{{ZRT}}\frac{{\partial {p_{1{\text{f}}}}}}{{\partial r}}} \right)} \right]=\frac{{{\phi _{1{\text{f}}}}{c_{{\text{t1f}}}}{p_{1{\text{f}}}}M}}{{ZRT}}\frac{{\partial {p_{1{\text{f}}}}}}{{\partial t}} - {q_{{\text{1m}}}},$$
(13)
$$\frac{{{\phi _{1{\text{m}}}}{c_{{\text{t1m}}}}{p_{1{\text{m}}}}M}}{{ZRT}}\frac{{\partial {p_{1{\text{m}}}}}}{{\partial t}}+{q_{{\text{1m}}}}=0,$$
(14)
$${q_{{\text{1m}}}}=\frac{{{\alpha _1}{k_{1{\text{m}}}}M}}{{\mu ZRT}}\left( {p_{{1{\text{m}}}}^{2} - p_{{1{\text{f}}}}^{2}} \right),$$
(15)

where \({c_{{\text{t1f}}}}={c_{{{\varvec{\uprho}1f}}}}+{c_{\phi 1{\text{f}}}}\) and \({c_{{\text{t1m}}}}={c_{{{\varvec{\uprho}1m}}}}+{c_{\phi 1{\text{m}}}}\).

For outer region (i.e., URV region) \(\left( {{r_{\text{f}}} \leq r<\infty } \right).\)

In the same way, the continuity equation for the fracture system can be expressed as

$$\frac{1}{r}\frac{{\partial \left( {r{\rho _{2{\text{f}}}}{\upsilon _{{\text{2f}}}}} \right)}}{{\partial r}}+\frac{{\partial \left( {{\rho _{{\text{2f}}}}{\phi _{{\text{2f}}}}} \right)}}{{\partial t}} - {q_{{\text{2m}}}}=0.$$
(16)

The continuity equation for the matrix system is

$$\frac{{\partial \left( {{\rho _{{\text{2m}}}}{\phi _{{\text{2m}}}}} \right)}}{{\partial t}}+{q_{{\text{2m}}}}=0,$$
(17)

and the matrix–fracture interporosity flow rate is given as (Warren and Root 1963)

$${q_{{\text{2m}}}}=\frac{{{\alpha _2}{k_{{\text{2m}}}}}}{\mu }\left( {{\rho _{{\text{2m}}}}{p_{{\text{2m}}}} - {\rho _{{\text{2f}}}}{p_{{\text{2f}}}}} \right).$$
(18)

The fractional Darcy law for the URV region is

$${\upsilon _{2{\text{f}}}}= - \frac{{{k_{{{2\varvec{\upbeta}}}}}}}{\mu }\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial {t^{1 - {\beta _2}}}}}\frac{{\partial {p_{2{\text{f}}}}}}{{\partial r}}.$$
(19)

The real-gas state equations for the URV region are written as

$${\rho _{{\text{2m}}}}=\frac{{{p_{{\text{2m}}}}M}}{{ZRT}},$$
(20)
$${\rho _{2{\text{f}}}}=\frac{{{p_{{\text{2f}}}}M}}{{ZRT}}{\text{.}}$$
(21)

The gas compressibility and rock compressibility in the URV region are, respectively, given as

$${c_\phi }_{{2j}}=\frac{1}{{{\phi _{{\text{2}}j}}}}\frac{{\partial {\phi _{{\text{2}}j}}}}{{\partial {p_{{\text{2}}j}}}},\left( {j={\text{m}},{\text{f}}} \right),$$
(22)
$${c_{{{\varvec{\uprho}2}}j}}=\frac{1}{{{\rho _{{\text{2}}j}}}}\frac{{\partial {\rho _{{\text{2}}j}}}}{{\partial {p_{{\text{2}}j}}}},\left( {j={\text{m}},{\text{f}}} \right).$$
(23)

Substituting Eqs. (19)–(23) into Eqs. (16)–(18), one can obtain that

$$\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial {t^{1 - {\beta _2}}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{{k_{2{{\varvec{\upbeta}}}}}}}{\mu }\frac{{{p_{{\text{2f}}}}M}}{{ZRT}}\frac{{\partial {p_{{\text{2f}}}}}}{{\partial r}}} \right)} \right]=\frac{{{\phi _{{\text{2f}}}}{c_{{\text{t2f}}}}{p_{{\text{2f}}}}M}}{{ZRT}}\frac{{\partial {p_{{\text{2f}}}}}}{{\partial t}} - {q_{{\text{2m}}}},$$
(24)
$$\frac{{{\phi _{{\text{2m}}}}{c_{{\text{t2m}}}}{p_{{\text{2m}}}}M}}{{ZRT}}\frac{{\partial {p_{{\text{2m}}}}}}{{\partial t}}+{q_{{\text{2m}}}}=0,$$
(25)
$${q_{{\text{2m}}}}=\frac{{{\alpha _2}{k_{{\text{2m}}}}M}}{{\mu ZRT}}\left( {p_{{{\text{2m}}}}^{2} - p_{{{\text{2f}}}}^{2}} \right),$$
(26)

where \({c_{{\text{t2f}}}}={c_{{{\varvec{\uprho}2f}}}}+{c_{\phi 2{\text{f}}}}\) and \({c_{{\text{t2m}}}}={c_{{{\varvec{\uprho}2m}}}}+{c_{\phi 2{\text{m}}}}\).

Introducing the pseudo-pressure

$$\psi =\int_{0}^{p} {\frac{{2p}}{{\mu Z}}} {\text{d}}p,$$
(27)

and then Eqs. (13)–(15) and (24)–(26) can be rewritten as

$$\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial {t^{1 - {\beta _1}}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{k_{1{{\varvec{\upbeta}}}}}\frac{{\partial {\psi _{1{\text{f}}}}}}{{\partial r}}} \right)} \right]={\phi _{1{\text{f}}}}{c_{{\text{t1f}}}}\mu \frac{{\partial {\psi _{1{\text{f}}}}}}{{\partial t}} - {\alpha _1}{k_{1{\text{m}}}}\left( {{\psi _{1{\text{m}}}} - {\psi _{1{\text{f}}}}} \right),\left( {0 \leq r \leq {r_{\text{f}}}} \right),$$
(28)
$${\phi _{1{\text{m}}}}{c_{{\text{t1m}}}}\mu \frac{{\partial {\psi _{1{\text{m}}}}}}{{\partial t}}+{\alpha _1}{k_{1{\text{m}}}}\left( {{\psi _{1{\text{m}}}} - {\psi _{1{\text{f}}}}} \right)=0,\left( {0 \leq r \leq {r_{\text{f}}}} \right),$$
(29)
$$\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial {t^{1 - {\beta _2}}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{k_{2{{\varvec{\upbeta}}}}}\frac{{\partial {\psi _{2{\text{f}}}}}}{{\partial r}}} \right)} \right]={\phi _{2{\text{f}}}}{c_{{\text{t2f}}}}\mu \frac{{\partial {\psi _{2{\text{f}}}}}}{{\partial t}} - {\alpha _2}{k_{{\text{2m}}}}\left( {{\psi _{{\text{2m}}}} - {\psi _{{\text{2f}}}}} \right),\left( {{r_{\text{f}}} \leq r<\infty } \right),$$
(30)
$${\phi _{2{\text{m}}}}{c_{{\text{t2m}}}}\mu \frac{{\partial {\psi _{{\text{2m}}}}}}{{\partial t}}+{\alpha _2}{k_{{\text{2m}}}}\left( {{\psi _{{\text{2m}}}} - {\psi _{{\text{2f}}}}} \right)=0,\left( {{r_{\text{f}}} \leq r<\infty } \right).$$
(31)

The point source is assumed to be placed in the coordinate origin and to produce at a constant rate, so the inner boundary condition can be written as

$$\mathop {\lim }\limits_{{r \to 0}} \frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial {t^{1 - {\beta _1}}}}}\left( {r\frac{{\partial {\psi _{1{\text{f}}}}}}{{\partial r}}} \right)=\frac{{{p_{{\text{sc}}}}q\left( {r=0,t} \right)T}}{{\pi {k_{1{{\varvec{\upbeta}}}}}h{T_{{\text{sc}}}}}}.$$
(32)

The outer boundary condition is

$${\psi _{{\text{2f}}}}\left( {r \to \infty ,t} \right)={\psi _{\text{i}}}.$$
(33)

The pseudo-pressure and gas velocity should be continuity at the interface between the SRV and URV regions, and thus interface boundary conditions are given as

$${\psi _{{\text{1f}}}}\left( {r={r_{\text{f}}},t} \right)={\psi _{{\text{2f}}}}\left( {r={r_{\text{f}}},t} \right),$$
(34)
$${\left. {\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial {t^{1 - {\beta _1}}}}}\left( {{k_{1{{\varvec{\upbeta}}}}}\frac{{\partial {\psi _{{\text{1f}}}}}}{{\partial r}}} \right)} \right|_{r={r_{\text{f}}}}}={\left. {\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial {t^{1 - {\beta _2}}}}}\left( {{k_{2{{\varvec{\upbeta}}}}}\frac{{\partial {\psi _{{\text{2f}}}}}}{{\partial r}}} \right)} \right|_{r={r_{\text{f}}}}}.$$
(35)

With the assumption of the uniform pressure distribution at initial time, the initial condition is expressed as

$${\psi _{{\text{1f}}}}\left( {r,t=0} \right)={\psi _{{\text{2f}}}}\left( {r,t=0} \right)={\psi _{{\text{1m}}}}\left( {r,t=0} \right)={\psi _{{\text{2m}}}}\left( {r,t=0} \right)={\psi _{\text{i}}}.$$
(36)

Introducing the dimensionless variables which are listed in Table 1, Eqs. (28)–(36) are, respectively, rewritten as

Table 1 Definition of dimensionless variables
Full size table
$$\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial t_{{\text{D}}}^{{1 - {\beta _1}}}}}\left[ {\frac{1}{{{r_{\text{D}}}}}\frac{\partial }{{\partial {r_{\text{D}}}}}\left( {{r_{\text{D}}}\frac{{\partial {\psi _{1{\text{fD}}}}}}{{\partial {r_{\text{D}}}}}} \right)} \right]={\omega _{1{\text{f}}}}\frac{{\partial {\psi _{1{\text{fD}}}}}}{{\partial {t_{\text{D}}}}}+{\lambda _1}\left( {{\psi _{1{\text{fD}}}} - {\psi _{1{\text{mD}}}}} \right),\left( {0 \leq {r_{\text{D}}} \leq {r_{{\text{fD}}}}} \right),$$
(37)
$$\left( {1 - {\omega _{1{\text{f}}}}} \right)\frac{{\partial {\psi _{1{\text{mD}}}}}}{{\partial {t_{\text{D}}}}} - {\lambda _1}\left( {{\psi _{1{\text{fD}}}} - {\psi _{1{\text{mD}}}}} \right)=0,\left( {0 \leq {r_{\text{D}}} \leq {r_{{\text{fD}}}}} \right),$$
(38)
$$\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial t_{{\text{D}}}^{{1 - {\beta _2}}}}}\left[ {\frac{{{g_{12}}}}{{{r_{\text{D}}}}}\frac{\partial }{{\partial {r_{\text{D}}}}}\left( {{r_{\text{D}}}\frac{{\partial {\psi _{{\text{2fD}}}}}}{{\partial {r_{\text{D}}}}}} \right)} \right]=\frac{{{M_{12}}{\omega _{{\text{2f}}}}}}{{{W_{12}}}}\frac{{\partial {\psi _{2{\text{fD}}}}}}{{\partial {t_{\text{D}}}}}+{\lambda _2}\left( {{\psi _{2{\text{fD}}}} - {\psi _{2{\text{mD}}}}} \right),\left( {{r_{{\text{fD}}}} \leq {r_{\text{D}}}<\infty } \right),$$
(39)
$$\frac{{{M_{12}}\left( {1 - {\omega _{{\text{2f}}}}} \right)}}{{{W_{12}}}}\frac{{\partial {\psi _{{\text{2mD}}}}}}{{\partial {t_{\text{D}}}}} - {\lambda _2}\left( {{\psi _{{\text{2fD}}}} - {\psi _{2{\text{mD}}}}} \right)=0,\left( {{r_{{\text{fD}}}} \leq {r_{\text{D}}}<\infty } \right),$$
(40)
$$\mathop {\lim }\limits_{{{r_{\text{D}}} \to 0}} \frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial t_{{\text{D}}}^{{1 - {\beta _1}}}}}\left( {{r_{\text{D}}}\frac{{\partial {\psi _{1{\text{fD}}}}}}{{\partial {r_{\text{D}}}}}} \right)= - {q_{\text{D}}}\left( {{r_{\text{D}}}=0,{t_{\text{D}}}} \right),$$
(41)
$${\psi _{{\text{2fD}}}}\left( {{r_{\text{D}}} \to \infty ,{t_{\text{D}}}} \right)=0,$$
(42)
$${\psi _{{\text{1fD}}}}\left( {{r_{\text{D}}}={r_{{\text{fD}}}},{t_{\text{D}}}} \right)={\psi _{{\text{2fD}}}}\left( {{r_{\text{D}}}={r_{{\text{fD}}}},{t_{\text{D}}}} \right),$$
(43)
$${\left. {\frac{{{\partial ^{1 - {\beta _1}}}}}{{\partial t_{{\text{D}}}^{{1 - {\beta _1}}}}}\frac{{\partial {\psi _{{\text{1fD}}}}}}{{\partial {r_{\text{D}}}}}} \right|_{{r_{\text{D}}}={r_{{\text{fD}}}}}}=\frac{{{g_{12}}}}{{{M_{12}}}}{\left. {\frac{{{\partial ^{1 - {\beta _2}}}}}{{\partial t_{{\text{D}}}^{{1 - {\beta _2}}}}}\frac{{\partial {\psi _{{\text{2fD}}}}}}{{\partial {r_{\text{D}}}}}} \right|_{{r_{\text{D}}}={r_{{\text{fD}}}}}},$$
(44)
$${\psi _{{\text{1fD}}}}\left( {{r_{\text{D}}},{t_{\text{D}}}=0} \right)={\psi _{{\text{2fD}}}}\left( {{r_{\text{D}}},{t_{\text{D}}}=0} \right)={\psi _{{\text{1mD}}}}\left( {{r_{\text{D}}},{t_{\text{D}}}=0} \right)={\psi _{{\text{2mD}}}}\left( {{r_{\text{D}}},{t_{\text{D}}}=0} \right)=0,$$
(45)

where

$${g_{12}}={\left[ {\frac{{{k_{{{1\varvec{\upbeta}}}}}}}{{\left( {{\phi _{{\text{1f}}}}{c_{{\text{t1f}}}}+{\phi _{{\text{1m}}}}{c_{{\text{t1m}}}}} \right)\mu {L^2}}}} \right]^{\frac{{{\beta _1} - {\beta _2}}}{{{\beta _1}}}}}.$$
(46)

The point source model in the composite system consists of Eqs. (37)–(46), which can be used to take into account the effect of the anomalous diffusion in fractured reservoirs with complex fracture network. When \({\beta _1}=1\) and \({\beta _2}=1\), the proposed point source model becomes the conventional one proposed by Zhao et al. (2014). Obviously, Eqs. (37)–(46) are fractional differential equations. Recently, the theories and solving methods for fractional differential equations have been investigated by many scholars (Guo 2010; Jiang et al. 2013; Zhu et al. 2016; Hao et al. 2017). Laplace transform is a widely used integral transform in mathematics and engineering that transforms a function of time into a function of complex frequency. Laplace transform from the time domain (i.e., the real space) to the frequency domain (i.e., the Laplace space) can transform differential equations into algebraic equations, and thus Laplace transform has been widely used to solve differential equations (Wang and Yi 2017; Wang et al. 2017; Ren and Guo 2018c).

Laplace transform will be employed to solve the above model and it is defined as follows:

$$\overline {f} \left( s \right)=\int_{0}^{\infty } f \left( {{t_{\text{D}}}} \right){e^{ - s{t_{\text{D}}}}}{\text{d}}{t_{\text{D}}},$$
(47)

where \(f\) is an arbitrary variable in real space. According to the above definition, the Laplace transform of the fractional derivative \({{{\partial ^\beta }f\left( {{t_{\text{D}}}} \right)} \mathord{\left/ {\vphantom {{{\partial ^\beta }f\left( {{t_{\text{D}}}} \right)} {\partial t_{{\text{D}}}^{\beta }}}} \right. \kern-0pt} {\partial t_{{\text{D}}}^{\beta }}}\) is given as (Caputo 1967)

$$\int_{0}^{\infty } {\frac{{{\partial ^\beta }f\left( {{t_{\text{D}}}} \right)}}{{\partial t_{{\text{D}}}^{\beta }}}{e^{ - s{t_{\text{D}}}}}} {\text{d}}{t_{\text{D}}}={s^\beta }\overline {f} \left( s \right) - {s^{\beta - 1}}f\left( 0 \right).$$
(48)

Employing the Laplace transform of Eqs. (37)–(44), one can derive the solution of the point source model (see Appendix A):

$${\overline {\psi } _{1{\text{fD}}}}=\frac{1}{{{s^{1 - {\beta _1}}}}}{\overline {q} _{\text{D}}}\left( {{r_{\text{D}}}=0,s} \right)\left[ {F{I_0}\left( {{\xi _1}{r_{\text{D}}}} \right)+{K_0}\left( {{\xi _1}{r_{\text{D}}}} \right)} \right],$$
(49)

where

$$F=\frac{{{s^{{\beta _2} - {\beta _1}}}{M_{12}}{\xi _1}{K_1}\left( {{\xi _1}{r_{{\text{fD}}}}} \right){K_0}\left( {{\xi _2}{r_{{\text{fD}}}}} \right) - {g_{12}}{\xi _2}{K_0}\left( {{\xi _1}{r_{{\text{fD}}}}} \right){K_1}\left( {{\xi _2}{r_{{\text{fD}}}}} \right)}}{{{s^{{\beta _2} - {\beta _1}}}{M_{12}}{\xi _1}{I_1}\left( {{\xi _1}{r_{{\text{fD}}}}} \right){K_0}\left( {{\xi _2}{r_{{\text{fD}}}}} \right)+{g_{12}}{\xi _2}{I_0}\left( {{\xi _1}{r_{{\text{fD}}}}} \right){K_1}\left( {{\xi _2}{r_{{\text{fD}}}}} \right)}},$$
(50)
$${\xi _1}=\sqrt {{s^{{\beta _1}}}{f_1}\left( s \right)} ,$$
(51)
$${\xi _2}=\sqrt {\frac{{{s^{{\beta _2}}}}}{{{g_{12}}}}{f_2}\left( s \right)} ,$$
(52)
$${f_1}\left( s \right)=\frac{{{\lambda _1}+s{\omega _{1{\text{f}}}}\left( {1 - {\omega _{1{\text{f}}}}} \right)}}{{{\lambda _1}+s\left( {1 - {\omega _{1{\text{f}}}}} \right)}},$$
(53)
$${f_2}\left( s \right)=\frac{{{\lambda _2}+s{\omega _{{\text{2f}}}}\left( {1 - {\omega _{{\text{2f}}}}} \right){\eta _{12}}}}{{{\lambda _2}+s\left( {1 - {\omega _{{\text{2f}}}}} \right){\eta _{12}}}}{\eta _{12}},$$
(54)
$${\eta _{12}}=\frac{{{M_{12}}}}{{{W_{12}}}}.$$
(55)

Model of the MSFH well with SRV

The pseudo-pressure solution of the point source model in a dual-porosity composite system has been derived above, and thus the pseudo-pressure solution for the MSFH well with SRV can be obtained by the superposition principle (Ozkan 1988):

$${\overline {\psi } _{1{\text{fD}}}}\left( {{x_{\text{D}}},{y_{\text{D}}},s} \right)=\frac{1}{{{s^{1 - {\beta _1}}}}}\sum\limits_{{i=1}}^{m} {\int_{{ - {L_{{\text{fLD}}i}}}}^{{{L_{{\text{fRD}}i}}}} {{{\overline {q} }_{{\text{fD}}}}\left( {\gamma ,{y_{{\text{wD}}i}},s} \right)\left[ {F{I_0}\left( {{\xi _1}{R_{\text{D}}}} \right)+{K_0}\left( {{\xi _1}{R_{\text{D}}}} \right)} \right]} {\text{d}}\gamma } ,$$
(56)

where

$${R_{\text{D}}}\left( {{x_{\text{D}}},{y_{\text{D}}};\,\gamma } \right)=\sqrt {{{\left( {{x_{\text{D}}} - \gamma } \right)}^2}+{{\left( {{y_{\text{D}}} - {y_{{\text{wD}}i}}} \right)}^2}} .$$
(57)

Based on the assumption of the infinite-conductivity hydraulic fractures, one can obtain that

$${\overline {\psi } _{{\text{wD}}}}(s)={\overline {\psi } _{1{\text{fD}}}}({x_{\text{D}}},{y_{{\text{wD}}i}},s),$$
(58)

where \(- {L_{{\text{fLD}}i}} \leq {x_{\text{D}}} \leq {L_{{\text{fRD}}i}}\).

The constraint condition of the flow rate can be expressed as

$$\sum\limits_{{i=1}}^{m} {\int_{{ - {L_{{\text{fLD}}i}}}}^{{{L_{{\text{fRD}}i}}}} {{{\overline {q} }_{{\text{fD}}}}\left( {\gamma ,{y_{{\text{wD}}i}},s} \right)} } {\text{d}}\gamma =\frac{1}{s}.$$
(59)

The model of the MSFH well with SRV including Eqs. (56)–(59) can be employed to study the pseudo-pressure behavior. The numerical discrete method (Wan 1999) will be used to solve the seepage model. The fracture wings are discretized into some segments and the flow rate in each segment is considered to stay the same at a certain time. The discrete schematic of the MSFH well in the given coordinate system is shown in Fig. 2.

Fig. 2
figure 2

Discrete schematic of the hydraulic fracture wings of an MSFH well

Full size image

And then, the discrete forms of Eqs. (56), (58) and (59) can be obtained as follows:

$${\overline {\psi } _{{\text{wD}}}}\left( s \right)=\sum\limits_{{i=1}}^{m} {\sum\limits_{{j=1}}^{{2{N_i}}} {\left[ {{{\overline {\psi } }_{1{\text{fD}}i,j}}\left( {{x_{{\text{mD}}k,v}},{y_{{\text{mD}}k,v}},s} \right)} \right]} } ,{\text{ }}(1 \leq v \leq 2{N_k},1 \leq k \leq m),$$
(60)
$$\sum\limits_{{i=1}}^{m} {\left\{ {\sum\limits_{{j=1}}^{{{N_i}}} {\left[ {\overline {q} _{{{\text{fD}}i,j}}^{{}}\left( s \right)\Delta {L_{{\text{fLD}}i}}} \right]} +\sum\limits_{{j={N_i}+1}}^{{2{N_i}}} {\left[ {\overline {q} _{{{\text{fD}}i,j}}^{{}}\left( s \right)\Delta {L_{{\text{fRD}}i}}} \right]} } \right\}=\frac{1}{s}} ,$$
(61)

where

$${\overline {\psi } _{1{\text{fD}}i,j}}\left( {{x_{{\text{mD}}k,v}},{y_{{\text{mD}}k,v}},s} \right)=\frac{1}{{{s^{1 - {\beta _1}}}}}\overline {q} _{{{\text{fD}}i,j}}^{{}}\left( s \right)\int_{{{x_{{\text{D}}i,j}}}}^{{{x_{{\text{D}}i,j+1}}}} {\left[ {F{I_0}\left( {{\xi _1}{R_{\text{D}}}} \right)+\,\,{K_0}\left( {{\xi _1}{R_{\text{D}}}} \right)} \right]{\text{d}}\gamma } ,$$
(62)
$${R_{\text{D}}}\left( {{x_{{\text{mD}}k,v}},{y_{{\text{mD}}k,v}};\,\,\gamma } \right)=\sqrt {{{\left( {{x_{{\text{mD}}k,v}} - \gamma } \right)}^2}+{{\left( {{y_{{\text{mD}}k,v}} - {y_{{\text{wD}}i}}} \right)}^2}} .$$
(63)

Equations (60)–(63) compose \(\left( {2\sum\nolimits_{{i=1}}^{m} {{N_i}} +1} \right)\) linear equations with \(\left( {2\sum\nolimits_{{i=1}}^{m} {{N_i}} +1} \right)\) unknowns. The unknowns are \({\overline {\psi } _{{\text{wD}}}}\left( s \right)\) and \(\overline {q} _{{{\text{fD}}k,v}}^{{}}\left( s \right)\)\((1 \leq v \leq 2{N_k},1 \leq k \leq m)\) which can be obtained by solving the linear equations. Finally, with the aid of the numerical inversion method (Stehfest 1970), one can obtain the bottomhole pseudo-pressure of the MSFH well with constant production rate.

Furthermore, if an MSFH well produces at a constant bottomhole pressure, the production rate of the MSFH well can be obtained by the following expression (Van Everdingen and Hurst 1949)

$${\overline {Q} _{\text{D}}}=\frac{1}{{{s^2}{{\overline {\psi } }_{{\text{wD}}}}}}.$$
(64)

Employing the numerical inversion method (Stehfest 1970), the production rate \({\overline {Q} _{\text{D}}}\) in Laplace space can be transformed into the production rate \({Q_{\text{D}}}\) in real space.

Results and analysis

The transient pseudo-pressure and transient rate of the MSFH well with SRV are generated based on the above model and the synthetic data listed in Table 2. The characteristics of the pseudo-pressure behavior and production rate decline are analyzed. In particular, the effects of the anomalous diffusion on the pseudo-pressure and production rate are discussed in detail.

Table 2 Synthetic data used for generating type curves
Full size table

Type curves and flow regimes

Type curves for the bottomhole pseudo-pressure of an MSFH well with SRV under the constant-rate-production (CRP) condition are shown in Fig. 3a. The type curves for the bottomhole pseudo-pressure consist of the pseudo-pressure curve (\(x\)-axis: \(t\), \(y\)-axis: \(\Delta {\psi _{\text{w}}}\)) and pseudo-pressure derivative curve (\(x\)-axis: \(t\), \(y\)-axis: \(\Delta {\psi ^{\prime}_{\text{w}}} \cdot t\)). Type curves for the production rate of an MSFH well with SRV under constant-pressure-production (CPP) condition are shown in Fig. 3b. The type curves for the production rate include the production-rate curve (\(x\)-axis: \(t\), \(y\)-axis: \({Q_{{\text{sc}}}}\)) and production-rate derivative curve (\(x\)-axis: \(t\), \(y\)-axis: \(- {Q^{\prime}_{{\text{sc}}}} \cdot t\)). Both the anomalous diffusion exponents for the SRV and URV regions are set to be 0.95. It is observed from Fig. 3 that there are seven possible flow regions in the type curves which are analyzed as follows:

Fig. 3
figure 3

Type curves for the bottomhole pseudo-pressure and the production rate (\({\beta _1}=0.95\), \({\beta _2}=0.95\))

Full size image
  1. 1.

    Early linear flow period in SRV The linear flow appears in the area around the hydraulic fractures and is perpendicular to the lateral surface of the main hydraulic fracture. Both the pseudo-pressure derivative curve and production-rate derivative curve exhibit as straight lines. It should be noted that the slope of the pseudo-pressure derivative curve is usually greater than 0.5 due to the effect of the anomalous diffusion.

  2. 2.

    Early pseudo-radial flow period in SRV If the hydraulic-fracture spacing is relatively large, the linear flow will develop into the pseudo-radial flow before the hydraulic-fracture interference occurs. Because of the impact of the anomalous diffusion, the pseudo-pressure derivative does not keep a constant value, but increases linearly with the time.

  3. 3.

    Late linear flow period in SRV The hydraulic-fracture interference has taken place and the linear flow appears beyond the hydraulic-fracture tips. The pseudo-pressure derivative curve exhibits as a straight line, but the slope of the straight line may not be equal to 0.5 owing to the effect of the anomalous diffusion.

  4. 4.

    Late pseudo-radial flow period in SRV If the SRV radius is large enough, this flow period may be observed in type curves. The pseudo-pressure derivative curve for the pseudo-radial flow usually exhibits as a straight line. Compared with the previous flow period (i.e., late linear flow period in SRV), the slope of the pseudo-pressure derivative curve is much smaller. But in reality this flow period may not exist because of the finite area of the SRV.

  5. 5.

    Matrix-fracture interporosity flow period During this period, the interporosity flow between the matrix and fracture systems occurs, so the pseudo-pressure under the CRP condition and the production rate under the CPP condition drop more slowly compared with the previous flow periods. In this flow period, both the pseudo-pressure derivative curve and the production-rate derivative curve exhibit as ‘dip’.

  6. 6.

    Transition flow period between SRV and URV During this period, the pressure wave propagates from the SRV region to the URV region. Since the flow capability in URV is much lower than that in SRV, the pseudo-pressure drop increases rapidly under the CRP condition and the production rate decreases sharply under the CPP condition in this period. Furthermore, this period and the matrix-fracture interporosity flow period usually occur simultaneously, so type curves in this period are usually influenced by the matrix–fracture interporosity flow.

  7. 7.

    Pseudo-radial flow period in URV When the pressure wave continues to travel in the URV region, the transition flow will develop into the pseudo-radial flow. In this period, slower growth of the pseudo-pressure drop under the CRP condition is observed and the production rate under the CPP condition decreases more slowly. Similarly, the magnitude of the pseudo-pressure derivative in this flow regime increases linearly with the time because of the effect of the anomalous diffusion.

Sensitivity analysis

Figure 4 shows the bottomhole pseudo-pressure under the CRP condition and the production rate under the CPP condition with different values of anomalous diffusion exponent in SRV region \(\left( {{\beta _1}} \right)\). It is obvious that \({\beta _1}\) has important effects on the pseudo-pressure behavior and production-rate performance in all flow periods. As the magnitude of the \({\beta _1}\) decreases, the pseudo-pressure drop becomes larger under the CRP condition and the production rate gets smaller under the CPP condition. Hence, the existence of the anomalous diffusion has a negative impact on the production performance of the MSFH well. The smaller the value of the \({\beta _1}\) is, the worse the production performance of the MSFH well is. Furthermore, with decreasing the value of the \({\beta _1}\), the duration of the linear flow becomes longer and the slopes of the pseudo-pressure derivative curves in the linear flow period and pseudo-radial flow period increase. It is interesting that the ‘dip’ in the pseudo-pressure derivative curve and the production-rate derivative curve is shifted right and becomes shallower when the \({\beta _1}\) decreases.

Fig. 4
figure 4

Effects of \({\beta _1}\) on the bottomhole pseudo-pressure and the production rate (\({\beta _2}=1\))

Full size image

Figure 5 shows the bottomhole pseudo-pressure under the CRP condition and the production rate under the CPP condition with different values of anomalous diffusion exponent in URV region \(\left( {{\beta _2}} \right)\). It can be observed that the \({\beta _2}\) only has an effect on the transient flow after the pressure wave propagates outside the SRV region. Decreasing the value of the \({\beta _2}\) gives rise to the increase of the pseudo-pressure drop in the CRP case and the decrease of the production rate in the CPP case. Furthermore, as the magnitude of the \({\beta _2}\) decreases, the ‘dip’ in the pseudo-pressure derivative curve and the production-rate derivative curve becomes shallower, indicating that the influence of the matrix-fracture interporosity flow on the performance of the MSFH well has been reduced. When \({\beta _2}<1\), the slope of the pseudo-pressure derivative curve in the pseudo-radial flow period is greater than zero and increases with the decrease of the \({\beta _2}\).

Fig. 5
figure 5

Effects of \({\beta _2}\) on the bottomhole pseudo-pressure and the production rate (\({\beta _1}=1\))

Full size image

Figure 6 shows the comparisons between the effects of \({\beta _1}\) and \({\beta _2}\) on the bottomhole pseudo-pressure under the CRP condition and the production rate under the CPP condition. It is interesting to find that both the \({\beta _1}\) and \({\beta _2}\) have effects on the pseudo-pressure behavior and production-rate performance in the flow periods after the pressure wave propagates outside the SRV region, but the effect of the \({\beta _2}\) is more pronounced than that of the \({\beta _1}\) in these flow periods. Therefore, it is concluded that the \({\beta _1}\) has a main effect on the production performance of the MSFH well in early flow periods, and the effect of the \({\beta _2}\) becomes more important than that of the \({\beta _1}\) in late flow periods.

Fig. 6
figure 6

Comparisons between the effects of \({\beta _1}\) and \({\beta _2}\) on the bottomhole pseudo-pressure and the production rate

Full size image

Figure 7 shows the bottomhole pseudo-pressure under the CRP condition and the production rate under the CPP condition with different values of the permeability of fracture system in SRV \(\left( {{k_{1{{\varvec{\upbeta}}}}}} \right)\). It is seen that the \({k_{1{{\varvec{\upbeta}}}}}\) affects the pseudo-pressure behavior and production-rate performance in the entire flow periods: A significant influence of the \({k_{1{{\varvec{\upbeta}}}}}\) on type curves is shown before the pressure wave propagates outside the SRV, while the influence of the \({k_{1{{\varvec{\upbeta}}}}}\) on type curves decreases with the increase of the time after the pressure wave propagates outside the SRV. Increasing the \({k_{1{{\varvec{\upbeta}}}}}\) reduces the pseudo-pressure drop in the CRP case and enhances the production rate in the CPP case. Therefore, improving the permeability of the SRV region is critical to obtain good performance of the MSFH well. Furthermore, as the magnitude of the \({k_{1{{\varvec{\upbeta}}}}}\) increases, the duration of the early linear flow period in SRV is shorter and the transition flow period between the SRV and URV regions appears earlier.

Fig. 7
figure 7

Effect of \({k_{1{{\varvec{\upbeta}}}}}\) on the bottomhole pseudo-pressure and the production rate (\({\beta _1}=0.95\), \({\beta _2}=0.95\))

Full size image

Figure 8 shows the bottomhole pseudo-pressure under the CRP condition and the production rate under the CPP condition with different values of the permeability of fracture system in URV \(\left( {{k_{2{{\varvec{\upbeta}}}}}} \right)\). It is clear that the \({k_{2{{\varvec{\upbeta}}}}}\) has no effect on the pseudo-pressure behavior and production-rate performance before the pressure wave arrives at the interface between the SRV and URV regions. After the pressure wave goes into the URV region, smaller value of \({k_{2{{\varvec{\upbeta}}}}}\) results in a substantial increase of the pseudo-pressure drop under the CRP condition and a large decrease of the production rate under the CPP condition. Therefore, compared with the \({k_{1{{\varvec{\upbeta}}}}}\), the \({k_{2{{\varvec{\upbeta}}}}}\) has a more significant effect on the performance of the MSFH well in the late flow periods.

Fig. 8
figure 8

Effect of \({k_{2{{\varvec{\upbeta}}}}}\) on the bottomhole pseudo-pressure and the production rate (\({\beta _1}=0.95\), \({\beta _2}=0.95\))

Full size image

Conclusions

We have incorporated the fractional Darcy law into the governing equations and established a novel model for the MSFH well with SRV. The proposed model includes anomalous diffusion exponents for the SRV region and the URV region, respectively, and thus this model has a much wider field of application and is more suitable for fractured reservoirs compared to the conventional models. The semi-analytical solution of the fractional model is derived, and type curves for pseudo-pressure and production rate are plotted. The influence of the relevant parameters on pseudo-pressure behavior and production rate decline is analyzed in detail. It is found that anomalous diffusion exponent has significant effects on the characteristics of the pseudo-pressure behavior and production rate decline. As the magnitude of anomalous diffusion exponent decreases, the pseudo-pressure drop becomes larger under the CRP condition and the production rate becomes smaller under the CPP condition. Furthermore, the anomalous diffusion has an effect on the characteristic of the type curves in different flow periods. The proposed model extends the conventional model of the MSFH well with SRV to take into account the effect of the anomalous diffusion, and thus it has an advantage over the previous models in interpreting production data and forecasting production performance.