On Three-Dimensional Non-linear Buoyant Convection in Ternary Solidification

Abstract

We consider the problem of three-dimensional non-linear buoyant convection in ternary solidification. Under the limit of large far-field temperature, the convective flow is modeled to be in a rectangular cube composing of a horizontal liquid layer above a primary mushy layer, which itself is over a secondary mushy layer. We first apply linear stability analysis to calculate the conditions at the onset of motion. Next, we carry out weakly non-linear analyses to determine solutions in the form of hexagons and their possible stability and to obtain information about tendency for chimney formation. We find that if the flow is driven either from both mushy layers with equal critical conditions at the onset of motion or only by the primary mushy layer, then the flow can be in the form of a double-cell structure vertically with down-hexagons below or above up-hexagons. There is tendency for vertically oriented chimney formation at different horizontal locations in each mushy layer. For the cases where only the critical conditions at the onset of motion are equal in both mushy layers and depending on the values of the mush Rayleigh numbers, the flow can be subcritical (or supercritical) in both mushy layers or mixed subcritical in one layer and supercritical in another layer.

1 Introduction

Convective buoyant flow during alloy solidification is known to affect the solid–liquid content within the region close to the solid–melt interface and influences the critical conditions for the generation of flow instabilities within the solidification system. It is important to understand such flow and its pattern and then find a way to reduce its undesirable effects in the region close to the solidification front that can lead to production of a class of defects known as freckles in the solidified alloy (Copley et al. 1970). There have been a number of analytical studies for understanding such flow such as those in the binary alloy cases by Anderson and Worster (1995), Chung and Chen (2000), Riahi (2002), and Roper et al. (2008) that were essentially based on the scaling and assumptions of the original model due to Amberg and Homsy (1993).

Although there have been many studies of the flow during the solidification of binary alloys in addition to those referred to in the previous paragraph, there have been relatively less number of studies of the ternary systems counterpart most of which are experimental in nature (Aitta et al. 2001a, b; Anderson 2003; Thompson et al. 2003a, b; Bloomfield and Huppert 2003; Anderson and Schulze 2005; Anderson et al. 2010). Ternary solidification systems belong to larger class of multi-component solidification systems that are very common in Earth sciences and metallurgical areas such as magma solidification and alloy casting.

Aitta et al. (2001a, b) were first to identify experimentally a double mushy layer geometry for their investigated aqueous ternary system water–potassium nitrate–nitrate. They found that two distinct mushy layers, which were referred to as the primary and secondary mushy layers, were formed between the completely solid and completely liquid regions. Thompson et al. (2003b) investigated the same type of ternary system for a convective flow case where the primary mushy layer was unstable, while the secondary mushy layer was stable and non-convective. Anderson (2003) investigated a diffusion-controlled solidification of ternary alloys in mushy layers and examined the corresponding similarity solution.

Anderson and Schulze (2005) investigated two-dimensional buoyancy-driven flow during the solidification of a ternary alloy. They used both a linear stability procedure and numerical computations to determine the results for linear and finite-amplitude steady states for the two-dimensional flow in the ternary state. This state was composed of a liquid layer and two distinct mushy layers referred to as the primary and secondary mushy layers that each has an independent Rayleigh number. They found that, in particular in the cases where one mushy layer was unstably stratified and one layer stably stratified, two-dimensional convection was primarily localized in the unstable layer and there was an adjacent set of rolls which circulated in the opposite direction in the stable layer. In such cases the solid fraction perturbation was found to be negative in one region and positive in another. In the case of convection driven in the primary mushy layer, the non-linear regime was detected to be in the form of supercritical rolls, while subcritical rolls were found for flow driven in the secondary layer.

In the present study, we are interested to uncover the types of three-dimensional flows in the form of hexagons that can possibly be stable and the tendency for chimney formation during the ternary alloy solidification for sufficiently small amplitude ${\vert } \varepsilon {\vert }$ of motion. Even though no experimental observation has been made so far for the observable convective flow patterns in the present type ternary problem, it is known in the binary system counterpart (Tait et al. 1992) that the observed convective flow is in the form of down-hexagons, and this has been one of the motivation for the present study of three-dimensional hexagonal flow in ternary solidification. We investigate theoretically a model of a three-dimensional ternary system by considering a large far-field temperature limit and for the flow close to its onset of motion. Due to a very complex ternary flow system, we restrict our non-linear studies to $O(\varepsilon ^{2})$ of terms in the non-linear system and determine the three-dimensional solutions in the form of hexagons, which is usually preferred in binary system counterpart for sufficiently small ${\vert }\varepsilon {\vert }$. We then make use of the corresponding solvability condition at $O(\varepsilon ^{2})$ to form an evolution type equation (Roper et al. 2008) and determine the preferred and stable hexagonal solutions subjected to the constraint of this evolution equation. We find some interesting results. In particular, we find that for the case that the flow is driven from both mushy layers with equal critical conditions at the onset of motion or only by the primary mushy layer, the convective flow can be in the form of double-layer structure vertically with up-hexagons above or below down-hexagons. Here by down-hexagons and up-hexagons we refer to those, respectively, with down- and up-flow at the cells’ centers and up- and down-flow at the cells’ boundaries. There is a tendency for vertically oriented chimney formation at different horizontal locations in each of the mushy layers, and such tendency first increases and then decreases with increasing the vertical variable.

2 Governing Systems

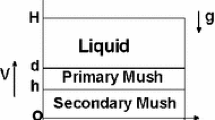
We consider a ternary alloy melt that is cooled from below and is solidified at a constant speed $V$. Following Anderson and Schulze (2005), we consider the ternary alloy in a horizontal region $z>$0 with a liquid region in $z>d$, a primary mushy layer $h<z<d$, and a secondary mushy layer 0$<z<h$. Here $z$ is the vertical variable, and $d$ and $h$ are two positive constants. Our ternary model considers a vertically finite system that includes both of these mushy layers and a finite sub-region of $z>d$ that contains a liquid layer $d<z<D$ on top of the primary mushy layer (Fig. 1). Our present model has some physical relations similar to those earlier models for the binary systems (Worster 1991; Amberg and Homsy 1993; Anderson and Worster 1995), and the temperature of the liquid as $z\rightarrow \infty$ is referred to as far-field temperature $T_\infty$. Our ternary system model is based on the ternary phase diagram used by Anderson (2003) and Anderson and Schulze (2005), which was presented in details by these later authors and, thus, will not be repeated here. We consider the solidification system to be three dimensional and in a moving frame of reference whose origin lies on the solidification front and translating at the speed $V$ with the solidification front in the upward direction. As in the work due to Anderson and Schulze (2005), we assume there is no latent heat release by the solidification process, no solute diffusion, no density change due to solidification, ternary system in local equilibrium with constant thermal properties, and the liquid density depends linearly upon temperature $T$ and compositions $A$ and $B$.

Fig. 1

This is a schematic diagram for the physical model of a ternary system

We consider the governing equations for momentum, under the assumption that the Stokes equation describes the fluid flow in the liquid layer and the Darcy equation describes the fluid flow in the mushy layers, and the equations for the mass conservation, heat, and solute for the ternary system. The necessary equations for the relations between the temperature and species composition in the mushy layers are due to the assumed thermodynamic equilibrium of the phase diagram (Anderson and Schulze 2005). The governing equations that are used in the present study are basically three-dimensional extension of those already derived in Anderson and Schulze (2005) who provided sufficient descriptions as well as experimental justification which will not be repeated here. Instead, the reader is referred to these authors’ paper for details. We make these equations dimensionless in the moving frame described before using $V$, $k/V, \Delta T=T^\mathrm{p}-T^\mathrm{E}$, $\mu k/\varPi _{0}$, and $V^{2}/k$ as scales for velocity, length, temperature excess ($T$–$T^\mathrm{p}$), pressure, and time, respectively (Anderson and Schulze 2005). Here $k$ is thermal diffusivity, $T^\mathrm{p}$ is the temperature at the primary mushy layer front, $T^\mathrm{E}$ is the temperature at the eutectic front, $\mu$ is the dynamic viscosity, and $\varPi _{0}$ is a reference scale for the permeability.

Following the above description to make the equations as well as the boundary conditions non-dimensional, we have the following three- dimensional systems in the liquid and the two mushy layers which are given below.

In the liquid layer we have

$$\begin{aligned}&\displaystyle D_\mathrm{a}\nabla ^{2}\mathbf{u}={\nabla }P+(R_\mathrm{a} A+R_\mathrm{b} B-RT)\mathbf{z},\end{aligned}$$

(1a)

$$\begin{aligned}&\displaystyle {\nabla } \cdot \mathbf{u}=0,\end{aligned}$$

(1b)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)T+\mathbf{u} \cdot {\nabla }T=\nabla ^{2}T,\end{aligned}$$

(1c)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)A+\mathbf{u}\cdot {\nabla }A=0,\end{aligned}$$

(1d)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)B+\mathbf{u}\cdot {\nabla }B=0,\end{aligned}$$

(1e)

$$\begin{aligned}&\displaystyle T=T^\mathrm{L}, A=A^\mathrm{L}, B=B^\mathrm{L}, \mathbf{u}=0 \;\hbox {at}\; z={\delta }L,\end{aligned}$$

(1f)

$$\begin{aligned}&\displaystyle [T]=[{\partial }T /{\partial }z]=[u]=[v]=[w]=[P]={\phi }_{\mathrm{a}}{\vert }^{-}=T {\vert }^{+}=0 \;\hbox {at}\; z=l\delta , \end{aligned}$$

(1g)

where $\mathbf{u}=(u, v, w)$ is the flux driven by the buoyancy with components $u, v$, and $w$ along the horizontal $x$-axis, horizontal $y$-axis, and the upward vertical $z$-axis, respectively; $P$ is the pressure; $A$ and $B$ are the two liquid compositions, which are measured in wt%; $t$ is time variable; $z$ is vertical variable; $D_\mathrm{a}=V^{2}\varPi _{0}/k^{2}$ is the Darcy number; $R=\beta _{\mathrm{t}}\,\varPi _{0}\,g{\Delta }T/(V v)$ is the thermal Rayleigh number representing stabilizing thermal buoyancy; $g$ is acceleration due to gravity; $v$ is kinematic viscosity; $\beta _\mathrm{t}$ is the coefficient of thermal expansion; z is a unit vector in the vertical $z$-axis; $R_\mathrm{a}=\beta _\mathrm{a}\,g\,\varPi _{0}/(Vv)$ and $R_\mathrm{b}=\beta _\mathrm{b}\,g\,\varPi _{0}/(Vv)$ are the compositional Rayleigh numbers due to the presence of the species composition; $\beta _\mathrm{a}$ and $\beta _\mathrm{b}$ are the corresponding expansion coefficients due to change in density with the species composition; ${\delta }L=DV/k$ is the non-dimensional value of the vertical variable at the top boundary of the liquid layer; $L=D/h$; $l$ is a constant of order one quantity to be determined later; $\delta =hV/k$ is the non-dimensional value of the vertical height of the secondary mushy layer; $T^{\mathrm{L}}, A^\mathrm{L}$, and $B^\mathrm{L}$ are constant quantities; and the square brackets $[\;] \equiv {\vert }^{+}-{\vert }^{-}$ denote the jump in the enclosed quantity across the interface.

In the primary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}/\varPi (\chi )=-{\nabla }P-(R_\mathrm{p}T+M_\mathrm{p})\mathbf{z},\end{aligned}$$

(2a)

$$\begin{aligned}&\displaystyle {\nabla }\cdot \mathbf{u}=0,\end{aligned}$$

(2b)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)T+ \mathbf{u}\cdot {\nabla }T={\nabla }^{2}T,\end{aligned}$$

(2c)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)({\chi }A+{\phi }_{\mathrm{a}})+ \mathbf{u}\cdot {\nabla }A=0,\end{aligned}$$

(2d)

$$\begin{aligned}&\displaystyle T=-1+M_{\mathrm{a}} (A-A^{\mathrm{E}})+M_{\mathrm{b}} (B-B^{\mathrm{E}}),\end{aligned}$$

(2e)

$$\begin{aligned}&\displaystyle \chi -1+{\phi }_{\mathrm{a}}={\phi }_{\mathrm{b}} =0,\end{aligned}$$

(2f)

$$\begin{aligned}&\displaystyle B=B^\mathrm{P} (1-A)/(1-A^\mathrm{P}),\end{aligned}$$

(2g)

$$\begin{aligned}&\displaystyle [T]=[{\partial }T/{\partial }z]=[P]=[\mathbf{u}]=[{\phi }_\mathrm{a}]={\phi }_\mathrm{b}{\vert }^{-}=T-T^\mathrm{s}{\vert }^{+} =0 \;\hbox {at}\; z =\delta , \end{aligned}$$

(2h)

where

$$\begin{aligned}&\displaystyle R_\mathrm{p}=-R+[R_\mathrm{a}(1-A^\mathrm{P})-R_\mathrm{b}\,B^\mathrm{P}]/[M_\mathrm{a}(1-A^\mathrm{P})-M_\mathrm{b}\,B^\mathrm{P}],\end{aligned}$$

(2i)

$$\begin{aligned}&\displaystyle M_\mathrm{p}=[M_\mathrm{a}\,A^\mathrm{E}+M_\mathrm{b}\,B^\mathrm{E} +1-M_\mathrm{b}\, B^\mathrm{P}/(1-A^\mathrm{P})]R_\mathrm{p}+R_\mathrm{b}\,B^\mathrm{P} /(1-A^\mathrm{P}), \end{aligned}$$

(2j)

$\chi$ is the liquid fraction in the primary mushy layer, which is also given in (2f) explicitly, ${\phi }_{\mathrm{b}}$ is the solid fraction due to composition $B$, and the value of constant temperature $T^\mathrm{s}$ was determined in Anderson and Schulze (2005) by identifying the intersection of the tie-line and the cotectic constraints on their considered phase diagram and apply the constraints on the primary mushy layer side of the interface. Additional equations given by (2e) and (2g) are of the type introduced and justified by Anderson and Schulze (2005), which are due to the assumed thermodynamic equilibrium of the mushy layers analog of the linear liquidus relation in the binary system (Anderson and Worster 1995). Here quantities with superscripts “P” and “E” represent constant quantities at the primary mushy layer front and the eutectic front, respectively, and the constants $M_\mathrm{a}$ and $M_\mathrm{b}$ are dimensionless liquidus slopes. Anderson and Schulze (2005) provided detail description, derivation, and experimental justification of equations (2e) and (2g) as well as derivation for the primary mushy layer Rayleigh number $R_\mathrm{p}$; thus, these will not be repeated here.

In the secondary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}/\varPi (\chi )=-{\nabla }P-(R_\mathrm{s}T +M_\mathrm{s})\mathbf{z},\end{aligned}$$

(3a)

$$\begin{aligned}&\displaystyle {\nabla }\cdot \mathbf{u}=0,\end{aligned}$$

(3b)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)T+ \mathbf{u}\cdot {\nabla }T={\nabla }^{2}T,\end{aligned}$$

(3c)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)({\chi }A+{\phi }_{\mathrm{a}})+ \mathbf{u}\cdot {\nabla }A=0,\end{aligned}$$

(3d)

$$\begin{aligned}&\displaystyle (\partial /{\partial }t-\partial /{\partial }z)({\chi }A+{\phi }_{\mathrm{b}})+ \mathbf{u}\cdot {\nabla }B=0,\end{aligned}$$

(3e)

$$\begin{aligned}&\displaystyle \chi = (1-{\phi }_{\mathrm{a}}-{\phi }_{\mathrm{b}}), A=A^\mathrm{E} + (T+1)/M_\mathrm{ac},\end{aligned}$$

(3f)

$$\begin{aligned}&\displaystyle B=B^\mathrm{E}+(T+1)/M_\mathrm{bc},\end{aligned}$$

(3g)

$$\begin{aligned}&\displaystyle T+1=\mathbf{u}\cdot \mathbf{z}=0\;\hbox {at}\;z=0, \end{aligned}$$

(3h)

where

$$\begin{aligned}&\displaystyle R_\mathrm{s}=-R+(R_\mathrm{a}/M_\mathrm{ac}+R_\mathrm{b} /M_\mathrm{bc}),\end{aligned}$$

(3i)

$$\begin{aligned}&\displaystyle M_\mathrm{s}=R_\mathrm{a}(A^\mathrm{E}+1/M_\mathrm{ac})+R_\mathrm{b}(B^\mathrm{E}+1/M_\mathrm{bc}), \end{aligned}$$

(3j)

$M_\mathrm{ac}$ and $M_\mathrm{bc}$ are constant dimensionless cotectic slopes and derivations of (3f)–(3g) are given in Anderson and Schulze (2005).

3 Analyses and Solutions

3.1 Scaling and Expansion Procedure

From the result found by Anderson and Schulze (2005) for the relation between the depth $\delta$ of the secondary mushy layer and the far-field temperature $T_\infty$, which we consider here to be large ($T_\infty \gg 1$) for large $z \gg 1$ and similar to the binary system counterpart described in Anderson and Worster (1995), we have

$$\begin{aligned} e^{\delta } =(T_\infty +1)/[T_\infty -T^\mathrm{s}+\hbox {e}^{-z}(T^\mathrm{s}+1)]. \end{aligned}$$

(4a)

Since ${\vert }T^\mathrm{s}{\vert }$ is taken to be less than 0.55 as in Anderson and Schulze (2005), (4a) implies that $\delta$ is small ($\ll$1) and to the first order in $\delta$, we have

$$\begin{aligned} 1+\delta = O(1+ 1/T_\infty ), \end{aligned}$$

(4b)

which implies that

$$\begin{aligned} \delta =O(1/T_\infty )\ll 1. \end{aligned}$$

(4c)

Similarly from the result obtained in Anderson and Schulze (2005), we have

$$\begin{aligned} l\delta =O(1/T_\infty )\ll 1, \end{aligned}$$

(4d)

which together with (4c) imply that $l$ is a constant of order one quantity.

In addition to the above explanation for the small value of $\delta$, we also later in Sect. 4 set our data collections for various results based on three base-state parameter values (Table 1) for our vertically bounded ternary system which together with the result due to Anderson and Schulze (2005) for the thickness of the secondary mushy layer, which is here in the form

$$\begin{aligned} \delta =l_{n}\{(1+T^\mathrm{L})/[T^\mathrm{L}-T^\mathrm{s}+\hbox {e}^{-{\delta }D} (1+T^\mathrm{s})]\}, \end{aligned}$$

(4e)

implies $\delta \ll 1$. Thus, similar to the well-known model for the binary system (Amberg and Homsy 1993), we find that the thickness of each mushy layer is small in the limit of large far-field temperature. Using this result, it motivated us a further scaling of the variables, and so we assume the limit of large far-field temperature in the present study and use $\delta$ as a small parameter. As noted in Roper et al. (2008), for values of $z$ smaller than $O(\delta ^{-1})$, we expect that temperature $T^\mathrm{L}$ at the top boundary of the rectangular cube region in the present study should be an order one quantity for $z={\delta }L$, which we consider to be a constant of at most order one in this paper.

Table 1 Parameter values for 3 base states I–III

We now scale all lengths with $\delta$ and time with $\delta ^{2}$. Then we expand the governing systems to derive the systems for small perturbations to the motionless steady basic state, which varies at most with respect to the vertical variable. Since the Darcy number is very small in applications (Worster 1992), we scale it with $\delta ^{2}(D_{\mathrm{a}}=\delta ^{2} d_\mathrm{a})$. Following Roper et al. (2008), we do some rescaling for u and the effective Rayleigh numbers for the mushy layers and consider each dependent variable to be sum of its basic state, which is designated with a subscript “B,” plus small perturbations, which vary in general with respect to three-dimensional space and time variables, and then make a double expansion in small amplitude $\varepsilon$ and $\delta$ of the perturbations

$$\begin{aligned}&\displaystyle T=T_\mathrm{B}+\varepsilon (T_{0}+{\delta }T_{01} +\cdots )+\varepsilon ^{2}(T_{1}+{\delta }T_{11} +\cdots )+\cdots ,\end{aligned}$$

(5a)

$$\begin{aligned}&\displaystyle \delta \mathbf{u}= \mathbf{0}+ \varepsilon (\mathbf{u}_{0}+\delta \,\mathbf{u}_{01}+\cdots )+\varepsilon ^{2}(\mathbf{u}_{1}+\delta \,\mathbf{u}_{11}+\cdots )+\cdots ,\end{aligned}$$

(5b)

$$\begin{aligned}&\displaystyle P=P_\mathrm{B}+\varepsilon (P_{0}+{\delta } P_{01}+\cdots )+\varepsilon ^{2}(P_{1}+{\delta }\,P_{11}+\cdots )+\cdots ,\end{aligned}$$

(5c)

$$\begin{aligned}&\displaystyle (A, B, \chi )=(A_\mathrm{B}, B_\mathrm{B}, \chi _\mathrm{B})+\varepsilon [(A_{0}+{\delta }A_{01}+\cdots ), (B_{0}+{\delta }B_{01}+\cdots ), (\chi _{0}+\delta \chi _{01}\nonumber \\&\displaystyle \quad +\cdots )]+\cdots ,\end{aligned}$$

(5d)

$$\begin{aligned}&\displaystyle ({\phi }_\mathrm{a}, {\phi }_{\mathrm{b}})=({\phi }_{\mathrm{aB}},{\phi }_{\mathrm{bB}})+\varepsilon [(\delta ^{-1}{\phi }_{\mathrm{a}(-1)}+{\phi }_{\mathrm{a}0}+\delta {\phi }_{\mathrm{a}01}+\cdots ), (\delta ^{-1}{\phi }_{\mathrm{b}(-1)}+{\phi }_{\mathrm{b}0}+\delta {\phi }_{\mathrm{b}01}\nonumber \\&\displaystyle \quad +\cdots )]+\cdots ,\end{aligned}$$

(5e)

$$\begin{aligned}&\displaystyle \delta (R_\mathrm{p}, R_\mathrm{s})=[(R_\mathrm{p0}+{\delta }R_\mathrm{p01}+\cdots ), (R_\mathrm{s0}+{\delta }R_\mathrm{s01}+\cdots )]+\varepsilon [(R_\mathrm{p1}+{\delta }R_\mathrm{p11}+\cdots ), (R_\mathrm{s1}\nonumber \\&\displaystyle \quad +\,{\delta }R_\mathrm{s11}+\cdots )]+\cdots , \end{aligned}$$

(5f)

where $\varepsilon \ll \delta \ll 1$ is assumed. It can be noted that the $O(\delta ^{-1})$-terms in (5e) were found to be needed to balance with the advection terms in the composition equations in order to determine non-trivial solutions for the solid fraction perturbations.

3.2 Basic State

Using (5a–5f) in (1a–1g)–(3a–3j) and considering the terms in the absence of perturbations by setting $\varepsilon =0$, we find the systems for the motionless basic state. In the liquid layer ($l \le z \le L$), we find to $O(\delta ^{2})$

$$\begin{aligned}&\displaystyle T_\mathrm{B}=T^\mathrm{L}\{[1-(z-L)/(l-L)]+0.5\delta [z^{2}-z(l+L)+lL]/(l-L)\},\end{aligned}$$

(6a)

$$\begin{aligned}&\displaystyle (A_\mathrm{B}, B_\mathrm{B})=(A^\mathrm{L}, B^\mathrm{L}),\end{aligned}$$

(6b)

$$\begin{aligned}&\displaystyle P_\mathrm{B}=z(-R_\mathrm{a}A^\mathrm{L}-R_\mathrm{b}B^\mathrm{L}+{\delta }RT_\mathrm{B})+P_{l0}, \end{aligned}$$

(6c)

where $P_{l0}$ is a constant.

In the primary mushy layer ($1 \le z \le l$), we find to $O(\delta ^{2})$

$$\begin{aligned}&\displaystyle T_\mathrm{B}=-T^\mathrm{s}\{(l-z)+0.5\delta [z^{2}-z(1+l)+l]\}/(1-l),\end{aligned}$$

(7a)

$$\begin{aligned}&\displaystyle \chi _{\mathrm{B}}=[M_\mathrm{a}(A^\mathrm{L}-1)+M_\mathrm{b}\,B^\mathrm{L}]/[M_\mathrm{a}(A^\mathrm{E}-1)+M_\mathrm{b}\,B^\mathrm{E}+1+T_\mathrm{B}],\end{aligned}$$

(7b)

$$\begin{aligned}&\displaystyle (A_\mathrm{B}, B_\mathrm{B}) =[1+(A^\mathrm{L}-1)/\chi _{\mathrm{B}}, B^\mathrm{L}/\chi _{\mathrm{B}}],\end{aligned}$$

(7c)

$$\begin{aligned}&\displaystyle {\phi }_{\mathrm{A}}-1+\chi _{\mathrm{B}}={\phi }_{\mathrm{B}}=0,\end{aligned}$$

(7d)

$$\begin{aligned}&\displaystyle P_\mathrm{B}=-M_\mathrm{p}(z-l)-R_\mathrm{p}T^\mathrm{s}(0.5 z^{2}-l\,z+0.5\, l^{2})-l(R_\mathrm{a}\,A^\mathrm{L}+R_\mathrm{b}\,B^\mathrm{L})+P_{l0}, \end{aligned}$$

(7e)

where the condition $[{\partial }T/{\partial }z]=0$ at the liquid–primary mush interface implies

$$\begin{aligned} T^\mathrm{L}/T^\mathrm{s}=(L-l)/(1-l). \end{aligned}$$

(7f)

In the secondary mushy layer ($0 \le z \le 1$), we find to $O(\delta ^{2})$

$$\begin{aligned}&\displaystyle T_\mathrm{B}=(T^\mathrm{s}+1)z-1+0.5\delta (T^\mathrm{s}+1)(z-z^{2}),\end{aligned}$$

(8a)

$$\begin{aligned}&\displaystyle (A_\mathrm{B}, B_\mathrm{B})=\{[A^\mathrm{E}+(T_\mathrm{B}+1)/M_\mathrm{ac}], [B^\mathrm{E}+(T_\mathrm{B}+1)/M_\mathrm{bc}]\},\end{aligned}$$

(8b)

$$\begin{aligned}&\displaystyle \chi _{\mathrm{B}}=(1-A^\mathrm{L}-B^\mathrm{L})/(1-A_\mathrm{B}-B_\mathrm{B}),\end{aligned}$$

(8c)

$$\begin{aligned}&\displaystyle {\phi }_{\mathrm{aB}}-(A^\mathrm{L}-\chi _{\mathrm{B}}A_{\mathrm{B}})={\phi }_{\mathrm{bB}}-(1-\chi _{\mathrm{B}}-{\phi }_{\mathrm{aB}})=0,\end{aligned}$$

(8d)

$$\begin{aligned}&\displaystyle P_\mathrm{B}=-R_\mathrm{s}\{1-z+0.5(1+T^\mathrm{s})[z-1+\delta (z^{2}/2-z^{3}/3-1/6)]\}+M_\mathrm{s}(1-z)\nonumber \\&\displaystyle \quad -(M_\mathrm{p}+0.5R_\mathrm{p}T^\mathrm{s})(1-l)-l(R_\mathrm{a}A^\mathrm{L}+R_\mathrm{b}B^\mathrm{L})+P_{l0}, \end{aligned}$$

(8e)

where the condition $[{\partial }T/{\partial }z]=0$ at the primary mush–secondary mush interface implies

$$\begin{aligned} l=1/(T^\mathrm{s}+1). \end{aligned}$$

(8f)

3.3 Linear Problem

We use the expansions (5a–5f) in (1a–1g)–(3a–3j) and similar to the work in Roper et al. (2008), we assume in the present study that $\varPi (\chi )\equiv 1$ in Darcy’s equations. Considering the systems in the liquid and mushy layers to the lowest order in $\varepsilon$, we find the linear problem whose leading order system is given below.

In the liquid layer we have

$$\begin{aligned}&\displaystyle d_\mathrm{a}{\nabla }^{2}\mathbf{u}_{0}={\nabla }P_{0}, {\nabla } \cdot \mathbf{u}_{0}=0, {\nabla }^{2}T_{0}=w_{0}\;\hbox {d}T_\mathrm{B}/\hbox {d}z, A_{0}=0, B_{0}=0,\end{aligned}$$

(9a)

$$\begin{aligned}&\displaystyle T_{0}= \mathbf{u}_{0}=0\;\hbox {at}\;z=L, [T_{0}]=[{\partial }T_{0}/{\partial }z]=[\mathbf{u}_{0}]=[P_{0}]={\phi }_{\mathrm{a}(-1)}{\vert }^{-}=T_{0}{\vert }^{+}\nonumber \\&\displaystyle \quad =0\;\hbox {at}\;z=l. \end{aligned}$$

(9b)

In the primary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}_{0}+{\nabla }P_{0}+R_\mathrm{p0}T_{0}\,\mathbf{z} =0, {\nabla }.\mathbf{u}_{0} =0, {\nabla }^{2} T_{0}=w_{0} \hbox {d}T_\mathrm{B}/\hbox {d}z, T_{0}=M_\mathrm{a}\,A_{0}+M_\mathrm{b}\,B_{0},\qquad \end{aligned}$$

(10a)

$$\begin{aligned}&\displaystyle B_{0}+B^\mathrm{p} A_{0} /(1-A^\mathrm{p}), \partial /{\partial }z \{{\phi }_{\mathrm{a}(-1)}[1-A_\mathrm{B}]\}=w_{0} \hbox {d}A_\mathrm{B}/\hbox {d}z,\end{aligned}$$

(10b)

$$\begin{aligned}&\displaystyle [T_{0}]=[{\partial }T_{0}/{\partial }z]=[\mathbf{u}_{0}]=[P_{0}]=[{\phi }_{\mathrm{a}(-1)}]={\phi }_{\mathrm{b}(-1)}{\vert }^{-}=T_{0}{\vert }^{+} =0\;\hbox {at}\;z =1.\qquad \end{aligned}$$

(10c)

In the secondary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}_{0}+{\nabla }P_{0}+R_\mathrm{s0} T_{0}\,\mathbf{z} =0, {\nabla } \cdot \mathbf{u}_{0} =0, {\nabla }^{2} T_{0}=w_{0} \hbox {d}T_\mathrm{B}/\hbox {d}z, (A_{0}, B_{0})\nonumber \\&\displaystyle \quad =T_{0} (1/M_\mathrm{ac}, 1/M_\mathrm{bc}),\end{aligned}$$

(11a)

$$\begin{aligned}&\displaystyle \partial /{\partial }z\{[{\phi }_{\mathrm{a}(-1)}-A_\mathrm{B}({\phi }_{\mathrm{a}(-1)}+{\phi }_{\mathrm{b}(-1)})], [{\phi }_{\mathrm{b}(-1)}-B_\mathrm{B}({\phi }_{\mathrm{a}(-1)}+{\phi }_{\mathrm{b}(-1)})]\}\nonumber \\&\displaystyle \quad =w_{0}\{\hbox {d}A_\mathrm{B}/\hbox {d}z, \hbox {d}B_{\mathrm{B}}/\hbox {d}z\},\end{aligned}$$

(11b)

$$\begin{aligned}&\displaystyle T_{0}=w_{0} =0\;\hbox {at}\;z =0. \end{aligned}$$

(11c)

The resulting leading order linear systems indicate that $\mathbf{u}_{0}, P_{0}$, and $T_{0}$ can be separable from the result of the equations for the other dependent variable. Since the systems for $\mathbf{u}_{0}, P_{0}$, and $T_{0}$ in the liquid and mushy layers contain the effective mush Rayleigh numbers $R_\mathrm{p}$ and $R_\mathrm{s}$, we consider these systems later whose analytical solutions will lead to the results at the onset of motion and for the neutral stability boundaries for the stationary perturbations. The non-linear extension of these systems at $O(\varepsilon ^{2})$ are also found to be sufficient to form the solvability conditions, which are derived later in this section.

In the liquid layer we find the following steady results at $O(\varepsilon )$

$$\begin{aligned}&\displaystyle w_{0}=[(b_{1}\,z+b_{2})\exp ({\alpha }z)+(b_{3}\, z+b_{4})\exp (-{\alpha }z)] H(x, y),\end{aligned}$$

(12a)

$$\begin{aligned}&\displaystyle H(x, y)\equiv \sum _{n=-N}^{N} E_{n}\, {\eta }_{n}(x, y),\eta _{n}(x,y){\equiv }\exp (i\,\varvec{\alpha }_{n} \cdot \mathbf{r}),\end{aligned}$$

(12b)

$$\begin{aligned}&\displaystyle T_{0}=[(b_{5}\,z+b_{6}\,z^{2})\exp ({\alpha }z)+(b_{0}+b_{7}\,z+b_{8}\, z^{2})\exp (-{\alpha }z)] H(x, y),\end{aligned}$$

(12c)

$$\begin{aligned}&\displaystyle P_{0}=l_{0} [2\,b_{1} \exp ({\alpha }z) +2\,b_{3} \exp (-{\alpha }z)+p_{00}]H(x, y), A_{0}=B_{0}=0,\end{aligned}$$

(12d)

$$\begin{aligned}&\displaystyle (u_{0}, v_{0})=(1/{\alpha }^{2})[(b_{1}+{\alpha }b_{2}+{\alpha }b_{1}z)\exp ({\alpha }z)+(b_{3}-{\alpha }b_{4}-{\alpha }b_{3}\, z)\exp (-{\alpha }z)\nonumber \\&\displaystyle \quad -p_{00}]\sum _{n=-N}^{N}[(i{\alpha }_{nx}, i{\alpha }_{ny})E_{n} {\eta }_{n}(x, y)], \end{aligned}$$

(12e)

where it is convenient for later references to designate the $z$-dependent coefficients for $u_{0}$ and $v_{0}$ in (12e) by $f_{1} (z, n)$ and $f_{2} (z, n)$, respectively, for $w_{0}$ in (12a) by $f_{3} (z)$ and for $T_{0}$ in (12c) by $f_{4} (z)$. In addition,

$$\begin{aligned} p_{00} \equiv -(1/{\alpha }^{2})[(b_{1}+{{\alpha }b}_{2}+b_{1}L)\exp ({\alpha }L)+(b_{3}-{\alpha }b_{4} -b_{3} L)\exp (-{\alpha }L)], \end{aligned}$$

(12f)

$x$ and $y$ are the horizontal variables, the unknown constants $b_{m} (m=0, 1, \ldots , 8)$ satisfy a set of lengthy linear algebraic equations, which are not given here, $i$ is pure imaginary number ($\surd -1$), the subscript “$n$” takes only non-zero integer values from –$N$ to $N$, $N$ is a positive integer, and the horizontal wave number vectors $\varvec{{\alpha }}_{n}\mathbf{=(}{\alpha }_{nx}, {\alpha }_{ny})$ satisfy the properties

$$\begin{aligned} \varvec{{\alpha }}_{n} \cdot \mathbf{z}=0, {\vert }\varvec{{\alpha }}_{n}{\vert }=\alpha , \varvec{{\alpha }}_{-n}=-\varvec{{\alpha }}_{n}. \end{aligned}$$

(13)

The constant coefficients $E_{n}$ satisfy the conditions

$$\begin{aligned} \sum _{n=-{N}}^{{N}} {\vert }E_{n}{\vert }^{2}=1, E_{n}^{*}=E_{-n}. \end{aligned}$$

(14a)

For the simplest types of solutions, which refer to as regular solutions and include those observed in the applications (Busse 1978) like hexagonal type solutions, all angles between two neighboring $\alpha$-vectors are equal and (14a) yields

$$\begin{aligned} {\vert }E_{1}{\vert }^{2}=\cdots ={\vert }E_{N}{\vert }^{2}=1/(2 N). \end{aligned}$$

(14b)

We have provided general form of the solutions in (12a–12e)–(14a, 14b) in terms of arbitrary positive integer $N$ so that the present paper can be used as a suitable reference for future extension of the present work, even though we shall later restrict our study to the cases for sufficiently small $\varepsilon$ where the hexagonal solutions with $N=3$ can be stable and preferred.

In the primary mushy layer the system at $O(\varepsilon )$ for the perturbations yields

$$\begin{aligned}&w_{0}=\{b_{9}\,\exp [({\gamma }^{0.5})z]+ b_{10} \,\exp [-({\gamma }^{0.5})z]+ b_{11} \,\exp [({\gamma }_{0})^{0.5} z]\nonumber \\&\quad +\,b_{12} \,\exp [-({\gamma }_{0})^{0.5} z]\}H(x, y),\end{aligned}$$

(15a)

$$\begin{aligned}&T_{0} =\{b_{13} \,\exp [({\gamma }^{0.5})z]+ b_{14} \,\exp [-({\gamma }^{0.5})z]+ b_{15} \,\exp [({\gamma }_{0})^{0.5} z]+ b_{16} \,\exp [\nonumber \\&\quad -\,({\gamma }_{0})^{0.5} z]\}H(x, y),\end{aligned}$$

(15b)

$$\begin{aligned}&{\gamma }\equiv {\alpha }^{2}+\alpha \beta (R_{\mathrm{p}0})^{0.5}, {\beta }^{2}{\equiv }T^\mathrm{s} /(1-l), {\gamma }_{0}\equiv {\alpha }^{2}-\alpha \beta (R_{\mathrm{p}0})^{0.5},\end{aligned}$$

(15c)

$$\begin{aligned}&{\phi }_\mathrm{a(-1)}=[1/(1-A_\mathrm{B})](\hbox {d} A_\mathrm{B}/\hbox {d}z)\int _{l}^{z} w_{0}\hbox {d}z, A_{0}=(1-A^\mathrm{P})T_{0}/[M_\mathrm{a}(1-A^\mathrm{P})\nonumber \\&\quad -\,M_\mathrm{b}\,B^\mathrm{P}], B_{0}=-B^\mathrm{P}A_{0}/(1-A^\mathrm{P}),\end{aligned}$$

(15d)

$$\begin{aligned}&P_{0}=\sum _{n=-N}^{N}\{-(1/{\gamma })^{0.5}(b_{9}+b_{13} R_\mathrm{p0})(\exp [({\gamma })^{0.5} z]\nonumber \\&\quad -\,\exp [({\gamma })^{0.5} l])+(1/{\gamma })^{0.5}(b_{10}+b_{14} R_\mathrm{p0})(\exp [-({\gamma })^{0.5}z]\nonumber \\&\quad -\,\exp [-({\gamma })^{0.5}l])-(1/{\gamma }_{0})^{0.5}(b_{11}+b_{15} R_\mathrm{p0})(\exp [({\gamma }_{0})^{0.5}z]\nonumber \\&\quad -\,\exp [({\gamma }_{0})^{0.5}l])+(1/{\gamma }_{0})^{0.5}(b_{12}+b_{16} R_\mathrm{p0})(\exp [-({\gamma }_{0})^{0.5}z]\nonumber \\&\quad -\,\exp [-({\gamma }_{0})^{0.5} l])+ l_{0} [2b_{1} \,\exp ({\alpha }l)+2b_{3}\,\exp (-{\alpha }l)+p_{00}]\}E_{n}{\eta }_{n},\end{aligned}$$

(15e)

$$\begin{aligned}&(u_{0}, v_{0})= -\sum _{n=-N}^{N} ({\alpha }_{nx}, {\alpha }_{ny}) P_{0}^{\prime } (z)E_{n}\,{\eta }_{n} \equiv \sum _{n= -N}^{N} [f_{5} (z, n), f_{6} (z, n)] E_{n}\, {\eta }_{n} (x, y), \end{aligned}$$

(15f)

where for the later references the expressions for the $z$-dependent coefficients for $u_{0}, v_{0}$, w, and $T_{0}$ in the above equations will be designated by $f_{i}$ ($i = 5, 6, 7, 8$), respectively, and $P_{0}^{\prime }$ is the $z$-dependent coefficient for $P_{0}$ in (15e). In addition, the unknown constants $b_{m}$ ($m=9, 10, \ldots , 16$) satisfy a set of lengthy linear algebraic equations, which are not given here.

In the secondary mushy layer the system at O($\varepsilon )$ for the perturbations yields

$$\begin{aligned}&w_{0}=\{b_{17} \,\exp [({\gamma }_{1})^{0.5}z]+b_{18} \,\exp [-({\gamma }_{1})^{0.5}z]+b_{19} \,\exp [({\gamma }_{2})^{0.5}z]+b_{20} \,\exp [\nonumber \\&\quad -({\gamma }_{2})^{0.5}z]\}H(x, y),\end{aligned}$$

(16a)

$$\begin{aligned}&T_{0}=\{\{b_{21} \,\exp [({\gamma }_{1})^{0.5}z]+b_{22} \,\exp [-({\gamma }_{1})^{0.5}z]+b_{23} \,\exp [({\gamma }_{2})^{0.5}z]+b_{24} \,\exp [\nonumber \\&\quad -({\gamma }_{2})^{0.5}z]\}H(x, y),\end{aligned}$$

(16b)

$$\begin{aligned}&(A_{0}, B_{0})=T_{0} (1/M_\mathrm{ac}, 1/M_\mathrm{bc}),\end{aligned}$$

(16c)

$$\begin{aligned}&{\gamma }_{1}\equiv {\alpha }^{2}+\alpha (1+T^\mathrm{s})(R_\mathrm{s0})^{0.5}, {\gamma }_{2}\equiv {\alpha }^{2}-\alpha (1+T^\mathrm{s})(R_\mathrm{s0})^{0.5},\end{aligned}$$

(16d)

$$\begin{aligned}&P_{0}=\sum _{n=-N}^{N} \{-(1/{\gamma }_{1})^{0.5}(b_{17}+b_{21} R_\mathrm{s0})(\exp [({\gamma }_{1})^{0.5}z]\nonumber \\&\quad -\exp [({\gamma }_{1})^{0.5}])+(1/{\gamma }_{1})^{0.5}(b_{18}+b_{22}R_\mathrm{s0})(exp[-({\gamma }_{1})^{0.5}z]\nonumber \\&\quad -\exp [-({\gamma }_{1})^{0.5}])-(1/{\gamma }_{2})^{0.5}(b_{19}+b_{23}R_\mathrm{s0})(exp[({\gamma }_{2})^{0.5}z]\nonumber \\&\quad -\exp [({\gamma }_{2})^{0.5}])+(1/{\gamma }_{2})^{0.5}(b_{20}+b_{24}R_\mathrm{s0})(exp[-({\gamma }_{2})^{0.5}z]\nonumber \\&\quad -\exp [-({\gamma }_{2})^{0.5}])+ P_{0}^{\prime }(1)\}E_{n}\,{\eta }_{n}(x, y),\end{aligned}$$

(16e)

$$\begin{aligned}&(u_{0}, v_{0})= -\sum _{n=-N}^{N} ({\alpha }_{nx}, {\alpha }_{ny})P_{0}^{\prime \prime }(z)E_{n}\,{\eta }_{n} (x, y),\end{aligned}$$

(16f)

$$\begin{aligned}&[{\phi }_{\mathrm{a}(-1)}, {\phi }_{\mathrm{b}(-1)}]=\{[(1-B_\mathrm{B})\,\hbox {d}A_\mathrm{B}/\hbox {d}z+A_\mathrm{B} \hbox {d}B_\mathrm{B}/\hbox {d}z, (1-A_\mathrm{B})\hbox {d}B_\mathrm{B}/\hbox {d}z\nonumber \\&\quad +B_\mathrm{B} \hbox { d}A_\mathrm{B}/\hbox {d}z]\int _{z}^{1} w_{0} \hbox {d}z+{\phi }_{\mathrm{ap}} [(1-A_\mathrm{B1})(1-B_\mathrm{B})\nonumber \\&\quad -A_\mathrm{B} B_\mathrm{B1}, (1-A_\mathrm{B1})B_\mathrm{B}-B_\mathrm{B1} (1-A_\mathrm{B})]\}/(1-A_\mathrm{B}-B_\mathrm{B}), \end{aligned}$$

(16g)

where ${\phi }_{\mathrm{ap}}$ is the value at $z=1$ of ${\phi }_{\mathrm{a}(-1)}$ in the primary mushy layer given in (15d), $A_\mathrm{B1}$ is the value at $z=1$ of $A_\mathrm{B}, B_\mathrm{B1}$ is the value at $z=1$ of $B_\mathrm{B}$, and for later references the expressions for the z-dependent coefficients for $u_{0}, v_{0}, w_{0}$, and $T_{0}$ in the above equations will be designated by $f_{i}$ ($i=9, 10, 11, 12$), respectively, and $P_{0}^{\prime \prime }$ is the $z$-dependent coefficient for $P$ in (16d). In addition, the unknown constants $b_{m}$ ($m=17, 18, \ldots , 24$) satisfy a set of lengthy linear algebraic equations, which are not given here.

We consider the 25 linear algebraic equations for the unknown constants $b_{m} (m=0, 1, \ldots , 24)$, whose expressions are lengthy and will not be given here. These equations can be written in matrix form like $M\,\mathbf{b}=0$, where $\mathbf{b}\equiv (b_{0}, b_{1}, \ldots , b_{24})^\mathrm{T}$ is the vertical vector of the unknown constants, whose components are the 25 unknown scalar constants, and $M$ is the matrix of coefficients of these 25 constants in the 25 equations. Setting ${\vert }M{\vert }=0$, where ${\vert }M{\vert }$ is the determinant of this matrix, we obtain by successive elimination approach a very lengthy form for the eigenvalue relation for the marginal stationary stability problem. For simplicity, the relation is in the form of an equation like

$$\begin{aligned} D(R_\mathrm{p0}, R_\mathrm{s0}, {\alpha }, L, l, d_\mathrm{a}, T^\mathrm{s}, T^\mathrm{L})=0. \end{aligned}$$

(17)

For given values of the constants $T^\mathrm{s}$, $l$, $d_\mathrm{a}$, $L$, and $T^\mathrm{L}$, this equation is a function of two effective mush Rayleigh numbers and the wave number at the onset of motion. Using iterative procedure, we then determine the relation between the two Rayleigh numbers for each given admissible value of the wave number, and consequently the critical conditions at the onset of motion can be found. It should also be noted that since the system of the 25 unknown constants $b_{m}$ ($m=0, 1, \ldots , 24$) is a linear homogeneous algebraic system of 25 equations for these unknowns, the solution for each of these unknowns can be written in terms of one of these constants that we have chosen to be $b_{1}$. This is due to the linearity property of this system.

3.4 Adjoint Systems

In order to compute the solvability condition for the non-linear systems, which can provide a non-linear evolution equation as well as an equation involving the non-linear coefficients $R_\mathrm{p1}$ and/or $R_\mathrm{s1}$ in the expansions (5f) for the mush Rayleigh numbers, the solutions to the adjoint problem of the linear system for the small perturbations are required. It turns out that the linear adjoint systems are needed here only to the leading order terms in ${\delta }$. As we also noted in the first paragraph in Sect. 3.3, it turns out to be sufficient that the adjoint problem to be presented here only by the following system for vertical volume flux, pressure, and temperature whose symbols are designated with a superscript “(a)”:

In the liquid layer we have

$$\begin{aligned}&\displaystyle d_\mathrm{a} {\nabla }^{2}\mathbf{u}^{(\mathrm{a})}={\nabla }P^{(\mathrm{a})}+T^{(\mathrm{a})} (\hbox {d}T_{\mathrm{B}}/\hbox {d}z) \mathbf{z},\end{aligned}$$

(18a)

$$\begin{aligned}&\displaystyle {\nabla }.\mathbf{u}^{(\mathrm{a})} =0,\end{aligned}$$

(18b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T^{(\mathrm{a})} = 0, \end{aligned}$$

(18c)

$$\begin{aligned}&\displaystyle T^{(\mathrm{a})}=\mathbf{u}^{(\mathrm{a})}0\;\hbox {at}\;z=L,\end{aligned}$$

(18d)

$$\begin{aligned}&\displaystyle [T^{(\mathrm{a})}]=[{\partial }T^{(\mathrm{a})}/{\partial }z]=[\mathbf{u}^{(\mathrm{a})}]=[P^{(\mathrm{a})}]\;\hbox {at}\;z=l. \end{aligned}$$

(18e)

In the primary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}^{(\mathrm{a})} ={\nabla }P^{(\mathrm{a})}+T^{(\mathrm{a})}(\hbox {d}T_{\mathrm{B}}/\hbox {d}z) \mathbf{z},\end{aligned}$$

(19a)

$$\begin{aligned}&\displaystyle {\nabla }.\mathbf{u}^{(\mathrm{a})}=0, \end{aligned}$$

(19b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T^{(\mathrm{a})}= -R_\mathrm{p0} w^{(\mathrm{a})},\end{aligned}$$

(19c)

$$\begin{aligned}&\displaystyle [T^{(\mathrm{a})}]=[{\partial }T^{(\mathrm{a})}/{\partial }z]=[\mathbf{u}^{(\mathrm{a})}]=[P^{(\mathrm{a})}]= T^{(\mathrm{a})}{\vert }^{+}=0\;\hbox {at}\;z=1. \end{aligned}$$

(19d)

In the secondary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}^{(\mathrm{a})}={\nabla }P^{(\mathrm{a})}+T^{(\mathrm{a})}(\hbox {d}T_\mathrm{B}/\hbox {d}z) \mathbf{z},\end{aligned}$$

(20a)

$$\begin{aligned}&\displaystyle {\nabla }.\mathbf{u}^{(\mathrm{a})}=0,\end{aligned}$$

(20b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T^{(\mathrm{a})}= -R_\mathrm{s0} w^{(\mathrm{a})},\end{aligned}$$

(20c)

$$\begin{aligned}&\displaystyle T^{(\mathrm{a})}=w^{(\mathrm{a})}=0\;\hbox {at}\;z=0. \end{aligned}$$

(20d)

Since it turns out that only the explicit form of the adjoint solution for the temperature and the vertical flux are needed to form the solvability condition, we provide such explicit form of solution in each of the three layers. From the system (18a–18e) for the liquid layer, we find

$$\begin{aligned} T^{(\mathrm{a})}&= [g_{0} \,\exp ({\alpha }z)+g_{1} \,\exp (-{\alpha }z)]H(x, y),\end{aligned}$$

(21a)

$$\begin{aligned} w^{(\mathrm{a})}&= \{[g_{2} z-(\hbox {d}T_\mathrm{B}/\hbox {d}z)g_{0} z^{2}/(8l_{0})]\exp ({\alpha }z)+[g_{3} z\nonumber \\&-(\hbox {d}T_\mathrm{B}/\hbox {d}z)g_{1} z^{2}/(8l_{0})]\exp ({\alpha }z)]\}H(x, y), \end{aligned}$$

(21b)

where for later references the $z$-dependent coefficients for $T^{(\mathrm{a})}$ and $w^{(\mathrm{a})}$ in (21a, 21b) will be designated by $T_\mathrm{a1} (z)$ and $w_\mathrm{a1} (z)$, respectively; the unknown constants $g_{m}$ ($m=0, 1, 2, 3$) satisfy a set of lengthy algebraic equations, which are not given here. From the system (–) and (18e) for the primary mushy layer, we find

$$\begin{aligned} (w^{(\mathrm{a})}, T^{(\mathrm{a})})&= \{(g_{4}, g_{8})\exp [({\gamma })^{0.5} z]+(g_{5}, g_{9})\exp [-({\gamma })^{0.5} z]+(g_{6}, g_{10})\exp [({\gamma }_{0})^{0.5} z]\nonumber \\&+(g_{7}, g_{11})\exp [-({\gamma }_{0})^{0.5} z]\}H(x, y), \end{aligned}$$

(22)

where for later references the $z$-dependent coefficients for $w^{(\mathrm{a})}$ and $T^{(\mathrm{a})}$ in (22) are designated by $w_\mathrm{a2}$ and $T_\mathrm{a2}$, the unknown constants $g_{m}$ ($m=4, \ldots , 11$) satisfy another set of lengthy algebraic equations that are not given here. From the equations (20a–20d) and (19d) for the secondary mushy layers, we find

$$\begin{aligned} (w^{(\mathrm{a})}, T^{(\mathrm{a})})&= \{(g_{12}, g_{16})\exp [({\gamma }_{1})^{0.5} z]+(g_{13}, g_{17})\exp [-({\gamma }_{1})^{0.5} z]\nonumber \\&+\,(g_{14}, g_{18})\exp [({\gamma }_{2})^{0.5} z]+(g_{15}, g_{19})\exp [-({\gamma }_{2})^{0.5} z]\nonumber \\&+\, (0, g_{20})\exp (-{\alpha }z)\}H(x, y)\equiv \sum [w_\mathrm{a}(z), T_\mathrm{a} (z)]E_{n}\,{\eta }_{n} (x, y), \end{aligned}$$

(23)

where for later references the $z$-dependent coefficients for $w^{(\mathrm{a})}$ and $T^{(\mathrm{a})}$ in (23) are designated by $w_\mathrm{a3}$ and $T_\mathrm{a3}$ and the unknown constants $g_{m}$ ($m=12, \ldots , 20$) satisfy a next set of lengthy algebraic equations that are not given here. The system of 20 equations for the $g_{m}$ ($m=1, \ldots , 20$) was then solved by a successive elimination method for given value of $g_{0}$, which is admissible due to the linearity of this system.

In addition for later use, we also designate the following form for the adjoint solution for the flux vector and the pressure in each of the three layers:

$$\begin{aligned}{}[\mathbf{u}^{(\mathrm{a})}, P^{(\mathrm{a})}]=\sum _{n=-N}^{N} [\mathbf{u}_\mathrm{a} (z, n), P_\mathrm{a}(z)]E_{n}\,{\eta }_{n} (x, y). \end{aligned}$$

(24)

As will be seen in the next subsection, such designation (24) will be needed to form the solvability condition, even though the explicit expressions for (24) will not be needed.

3.5 Non-linear Problem

Next, we analyze the non-linear problem for the governing systems (1a–1g)–(3a–3j) at order $\varepsilon ^{2}$. The solutions to these systems are very lengthy and will not be presented here. The systems for the dependent variables $\mathbf{u}, P$, and $T$ at $O(\varepsilon ^{2})$, which are needed to form the solvability condition, are given by (37a–37e)–(39a–37d) in Appendix. The solvability condition for the non-linear system requires the following special solutions $\mathbf{u}_{\mathrm{an}}$, $P_\mathrm{an}$, and $T_\mathrm{an}$ of the adjoint system in each of the three layers:

$$\begin{aligned} (\mathbf{u}_{\mathrm{an}}, P_\mathrm{an}, T_\mathrm{an})=([\mathbf{u}_\mathrm{a} (z, n), P_\mathrm{a}(z), T_\mathrm{a}(z)]E_{n}\,{\eta }_{n} (x, y). \end{aligned}$$

(25)

Consider the systems (37a–37e), (38a–38d), and (39a–39d) given in the appendix. First, we consider the liquid layer. Taking dot product of the equation (37a) by $\mathbf{u}_{\mathrm{an}}$, multiplying the equation (37b) by $P_\mathrm{an}$ and (37c) by $T_\mathrm{an}$, adding, applying integration by parts, using the boundary conditions (37d, 37e) and (18d, 18e), and averaging over the liquid layer, we obtain an integral equation which also contains several terms evaluated at the primary mush–liquid interface. We refer to this resulting equation as $I_\mathrm{L} =0$. Now we consider the primary mushy layer. Taking dot product of Eq. (38a) by $\mathbf{u}_{\mathrm{an}}$, multiplying the equation (38b) by $P_\mathrm{an}$ and (38c) by $T_\mathrm{an}$, adding, applying the integration by parts, using the boundary conditions (38d) and (19d), and averaging over the primary mushy layer, we find an integral equation which also contains several terms evaluated at the primary mush–liquid and primary mush–secondary mush interfaces. We refer to this resulting equation as $I_\mathrm{P} =0$. Similarly, we consider the secondary mushy layer. Taking dot product of Eq. (39a) by $\mathbf{u}_{\mathrm{an}}$, multiplying (39b) by $P_\mathrm{an}$ and (39c) by $T_\mathrm{an}$, adding, applying the integration by parts, using the boundary conditions (39d) and (20d), and averaging over the secondary mushy layer, we find a third integral equation, referred to here as $I_{S} =0$, which also contains several terms evaluated at the secondary mush–primary mush interface. Next, we simplify the equation $I_\mathrm{L}+I_\mathrm{P}+I_{S} =0$ using the adjoint equations and the boundary conditions for both adjoint systems and the finite amplitude systems at $o(\varepsilon ^{2})$. This leads to the solvability condition for the present ternary system which is simplified to the form

$$\begin{aligned} (R_\mathrm{p1} S_{2}+R_\mathrm{s1} S_{4}){\vert }E_{n}{\vert }^{2}&=\sum _{p, q=-N}^{N} (S_{lpq}+S_{3pq}+S_{5pq})E_{n}\, E_{p}\, E_{q} \langle {\eta }_{n} {\eta }_{{p}} {\eta }_{\mathrm{q}}\rangle ,\nonumber \\&\quad \times (n= -N, \ldots , -1, 1, \ldots , N), \end{aligned}$$

(26)

where an angular bracket indicates an average over the horizontal plane, and the expressions for the quantities $S_{1pq}, S_{2}, S_{3pq}, S_{4}$, and $5_{5pq}$ are given by (40a–40e) in the appendix. The right-hand side of (26) is zero, unless

$$\begin{aligned} {\alpha }_{n}+{\alpha }_{{p}}+{\alpha }_{\mathrm{q}} =0, \end{aligned}$$

(27)

for at least some $p$ and $q$. The condition (27) can be satisfied in the case where convection is in the form of hexagons ($N=3$), which is the focus of present study.

For convective flow in the form of hexagons ($N=3$), where (27) holds and $E_{n}=(1/6)^{0.5}$, (26) becomes

$$\begin{aligned} R_\mathrm{p1}=S_{9} R_\mathrm{s1} -S_{10}, S_{9}\equiv -S_{4}/S_{2}, S_{10} \equiv -[2/(6)^{0.5}](S_{1}+S_{3}+S_{5})/S_{2}, \end{aligned}$$

(28a)

where $S_{1}, S_{3}$, and $S_{5}$ are the expressions for $S_{1pq}, S_{3pq}$, and $S_{5pq}$ evaluated at ${\Phi }_{pq} = -1/2$ and

$$\begin{aligned} {\phi }_{pq} \equiv \varvec{{\alpha }}_{p}\cdot \varvec{{\alpha }}_{\mathrm{q}}/{\alpha }^{2}. \end{aligned}$$

(28b)

It can be seen from the above description for $S_{1}, S_{3}$, and $S_{5}$ and the expressions given in (40a–40e) that $S_{1}$ is due to the liquid layer, $S_{2}$–$S_{3}$ are due to the primary mushy layer, and $S_{4}$–$S_{5}$ are due to the secondary mushy layer. We numerically calculated $S_{1}$–$S_{5}$ using Simpson’s Rule (Isaacson and Keller 1966) for several cases, which are presented and discussed in the next section.

As we noted earlier in Sect. 3.3, the linear solutions for the dependent variables depend on the arbitrary constant $b_{1}$. Hence, non-linear solutions at $O(\varepsilon ^{2})$ for the dependent variables are also dependent on $b_{1}$. As a kind of normalization procedure, we kept a fixed magnitude for this constant in each case of calculation and found two distinct non-linear solutions depending on whether this constant is positive or negative.

3.6 Non-linear Evolution Problem

Similar to the work in Roper et al. (2008) for the binary system case, we first write all the dependent variables at $O(\varepsilon )$ in the three layers in terms of an unknown amplitude function $C(\tau )$ so that, for example, the expression for the vertical flux (12a) in the liquid layer can be in the form

$$\begin{aligned} w_{0}=C(\tau )\sum _{n=-N}^{N} f_{3} E_{n}\,{\eta }_{n} (x, y), \end{aligned}$$

(29)

where in the case of hexagonal planforms (Busse 1978) $N=3$, amplitude of each of the three modes $C(\tau )E_{n} (n=1, 2, 3)$ in (29) are equal to $C(\tau )[1/(6)^{0.5}$], and the slowly varying time $\tau$ (Roper et al. 2008) is defined here by $\tau ={\vert }\varepsilon {\vert }t$. It should be noted that here the amplitude function $C(\tau )$ is taken as real since in our actual calculation of various quantities, we made each solution real by making use of real functions, even though the formal expressions of various solutions provided in this paper have z-dependent complex coefficients. We provided such formal expressions since the equivalent real expressions were found to be more lengthy and different for different investigated cases and so were not instructional to be provided for the readers.

Next, following a similar procedure to that described in Sect. 3.5 to form the solvability condition at $O(\varepsilon ^{2})$, we find the following result:

$$\begin{aligned} {\gamma }(S_{6}+S_{7}+S_{8})(\hbox {d}C(\tau )/\hbox {d}\tau )=(R_\mathrm{p1} S_{2}+R_\mathrm{s1} S_{4})C -[2/(6)^{0.5}](S_{1}+S_{3}+S_{5})C^{2}, \end{aligned}$$

(30)

where ${\gamma }=1$ for $\varepsilon >0$ and -1 for $\varepsilon <0$, and the expressions for the quantities $S_{6}$–$S_{8}$ are given by (41) in the Appendix.

The solution to the non-linear equation (30) can be readily found to be

$$\begin{aligned} (C/C_{0})=M \,\exp (M \tau /\theta )/[(M-{\lambda }C_{0})+{\lambda }C_{0} \,\exp (M \tau /\theta )], \end{aligned}$$

(31a)

where $C_{0}$ is some initial condition for $C$,

$$\begin{aligned} M\equiv (R_\mathrm{p1} S_{2}+R_\mathrm{s1} S_{4}), \theta \equiv {\gamma }(S_{6}+S_{7}+S_{8}), \lambda \equiv [2/(6)^{0.5}](S_{1}+S_{3}+S_{5}). \end{aligned}$$

(31b)

Here the quantities $M, \theta$, and $\lambda$ in (31b) are given in terms of the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$ and the $S_{1}$–$S_{8}$ whose numerical values are given for different cases in Sect. 4. The time-dependent evolution of the finite amplitude solution can then be determined by the way the amplitude function $C$ can vary in the slow time $\tau$. However, if the initial value of the amplitude takes the value $M/\lambda$, then (31a) implies that $C=C_{0}$ for all times so that a constant amplitude prevails here for all times in this case.

It can be seen from (31a, 31b) that asymptotic solutions for $C$ as $\tau \rightarrow \infty$ can be

$$\begin{aligned}&C{\rightarrow }M/{\lambda }\hbox { as }\tau \rightarrow \infty \hbox { for }M/\theta >0\hbox { if }M/({\lambda }C_{0})>0,\end{aligned}$$

(32a)

$$\begin{aligned}&C{\rightarrow }0\hbox { as }\tau \rightarrow \infty \hbox { for }M/\theta <0\hbox { if either }M/({\lambda }C_{0})>1\hbox { or }M/({\lambda }C_{0})<0. \end{aligned}$$

(32b)

The solution in (32a) is the equilibrium solution for the amplitude $C$ of the finite-amplitude solution, which we take into account to determine the steady finite amplitude solutions. It can be seen from (31b) and (32a) that, for given parameter values, the equilibrium solution cannot exist if both Rayleigh numbers are too close to their respective critical values.

It should be noted that there are also conditions under which solution can break down after a finite time, so that

$$\begin{aligned} {\vert }C{\vert }\rightarrow \infty \hbox { as }\tau \rightarrow (\theta /\,M) \,ln\, [1-M/(\lambda \,C_{0})], \end{aligned}$$

(33a)

provided if

$$\begin{aligned} (\theta /M)<0\hbox { and }0<M/({\lambda }C_{0})<1, \end{aligned}$$

(33b)

or

$$\begin{aligned} (\theta /M)>0\hbox { and }M/(\lambda \,C_{0})<0. \end{aligned}$$

(33c)

It can be seen that the finite time given in (33a), as ${\vert }C{\vert }\rightarrow \infty$, depends on the initial condition $C_{0}$ of $C$, and this initial condition needs to be in particular domain either in (33b) or (33c). It is suggested (Landau and Lifshitz 1987) that in this case for subcritical flow in a shear flow or convection problem there should be a lower critical $R_{G}$ of the corresponding effective controlling parameter below which the bifurcated solution does not exist so that the value of ${\vert }C{\vert }$ begins to increase in the subcritical domain with the effective controlling parameter (Drazin and Reid 1981). It is expected that the motionless basic state is globally asymptotically stable with respect to all disturbances for the effective controlling parameter less than $R_{G}$.

In the previous investigations of amplitude equations, the interest had been on the stability of the equilibrium solutions (Anderson and Worster 1995; Chung and Chen 2000), despite the existence of some solutions of those equations that could break down under certain initial conditions. Similarly, in the present study the equilibrium solution (32a), which can possibly lead to a stable hexagonal solution, is of interest. We investigate its linear stability using the amplitude equation approach (Chung and Chen 2000). We superpose a small perturbation amplitude $c(\tau )$ onto the solution (32a), use the resulting sum and (31b) in (30), subtract the equation for the equilibrium solution from the resulting equation for ($M/\lambda +c$), and linearize the subsequent equation with respect to $c$. We also assume $c=a\,\exp (\sigma \tau )$, where $a$ is a constant and $\sigma$ is the growth rate of the perturbation. Then the equation for such perturbation amplitude reduces to the condition

$$\begin{aligned} \sigma = -M/\theta , \end{aligned}$$

(34a)

so that equilibrium solution is stable if

$$\begin{aligned} M/\theta >0. \end{aligned}$$

(34b)

We calculated values of the quantities $S_{6} -S_{8}$ given in (41) using a Simpson’s Rule for several cases under the condition (32a) for the equilibrium solution, which are presented and discussed in the next section. As we explained in Sect. 3.5, we have found two distinct non-linear solutions for given fixed values of the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$, and it turns out that for all the calculations that we carried out for different cases (34b) is satisfied only for one of these solutions. So subjected to (30), one of the two solutions is stable and another unstable.

4 Results and Discussion

Following Anderson and Schulze (2005), we consider zero thermal Rayleigh number and a fully compositionally symmetric ternary phase diagram, where $A^\mathrm{E}=B^\mathrm{E} =1/3, M_\mathrm{b} =0, M_\mathrm{a}=M_\mathrm{ac}=M_\mathrm{bc} =1/(A^\mathrm{P} -1/3), A^\mathrm{P}=A^\mathrm{L} =0.37$, and $B^\mathrm{P}=B^\mathrm{L} =0.35$. These values, which do not affect the main systems, were found to be typical for our calculations. We also tried different values for $A^\mathrm{L}$ and $B^\mathrm{L}$ and found no change on the qualitative behavior of the solutions for the solid fractions. About the effects of the Darcy parameter, we calculated the results for several values of $d_\mathrm{a}$ and found that its higher value has a slight stabilizing effect, which is consistent with its increasing frictional role in the liquid layer. Hence, for the finally produced results and figures, we kept the value of $d_\mathrm{a}$ at 0.8. We focused our study on several different values of the constants $T^\mathrm{L}, T^\mathrm{s}, L$, and $l$ that were found to affect the results due to the main systems. However, due to the constraints (7f) and (8f), given values for two of these constants determine the values of the other two constants. Thus, we provide here three base-state parameter values (Table 1), which are found to be representative under which the main results of the present study are determined.

It should also be noted that $\delta$, which is the thickness of the secondary mushy layer, is one of the assumed small perturbation parameter that is used in the expansion procedure (5a, 5b, 5c, 5d, 5e, 5f) and is also used to determine the basic state solutions up to $o (\delta ^{2})$.

4.1 Motionless Basic State

We generated data for the motionless basic state based on (6a–6c)–(8a–8e) for the base state I (Table 1), which turns out to provide typical results for the temperature, compositions, and solid fractions. As can be seen from (6a–6c) to (8a–8e), the basic state solutions are all independent of the mush Rayleigh numbers. Our generated data indicated that the basic state temperature is continuous due to the zero jump conditions for the temperature across the interfacial boundaries. As expected physically, the basic state temperature was found to increase with the vertical variable. The temperature profile is slightly non-linear due to the second-order contribution of $\delta$ in the expressions for the basic state temperature. Since $\delta$ represents a length scale for the thickness of each of the three layers as well as the thickness of the secondary mushy layer, we also generated data for $T_\mathrm{B}$ for two different values of $\delta$ to see the effect of such length scale and found that the basic state temperature increases with $\delta$.

Our generated data for the basic state compositions $A_\mathrm{B}$ and $B_\mathrm{B}$ versus $z$ indicated that both compositions increase vertically in the secondary mushy layer. In the primary mushy layer the composition $A_\mathrm{B}$ increases with $z$, while $B_\mathrm{B}$ decreases with increasing $z$. In the liquid layer both compositions are constant. Note that due to the symmetry of the phase diagram, both compositions are found to be equal at the interface between the primary and secondary mushy layers as well as at the eutectic front. Our generated data for different values of $\delta$ indicate that the basic state compositions increases with $\delta$.

Our calculation for the basic state solid fractions ${\phi }_{\mathrm{aB}}$ and ${\phi }_{\mathrm{bB}}$ as well as the sum ${\phi }_{\mathrm{aB}}+{\phi }_{\mathrm{bB}}$ indicated that these decrease with increasing $z$ in the secondary mushy layer, but rate of decrease with respect to $z$ for ${\phi }_{\mathrm{bB}}$ is higher. Due to the structure of each mushy layer, there is no solid fraction for composition $B$ in the primary mushy layer (${\phi }_{\mathrm{bB}} =0$). The solid fraction ${\phi }_{\mathrm{aB}}$ also decreases with increasing $z$ in the primary mushy layer. The positive rate of decrease of the solid fraction ${\phi }_{\mathrm{bB}}$ in the secondary mushy layer is due to the zero value of this solid fraction in the primary mushy layer and the highest value at the solid–secondary mushy layer interface.

4.2 Linear Stability

The eigenvalue relation (17) for the onset of motion was calculated by applying an iterative procedure for fixed values of the constants in each of the base states I, II, and III listed in Table 1 as well for other cases with different values of the constants, and we found qualitatively similar results. For given values of the constants in (17), this equation is a function of two effective Rayleigh numbers and the wave number. Typical reported results here are for the base state I. Using the iterative procedure we consider three specific convection scenarios and determine the relation between the two Rayleigh numbers at the onset of motion for each given admissible value of the wave number.

(i) Case 1 Here we assume that convection at the onset of motion is driven equally from both mushy layers ($R_\mathrm{p}=R_\mathrm{s}$). We generated data for the neutral stability curve, and the numerical values of the critical Rayleigh numbers and the wave number at the lowest point on this curve are found to be $R_\mathrm{pc}=R_\mathrm{sc}=9.38$ and ${\alpha }_{\mathrm{c}}=1.54$. Our results are in qualitative agreement with the numerical results due to Anderson and Schulze (2005) using a pseudo-spectral Chebyshev method.

(ii) Case 2 Here we assume that convection at the onset of motion is driven mainly from the primary mushy layer ($R_\mathrm{s0} =0.00001$). We generated data for the neutral stability curve for this case. Numerical values of the critical primary mush Rayleigh number and the wave number at the lowest point on this curve are found to be $R_\mathrm{pc}=9.40$ and ${\alpha }_{\mathrm{c}}=1.56$, which are also in qualitative agreement with those for $R_\mathrm{s}=0$ given in Anderson and Schulze (2005). We also calculated this case for $R_\mathrm{s0}=0$ by implementing different analytical expressions for the solutions in the primary mushy layers, and we found that the results remain unchanged as compared with those for $\hbox {R}_{\mathrm{s}0}=0.00001$. The results indicate that the critical values for the primary mush Rayleigh number and the wave number are very slightly higher if convection is insignificant in the secondary mushy layer. This result is reasonable since less flow efforts can be stabilizing.

(iii) Case 3 Here we assume that convection at the onset of motion is driven mainly from the secondary mushy layer ($R_\mathrm{p0} =0.00001$). We generated data for the neutral stability curve. Numerical values of the critical secondary mush Rayleigh number and the wave number at the lowest point on this curve are found to be $R_\mathrm{sc} =60.78$ and ${\alpha }_{\mathrm{c}} =3.12$. Again we found qualitative agreement with those for $R_\mathrm{p} =0$ given in Anderson and Schulze (2005). We also calculated this case for $R_\mathrm{p0} =0$ by implementing different analytical expressions for the solutions in the secondary layer and found that the results remain unchanged as compared with those for the case $R_\mathrm{p0} =0.00001$. Here the critical conditions are significantly higher than those for the previous 2 cases (i)–(ii).

From the linear results presented above, it can be seen that convective flow in the primary mushy layer is more significant than that in the secondary mushy layer, which appear reasonable since the primary mushy layer contains solid dendrites due to only composition $A$; while the secondary mushy layer contains solid dendrites due to both compositions $A$ and $B$, even though the secondary mushy layer is adjacent to the solidification front. In addition, the flow significantly stabilizes and is of the lower horizontal wavelength if the flow is driven mainly from the secondary mushy layer.

4.3 Non-linear Problem

We numerically evaluated the expressions for $S_{1}$–$S_{10}$, which were defined in Sects. 3.5 and 3.6, using Simpson’s Rule (Isaacson and Keller 1966) for each of the three base states I–III (Table 1) and for the two detected solutions noted in the Sects. 3.5 and 3.6. In addition to these calculations, we also generated data for several other cases and found that the sign of the values for these expressions remain unchanged for each of the two solutions. Tables 2, 3, and 4 present numerical values of $S_{1}$–$S_{8}$ for the three base states I–III, respectively, for the stable type solution that satisfies (33b), and each of these tables provides also the corresponding values for three cases of $R_\mathrm{p}=R_\mathrm{s}$, $R_\mathrm{s} =0$, and $R_\mathrm{p}=0$, which are referred to here, respectively, as the cases (i)–(iii). Since each of these three cases corresponds to different critical onset parameters that enter the solvability condition, we had to carry out separate calculation for each case to determine the values of $S_{1}$–$S_{8}$. It can be seen that Tables 2, 3, and 4 also provide values for the critical onset conditions as well as for the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$ for each of the above three cases. We also calculated the expressions for $S_{1}$–$S_{8}$ in each of the three cases for the unstable solution and found that the magnitudes of $S_{1}$–$S_{8}$ as well as the signs of $S_{1}, S_{3}$, and $S_{5}$ remain unchanged, but the sign of the expressions for $S_{2}, S_{4}$, and $S_{6}$–$S_{8}$ are changed.

Case (i) Convective flow is driven equally both at the onset and beyond from both mushy layers ($R_\mathrm{p}=R_\mathrm{s})$. We calculated the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$, volume flux, and the solid fraction for the stable finite amplitude solution, which satisfies the condition (34b), for various values of the parameters for the base states I–III in Table 1 and also for other cases for $\delta =0.5$ and ${\vert }\varepsilon {\vert }=0.03$, which is found to be the maximum value of ${\vert }\varepsilon {\vert }$ beyond which the total solid fraction (basic state plus the perturbation) becomes negative and subsequently physically unrealistic. The values of $R_\mathrm{p1}$ and $R_\mathrm{s1}$ for the stable solution, which were found to be the case for $\varepsilon >0$, are given in Tables 2, 3, and 4 for the base states I–III, respectively. Hence, stable flow was found to be supercritical. Comparing the results given in Tables 2, 3, and 4 for the base states I–III, we find that flow is more supercritical for higher values of either the thickness of the primary mushy layer or the temperature at the top of the liquid layer.

-24pt

Table 2 Values of $S_{1}$–$S_{8}$ for the base state I and for 3 cases $R_\mathrm{p}=R_\mathrm{s}, R_\mathrm{s} =0$, and $R_\mathrm{p} =0$

Table 3 The same as in Table 2 but for the base state II

Table 4 The same as in Table 2 but for the base state III

Typical results are presented in Figs. 2 and 3 for the vertical distribution of vertical volume flux and total solid fraction and for the base state I at center and a node of a hexagonal cell. As is expected and we also inspected that the results to be reported in this paper at center and a node of a cell are representative for center and node of any cell. It can be seen from Fig. 2 that in the secondary mushy layer flow is downward at the cell center and upward at the node, and the magnitude of the vertical flux increases with $z$ both at the center and at the node. In the primary mushy layer up to the horizontal level about $z=1.282$ flow is downward at the cell center and upward at the node, but now the magnitude of the vertical flux decreases with increasing $z$ and becomes zero at the level $z=1.282$. From this level to top of the primary mushy layer, the flow is upward at the cell center and downward at the node, and the magnitude of the vertical flux increases with $z$ both at the center and at the node. In the liquid layer the flow direction remains the same as in the upper section of the primary layer for $z>1.282$, but now magnitude of the vertical flux decreases with increasing $z$. So double cellular structure in the vertical direction is evident from these results with down-hexagons in the lower region and up-hexagons in the upper region of the ternary system.

Figure 3 presents total solid fraction versus $z$ at center and a node of a cell. It can be seen and implied from this figure as well as from the actual generated data that there is solid fraction reduction, referred to hereafter as tendency for chimney formation, that varies with respect to $z$ and exists in both mushy layers. In the secondary mushy layer such tendency for chimney formation initiates at different horizontal locations of the bottom of the layer, is along the vertical direction, and it first increases slightly and then decreases with increasing $z$ until it becomes negligible at the top of the secondary layer. These horizontal locations are the vertical projections of the nodes of the down-hexagonal cells on the bottom of the secondary layer. In the primary mushy layer the tendency for vertically oriented chimneys formation begins on the internal horizontal level $z =1.282$ between the two cellular flow structures. Below this internal level such tendency decreases with decreasing $z$ until it is negligible on the bottom of the primary layer, while above this level such tendency increases first slightly before decreases with increasing $z$ until it ends at the top of the layer. The horizontal locations of tendency for chimney formation in the primary mushy layer, which are vertical projections of centers of down-hexagons and up-hexagons on this level, are all, in general, different from those in the secondary mushy layer. The amount of solid fraction reduction in the primary mushy layer are relatively less than those in the secondary mushy layer, but the tendency for chimney formation is again vertically oriented at discrete locations and over this layer such tendency first increases and then decreases with increasing $z$.

Fig. 2

Vertical volume flux versus $z$ at center of a cell (solid line) and at a node of the same cell (dashed line) for base state I listed in Table 1 and $R_\mathrm{p}=R_\mathrm{s}$ case. Here $\varepsilon =0.03$ and $\delta =0.5$. Dotted lines indicate interfaces, and dash-dot line represents the level that separates the two vertical cellular structures

Case (ii) Convection is driven both at the onset and beyond by the primary mushy layer ($R_\mathrm{s}=0$). We calculated the non-linear coefficient $R_\mathrm{p1}$, volume flux, and the solid fraction for the stable solution for various values of the parameters and for the three base states in Table 1 for $\delta =0.5$ and ${\vert }\varepsilon {\vert }=0.01$, which is found to be the maximum value of ${\vert }\varepsilon {\vert }$ beyond which total solid fraction becomes negative and, thus, physically meaningless. The values of $R_\mathrm{p1}$ for the stable solution, which was found to be the case for $\varepsilon >0$, are given in Tables 2, 3, and 4 for the base states I–III, respectively. Hence, we found that the stable flow is supercritical. Comparing the results given in Tables 2, 3, and 4 for the base states I–III, we found that flow is more supercritical for higher values of thickness of the primary mushy layer or the temperature on top of liquid layer.

Fig. 3

Total solid fraction versus $z$ at center (solid line), a node (dashed line) of a cell for basic state I listed in Table 1 and $R_\mathrm{p}=R_\mathrm{s}$ case. Here $\varepsilon =0.03, \delta =0.5$, and the basic state total solid fraction is also given (dotted line) for comparison

Typical results are presented in Figs. 4 and 5 for the vertical distribution of the vertical volume flux and total solid fraction for the base state I at center and a node of a hexagonal cell. It can be seen from Fig. 4 that in the secondary mushy layer flow is upward at the center of the cell and downward at the node. The magnitude of the vertical flux increases with $z$ both at the center and the node. In the primary mushy layer and the liquid layer the results shown in this figure as well as from our additional generated data indicate that flow continues to be upward at the center in the lower part of the primary mushy layer up to the horizontal level $z=1.285$, beyond which the flow is downward. At the node of the cell flow direction is opposite to that at the center. At $z=1.285$, the vertical flux is zero. The magnitude of the vertical flux decreases with increasing $z$ both at the center and the node in the lower part of the primary mushy layer for $1<z<1.285$ and also in the liquid layer, while the magnitude of the vertical flux increases with $z$ both at the center and the node in the upper part of the primary mushy layer for $1.54>z>1.285$. These results indicate the presence of double-cell structure in the vertical direction with down-hexagons above up-hexagons.

Figure 5 presents total solid fraction versus vertical variable at center and a node of a cell, and it also shows vertical distribution of the basic state solid fraction. It can be implied from this figure as well as from the quantitative values of the generated data that in the secondary mushy layer the tendency for chimney formation is initiated at the bottom of the layer. Then, it takes place at different horizontal locations, which are vertical projections of centers of up-hexagons on the bottom of the secondary layer, and such tendency is along the vertical direction but first increases slightly before it decreases with increasing $z$ until it becomes negligible at top of the layer. In the primary mushy layer the tendency for chimney formation begins on the internal horizontal level $z=1.285$. This is the level between the two cellular flow structures, where chimney formation begins at different horizontal locations, which are vertical projections of the nodes of up-hexagons and down-hexagons on this level, and are all, in general, different from those in the secondary mushy layer. Such tendency, which is relatively less than the one in the secondary mushy layer, is again vertically oriented, first slightly increases and then decreases with increasing $z$ for $z>1.285$ and decreases with decreasing $z$ for $1<z<1.285$. Again as in the case (i), the tendency for chimneys formation in each of the mushy layers takes place at different vertically oriented locations and the vertical extension of each chimney is limited within each mushy layer.

Case (iii) Convection is driven both at the onset and beyond from the secondary mushy layer ($R_\mathrm{p}=0$). We calculated the non-linear coefficient $R_\mathrm{s1}$, volume fluxm and the solid fraction for the stable finite amplitude solution which satisfies the stability condition (34b) for various values of the parameters and for those of the base states I–III in Table 1 for $\delta =0.5$ and ${\vert }\varepsilon {\vert }=0.03$, which is found to be the maximum accepted value of ${\vert }\varepsilon {\vert }$ above which the total solid fraction is negative. The values of $R_\mathrm{s1}$ for the stable solution, which were found to be for $\varepsilon >0$, are given in Tables 2, 3, and 4 for the base states I–III, respectively. Hence stable flow is subcritical. Comparing the results given in Tables 2, 3, and 4 for the base states I–III, we find that the flow is more subcritical if the value of the primary mushy layer’s thickness or the temperature at the top of the liquid layer is higher.

Fig. 4

The same as in Fig. 2 but for $\varepsilon =0.01$ and $R_\mathrm{s} =0$ case

Fig. 5

The same as in Fig. 3 but for $\varepsilon =0.01$ and $R_\mathrm{s} =0$ case

Typical results are presented in Figs. 6 and 7 for the vertical distribution of the vertical volume flux and total solid fraction, respectively, for the base state I at center and a node of a cell. It can be seen from Fig. 6 as well as from the actual generated data that flow occurs mainly in the secondary mushy layer and very slightly in the lower part of the primary mushy layer up to about $z =1.33$, where flow is downward at the center and upward at the node. The magnitude of the vertical flow increases with $z$ for $z<0.48$ and decreases with increasing $z$ for $z>0.48$. These results indicate the presence of only a single-cell structure in the vertical direction, where flow is in the form of down-hexagons.

Fig. 6

The same as in Fig. 2 but for $R_\mathrm{p} =0$ case

Fig. 7

The same as in Fig. 3 but for $R_\mathrm{p} =0$ case

Figure 7 presents total solid fraction versus $z$. It can be seen from this figure as well as from the actual generated data that the tendency for chimney formation exists only in the secondary mushy layer. This tendency begins at the bottom of this layer at different horizontal locations, which are vertical projections of the nodes of down-hexagonal cells on the bottom of this layer, and it is along vertical direction where it first increases slightly with $z$ up to about $z=0.12$ and then decreases with increasing $z$ until it becomes negligible at the top of the layer.

Case (iv) Onset of motion is driven equally from both mushy layers ($R_\mathrm{pc}=R_\mathrm{sc}$). This case is more general than the case (i) since here only the onset of motion takes place at the same values of both mush Rayleigh numbers, but the Rayleigh numbers can have different values. In this case we have the relation given in (28a) between the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$, where the values of the constants $S_{9}$ and $S_{10}$ for both of the solutions and the three base states I–III are given in Table 5. The positive sign for $S_{10}$ corresponds to the stable solution as detected also in the case (i), which is considered a sub-case of the case (iv), while the negative sign for this constant corresponds to the unstable solution as detected in the case (i). It can be seen from the results in Table 5 that the magnitudes of both of these constants are higher if the primary mushy layer is thicker or if the value of the temperature at the top of the liquid layer is higher. We also calculated these constants for other parameter values and found that the signs for $S_{9}$ and $S_{10}$ remain unchanged for either type of solution.

Table 5 Values of $S_{9}$–$S_{10}$ for 3 base states

It should be noted that due to the relation (28a), any of the two solutions in the case (i) now can correspond to a set of solutions satisfying (28a) with a linear relationship between the non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$. The values of the constants $S_{1}$–$S_{8}$ that are given for the stable solution of the case (i) in the three base states (Tables 2, 3, 4), were found to be the same as those in the case (iv) corresponding to a first set of solutions since both non-linear coefficients $R_\mathrm{p1}$ and $R_\mathrm{s1}$ can take different values satisfying (28a). The corresponding values for $S_{1}$–$S_{8}$ for a second set of solutions in this case are found to have the same magnitudes as those for the first one but with opposite signs for only $S_{2}, S_{4}$, and $S_{6}$–$S_{8}$. Using the stability analysis presented in Sect. 3.6 and applying (5f) to $O(\varepsilon )$, we find that the stable solutions subjected to either of the base states I–III satisfy the following relation between the mush Rayleigh numbers:

$$\begin{aligned} R_\mathrm{p}-S_{9}\,R_\mathrm{s}=(1-S_{9})R_\mathrm{pc} -{\vert }\varepsilon {\vert }\,S_{10}. \end{aligned}$$

(35)

Here the value of $S_{10}$ in Table 5 corresponds to the one with positive sign. The relation (35) can be useful for the experimentalists to investigate the flow features using this type of relation between the two mush Rayleigh numbers for the flow near its onset of motion and for the prescribed value of the amplitude of the perturbation that is maintained in their experimental systems.

For the base states I–III (Table 1), there is an important issue about the type of convection that may prevail in this case. To address this issue, which turns out to be peculiar and very particular for the ternary system, we extended further investigation and found that depending on a prescribed value of either $R_\mathrm{p}$ or $R_\mathrm{s}$, the resulting stable flow can be subcritical (or supercritical) in both mushy layers or mixed subcritical in one mushy layer and supercritical in another mushy layer. To show this result explicitly, we suppose that the flow in the secondary mushy layer is supercritical, so that

$$\begin{aligned} R_\mathrm{s}=R_\mathrm{pc}+{\vert }\varepsilon {\vert }{\vert }R_\mathrm{s1}{\vert }. \end{aligned}$$

(36a)

Using this in (35), we find

$$\begin{aligned} R_\mathrm{p}=R_\mathrm{pc}+{\vert }\varepsilon {\vert }(S_{9} {\vert }R_\mathrm{s1} {\vert }-S_{10}). \end{aligned}$$

(36b)

Thus, since $S_{9}>0$ and $S_{10}>0$, convection in the primary mushy layer is supercritical if ${\vert }R_\mathrm{s1} {\vert }>S_{10}/S_{9}$ and subcritical if ${\vert }R_\mathrm{s1}{\vert }<S_{10}/S_{9}$. If convection in the secondary mushy layer is subcritical, so that

$$\begin{aligned} R_\mathrm{s}=R_\mathrm{pc} -{\vert }R_\mathrm{s1}{\vert }, \end{aligned}$$

(36c)

then (35) implies that

$$\begin{aligned} R_\mathrm{p}=R_\mathrm{pc}-{\vert }\varepsilon {\vert }(S_{9} {\vert }R_\mathrm{s1} {\vert }+S_{10}). \end{aligned}$$

(36d)

Thus, in this case flow is also subcritical in the primary mushy layer. As specific examples, we also generated data for the volume flux and the solid fraction under the base state I (Tables 1, 2) for three sub-cases of $R_\mathrm{s1}=10.0, R_\mathrm{s1} =5.0$, and $R_\mathrm{s1} =-10.0$ corresponding, respectively, to both supercritical mushy layers ($\varepsilon =0.03, R_\mathrm{p1} =4.916$), supercritical secondary mushy layer and subcritical primary mushy layer ($\varepsilon =0.03, R_\mathrm{p1} =-3.965$), and both subcritical mushy layers ($\varepsilon =0.03, R_\mathrm{p1} = -30.624$). Due to some similarities between this case and its sub-case (i), and the weak non-linear approach of present study, we find that the results for the vertical flux and total solid fraction are qualitatively the same as those described for the case (i) and in Figs. 2 and 3 and only differ quantitatively, and, thus, no figures were produced for these three sub-cases. Hence, the results for the preferred flow pattern and the tendency for chimney formation are qualitatively the same as those described for the case (i) and will not be repeated here.

4.4 Discussion on the Three-Dimensional Results

We already provided a paragraph in the introduction section about the main results of the two-dimensional steady rolls of the ternary system that was investigated by Anderson and Schulze (2005). Here we present the main differences between that study and the results and the corresponding ones in the present investigation. In contrast to the work in Anderson and Schulze (2005), the present study considered three-dimensional convection in a naturally fitted ternary system and investigated stability of the resulting three-dimensional hexagons. It is known from previous theoretical and experimental studies of convective flow in binary systems (Tait et al. 1992; Amberg and Homsy 1993; Roper et al. 2008) that three- dimensional hexagons are the preferred and observable flow structure at least for sufficiently small amplitude of the flow cases. Although no experimental investigation has yet been done to determine the preferred patterns in a present type ternary system, it has been a motivation for the present three-dimensional hexagonal studies to stimulate future experimental work to uncover the observable flow patterns in ternary system.

The preferred flow structures that were detected in the present study such as down-hexagons over or under up-hexagons in supercritical or subcritical states were completely different from the results for two-dimensional rolls reported in Anderson and Schulze (2005). The present study also uncovered for the first time new flow phenomena and mechanisms that can play in the present system such as depending on the given parameter values one mushy layer can be in supercritical state, while another layer in subcritical state. In addition, other main results of the present study about tendency for chimney formation and its mechanisms for various hexagonal convection scenarios that we presented in this paper and concluded in this section are completely new and none of such results were detected in Anderson and Schulze (2005) for the two-dimensional rolls counterpart.

Despite the lack of any experimental results about the preferred patterns in a ternary type flow system such as the present one and the fact that no other numerical or theoretical studies have been available so far for the three-dimensional flow patterns near the onset of motion in such ternary system, we would like to provide the following explanations that can provide some support for the present three-dimensional results.

First, from the part (iii) of Sect. 4.3, we presented results for the case where the convective flow is driven only by the secondary mushy layer, which is bounded from below by the solidification front and from above by a passive primary layer with zero Rayleigh number and a liquid layer. This is a limiting type ternary flow model, which is closet to the single mushy layer model of a binary system (Worster 1992; Tait et al. 1992), where the mushy layer is bounded from below by a solidification front and from above by a liquid layer. According to the experimental results for the binary system due to Tait et al. (1992), the observed flow pattern was in the form of down-hexagons with flow downward at the center of each cell and with chimneys convective flow in the upward direction along the nodes of the hexagonal cells. These are precisely the type of results that we found and presented in part (iii) of Sect. 4.3 in the case of a passive primary layer ($R_\mathrm{p} =0$) with convection driven only by the secondary mushy layer.

Next, a comparison between the present three-dimensional results and the two-dimensional ones (Anderson and Schulze 2005), which were already described in Sect. 1, indicate some general features which agree between the two studies such as supercritical realization of flow driven by the primary layer, subcritical realization of flow driven by the secondary layer, and the direction of flow circulation and the sign of the solid fraction perturbation in the case of flow driven by one mushy layer.

In the present investigation non-linear examination of the three-dimensional ternary system was restricted to $O(\varepsilon ^{2})$ of the perturbations superimposed on the basic state which enabled us to examine the hexagonal type solutions that can be preferred for the smallest values of the amplitude $\varepsilon$ and the mush Rayleigh numbers. However, computation of the non-linear properties of such flows for $O(\varepsilon ^{3})$ for three-dimensional hexagonal and non-hexagonal type solutions will be quite complex requiring very extensive algebras and remain a subject for future work.

5 Conclusion

We studied the problem of three-dimensional buoyant convection during the solidification of ternary alloy and under the assumption of large far-field temperature and sufficiently small amplitude of convection ${\vert }\varepsilon {\vert }$. We determined the motionless basic state solution and then carried out linear stability analysis to determine the critical conditions at the onset of convection for several cases. Applying weakly non-linear analyses up to and including $O(\varepsilon ^{2})$, we examined the linear and non-linear properties of the three-dimensional flow in the form of hexagons and found the stable non-linear solutions for several convection scenarios.

We found for the cases that the flow is driven from both mushy layers with equal critical conditions at the onset of motion in both mushy layers; and depending on the values of the mush Rayleigh numbers, the stable flow can be supercritical or subcritical in either of the two mushy layers. Such flow is in the form of double cellular structure in the vertical direction with down-hexagons under up-hexagons. There is a tendency for chimney formation in both of the mushy layers. In the secondary mushy layer such tendency initiates at different horizontal locations on the bottom of the layer and is vertically oriented where its amount first slightly increases and then decreases with increasing the vertical variable $z$ until it becomes negligible at the top of this layer. In the primary mushy layer, tendency for chimney formation initiates at different horizontal locations on an internal horizontal level within the layer. The amount of tendency for chimney formation in this layer is relatively less than that in the secondary layer but is again vertically oriented at discrete locations. Here the amount of such tendency above the internal level first increases slightly and then decreases with increasing $z$ in the upward flow direction until ends at the top of the layer, while under the internal level this tendency decreases with decreasing $z$ in the downward flow direction until becomes negligible at the bottom of the layer.

If the flow is driven only by the primary mushy layer, then the stable flow is supercritical and has double cellular structure vertically but now down-hexagons are above up-hexagons. The tendency for chimney formation in both mushy layers is similar to the corresponding one described in the previous paragraph but the amount of such tendency is now relatively less. For the case that the flow is driven only by the secondary mushy layer, the stable flow is subcritical and has only a single cellular structure in the form of down-hexagons. Here convection is mainly restricted to the secondary mushy layer and very slightly to the lower part of the primary layer, and the tendency for chimney formation, which exists only in the secondary mushy layer, is similar to the previous cases but is relatively less. The tendency for chimney formation is found to be higher if the convection is driven by both mushy layers with equal critical onset conditions for motion.

Since no experimental investigation has been done yet to determine the preferred patterns in a ternary system, it has been a motivation for the present three-dimensional hexagonal studies to stimulate future experimental work to uncover the observable flow patterns in ternary systems. The present study detected for the first time new types of preferred flow structures such as down-hexagons over or under up-hexagons in supercritical or subcritical states as well as new flow phenomena and mechanisms that can play in the present ternary system such as one mushy layer can be in supercritical state, while another layer can be in subcritical state for the same values of the parameters of the flow system. In addition, other main results of the present study about tendency and mechanisms for chimney formation in different hexagonal convection scenarios that we also summarized in the last two paragraphs of this section are completely new and none of such results have been detected before.

Although there have been some notable experimental results and discoveries in the ternary systems (Aitta et al. 2001a, b; Thompson et al. 2003b) about the presence of distinct primary and secondary mushy layers, which can form between solid and liquid layers, no experimental result is known about the form of buoyancy driven convective flow near the onset of motion that could operate in the ternary system cooled from below. It is hoped that the present analytical results for the realizable type of flow near the onset of motion can stimulate future experimental investigation on the subject.

Appendix

The systems for dependent variables $\mathbf{u}$, $P$, and $T$ at order $\varepsilon ^{2}$ in each of the three layers are given below: In the liquid layer we have

$$\begin{aligned}&\displaystyle d_\mathrm{a} {\nabla }^{2}\mathbf{u}_{1}={\nabla }P_{1},\end{aligned}$$

(37a)

$$\begin{aligned}&\displaystyle {\nabla } \cdot \mathbf{u}_{1} =0,\end{aligned}$$

(37b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T_{1}-(\hbox {d}T_{\mathrm{B}}/\hbox {d}z)w_{1}= \mathbf{u}_{0} \cdot {\nabla }T_{0},\end{aligned}$$

(37c)

$$\begin{aligned}&\displaystyle T_{1}=\mathbf{u}_{1}=0\;\hbox {at}\;z =L,\end{aligned}$$

(37d)

$$\begin{aligned}&\displaystyle [T_{1}]=[{\partial }T_{1}/{\partial }z]= [\mathbf{u}_{1}]=[P_{1}]= T_{1}{\vert }^{+}=0\;\hbox {at}\;z=l. \end{aligned}$$

(37e)

In the primary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}_{1}+{\nabla }P_{1}= -(R_\mathrm{p0} T_{1}+R_\mathrm{p1}T_{0}) \mathbf{z},\end{aligned}$$

(38a)

$$\begin{aligned}&\displaystyle {\nabla } \cdot \mathbf{u}_{1}=0,\end{aligned}$$

(38b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T_{1}-(\hbox {d}T_{\mathrm{B}}/\hbox {d}z)w_{1}= \mathbf{u}_{0} \cdot {\nabla }T_{0},\end{aligned}$$

(38c)

$$\begin{aligned}&\displaystyle [T_{1}]=[{\partial }T_{1} /{\partial }z]=[\mathbf{u}_{1}]=[P_{1}]=T_{1}{\vert }^{+}=0\;\hbox {at}\;z =1. \end{aligned}$$

(38d)

In the secondary mushy layer we have

$$\begin{aligned}&\displaystyle \mathbf{u}_{1}+{\nabla }P_{1}= -(R_\mathrm{s0} T_{1}+R_\mathrm{s1}T_{0}) \mathbf{z},\end{aligned}$$

(39a)

$$\begin{aligned}&\displaystyle {\nabla } \cdot \mathbf{u}_{1}=0,\end{aligned}$$

(39b)

$$\begin{aligned}&\displaystyle {\nabla }^{2}T_{1}-(\hbox {d}T_{\mathrm{B}}/\hbox {d}z)w_{1} = \mathbf{u}_{0} \cdot {\nabla }T_{0},\end{aligned}$$

(39c)

$$\begin{aligned}&\displaystyle T_{1}=w_{1}=0\;\hbox {at}\;z =0. \end{aligned}$$

(39d)

The expressions for $S_{1pq}, S_{2}, S_{3pq}, S_{4}$, and $S_{5pq}$, which were introduced in (26) are

$$\begin{aligned}&\displaystyle S_{1pq}=\int _{l}^\mathrm{L} T_\mathrm{a1}(z)\{i\,f_{4}(z)[{\alpha }_{\mathrm{px}}\, f_{1}(z, q)+{\alpha }_\mathrm{py} f_{2}(z, q)]+f_{3}(z)[\hbox {d}\,f_{4}(z)/\hbox {d}z]\}\hbox {d}z,\end{aligned}$$

(40a)

$$\begin{aligned}&\displaystyle S_{2}=\int _{1}^{l} [w_\mathrm{a2 }(z) f_{8} (z)]\hbox {d}z,\end{aligned}$$

(40b)

$$\begin{aligned}&\displaystyle S_{3pq}=\int _{1}^{l} T_\mathrm{a2 }(z)\{i\,f_{8}(z)[{\alpha }_{\mathrm{px}}\, f_{5}(z, q)+{\alpha }_{\mathrm{py}}\, f_{6}(z, q)]+f_{7} (z)[\hbox {d}\, f_{8}(z)/\hbox {d}z]\}\hbox {d}z,\end{aligned}$$

(40c)

$$\begin{aligned}&\displaystyle S_{4}=\int _{0}^{1} [w_\mathrm{a3}(z) f_{12}(z)]\hbox {d}z,\end{aligned}$$

(40d)

$$\begin{aligned}&\displaystyle S_{5pq}{=}\int _{0}^{1} T_\mathrm{a3}(z)\{i\,f_{12}(z)[{\alpha }_{\mathrm{px}} \,f_{9}(z, q){+}{\alpha }_{\mathrm{py}}\, f_{10}(z, q)]{+}f_{11}(z)[\hbox {d}\, f_{12}(z)/\hbox {d}z]\}\hbox {d}z. \end{aligned}$$

(40e)

The expressions for $S_{6}$–$S_{8}$, which were introduced in (31a, 31b) are given below

$$\begin{aligned} S_{6}=\int ^\mathrm{L}_{l} [T_\mathrm{a1}(z)f_{4}(z)]\hbox {d}z, S_{7}=\int _{1}^{l} [T_\mathrm{a2}(z)f_{8}(z)]\hbox {d}z, S_{8}=\int _{0}^{1}[T_\mathrm{a3}(z)f_{12}(z)]\hbox {d}z. \end{aligned}$$

(41)