1 Introduction

Earlier investigations of convective flow during alloy solidification were for the binary alloy solidification cases with notable work due to Worster (1992), Tait et al. (1992), Amberg and Homsy (1993), Anderson and Worster (1995) and Chung and Chen (2000). Worster (1992) studied linear stability analysis of the flow in the liquid and mushy-layer regions during the solidification of binary alloys. Mushy layer is a layer composed of both solid dendrites and fluid. He uncovered, in particular, two modes of compositional convection at the onset of motion, where one of these modes, which was referred to as the mushy-layer mode, was driven by the flow within the mushy layer. Amberg and Homsy (1993) developed a single-mushy-layer model of the mushy zone alone for the binary alloy solidification system. A number of reasonable assumptions including a thin horizontal mushy layer in the limit of large far-field temperature, which is the temperature far away in the fluid above the mushy layer, were considered that allowed the authors to examine the weakly nonlinear dynamics of the flow in the mushy layer.

Guba (2001) studied finite-amplitude steady convection in rotating mushy layers during the solidification of binary alloys. Guba (2001) excluded interactions between the solid fraction and the convection associated with the Coriolis term, which can exist in the presence of rotation, by setting the solid fraction at a constant value in the term modeling the effect of rotation. Applying the modeling approach due to Amberg and Homsy (1993), Guba (2001) determined two- and three-dimensional flow in the form of oblique rolls and distorted hexagons, which are the form of regular rolls and hexagonal pattern in the presence of rotation (Veronis 1959; Busse 1978), and found, in particular, that distorted hexagons can change their form from up-hexagons, where convection is upward at the cells’ centers and downward at the cells’ boundaries, to down-hexagons, where convection is downward at the cells’ centers and upward at the cells’ boundaries, for a rotation rate beyond some value.

Riahi (2003) studied steady convection in rotating mushy layers during the solidification of binary alloys and extended the work due to Guba (2001) by including the interactions between the solid fraction and the flow associated with the Coriolis term in the momentum Darcy equation. His linear analysis provided results for the critical values of the Rayleigh number and the wave number at the onset of motion for both cases where the above-noted interactions were taken into consideration or not. He also carried out stability analysis for several different types of flow patterns that were determined by a weakly nonlinear analysis and found, in particular, that depending on the values of the parameters and the amplitude of convection distorted down-hexagons or up-hexagons can be stable.

In contrast to many studies that have been done in the last several decades for the flow during the solidification of binary alloys, there have been relatively few studies of the ternary alloy systems (Aitta et al. 2001a, b; Anderson 2003; Thompson et al. 2003a, b; Bloomfield and Huppert 2003; Anderson and Schulze 2005; Anderson et al. 2010; Riahi 2014). Aitta et al. (2001a, b) were the first to identify experimentally two distinct mushy layers, which were referred to as the primary and secondary mushy layers, for their investigated aqueous ternary system. Thompson et al. (2003b) investigated the same type of ternary system for a convective flow case where the primary mushy layer was unstable, while the secondary mushy layer was stable and nonconvective. Anderson (2003) investigated a diffusion-controlled solidification of ternary alloys in mushy layers and examined the corresponding similarity solution.

Anderson and Schulze (2005) investigated two-dimensional buoyancy-driven flow during the solidification of a ternary alloy. They used both a linear stability procedure and numerical computations to determine the results for linear and finite-amplitude steady states for the flow in their considered ternary state, which was composed of a liquid layer and two distinct mushy layers referred to as the primary and secondary mushy layers that each have its own independent Rayleigh numbers.

Recently Riahi (2014) studied theoretically a three-dimensional weakly nonlinear version of the two-dimensional ternary system that was used before in Anderson and Schulze (2005) by considering a large far-field temperature limit and for the flow close to its onset of motion. Since the three-dimensional nonlinear ternary flow system was quite complicated, Riahi (2014) restricted his investigation to the system only up to order \(\varepsilon ^{2}\) where \(\varepsilon \) is the magnitude of the small-amplitude convection. He found, in particular, that for sufficiently small amplitude of motion and over a wide range of values of the mush Rayleigh numbers, the stable convection that existed for the smallest values of the mush Rayleigh numbers for both primary and secondary mushy layers, was in the form of subcritical down-hexagons. Although no experimental result is known for the preferred flow pattern in the ternary flow system, this result agreed with the available experimental results for the binary counterpart system (Tait et al. 1992).

In the present study we investigate the low rotating rate extension of a simple version of the nonrotating ternary flow system that was studied before by Riahi (2014). We study the linear ternary flow system at the onset of motion within a double-horizontal mushy layers, which is due to the presence of additional complexity of the imposed rotational constraint. We find some interesting results. In particular, we find that the rotating flow at low rate exhibits multi-minima on the neutral stability boundary. The rotational effect in the present ternary flow system is less stabilizing as compared to the binary alloy counterpart case, and the present rotational force can increase the magnitude of the vertical volume flux and the solid fraction at certain vertically oriented fluid lines in the ternary system.

In the following, we describe in Sect. 2 the present physical ternary system and the corresponding governing equations and the associated boundary conditions. In Sect. 3 we present the linear stability analysis and the associated solutions, and then the corresponding results and discussion are given in Sect. 4. Section 4 is then followed by the conclusion in Sect. 5.

2 Governing Systems

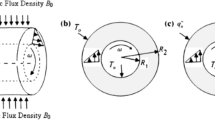
We consider a ternary alloy melt that is cooled from below and is solidified at a constant speed V. Following Riahi (2003) for the rotating binary system and Riahi (2014) for the ternary counterpart of the binary model due to Amberg and Homsy (1993), we consider the ternary alloy in a horizontal region \(0<z<d\), which is composed of a primary mushy layer \(h<z<d\) and a secondary mushy layer \(0<z< h\) (Fig. 1). Here h and d are 2 positive constants (\(d>h)\). Our ternary system model is based on the ternary phase diagram used by Anderson and Schulze (2005) and Riahi (2014), which was presented in details by Anderson (2003) and Anderson and Schulze (2005) and, thus, will not be repeated here. We consider the solidification system to be rotating at a constant angular velocity vector with small magnitude M about a vertical axis anti-parallel to the gravity vector and in a moving frame of reference whose origin lies on the solidification front and translating at the speed V with the solidification front in the upward direction. As in the work due to Anderson and Schulze (2005) and Riahi (2014), we assume that there is no latent heat release, there is no solute diffusion, no density change due to solidification, the ternary system is in local equilibrium with constant thermal properties, and the liquid density depends linearly upon temperature T and compositions A and B.

Fig. 1
figure 1

This is a schematic diagram for a physical ternary system

Full size image

We consider the governing equations for momentum, under the assumption that the Darcy equation describes the fluid flow in the mushy layers, the equations for the mass conservation, heat and solute for the ternary fluid flow system and the necessary equations for the relations between the temperature and species composition in the mushy layers due to the assumed thermodynamic equilibrium of the phase diagram (Anderson and Schulze 2005). The governing equations for the flow in the mushy layers that are used in the present study are basically rotating extension of those already derived in Anderson and Schulze (2005) who provided sufficient descriptions as well as experimental justification which will not be repeated here. Instead, the reader is referred to these authors’ paper for details. We make these equations dimensionless in the moving frame described before by using V, k / V, \(\Delta T=T^{p}-T^{E}\), \(\mu k/\Pi _{0}\) and \(V^{2}/k\) as scales for velocity, length, temperature excess \((T-T^{p})\), pressure and time, respectively (Anderson and Schulze 2005). Here k is thermal diffusivity, \(T^{p}\) is the temperature at the primary mushy-layer front, \(T^{E}\) is the temperature at the eutectic front, \(\mu \) is the dynamic viscosity, and \(\Pi _{0}\) is a reference scale for the permeability.

Following above description to make the equations as well as the boundary conditions nondimensional, we have the following systems in the two mushy layers which are given below.

In the primary mushy layer we have

$$\begin{aligned}&\mathbf{u}/\Pi (\chi )= -\nabla P-(R_{ap}T+M_{E})\mathbf{z},+\tau \; \mathbf{u}\times \mathbf{z}/\chi , \end{aligned}$$
(1a)
$$\begin{aligned}&\nabla \cdot \mathbf{u}=0, \end{aligned}$$
(1b)
$$\begin{aligned}&(\partial /\partial t-\partial /\partial z)T+ \mathbf{u}\cdot \nabla T=\nabla ^{2}T, \end{aligned}$$
(1c)
$$\begin{aligned}&(\partial /\partial t-\partial /\partial z)(\chi A+\phi _{{a}})+ \mathbf{u}\cdot \nabla A=0, \end{aligned}$$
(1d)
$$\begin{aligned}&T=-1+{M}_{{a}} (A-{A}^{{E}})+{M}_{{b}} (B-{B}^{{E}}) \end{aligned}$$
(1e)
$$\begin{aligned}&\chi =1-\phi _{{a}}, \phi _{{b}} =0, \end{aligned}$$
(1f)
$$\begin{aligned}&B=B^{P} (1-A)/(1-A^{P}), \end{aligned}$$
(1g)
$$\begin{aligned}&T=w=\phi _{{a}}=A-A^{H}=B-B^{H} =0\; \hbox {at}\; z=\delta l, \end{aligned}$$
(1h)
$$\begin{aligned}&[T]=[\partial T/\partial z]=[P]=[\mathbf{u}]=[\phi _{{a}}]=\phi _{{b}}{\vert }^{-}=T-T^{s}{\vert }^{+} =0\; \hbox {at}\; z =\delta , \end{aligned}$$
(1i)

where \(\mathbf{u}=(u, v, w)\) is the flux driven by the buoyancy with components u, v and w along the horizontal x-axis, horizontal y-axis and the upward vertical z-axis, respectively, P is the pressure, A and B are the two liquid compositions, which are measured in wt%, t is time variable, z is vertical variable, \(\Pi \) is the permeability of the porous medium, l is a positive constant, \(\delta = { hV}/k\) is the nondimensional value of the vertical height of the secondary mushy layer, \(A^{H}\) and \(B^{H}\) are positive constant quantities, the square brackets \([]\equiv {\vert }^{+} - {\vert }^{-}\) denote the jump in the enclosed quantity across the interface, \(R_{p}=-R+[R_{a}(1-A^{P})-R_{b} B^{P}]/[M_{a}(1-A^{P})-M_{b}B^{P}]\), \(M_{E} =[M_{a} A^{E}+M_{b} B^{E} +1-M_{b} B^{P}/(1-A^{P})]R_{p}+R_{b}B^{P} /(1-A^{P})\), \(R=\beta _{{t}} \Pi _{0} g \Delta T/(V \nu )\) is the thermal Rayleigh number representing stabilizing thermal buoyancy, g is acceleration due to gravity, \(\nu \) is kinematic viscosity, \(\beta _{{t}}\) is the coefficient of thermal expansion, \(M_{a}\) and \(M_{b}\) are dimensionless liquidus slopes (Anderson and Schulze 2005), z is a unit vector in the vertical z-axis, \(R_{a}=\beta _{{a}} g \,\Pi _{0} /(V\nu )\) and \(R_{b}=\beta _{{b}} g \,\Pi _{0} /(V\nu )\) are the compositional Rayleigh numbers due to the presence of the species composition, \(\Pi _{0}\) is a constant reference value of the permeability, \(\beta _{{a}}\) and \(\beta _{{b}}\) are the corresponding expansion coefficients due to change in density with the species composition, \(\tau =2M\Pi _{0}/\nu \) is the rotational parameter, which is the square root of a Taylor number, M is the constant magnitude of the angular velocity vector M, which is assumed to be small, \(\chi \) is the liquid fraction in the primary mushy layer, which is given in (1f) explicitly, \(\phi _{{ a}}\) and \(\phi _{{b}}\) are the solid fractions due to the compositions A and B, respectively, and the constant temperature \(T^{s}\) is the prescribed temperature at the interface between the two mushy layers (Anderson and Schulze 2005). Additional equations (1e) and (1g) for the relations between temperature and compositions are of the type introduced and justified in Anderson and Schulze (2005). Here quantities with superscripts “P” and “E” represent constant quantities at the primary mushy-layer front and the eutectic front, respectively. Anderson and Schulze (2005) provided detail description, derivation and experimental justification of Eqs. (1e) and (1g) as well as derivation for the primary mushy-layer Rayleigh number \(R_{ap}\), and thus, these will not be repeated here.

In the secondary mushy layer we have

$$\begin{aligned}&\mathbf{u}/\Pi (\chi )=-\nabla P -(R_{as}T +M_{F})\mathbf{z} +\tau \; \mathbf{u}\times \mathbf{z}/\chi , \end{aligned}$$
(2a)
$$\begin{aligned}&\nabla \cdot \mathbf{u}=0, \end{aligned}$$
(2b)
$$\begin{aligned}&(\partial /\partial t-\partial /\partial z)T + \mathbf{u}\cdot \nabla T=\nabla ^{2}T, \end{aligned}$$
(2c)
$$\begin{aligned}&(\partial /\partial t-\partial /\partial z)(\chi A+\phi _{{a}})+ \mathbf{u}\cdot \nabla A=0, \end{aligned}$$
(2d)
$$\begin{aligned}&(\partial /\partial t-\partial /\partial z)(\chi A+\phi _{{b}})+ \mathbf{u}\cdot \nabla B=0, \end{aligned}$$
(2e)
$$\begin{aligned}&\chi = (1-\phi _{{a}}-\phi _{{b}}), \end{aligned}$$
(2f)
$$\begin{aligned}&A=A^{E} + (T+1)/M_{ac}, \end{aligned}$$
(2g)
$$\begin{aligned}&B=B^{E}+(T+1)/M_{bc}, \end{aligned}$$
(2h)
$$\begin{aligned}&T+1=\mathbf{u}\cdot \mathbf{z}=0\; \hbox {at}\; z=0, \end{aligned}$$
(2i)

where \(R_{as} =-R+(R_{a} /M_{ac}+R_{b} /M_{bc})\), \(M_{F}=R_{a} (A^{E} +1/M_{ac})+R_{b} (B^{E}+1/M_{bc})\), \(M_{ac}\) and \(M_{bc}\) are the constant dimensionless cotectic slopes (Anderson and Schulze 2005) and derivations of (2f)–(2h) are given in this reference.

3 Analysis and Solutions

3.1 Scaling and Expansion Procedure

From the result found by Anderson and Schulze (2005) for the relation between the depth \(\delta \) of the secondary mushy layer and the far-field temperature \(T_{\infty }\), which we consider here to be large (\(T_{\infty }>>1\)) for large \(z =Z>>1\), we have

$$\begin{aligned} \hbox {e}^{\delta } =(T_{\infty }+1)/[T_{\infty }-T^{s} + \hbox {e}^{-Z}(T^{s} +1)]. \end{aligned}$$
(3a)

Since \({\vert }T^{s}{\vert }<1\) (Anderson and Schulze 2005), (3a) implies that \(\delta \) is small (\(<<1\)) and to the first order in \(\delta \), we have

$$\begin{aligned} 1+\delta \sim 1+ 1/ T_{\infty }, \end{aligned}$$
(3b)

which implies that

$$\begin{aligned} \delta \sim 1/T_{\infty }<<1. \end{aligned}$$
(3c)

Thus similar to the binary system (Amberg and Homsy 1993), we find that the thickness of the secondary mushy layer is small in the limit of large far-field temperature. Using this result, it motivated us a further scaling of the variables, and so we assume the limit of large far-field temperature in the present study and use \(\delta \) as a small parameter.

As in Riahi (2014), we now scale all lengths with \(\delta \) and time with \(\delta ^{2}\). Then we expand the governing systems to derive the systems for small perturbations to the motionless steady basic state, which varies at most with respect to the vertical variable. Following Amberg and Homsy (1993), we do some rescaling for u and the effective Rayleigh numbers for the mushy layers and consider each dependent variable to be sum of its basic state, which is designated with a subscript “B,” plus small perturbations, which vary in general with respect to three-dimensional space and time variables

$$\begin{aligned} T= & {} T_{B}+\varepsilon (T_{0}+\delta T_{01} +{\cdots }), \end{aligned}$$
(4a)
$$\begin{aligned} \delta \mathbf{u}= & {} \mathbf{0}+ \varepsilon (\mathbf{u}_{0}+\delta \; \mathbf{u}_{01}+{\cdots }), \end{aligned}$$
(4b)
$$\begin{aligned} P= & {} P_{B}+\varepsilon (P_{0}+\delta \,P_{01}+{\cdots }), \end{aligned}$$
(4c)
$$\begin{aligned} (A, B, \chi )= & {} (A_{B}, B_{B}, \chi _{B})+\varepsilon [(A_{0}+\delta A_{01}+{\cdots }), (B_{0}+\delta B_{01}+{\cdots }),\nonumber \\&(\chi _{0}+\delta \chi _{01}+{\cdots })], \end{aligned}$$
(4d)
$$\begin{aligned} (\phi _{{a}}, \phi _{{b}})= & {} (\phi _{{aB}},\phi _{{bB}})+\varepsilon [(\delta ^{-1} \phi _{{a}(-1)}+\phi _{{a}0}+\delta \phi _{{a}01}+{\cdots }),\nonumber \\&(\delta ^{-1}\phi _{{b}(-1)}+\phi _{{b}0}+\delta \phi _{{b}01}+{\cdots })], \end{aligned}$$
(4e)
$$\begin{aligned} {\mathrm {\delta ({ R_{p}}, { R_{s}})}}= & {} {\mathrm {[({ R_{p}}0+\delta { R_{p}}01+{\cdots }), ({ R_{s}}0+\delta { R_{s}}01+{\cdots })],}} \end{aligned}$$
(4f)

where \(\varepsilon<<\delta <<\)1 is assumed. As described in Riahi (2014), the order O(\(\delta ^{-1})\)-terms in (4e) were needed to balance with the advection terms in the composition equations in order to determine nontrivial solutions for the solid fraction perturbations.

3.2 Basic State Motionless

Using (4) in (1), (2) and considering the terms in the absence of perturbations by setting \(\varepsilon \)=0 and keeping leading order terms in \(\delta \) for simplicity, we find the systems for the basic state. In the primary mushy layer \((1\le z \le l)\), we find

$$\begin{aligned} T_{B}= & {} -T^{s} \{(l-z)/(1-l), \end{aligned}$$
(5a)
$$\begin{aligned} \chi _{{B}}= & {} [M_{a} (A^{H} -1)+M_{b} \, B^{H}]/[M_{a} (A^{E} -1)+M_{b} \, B^{E} +1 +T_{B} ], \end{aligned}$$
(5b)
$$\begin{aligned} (A_{B}, B_{B})= & {} [1+(A^{H} -1)/\chi _{{B}}, B^{H}/\chi _{{B}}], \end{aligned}$$
(5c)
$$\begin{aligned} \phi _{{B}}= & {} 1-\chi _{{B}}, \phi _{{B}}=0, \end{aligned}$$
(5d)
$$\begin{aligned} P_{B}= & {} -M_{E} (z-l)-R_{p} \; T^{s} (0.5 z^{2}-l \;z+0.5 l^{2}) \nonumber \\&-l(R_{a} A^{L}+R_{b} \; B^{L})+P_{l0}. \end{aligned}$$
(5e)

In the secondary mushy layer (\(0\le z \le 1\)), we find

$$\begin{aligned} T_{B}= & {} (T^{s} +1)z -1, \end{aligned}$$
(6a)
$$\begin{aligned} (A_{B}, B_{B})= & {} \{[A^{E}+(T_{B}+1)/M_{ac}], [B^{E}+(T_{B}+1)/M_{bc}]\}, \end{aligned}$$
(6b)
$$\begin{aligned} \chi _{{B}}= & {} (1-A^{H}-B^{H})/(1-A_{B}-B_{B}), \end{aligned}$$
(6c)
$$\begin{aligned} \phi _{{aB}}= & {} (A^{H}-\chi _{{B}} A_{{B}}), \phi _{{bB}}=(1-\chi _{{B}}-\phi _{{aB}}), \end{aligned}$$
(6d)
$$\begin{aligned} P_{B}= & {} -R_{s}\{1-z+0.5(1+T^{s})[z -1]\}+M_{s}(1-z)\nonumber \\&-(M_{p}+0.5R_{p}T^{s})(1-l)-l(R_{a }A^{L }+R_{b }B^{L})+P_{l0}, \end{aligned}$$
(6e)

where the condition \([\partial T/\partial z]=0\) at the primary mush–secondary mush interface implies

$$\begin{aligned} l=1/(T^{s} +1). \end{aligned}$$
(6f)

3.3 Linear Stability

We use the expansions (4) in (1), (2), and similar to the work in Roper et al. (2008), we assume in the present study that \(\Pi (\chi )\equiv 1\) in Darcy’s equations. In addition, in order to reduce the already complex rotating ternary system, we follow Guba (2001) and do not include the interaction between the local solid fraction and the flow associated with the Coriolis term in the Darcy momentum equations in both mushy layers by fixing the local solid fraction at constant value 1 in the Coriolis term. Considering the corresponding systems at \(o(\varepsilon ^{1} \; \delta ^{0})\), we find that in the resulting systems the equations and the boundary conditions for the dependent variables \(\mathbf{u}_{0}\), \(P_{0}\) and \(T_{0}\) can be separable from the result of the equations for the other dependent variable. Since the systems for \(\mathbf{u}_{0}\), \(P_{0}\) and \(T_{0}\) contain the effective mush Rayleigh numbers \(R_{ap}\) and \(R_{as}\), we consider these systems and then solve the steady form of these systems analytically to obtain the results for the linear eigenvalue problem at the onset of motion and for the neutral stability boundaries for the stationary perturbations.

In the primary mushy layer we have the system at \(o(\varepsilon )\)

$$\begin{aligned} \mathbf{u}_{0}= & {} -\nabla P_{0} -R_{p0} \; T_{0} \mathbf{z},+\tau \mathbf{u}\times \mathbf{z}, \nabla \cdot \mathbf{u}_{0} =0,\nonumber \\&(\nabla ^{2}-\partial /\partial t)T_{0} =[T^{s} /(1-l)]w_{0}, \end{aligned}$$
(7a)
$$\begin{aligned} T_{0}= & {} M_{a} \; A_{0}+M_{b}B_{0}, B_{0} = -B^{p} \; A_{0} /(1-A^{p}), \nonumber \\&\partial /\partial z \{ \phi _{{a}(-1)}[1-A_{B}]\}=w_{0}\,\,\hbox {d}A_{B}/\hbox {d}z, \end{aligned}$$
(7b)
$$\begin{aligned} T_{0}= & {} w_{0}=\phi _{{a}(-1)}=A_{0}=B_{0} =0 \;\hbox {at}\; z=l, \end{aligned}$$
(7c)
$$\begin{aligned}{}[T_{0}]= & {} [\partial T_{0}/\partial z]=[P_{0}]=[\mathbf{u}_{0}]=T_{0}{\vert }^{+}=0\; \hbox {at}\; z=1. \end{aligned}$$
(7d)

Solving this system analytically for the stationary perturbations, we find

$$\begin{aligned} w_{0 }= & {} \{b_{1}\; {\exp }[(\gamma ^{0.5})z]+ b_{2}\; {\exp }[-(\gamma ^{0.5})z]+ b_{3}\; {\exp }[(\gamma _{0})^{0.5} \; z]\nonumber \\&+ b_{4}\; {\exp }[(\gamma _{0})^{0.5} \; z]\}H(x, y), \end{aligned}$$
(8a)
$$\begin{aligned} T_{0}= & {} \{b_{5}\; {\exp }[(\gamma ^{0.5})z]+ b_{6}\; {\exp }[-(\gamma ^{0.5})z]+ b_{7}\; {\exp }[(\gamma _{0})^{0.5} \; z]\nonumber \\&+ b_{8}\; {\exp }[-(\gamma _{0})^{0.5} \; z]\}H(x, y), \end{aligned}$$
(8b)
$$\begin{aligned} \gamma\equiv & {} [\alpha ^{2} /(2+2\tau ^{2})]\{(2+\tau ^{2})+[\tau ^{4}+4(1+\tau ^{2})\alpha ^{-2}\beta ^{2} {R}_{{p}0}]^{0.5}\},\nonumber \\&\beta ^{2}\equiv T^{s} /(1-l), \end{aligned}$$
(8c)
$$\begin{aligned} \gamma _{0}\equiv & {} [\alpha ^{2} /(2+2\tau ^{2})]\{(2+\tau ^{2})-[\tau ^{4}+4(1+\tau ^{2})\alpha ^{-2}\beta ^{2} {R}_{{p}0}]^{0.5}\}, \end{aligned}$$
(8d)
$$\begin{aligned} H(x, y)\equiv & {} \sum \limits ^{N}_{{n}=-N} \; E_{n}\eta _{{n}}(x, y), \eta _{{n}}(x, y)\equiv {\exp }(i {{\varvec{\upalpha }}}_{{n}}.\mathbf{r}), \end{aligned}$$
(8e)
$$\begin{aligned} P_{0}= & {} \sum \limits ^{N}_{n=-N}\{-(1/\gamma )^{0.5}(b_{1}+b_{5} \; R_{p0})({\exp }[(\gamma )^{0.5} \; z]-{\exp }[(\gamma )^{0.5} \; l])\nonumber \\&+(1/\gamma )^{0.5}(b_{2}+b_{6} \; R_{p0})({\exp }[-(\gamma )^{0.5}z ]-{\exp }[-(\gamma )^{0.5}l])\nonumber \\&-(1/\gamma _{0})^{0.5}(b_{3}+b_{7} \; R_{p0})({\exp }[(\gamma _{0})^{0.5}z]-{\exp }[(\gamma _{0})^{0.5} \; l])\nonumber \\&+(1/\gamma _{0})^{0.5}(b_{4}+b_{8} \; R_{p0})({\exp }[-(\gamma _{0})^{0.5}z]\nonumber \\&-{\exp }[-(\gamma _{0})^{0.5} \; l])+ p_{0c}\}E_{n}\eta _{{n}}, \end{aligned}$$
(8f)
$$\begin{aligned} (u_{0}, v_{0})= & {} -[1/(1+\tau ^{2})]\sum \limits ^{N}_{n=-N} {i}[\alpha _{{nx}}+\alpha _{{ny}}\tau , \alpha _{{ny}}-\alpha _{{nx}}\tau ) \; P_{00} (z){E}_{{n}} \; \eta _{{n}}, \end{aligned}$$
(8g)
$$\begin{aligned} A_{0}= & {} T_{0} /[M_{a}-M_{b}B^{P}/(1-A^{P})], B_{0}=-A_{0}B^{P}/(1-A^{P}), \phi _{{b}(-1)}=0, \phi _{{a}(-1)}\nonumber \\= & {} (\hbox {d}A_{B}/\hbox {d}z){\smallint }_{l}^{z} \; w_{0}\hbox {d}z/(1-A_{B}), \end{aligned}$$
(8h)

where x and y are the horizontal variables, the unknown constants \(b_{m} (m=1, {\ldots }, 8)\) satisfy a set of linear algebraic equations, which are given by (14) in “Appendix” section, i is pure imaginary number (\(\surd -1\)), \(p_{0c}\) is a constant, \(P_{00}\) (z) is the z-dependent coefficient for \(P_{0}\) in (8f), subscript “n” takes only nonzero integer values from \(-N\) to N, N is a positive integer, and the horizontal wave number vectors \({\varvec{\alpha }}_{n}=(\alpha _{{nx}}, \alpha _{{ny}})\) satisfy the properties

$$\begin{aligned} {{\varvec{\upalpha }}}_{{n}}\cdot \mathbf{z}=0, {\vert }{{\varvec{\upalpha }}}_{{n}}{\vert }=\alpha , {{\varvec{\upalpha }} }_{-{n}} = - {\varvec{\upalpha }}_{{n}}. \end{aligned}$$
(9)

The constant coefficients \(E_{n}\) satisfy the conditions

$$\begin{aligned} \sum \limits ^{{N}}_{{n}=-{N}}{\vert }E_{n}{\vert }^{2}=1, E_{n}^{*}=E_{-n}. \end{aligned}$$
(10a)

The solutions given in (8) are in the form of cellular structure for the convective flow that is known to be the relevant one near and at the onset of motion. For the simplest type of such solutions, which refer to as regular solutions and include those observed in the applications (Busse 1978) like hexagonal-type solutions, all angles between two neighboring \({\varvec{\upalpha }}\) vectors are equal and (10a) yields

$$\begin{aligned} {\vert }{E}_{1}{\vert }^{2} ={\cdots }={\vert }{E}_{{N}}{\vert }^{2}=1/(2\; N). \end{aligned}$$
(10b)

We have provided general form of the solutions in (8)–(10) in terms of arbitrary positive integer N so that the present paper can be used as a suitable reference for future extension of the present work, even though we shall later restrict our study to the cases for sufficiently small \(\varepsilon \) where, as an example, the flow solution is in the form of hexagons with N=3. Such form of solutions was studied in Riahi (2014) in the absence of rotational constraint, and one of such solutions was found to be stable.

In the secondary mushy layer we have the system at \(o(\varepsilon )\)

$$\begin{aligned} \mathbf{u}_{0}= & {} -\nabla P_{0}-{R}_{s0}{T}_{0} \mathbf{z}+\tau \; \mathbf{u}\times \mathbf{z}, \nabla \cdot \mathbf{u}_{0}=0, (\nabla ^{2}-\partial /\partial t)T_{0} =(1+T^{s})w_{0}, \end{aligned}$$
(11a)
$$\begin{aligned} A_{B}= & {} A^{E}+(T_{B}+1)/M_{ac}, \partial /\partial z\{-[\phi _{{a}(-1)}+\phi _{{ b}(-1)}]A_{B}+\phi _{{a}(-1)}\}\nonumber \\= & {} w_{0} (\hbox {d}A_{B}/\hbox {d}z), \end{aligned}$$
(11b)
$$\begin{aligned} B_{B}= & {} B^{E}+(T_{B} +1)/M_{bc}, \partial /\partial z\{-[\phi _{{a}(-1)}+\phi _{{ b}(-1)}]B_{B}+\phi _{{b}(-1)}\}\nonumber \\= & {} w_{0} (\hbox {d}B_{B}/\hbox {d}z), \end{aligned}$$
(11c)
$$\begin{aligned} T_{0}= & {} w_{0}=0\; \hbox {at}\; z=0. \end{aligned}$$
(11d)

Solving this system analytically for the stationary perturbations, we find

$$\begin{aligned} w_{0}= & {} \{b_{9}\; {\exp }[(\gamma _{1})^{0.5}z]+b_{10} \;{\exp }[-(\gamma _{1})^{0.5}z]+b_{11}\; {\exp }[(\gamma _{2})^{0.5}z]\nonumber \\&+b_{12}\; {\exp }[-(\gamma _{2})^{0.5}z]\}H(x, y), \end{aligned}$$
(12a)
$$\begin{aligned} T_{0}= & {} \{\{b_{13} {\exp }[(\gamma _{1})^{0.5}z]+b_{14} {\exp }[-(\gamma _{1})^{0.5}z]+b_{15} {\exp }[(\gamma _{2})^{0.5}z]\nonumber \\&+b_{16} {\exp }[-(\gamma _{2})^{0.5}z]\}H(x, y), \end{aligned}$$
(12b)
$$\begin{aligned} \gamma _{1}\equiv & {} [\alpha ^{2}/(2+2\tau ^{2})]\{(2+\tau ^{2})+[\tau ^{4}+4(1+\tau ^{2}) \alpha ^{-2}\beta _{1}^{2}R_{s0}]^{0.5}\},\nonumber \\&\beta _{1}^{2}\equiv {T}^{{s}}+1, \end{aligned}$$
(12c)
$$\begin{aligned} \gamma _{2}\equiv & {} [\alpha ^{2}/(2+2\tau ^{2})]((2+\tau ^{2})-[\tau ^{4}+4(1+\tau ^{2}) \alpha ^{-2} \;\beta _{1}^{2}R_{s0}]^{0.5}\}, \end{aligned}$$
(12d)
$$\begin{aligned} P_{0}= & {} \sum \limits ^{N}_{n=-N} \{-(1/\gamma _{1})^{0.5}(b_{17}+b_{21} \; R_{s0})({\exp }[(\gamma _{1})^{0.5}z]-{\exp }[(\gamma _{1})^{0.5}])\nonumber \\&+(1/\gamma _{1})^{0.5}(b_{18}+b_{22}R_{s0})({\exp }[-(\gamma _{1})^{0.5} \; z]-{\exp }[-(\gamma _{1})^{0.5}])\nonumber \\&-(1/\gamma _{2})^{0.5}(b_{19}+b_{23}R_{s0})({\exp }[(\gamma _{2})^{0.5}z]-{\exp }[(\gamma _{2})^{0.5}])\nonumber \\&+(1/\gamma _{2})^{0.5}(b_{20}+b_{24}R_{s0})({\exp }[-(\gamma _{2})^{0.5}z]-{\exp }[-(\gamma _{2})^{0.5}])\nonumber \\&+ P_{00}(1)\}E_{n} \;\eta _{{n}}(x, y), \end{aligned}$$
(12e)
$$\begin{aligned} (u_{0}, v_{0})= & {} -[1/(1+\tau ^{2})]\sum \limits ^{N}_{n=-N} {i}(\alpha _{{nx}}\nonumber \\&+\alpha _{{ny}}\tau , -\alpha _{{nx}}\tau +\alpha _{{ny}})P_{01}(z)E_{n} \; \eta _{{n}} (x, y), \end{aligned}$$
(12f)
$$\begin{aligned} A_{0}= & {} T_{0} /M_{ac}, B_{0}=T_{0} /M_{bc}, \end{aligned}$$
(12g)
$$\begin{aligned} \phi _{{a}0}= & {} [1/(1-2A_{B})]\{(1-A_{B})(\hbox {d}A_{B}/\hbox {d}z)[{\smallint }_{1}^{z} \; w_{0} \hbox {d}z+a_{1}]\nonumber \\&+B_{B}(\hbox {d} B_{B}/\hbox {d}z)[{\smallint }_{1}^{z} \; w_{0} \hbox {d}z+a_{2}]\}, \end{aligned}$$
(12h)
$$\begin{aligned} \phi _{{ b}0}= & {} [1/(1-2B_{B})]\{A_{B}(\hbox {d}A_{B}/\hbox {d}z)[{\smallint }_{1}^{z} \; w_{0} \hbox {d}z+a_{1}]\nonumber \\&+(1-B_{B})(\hbox {d}B_{B}/\hbox {d}z)[{\smallint }_{1}^{z} \; w_{0} \hbox {d}z+a_{2}]\}, \end{aligned}$$
(12i)

where \(P_{01}(z)\) is the z-dependent coefficient for \(P_{0}\) in (12e), \(a_{1}\) and \(a_{2}\) are values of \((1-A_{B})\phi _{{a}0}\) and \((-B_{B} \;\phi _{{b}0})\), respectively, at \(z=1\) for the primary mushy-layer solution given in (8h), the expressions for the unknown constants \(b_{m}\; (m=9, 10, {\ldots }, 16)\) satisfy a set of linear algebraic equations, which are given by (15) in “Appendix” section.

Considering the 16 linear algebraic equations for the unknown constants \(b_{m}\; (m=1, 2, {\ldots }, 16)\) which are given by (14) and (15) in “Appendix” section, these equations can be written in matrix form like \(M\; \mathbf{b}=0\), where \(\mathbf{b}\equiv (b_{1}, b_{2}, {\ldots }, b_{16})^{{T}}\) is the vertical vector of the unknown constants, whose components are the 16 unknown scalar constants, and M is the matrix of coefficients of these 16 constants in the 16 equations. Setting \({\vert }M{\vert }=0\), where \({\vert }M{\vert }\) is the determinant of this matrix, we obtain by successive elimination approach a very lengthy form for the eigenvalue relation for the marginal stationary stability problem. For simplicity, the relation is in the form of an equation like

$$\begin{aligned} D(R_{p0}, R_{s0}, \alpha , l, \tau , T^{s})=0. \end{aligned}$$
(13)

We choose fixed values for constants \(T^{s}=-0.9\) and \(l=10.0\), which satisfy the constraint (6f). Thus, for given values of these constants in (13) as well as given value of the rotational parameter \(\tau \), this equation is a function of two effective mush Rayleigh numbers and the wave number at the onset of motion. Since we are going to present the results to the leading orders of the mush Rayleigh numbers for the primary and secondary mushy layers, we are going to refer to them, hereafter, as \(R_{p}\) and \(R_{s}\) without an extra subscript “0,” respectively.

4 Results and Discussion

Following the cases of previous studies (Anderson and Schulze 2005; Riahi 2014), we consider zero thermal Rayleigh number with \(A^{E}=B^{E}=1/3\), \(M_{b}=0\), \(M_{a}=M_{ac}=M_{bc} =1/(A^{P}-1/3)\), \(A^{P}=A^{H} =0.55\) and \(B^{P}=B^{H} =0.35\). These values are similar to those in Anderson and Schulze (2005) for the case where the secondary mushy layer is thin and the primary mushy layer is relatively thick, which is the type of model in the present study. We also tried different values for \(A^{H}\) and \(B^{H}\) and found no qualitative change in the behavior of the resulting solutions.

Using the iterative procedure to solve the eigenvalue relation (13), we consider three specific cases and determine the results for the convective flow in the absence or presence of the rotational constraint at small rate: (i) Case I where we assume that convection at the onset of motion is driven equally from both mushy layers \((R_{p}=R_{s})\); (ii) Case II where we assume that convection at the onset of motion is driven more from the primary mushy layer \((R_{p}>R_{s})\); Case III where we assume that convection at the onset of motion is driven more from the secondary mushy layer \((R_{p}<R_{s})\).

4.1 Neutral Stability Boundaries and Critical Values

The eigenvalue relation (13) was calculated by applying an iterative procedure for several values of the rotational parameter and for the three cases that we described earlier in this section.

(i) Case I Here we assume that the convection at the onset of motion is driven equally from both mushy layers \((R_{p}=R_{s})\). For each value of the rotational parameter \(\tau \), which is assumed to be smaller than unity, we detected two neutral stability curves of similar shapes. We refer to each of these two cases as one due to mode 1, which has the smaller value of the critical \(R_{pc}\) at the onset of motion, and another one due to mode 2. In addition, in the presence of rotation, we found more than one local minimum on each neural stability curves, and one of these local minima is the global minimum providing the critical values of the mush Rayleigh number and the corresponding critical wave number. In order to make sure about numerical correctness of these results, we use two iterative procedures each with particular scaling, and we confirmed the existence of such minima on the neutral stability boundaries in the presence of rotational constraint. It should also be noted that existence of local minima on the neutral stability boundaries has also been found before for multi-component flow at the onset of convection under certain conditions, such as, for example, convection due to the surface tension variations (Skarda and McCaughan 1999). Figures 2, 3 and 4 present \(R_{p}\) versus the horizontal wave number \(\alpha \) for different values of \(\tau \) on the neutral stability curves for this case. The flow is unstable in the region above each of the curves and stable in the region under the curve. Figure 2 presents three neural stability curves for the mode 1 and for three different values of \(\tau =0, 0.47 \,\text {and}\, 0.94\), which were selected for producing these figures just to make sure the corresponding produced figures can provide relatively clear indications of the results. Numerical values of the critical Rayleigh numbers and the wave number at the lowest point on this curve are found to be \(R_{pc}=R_{sc}=4.82\) and \(\alpha _{{c}}=0.35\) for \(\tau =0\). For \(\tau =0.47\), \(R_{pc}=R_{sc} =5.53\) and \(\alpha _{{c}}=0.40\). For \(\tau =0.94\), \(R_{pc}=R_{sc} =7.33\) and \(\alpha _{{c}}=0.44\). It can be seen from this figure that both \(R_{p}\) and \(\alpha \) increase with \(\tau \) implying the result of stabilizing effect of rotation, which confirms to be true in a ternary flow system as is also known to be valid in the binary flow system (Riahi 2003) as well as in the thermal convection problems (Busse 1978). However, comparing these results for the present ternary system with those for the rotating binary counterpart system (Riahi 2003) indicates that the present results for the critical values are smaller than those for the binary problem, so that the present ternary system is less stabilizing. Comparing our result for zero-rotation case to the ternary case calculated in Riahi (2014), it is seen that the present values for both critical mush Rayleigh number and wave number are smaller than the corresponding values reported in Riahi (2014), which is expected due to the relatively thick primary mushy layer in the present case that can lead to lower critical values. About the existence of more than one local minimum on the neutral stability curves that we found for the nonzero-rotation cases, we referred to this result earlier, as an example in the case of \(\tau =0.47\), and for the mode 1, we found local minima are at about \(\alpha =0.35\) \((R_{p} =5.54)\), \(\alpha =40\,(R_{p} =5.53)\) and \(\alpha =0.44\,(R_{p}=5.61)\). Since the differences between these minimum values for \(R_{p}\) are rather small, Fig. 2 does not show the differences clearly, but our generated data clearly indicated these results. Figure 3 presents the neutral stability boundaries for the values of the rotational parameter that were stated before but now for the mode 2. As in the case of the mode 1, the mush Rayleigh number and the wave number again increase with the rotation rate. But here for the mode 2, \((R_{pc}, \alpha _{{ c}})=(5.30, 0.35)\) for \(\tau =0, (R_{pc}, \alpha _{{c}})=(6.02, 0.40)\) for \(\tau =0.47\) and \((R_{pc}, \alpha _{{c}})=(7.99, 0.44)\) for \(\tau =0.94\). Comparing the results for both modes as provided in Figs. 2 and 3, it can be concluded that the preferred critical values are those based on the mode 1. Figure 4 presents the neutral stability curves for the two modes 1 and 2 for \(\tau =0.94\). It can be seen the similarity between the shapes of the 2 curves and the clear preference of the mode 1.

Fig. 2
figure 2

The neutral stability curves for the primary Rayleigh number \(R_{p}\) versus the wave number \(\alpha \) for the case of the critical mode 1 with \(R_{p}=R_{s}\) at \(\tau =0\) (dotted line, \(R_{pc} =4.82, \alpha _{{c}}=0.35)\), \(\tau =0.47\) (solid line, \(R_{p} =5.53, \alpha _{{c}}=0.40\)) and \(\tau =0.94\) (dashed line, \(R_{pc}= 7.33, \alpha _{{c}} =0.44\))

Full size image
Fig. 3
figure 3

The same as in Fig. 2 but for the mode 2 at \(\tau =0\) (dotted line, \(R_{pc}=5.36\), \(\alpha _{{c}}=0.36\)), \(\tau =0.47\) (solid line, \(R_{pc}=6.02\), \(\alpha _{{c}}=0.40\)) and \(\tau =0.94\) (dashed line, \(R_{pc} =7.99\), \(\alpha _{{c}}=0.44\))

Full size image
Fig. 4
figure 4

The neutral stability curves for \(R_{p}\) versus \(\alpha \) for \(R_{p}=R_{s}\) and \(\tau =0.94\) for the mode 1 (dashed line) and the mode 2 (solid line)

Full size image

(ii) Case II Here we assume that the convection at the onset of motion is driven more from the primary mushy layer \((R_{s}\; <R_{p})\). Generating data for several different values for \(R_{s}\) in this case, we found that a typical value can be \(R_{s}\) =0.01. Figures 5 and 6 present the neutral stability curves for this case. Figure 5 is the analog of Fig. 2 for the mode 1 with the primary mush Rayleigh number versus the wave number with different values of the rotational parameter. The critical values of the parameters are found to be \((R_{pc}, \alpha _{{c}})=(4.84, 0.37)\) for \(\tau =0, (R_{pc}, \alpha _{{c}})=(5.55, 0.41)\) for \(\tau =0.47\) and \((R_{pc}\), \(\alpha _{{c}})=(7.34, 0.45)\) for \(\tau =0.94\). It can be seen from these critical values and those results given for Fig. 2 that the critical values for the primary mush Rayleigh number and wave number are slightly higher in the Case II than those in the Case I. These results are found to be due to the facts that the secondary mushy layer is thin and the value of the secondary mush Rayleigh number is small in the Case II as compared to the one in the Case I, and, thus, it requires higher values for the critical parameters at the onset of motion. Figure 6 is analog to Fig. 4 for the Case I. It presents the neutral stability curves for both modes at \(\tau =0.94\). It can be seen a clear preference of the mode 1 at this value of \(\tau \), which according to our additional generated data indicates to be true for other values of the rotational parameter as well. So, the flow is unstable in the region above the neutral curve for the mode 1 in the plane \((R_{p}, \alpha )\) and stable in the region below the curve. For zero-rotation case, the numerical values of the critical primary mush Rayleigh number and the wave number at the lowest point on this curve are found to be smaller than the corresponding ones reported in Riahi (2014), which is due to the fact that the primary mushy layer is relatively thick in the present model as compared to the corresponding one in the model studied by Riahi (2014).

Fig. 5
figure 5

The neutral stability curves for \(R_{p}\) versus \(\alpha \) for the critical mode 1 with \(R_{s}\)=0.01 at \(\tau =0\) (dotted line, \(R_{pc} =4.84\), \(\alpha _{{c}}=0.37\)), \(\tau =0.47\) (solid line, \(R_{pc}=5.52\), \(\alpha _{{c}}=0.41\)) and \(\tau =0.94\) (dashed line, \(R_{pc} =7.31, \alpha _{c} = 0.45\))

Full size image
Fig. 6
figure 6

The same as in Fig. 4 but for \(R_{s}=0.01\)

Full size image

(iii) Case III Here we assume that the convective flow at the onset of motion is driven more from the secondary mushy layer \((R_{s}>R_{p})\). Generating data for several values of \(R_{p}\) in this case, we found that a typical case can be \(R_{p}=0.9\; R_{s}\). Figures 7 and 8 present the neutral stability curves for this case. Figure 7 presents the neural stability curves with \(R_{s}\) versus \(\alpha \) for the more critical mode 1 and for three different values of the rotational parameter. For each value of the rotational parameter, the convective flow is unstable in the region above the curve in the plane \((R_{s}, \alpha )\) and stable in the region below the curve. It can be seen from this figure that both secondary mush Rayleigh number and the wave number increase with the rotation rate. Numerical values of the critical secondary mush Rayleigh number and the wave number at the lowest point on this curve were found to be \((R_{sc}, \alpha _{c})=(5.45, 0.38)\) for \(\tau =0\), \((R_{sc}, \alpha _{{c}})=(6.11, 0.41)\) for \(\tau =0.47\) and \((R_{sc}, \alpha _{{c}})=(8.11, 0.45)\) for \(\tau =0.94\). Comparing these critical values with the corresponding ones in the Case I, we find that the critical values for the Case III are higher than the corresponding ones for the Case I. These results are again due to the facts that since the primary mush Rayleigh number is smaller than the secondary mush Rayleigh number in the Case III, it requires higher values for the secondary mush Rayleigh number to initiate convective flow in the ternary system. Also similar to the previous 2 cases, we were able to detect more than one local minimum on each neutral stability curve for both mode 1 and mode 2 in the rotating case. Figure 8 is analog to Fig. 4 for this case, which shows neutral stability curves for both mode 1 and mode 2 for \(\tau =0.94\). It can also be seen from this figure and from our additional generated data the preference of mode 1, which was found to be the case for other values of the rotation rate that we calculated.

Fig. 7
figure 7

The neutral stability curves for \(R_{p}\) versus \(\alpha \) for the critical mode 1 with \(R_{p} =0.9R_{s}\) at \(\tau =0\) (dotted line, \(R_{sc}=5.45\), \(\alpha _{{c}}=0.38\)), \(\tau =0.47\) (solid line, \(R_{sc}=6.12\), \(\alpha _{{c}}=0.40\)) and \(\tau =0.94\) (dashed line, \(R_{sc}=8.11\), \(\alpha _{{c}}=0.44\))

Full size image
Fig. 8
figure 8

The same as in Fig. 4 but for \(R_{p}=0.9R_{s}\)

Full size image

From the results presented in Figs. 2, 3, 4, 5, 6, 7 and 8, it can be seen that the convective flow in the primary mushy layer is more significant than that in the secondary mushy layer for both in the absence and presence of the rotational effect, which appear to be reasonable since the primary mushy layer is relatively thick in comparison with the secondary mushy layer, and, in addition, the primary mushy layer contains solid dendrite due to only composition A, while the secondary mushy layer contains solid dendrites due to both compositions A and B, even though the secondary mushy layer is adjacent to the solidification front.

4.2 Vertical Volume Flux and Perturbation to Solid Fraction

In this subsection we present results and the associated discussion for the vertical volume flux and the perturbation to solid fraction for the two solutions that we found after solving system of 16 linear equations for 16 unknowns \(b_{m} (m=1, 2, {\ldots }, 16)\) constants that we described before in Sect. 3. Since the solution is linear, then these unknown constants are determined in terms of one of them say \(b_{1}\). Hence, depending on the sign of this constant, we have 2 solutions as in the case studied in Riahi (2014) for the three-dimensional flow solution in the form of hexagons.

To be specific, we also consider the solution of the convective flow to be in the form of hexagons, which is known to be one of the observable and the simplest types of the convective flow in thermal convection (Busse 1978) that is also known to be observed in the convection during the solidification of binary alloys (Tait et al. 1992). However, it should be noted that the present cellular convective flow in the horizontal mushy layers is of the type of standard convection in a semi-infinite region in the horizontal direction with no vertical walls, and the linear solutions exhibit, in particular, pattern degeneracy (Busse 1978). Thus, the present results to be described here for the case of convection in the form of hexagons can also be applicable, in general, to any other form of the cellular solutions but at different horizontal locations of such form. Even though no experimental observations have been done so far for the observable form of convection in the present type of ternary problem, we follow Riahi (2014) and consider the present convective flow is in the form of hexagons. According to the results reported in Riahi (2014), there are two hexagonal-type solutions one of which was found to be stable. Hence, in the present investigation we consider the solution that is the analog of the stable-type solution in Riahi (2014) which turns out to correspond to positive sign for \(b_{1}\) and \(\varepsilon \). We then determined the results for the leading terms of the vertical volume flux \(w_{0}\) and the perturbation to solid fraction \([\phi _{{a}(-1)}+\phi _{{b}(-1)}]\) for such solution for the three Cases I–III, which are described below.

Fig. 9
figure 9

Vertical volume flux at a hexagonal cell’s center versus vertical variable z for \(R_{p} ={R}_{{s}}\), \(\tau =0\) (dotted line), \(\tau \)=0.47 (solid line) and \(\tau =0.94\) (dashed line)

Full size image
Fig. 10
figure 10

The same as in Fig. 9 but at a node of the same hexagonal cell

Full size image

(i) Case I where \(R_{p}=R_{s}\). Figures 9 and 10 present the vertical distribution of vertical volume flux versus z at the center and at a node of a hexagonal cell, respectively. As is expected, we also inspected that the present results at the center and at a node of a cell (Chandrasekhar 1961) are representative for the center and node of any cell. It can be seen from Figs. 9 and 10 that in both mushy layers the flow is downward at cell center and upward at the node for zero- and nonzero-rotation cases. Thus, the hexagonal convection is in the form of down-hexagons, which actually was the type of convection pattern observed by Tait et al. (1992) for the binary system and in the absence of rotation. In contrast to the linear result for the binary counterpart system (Riahi 2003), where the magnitude of the vertical volume flux to the leading order term was constant; in the present case the vertical volume flux increases with the rotation rate which indicates that the rotational force has more destabilizing effects in the present ternary system. For both zero- and nonzero-rotation cases, the magnitude of the vertical volume flux at both center and the node of the cell increases with the vertical variable up to a horizontal level about \(z=5.5\), beyond which it decreases with increasing z. The rate of change of the vertical volume flux with respect to the vertical variable increases by the rotational effect in both of the mushy layers. Vertical rate of increase of the magnitude of the vertical volume flux increases with the rotational parameter and is largest in the secondary mushy layer. In the primary mushy layer such rate increases with the rotational parameter up to about \(z=5.5\) level, beyond which such rate decreases with increasing \(\tau \).

Fig. 11
figure 11

The same as in Fig. 9 but for the perturbation to solid fraction

Full size image
Fig. 12
figure 12

The same as in Fig. 10 but for the perturbation to solid fraction

Full size image

Figures 11 and 12 present the perturbation to solid fraction versus z at center and a node of a hexagonal cell, respectively. It can be seen and implied from these figures as well as from the actual generated data that there is a total solid fraction (basic state plus perturbation) enhancement at the center of the cell, but there is a total solid fraction reduction at the node of the cell. The total solid fraction increases with the rotation rate at the center of the cell, while the total solid fraction decreases with increasing the rotation rate at the nodes of the cell. Since these results correspond to particular horizontal locations of the cells’ centers and nodes and are independent of the vertical variables, such results can be said to hold at particular vertical fluid lines in the flow system. Furthermore, these figures as well as our actual generated data indicate that the perturbation to solid fraction at the center of the cell increases with z up to a horizontal level about \(z=1.5\), which is at a horizontal level close to the interface between the two mushy layers, beyond which it decreases with increasing z. At the node of the cell, the magnitude of the perturbation to solid fraction increases with z up to \(z=1.5\) and then decreases with increasing z for \(z>1.5\). If these results can be also valid qualitatively beyond the linear regime, then under such possibility it may be concluded that the tendency for chimney formation with least solid fraction may initiate at different horizontal locations on the horizontal level at \(z=1.5\), and such tendency is along the vertical direction. This later implication is in agreement with the experimental observation (Sample and Hellawell 1984; Tait et al. 1992) that chimney and dendrite generally form in the vertical direction in the presence of rotation (Sample and Hellawell 1984) or in the absence of rotation (Tait et al. 1992) in the binary systems. No experimental results are available about such flow features in a ternary system. Based on our additional generated data, we confirm that rate of increase of the total solid fraction with respect to the rotation rate at the center of the cell of down-hexagons increases in the secondary mushy layer. The same can be valid for the up-hexagonal case, if the location of center of the cell is replaced by a node of the cell. Rate of change of the total solid fraction with respect to the vertical variable increases by the rotation rate in both of the mushy layers. The Coriolis force appears to strengthen the magnitude of the perturbation to solid fraction in a region close to the interface between the two mushy layers. In contrast to the binary alloy counterpart case (Riahi 2003) where the magnitude of the perturbation to solid fraction decreases with increasing z, here in the ternary alloy case such magnitude increases with increasing z in the secondary mushy layer and reaches a maximum value in the primary mushy layer but near the interface between the two mushy layers.

(ii) Case II where \(R_{s} =0.01\). Similar to the Case I, we carried out our calculation for the vertical volume flux and the perturbation to the solid fraction. Our generated data indicate qualitative results similar to those presented in Figs. 9, 10, 11 and 12, provided the results presented by Figs. 9 and 11 be applied at a node of the cell, and the results presented by Figs. 10 and 12 be applied at the center of the cell. Thus, no additional figures are produced for this case.

(iii) Case III where \(R_{p}=0.9\, R_{s}\). Similar to the Case I, we carried out our calculation for the vertical volume flux and the perturbation to the solid fraction, and we found the results to be qualitatively similar to those presented in Figs. 9, 10, 11 and 12. Thus, no additional figures are produced for this case.

4.3 Comparison with Other Related Studies

Guba (2001) studied the effect of uniform rotation on convection in a mushy layer during binary alloy solidification. As in the present study, the author did not take into account the interaction between the local solid fraction and the flow associated with the Coriolis term in the Darcy momentum equation. For the linear convection, the results given in Guba (2001) indicated, in particular, that in contrast to the present rotating ternary counterpart system, there was a single neutral stability curve for a given rotational parameter with no more than one minimum on such curve. Similar to the present result, the values of the critical mush Rayleigh number and the associated wave number were increased with the rotation rate. However, the present results indicate that the critical values for the mushy Raleigh number and wave number are relatively smaller than the corresponding values in the binary flow case, which implies less stabilizing effect by the rotational constraint in the present ternary flow case. No results were provided by Guba on the vertical volume flux and the perturbation to solid fraction in the linear regime of his studies for a binary alloy system.

Riahi (2003) extended the work due to Guba (2001) by taking into account the interaction between the local solid fraction and the convection associated with the Coriolis term in the momentum Darcy equation and carrying out a stability analysis of several types of finite-amplitude steady solutions. However, the linear results reported in Riahi (2003) also indicate results without the presence of above interaction and found, in particular, that in contrast to the present ternary flow case, the leading order vertical volume flux was independent of the rotation rate, and the critical values for the mush Rayleigh number and the wave number had higher values as compared to the corresponding present ternary counterpart results at the same rotation rate. In contrast to the present result that the magnitude of perturbation to solid fraction increases with the vertical variable in the secondary mushy layer, Riahi (2003) found that such magnitude decreases with increasing z in the mushy layer of the studied binary alloy flow case.

Riahi (2014) studied three-dimensional convection in the form of hexagons in mushy layers during ternary alloy solidification and in the absence of rotation. He considered the case where the thickness of the primary mushy layer was moderate. For the linear convection, the results determined by Riahi (2014) indicated that in contrast to the present zero-rotation result, no multi-modal existed for the neutral stability boundary. The critical values for the mush Rayleigh numbers and the associated wave numbers were calculated in Riahi (2014) where relatively larger than the corresponding ones determined in the present study, which is expected to be due to the fact that in contrast to the system studied in Riahi (2014), in the present study the thickness of the primary mushy layer is relatively thick, so that smaller values of the critical values at the onset of motion can initiate convective motion. To the author’s best knowledge, the present study is the first one that takes into account the rotational effect for the problem of convection in mushy layers during ternary alloy solidification, and, thus, no comparison with other related investigation on this aspect can be possible.

5 Conclusion

We studied theoretically the problem of convection during the solidification of ternary alloys and rotating at a constant and low rate about the vertical axis. Under the assumption of large far-field temperature, our model for the ternary flow system was considered to be composed of a primary mushy layer above a secondary mushy layer, which is above the solidification front. We determined the motionless basic state solution for the ternary system which holds for sufficiently small values of the effective mush Rayleigh numbers. We then carried out linear stability analysis for the basic state and determined the results for the neutral stability boundaries, critical conditions at the onset of convection, vertical volume flux and the perturbation to solid fraction for several cases in the presence or absence of the rotational constraint. We found, in particular, that for each value of the rotation rate there are two convective modes with distinct neutral stability curves. For nonzero low rotation rate, there can be more than one local minimum on each neutral stability boundary. Similar to the binary flow system (Riahi 2003), our present result for a ternary flow system confirms that the critical values of the mush Rayleigh numbers and the wave number increase with the low rotation rate. However, our results indicate that the present ternary flow system is less stabilizing than the one for the binary flow counterpart. For the case of convection in the form of hexagons, we determined the effect of rotation on the vertical volume flux and the perturbation to the solid fraction. We found that the magnitude of the vertical volume flux and the magnitude of the perturbation to solid fraction increase with the low rotation rate. Such rate of increase of the magnitude of the vertical volume flux increases in the secondary mushy layer and is higher in this layer, while the rate of increase of the magnitude of the perturbation to solid fraction decreases with increasing the rotation rate in this layer. For down-hexagons, the total solid fraction at the node and center of any hexagonal cell reduces and enhances, respectively, with respect to the low rotation rate. For up-hexagons, the total solid fraction at the node and center of any hexagonal cell enhances and reduces, respectively, with respect to the low rotation rate. For general cellular structures, presence of rotation can enhance solid and liquid fractions vertically at particular horizontal locations in the ternary flow system.

In the present investigation linear examination of the rotating ternary system at low rate was restricted to \(o(\varepsilon )\) of the perturbations superimposed on the motionless basic state which enabled us to examine the effect of rotation at low rate on the linear hexagonal-type solutions that can be preferred for the smallest values of the amplitude \(\varepsilon \) and the mush Rayleigh numbers. However, computation of the nonlinear properties of such rotating ternary flows up to \(o(\varepsilon ^{2})\) for the hexagonal- and nonhexagonal-type solutions will be quite complex requiring very extensive algebras and remain a subject for future work. In addition, our present study was restricted to low ration case with the rotational parameter values less unity. For moderate or high rotation rates, our initial investigation indicated that the linear eigenvalue value system did not converge, and perhaps a more numerical approach may be needed to investigate possible moderate and high values of the rotation rate cases, and thus, it also remains a subject for future studies.

Although there have been some notable experimental results and discoveries in the nonrotating ternary systems (Aitta et al. 2001a, b; Thompson et al. 2003b) about the presence of distinct primary and secondary mushy layers, which can form between solid and liquid layers, no experimental result is known for either rotating or nonrotating cases about the effect of rotation and/or the form of convection pattern near the onset of motion that could operate in the ternary system cooled from below. It is hoped that the present analytical results for the effect of rotation at the onset of motion can stimulate future experimental investigation on the subject.