Double-Diffusive Natural Convection in Anisotropic Porous Medium Bounded by Finite Thickness Walls: Validity of Local Thermal Equilibrium Assumption

Abstract

Double-diffusive natural convection in fluid-saturated porous medium inside a vertical enclosure bounded by finite thickness walls with opposing temperature, concentration gradients on vertical walls as well as adiabatic and impermeable horizontal ones has been performed numerically. The Darcy model was used to predict fluid flow inside the porous material, while thermal fields are simulated based on two-energy equations for fluid and solid phases on the basis of a local thermal non-equilibrium model. Computations have been performed for different controlling parameters such as the buoyancy ratio $N$, the Lewis number Le, the anisotropic permeability ratio $R_\mathrm{p}$, the fluid-to-solid thermal conductivity ratio $R_\mathrm{c}$, the interphase heat transfer coefficient $\mathcal{H}$, the ratio of the wall thickness to its height $D$, the wall-to-porous medium thermal diffusivity ratio $R_\mathrm{w}$, and the solid-to-fluid heat capacity ratio $\gamma$. Thus, the effects of the controlling parameters on heat and mass transfer characteristics are discussed in detail. Moreover, the validity domain of the local thermal equilibrium (LTE) assumption has been delimited for different set of the governing parameters. It has been shown that Le has a noticeable significant effect on fluid temperature profiles and that higher $N$ values lead to a significant enhancement in heat and mass transfer rates. Moreover, for higher $\mathcal{H}, R_\mathrm{c}$, $R_\mathrm{p}, R_\mathrm{w}$, or $D$ values and/or lower $\gamma$ values, the solid and fluid phases tend toward LTE.

1 Introduction

The problem of double-diffusive convection in porous media has been the subject of several surveys due to its emerging practical applications, from the solidification of binary mixtures to the migration of solutes in water-saturated soils. The other examples include geophysical systems, electrochemistry, and migration of moisture through air contained in fibrous insulation, just to name a few applications.

The most available studies on double-diffusive natural convection in fluid-saturated porous media were under the assumption that the solid and fluid phases are in local thermal equilibrium (LTE).

Mamou and Vasseur (1999) have studied double-diffusive instability in a horizontal rectangular porous enclosure subjected to vertical temperature and concentration gradients.

A numerical investigation of double-diffusive convection in vertical annulus with opposing temperature and concentration gradients has been studied by Chen et al. (2010) for higher Rayleigh numbers using a simple Lattice Boltzmann Model.

Double-diffusive convection in a vertical enclosure filled with anisotropic porous media has been studied numerically by Bennacer et al. (2001). Mamou et al. (2001) performed both analytical and numerical stability analyses of double-diffusive convection in a confined horizontal rectangular enclosure based on Galerkin and finite element methods using the Darcy–Brinkman model.

Bennacer et al. (2002) have studied thermosolutal convection in a two-dimensional rectangular cavity filled with a saturated homogeneous porous medium that is thermally anisotropic. They have presented an analytical and numerical study of combined heat and mass transfer driven by buoyancy forces due to temperature and concentration variations.

Al-Farhany and Turan (2012) have presented numerical study of double-diffusive natural convective heat and mass transfers in an inclined rectangular cavity filled with a porous material. The authors have demonstrated that as the aspect ratio increases, the average Nusselt and Sherwood numbers are reduced, although they decrease when the inclination angle increases.

A steady conjugate double-diffusive natural convective heat and mass transfer in a two-dimensional variable porosity layer sandwiched between two walls has been studied numerically using Forchheimer–Brinkman–extended Darcy model by Al-Farhany and Turan (2011).

However, in some applications, there are situations where the local thermal equilibrium LTE assumption is not valid. In fact, when a substantial temperature difference exists between the solid and fluid phases (Vafai 2000), it is essential that the phases of the porous material should be modeled separately, and, therefore, the adoption of a two-temperatures model known as local thermal non-equilibrium (LTNE) model has now become quite common place for convecting flows in saturated porous media problems. A review by Rees and Pop (2005) summarizes much of the present knowledge, including the various models used for LTNE and their applications to free, mixed, and forced convective flows and stability analyses problems.

Several numbers of papers dealing with natural convection in fluid-saturated porous media problems based on LTNE approach have been studied by many authors (Baytaş and Pop 2002; Saeid 2004; Borujerdi et al. 2007). Baytaş (2003) has studied thermal non-equilibrium natural convection in a square enclosure filled with a heat-generating solid phase non-Darcy porous medium. Wang et al. (2007) have presented a numerical investigation of natural convection (without mass transfer) in an inclined square enclosure filled with a porous medium and submitted to a strong magnetic field using a LTNE model. Vadász (2011) has studied the problem of natural convection in a vertical porous layer differentially heated from its sidewalls. He has found that the LTNE state destroys the symmetry of the problem via deviatoric terms in the solutions. Saeid (2006) has applied the LTNE model to study free convection from a horizontal cylinder immersed in a porous medium (PM) using an implicit finite difference method based on Keller box algorithm. A two-temperature model for predicting heat and fluid flow by natural convection and radiation within a saturated porous vertical channel has been studied numerically by Slimi (2009).

Double-diffusive convection in a porous layer using a LTNE model has been studied by Malashetty et al. (2008). It has been concluded that small interphase heat transfer coefficient has significant effect on the stability of the system. Ahmed (2011) has numerically analyzed the problem of mixed convection in a vertical annular cylinder saturated with a PM using a LTNE approach. Numerical results indicate that the LTNE approach gives more realistic predictions of heat transfer rate and fluid flow behavior in the PM confined in the annular cylinder.

Harzallah et al. (2010) have studied the problem of unsteady natural convection in an anisotropic PM bounded by finite thickness walls. Their results have shown that as the wall-to-porous thermal conductivity ratio and the heat capacity ratio are increased, conductive heat transfer mode is enhanced. For larger longitudinal anisotropic permeability ratio, convective heat transfer mode is dominant. It was put in evidence that as the transverse thermal conductivity ratio increases and/or the ratio of the wall thickness to its height decreases, the heating rate of the medium increases.

The stability analysis of thermosolutal convection in a horizontal porous layer using a LTNE model was studied by Chen et al. (2011). It has been demonstrated how the reaction and non-equilibrium model affect the double-diffusive convection in porous media. Free convection heat and mass transfers of fluid in a square packed bed enclosure have been recently numerically studied by Mehdy (2012) using a LTNE model.

The present paper gives more attention to examine the effects of finite thickness conducting walls as well as the mechanical anisotropy on the unsteady double-diffusive natural convection taking place in a porous material sandwiched between two-vertical finite thickness walls maintained at constant but different temperatures. The two-vertical left and right interfaces wall-porous material are, respectively, kept at constant high and low concentration values. The remaining two-horizontal walls are assumed to be impermeable to mass transfer and thermally insulated. A LTNE model will be used to derive the energy conservation equations for the two phases. Furthermore, the validity of The LTE assumption will be examined for different set of the controlling parameters.

First, the governing macroscopic equations along with the appropriate initial and boundary conditions will be written in a dimensionless form on the basis of appropriate hypotheses. The obtained set of the dimensionless governing equations along with the appropriate initial and boundary conditions will be numerically solved using the classical finite volume method (Patankar 1980). Then, a sensitivity study restricted to the effects of the Lewis number Le, the buoyancy ratio $N$, on fluid flow and heat and mass transfer rates will be examined and discussed in detail. We shall precise that the effects of the other remaining parameters have been previously done by the co-authors (see for instance, Slimi et al. 1998; Amara and Slimi 2000; Slimi 2009; Harzallah et al. 2010). Our attention will also be paid to determine the validity domain of the LTE assumption for different set of the controlling parameters.

2 Mathematical Formulation

2.1 Problem Definition

A double-diffusive natural convective flow and heat and mass transfers inside a vertical enclosure filled with a fluid-saturated PM sandwiched between two equal-thickness walls are considered and displayed in Fig. 1.

Fig. 1

Physical model and coordinates system

The PM is assumed to be anisotropic in permeability. The left and right vertical walls are kept at constant high and low temperatures, respectively, $T_\mathrm{h}$ and $T_\mathrm{c}$. While the vertical wall’s interfaces to porous material left and right are to be, respectively, kept at constant high and low concentrations. The remaining horizontal walls are assumed thermally insulated and impermeable to mass transfer.

In order to predict thermal fields, energy conservation equations for the fluid and solid phases are separately derived on the basis of a LTNE model. The mathematical model takes also into account the energy transfer equation through the bounding finite thickness walls. The Darcy model and the Oberbeck–Boussinesq approximations are used. Viscous dissipation, compression work, radiative transfer, and the Soret as well as Dufour effects are assumed to be neglected.

2.2 Governing Equations

The governing set of macroscopic equations of the problem under investigation is rendered dimensionless on the basis of the following scales and non-dimensional variables:

$$\begin{aligned} \left( {X,Z} \right)&= \left( {\frac{x}{L_\mathrm{ref} },\frac{z}{L_\mathrm{ref} }} \right) ; \tau =\frac{t}{t_\mathrm{ref} }; \left( {U,W} \right) =\left( {\frac{u}{V_\mathrm{ref} },\frac{w}{V_\mathrm{ref} }} \right) ; \nonumber \\ \varPi&= \frac{P-P_0 }{P_\mathrm{ref} }; \theta =\frac{T-T_\mathrm{c} }{\varDelta T_\mathrm{ref} }; C=\frac{c-c_\mathrm{c} }{\varDelta c_\mathrm{ref} }; \theta _\mathrm{w} =\frac{T_\mathrm{w} -T_\mathrm{c} }{\varDelta T_\mathrm{ref} } \end{aligned}$$

(1)

with: $\;L_\mathrm{ref} \;=\;L\; ; t_\mathrm{ref} =\frac{L}{V_\mathrm{ref} }; P_\mathrm{ref} =\frac{\alpha \mu _\mathrm{f} }{K_x} ;V_\mathrm{ref} =\frac{\alpha }{L}; \varDelta T_\mathrm{ref} =T_\mathrm{h}-T_\mathrm{c}; \varDelta c_\mathrm{ref} =c_\mathrm{h}-c_\mathrm{c}$

The basic dimensionless macroscopic equations governing unsteady double-diffusive natural convection in Cartesian coordinates system $(X, Z)$ can be written as (Harzallah et al. 2010; Jbara et al. 2013)

Mass conservation equation

$$\begin{aligned} \frac{\partial U}{\partial X}+\frac{\partial W}{\partial Z}=0 \end{aligned}$$

(2)

Momentum conservation equation

$$\begin{aligned} U&= -\frac{\partial \varPi }{\partial X}\end{aligned}$$

(3)

$$\begin{aligned} W&= -R_\mathrm{p} \left[ {\frac{\partial \varPi }{\partial Z}-Ra\left( {\theta _\mathrm{f} +NC} \right) } \right] \end{aligned}$$

(4)

Substituting Eqs. (3) and (4) into Eq. (2) leads to Poisson equation for pressure.

$$\begin{aligned} \frac{\partial ^{2}\varPi }{\partial X^{2}}+R_\mathrm{p} \frac{\partial ^{2}\varPi }{\partial Z^{2}}-R_\mathrm{p} Ra\left( {\frac{\partial \theta _\mathrm{f} }{\partial Z}+N\frac{\partial C}{\partial Z}} \right) =0 \end{aligned}$$

(5)

Transport equation for fluid phase

$$\begin{aligned} \varepsilon \frac{\partial \theta _\mathrm{f} }{\partial \tau }+U\frac{\partial \theta _\mathrm{f} }{\partial X}+W\frac{\partial \theta _\mathrm{f}}{\partial Z}=\left[ {\frac{\varepsilon R_\mathrm{c} }{\left( {1-\varepsilon } \right) +\varepsilon R_\mathrm{c} }} \right] \left( {\frac{\partial ^{2}\theta _\mathrm{f} }{\partial X^{2}}+\frac{\partial ^{2}\theta _\mathrm{f} }{\partial Z^{2}}} \right) + \mathcal{H} \left( {\theta _\mathrm{s} -\theta _\mathrm{f} } \right) \end{aligned}$$

(6)

Transport equation for solid phase

$$\begin{aligned} \left( {1-\varepsilon } \right) \gamma \frac{\partial \theta _\mathrm{s} }{\partial \tau }=\left[ {\frac{\left( {1-\varepsilon } \right) R_\mathrm{c} }{\left( {1-\varepsilon } \right) +\varepsilon R_\mathrm{c} }} \right] \left( {\frac{\partial ^{2}\theta _\mathrm{s} }{\partial X^{2}}+\frac{\partial ^{2}\theta _\mathrm{s} }{\partial Z^{2}}} \right) + \mathcal{H} \left( {\theta _\mathrm{f} -\theta _\mathrm{s} } \right) \end{aligned}$$

(7)

Transport equation for the wall

$$\begin{aligned} \frac{\partial \theta _\mathrm{w} }{\partial \tau }=R_\mathrm{w} \left( {\frac{\partial ^{2}\theta _\mathrm{w} }{\partial X^{2}}+\frac{\partial ^{2}\theta _\mathrm{w} }{\partial Z^{2}}} \right) \end{aligned}$$

(8)

Concentration conservation equation

$$\begin{aligned} \varepsilon \frac{\partial C}{\partial \tau }+U\frac{\partial C}{\partial X}+W\frac{\partial C}{\partial Z}=\frac{1}{Le}\left( {\frac{\partial ^{2}C}{\partial X^{2}}+\frac{\partial ^{2}C}{\partial Z^{2}}} \right) \end{aligned}$$

(9)

Thus, the controlling parameters for the problem under consideration are the modified Rayleigh number $Ra\left( {=\frac{K_x g\beta _\mathrm{T} L\varDelta T}{\alpha \nu _f }} \right)$, the interphase heat transfer coefficient $\mathcal{H}\left( {=\frac{h_\mathrm{fs} a_\mathrm{fs} L^{2}}{\lambda }} \right)$, the Lewis number $Le\left( {=\frac{\alpha }{D_\mathrm{c} }} \right)$, the buoyancy ratio $N\left( {=\frac{\beta _\mathrm{C} \varDelta c}{\beta _\mathrm{T} \varDelta T}} \right)$, the anisotropic permeability ratio $R_\mathrm{p}\left( {=\frac{K_z }{K_x }} \right)$, the wall-to-porous medium thermal diffusivity ratio $R_\mathrm{w}\left( {=\frac{\alpha _\mathrm{w} }{\alpha }} \right)$, the fluid-to-solid thermal conductivity ratio $R_\mathrm{c}\left( {=\frac{\lambda _\mathrm{f} }{\lambda _\mathrm{s} }} \right)$, and the solid-to-fluid heat capacity ratio $\gamma \left[ {=\frac{\left( {\rho c_\mathrm{p} } \right) _\mathrm{s} }{\left( {\rho c_\mathrm{p} } \right) _\mathrm{f} }} \right]$.

2.3 Initial and Boundary Conditions

Initially, the porous medium is in hydrostatic equilibrium state and kept at cold uniform temperature $T_\mathrm{c}$. Relying on that, we get the following boundary conditions:

$$\begin{aligned}&\hbox {t}=0:P=\theta _\mathrm{f,s} =\theta _\mathrm{w} =0 \quad \hbox {at} \quad 0\le X\le 1 \quad \hbox {and} \quad 0\le Z\le A\end{aligned}$$

(10)

$$\begin{aligned}&\hbox {t}=0\,: C=0 \hbox { at } D\le X\le 1-D\quad \hbox {and}\quad 0\le Z\le A \end{aligned}$$

(11)

The bounding vertical walls of the enclosure (i. e., at $X=0, 1)$ are impermeable and maintained at uniform hot and cold temperatures, respectively. This leads to:

$$\begin{aligned} t>0:\left. {\frac{\partial \Pi }{\partial X}} \right) _{X=D,Z} =\left. {\frac{\partial \Pi }{\partial X}} \right) _{X=1-D,Z} =0 \quad \hbox {and}\quad \theta _\mathrm{w} \left( {0,Z,\tau } \right) =1 \quad \hbox {and} \quad \theta _\mathrm{w} \left( {1,Z,\tau } \right) =0\nonumber \\ \end{aligned}$$

(12)

The bounding interfaces between vertical walls and the PM (i.e., at $X=D, 1-D)$ are impermeable and maintained at uniform high and low concentrations, respectively. This leads to:

$$\begin{aligned} t>0:C\left( {D,Z,\tau } \right) =1 \quad \hbox {and}\quad C\left( {1-D,Z,\tau } \right) =0 \end{aligned}$$

(13)

The bounding horizontal walls of the enclosure (i.e., at $Z=0, A$) are impermeable and insulated. Relying on that, the hydrodynamic and thermal boundary conditions can be expressed as follows:

$$\begin{aligned} \left. {\frac{\partial \varPi }{\partial Z}} \right) _{X;Z=0,A}&= Ra\left[ {\theta _\mathrm{f} \left( {X;Z=0,A} \right) +NC\left( {X;Z=0,A} \right) } \right] \end{aligned}$$

(14a)

$$\begin{aligned} \left. {\frac{\partial \theta _\mathrm{w} }{\partial Z}} \right) _{X;Z=0,A}&= 0\; \hbox {for } 0\le X\le D \quad \hbox {and} \quad 1-D\le X\le 1\end{aligned}$$

(14b)

$$\begin{aligned} \left. {\frac{\partial \theta _\mathrm{f,s} }{\partial Z}} \right) _{X;Z=0,A}&= 0\; \hbox {for}\;D\le X\le 1-D\end{aligned}$$

(14c)

$$\begin{aligned} \left. {\frac{\partial C}{\partial Z}} \right) _{X;Z=0,A}&= 0\;\hbox {for}\;D\le X\le 1-D \end{aligned}$$

(14d)

The continuity of the thermal field at the two interfaces located at $X=D$ and $X=1-D$ can be expressed as follows:

$$\begin{aligned} \theta _\mathrm{w} \left( {D,Z,\tau } \right) =\theta _\mathrm{f,s} \left( {D,Z,\tau } \right) ; \;\theta _\mathrm{w} \left( {1-D,Z,\tau } \right) =\theta _\mathrm{f,s} \left( {1-D,Z,\tau } \right) \end{aligned}$$

(15)

The continuity of the conduction heat flux density across the two interfaces can be written as follows (Nield 2012):

$$\begin{aligned}&\left. {\frac{\partial \theta _\mathrm{w} }{\partial X}} \right) _{X=D,1-D;Z} =\left. {\varepsilon \frac{\partial \theta _\mathrm{f} }{\partial X}} \right) _{X=D,1-D;Z}\end{aligned}$$

(16a)

$$\begin{aligned}&\left. {\frac{\partial \theta _\mathrm{w} }{\partial X}} \right) _{X=D,1-D;Z} =\left. {\left( {1-\varepsilon } \right) \frac{\partial \theta _\mathrm{s} }{\partial X}} \right) _{X=D,1-D;Z} \end{aligned}$$

(16b)

3 Numerical Procedure

Equations (2)–(9) along with the associated initial and boundary conditions (10)–(16) have been numerically solved by the classical finite volume approach (Patankar 1980).

The calculated domain is discretized by a uniform rectangular grid of $N_{x} \times N_{z}$ control volumes of dimension $\varDelta x\times \varDelta z$. A fully implicit discretization scheme is used for temporal derivative terms in energy and concentration equations, while a power law scheme is used for convection–diffusion terms and a central scheme is used for diffusive terms.

The resulting discretized two-energy conservation equations and that of the wall, and concentration equation as well as the Poisson equation for pressure were solved by the alternating direction implicit (ADI) method. ADI leads to a tridiagonal matrix, which was solved with the tridiagonal matrix algorithm (TDMA).

After initializing all the variables (i.e., the wall as well as fluid and solid phase temperatures, respectively, $\theta _\mathrm{w}$ and $\theta _\mathrm{f,s}$, concentration $C$, and the pressure, $\varPi$) and choosing arbitrary values of these variables, the pressure field is determined by resolving Eq. (5). The velocity field is then deduced from Eqs. (3) and (4). The updated velocity field is then used to update the thermal fields by resolving the transport Eqs. (6)–(8) and the concentration conservation Eq. (9).

The numerical iterations were advanced in time until the satisfaction of the following convergence criteria:

$$\begin{aligned} \mathrm{Max}\left| {\frac{\varPhi _{m,n}^{i+1} -\varPhi _{m,n}^i }{\varPhi _{m,n}^i }} \right| <10^{-5} \end{aligned}$$

(17)

where $\varPhi$ stands for $\varPi , \theta _\mathrm{w}, \theta _\mathrm{f,s}$, and $C$ at point $(m, n)$, and $i$ is the iteration level.

Various grid sizes and time steps have been tested in order to determine the sensitivity of the numerical code to spatial mesh and time step as well. A calculation of the relative variations of the average Nusselt and Sherwood numbers, $\overline{Nu}$ and $\overline{Sh}$, between two consecutive grids has been performed for different combination of $N_{x} \times N_{z}$. $\overline{Nu}$ and $\overline{Sh}$ are, respectively, written as follows:

$$\begin{aligned} \overline{Nu}&= \frac{1}{A}\int \limits _0^A {Nu{\text {d}}Z} \quad \quad \hbox {with}\quad \quad Nu=\left. {\frac{\partial \theta }{\partial X}} \right| _{X=D,1-D}\end{aligned}$$

(18)

$$\begin{aligned} \overline{Sh}&= \frac{1}{A}\int \limits _0^A {Sh{\text {d}}Z} \quad \quad \hbox {with}\quad \quad Sh=\left. {\frac{\partial C}{\partial X}} \right| _{X=D,1-D} \end{aligned}$$

(19)

According to Table 1, a grid of $81 \times 81$ nodes and a constant time step $\varDelta \tau =1.38\times 10^{-7 }$ were selected as a tradeoff between numerical accuracy, stability, and reasonable computational time in all the calculations performed in the present study.

Table 1 Variations of $\overline{Nu}_\mathrm{f}, \overline{Nu}_\mathrm{s}$, and $\overline{Sh}$ at $X=D$ for various grid sizes, with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Ra=250, Le=1, N=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5, R_\mathrm{p}=1$, and $t \rightarrow \infty$

The validation of the present numerical code has been done by comparing our results with the most available related published results (Harzallah et al. 2010; Al-Farhany and Turan 2011) in the case of pure natural convection problem driven only by thermal buoyancy force (i.e., for $N=0$) and also for higher interphase heat transfer coefficient when dealing with LTNE model. The obtained isotherm contours (Fig. 2) are in good agreement with those given by Harzallah et al. (2010) and Al-Farhany and Turan (2011).

Fig. 2

Comparison of present results of isotherms at steady state with Harzallah et al. (2010) and Al-Farhany and Turan (2011) for Darcy model $N=0)$ with: $Ra=1000$, $\mathcal{H}=1000$ a $(R_\mathrm{c}=1, R_\mathrm{p}=1, D=0.1, R_\mathrm{w}=10)$ and b $(R_\mathrm{c}=1, R_\mathrm{p}=1, D=0.2, R_\mathrm{w}=1)$

4 Results and Discussion

4.1 Time–Space Variations of Thermal Fields

In this section, the results are presented in terms of time–space variations for fluid and solid phase temperatures, iso-concentration, and velocity fields for $\varepsilon =0.4, R_\mathrm{p}=1, Ra=250, D=0.1, A=1, \mathcal{H}=1, Le=1$, and $N=1$.

Figure 3a delineates the evolution of isotherm curves of the fluid phase in response to time. It can be concluded that the temperature gradients in the vicinity of the enclosure walls continue to increase as time goes on and that the isotherms are almost parallel near the left wall and increase near the left upper corner of the cold interface of the enclosure as a result of the fluid rising due to the influence of buoyancy forces. For solid isotherm curves, it can be deduced from Fig. 3b that they are almost parallel in the bulk of the enclosure and as time progresses the heat transfer increases from hot to cold wall’s interface.

Fig. 3

Time–space variations of the a fluid temperature, b solid temperature, and c absolute difference isotherms $\left| {\varDelta \theta } \right|$ with: $\varepsilon =0.4, \hbox {A}=1, D=0.1, \mathcal{H}=1, Le=1, N=1, Ra=250, R_\mathrm{p}=1$

Figure 3c gives the absolute difference isotherms curves between fluid and solid phase temperatures for different time values. As observed by these plots, the temperature difference $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ is more significant near the cavity boundaries at the beginning of the process and higher values are depicted at first near the bottom left corner as well as the upper right one. As time goes on, this difference decreases mainly in the bulk region.

4.2 Sensitivity Study

4.2.1 Effect of the Lewis Number Le

To examine the effect of Lewis number Le, on thermal fields, we have varied this number between $0.5$ and $10$ in order to cover the two-limiting cases: porous media with relatively low thermal diffusivity and high diffusivity coefficient and vice versa.

Figure 4a, b illustrate the effects of Lewis number, Le, on the fluid temperature profiles at $X=0.5$ and $Z=0.5$, respectively. It can be observed that for a given value of Le number, the fluid temperature increases and reaches a maximum value near the top of the enclosure. In addition, one can depict a sharp decrease of this temperature at the horizontal adiabatic wall. Moreover, the fluid temperature decreases when Le increases at the bottom and increases at the top of the porous enclosure. Furthermore, for $Le <1$, the fluid temperature decreases asymptotically to a constant value. However, for $Le >1$, a sharply decrease of fluid temperature can be depicted inside the porous medium.

Fig. 4

Effect of Lewis number Le on fluid temperature profiles for a $X=0.5$ and b $Z=A/2$ with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, N=1, Ra=250, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Figure 5a, b display the effect of Le number on solid temperature profiles at $X=0.$5 and $Z=0.$5, respectively. As demonstrated by these figures, Le has no significant effect on solid temperature profiles at the centerline as well as on mid-height of the porous enclosure. In addition, for a given value of Le, the solid temperature increases with $Z$-coordinate to reach a highest value near the top of the enclosure. Moreover, it resorts that the solid temperature at mid-height decreases with $X$.

Fig. 5

Effect of Lewis number Le on solid temperature profiles for a $X=0.5$ and b $Z=A/2$ with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, N=1, Ra=250, R_\mathrm{p}=1$, and $t \rightarrow \infty$

4.2.2 Effect of the Buoyancy Ratio N

The exam of the influence of the buoyancy ratio $N$ on fluid and solid temperature fields is carried out by varying this number between $0.1$ and $5$ in order to cover the two-limiting cases: thermal buoyancy force dominates mass buoyancy force and vice-versa.

The variations of the fluid temperature at the centreline (i. e., at $X=0.5)$ and at mid-height (i. e., at $Z=0.5)$ of the enclosure for different values of the buoyancy ratio $N$, are drawn, respectively, in Fig. 6a, b. It can be concluded from Fig. 6a that, for a given value of $N$, the fluid temperature increases with the longitudinal coordinate $Z$, and is at its maximum near the top of the enclosure. In addition, one can depict a sharp decrease at the horizontal adiabatic walls. Moreover, the temperature increases at the bottom with the increase of $N$ and will tend to approximately constant value in the porous medium for higher values of $N$.

Fig. 6

Effect of Buoyancy ratio $N$on fluid temperature profiles for a $X=0.5$ and b $Z=A/2$ with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Le=1, Ra=250, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Figure 6b shows that, for a given value of $N$, the fluid temperature decreases with the transverse coordinate $X$. Furthermore, the fluid temperature is insensitive to higher values of $N$.

Solid temperature variations at the mid-height and the centreline of the porous enclosure as a function of the buoyancy ratio, $N$, have been displayed in Fig. 7a, b. It is deduced from Fig. 7a that for a given value of $N$, the solid temperature increases with the longitudinal coordinate $Z$. In addition, as $N$increases, the solid temperature decreases at the lower and the upper parts of the porous enclosure as well.

Fig. 7

Effect of Buoyancy ratio $N$ on solid temperature profiles for a $X=0.5$ and b $Z=A/2$ with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Le=1, Ra=250, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Figure 7b shows that for a given value of buoyancy ratio $N$, the solid temperature decreases along the transverse distance at the mid-height of the porous medium. As $N$ increases, the solid temperature profiles remain unchanged except near the two-wall porous interfaces. However, the solid temperature decreases at the hot wall-porous interface and increases at the cold one.

4.3 Validity Domain of the LTE Assumption

In this section, we aim to determine the validity domain of the well-known LTE assumption. To this end, we have made different comparisons between:

• Local absolute difference between fluid and solid temperature values, $\left| {\varDelta \theta } \right|$

• Computed values of the relative difference in dimensionless temperatures between fluid and solid phases $\theta _\mathrm{LTNE}$ defined as:

  $$\begin{aligned} \theta _\mathrm{LTNE} =\frac{1}{N_x \times N_z }\sum _{i,j} {\left| {\frac{\theta _\mathrm{f} \left( {i,j} \right) -\theta _\mathrm{s} \left( {i,j} \right) }{\theta _\mathrm{f} \left( {i,j} \right) }} \right| } \end{aligned}$$

  (20)

where $N_{x}$ and $N_{z}$ are the total number of nodes along X-axis and Z-axis, respectively; ($i, j$) denote spatial indexes according to X and Z-direction, respectively.

The average relative error difference in dimensionless temperature between solid and fluid phases can lead to the validity of LTE assumption when $\theta _\mathrm{LTNE}$ approaching zero.

Figure 8 illustrates the effect of buoyancy ratio $N$ on the temperature difference $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ for different wall thickness $D$ values. For a given value of $N$, it is observed that at the bottom left and upper corners, $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ is important in vicinity of wall’s interface-porous cavity and decreases when approaching the central zone.

Fig. 8

Effect of wall thickness $D$ on local $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ values for different values of Buoyancy ratio $N$ for a $D=0.1$, b $D=0.2$ and c $D=0.4$ with: $\varepsilon =0.4, A=1, Ra=250, \mathcal{H}=1, N=1, R_\mathrm{p}=1$, and $t \rightarrow \infty$

This figure indicates also that $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ decreases as $D$ increases. Besides, a maximum value is depicted for natural convection induced only by temperature difference (i.e., for $N=0$) and minimum value is recorded for thick walls.

Effects of Lewis number Le and wall thickness $D$ on $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ are presented in Fig. 9. As it is deduced from this figure, for a given value of $D$, $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ increases at the bottom left and upper corners when Le increases. A smaller temperature difference for thick walls can also be seen.

Fig. 9

Effect of wall thickness $D$ on local $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ values for different values of Lewis number Le for a $D=0.1$, b $D=0.2$ and c $D=0.4$ with: $\varepsilon =0.4, A=1, Ra=250, \mathcal{H}=1, N=1, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Figure 10 displays the effects of anisotropic permeability ratio $R_\mathrm{p}$ as well as wall thickness $D$, on $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$. It can be concluded from this figure that, for a given value of $R_\mathrm{p}, \left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ is important near the two-wall’s interface-porous cavity and decreases when approaching the bulk region of the cavity while the wall thickness $D$ increases.

Fig. 10

Effect of wall thickness $D$ on local $\left| {\theta _\mathrm{f} -\theta _\mathrm{s} } \right|$ values for different values of the anisotropic permeability ratio Rp for a $D=0.1$, b $D=0.2$ and c $D=0.4$ with: $\varepsilon =0.4, A=1, Ra=250, \mathcal{H}=1, N=1, Le=1$, and $t \rightarrow \infty$

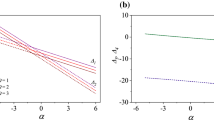
Figure 11a presents the anisotropic permeability ratio $R_\mathrm{p}$ effects on temporal variation of $\theta _\mathrm{LTNE}$. As observed, $\theta _\mathrm{LTNE}$ decreases as time goes on increasing and tends asymptotically to a constant value when $R_\mathrm{p}$ gets higher, which indicates that the two phases are in local thermal equilibrium.

Fig. 11

Time-evolution of the error relative difference $\theta _\mathrm{LTNE}$ for different values of a anisotropic permeability ratio $R_\mathrm{p}$ for: $D=0.1, Le=1, N=1, \mathcal{H}=1$; b wall thickness $D$ for: $N=1, Le=1, R_\mathrm{p}=1, \mathcal{H}=1$; c Buoyancy Number $N$ for: $D=0.1, Le=1, R_\mathrm{p}=1, \mathcal{H}=1$; d Lewis Number Le for: $D=0.1, N=1, R_\mathrm{p}=1, \mathcal{H}=1$; e Interphase heat transfer coefficient ${\mathcal {H}}$ for: $D=0.1, N=1, R_\mathrm{p}=1$; f Wall-to-porous medium thermal diffusivity ratio $R_\mathrm{w}$ for: $D=0.1, N=1, R_\mathrm{p}=1, {\mathcal {H}}=1$; g Thermal conductivity ratio $R_\mathrm{c}$ for: $D=0.1, N=1, R_\mathrm{p}=1, {\mathcal {H}}=1$ and h Solid-to-fluid heat capacity ratio $\gamma$ for: $D=0.1, N=1, R_\mathrm{p}=1, {\mathcal {H}}=1$: with: $\varepsilon =0.4, Ra=250, A=1$

Figure 11b illustrates the time progresses of $\theta _\mathrm{LTNE}$ with the variation of the wall thickness $D$. These curves demonstrate that the declination of $\theta _\mathrm{LTNE}$ with time is as rapid as $D$ is higher. Furthermore, for higher $D$ values (i.e., for thick walls), $\theta _\mathrm{LTNE}$ tends asymptotically to a lower constant value when steady-state regime is reached. Consequently, for thick walls, the LTE assumption is valid.

The effect of the buoyancy ratio $N$ on $\theta _\mathrm{LTNE}$ has been examined (Fig. 11c). For a given value of $N, \theta _\mathrm{LTNE}$ decreases as time goes on. As illustrated, the higher the $N$ values are, the lower is $\theta _\mathrm{LTNE}$.

Figure 11d shows the effects of the Lewis number Le on temporal variations of $\theta _\mathrm{LTNE}$. It comes out from this figure that increasing Le leads to an increase in $\theta _\mathrm{LTNE}$ values. In addition, $\theta _\mathrm{LTNE}$ tends asymptotically to a constant value as Le gets lower indicating that the two phases tend toward LTE for small Le values.

Figure 11e displays the effects of the interphase heat transfer coefficient $\mathcal{H}$ on temporal variations of $\theta _\mathrm{LTNE}$ . As expected, $\theta _\mathrm{LTNE}$ decreases with the increasing of $\mathcal{H}$. The steady-state regime is reached as rapidly as $\mathcal{H}$ value is higher. Consequently, the fluid and solid phases are in LTE for higher values of $\mathcal{H}$.

Figure 11f depicts the effect of the wall-to-porous medium thermal diffusivity ratio $R_\mathrm{w}$ on time variations of $\theta _\mathrm{LTNE}$. Obviously, higher wall thermal diffusivity compared to that of the porous medium leads to a substantial decrease in $\theta _\mathrm{LTNE}$ values. Hence, LTNE tends toward LTE for higher $R_\mathrm{w}$ values.

Figure 11g presents the effects of the fluid-to-solid thermal conductivity ratio $R_\mathrm{c}$ on temporal variations of $\theta _\mathrm{LTNE}$. Similarly, it can be illustrated from this figure that the steady-state regime is reached as rapidly as $R_\mathrm{c}$ is higher. Consequently, the higher the $R_\mathrm{c}$ values are, the lower is $\theta _\mathrm{LTNE}$.

Figure 11h displays the time progress of $\theta _\mathrm{LTNE}$ with different values of solid-to-fluid heat capacity ratio $\gamma$. It comes out from this figure that the steady-state regime is reached as rapidly as $\gamma$ gets higher. It can also be observed from this figure that $\theta _\mathrm{LTNE}$ is small as $\gamma$ is lower.

Computations of $\theta _\mathrm{LTNE}$ for different values of the anisotropic permeability ratio $R_\mathrm{p}$, the buoyancy ratio $N$, the Lewis number Le, the interphase heat transfer coefficient $\mathcal{H}$, the wall thickness $D$, and the solid-to-fluid thermal conductivity ratio $R_\mathrm{c},$ have been done and summarized in Tables  2, 3, 4, 5, 6, 7, 8, 9.

As provided by Table 2, increasing Le, or decreasing $R_\mathrm{p}$, leads to an increase in $\theta _\mathrm{LTNE}$ value. Therefore, it can be concluded that LTE assumption is not valid for higher values of Le and/or lower values of $R_\mathrm{p}$. For a lower given value of Le, $\theta _\mathrm{LTNE}$ decreases as $R_\mathrm{p}$ gets higher.

Table 2 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of Le and $R_\mathrm{p}$, with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Ra=250, N=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5$, and $t\rightarrow \infty$

Table 3 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $N$ and $R_\mathrm{p}$, with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Ra=250, Le=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5$, and $t \rightarrow \infty$

Table 4 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $\mathcal{H}$ and $R_\mathrm{p}$, with: $\varepsilon =0.4, A=1, D=0.1, Ra=250, Le=1, N=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5$, and $t \rightarrow \infty$

Table 5 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $D$ and $R_\mathrm{p}$, with: $\varepsilon =0.4, A=1, \mathcal{H}=1, Ra=250, Le=1, N=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5$, and $t \rightarrow \infty$

Table 6 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $D$ and $\mathcal{H}$, with: $\varepsilon =0.4, A=1, Ra=250, Le=1, N=1, R_\mathrm{c}=3.83, R_\mathrm{w}=3.5, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Table 7 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of Le and $R_\mathrm{c}$, with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Ra=250, N=1, R_\mathrm{w}=3.5, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Table 8 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $N$ and $R_\mathrm{c}$, with: $\varepsilon =0.4, A=1, D=0.1, \mathcal{H}=1, Ra=250, Le=1, R_\mathrm{w}=3.5, R_\mathrm{p}=1$, and $t \rightarrow \infty$

Table 9 Computed average relative error difference $\theta _\mathrm{LTNE}$ for different values of $D$ and $R_\mathrm{c}$, with: $\varepsilon =0.4, A=1, \mathcal{H}=1, Ra=250, Le=1, N=1, R_\mathrm{w}=3.5, R_\mathrm{p}=1$ and $t \rightarrow \infty$

Table 3 illustrates the effects of the buoyancy ratio $N$ and the anisotropy permeability $R_\mathrm{p}$ on LTNE approach. For a given value of $N, \theta _\mathrm{LTNE}$ decreases with the increasing of $R_\mathrm{p}$. Besides, for a given value of $R_\mathrm{p}$, an increase in the buoyancy ratio $N$ values decreases $\theta _\mathrm{LTNE}$.

Table 4 shows that $\theta _\mathrm{LTNE}$ decreases with the increasing of $\mathcal{H}$ and $R_\mathrm{p}$. Therefore, LTNE approaches LTE assumption between solid and fluid phases.

As expected, with higher values of $\mathcal{H}$, there is significant heat transfer between the fluid and solid phases leading to classical LTE assumption limit. Table 4 indicates also a sharply decrease of $\theta _\mathrm{LTNE}$ for higher values of $R_\mathrm{p}$. Consequently, LTNE tends to LTE assumption even for small value of $\mathcal{H}$.

The effects of $R_\mathrm{p}$ and $D$ on $\theta _\mathrm{LTNE}$ are computed in Table 5. The increase of $D$ and $R_\mathrm{p}$ reduces the value of $\theta _\mathrm{LTNE}$. Therefore, for higher values of $R_\mathrm{p}$ and for thick walls, the solid and fluid phases can be considered as in LTE. For that reason, LTE assumption can be assumed to be valid for higher $D$ and $R_\mathrm{p}$ values.

Results presented in Table 6 show the effects of $D$ and $\mathcal{H}$ on $\theta _\mathrm{LTNE}$. As $D$ increases or for high values of $\mathcal{H}$, the error in using the LTNE model decreases and consequently the LTE assumption is valid.

In Table 7, the effects of both $R_\mathrm{c}$ and Le on $\theta _\mathrm{LTNE}$ are computed. For a given value of $R_\mathrm{c} \le 1$, it comes out that $\theta _\mathrm{LTNE}$ gets lower for $Le =1$ and sharply increases for $Le>1$ or $Le<1$. On the other hand, $\theta _\mathrm{LTNE}$ increases with the increasing of Le for higher values of $R_\mathrm{c}>1$. For a given value of Le, $\theta _\mathrm{LTNE}$ decreases with the increase of $R_\mathrm{c}$. Consequently, the LTE approach is valid for large values of $R_\mathrm{c}$ and lower values of Le.

The effects of $N$ and $R_\mathrm{c}$ on $\theta _\mathrm{LTNE}$ are illustrated in Table 8. From this table, it comes out that $\theta _\mathrm{LTNE}$ is higher for small values of $N$ and sharply decreases with the increasing of $N$.

For a given value of $N, \theta _\mathrm{LTNE}$ decreases with the increase of $R_\mathrm{c}$. This implies that for small values of $N$ and $R_\mathrm{c}$, the LTE assumption is not valid.

The influence of $D$ and $R_\mathrm{c}$ on $\theta _\mathrm{LTNE}$ is depicted in Table 9. As expected, for a given value of $D, \theta _\mathrm{LTNE}$ decreases with the increase of $R_\mathrm{c}$. Furthermore, for a given value of $R_\mathrm{c}, \theta _\mathrm{LTNE}$ decreases when $D$ increases.

5 Concluding Remarks

In the present study, a two-dimensional unsteady double-diffusive natural convection in a fluid-saturated porous medium sandwiched between two-finite equal-thickness walls has been numerically investigated using a two-energy equations model (or the LTNE model) and the Darcy model. The porous medium was assumed to be hydrodynamically anisotropic. The vertical walls of the porous enclosure are thick, impermeable, and maintained at different temperatures. The wall’s interfaces to porous medium are kept at different concentration while the horizontal walls are adiabatic and impermeable.

The main obtained results can be summarized as follows:

• 1. The Lewis number, Le, has an unperceived effect on the solid temperature profiles and significant effect on the fluid temperature profiles for high values of Le.

• 2. An increase in the buoyancy ratio $N$ leads to an increasing heat and mass transfer’s rates.

• 3. The temperature difference between fluid and solid phases is important in vicinity of wall’s interface-porous cavity and decreases when approaching the central zone.

• 4. The average relative error difference in dimensionless temperatures $\theta _\mathrm{LTNE}$ decreases as time goes on increasing and tends asymptotically to a lower constant value. The steady-state regime is reached as rapidly as the anisotropic permeability ratio $R_\mathrm{p},$ the buoyancy ratio $N,$ the interphase heat transfer coefficient $\mathcal{H},$ fluid-to-solid thermal conductivity ratio $R_\mathrm{c},$ the solid-to-fluid heat capacity ratio $\gamma ,$ the wall-to-porous medium thermal diffusivity ratio $R_\mathrm{w}$, and the dimensionless walls thickness $D$ get higher or for lower Lewis number Le values which indicates that the two phases are in LTE.

• 5. The solid and fluid phases tend toward LTE assumption even for small value of the interphase heat transfer coefficient $\mathcal{H},$ with higher values of the anisotropy permeability $R_\mathrm{p}$.

• 6. For higher fluid-to-solid thermal conductivity ratio $R_\mathrm{c}$, the fluid conduction dominates and the system behaves like in the case when LTE assumption is valid for lower values of Le or higher values of $D$.