Fault-tolerant and real-time scheduling for mixed-criticality systems

Abstract

The design and analysis of real-time scheduling algorithms for safety-critical systems is a challenging problem due to the temporal dependencies among different design constraints. This paper considers scheduling sporadic tasks with three interrelated design constraints: (i) meeting the hard deadlines of application tasks, (ii) providing fault tolerance by executing backups, and (iii) respecting the criticality of each task to facilitate system’s certification. First, a new approach to model mixed-criticality systems from the perspective of fault tolerance is proposed. Second, a uniprocessor fixed-priority scheduling algorithm, called fault-tolerant mixed-criticality (FTMC) scheduling, is designed for the proposed model. The FTMC algorithm executes backups to recover from task errors caused by hardware or software faults. Third, a sufficient schedulability test is derived, when satisfied for a (mixed-criticality) task set, guarantees that all deadlines are met even if backups are executed to recover from errors. Finally, evaluations illustrate the effectiveness of the proposed test.

1 Introduction

Safety-critical systems, e.g., automotive, aircraft, space shuttle, have strict real-time and fault-tolerant requirements. In addition, the manufacturers of safety-critical systems are considering mixed-criticality design by hosting tasks having different criticality on the same computing platform due to space, weight and power (SWaP) concerns. Ensuring the real-time properties of such systems is challenging because the schedule to satisfy real-time constraints, i.e., meeting deadlines, can influence or be influenced by the fault-tolerant and/or mixed-criticality constraints. This paper proposes a new uniprocessor fixed-priority (FP) scheduling algorithm, called fault-tolerant mixed-criticality (FTMC), for scheduling constrained-deadline sporadic tasks by taking into account three interrelated design constraints: (i) meeting the deadlines of the tasks (real-time constraints), (ii) providing fault tolerance using time-redundant execution of backup tasks (fault-tolerant constraints), and (iii) respecting the statically-assigned criticality of each task to facilitate system’s certification (mixed-criticality constraints).

This paper considers safety-critical application (e.g., control and monitoring) modeled as a collection of sporadic real-time tasks, i.e., a task potentially releases infinite number of instances, called jobs. Consecutive jobs of a task are separated by a minimum inter-arrival time. Each job must deliver correct output before its deadline even in the presence of faults. According to Avižienis et al. (2004), a fault is a source of an error which is an incorrect state in the system that may cause deviation from correct service, called failure. When a task’s behavior is incorrect (e.g., wrong output generated or wrong execution path is taken) due to some fault, we categorize such behavior as task error, not as task failure because we aim to mask task errors to avoid task failures.

In addition to satisfying the temporal correctness, the functional correctness of safety-critical systems ought to be guaranteed even in the presence of faults; otherwise, the consequence may be disastrous, like death or severe economic loss. To guarantee both temporal and functional correctness, the proposed FTMC algorithm considers fault-tolerant scheduling to recover from task errors caused by hardware transient faults or software bugs. When a fault adversely affects the functionality of a task, the task is said to be erroneous. Hardware transient faults may occur due to, for example, hardware defects, electromagnetic interferences, or cosmic ray radiation (Koren and Krishna 2007). Hardware transient faults are the most common, and their number is continuously increasing due to high complexity, smaller transistor sizes and low operating voltage for computer electronics (Baumann 2005). In addition, software faults (bugs) may remain undetected even after months of software testing.

Real-time scheduling with fault-tolerant capability is implemented using redundancy either in time or space (Koren and Krishna 2007). However, time redundancy rather than space redundancy is often viable and cost-efficient means to achieve fault-tolerance due to SWaP concerns in many resource-constrained systems. The proposed FTMC algorithm employs time redundancy to recover from task error while also ensuring the real-time constraints.

In time redundancy, each task is considered to have one primary and several backups. Multiple task errors due to multiple of faults may affect the same job of a task in such a way that the primary and multiple backups of that job may become erroneous. Multiple task errors may also affect different jobs of the same task or may affect different jobs of different tasks. The FTMC algorithm has to ensure that each job (including its backups) of each task completes execution before its deadline to guarantee both temporal and functional correctness of the system. Whenever a job of some task is ready to execute, the FTMC algorithm first dispatches the primary. If the primary is detected to be erroneous, then one-by-one backup is dispatched until the output is correct. The priority of the backup is same as the primary. The backup can either be the re-execution of the primary or a diverse-implementation execution of the same task. Note that the WCET of a backup which is implemented diversely may be smaller or larger than that of the original task.

Algorithm FTMC also considers the mixed-criticality aspect of safety-critical system to facilitate certification—which is about ensuring certain level of confidence regarding the correct behavior (e.g., meeting deadline, producing non-erroneous output) of different multi-criticality functions hosted on a common computing platform. The need for research in the domain of mixed-criticality MC systems is motivated in Barhorst et al. (2009) using an example of unmanned aerial vehicle (UAV) which is expected to operate over or close to civilian airspace. Such a system has both flight-critical and mission-critical functionalities that require safety, reliability and timeliness guarantee. In addition, the design of such safety-critical MC systems is often subject to certification by standard statutory certification authority (CA), for example, by Federal Aviation Authority (FAA) in the US or the European Aviation Safety Agency (EASA) in Europe for avionics systems. A certified product is considered safe and also promotes confidence among the end-users in buying that product.

Traditionally, the design of a non-mixed-criticality system assumes the same criticality level for all the functions present in the system. In contrast, an MC system has multiple criticality levels where each function is assigned one unique criticality based on its “importance”. For example, the ABS function in a car is assigned a safety criticality level that is relatively higher than that is assigned to the DVD player function. Higher criticality level assigned to a function means that higher degree of assurance is needed regarding the correct behavior of the function. The FTMC algorithm considers scheduling MC tasks having two criticality levels (called, dual-criticality system): each task’s criticality is either low (LO-critical task) or high (HI-critical task). Extending the FTMC algorithm for more than two criticality levels adds no fundamental challenge, and for simplicity of presentation, this paper considers dual-criticality system. The main principle to extend the result of this paper for more than two criticality levels is briefly presented in Sect. 7.2.

The degree of assurance needed for certifying the behavior of an MC system as “correct” is a function of different criticality levels. In this paper, the correct behavior of an MC system is modeled using timing constraints (i.e., deadlines). Certification of MC system is a challenging and costly approach since such system is relatively complex due to the integration of functionalities with different criticality levels. The run-time behavior of MC system like other systems varies based on the operating environment, hardware dynamics, input parameters, and so on. The behavior of the system at each time instant determines the criticality behavior of the system at that time instant. The criticality behavior of the system changes from one time instant to another while the statically-assigned criticality of each function does not change. The criticality behavior of an MC system can be modeled based on many different run-time parameters. This paper considers two such parameters to model the run-time criticality behavior of MC systems: the WCET of application tasks and the frequency of errors detected in the system.

Whether the deadline of a function is met or not depends on the WCET of the function, which is the maximum CPU time the function requires to complete its execution. The WCET of a function can be approximated at varying degrees of confidence or assurance, depending on the inaccuracy or difficulty in estimating the true WCET, for example, due to the variability in inputs, operating environment, hardware dynamics, and so on. The higher degree of assurance needed in estimating the WCET of a function, the larger (more conservative) the WCET bound tends to be in practice (pointed by Honeywell’s engineer Vestal in 2007).

Building upon Vestal’s seminal work (Vestal 2007), there have been several approaches (Baruah and Vestal 2008; Baruah et al. 2010, 2011b, 2012b; Li and Baruah 2010b; Guan et al. 2011; Ekberg and Yi 2012; Baruah and Fohler 2011; Santy et al. 2012) to design certification-cognizant scheduling of MC system based on a particular run-time aspect: the WCET of the tasks. In order to certify an MC system as being correct, the worst-case assumptions by the CA regarding the system’s run-time behavior tend to be more conservative in comparison to that of assumed by the manufacturer. Based on Vestal’s model, each task in a dual-criticality system is considered to have two different WCETs: $C^{\mathtt{LO}}$ (LO-criticality WCET) and $C^{\mathtt{HI}}$ (HI-criticality WCET) such that $C^{\mathtt{LO}} \le C^{\mathtt{HI}}$. The assumption regarding the WCET of the tasks holding during run-time determines the criticality behavior of the system. The criticality behavior of the system is determined by comparing the actual execution time of each task with the WCET that is estimated using different degrees of assurance. When some task’s actual execution time exceeds $C^{\mathtt{LO}}$, the system is considered to switch from LO to HI criticality behavior.

Inspired by Vestal’s model, this paper also considers that each primary and backup of a task has two different WCETs corresponding to LO and HI criticality behaviors. In addition, this paper considers another important run-time parameter to model MC system—the number of task errors detected in any interval no larger than $D_{max}$—where $D_{max}$ is the maximum relative deadline of the tasks. The term “task error” refers to the situation when the output of a primary/backup of some job of a task is erroneous. Multiple task errors may be detected in the same job of a task or in multiple jobs of the same task or in jobs of different tasks. In this paper, it is assumed that the frequency of task errors at higher criticality behavior is larger than the frequency of errors at lower criticality behavior. In other words, the CA assumes higher frequency of errors in comparison to that of the manufacturer. In any interval of no larger than $D_{max}$, the manufacturer considers to recover at most $\mathtt{f}$ errors while the CA considers to recover at most $\mathtt{F}$ errors where $\mathtt{F} \ge \mathtt{f}$. This way to model the criticality behavior of the MC system will be used to generate robust schedule for tolerating WCET overrun and higher number of errors. Based on the different constraints regarding the WCET and frequency of errors, the criticality behavior of an MC system is defined as follows:

Definition 1

(Mixed-Criticality Behavior) An MC system exhibits LO-criticality behavior if

• each task’s primary or backup executes no more than the WCET estimated for the LO criticality behavior, and

• the number of task errors detected in any interval no larger than $D_{max}$ is at most $\mathtt{f}$.

Otherwise, the system exhibits HI-criticality behavior if

• any task’s primary or backup executes at most the WCET estimated for the HI criticality behavior, and

• the number of task errors detected in any interval no larger than $D_{max}$  is at most $\mathtt{F}$, where ${\mathtt{F} } \ge \mathtt{f}$.

Otherwise, the behavior of the system is erroneous. $\square$

The HI-criticality behavior of the system requires higher computation power because tolerating WCET overrun or higher frequency of errors need additional processing capacity to meet the deadlines of the tasks. Based on Definition 1, the system is considered to switch from LO to HI criticality behavior at time $t$ if one of the following events (denoted by E1 and E2) is detected at $t$:

• E1 Some job’s primary or backup does not signal completion after finishing its LO-criticality WCET.

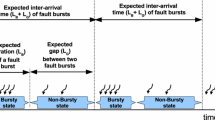
• E2 There is an error detected at time $t$ and this is the $(\mathtt{f}+1)^{th}$ error detected in $[t-t^\prime ,t]$ such that $t^\prime \le D_{max}$. This is illustrated in Fig. 1 for $D_{max}=5$ and $\mathtt{f}=1$.

Fig. 1

Staring from time $t=0$, the error detected at $t=12$ is the first occurrence of $(f+1)^{th}$ (i.e., second) error in an interval no larger than $D_{max}=5$. By assuming that no job’s primary/backup exceeds LO-criticality WCET before $t=12$, the system exhibits LO-criticality behavior in $[0, 12)$ and switches to HI-criticality behavior at $t=12$. However, if some job’s primary/backup exceeds LO-criticality WCET before $t=12$, then the system switches to HI-criticality behavior earlier than $t=12$. The error detected at $t=14$ occurs during the HI-criticality behavior

According to Definition 1, this paper considers restricting certain number of task errors in any interval no larger than $D_{max}$ during the LO- and HI-criticality behavior of the system. No fault-tolerant system can mask infinite number of task errors in a bounded interval. Therefore, the schedulability guarantee of fault-tolerant systems is this paper is provided by assuming a bounded number of errors in an interval.

Assuming a bounded number of task errors in any interval no larger than $D_{max}$ is a system-level property that applies to all the tasks in the system rather than only being applicable to some specific task. This enables to perform (as will be evident later) the schedulability analysis of each task by applying the analysis only to an arbitrary job of each task; rather than doing so for all the (potentially infinite number of) jobs of the task. This is because the maximum number of errors between the release time and deadline of any job of any task is not larger than the maximum number of errors assumed to occur in any interval of length $D_{max}$ since no job’s deadline is larger than $D_{max}$.

No other restriction regarding the occurrences of task errors is assumed for FTMC scheduling: (i) errors can occur in any job of any task at any time, (ii) there is no separation restriction regarding the occurrences of consecutive errors, and (iii) there is no probability distribution assumed for the occurrences of task errors. Consequently, assuming a bounded number of task errors in $D_{max}$ also covers the case where all these errors may occur in an interval smaller than $D_{max}$. To that end, the schedulability analysis of this paper in fact considers the worst-case occurrences of a bounded number of errors in the busy-period ¹ of each task where the length of the busy period may be smaller than $D_{max}$.

The proposed FTMC scheduling is based FP scheduling paradigm. The dominating scheduling approach in industry for meeting the hard deadlines of application tasks is the FP scheduling policy, due to its flexibility, ease of debugging, and predictability. Under the FP scheduling strategy, each task is assigned a priority that never changes during the execution of the task. This paper addresses preemptive FP scheduling of sporadic tasks on uniprocessor platform. In preemptive FP scheduling, at each time instant, the highest-priority runnable² task is dispatched for execution. If the processor is busy for executing a relatively lower-priority task, then the highest-priority runnable task is dispatched for execution by preempting the lower-priority (executing) task. The preempted task may later resume its execution when it becomes the highest-priority runnable task. As will be evident in next paragraph if some LO -critical task is preempted before the criticality switch and becomes ready after the criticality switch, then such LO-critical task will not be allowed to resume their executing after the criticality switch in FTMC scheduling.

The proposed FTMC algorithm (formally presented later) is same as traditional uniprocessor FP scheduling with three additional features: run-time monitoring to detect the events E1 and E2 (i.e., when the system switches to HI-criticality behavior); dropping the LO-criticality tasks after the system switches to HI-criticality behavior; and finally, dispatching backup whenever task error is detected. Based on run-time monitoring, as soon as it is detected that the system has switched to HI-criticality behavior (i.e., the assumptions for LO-criticality behavior are no more valid), only the HI-criticality tasks including their backups are scheduled. When the system switches to HI-criticality behavior, rather than dropping the LO-critical tasks, the execution of the LO-critical tasks may be suspended until the system’s criticality behavior is restored to LO-criticality behavior. However, this paper considers dropping (rather than suspending) the LO -critical tasks since for certification it is enough to show that the system is schedulable in both LO and HI critical behaviors.

The FTMC algorithm schedules MC sporadic tasks with both real-time and fault-tolerant constraints while facilitating system’s certification. The FTMC algorithm needs to recover at most $\mathtt{f}$ and $\mathtt{F}$  task errors during the LO- and HI-criticality behaviors in any interval no larger than $D_{max}$, respectively. And, the execution time of the primary and backups of each task may be up to the corresponding WCET assumed for each criticality behavior.

The major contribution in this paper is the derivation of a sufficient schedulability test for FTMC algorithm. As will be evident later deriving an exact schedulability test for the FTMC algorithm is computationally impractical. When the proposed test is satisfied for a task set, it is ensured that all deadlines are met even if backups are executed to recover from task errors, which facilitates certification. Deriving such a schedulability test is important to guarantee offline that all the deadlines will be met during the mission of the system. Experimental results show that the proposed test is very close to the theoretical upper bound of the fraction of schedulable, randomly-generated task sets. In other words, the sufficient schedulability analysis presented in this paper is quite close to the exact analysis, i.e., does not suffer from too much pessimism.

Another challenge in the design of mixed-criticality scheduling is the priority assignment problem for the MC tasks. The priority and criticality of a task are not necessarily positively correlated in the sense that always assigning higher priority to a higher criticality task may not yield the best performance (Vestal 2007; Baruah and Vestal 2008; Baruah et al. 2011b). The criticality level of a task is statically assigned based on the degree of assurance needed regarding its correct behavior (which in this paper is about meeting its deadline). In case of FP scheduling, a task with higher criticality level may sometimes be assigned higher fixed priority to ensure, for example, that all the HI-criticality tasks get processing resources before the LO-critical ones. However, a task with higher criticality level may sometimes need to be assigned a relatively lower fixed priority to allow the deadlines of all the LO- and HI-critical tasks to be met. The deadline-monotonic (DM) priority ordering—which is optimal for traditional FP scheduling of constrained-deadline sporadic tasks (Leung and Whitehead 1982)—is already shown to be suboptimal for scheduling MC tasks (Vestal 2007; Baruah et al. 2011b). Therefore, determining a good FP priority assignment policy is very important for MC systems and this problem is addressed in this paper. Another salient feature of the proposed schedulability test is that it can be used to find effective fixed-priority ordering of the tasks based on Audsley’s optimal priority assignment (OPA) algorithm (Audsley 2001).

The derivation of a schedulability test that does not suffer mush from pessimism and finding an effective priority ordering that makes a task set schedulable on a given platform have several advantages. First, it reduces the demand on computing resources which in turn reduces the cost of the system for mass production. Second, lower computing resource means less SWaP consumption which are desirable in many resource-constrained embedded systems. Finally, efficient use of system resources enables incorporating more functionalities on the same computing platform without buying additional hardware. All these advantages provide better competitiveness of a product in the market.

Certification of safety-critical system is a complex and broad issue. In reality, the CA does not certify only a piece of software, e.g., scheduler, rather the entire system (e.g., aircraft or car) is certified. The aim of certification is to check that the required verification and validation (V&V) activities, depending on the criticality level, have been successfully completed by the manufacturer. It must be noted that the manufacturer and the CA do not have different or conflicting aims in developing and certifying a product. Addressing the entire spectrum of certification of MC system is outside the scope of this paper. The certification issue of MC system, addressed in this paper, is tailored to the issue of real-time and fault-tolerant scheduling. The scheduling algorithm proposed in this paper is to facilitate certification of MC systems by ensuring different levels of assurance for different criticality behavior. In this paper, the different values of WCET and frequency of errors are considered to model the criticality of the software and to show the robustness of the system in tolerating WCET overrun and mitigating the effect of higher number of errors than predicted. Based on such model, the manufacturer would be able to show that the required V&V activities (regarding the system’s schedule) have been performed which guarantees correctness of the system in case of WCET overrun and increase in frequency of errors.

The paper is organized as follows. The fault and task models are presented in Sect. 2. The FTMC algorithm is formally presented in Sect. 3. Important considerations and an overview of the worst-case schedulability analysis of FTMC algorithm are presented in Sects. 4 and 5. The schedulability tests for both criticality behaviors are presented in Sects. 6 and 7. Empirical investigation into the proposed schedulability test is presented in Sect. 8. Finally, related works are presented in Sect. 9 before concluding the paper in Sect. 10.

2 Fault and task model

The category of real-time systems having stringent timing constraints is called hard real-time systems. If the timing constraints of a hard real-time system are not satisfied, then the consequences may be catastrophic, for instance, threat to human lives. Consequently, it is of utmost importance for designers of hard real-time systems to ensure a priori that all the timing constraints will be met when the system is in mission. The timing constraints of hard real-time applications can be fulfilled using appropriate scheduling of the tasks on a particular hardware platform. Scheduling is the policy of allocating resources (e.g., CPU time, communication bandwidth) to the tasks of the application that are competing for the same resource. Scheduling algorithms and their analysis that can be used to verify the timing constraints of hard real-time systems are at the heart of the research presented in this paper. The design and analysis of hard real-time scheduling algorithms is based on appropriate modeling of the target system. This is because a priori knowledge of the workload and available resources is necessary to analyze and ensure predictability of the system. The task and fault models are presented in this section.

2.1 Fault model

The nature and frequency of faults considered for the design of a particular fault-tolerant system are specified using a fault model. The fault model used for analyzing the predictability of different computer systems varies. For example, the fault model considered during the design of a space shuttle is different from that of personal computers. Identifying the characteristics of the faults and the corresponding errors is an important issue for the design of an effective fault-tolerant system. Based on persistence, faults can be classified as permanent, intermittent, and transient (Koren and Krishna 2007). Faults can occur in hardware or/and software.

Hardware faults A permanent failure of the hardware is an erroneous state that is continuous and stable. Such erroneous state is caused by some permanent fault in the hardware. This paper does not consider tolerating permanent hardware faults, for example, failure of a processor permanently. Such failure needs to be tolerated using hardware redundancy, for example, using TMR approach.

Transient hardware faults are temporary malfunctioning of the computing unit or any other associated components which causes incorrect state in the system. Intermittent faults are repeated occurrences of transient faults. Transient faults and intermittent faults manifest themselves in a similar manner. They happen for a short time and then disappear without causing a permanent damage. If the error caused by such transient faults are recovered, then it is expected that the same error will not re-appear since transient faults are short lived.

• Sources and rate of hardware transient faults  The main sources of transient faults in hardware are environmental disturbances like power fluctuations, electromagnetic interference and ionization particles. Transient faults are the most common, and their number is continuously increasing due to high complexity, smaller transistor sizes and low operating voltage for computer electronics (Baumann 2005). It has been shown that transient faults are significantly more frequent than permanent faults (Siewiorek et al. 1978; Castillo et al. 1982; Iyer et al. 1986; Campbell et al. 1992; Baumann 2005; Srinivasan et al. 2004). Experiments by Campbell, McDonald, and Ray using an orbiting satellite containing a microelectronics test system found that, within a small time interval ($\sim$15 min), the number of errors due to transient faults is quite high (Campbell et al. 1992). It was shown by Shivakumar et al. (2002) that the error rate in processors due to transient faults is likely to increase by as much as eight orders of magnitude in the next decade.

Software faults All software faults, known as software bugs, are permanent. However, the way software faults are manifested as errors leads to categorize the effect as: permanent and transient errors. If the effect of a software fault is always manifested, then the error is categorized as permanent. For example, initializing some global variable with incorrect value which is always used to compute the output is an example of a permanent software error. On the other hand, if the effect of a software fault is not always manifested, then the error is categorized as transient. Such transient error may be manifested in one particular execution of the software and may not manifest at all in another execution. For example, when the execution path of a software varies based on the input (for example, sensor values) or the environment, a fault that is present in one particular execution path may manifest itself as a transient error only when certain input values are used. This fault may remain dormant when a different execution path is taken, for example, due to a change in the input values or environment.

Fault model of this paper The fault-tolerant scheduling algorithms proposed in this paper considers tolerating multiple task errors due to hardware transient faults and software faults (errors due to which may be transient or permanent in nature). Hardware transient faults that can cause transient task errors are considered in the fault model of the paper. Hardware transient faults are short lived and generally cause no permanent error to the hardware. Therefore, re-executing the primary as backup is a cost-efficient and simple means for tolerating such faults. Software faults that leads to transient errors can be masked using simple re-execution. Such software faults which result in transient errors are considered in the fault model. Finally, software faults which result in permanent task errors (therefore, cannot be tolerated using re-execution) are also considered in the fault model. A diverse implementation of the same task (e.g., exception handler) needs to be executed as backup to recover from such permanent error due to software faults. To this end, the FTMC algorithm considers original-task re-execution or diverse-implementation execution as backup.

The FTMC algorithm needs to recover during the LO- and HI-criticality behaviors at most $\mathtt{f}$ and $\mathtt{F}$  errors in any interval no larger than $D_{max}$, respectively. And, during the LO-criticality behavior of the system, no task’s primary/backup executes more than its LO-criticality WCET while it can execute up to its HI-criticality WCET during the HI-criticality behavior of the system. Regardless of how errors are propagated, the FTMC algorithm can recover errors as long as the errors are contained at the task level (i.e., error-containment region) and the frequency of errors is bounded according to the assumed fault model. Faults that affect the system software (e.g., RTOS) or cause permanent hardware error (e.g., processor failure) need to be tolerated using system level fault-tolerance, for example, using triple-modular (space) redundancy. This paper does not address system level fault-tolerance rather proposes fault-tolerant technique for application level.

Masking task errors based on time redundancy have been proposed for non-MC task systems in many other works considering hardware transient faults (Pandya and Malek 1998; Liberato et al. 2000; Punnekkat et al. 2001; Aydin 2007; Lima and Burns 2003; Many and Doose 2011; Short and Proenza 2013) and software faults (Chetto and Chetto 1989; Han et al. 2003). However, many of these earlier works are based on a relatively restricted fault model assuming, for example, that (i) the inter-arrival time of two faults must be separated by a minimum distance (Ghosh et al. 1995; Pandya and Malek 1998; Burns et al. 1996 Lima and Burns 2003; Punnekkat et al. 2001), (ii) at most one fault may occur in one task (Punnekkat et al. 2001; Han et al. 2003), (iii) the backup is simply the re-execution of the original task, i.e., do not consider diverse implementation of the task (Ghosh et al. 1995; Pandya and Malek 1998; Punnekkat et al. 2001; Liberato et al. 2000; Many and Doose 2011). In contrast, the fault model considered for the FTMC algorithm is very powerful in the sense that it covers variety of hardware/software faults and can recover multiple errors in any task, at any time even during the execution of backups. The fault model allows to consider many different situations, for example, where (i) a single job of a particular task is affected by multiple faults, (ii) a single fault causes multiple task errors, (iii) different jobs are affected by different number of faults, (iv) faults that may occur in bursts, and (v) the inter-arrival time of faults is not predictable.

Error-detection mechanisms In order to tolerate a fault that leads to an error, fault-tolerant systems rely on effective error detection mechanisms. The design of many fault-tolerant scheduling algorithm relies on effective mechanisms to detect errors. Error detection mechanisms and their coverage (e.g., percentage of errors that are detected) determine the effectiveness of the fault-tolerant scheduling algorithms.

The fault-tolerant scheduling algorithm proposed in this paper relies on effective error-detection mechanisms that are already part of the safety-critical system’s health monitoring functions. We assume 100 % error-detection coverage, i.e., each error is detected based on existing hardware/software based error-detection mechanisms. Errors that skipped detection at a partition-level must be masked at the system level using, for example space redundancy, which is not addressed in this paper.

Error detection can be implemented in hardware or software. Hardware implemented error detection can be achieved by executing the same task on two processors and compare their outputs for discrepancies (duplication and comparison technique using hardware redundancy). Another cost-efficient approach based on hardware is to use a watchdog processor that monitors the control flow or performs reasonableness checks on the output of the main processor (Madeira et al. 1991). Control flow checks are done by verifying the stored signature of the program control flow with the actual program control flow during runtime. In addition, today’s modern microprocessors have many built-in error detection capabilities like, error detection in memory, cache, registers, illegal op-code detection, and so on (Meixner et al. 2007; Kalla et al. 2010; Al-Asaad et al. 1998).

There are many software-implemented error-detection mechanisms: for example, executable assertions, time or information redundancy-based checks, timing and control flow checks, and etc. Executable assertions are small code in the program that checks the reasonableness of the output or value of the variables during program execution based on the system specification (Jhumka et al. 2002; Hiller 2000). In time redundancy, an instruction, a function or a task is executed twice and the results are compared to allow errors to be detected (duplication and comparison technique used in software) (Aidemark et al. 2005). Additional data (for example, error-detecting codes or duplicated variables) are used to detect occurrences of an error using information redundancy (Koren and Krishna 2007).

2.2 Task model

A task model specifies the workload and timing constraints of the real-time application. A task is a particular piece of program code that performs some computation, e.g., reading sensor data, writing actuator value, executing a control loop, etc. The recurrent task model considered in this paper is the sporadic task model where the inter-arrival time (period) of each task has a lower bound and the relative deadline of each task is not greater than its period. An instance (also, called job) of the task is said to be released when it becomes available for execution. The releases of two consecutive jobs are separated by at least the period of the task. The deadline is “relative” in the sense that whenever a job is released, the deadline for that job applies with respect to its release time.

The uniprocessor preemptive FP scheduling of $n$ sporadic tasks in $\Gamma =\{\tau _1 \ldots \tau _n\}$ is considered. Task $\tau _{i}$ is characterized by a 5-tuple $(L_i, D_i, T_i, \overrightarrow{C}_i^L, \overrightarrow{C}_i^H)$, where

• $L_i \in \{\mathtt{LO}, \mathtt{HI}\}$ is the criticality of the task;

• $T_i \in \mathbb {N}^+$ is the minimum inter-arrival time (also called period) of consecutive jobs of the task;

• $D_i \in \mathbb {N}^+$ is the relative deadline such that $D_i \le T_i$;

• $\overrightarrow{C}_i^L$ is a vector $<C_{i,p}, B_{{i},{1}}, \ldots B_{{i},{\mathtt{f}}}>$ where the LO-criticality WCET of $\tau _i$’s primary is $C_{i,p}$ and the LO-criticality WCET of $a^{th}$ backup of $\tau _i$ is $B_{{i},{a}}$.

• $\overrightarrow{C}_i^H$ is a vector $<\widehat{C}_{i,p}, \hat{B}_{{i},{1}}, \ldots \hat{B}_{{i},{\mathtt{f}}}, \ldots \hat{B}_{{i},{\mathtt{F}}}>$ where the HI-criticality WCET of $\tau _i$’s primary is $\widehat{C}_{i,p}$ and the HI-criticality WCET of $a^{th}$ backup of $\tau _i$ is $\hat{B}_{{i},{a}}$.

The WCET of a piece of code is generally an upper bound on true WCET and the more confidence one needs in estimating the true WCET of a piece of code, the more pessimistic this upper bound tends to be in practice (Vestal 2007). Accurately estimating the WCET of a piece of code is challenging and also an active research area (Yoon et al. 2011; Huynh et al. 2011; Guan et al. 2012; Chattopadhyay et al. 2012). One reason for this problem is because modern processors include performance enhancing micro-architectural features (e.g., pipelining, caching) that make WCET estimation complicated. Another reason is that software is becoming more complex as new services/function are added to the system, for example, advanced safety features in modern cars. The different parts of hardware and possible paths in software that are exercised during a particular run of a system is quite difficult to predict, which makes the WCET estimation challenging. The different values of WCET of the same task used in this paper is to model the possibility of WCET overrun. To this end, it is assumed that $C_{i,p} \le \widehat{C}_{i,p}$ and $B_{{i},{a}} \le \hat{B}_{{i},{a}}$ for $a=1 \ldots \mathtt{F}$.

A sporadic task $\tau _{i}$ potentially generates an infinite sequence of instances or jobs with consecutive arrivals separated by at least $T_i$ time units. The $j{th}$ instance or job of task $\tau _{i}$ is denoted by $J_i^j$. All time values (e.g, WCET, relative deadline, inter-arrival time, time intervals) are assumed to be positive integer. This is a reasonable assumption since all the events in the system happen only at clock ticks.

We denote $\mathtt{hpe}_i$ the set of all tasks having priority higher than or equal to the priority of task $\tau _i$. We denote $\mathtt{hp}_i$ the set of all the higher priority tasks of task $\tau _i$. We denote $\mathtt{hpL}_i$ the set of higher-priority and lower-critical tasks of task $\tau _i$. Similarly, we denote $\mathtt{hpH}_i$ the set of higher-priority and higher/equal-critical tasks of task $\tau _i$. Note that, $\mathtt{hp}_i=\mathtt{hpL}_i\cup \mathtt{hpH}_i$ and $\mathtt{hpe}_{i}=\mathtt{hpL}_i\cup \mathtt{hpH}_i\cup \{\tau _i\}$.

We finally denote $\mathtt{E}_{i,\alpha }$and $\hat{\mathtt{E}}_{i,\alpha }$respectively the total LO- and HI-criticality WCET required for the recovery of a job of task $\tau _{i}$ if exactly $\alpha$ task errors³ are detected in that particular job. Note that $\alpha$ task errors affect the same job of task $\tau _{i}$ such that the primary of $(\alpha -1)$ backups of that job suffer task error. The values of $\mathtt{E}_{i,\alpha }$and $\hat{\mathtt{E}}_{i,\alpha }$are computed as follows:

$$\begin{aligned}&\mathtt{E}_{i,\alpha } =C_{i,p}+\sum _{a=1}^{\alpha } {B_{{i},{a}} } \end{aligned}$$

(1)

$$\begin{aligned}&\hat{\mathtt{E}}_{i,\alpha } =\hat{C}_{i,p}+\sum _{a=1}^{\alpha } {\hat{B}_{{i},{a}} } \end{aligned}$$

(2)

When all the backups of task are same as the primary, then $B_{{i},{a}} =C_{i,p}$ and $\hat{B}_{{i},{a}} =\widehat{C}_{i,p}$ for any $a$. In such case, $\mathtt{E}_{i,\alpha }= (\alpha +1) \cdot C_{i,p}$ and $\hat{\mathtt{E}}_{i,\alpha }= (\alpha +1) \cdot \widehat{C}_{i,p}$. The assumption that all the backups are same as the primary does not provide any advantage in terms of run-time dispatching of FTMC algorithm and does not simplify the schedulability analysis since the worst-case occurrence of multiple faults affecting different tasks is still need to be considered. Moreover, when all backups are same, then software faults that cause permanent errors cannot be masked using time redundancy.

Example 1

Consider the dual-criticality task set in Table 1 where $\mathtt{f}=1$ and $\mathtt{F}=2$. Since FTMC drops the LO-critical tasks when the system switches to HI-criticality behavior, the HI-criticality WCET of the LO-critical task $\tau _2$ is not specified in Table 1.

Based on Eqs. (1) and (2), the total LO- and HI-criticality WCET for the recovery of one job of task $\tau _i$ that exclusively suffers and recovers $\alpha$ errors are given in Table 2 for $\alpha =0,1,2$.

For example, the total HI-criticality WCET for the recovery of any particular job of $\tau _3$ that suffers $\alpha =2$ errors is computed using Eq. (2) as follows (shaded in Table 2):

$$\begin{aligned} \hat{\mathtt{E}}_{3,{\alpha }}=\hat{\mathtt{E}}_{3,{2}}=\widehat{C}_{3,p}+\hat{B}_{{3},{1}}+\hat{B}_{{3},{2}}=4+3+3=10 \end{aligned}$$

$\square$

Table 1 An example of dual-criticality task set

Table 2 Execution requirement of any job of $\tau _{i}$ affected by $\alpha$ errors

Definition 2

(Busy Period) The notion of level-$i$ busy period will be used in this paper. We define the level-$i$ busy period as the interval $[a,b)$ such that

• $b>a$;

• only the primary and backups of jobs of tasks in set $\mathtt{hpe}_i$ execute in $[a,b)$;

• the processor is busy throughout $[a,b)$; and

• the processor is not executing any task from $\mathtt{hpe}_i$ just prior to $a$ or just after $b$.

A note on mixed-criticality system design and its challenges The advent of powerful processors and the SWaP concerns drive the design of safety-critical systems towards integrating multiple functionalities having multiple criticality levels on the same computing platform. There are many standards that specify multiple criticality levels of the application tasks. For example, the RTCA DO-178B and ISO 26262 standards specify multiple criticality for different software functions in avionics and automotive systems, respectively.

One of the challenges regarding the design of such MC systems is to ensure the isolation property, i.e., that functions, tasks or components at a lower criticality level do not interfere adversely with those at a higher criticality level. The real time, fault tolerance and mixed criticality aspects are already addressed in avionics certification. Aviation industry considers “Integrated Modular Avionics” (IMA) to achieve economic advantage by hosting multiple avionics functions on a single platform.

The ARINC-653 standard provides application programming interfaces (APIs) to employ temporal and spatial partitions in IMA-based avionic systems. Mixed criticality is addressed by the IMA standard which creates real-time virtual processors called IMA partition and then allocating applications with different criticality to different IMA partitions. Such partitioning ensures that the failure of software in any form in any partition cannot cause other partitions to fail in either time or space. Hardware (permanent) fault tolerance is then addressed by hardware redundancy using quad or triple redundancy. The intra-partition software fault avoidance / tolerance is then done by application developers to meet the software reliability requirement for each criticality level mandated by FAA or EASA. However, providing such dedicated resource, i.e., virtual processors, for each critical application may not be cost- and resource-efficient. Therefore, (truly) sharing the computing resources among the tasks having multiple criticality levels needs to be considered. To this end, the processing platform is not divided into multiple virtual processors (each dedicated to one application); rather, the entire platform is shared among all the tasks of all the application.

The main aspect of MC system design that is addressed in this paper is static verification, which is related to the certification of safety-critical systems by CA. For example, in order to operate UAV over civilian airspace, the flight-critical functionalities must be certified as “correct” by the CA while the manufacturer needs to ensure the correctness of both mission-critical and flight-critical functionalities. Conventional scheduling strategies, that address both the “criticality” (i.e., multiple WCET of the same task or frequency of errors) and “deadline” aspects of MC systems, are not cost- and resource-efficient. The major challenge in the design of MC system is devising a FP scheduling strategy that addresses both the criticality and deadline aspects of the tasks while facilitating certification and efficient resource usage. This challenge is addressed in this paper.

3 Certification and the FTMC algorithm

An MC system is certified as correct if and only if the system is schedulable at each criticality level. An MC task system is schedulable at $\ell$ -criticality level, where $\ell \in \{\mathtt{LO}, \mathtt{HI}\}$, if and only if the primary and backups of the jobs of each task $\tau _i$ satisfying $L_i \ge \ell$ complete by their deadlines for all the $\ell$-criticality behaviors of the system. According to the definition of correctness, when the system switches to HI-criticality behavior, the LO-critical tasks can be dropped to efficiently utilize the processor. The FTMC algorithm for dispatching the jobs of the tasks is designed as follows:

• There is a criticality level indicator $\ell$, initialized to the lowest criticality level, $\ell \leftarrow \mathtt{LO}$.

• While (true), at each time-instant $t$, do the following

  • if event E1 is detected, i.e., a currently executing primary or backup exceeds its LO-criticality WCET without signaling completion at time $t$, then $\ell \leftarrow \mathtt{HI}$; or

  • if event E2 is detected, i.e., an error is detected at time $t$ and this is the $(\mathtt{f}+1)^{th}$ error in an interval $[t^\prime ,t]$ where $t^\prime \le D_{max}$, then $\ell \leftarrow \mathtt{HI}$.

  • if an error is detected at time $t$, then the next backup of the faulty task becomes ready for execution;

  • the ready job (i.e, its primary or backup) of the highest priority task $\tau _{i}$, satisfying $L_i \ge \ell$, is dispatched for execution;

Algorithm FTMCnospace, as defined above, works exactly same as the uniprocessor FP scheduling with the following three additional features:

• The system employs run-time monitoring to detect the events E1 and E2. As soon as any one of the events is detected, the system switches from LO to HI criticality behavior. Such run-time monitoring support to detect events E1 and E2 can be incorporated as part of system’s health-monitoring functions (Pellizzoni et al. 2008; Raju et al. 1992).

• As soon as the system switches to HI-criticality behavior, the FTMC algorithm drops the LO-criticality tasks to better utilize the processor for HI-critical tasks while not compromising the certification requirement.

• In FTMC algorithm, whenever a job of a task arrives, the primary of the job is executed; and if an error is detected in the primary, then one-by-one backup is executed until no error is detected. The priority of the backup is equal to the priority of the primary.

Regardless of what task corresponds to event E1 or E2, the FTMC algorithm increases the criticality and drops the jobs of the LO-critical tasks after event E1 or E2 is detected. Switching the criticality $\ell$ of the system by setting $\ell \leftarrow \mathtt{HI}$ is a “flag” that is used at run-time to ensure that no job of any LO-critical task is dispatched after the criticality of the system is switched. If criticality behavior $\ell$ is not switched, then the LO-critical tasks may consume processor bandwidth that should be used for executing the HI-critical tasks. And, such uncontrolled provision of processing bandwidth to LO-critical tasks can cause HI-critical task to miss their deadlines.

Clarification of the assumption that $\mathtt{f}\le \mathtt{F}$. Remember that $\mathtt{f}$ and $\mathtt{F}$ are assumed to be the maximum number of errors detected in an interval no larger than $D_{max}$ respectively during the LO- and HI-criticality behavior of the system. And, we assume $\mathtt{f}\le \mathtt{F}$. We think this assumption warrants some explanation, which is given below.

Consider an interval $[r_i,r_i+D_i)$ where $r_i$ and $(r_i+D_i)$ are the release time and deadline of some job of task $\tau _{i}$. Also assume that the system has not switched to HI-criticality behavior before time instant $r_i$. And, the time instant $(r_i+s)$ is when event E1 and/or E2 is detected, i.e., the system switches to HI-criticality behavior at time $(r_i+s)$ for some $s$, where $0 \le s \le D_i$. This situation is depicted in Fig. 2.

Fig. 2

At most $\mathtt{F}$ errors are detected in $[r_i, r_i+D_i)$ where at most $\mathtt{f}$ errors are detected in $[r_i,r_i+s]$ and at most $(\mathtt{F}-\mathtt{f})$ errors are detected in $(r_i+s, r_i+D_i)$

The system exhibits LO-criticality behavior in $[r_i, r_i+s]$ and exhibits HI-criticality behavior in $[r_i+s, r_i+D_i]$ in Fig. 2. Based on the fault model in this paper, the maximum number of errors that can be detected in any interval of length $D_{max}$ during the LO- and HI-criticality behavior of the system is $\mathtt{f}$ and $\mathtt{F}$, respectively. Since $D_i \le D_{max}$, at most $\mathtt{F}$ errors can be detected in $[r_i,r_i+D_i]$ where

• at most $\mathtt{f}$ errors are detected in $[r_i,r_i+s]$ where these errors are detected in the jobs of both LO- and HI-critical tasks, and

• at most $(\mathtt{F}-\mathtt{f})$ errors are detected in $(r_i+s, r_i+D_i)$ where these errors are detected in the jobs of the HI-critical tasks since only HI-critical tasks are allowed to execute beyond $(r_i+s)$ in FTMC scheduling.

Note that if $s=D_i$, then the entire interval $[r_i,r_i+D_i)$ exhibits LO-criticality behavior and at most $\mathtt{f}$ task errors can be detected in that interval. On the other hand, if $s=0$, then the entire interval $[r_i,r_i+D_i)$ exhibits HI-criticality behavior and at most $\mathtt{F}$ task errors can be detected in $[r_i,r_i+D_i)$. Finally, as is shown in Fig. 2, if $0 < s < D_i$, then at most $\mathtt{f}$ errors are detected in $[r_i,r_i+s]$ and at most $(\mathtt{F}-\mathtt{f})$ errors are detected in $(r_i+s, r_i+D_i)$. Note that $\mathtt{f}\le \mathtt{F}$ does not necessary imply that the number of errors in $(r_i+s, r_i+D_i)$, i.e., during the HI-criticality behavior is larger than the number of errors during the LO-criticality behavior in $[r_i,r_i+s]$. This is because $(\mathtt{F}-\mathtt{f})$ can be smaller than $\mathtt{f}$ if the values of $\mathtt{F}$ and $\mathtt{f}$ are such that $2 \cdot \mathtt{f} >\mathtt{F}$. $\square$

Our main objective is to derive schedulability tests of each task $\tau _{i}\in \Gamma$ during both LO and HI criticality behaviors of FTMC algorithm. Section 4 presents important considerations for the worst-case schedulability analysis of FTMC algorithm. The detailed schedulability analysis of FTMC algorithm is presented in Sects. 5 and 7.

4 Considerations for schedulability analysis

We will derive response-time-based schedulability test of each task $\tau _{i}\in \Gamma$ for both LO and HI criticality behaviors. The response time of a task is the largest difference between the completion time and release time of any job of the task. We denote $R_i^{\mathtt{LO}}$ and $R_i^{\mathtt{HI}}$ the response times of task $\tau _i$ respectively for the LO- and HI-criticality behaviors. We compute the response time of a generic job, denoted by $J_i$, of task $\tau _{i}$based on the schedulability analysis during the level-$i$ busy period $[r_i, r_i+t)$ of length $t$, where $r_i$ is the release time of the generic job. An interval is called level-$i$ busy period if and only if jobs of the tasks only in $\mathtt{hpe}_i$ execute in that interval. By computing the worst-case workload (i.e., maximum CPU time required) in the level-$i$ busy period, the response-time of task $\tau _{i}$ is derived.

The workload of the tasks in $\mathtt{hpe}_i$ during the level-$i$ busy period for traditional uniprocessor FP scheduling of constrained-deadline sporadic tasks⁴ is maximized under the following two assumptions (Audsley et al. 1991):

• A1: when all tasks arrive simultaneously, and

• A2: when jobs of the tasks arrive strictly periodically.

Assumptions A1 and A2 also correspond to the worst-case schedulability analysis of FTMC algorithm for LO-criticality behavior. This is because the execution of the jobs during the LO-criticality behavior in FTMC algorithm is same as traditional uniprocessor FP scheduling of (non-MC) sporadic tasks with the exception that backups are executed to recover from task errors. And, if the completion of job $J$ of a task is delayed by $\Delta$ time units due to executing backups of $J$ or its higher-priority jobs, then some other lower priority job $J^\prime$ will be delayed by at most $\Delta$ time unit if both $J$ and $J^\prime$ are released simultaneously (i.e., A1 holds). And, it is not difficult to realize that when jobs of the tasks are released strictly periodically during the LO-criticality behavior, the workload in the busy period is maximized (i.e., A2 holds).

However, A1 and A2 do not correspond to the worst-case schedulability analysis of FTMC algorithm for HI-criticality behavior. This is due to the following reason:

The workload of HI- and LO -critical jobs in a level-i busy period cannot be computed independent of the release times of other jobs when analyzing the HI -criticality behavior of the system.

Whether a HI-critical job executes beyond its LO-criticality WCET depends on when event E1 or E2 is detected relative to the execution of that HI-critical job. Because FTMC algorithm drops the LO-critical tasks when event E1 or E2 is detected, the workload of the LO-critical tasks in the level-$i$ busy period depends on the release time of the jobs that could trigger the events. Considering all possible releases of the jobs of sporadic tasks to exactly analyze the the HI-criticality behavior in the busy period is computationally impractical. We, therefore, concentrate on sufficient schedulability analysis of FTMC algorithm for the HI-criticality behavior of the system (Sect. 7).

The schedulability analysis of FTMC algorithm assumes that an error is detected (using some built-in error-detection mechanism as part of the system’s health monitoring) at the end of execution of a job’s primary or backup since detection of the error at the end of execution corresponds to larger wasted CPU time. Without loss of generality, assume that job $J_k^{o_{k}}$ is the first job of task $\tau _{k}\in \mathtt{hpe}_i$ released in the level-$i$ busy period $[r_i, r_i+t)$. The actual values of $r_i$ and $o_{k}$ are not needed to be known for the schedulability analysis (i.e., any positive integer for $r_i$ and $o_{k}$ can be assumed).

5 Overview of schedulability analysis

In this section, an overview of the schedulability analysis of the FTMC algorithm in the level-$i$ busy period $[r_i, r_i+t)$ is presented. Computing the response time of task $\tau _{i}$ requires to find the workload of the tasks in set $\mathtt{hpe}_i$ during the level-$i$ busy period $[r_i, r_i+t)$. The response time $R_i^{\mathtt{LO}}$ and $R_i^{\mathtt{HI}}$ of task $\tau _{i}$ respectively for LO- and HI-criticality behaviors are computed based on the following two steps.

Step 1 (job characterization) When analyzing a particular criticality behavior, we first determine the jobs of each task $\tau _k \in \mathtt{hpe}_i$that can execute in the level-$i$ busy period. And, for each such job of task $\tau _{k}$, say the $h^{th}$ job⁵ of task $\tau _{k}$, we also decide whether $J_k^h$ executes up to its LO- or HI-criticality WCET in the busy period. If job $J_k^h$ is considered to execute up to its LO-criticality WCET, then it is characterized as $J_k^h(\mathtt{LO})$; otherwise, it is characterized as $J_k^h(\mathtt{HI})$.

The purpose of characterizing job $J_k^h$ either as $J_k^h(\mathtt{LO})$ or $J_k^h(\mathtt{HI})$ is to consider the corresponding LO- or HI-criticality WCET when computing the workload in the busy period. It is important to characterize each job this way in order to reduce pessimism during the schedulability analysis because if job $J_k^h$ executes in LO-criticality behavior, then (i) the maximum number of faults that can affect this job is limited to $\mathtt{f}$ (not $\mathtt{F}$) according to the fault model considered in this paper, and (ii) the WCET of the primary and backup of job $J_k^h$ corresponds to the LO-criticality WCET of task $\tau _{k}$. Consequently, the total CPU time required for job $J_k^h$ which is characterized as $J_k^h(\mathtt{LO})$ can be computed using the relatively less pessimistic assumption regarding the frequency of faults and WCET.

Step 2 (workload computation) The maximum total execution time (i.e., workload) that needs to be completed by jobs of the tasks in set $\mathtt{hpe}_i$ during the busy period is computed in this step. Since the length of the busy period will be bounded by $D_{max}$, the workload computation must consider that the jobs determined in Step 1 may need to recover from at most $\mathtt{f}$ and $\mathtt{F}$ errors when analyzing the LO and HI-criticality behaviors, respectively. To this end, we are interested in solving the following problem:

Workload Computation Problem Let $\mathcal {A}$ be a set of jobs where each particular job $J_k^h$ in $\mathcal {A}$ is characterized as $J_k^h(\mathtt{LO})$ if job $J_k^h$ of task $\tau _{k}$ must complete its execution in FTMC scheduling during the LO-criticality behavior; otherwise, job $J_k^h$ is characterized as $J_k^h(\mathtt{HI})$. Set $\mathcal {A}$ may contain jobs of different tasks. Assume that the jobs of set $\mathcal {A}$ suffer $\alpha$ task errors such that these errors affect the primaries and backups of different jobs in set $\mathcal {A}$ during run-time. What is the maximum total execution time required by the jobs in set $\mathcal {A}$ such that these jobs suffer and recover from $\alpha$ task errors?

To compute the response time of task $\tau _{i}$ for each criticality behavior, Step 1 finds the set of jobs of the tasks in $\mathtt{hpe}_i$ that can execute in the level-$i$ busy period. Then, Step 2 computes the workload by solving the workload computation problem by considering $\alpha =\mathtt{f}$ and $\alpha =\mathtt{F}$ for analyzing the LO- and HI-criticality behaviors in the busy period, respectively. The solution to the workload computation problem is presented in the remainder of this section by assuming $\mathcal {A}$ and $\alpha$ are known. The details of Step 1, i.e., characterizing the set of jobs that can execute in the busy period for each criticality behavior, are presented in Sects. 6 and 7.

We denote ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ the maximum workload that needs to be completed by the jobs in set $\mathcal {A}$ where $\alpha$ errors are detected in these jobs and recovered. Inspired by Aydin’s work in Aydin (2007), technique to compute the maximum workload ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ is presented. In order to compute ${\mathtt{W}}_{\alpha }({\mathcal {A}})$, we need to consider the worst-case occurrences of $\alpha$ errors affecting the jobs in $\mathcal {A}$ such that the sum of the execution time required by the primaries and backups of the jobs in $\mathcal {A}$ is maximized. The value of ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ is recursively computed as follows.

The basis of the recursion considers exactly one job (say, job $J_k^h(\ell )$) in $\mathcal {A}$ such that $J_k^h$ suffers $\alpha$ errors during the $\ell$-criticality behavior. Since there are at most $\mathtt{f}$ and $\mathtt{F}$ errors in any interval no larger than $D_{max}$respectively during the LO and HI criticality behaviors, job $J_k^h$ suffers at most $min\{\mathtt{f}, \alpha \}$ errors if $J_k^h(\mathtt{LO}) \in \mathcal {A}$; otherwise, it suffers at most $min\{\mathtt{F}, \alpha \}$ errors. The basis is computed as follows:

$$\begin{aligned} {\mathtt{W}}_{\alpha }({\mathcal {A}})={\mathtt{W}}_{\alpha }({{\{J_k^h(\ell )\}}})= {\left\{ \begin{array}{ll} \mathtt{E}_{k,min\{\alpha , \mathtt{f}\}} &{}\text {if}\;\, \ell =\mathtt{LO} \\ \hat{\mathtt{E}}_{k,min\{\alpha , \mathtt{F}\}} &{}\text {if}\;\, \ell =\mathtt{HI} \end{array}\right. } \end{aligned}$$

(3)

where $\mathtt{E}_{k,min\{\alpha , \mathtt{f}\}}$ and $\hat{\mathtt{E}}_{k,min\{\alpha , \mathtt{F}\}}$ are computed using Eqs. (1) and (2), respectively.

Let $\mathcal {B}=\mathcal {A}-\{J_k^h\}$. The value of ${\mathtt{W}}_{\alpha }({\mathcal {A}})$, where $|A|>1$, is computed as follows:

$$\begin{aligned} {\mathtt{W}}_{\alpha }({\mathcal {A}})=\mathop {max}\limits _{q=0}^{\alpha } \Big \{ {{\mathtt{W}}_{q}({{\mathcal {B}}})} + {{\mathtt{W}}_{(\alpha -q)}({{\{J_k^h(\ell )\}}})}\Big \} \end{aligned}$$

(4)

using values of ${\mathtt{W}}_{q}({{\mathcal {B}}})$ that are computed for $q=0,1, \ldots \alpha$ before ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ is computed. The value of ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ is the maximum for one of the $(\alpha +1)$ possible values of $q$ for the right hand side of Eq. (4). The value of $q$ is selected such that, if there are $q$ errors detected in the jobs of set $\mathcal {B}$ and the remaining $(\alpha -q)$ errors are detected in job $J_k^h$, then ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ is maximum for some $q$, $0 \le q \le \alpha$. Starting with one job in set $\mathcal {A}$, and then including one-by-one job in the calculation of workload in Eq. (4), the value of ${\mathtt{W}}_{\alpha }({\mathcal {A}})$ can be computed using $O(|\mathcal {A}| \cdot \mathtt{F}^2)$ operations for all $\alpha =0, 1, \ldots \mathtt{F}$.

Example 2

Consider the task set in Table 1 where $\mathtt{f}=1$ and $\mathtt{F}=2$. We will show how to compute ${\mathtt{W}}_{2}({\mathcal {A}})$ where $\mathcal {A}=\{J_1^1(\mathtt{LO}), J_3^1(\mathtt{HI})\}$. The value ${\mathtt{W}}_{2}({\mathcal {A}})$ is the maximum workload of the jobs in $\mathcal {A}$ such that these jobs suffer and recover from $\alpha =2$ errors. The workload of each individual job in $\mathcal {A}$—affected by $0,1$ and $2$ errors—is computed using Eq. (3) as follows:

$$\begin{aligned}&{{\mathtt{W}}_{0}({\{J_1^1(\mathtt{LO})\}})}=\mathtt{E}_{1,min\{0, \mathtt{f}\}}=\mathtt{E}_{1,min\{0, 1\}}=\mathtt{E}_{1,0}=1\\&{{\mathtt{W}}_{1}({\{J_1^1(\mathtt{LO})\}})}=\mathtt{E}_{1,min\{1, \mathtt{f}\}}=\mathtt{E}_{1,min\{1, 1\}}=\mathtt{E}_{1,1}=2\\&{{\mathtt{W}}_{2}({\{J_1^1(\mathtt{LO})\}})}=\mathtt{E}_{1,min\{2, \mathtt{f}\}}=\mathtt{E}_{1,min\{2, 1\}}=\mathtt{E}_{1,1}=2\\&{{\mathtt{W}}_{0}({\{J_3^1(\mathtt{HI})\}})}=\hat{\mathtt{E}}_{3,min\{0, \mathtt{F}\}}=\hat{\mathtt{E}}_{3,min\{0, 2\}}=\mathtt{E}_{3,0}=4\\&{{\mathtt{W}}_{1}({\{J_3^1(\mathtt{HI})\}})}=\hat{\mathtt{E}}_{3,min\{1, \mathtt{F}\}}=\hat{\mathtt{E}}_{3,min\{1, 2\}}=\mathtt{E}_{3,1}=7\\&{{\mathtt{W}}_{2}({\{J_3^1(\mathtt{HI})\}})}=\hat{\mathtt{E}}_{3,min\{2, \mathtt{F}\}}=\hat{\mathtt{E}}_{3,min\{2, 2\}}=\mathtt{E}_{3,2}=10 \end{aligned}$$

Note that ${\mathtt{W}}_{2}({\{J_1^1(\mathtt{LO})\}})$ is equal to $\mathtt{E}_{1,1}$ rather than $\mathtt{E}_{1,2}$ even if $\alpha =2$. This is due to the “min” function in Eq. (3) which accounts the important fact that job $J_1^1$ executes in LO-criticality behavior since it is characterized as $J_1^1(\mathtt{LO})$ and thus can suffer at most $\mathtt{f}=1$ error. Therefore, the use of “min” function in Eq. (3) helps to tighten the computed workload which reduces the demand on processing capacity. The value of ${\mathtt{W}}_{2}({\{J_1^1(\mathtt{LO}),J_3^1(\mathtt{HI})\}})$ is computed using Eq. (4) as follows:

$$\begin{aligned} {{\mathtt{W}}_{2}({\{J_1^1(\mathtt{LO}),J_3^1(\mathtt{HI})\}})}&=\mathop {max}_{q=0}^{2} \Big \{ {{\mathtt{W}}_{q}({{\{J_1^1(\mathtt{LO})\}}})} + {{\mathtt{W}}_{(2-q)}({{\{J_3^1(\mathtt{HI})\}}})}\Big \} \\&=max\{{{\mathtt{W}}_{0}({{\{J_1^1(\mathtt{LO})\}}})} + {{\mathtt{W}}_{2}({{\{J_3^1(\mathtt{HI})\}}})}, \\&\quad \quad \quad \quad \quad {{\mathtt{W}}_{1}({{\{J_1^1(\mathtt{LO})\}}})} + {{\mathtt{W}}_{1}({{\{J_3^1(\mathtt{HI})\}}})}, \\&\quad \quad \quad \quad \quad {{\mathtt{W}}_{2}({{\{J_1^1(\mathtt{LO})\}}})}+ {{\mathtt{W}}_{0}({{\{J_3^1(\mathtt{HI})\}}})} \}\\&=max\{1+10, 2+7, 2+4\}=11 \end{aligned}$$

$\square$

The details schedulability analysis of the FTMC algorithm to compute $R_i^{\mathtt{LO}}$ and $R_i^{\mathtt{HI}}$ are now presented in Sects. 6–7.

6 Schedulability analysis: LO criticality

In this section, we compute the response-time $R_i^{\mathtt{LO}}$ of each task $\tau _i \in \Gamma$ considering the occurrences of at most $\mathtt{f}$ task errors in a level-$i$ busy period $[r_i, r_i+t)$ of length $t$. First, we determine the set of jobs of the tasks in $\mathtt{hpe}_i$ that are eligible to execute in the busy period during the LO-criticality behavior. Then, the maximum workload of these jobs due to the recovery of at most $\mathtt{f}$ task errors is computed using Eq. (4). Finally, a recursion to compute $R_i^{\mathtt{LO}}$ is presented.

We denote ${\mathtt{JB}}_i(t)$ the set of all jobs of the tasks in $\mathtt{hpe}_i$ that are released in the level-$i$ busy period $[r_i, r_i+t)$. Since A1 and A2 correspond to the worst-case schedulability analysis of FTMC algorithm during the LO-criticality behavior (as discussed in Sect. 4), there are at most $\lceil \frac{t}{T_k}\rceil$ jobs of task $\tau _k \in \mathtt{hpe}_i$that are released in the busy period $[r_i, r_i+t)$. If job $J_k^{o_{k}}$ of task $\tau _k \in \mathtt{hpe}_i$ is released at time $r_i$, the set ${\mathtt{JB}}_i(t)$ is computed as follows:

$$\begin{aligned} {\mathtt{JB}}_i(t)= \mathop {\bigcup }_{\tau _k \in \mathtt{hpe}_{i}} \left\{ J_k^{h}(\mathtt{LO}) | h=o_{k} \ldots \left( o_{k}+\lceil \frac{t}{T_k} \rceil -1\right) \right\} \end{aligned}$$

(5)

Since during the LO-criticality behavior, no primary/backup of task $\tau _k$ executes more than its LO-criticality WCET, each job $J_k^h$ is characterized as $J_k^h(\mathtt{LO})$ in ${\mathtt{JB}}_i(t)$. The generic job $J_i$ is captured in set ${\mathtt{JB}}_i(t)$ as $J_i^{o_i}$. Since at most $\mathtt{f}$ task errors need to be recovered in the busy period, the response time $R_{i}^{\mathtt{LO}}$ of task $\tau _{i}$ is given as follows:

$$\begin{aligned} R_{i}^{\mathtt{LO}} \leftarrow {\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_i(R_i^{\mathtt{LO}})}}) \end{aligned}$$

(6)

where ${\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_i(R_i^{\mathtt{LO}})}})$ is computed using Eq. (4). We can solve Eq. (6) by searching the least fixed point starting with $R_{i}^{\mathtt{LO}}=\mathtt{E}_{i,\mathtt{f}}$ for the right-hand side of Eq. (6). Example 3 in page 32 demonstrates how to compute $R_{i}^{\mathtt{LO}}$.

When certifying a system at LO-criticality level, Eq. (6) can be used to determine whether task $\tau _i \in \Gamma$ meets its deadline during all the LO -criticality behavior of the system or not. The test in Eq. (6) is an exact test for the FTMC scheduling algorithm when considering the LO-criticality behavior of the system under the assumed fault model. Note that Eq. (6) can be used to test the fault-tolerant schedulability of traditional (non-MC) sporadic tasks where at most $\mathtt{f}$ task errors are detected in any interval of length $D_{max}$. Moreover, if $\mathtt{f} =0$, then Eq. (6) becomes the well-known uniprocessor response-time analysis, as is proposed by Audsley et al. (1993), for traditional non-MC and non-fault-tolerant fixed-priority scheduling of sporadic tasks.

7 Schedulability analysis: HI criticality

In this section, we compute the response-time $R_i^{\mathtt{HI}}$ of each HI-critical task $\tau _i$ considering the occurrences of at most $\mathtt{F}$ task errors in a level-$i$ busy period $[r_i, r_i+t)$ of length $t$. The primary and backups of each task $\tau _k \in \mathtt{hpe}_i$in the busy period may execute up to the WCET estimated for the HI-criticality behavior.

Assume $s$ be the time instant relative to $r_i$ at which the system switches from $\mathtt{LO}$ to $\mathtt{HI}$ criticality behavior (as is shown in Fig. 3). If $s > R_i^{\mathtt{LO}}$, then the generic job $J_i$ finishes its execution before $(r_i+s)$ since the response time of task $\tau _{i}$ during the LO-criticality behavior is $R_i^{\mathtt{LO}}$. Because we are interested to find the response time of HI-critical task $\tau _i$ during the HI-criticality behavior of the system, we only consider $0 \le s \le R_i^{\mathtt{LO}}$ to compute $R_i^{\mathtt{HI}}$.

Fig. 3

The level-$i$ busy period $[r_i, r_i+t)$. System switches to HI-criticality at $(r_i+s)$ because either event E1 or E2 is detected at $(r_i+s)$. Notice that $s=0$ considers the scenario when the criticality of the system switches at or before the start of the busy period $[r_i, r_i+t)$

We denote $\overline{R}^{\mathtt{HI} }_{i,s}$ the response time of task $\tau _i$ during the HI-criticality behavior for some given $s$. The response time $R_i^{\mathtt{HI}}$ is the largest $\overline{R}^{\mathtt{HI}}_{i,s}$ for some $s$ where $0\le s \le R_i^{\mathtt{LO}}$. To compute $\overline{R}^{\mathtt{HI}}_{i,s}$, first we determine the set of jobs of the tasks in $\mathtt{hpe}_i$ that can execute in the busy period $[r_i, r_i+t)$ for some given $s$. And, for each such job, say job $J_k^h$ of task $\tau _{k}\in \mathtt{hpe}_{i}$, we decide whether $J_k^h$ executes during the LO- or HI-criticality behavior in the busy period to characterize it either as $J_k^h(\mathtt{LO})$ or $J_k^h(\mathtt{HI})$. Then, the workload due to these jobs suffering from at most $\mathtt{F}$ task errors is computed using Eq. (4). Finally, a recursion to compute $\overline{R}^{\mathtt{HI}}_{i,s}$ is presented.

We denote $\mathcal {X}_{i,s}(t)$ and $\mathcal {Y}_{i,s}(t)$ respectively the set of all LO- and HI-critical jobs of the tasks in $\mathtt{hpe}_i$ that can execute in the busy period $[r_i,r_i+t)$ for some given $s$ and $t$. First, we present how sets $\mathcal {X}_{i,s}(t)$ and $\mathcal {Y}_{i,s}(t)$ are computed. Then, the maximum workload due to the execution of the jobs in set $\mathcal {X}_{i,s}(t) \cup \mathcal {Y}_{i,s}(t)$ subjected to $\mathtt{F}$ errors is computed.

Computing $\mathcal {X}_{i,s}(t)$ This set contains only the jobs of the LO-critical tasks in $\mathtt{hpe}_i$ (i.e., jobs of the tasks in $\mathtt{hpL}_i$) that can execute in the busy period $[r_i, r_i+t)$. Since FTMC drops the LO-critical jobs after the criticality switches at $(r_i+s)$, set $\mathcal {X}_{i,s}(t)$ only contains the jobs of tasks in set $\mathtt{hpL}_i$ that are released in $[r_i, r_i+s)$. Since jobs in $\mathcal {X}_{i,s}(t)$ execute only in LO-criticality behavior, the assumptions A1 and A2 correspond to the worst-case analysis in the busy period. And, there are at most $\lceil \frac{s}{T_k}\rceil$ jobs of each task $\tau _k \in \mathtt{hpL}_i$released in $[r_i, r_i+s)$. This is depicted in Fig. 4.

Fig. 4

At most $\lceil \frac{s}{T_k}\rceil$ jobs of $\tau _k \in \mathtt{hpL}_i$can execute in $[r_i, r_i+s)$. The upward arrow indicates job arrival and the downward arrow indicates job’s deadline

If job $J_k^{o_k}$ is the first job of task $\tau _k \in \mathtt{hpL}_i$ released in the busy period, set $\mathcal {X}_{i,s}(t)$ is computed for some given $s$ and $t$ as follows (note that if $s=0$, then this set is empty):

$$\begin{aligned} \mathcal {X}_{i,s}(t)= \mathop {\bigcup }_{\tau _k \in \mathtt{hpL}_i} \left\{ J_k^h(\mathtt{LO}) | h=o_k, \ldots , \left( o_k+\lceil \frac{s}{T_k}\rceil -1\right) \right\} \end{aligned}$$

(7)

Note that Eq. (7) considers exactly $\lceil \frac{s}{T_k}\rceil$ jobs of each task $\tau _k \in \mathtt{hp}_i$ in set $\mathcal {X}_{i,s}(t)$ since both A1 and A2 are satisfied for the analysis of the system in $[r_i, r_i+s]$ which exhibits LO-criticality behavior. In others words, we assume one job of all the tasks in $\mathtt{hpL}_i$ arrives simultaneously at time $r_i$ and subsequent jobs of each task $\tau _{k}\in \mathtt{hpL}_i$ arrive as soon as possible in $[r_i, r_i+s]$.

Computing $\mathcal {Y}_{i,s}(t)$ This set contains only the jobs of the HI-critical tasks in $(\mathtt{hpH}_i\cup \{\tau _i\})$. Note that the generic job $J_i$ belongs to this set because $\tau _i$ is a HI-critical task.

The number of jobs of task $\tau _{k}\in \mathtt{hpH}_i\cup \{\tau _i\}$ that are released in $[r_i, r_i+t)$ is at most $\lceil \frac{t}{T_k}\rceil$. This is because A1 and A2 correspond to the release of maximum number of jobs of any task that may execute during the busy period in any uniprocessor FP scheduling, of which FTMC is an example. However, assumptions A1 and A2 do not correspond to the worst-case for computing the maximum workload of the HI-critical tasks in the busy period (as discussed in Sect. 4). The workload of the HI-critical task $\tau _{k}$ can be computed by finding how many (out of $\lceil \frac{t}{T_k}\rceil$) jobs of $\tau _{k}$ may execute up to their HI-criticality WCET in the busy period.

A trivial way to compute the maximum workload due to the execution of the jobs of task $\tau _{k}$ in the busy period is to consider that the primary and backups of each of the $\lceil \frac{t}{T_k}\rceil$ jobs of task $\tau _{k}$ take up to their HI-criticality WCET. However, computing the workload based on this trivial approach may be pessimistic if some of these jobs must finish execution before the criticality is switched; hence, only allowed to execute up to their LO-criticality WCET. Therefore, our aim is to find a safe but tight upper bound on the number of jobs of task $\tau _{k}$ that can execute in the HI-criticality behavior. The maximum number of jobs of task $\tau _{k}$ that are eligible for execution in the interval $[r_i+s, r_i+t)$, i.e., in an interval of length $(t-s)$, is bounded by the following quantity:

$$\begin{aligned} \bigg \lceil \frac{t-s}{T_k}\bigg \rceil +1 \end{aligned}$$

by assuming $T_k=D_k$. However, if $D_k<T_k$, then there is forced to be an interval of length $(T_k-D_k)$ after the completion of each job of task $\tau _{k}$ during which no job of task $\tau _{k}$ is allowed to be released since the minimum inter-arrival time of the jobs of task $\tau _{k}$ is $T_k$. Therefore, the maximum number of jobs of task $\tau _{k}$ that are eligible for execution in an interval of length $(t-s)$ is bounded by the following quantity, as is shown by Baruah et al. (2011b):

$$\begin{aligned} \bigg \lceil \frac{t-s-(T_k-D_k)}{T_k}\bigg \rceil +1 \end{aligned}$$

However, if $s+(T_k-D_k)$ is small, then we may have $\lceil \frac{t-s-(T_k-D_k)}{T_k}\rceil +1 > \lceil \frac{t}{T_k}\rceil$. Based on these observations, the work in Baruah et al. (2011b) without considering fault-tolerance proposed an upper bound on the number of jobs of task $\tau _{k}$ that can execute up to their HI-criticality WCET in the busy period for some given $s$ and $t$. This upper bound (please see Eq. (11) in reference Baruah et al. 2011b) is given as follows:

$$\begin{aligned} min\bigg \{\bigg \lceil \frac{t-s-(T_k-D_k)}{T_k} \bigg \rceil +1, \bigg \lceil \frac{t}{T_k}\bigg \rceil \bigg \} \end{aligned}$$

The crucial observation regarding this upper bound is that it is independent of the WCET parameter of task $\tau _{k}$. Consequently, regardless of how the primaries and backups of the jobs of task $\tau _{k}$ are executed in the busy period, this upper bound is also applicable to bound the number of jobs of $\tau _{k}$ that may execute up to their HI-criticality WCET in the busy period for FTMC algorithm. To this end, we define $x_k$ the minimum number of jobs of $\tau _{k}$ that can execute up to their LO-criticality WCET in the busy period as follows:

$$\begin{aligned} x_k=\bigg \lceil \frac{t}{T_k}\bigg \rceil - min\bigg \{\bigg \lceil \frac{t-s-(T_k-D_k)}{T_k} \bigg \rceil +1, \bigg \lceil \frac{t}{T_k}\bigg \rceil \bigg \} \end{aligned}$$

(8)

Note that if $s \le D_k$, then $x_k=0$., i.e., all $\lceil \frac{t}{T_k}\rceil$ jobs of $\tau _{k}$ can execute up to their HI-criticality WCET (as is shown in Fig. 5).

Fig. 5

All the $\lceil \frac{t}{T_k} \rceil$ jobs of task $\tau _{k}$ can execute up to their HI-criticality WCET in the busy period if $0 \le s \le D_k$

In summary, there are at least $x_k$ jobs of $\tau _{k}$ that execute no more than their LO-criticality WCET while the remaining $(\lceil \frac{t}{T_k} \rceil -x_k)$ jobs may execute up to their HI-criticality WCET in the busy period $[r_i, r_i+t)$. If job $J_k^{o_k}$ is the first job of $\tau _k \in \mathtt{hpH}_i\cup \{\tau _i\}$ released in $[r_i, r_i+t)$, then the set of jobs of the tasks in $\mathtt{hpH}_i\cup \{\tau _i\}$ that execute no more than their LO-criticality WCET in the busy period is:

$$\begin{aligned} \mathop {\bigcup }_{\tau _k \in \mathtt{hpH}_i\cup \{\tau _i\}} \left\{ J_k^h(\mathtt{LO}) | h=o_k, \ldots , (o_k+x_k-1)\right\} \end{aligned}$$

(9)

And, the set of jobs of tasks in $\mathtt{hpH}_i\cup \{\tau _i\}$ that may execute up to their HI-criticality WCET in the busy period is:

$$\begin{aligned} \mathop {\bigcup }_{\tau _k \in \mathtt{hpH}_i\cup \{\tau _i\}} \left\{ J_k^h(\mathtt{HI}) | h=o_k+x_k, \ldots , \left( o_k+\lceil \frac{t}{T_k} \rceil -1\right) \right\} \end{aligned}$$

(10)

Therefore, set $\mathcal {Y}_{i,s}(t)$ which is the set of jobs of all the HI-critical tasks that execute in the busy period is:

$$\begin{aligned} \mathcal {Y}_{i,s}(t)=\mathrm{Eq.}\, (9) \bigcup \mathrm{Eq.}\,(10) \end{aligned}$$

(11)

Computing $\overline{R}^{\mathtt{HI}}_{i,s}$ The set $\mathcal {X}_{i,s}(t)\cup \mathcal {Y}_{i,s}(t)$ is the set of all the jobs of the tasks in $\mathtt{hpe}_{i}=\mathtt{hpL}_i\cup \mathtt{hpH}_i\cup \{\tau _i\}$ that execute in the busy period where $\mathcal {X}_{i,s}(t)$ and $\mathcal {Y}_{i,s}(t)$ are computed using Eqs. (7) and (11), respectively. To find $\overline{R}^{\mathtt{HI}}_{i,s}$, we have to consider the worst-case occurrences and recovery of $\mathtt{F}$ errors in the jobs of $(\mathcal {X}_{i,s}(t) \cup \mathcal {Y}_{i,s}(t))$ such that the workload in the busy period is maximum. In other words, we are interested in computing $\mathtt{W}_{\mathtt{F}}({{\mathcal {X}_{i,s}(t) \cup \mathcal {Y}_{i,s}(t)}})$. The response time of HI-critical task $\tau _i$ for some given $s$ is given as follows:

$$\begin{aligned} \overline{R}_{i,s}^{\mathtt{HI}} \leftarrow \mathtt{W}_{\mathtt{F}}({{\mathcal {X}_{i,s}(\overline{R}_{i,s}^{\mathtt{HI}}) \cup \mathcal {Y}_{i,s}(\overline{R}_{i,s}^{\mathtt{HI}})}}) \end{aligned}$$

(12)

The Eq. (12) can be solved by iteratively searching the least fixed point starting with $R_{i,s}^{\mathtt{HI}}=\hat{\mathtt{E}}_{i,\mathtt{F}}$ for the right-hand side of Eq. (12). The response time $R_i^{\mathtt{HI} }$ of task $\tau _i$ during any HI-criticality behavior of the system is given as follows:

$$\begin{aligned} R_i^{\mathtt{HI}}= \mathop {max}_{0 \le s \le R_i^{\mathtt{LO}}} \left\{ \overline{R}^{\mathtt{HI}}_{i,s}\right\} \end{aligned}$$

(13)

When certifying the system at HI-criticality level, Eq. (13) can be used to determine whether the HI-critical task $\tau _i$ meets its deadline during all HI-criticality behaviors of the system or not. The response-time calculation in Eq. (6) for LO-criticality behavior is an exact test while the response-time calculation in Eq. (13) for HI-criticality behavior is a sufficient test.

Time-complexity As mentioned earlier, the time-complexity of computing ${\mathtt{W}}_{\alpha }({{\mathcal {A}}})$ for all $\alpha =0, 1, \ldots \mathtt{F}$ using Eq. (4) is $O(|\mathcal {A}| \cdot \mathtt{F}^2)$. There are pseudo-polynomial number of jobs of the higher priority tasks that can be released between the release time and deadline of any job. Therefore, the workload computation problem considering a collection of jobs in set $\mathcal {A}$ has pseudo-polynomial time complexity in the representation of the system. Because the response-time calculation in Eqs. (6) and (13) apply the workload computation in Eq. (4) at most $O(n \cdot D_{max})$ times for all the $n$ tasks, the proposed schedulability test for the FTMC algorithm has pseudo-polynomial time complexity.

Example 3

Consider the task set in Table 1 where $\mathtt{f}$ = 1 and $\mathtt{F}$ = 2. Assume that $\tau _1$ and $\tau _2$ are the higher priority tasks of $\tau _3$. We will show how $R_3^{\mathtt{LO}}$ and $R_3^{\mathtt{HI} }$ are computed based on Eqs. (6) and (13), respectively. Without loss of generality, assume $r_i=r_3=0$ (busy period starts at 0) and $o_k=1$ for each task $\tau _k$.

Computing $R_3^{\mathtt{LO}}$ Initially, the length of the busy period is $R_3^{\mathtt{LO}}=\mathtt{E}_{3,\mathtt{f}}=\mathtt{E}_{3,1}=6$. The set of jobs that are eligible for execution in the busy period $[0, 6)$ is ${\mathtt{JB}}_{3}(6)$. Based on Eq. (5), the set ${\mathtt{JB}}_{3}(6)$ is given as follows:

$$\begin{aligned} {\mathtt{JB}}_{3}(6)=\left\{ J_1^1(\mathtt{LO}), J_2^1(\mathtt{LO}), J_3^1(\mathtt{LO})\right\} \end{aligned}$$

Note that the generic job $J_3$ is captured in ${\mathtt{JB}}_{3}(6)$ as $J_3^1(\mathtt{LO})$. The maximum workload of the jobs in set ${\mathtt{JB}}_{3}(6)$ such that these jobs can suffer and recover at most $\mathtt{f}=1$ error is ${\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_{3}(6)}})$. Based on Eq. (4), the value of ${\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_{3}(6)}})$ is given as follows:

$$\begin{aligned}&{\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_{3}(6)}})=\Big ({\left\{ J_1^1(\mathtt{LO}), J_2^1(\mathtt{LO}),J_3^1(\mathtt{LO})\right\} \Big )}{1}=9 \end{aligned}$$

Since this computed workload is larger than the length of the busy period, the new length of the busy period is reset to $R_3^{\mathtt{LO} }=9$. Based on Eq. (5), the jobs released in the busy period $[0, 9)$ is given as:

$$\begin{aligned} {\mathtt{JB}}_{3}(9)=\left\{ J_1^1(\mathtt{LO}), J_1^2(\mathtt{LO}), J_2^1(\mathtt{LO}), J_3^1(\mathtt{LO})\right\} \end{aligned}$$

Based on Eq. (4), the maximum workload of the jobs in set ${\mathtt{JB}}_{3}(9)$ subjected to at most $\mathtt{f}=1$ error is given as follows:

$$\begin{aligned}&{\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_{3}(9)}})=\Big ({\left\{ J_1^1(\mathtt{LO}),J_1^2(\mathtt{LO}), J_2^1(\mathtt{LO}),J_3^1(\mathtt{LO})\right\} \Big )}{1}=10 \end{aligned}$$

And, the new length of the busy period is $R_3^{\mathtt{LO} }=10$. The jobs released in the busy period $[0, 10)$ is given as follows:

$$\begin{aligned} {\mathtt{JB}}_{3}(10)=\left\{ J_1^1(\mathtt{LO}), J_1^2(\mathtt{LO}), J_2^1(\mathtt{LO}), J_3^1(\mathtt{LO})\right\} \end{aligned}$$

And, we have ${\mathtt{W}}_{\mathtt{f}}({{{\mathtt{JB}}_{3}(10)}})={\mathtt{W}}_{1}({{{\mathtt{JB}}_{3}(10)}})=10$ because ${\mathtt{JB}}_{3}(10)={\mathtt{JB}}_{3}(9)$. Since the computed workload is equal to length of the busy period, the response time computation converges and $R_3^{\mathtt{LO}}=10$. Since $R_3^{\mathtt{LO}} \le D_3=14$, task $\tau _3$ meets its deadline in all LO-criticality behaviors.

Computing $R_3^{\mathtt{HI}}$ According to Eq. (13), the values of $s$ ranges in $[0, R_3^{\mathtt{LO}}]$. Here we only show here how to compute $R_{3,s}^{\mathtt{HI}}$ for $s=9$. Initially, the length of the busy period is $\overline{R}_{3,s}^{\mathtt{HI}}=\hat{\mathtt{E}}_{3,\mathtt{F}}=\hat{\mathtt{E}}_{3,2}=10$. The jobs that are released in the busy period $[0, 10)$ are in set $(\mathcal {X}_{i,s}(t) \cup \mathcal {Y}_{i,s}(t))$ where $i=3$, $s=9$ and $t=R_{3,s}^{\mathtt{HI}}=10$.

We have $\mathcal {X}_{3,9}(10)=\{J_2^1(\mathtt{LO})\}$ and $\mathcal {Y}_{3,9}(10)=\{J_1^1(\mathtt{LO}), J_1^2(\mathtt{HI}), J_3^1(\mathtt{HI})\}$ based on Eqs. (7) and (11) , respectively. The generic job $J_3$ is included in $\mathcal {Y}_{3,9}(10)$ as $J_3^1(\mathtt{HI})$.

Based on Eq. (4), the maximum total workload due to the execution of the jobs in set $\mathcal {X}_{3,9}(10) \cup \mathcal {Y}_{3,9}(10)$ that can suffer and recover at most $\mathtt{F}=2$ errors is given as follows:

$$\begin{aligned}&{\mathtt{W}}_{2}({{\{J_2^1(\mathtt{LO}), J_1^1(\mathtt{LO}), J_1^2(\mathtt{HI}), J_3^1(\mathtt{HI}) \}}})=15 \end{aligned}$$

Since the computed workload is larger than the deadline $D_3=14$ of task $\tau _3$, the response time $R_{i,s}^{\mathtt{HI} } > D_3=14$, which implies [based on Eq. (13)] that $R_i^{\mathtt{HI}}> D_3$. So, task $\tau _3$ cannot be guaranteed to be schedulable during all HI-criticality behaviors. $\square$

7.1 Priority assignment using audsley’s OPA algorithm

The proposed response-time test in Eqs. (6) and (13) can be used to find the fixed priorities of the tasks using Audsley’s OPA algorithm (Audsley 2001). The following three conditions, proposed by Davis and Burns (2009) are used to check whether a shcedulability test $S$ is OPA-compatible, i.e., can be applied along with Audsley’s OPA algorithm to find fixed-priority ordering of the tasks.

• Condition 1 The schedulability of a task $\tau _i$ may, according to test S, be dependent on the set of higher priority tasks, but not on the relative priority ordering of those tasks.

• Condition 2 The schedulability of a task $\tau _i$ may, according to test S, be dependent on the set of lower priority tasks, but not on the relative priority ordering of those tasks.

• Condition 3 When the priorities of any two tasks of adjacent priority are swapped, the task being assigned the higher priority can not become unschedulable according to test S, if it was previously schedulable at the lower priority. (As a corollary, the task being assigned the lower priority can not become schedulable according to test S, if it was previously unschedulable at the higher priority).

Now we briefly describe how these conditions are satisfied for both schedulability tests in Eqs. (6) and (13). Note that both Eqs. (6) and (13) are computed based on the workload of the higher priority tasks. And, the workload of all the higher priority tasks is the sum of the workloads of jobs of each higher priority task considering the occurrences of a particular number of faults in each such job. Computing the workload of each job of each particular task entirely depends on the corresponding task’s parameters (please observe that the workload computation in Eq. (4) accumulates workload of each job separately). In other words, the workload of a job of each particular task can be computed independent of any parameters of its higher or lower priority tasks. This implies that Eqs. (6) and (13) satisfy both Condition 1 and Condition 2 for a schedulability test to be OPA-compatible.

The tests in Eqs. (6) and (13) are derived for FTMC algorithm, which is a fixed-priority based algorithm. If the priorities of any two tasks of adjacent priority are swapped, then the task being assigned the higher priority cannot suffer more interference than that of when it was assigned lower priority in fixed-priority based scheduling. Consequently, the task being assigned the higher priority cannot become unschedulable according to tests Eqs. (6) and (13) if it was previously deemed schedulable at the lower priority using Eqs. (6) and (13). Therefore, schedulability tests in Eqs. (6) and (13) also satisfy Condition 3 for a schedulability test to be OPA-compatible.

Given that the schedulability tests in Eqs. (6) and (13) are OPA-compatible, the OPA algorithm is combined with Eqs. (6) and (13) as follows in Fig. 6. The OPA algorithm is applied to find the priorities of the MC tasks as follows. Initially, no task is assigned any priority (i.e., all tasks are priority-unassigned). Priorities are assigned from lowest to highest priority level (loop in line 1). At each new priority level, if any priority-unassigned task $\tau _{i}$ satisfies $R_i^{\ell } \le D_i$ for all $\ell \le L_i$ assuming the higher priorities for all other priority-unassigned tasks (line 2–5), then $\tau _{i}$ is assigned the current priority level (line 6) and priority assignment for next (higher) priority level starts (jumping from line 7 to next iteration in line 1). The value of $R_i^{\mathtt{LO}}$ and $R_i^{\mathtt{HI}}$ are computed using Eqs. (6) and (13), respectively. If no task can be assigned the current priority, then priority assignment fails (line 8). If each task is assigned a priority, then OPA algorithm declares success (line 9) and all tasks are guaranteed to met their deadlines using FTMC algorithm. The response time tests in Eqs. (6) and (13) combined with OPA is called the OPA-FTMC test.

Fig. 6

OPA algorithm for MC tasks scheduled using FTMC. The value of $R_i^{\mathtt{LO}}$ and $R_i^{\mathtt{HI}}$ are computed using Eqs. (6) and (13), respectively

Since the OPA algorithm considers at most $O(n^2)$ different priority ordering and the response time tests in Eqs. (6) and (13) have pseudo-polynomial time complexity, the OPA-FTMC test also has pseudo-polynomial time complexity in the representation of the task set and fault model.

7.2 Dealing with more than two criticality levels

There are many safety-critical systems having functions with more than two criticality levels. In this subsection, the main principle to extend the result of this paper for more than two criticality levels is briefly presented. A system having $\mathcal {L}$ different criticality levels is called $\mathcal {L}$ -criticality system. An approach to perform the schedulability analysis for MC systems having more than two criticality levels but without considering fault tolerance is discussed by Pathan (2012). To deal with MC systems having more than two criticality levels and considering fault tolerance, the fault and task models of this paper need to be extended. And, the criticality behavior of the system is defined based on the extended fault and task model as follows:

• Similar to dual-criticality system that exhibits either LO- or HI-criticality behaviors, an $\mathcal {L}$-criticality system exhibits $\mathcal {L}$ different criticality behaviors. An $\mathcal {L}$-criticality system exhibits $\ell$ -criticality behavior if the number of errors within any interval of length $D_{max}$ is at most $\eta (\ell )$ for $\ell =1,2 \ldots \mathcal {L}$. For dual-criticality system, we have $\eta (\mathtt{LO})=\mathtt{f}$ and $\eta (\mathtt{HI})=\mathtt{F}$ respectively for the LO- and HI-criticality behaviors of the dual-criticality system. When the number of errors in any interval of length $D_{max}$ exceeds $\eta (\ell )$, then the system switches to $(\ell +1)$-criticality behavior.

• The criticality $L_i$ of task $\tau _{i}$ in $\mathcal {L}$-criticality system is equal to exactly one element in set $\{1,\ldots \mathcal {L}\}$. Similar to the WCET vectors $\overrightarrow{C}_i^L$ and $\overrightarrow{C}_i^H$ in dual-criticality systems for each task $\tau _{i}$, we define total $|L_i|$ different vectors $\overrightarrow{C}_i^{1}, \overrightarrow{C}_i^{2}, \ldots \overrightarrow{C}_i^{L_i}$ for task $\tau _{i}$ in $\mathcal {L}$-criticality system. The WCET vector $\overrightarrow{C}_i^\ell$ is equal to $<C^{\ell }_{i,p}, B^{\ell }_{{i},{1}}, \ldots B^{\ell }_{{i},{\eta (\ell )}}>$ where $1 \le \ell \le L_i$. The WCET of $\tau _i$’s primary is $C^{\ell }_{i,p}$ and the WCET of $a^{th}$ backup of $\tau _i$ is $B^{\ell }_{{i},{a}}$ during the $\ell$-criticality behavior of the system. If some task’s primary or backup does not signal completion after executing for its $\ell$-criticality WCET, then the system switches to $(\ell +1)$-criticality behavior.

For of each task $\tau _{i}$in $\mathcal {L}$-criticality system, we are interested in computing the response time $R_i^{\ell }$ considering the $\ell$-criticality behavior of the system where $1 < \ell \le L_i$. When computing $R_i^{\ell }$ for task $\tau _{i}$, we have to consider the time instants within the problem window of a generic job of $\tau _{i}$ when the system switches its behavior from $q$ to $(q+1)$-criticality behavior where $1 \le q < \ell$. In other words, to compute $R_i^{\ell }$ for $\mathcal {L}$-criticality system, we have to consider $(\ell -1)$ possible criticality switching instants within the problem window of a generic job of task $\tau _{i}$, i.e., from $q$-criticality behavior to $(q+1)$-criticality behavior for $q=1,2 \ldots (\ell -1)$. By computing the workload considering the worst-case occurrences of $\eta (q)$ faults in the problem window of a generic job of task $\tau _{i}$during the $q$-criticality behavior of the system for $q=1, 2, \ldots \ell$, an upper bound on response time $R_i^{\ell }$ can be computed for each task $\tau _{i}$. According to the RTCA DO-178B standard, there are five different Design Assurance Levels (DAL A to DAL E) for software in avionics systems, and according to ISO 26262 standard, the safety functions in automotive systems can have four different Automotive Safety Integrity Levels (ASIL A to ASIL D). Since the number of different criticality levels for such practical systems are generally not very high, the time complexity of the solution proposed in this paper for such systems is still pseudo-polynomial.

8 Empirical investigation

In this section, result of empirical investigation to measure the performance of OPA-FTMC test using randomly generated task sets is presented. In particular, the OPA-FTMC test is compared with the following two tests:

• DM-FTMC test: This test applies the proposed response-time tests in Eqs. (6) and (13) where all the tasks are assigned DM priorities.

• UBound test: This test is satisfied for a task set if (i) all the tasks with DM priorities are deemed schedulable based on Eq. (6), and (ii) all the HI-critical tasks with DM priorities are deemed schedulable based on Eq. (12) for $s=0$, i.e., considering that only HI-critical tasks executes in the entire busy period.

The UBound test is not a sufficient schedulability test that can be used to verify whether a task set is schedulable. But UBound test is a necessary schedulability test, i.e., any task set that fails to satisfy UBound test is unschedulable using any FP scheduling algorithm for the assumed task and fault models. This is because if the entire busy period exhibits the same criticality behavior and backups have the same priority as the primary, then the DM priority ordering can be shown to be the optimal using similar reasoning as used by Leung and Whitehead (1982). The UBound test is an upper bound on the schedulable task sets by FTMC algorithm. The task set generation algorithm is presented next.

Task set generation The UUnifast algorithm is proposed by Bini and Buttazzo (2005) to generate utilizations of a task set to study uniprocessor scheduling (given in Fig. 7). The utilization of a task $\tau _{i}$, denoted by $u_i$, is the ratio between $C_i$ and $T_i$, i.e., $u_i=C_i/T_i$.

Fig. 7

The UUnifast algorithm (Bini and Buttazzo 2005). The function pow(x,y) returns $x^y$ and rand() returns a random number in the range [0,1]

The UUnifast algorithm is used to generate utilizations for $n$ tasks with total utilization equal to $U$. These utilizations correspond to LO-criticality WCET of the primaries of $n$ tasks. Once a set of $n$ utilizations $\{u_1, u_2, \ldots u_n\}$ of a task set is generated, the other parameters of each task $\tau _i$ are generated as follows:

• The period $T_i$ of task $\tau _i$ is generated from the uniform random distribution in the range $[10ms, 1000ms]$. Task $\tau _{i}$’s deadline is set equal to its period. The inter-arrival time of the tasks in many practical real-time systems (e.g., robotics and control applications) often belong to this interval.

• The LO-criticality WCET of the primary of task $\tau _{i}$ is set to $C_{i,p}=u_i \cdot T_i$.

• The criticality of task $\tau _{i}$ is set to HI (i.e., $L_i=\mathtt{HI}$) with a probability of 50 %.

• The HI-criticality WCET of the primary is set to $\widehat{C}_{i,p}=C_{i,p} \cdot \mathtt{CF}$ where $\mathtt{CF} \ge 1$. For different experiments, we considered different values of CF as will be discussed below.

• Backups are considered to be the re-execution of the primary, i.e., $B_{{i},{a}}=C_{i,p}$ and $\hat{B}_{{i},{a}}=\widehat{C}_{i,p}$ for any $a=0, 1, \ldots \mathtt{F}$.

For each experiment, total 40 different utilization levels $\{0.025, \ldots 0.975, 1\}$ are considered. For each utilization level $U \in \{0.025, \ldots 0.975, 1\}$, total 1000 task sets are generated with simulation parameters $n$, $U$ and $\mathtt{CF}$. The value of CF we considered are $\mathtt{CF}=1$ and $\mathtt{CF}=2$ where the former is to experiment that the CA is not more pessimistic than the system designer regarding the WCET of the tasks while the latter is to experiment that the CA is more pessimistic than the system designer regarding the WCET of the tasks. The fault-tolerant requirement for each experiment is specified using simulation parameter $(\mathtt{f}, \mathtt{F})$.

Result analysis Figures 8 and 9 plot fraction of schedulable task sets deemed schedulable by the UBound, OPA-FTMC and DM-FTMC tests for a system with $n=20$ tasks. The experiment presented in Fig. 8 considers $\mathtt{CF}=1$ and $(\mathtt{f}=0,\mathtt{F}=1)$ to investigate the fact that the CA is not pessimistic regarding the WCET of the tasks but pessimistic regarding frequency of errors. The fault-tolerant requirement $(\mathtt{f}=0,\mathtt{F}=1)$ specifies that as long as the system exhibits LO-criticality behavior, no error recovery is required while one error needs to be recovered in any interval no larger than $D_{max}$ during the HI-critical behavior. In other words, one error is recovered in any interval no larger than $D_{max}$ when the system executes (only) the HI-critical tasks during the HI-criticality behavior.

Fig. 8

Schedulable tasksets with $(n=20, \mathtt{f}=0, \mathtt{F}=1, \mathtt{CF}=1)$

Fig. 9

Schedulable tasksets with $(n=20, \mathtt{f}=1, \mathtt{F}=2, \mathtt{CF}=2)$

The experiments presented in Fig. 9 considers $\mathtt{CF}=2$ and $(\mathtt{f}=1,\mathtt{F}=2)$ to experiment the fact that the CA is pessimistic regarding both the WCET and the frequency of errors. The HI-criticality WCET of each primary/backup is two times (i.e., $\mathtt{CF}=2$) the LO-criticality WCET of the corresponding primary/backup. The fault-tolerant requirement $(\mathtt{f}=1,\mathtt{F}=2)$ specifies that at most one error needs to be recovered during the LO-critical behavior while at most two errors need to be recovered during the HI-critical behavior in any interval no larger than $D_{max}$.

The performance of the OPA-FTMC test in both Figs. 8 and 9 is very close to the upper limit illustrated by the UBound test. This demonstrates that sufficient schedulability analysis presented in this paper is very close to the exact analysis of FTMC algorithm for implicit-deadline tasks.

The OPA-FTMC test performs significantly better than the DM-FTMC test with higher pessimism in WCET and frequency of errors. For example, the percentage of task sets deemed schedulable by OPA-FTMC test in Fig. 9 at $U=0.5$ is 74 % while that of by DM-FTMC test is only 31 % (an improvement of 238 %). This is because the OPA-FTMC test applies the OPA algorithm to search for a priority assignment, if there exists one, for which the task set passes the proposed response-time test.

The performance of each test decreases with increasing CF or stricter fault-tolerance requirement. This is expected since increasing CF or fault-tolerant requirement results in increased workload in the busy period. And, task with higher workload in its busy period is more difficult to schedule.

The result for constrained-deadline tasks is presented in Fig. 10 where the deadline of $\tau _{i}$ is selected from a uniform distribution in the range $[\mathtt{E}_{i,\mathtt{f}}, T_i]$ and $[\hat{\mathtt{E}}_{i,\mathtt{F}}, T_i]$ if $L_i=\mathtt{LO}$ and $L_i=\mathtt{HI}$, respectively. The OPA-FTMC test performs much better than the DM-FTMC test and quite close to the upper limit given by the UBound test in Fig. 10.

Fig. 10

Schedulable tasksets with $(n=20, \mathtt{f}=1, \mathtt{F}=2, \mathtt{CF}=2)$

Comparing OPA-FTMC with non-(MC) fault-tolerant scheduling The response-time computation in Eq. (6) computes $R_{i}^{\mathtt{LO}}$. If $R_{i}^{\mathtt{LO}} \le D_i$ for each task $\tau _{i} \in \Gamma$, then at most $\mathtt{f}$ errors can be tolerated between the release time and deadline of each job of task $\tau _{i}$ during the LO-criticality behavior of the system. By applying the test in Eq. (6) for all the tasks, we can determine whether at most $\mathtt{f}$ task errors can be masked in any interval not larger than $D_{max}$ for traditional non-MC task system. And, DM is the OPA in such case. We call the response time test in Eq. (6) assuming DM priority ordering the nonMC-FTDM test.

To compare OPA-FTMC and nonMC-FTDM, we randomly generated implicit-deadline task sets using simulation parameters $n=20$, $\mathtt{f}=1$, and $\mathtt{F}=2$. To measure the impact of pessimism regarding the WCET of the HI-critical tasks in FTMC scheduling, we considered two different value of CF such that $\mathtt{CF}=1$ and $\mathtt{CF}=2$. The fraction of schedulable task sets that pass the OPA-FTMC for $\mathtt{CF} =1$ and $\mathtt{CF} =2$ are compared with the fraction of schedulable task sets that pass the nonMC-FTDM test. The results are presented in Fig. 11.

Fig. 11

Schedulable tasksets with $(n=20, \mathtt{f}=1, \mathtt{F}=2)$

The nonMC-FTDM test performs better than the OPA-FTMC test for both $\mathtt{CF}=1$ and $\mathtt{CF}=2$ in Fig. 11. The fraction of schedulable task sets using OPA-FTMC test with $\mathtt{CF}=2$ at higher utilization level is much smaller than that of using OPA-FTMC test with $\mathtt{CF}=1$. This is because when $\mathtt{CF}=2$, the WCET of each HI-critical task during the HI-criticality behavior is two times larger (i.e., more pessimistic) in comparison to that of when $\mathtt{CF}=1$. Capturing such pessimism in the OPA-FTMC test degrades the performance of OPA-FTMC for $\mathtt{CF}=2$ in comparison to OPA-FTMC for $\mathtt{CF}=1$.

Note that when $\mathtt{CF}=1$, then there is no pessimism regarding the WCET of the MC tasks in OPA-FTMC test. And, the system only switches the criticality and drops LO-critical tasks if more than $\mathtt{f}$ task errors are detected in the problem window of a task. Therefore, at run-time FTMC never needs to complete higher amount of execution (due to dropping of tasks) in comparison to non-MC scheduling, which is assumed for the nonMC-FTDM test. Surprisingly, the OPA-FTMC does not perform better than nonMC-FTDM scheduling although less work is done in FTMC scheduling. This is due to the sufficient (not exact) analysis of the FTMC scheduling during the HI-criticality behavior.

Since an upper bound on the number of jobs of the higher priority tasks in a problem window is considered, the OPA-FTMC test suffers from this pessimism. And, this pessimism is not offset by the fact that FTMC is performing less work due to dropping of LO-critical tasks. However, the performance of OPA-FTMC with $\mathtt{CF}=1$ is quite close to the nonMC-FTDMin Fig. 11. And, this implies the pessimism is not in OPA-FTMC test is insignificant when comparing with non-MC fault tolerant scheduling.

Comparing OPA-FTMC with non-fault-tolerant (MC) scheduling When $\mathtt{f} =0$ and $\mathtt{F} =0$, the FTMC algorithm is equivalent to scheduling of MC tasks without fault tolerance. We conducted a series of experiments for OPA-FTMC test using randomly generated implicit-deadline task sets using simulation parameters $n=20$, $\mathtt{f}=0$ and $\mathtt{F}=0$.

To measure the impact of pessimism regarding the WCET of the high criticality tasks, we considered $\mathtt{CF}=1$, $\mathtt{CF}=2$, and $\mathtt{CF}=3$. The results are presented in Fig. 12. As expected, the higher is the pessimism regarding the WCET of the HI-critical tasks (i.e., larger value of CF) the smaller is the fraction of schedulable task sets at relatively higher utilization level. This is because, as the utilization of the task set increases, each task in a task set has a relatively higher individual utilization since number of tasks in a task set remains unchanged. Moreover, the HI criticality utilization of each task increases as CF increases. As a result, the total HI-criticality utilization of each random task set at higher utilization level increases with increasing CF. And, task set with relatively higher total utilization is more difficult to schedule. Consequently, the fraction of schedulable task sets that passes the OPA-FTMC test decreases with increasing CF and increasing utilization level in Fig. 12.

Fig. 12

Schedulable tasksets with $(n=20, \mathtt{f}=0, \mathtt{F}=0)$ by varying $\mathtt{CF} =1,2,3$

9 Related work

The seminal work by Vestal in first proposed the MC task model and its analysis based on FP scheduling algorithm on uniprocessor platform (Vestal 2007). Vestal’s algorithm is proved by Dorin et al. as the optimal for traditional FP scheduling on uniprocessor where lower critical tasks are not dropped (Dorin et al. 2010). By showing that neither FP nor earliest-deadline-first (EDF) scheduling of MC tasks on uniprocessor dominates the other, Baruah and Vestal proposed a hybrid algorithm by combining the benefits of both FP and EDF policies (Baruah and Vestal 2008). A variant of FP scheduling algorithm and its analysis on uniprocessor platform is proposed by Baruah et al. based on the following observation (Baruah et al. 2011b): the run-time monitoring of execution time of the jobs can be used to drop jobs of $\ell$-critical tasks as soon as the system switches to $(\ell +1)$-criticality behavior. The FTMC algorithm proposed in this paper also uses this observation.

Several works addressed MC scheduling of a finite collection of jobs on uniprocessors. It has been proved by Baruah et al. (2012a) that determining the feasibility of a collection of MC jobs is strongly NP-hard, even when all release times are identical and there are only two criticality levels. Baruah et al. (2010) proposed own criticality based priority (OCBP) algorithm for scheduling a finite collection of jobs on uniprocessor. Algorithm OCBP works as follows: jobs are assigned fixed-priorities in offline, and the highest priority ready job is always dispatched at run-time. The processor speed-up factor of the OCBP algorithm for dual-criticality system is 1.619, i.e., any feasible instance of dual-criticality jobs on unit-capacity processor is also OCBP-schedulable on a processor that is 1.619 times faster (Baruah et al. 2010). An improved load-based sufficient schedulability condition of the OCBP algorithm is proposed by Li and Baruah (2010a).

By assuming the earliest releases of the jobs within a busy interval, Li and Baruah proposed interesting techniques to apply the OCBP algorithm for scheduling sporadic MC tasks on uniprocessor platform (Li and Baruah 2010b). However, Due to the sporadic nature of the tasks, the priorities of the jobs are recomputed at run-time and such priority recomputation at run-time has pseudo-polynomial time complexity (Li and Baruah 2010b). Recently, Guan et al. (Guan et al. (2011)) proposed a novel polynomial time algorithm for recomputing the priorities at run-time for scheduling sporadic tasks using the OCBP algorithm. Although OCBP and the proposed OPA-FTMC uses the Audsley’s approach for assigning the priorities, the main differences are: (i) OCBP is based on dynamic-priority-based dispatching algorithm where different jobs of the same task may have different priorities. In contrast, all the jobs of each task are assigned the same priority in FTMC algorithm, (ii) OCBP may need to recompute the priorities of the jobs during run-time while there is no recomputation of priorities during run-time in FTMC scheduling.

An EDF-based scheduling algorithm, called EDF-VD (EDF Virtual-Deadline), in which the deadlines of the implicit-deadline sporadic tasks are modified online, is proposed by Baruah et al. (2011a). The algorithm EDF-VD modifies the deadlines of the tasks depending of the behavior of the system at different criticality levels and schedule the tasks based on EDF scheduling according to the modified deadlines. The processor speed-up factor of EDF-VD scheduling for dual-criticality system is 1.619. By performing a more precise analysis of the EDF-VD scheduling of implicit-deadline MC sporadic tasks, the speed-up factor of EDF-VD is further improved by Baruah et al. to 1.333 (Baruah et al. 2012b). Ekberg and Yi (2012) recently proposed interesting technique to compute the demand-bound (Baruah et al. 1990b) function to determine the EDF schedulability of constrained-deadline MC sporadic tasks. The demand-bound of the tasks at each criticality level is determined by adjusting the deadline of the tasks when the system switches from LO to HI criticality behavior. The purpose of shaping or adjusting the demand is to respect the supply-bound (Mok et al. 2001) function of the underlying uniprocessor platform to ensure schedulability.

Time-triggered (TT) scheduling of MC jobs on uniprocessor platform is proposed by Baruah and Fohler (2011). The TT-scheduling essentially computes in offline, for each criticality levels, the scheduling table that stores the time instant at which jobs will be dispatched for execution. When the criticality behavior of the system switches from $\ell$ to $(\ell +1)$, then jobs are scheduled based on the scheduling table computed for criticality level $(\ell +1)$. The processor speed-up factor for TT-scheduling is 1.619.

Many of the scheduling algorithms for MC systems considers dropping tasks of lower criticality levels when the system switches to a higher criticality level. However, the lower criticality tasks may not need to be dropped as long as they are not causing a higher criticality task to miss its deadline. Based on this observation, Santy et al. (2012) proposed a method, called latest completion time (LCT), that allows lower criticality task to execute using uniprocessor FP scheduling until time instant at which the lower criticality task is suspended to allow execution of a higher criticality task to avoid missing its deadline. The lower-criticality task may resume its execution later when the system switches back to lower-criticality behavior.

Many other works addressed scheduling of MC systems for aspects other than certification. Pellizzoni et al. (2009) and Petters et al. (Petters et al. (2009)) proposed techniques for isolating (either in time or space) subsystems having different criticality levels based on reservation based approach. However, these work concentrate on providing isolation through worst-case reservation of resources and do not efficiently utilize the resources. The work proposed by de Niz et al. (2009) observed that isolation among multiple subsystems that are based on reservation based approach may suffer from, so called criticality inversion problem: the deadline of a higher-criticality job may be missed while allowing a lower criticality job to meet its deadline. In addition, assigning priorities based on criticality to avoid criticality-inversion is not a good priority assignment policy for meeting the deadlines. They have proposed slack-aware scheduling that dynamically assigns the priorities to tasks or jobs to avoid criticality inversion while focusing on efficient use of the resources (Niz et al. 2009). This algorithm avoids criticality inversion under which low-criticality task can not interfere with high-criticality task but high-criticality task can steal cycles from the low-criticality task under overload situations to meet deadlines. The work in Niz et al. (2009) is further extended for non-preemptable shared resources (Lakshmanan et al. 2010) and distributed systems (Lakshmanan et al. 2011). Mollison et al. (2010) proposed an architecture for scheduling MC tasks based on criticality-monotonic scheduling on multicore. The allocation of MC tasks in a distributed systems is considered in Tamas-Selicean and Pop (2011), where each task allocated to a processor is given a time partition by determining the sequence and size of each partition in addition to finding the scheduling table for each processor.

Many approaches exist in the literature for tolerating faults for (non-MC) real-time tasks. Ghosh et al. (1995) proposed fault-tolerant uniprocessor scheduling of aperiodic tasks considering transient faults by inserting enough slack in the schedule to allow for the re-execution of tasks when an error is detected. They assumed that the occurrences of two faults are separated by a minimum distance. Pandya and Malek analyzed fault-tolerant rate-monotonic (RM) scheduling on a uniprocessor for tolerating one fault and proved that the minimum achievable utilization bound is 50 % (Pandya and Malek 1998). The authors also demonstrated the applicability of their scheme for tolerating multiple faults if two faults are separated by a minimum time distance equal to maximum period $T_{max}$ of a task set. In this paper, the proposed FTMC algorithm place no restriction in time distance between occurences of two consecutive faults within $D_{max}$.

Liberato, Melhem and Mossé derived both exact and sufficient feasibility conditions for tolerating f transient faults for a set of aperiodic tasks using EDF scheduling (Liberato et al. 2000). However, the authors of Liberato et al. (2000) consider backup of a faulty task simply as a re-execution of the primary copy and do not consider the execution of a diverse implementation of a task possibly having a different execution time as backup.

Burns, Davis, and Punnekkat derived an exact fault-tolerant feasibility test for any fixed-priority system using backup that could be simple re-execution or a diverse implementation of the same task Burns et al. (1996). This work is extended in Punnekkat et al. (2001) to provide the exact schedulability tests employing check-pointing for fault recovery. In Lima and Burns (2003), proposed an optimal fixed-priority assignment to tasks for fault-tolerant scheduling based on re-execution. The fixed priorities of the tasks can be determined in $O(n^2)$ time for a set of $n$ periodic tasks. The schedulability analysis in Burns et al. (1996, Lima and Burns 2003) require the information about the minimum time distance between any two consecutive occurrences of transient faults within the schedule, and only considers simple re-execution or exactly one different implementation when an error is detected. In the latter case, the execution time of the backup is the same regardless of the number of errors affecting a particular job. This is in contrast to the proposed method in this paper where each backup for a particular job may have different execution time.

Based on the last chance strategy of Chetto and Chetto (1989) (in which backups execute at late as possible), software faults are tolerated by considering two versions of each periodic tasks: a primary and a backup (Han et al. 2003). Backups are scheduled as late as possible using a backward RM algorithm (schedule from backward in time). Similar to the work in Lima and Burns (2003), the work in Han et al. (2003) considers that there is only one backup for each task and therefore does not have the provision for considering different backups of the same task if more than one fault affect the same task.

A fault-burst model is recently defined by Many and Doose in Many and Doose (2011) as a bounded time interval during which the execution of the tasks are disturbed due to the occurrences of faults for which the distribution of the faults is unknown. Although the work in Many and Doose (2011) assumes arbitrary number of faults in a fault burst, the proposed recovery strategy in fact considers a finite number of errors to be tolerated within an interval of length $D_{max}$ where only one job of each task is assumed to be faulty. In contrast, the proposed FTDM algorithm considers that multiple jobs of the same task can be disturbed due to burst of faults within an interval of length $D_{max}$.

Aydin (2007) proposed aperiodic and periodic task scheduling based on an exact EDF feasibility analysis in which a backup of a task can be different from the primary. Aydin considers a fault model in which a maximum of f transient errors could occur in tasks of the aperiodic task set. The schedulability analysis in Aydin (2007) is based on processor demand analysis proposed by Baruah et al. (1990a). For periodic task systems, the proposed exact feasibility test in Aydin (2007) has exponential time complexity.

The fault model considered for the FTMC algorithm is more general (e.g., no separation constraints between two errors, multiple diverse backups, multiple errors in the same job) in comparison to many of the earlier works. In addition to fault tolerance, the FTMC algorithm also considers the mixed-criticality aspect of safety-critical systems.

10 Conclusion

This paper proposes a new approach to model MC systems from the perspective of fault tolerance which is an important aspect of safety-critical systems. The proposed FTMC algorithm and its analysis address the challenge of satisfying real-time, fault-tolerance, and mixed-criticality constraints. The fault model that FTMC algorithm assumes is very powerful in the sense that it considers different types of faults and covers many different scenarios for error recovery. The derived OPA-FTMC test enables the system designer to judge the resilience of the system by experimenting with different values of $\mathtt{f}$ and $\mathtt{F}$. The performance of the proposed test is close to the theoretical upper bound in simulation. Extending the FTMC algorithm and its analysis for multiprocessors is an interesting future work.