A fault-tolerant time-triggered scheduling algorithm of mixed-criticality systems

Abstract

Real-time and safety-critical systems are an integration of multiple functionalities onto a single computing platform. Some of the functionalities are safety-critical and subject to certification while the rest of the functionalities are nonsafety-critical and do not need the certification. Various researches have been done for the scheduling theory of mixed-criticality systems. But the time-triggered scheduling of mixed-criticality systems is very popular and used in industry. Since the schedule is prepared offline in a time-triggered mixed-criticality system, we need to prepare the schedule in such a way that the schedule must tolerate fault online. Hence the problem of fault-tolerance in the time-triggered system is important. This work proposes a new and novel time-triggered fault-tolerant algorithm for mixed-criticality systems. Then we show that the proposed algorithm is correct and tolerate at most one fault over the hyperperiod. Finally, we compare the proposed algorithm with the existing time-triggered scheduling algorithms for mixed-criticality systems.

1 Introduction

A real-time system [11, 20] is required to not only generate correct results but also produce such results within a stipulated time called deadline. Typical applications of real-time systems span across various domains including defense and space systems, networked multimedia systems, embedded automotive and avionics systems etc. In real-time systems, satisfying the timing specifications for a given set of tasks by determining an appropriate order among task executions boils down to a challenging scheduling problem. Traditional scheduling schemes have primarily dealt with scenarios in which all tasks belong to a single criticality level. In these systems, tasks at distinct criticality levels are typically handled by allocating a dedicated server for each criticality level. However, such federated schemes often make the resulting systems prone to severe resource under-utilization. In recent years, there is an increasing trend towards integrating applications at different importance/criticality levels and implementing them onto a single computation platform. Such an integrated system, often referred to as a mixed-criticality system [3, 30], helps to reduce cost, energy consumption and resource under-utilization. For example, let us consider a UAV (Unmanned Aerial Vehicle) [29] whose primary mission is to capture the ground images. The functionalities (jobs) of such a UAV can be easily classified into two criticality-based categories: (i) safety-critical—functionalities related to safe flight operation of the UAV; higher in criticality (HI-criticality) and (ii) mission-critical—functionalities related to image capturing; relatively lower in criticality (LO-criticality). Satisfying the timing specifications of the HI-criticality functionalities even under worst-case scenarios is very important as they are related to safe flight operation and are typically certified by Certification Authorities (CAs). In order to ensure safety, the CAs typically use very conservative worst-case execution time (WCET) estimates for the tasks and actual task execution times may typically be expected to be significantly less than these conservative WCETs (also called HI-criticality WCETs) in most cases. On the other hand, the general goal of the System Designers (SDs) is to satisfactorily execute both HI-criticality and LO-criticality functionalities within limited resource budgets, so that cost overhead may be controlled. In order to achieve their objective, an important design strategy adopted by SDs is to assume less conservative WCET estimates for the HI-criticality tasks (referred to as LO-criticality WCETs of HI-criticality tasks). As only SDs are concerned about the timely execution of LO-criticality tasks and hence they are assumed to have only a single WCET (referred to as LO-criticality WCETs of LO-criticality tasks). The CAs are not concerned about the execution of LO-criticality tasks. They are only concerned about the execution of HI-criticality tasks. We know that estimating the WCET is a difficult job. The CAs use very pessimistic tools to estimate the WCET of a job. Hence the CAs expect a higher WCET for the HI-criticality jobs than that estimated by the SDs. Let us understand the technicality of the mixed-criticality schedulability problem using the following example.

Example 1

Consider the instance given in the following table which has three jobs.

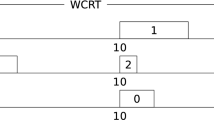
The given instance is EDF schedulable from the perspective of system designers (SDs) and certification authorities (CAs), as shown in the Figs. 1 and 2, respectively.

The CAs use very conservative tools, and their estimates are given in the last column of Table 1. When we consider the WCET estimated by the CAs, it is easily verifiable that EDF fails to schedule the given instance. On the other hand, we know that CAs do not care about the schedulability of the LO-criticality jobs. So they certify the system only if the HI-criticality jobs are schedulable. We can verify that the HI-criticality jobs are schedulable with respect to the WCET estimation of the CAs as shown in Fig. 2 where we ignore job $j_1$. This is because $j_3$ and $j_2$ can be scheduled in the interval [0,2] and [2,6]. SDs also verify the system as correct as they consider WCET estimated by them as shown in Fig. 1. But if job $j_3$ and $j_2$ executes for more than its WCET that estimated by the SDs in the schedule given in Fig. 1, then the instance is not schedulable. It is a hazardous situation when both the SDs and CAs certify the system to be correct and the jobs of the system behave according to the estimation of CAs. In this case, it is not possible to correctly schedule each job in the system as we do not know the actual execution time of a job a prior to the run time. Hence the MC-schedulability is hard and popular among the real-time system researchers’ community.

Table 1 Instance for Example 1

Fig. 1

Schedule according to the SDs

Fig. 2

Schedule according to the CAs

In this paper, we focus on the time-triggered schedule [4,5,6,7, 15] of a mixed-criticality system. As we know, the whole schedule of the jobs is prepared prior to the run-time in a time-triggered system and generally kept in a tabular format. When the system goes online, the tables are followed to dispatch the jobs for each time instant t. There are various algorithms discussed [4, 5, 25] to find the time-triggered schedule of a uniprocessor mixed-criticality systems. But none of the above algorithms discussed the fault-tolerant aspect of the uniprocessor mixed-criticality approach.

1.1 Fault-tolerant mixed-criticality systems

Real-time systems are marked by their necessity to react to events in the environment within specified time bounds. Thus, the correct behavior of Real-time systems depends not only on the value of the computation but also on the time at which the results are produced [11]. Here we consider the hard real-time systems, i.e. the real-time systems which have stringent timing constraints. If the timing constraints are not satisfied, then a hard real-time system may lead to catastrophic results. This may lead to the loss of life. So the system designers do their best to ensure that all the timing constraints will meet before the system is deployed to the mission. Hence the designers design an appropriate model of the target system which is analyzed for any fault that may occur during the mission. A fault [22] is an event which may occur in the system that leads to a system failure. Apart from satisfying the timing constraints, most researchers emphasis towards the fault-tolerant real-time systems. A fault-tolerant real-time system [16, 22] not only ensures the timing constraints but also ensures the functional correctness of the system. Generally, there are two major faults occur in a real-time system, i.e., permanent and transient faults. A transient fault is one that does not reoccur if you retry the operation. A permanent fault is not transient; it is repeatable.

In this paper, we focus on the transient faults [32] only. From the definition of the transient faults, we know that if the operation is retried then the fault will not reoccur. Our main goal is to design a fault-tolerant algorithm that can tolerate at most one fault over the hyperperiod. Since we are considering a time-triggered system, the scheduling table related to the instance is constructed prior to the run-time.

The fault-tolerant aspect in a time-triggered system [17] is an interesting problem, because the whole schedule is prepared prior to the run-time but the faults can occur at the run-time only. Hence we must allocate sufficient time for each job such that they can tolerate the faults occur at the run-time. Here we assume that the proposed algorithm can tolerate at most one fault in one hyperperiod. This is a fair assumption, because no system can tolerate n number of faults. Apart from that if a uniprocessor system encounters n number of faults, then the system will lead to failure and difficult to recover.

We present a new time-triggered scheduling algorithm in this paper on investigating the fault-tolerant aspect of the time-triggered uniprocessor mixed-criticality systems. To our best knowledge, these are the first results in this setting. Our detailed contributions are as follows:

• We point out the requirement of the fault-tolerant aspect of the time-triggered uniprocessor mixed-criticality systems.

• We construct a fault-tolerant algorithm to find the time-triggered schedule for mixed-criticality uniprocessor systems.

• We demonstrate various trade offs for the fault-tolerant algorithm of time-triggered mixed-criticality systems with both theoretical and experimental results.

The rest of the paper is organized as follows: Sect. 2 describes the system model and presents definitions and related work on fault-tolerant algorithm of mixed-criticality real-time systems and time-triggered scheduling. In Sect. 3, we propose a new fault-tolerant algorithm which constructs multiple tables to find a time-triggered schedule for a dual-criticality MC instance. Section 4 includes experimental results based on a large number of randomly generated mixed-criticality instances. Section 5 concludes the paper.

2 System models and literature review

Here we describe the mixed-criticality job model used in this paper. The mixed-criticality model used in this paper is based on at most two levels of criticality, LO and HI. A job is characterized by a 5-tuple of parameters: $j_i = (a_i, d_i, \chi _i, C_i(\mathrm {LO}), C_i(\mathrm {HI}))$, where

• $a_i \in {\mathbb {N}}$ denotes the arrival time.

• $d_i \in {\mathbb {N}}^+$ denotes the absolute deadline.

• $\chi _i \in \{LO, HI\}$ denotes the criticality level.

• $C_i(\mathrm {LO}) \in {\mathbb {N}}^+$ denotes the LO-criticality worst-case execution time.

• $C_i(\mathrm {HI}) \in {\mathbb {N}}^+$ denotes the HI-criticality worst-case execution time.

We assume that the system is preemptive and $C_i(\mathrm {LO}) \le C_i(\mathrm {HI})$ for $1 \le i \le n$. Note that in this paper, we consider arbitrary arrival times of jobs.

An instance of mixed-criticality (MC) [3, 9] job set can be defined as a finite collection of MC jobs, i.e., $I = \{j_1, j_2,\ldots , j_n\}$. The job $j_i$ in the instance I is available for execution at time $a_i$ and should finish its execution before $d_i$. The job $j_i$ must execute for $c_i$ amount of time which is the actual execution time between $a_i$ and $d_i$, but this can be known only at the time of execution. The collection of actual execution time ($c_i$) of the jobs in an instance I at run-time is called a scenario. The scenarios in our model can be of two types, i.e., LO-criticality scenarios and HI-criticality scenarios. When each job $j_i$ in instance I executes $c_i$ units of time and signals completion before its $C_i(\mathrm {LO})$ execution time, it is called a LO-criticality scenario. If any job $j_i$ in instance I executes $c_i$ units of time and doesn’t signal its completion after it completes the $C_i(\mathrm {LO})$ execution time, then this is called a HI-criticality scenario.

Each mixed-criticality instance needs to be scheduled by a scheduling strategy where both kinds of scenarios (LO and HI) can be scheduled. If we have prior knowledge about the scenario, then the scheduling strategy is known as a clairvoyant scheduling strategy. If we don’t have prior knowledge about the scenario, then the scheduling strategy is called an online scheduling strategy. Here we assume that if any job continues its execution without signaling its completion at $C_i(\mathrm {LO})$ then no LO-criticality jobs are required to complete by their deadlines. Now, we define the notion of MC-schedulability.

Definition 1

An instance I is MC-schedulable if it admits a correct online scheduling policy.

First, we present the conventional time-triggered scheduling [4] strategy of MC instances. Later in this section, we define the time-triggered scheduling strategy in the presence of a fault. As we know, the schedule of the jobs in a time-triggered system is generally prepared in a tabular format, prior to the runtime. Since we are considering a dual-criticality system, we will construct two tables ${\mathcal {S}}_{\mathrm {HI}}$ and ${\mathcal {S}}_{\mathrm {LO}}$ for a given instance I which will be used at run-time. The length of the tables is the length of the interval $[\min _{j_i \in I}\{a_i\},\max _{j_i \in I}\{d_i\}]$. The rules to use the tables ${\mathcal {S}}_{\mathrm {HI}}$ and ${\mathcal {S}}_{\mathrm {LO}}$ at run-time, (i.e., the scheduler) are as follows:

• The criticality level indicator $\Gamma$ is initialized to LO.

• While ($\Gamma = \mathrm {LO}$), at each time instant t the job available at time t in the table ${\mathcal {S}}_{\mathrm {LO}}$ will execute.

• If a job executes for more than its LO-criticality WCET without signaling completion, then $\Gamma$ is changed to HI.

• While ($\Gamma = \mathrm {HI}$), at each time instant t the job available at time t in the table ${\mathcal {S}}_{\mathrm {HI}}$ will execute.

Now we present the system model in presence of a fault.

Definition 2

A dual-criticality MC instance I is said to be time-triggered schedulable [4] if it is possible to construct the two schedules ${\mathcal {S}}_{\mathrm {HI}}$ and ${\mathcal {S}}_{\mathrm {LO}}$ for I, such that the run-time scheduler algorithm described above schedules I in a correct manner.

Here We assume that the proposed fault-tolerant algorithm tolerates at most one fault over a hyperperiod. We construct a scheduling table for each job in the instance I which will be used to dispatch jobs according to the following dispatcher (i.e., the scheduler). Initially, we begin with the tables ${\mathcal {S}}_{\mathrm {LO}}$ and ${\mathcal {S}}_{\mathrm {HI}}$. If job $j_i$ encounters a fault in LO-criticality, then the scheduler will switch to table ${\mathcal {S}}_{\mathrm {LO}}^i$. On the other hand, if job $j_i$ encounters a fault in HI-criticality, then the scheduler will switch to table ${\mathcal {S}}_{\mathrm {HI}}^i$. The rules of the scheduler are as follows:

• The criticality level indicator $\Gamma$ is initialized to LO.

• The fault table indicator ${\mathscr {F}}$ is initialized to the table ${\mathcal {S}}_{\mathrm {LO}}$.

• While ($\Gamma = LO$), at each time instant t the job available at time t in the table indicated by the fault table indicator ${\mathscr {F}}$ will be executed.

  • If a fault occurs for a job $j_i$, then the fault table indicator ${\mathscr {F}}$ will be changed to ${\mathcal {S}}_{\mathrm {LO}}^i$ and the jobs will be dispatched according to the table ${\mathcal {S}}_{\mathrm {LO}}^i$.

• If a job $j_i$ executes for more than its LO-criticality WCET without signaling completion, then $\Gamma$ is changed to HI.

• While ($\Gamma = \mathrm {HI}$ and ${\mathscr {F}} = {\mathcal {S}}_{\mathrm {LO}}$), at each time instant t the job available at time t in the table ${\mathcal {S}}_{\mathrm {HI}}$ will execute.

  • If a fault occurs for a job $j_i$, then the fault table indicator ${\mathscr {F}}$ will be changed to ${\mathcal {S}}_{\mathrm {HI}}^i$ and the jobs will be dispatched according to the table ${\mathcal {S}}_{\mathrm {HI}}^i$.

• While ($\Gamma = \mathrm {HI}$ and ${\mathscr {F}} = {\mathcal {S}}_{\mathrm {HI}}^i$), at each time instant t the job available at time t in the table ${\mathcal {S}}_{\mathrm {HI}}^i$ will execute.

2.1 Literature review

In 2007, Vestal [30] introduced the mixed-criticality model to the real-time system’s research community. He proposed a fixed-task-priority scheduling strategy, which was later [10] proven to be optimal. Since then, the mixed-criticality model is the center of attraction for all the researchers of the real-time system community. In 2011, Baruah et al. [4] proposed an algorithm to find the time-triggered schedule for given mixed-criticality instances based on OCBP [3]. Socci et al. [25] also proposed a time-triggered scheduling algorithm which was a priority-based algorithm. Behera and Bhaduri [5] proposed a time-triggered scheduling algorithm, hereafter abbreviated as TT-Merge, which directly constructs the scheduling tables for a given mixed-criticality instance without using any priority order for the jobs. They also prove the dominance of the TT-Merge algorithm over the algorithms proposed in [4, 25] with respect to the number of instances scheduled successfully. Apart from these, there are various fault-tolerant algorithms [14, 18, 21, 27] proposed for mixed-criticality systems. In 2017, Burns and Davis [10] published a survey paper where various fault-tolerant scheduling algorithm for mixed-criticality systems are discussed.

RM Pathan [21] proposed an approach to model the mixed-criticality system from the perspective of fault-tolerant. Then they presented a fault-tolerant mixed-criticality algorithm for their proposed model. They used a backup strategy to tolerate the fault that occurs at the run-time. In 2014, Huang et al. [14] proposed a fault-tolerant mixed-criticality scheduling algorithm that models safety requirements for tasks of varying criticalities in the presence of transient faults. Lin et.al [18] proposed a novel online slack-reclaiming algorithm is also proposed to recover from as many faults as possible before the jobs’ deadline. In 2015, Thekkilakattil et al. [26] proposed a fault-tolerant scheduling scheme that promised to tolerate permanent faults and influences the associated safety assurance. In another research, Thekkilakattil et al. [28] derived a sufficient test that determines the fault-tolerant feasibility of a set of mixed-criticality real-time tasks under the assumption that the inter-arrival time between two consecutive error bursts is at least equal to the hyper-period of the task set.

Al-bayati et al. [1] proposed a four mode model that addresses fault and execution time overrun with separate modes. In 2017, Zhou et al. [35] proposed a non-time-triggered fault-tolerant algorithm for mixed-criticality systems where re-execution of tasks was adopted to tolerate a transient fault. In 2021, Ranjbar et al. [23] proposed a design-time task-drop aware schedulability analysis based on the EDF-VD algorithm that bounds the LO-criticality tasks drop in the HI-criticality scenario.

Apart from the above, there are many articles available those proposed fault-tolerant scheduling algorithm for multiprocessor mixed-criticality systems. Zeng et al. [33] proposed a fault-tolerant scheduling algorithm for multiprocessor mixed-criticality systems that relies on the task replication and re-execution to tolerate a fault. Al-bayati et al. [2] proposed a fault-tolerant technique for multi-core mixed-criticality systems where the HI-criticality tasks executing on the core that exhibit fault are moved to other cores, and the LO-criticality tasks are discarded if required in the newly assigned core. This work also useful for permanent faults in multi-core systems. Safari et al. [24] proposed a technique that uses the inherent redundancy of multicores to apply the standby-sparing technique for fault-tolerance. There are few scheduling techniques proposed in [13, 31, 34] which are not fault-tolerant but must be investigated in terms of fault-tolerant and mixed-criticality systems. We are not discussing the other fault-tolerant multiprocessor algorithms as our work is focused on uniprocessor mixed-criticality systems.

The above discussion clarifies that all the fault-tolerant scheduling algorithms are proposed for either uniprocessor or multiprocessor mixed-criticality systems. There does not exist a fault-tolerant scheduling algorithm for a time-triggered system in mixed-criticality systems. There is no time-triggered fault-tolerance scheduling algorithm for mixed-criticality systems because the computation of a table is challenging that can not be changed during the run-time. Since we do not know the exact time of a fault, preparing a scheduling table prior to run-time is difficult. That means we need to find a scheduling table that can handle fault online and need not be changed at run-time. Hence we propose a fault-tolerant time-triggered scheduling algorithm for the uniprocessor mixed-criticality systems, which constructs a scheduling table for each job. Since the TT-Merge algorithm outperforms all the time-triggered algorithms in the literature, we apply the TT-Merge algorithm to find the fault-tolerant schedule for any instance I.

2.2 Recap of TT-merge algorithm

In this section, we briefly review the TT-Merge algorithm from [5] which constructs two scheduling tables ${\mathcal {S}}_{\mathrm {LO}}$ and ${\mathcal {S}}_{\mathrm {HI}}$. If the jobs of an instance are dispatched according to these tables, then no job will miss its deadline. The scheduling table length is equal to the maximum deadline among all the jobs in the instance. Initially, the TT-Merge algorithm constructs two temporary tables, ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$. Then the temporary tables ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are merged to construct the table ${\mathcal {S}}_{\mathrm {LO}}$. Finally, the TT-Merge algorithm uses table ${\mathcal {S}}_{\mathrm {LO}}$ to construct ${\mathcal {S}}_{\mathrm {HI}}$. We have constructed our fault-tolerant algorithm based on the TT-Merge algorithm.

2.2.1 Construction of tables ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$

As discussed above, the construction of ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ is a preliminary phase. The table ${\mathcal {T}}_{\mathrm {LO}}$ is constructed using LO-criticality jobs only where table ${\mathcal {T}}_{\mathrm {HI}}$ is constructed using HI-criticality jobs only. The jobs in the tables ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are arranged using the EDF algorithm [19]. Then the jobs in both the tables are then moved as close to their deadline as possible. In table ${\mathcal {T}}_{\mathrm {HI}}$, the initial $C_i({\mathrm {LO}})$ units of allocations of each HI-criticality job are retained and the remaining $C_i({\mathrm {HI}}) - C_i({\mathrm {LO}})$ units of allocation are unallocated.

For example, consider the instance in Table 2. The hyperperiod of the task set is 18. Here deadline of the two LO-criticality jobs $j_1$ and $j_3$ are 6 and 14, respectively. Now we schedule $j_1$ and $j_3$ as close to their deadline as possible in the interval [4, 6] and [12, 14] in table ${\mathcal {T}}_{\mathrm {LO}}$. Similarly, the two HI-criticality jobs $j_2$ and $j_4$ are scheduled in the interval [9, 12] and [14, 18] in table ${\mathcal {T}}_{\mathrm {HI}}$. But we need to retain the initial $C_i({\mathrm {LO}})$ units of execution time and unallocate the remaining $C_i({\mathrm {HI}}) - C_i({\mathrm {LO}})$ units of execution time from table ${\mathcal {T}}_{\mathrm {HI}}$. The final table ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are given in Fig. 3.

2.2.2 Construction of tables ${\mathcal {S}}_{\mathrm {LO}}$ and ${\mathcal {S}}_{\mathrm {HI}}$

The tables ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are then merged to construct the table ${\mathcal {S}}_{\mathrm {LO}}$, starting from time instant 0 going up to P. At each time instant t, four situations can occur: (1) ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are both empty (2) ${\mathcal {T}}_{\mathrm {LO}}$ is empty but ${\mathcal {T}}_{\mathrm {HI}}$ is non-empty (3) ${\mathcal {T}}_{\mathrm {LO}}$ is non-empty but ${\mathcal {T}}_{\mathrm {HI}}$ is empty and (4) ${\mathcal {T}}_{\mathrm {LO}}$ and ${\mathcal {T}}_{\mathrm {HI}}$ are both non-empty. In case of situation 4, the algorithm declares failure and in all other cases, a job is allocated at the time slot t, if ready; see [5] for the details.In Example 2, we have explained the construction of table ${\mathcal {S}}_{\mathrm {LO}}$. Once the table ${\mathcal {S}}_{\mathrm {LO}}$ is constructed, the algorithm starts the construction of table ${\mathcal {S}}_{\mathrm {HI}}$. The same example also shows how the TT-Merge algorithm works along with the fault-tolerant algorithm. For further details about TT-Merge, we refer the reader to [5].

3 Our work

In this section, we propose a fault-tolerant algorithm which is based on the TT-Merge algorithm and tolerate at most one fault in the entire schedule over the hyperperiod. Here we consider the jobs which have only one instance. Hence the hyperperiod for the instance I is $\max \limits _{\forall j_i}\{d_i\}$. The proposed algorithm produces the fault-tolerant tables ${\mathcal {S}}_{\mathrm {LO}}^i$ and ${\mathcal {S}}_{\mathrm {HI}}^i$ as output, where table ${\mathcal {S}}_{\mathrm {LO}}^i$ represents the LO-criticality table for $\mathrm {i}^{\mathrm {th}}$ LO-criticality job and table ${\mathcal {S}}_{\mathrm {HI}}^i$ represents the HI-criticality table for $\mathrm {i}^{\mathrm {th}}$ HI-criticality job. Here we assume that the context switch time between two jobs and the context switch time to change from one scheduling table to the other is negligible. It is easy to check whether the instance I can tolerate at most one fault over a hyperperiod.

Theorem 1

An instance I is schedulable and tolerate at most one fault over a hyperperiod if and only if the following equations hold:

For LO-criticality scenario:

$$\begin{aligned} \sum _{\forall j_i}^{} C_i(\mathrm {LO}) + \max \limits _{\forall j_i}\{C_i(\mathrm {LO})\} \le \max \limits _{\forall j_i}\{d_i\} \end{aligned}$$

(1)

For HI-criticality scenario:

$$\begin{aligned} \sum _{\forall j_i \wedge \chi _i = \mathrm {LO}}^{} C_i(\mathrm {LO}) + \sum _{\forall j_i \wedge \chi _i = \mathrm {HI}}^{} C_i(\mathrm {HI}) + \max \limits _{\forall j_i}\{C_i(\mathrm {\chi _i})\} \le \max \limits _{\forall j_i}\{d_i\} \end{aligned}$$

(2)

Proof

($\Rightarrow$) In this part of the proof, we assume that the instance I is schedulable and tolerate at most one fault. We need to show that the Eqs. 1 and 2 are correct.

Let us assume that the scenario is in LO-criticality. Since the instance I is schedulable and tolerate at most one fault, there must be sufficient time for a job $j_i$ to complete its execution after all the jobs finish their execution before its deadline, i.e., $d_i$. Suppose job $j_i$ is the job with maximum execution time among all the jobs in the instance I. Then the total time required to execute all the jobs is $\sum \nolimits _{\forall j_i}^{} C_i(\mathrm {LO}) + \max \nolimits _{\forall j_i}\{C_i(\mathrm {LO})\}$. Since it is schedulable it must be less than or equal to $\max \nolimits _{\forall j_i}\{d_i\}$.

Now assume that the scenario is in HI-criticality. In other words, a job $j_i$ has not signaled its completion after finishing the execution of $C_i(\mathrm {LO})$ units of execution time. Hence the scenario is in HI-criticality. In the worst-case situation, a HI-criticality job $j_i$ will trigger the scenario change (by not signaling its completion after finishing the execution of $C_i(\mathrm {LO})$ units of execution time) after all the LO-criticality jobs finish their execution and no HI-criticality job other than $j_i$ have started their execution. Since all the jobs have scheduled correctly, we can write the equation as follows

$$\begin{aligned} \sum _{\forall j_i \wedge \chi _i = \mathrm {LO}}^{} C_i(\mathrm {LO}) + \sum _{\forall j_i \wedge \chi _i = \mathrm {HI}}^{} C_i(\mathrm {HI}) \le \max \limits _{\forall j_i}\{d_i\} \end{aligned}$$

(3)

We know that the instance can tolerate at most one fault over the hyperperiod. As in the LO-criticality scenario case, we add the execution time of the job with maximum execution time to the already calculated time in Eq. 3. Hence we prove that if the instance I is schedulable and tolerate at most one one fault, then the Eqs. 1 and 2 hold.

($\Leftarrow$) In this part of the proof, we assume that the the Eqs. 1 and 2 are correct. We need to show that the instance I is schedulable and tolerate at most one fault.

Let us assume that the scenario is in LO-criticality. From Eq. 1, it is clearly seen that all the jobs can finish their Lo-criticality execution as well as a job $j_i$ with maximum LO-criticality execution before $\max \nolimits _{\forall j_i}\{d_i\}$. Hence an instance I can be scheduled in the LO-criticality scenario and can tolerate at most one fault over the hyperperiod.

Now assume that the scenario is in HI-criticality. From Eq. 2, we can check infer that the left hand side of the equation is a sum of three terms. The first term is the sum of all the execution time of LO-criticality jobs. The second term is the sum of the HI-criticality execution time of all the HI-criticality jobs. The third term is the maximum execution time among all the jobs. The sum of first two terms depict the total execution time required for all the jobs to be scheduled over the hyperperiod. In the worst case situation, we know that a HI-criticality job will trigger the scenario change after all the LO-criticality jobs finish their execution. If a fault has already been occurred for a LO-criticality job, then the third term is added which will be the execution time of a LO-criticality job. On the other hand, if a fault has already been occurred for a HI-criticality job, then the third term is added which will be the execution time of a HI-criticality job. In Eq. 2, the third term is the maximum execution time among all the jobs in the instance. So, the instance is schedulable in HI-criticality scenario when Eq. 2 holds. Hence we prove that if the Eqs. 1 and 2 hold, then instance I is schedulable and tolerate at most one one fault. $\square$

A fault can occur in a job at any time while in execution. We check the occurrence of a fault at the end of its execution. If a fault is found then the job is re-executed immediately after its faulty execution. We assume that the time taken to check for the occurrence of a fault is negligible. We know that a fault can occur at any point of time while the system is running online and the time-triggered tables are prepared prior to the run-time. Hence we need to allocate sufficient extra times for each job, so that, each job can complete their execution correctly on time.

We recall Algorithm 1 from [5] that constructs the table ${\mathscr {T}}_{\mathrm {LO}}$ which includes only the LO-criticality jobs. This algorithm chooses the LO-criticality jobs from the instance I and orders them in EDF order [19]. Then, all the job segments of the EDF schedule are moved as close to their deadline as possible so that no job misses its deadline in table ${\mathscr {T}}_{\mathrm {LO}}$.

Note that, if the arrival times of the jobs are not the same, then the jobs may execute in more than one segment, in general. If the arrival times of all the jobs are the same then, the jobs will execute in one segment.

Algorithm 2, also from [5], constructs the table ${\mathscr {T}}_{\mathrm {HI}}$ which contains only the HI-criticality jobs. This algorithm chooses the HI-criticality jobs from the instance I and orders them in EDF order. Then, all the job segments of the EDF schedule are moved as close to their deadline as possible so that no job misses its deadline in table ${\mathscr {T}}_{\mathrm {HI}}$. Then, out of the total allocation so far, the algorithm allocates $C_i(\mathrm {LO})$ units of execution of job $j_{ik}$ in table ${\mathscr {T}}_{\mathrm {HI}}$ from the beginning of its slot and leaves the rest of the execution time of $j_i$ unallocated in table ${\mathscr {T}}_{\mathrm {HI}}$.

Algorithm 3 constructs a general time-triggered scheduling table ${\mathcal {S}}_{\mathrm {LO}}$ which can be used to dispatch jobs in a LO-criticality scenario without the presence of a fault. Hence we call the function Faulttolerant(${\mathscr {T}}_{\mathrm {LO}}$,${\mathscr {T}}_{\mathrm {HI}}$,${\mathcal {S}}_{\mathrm {LO}}$) which constructs the scheduling tables for LO-criticality and HI-criticality scenario at the presence of a fault.

Algorithm 4 (Function Faulttolerant(I,${\mathcal {T}}_{\mathrm {LO}}$,${\mathcal {T}}_{\mathrm {HI}}$,${\mathcal {S}}_{\mathrm {LO}}$,${\mathcal {S}}_{\mathrm {HI}}$)) constructs a LO-criticality and a HI-criticality time-triggered fault-tolerant scheduling table for each job. The algorithm is divided into two parts. In the first part, from line 1 to line 8, a LO-criticality and HI-criticality time-triggered fault-tolerant scheduling table for each job is constructed. Line 3 copies all the jobs in the table ${\mathcal {S}}_{\mathrm {LO}}$ to table ${\mathcal {S}}_{\mathrm {LO}}^i$. Then $C_i({\mathrm {LO}})$ units of back up execution time is allocated after $C_i({\mathrm {LO}})$ units of primary execution of the job $j_i$ in table ${\mathcal {S}}_{\mathrm {LO}}^i$. This is done by shifting all the jobs after the last segment of job $j_i$ in table ${\mathcal {S}}_{\mathrm {LO}}^i$ such that no job misses its finishing time in table ${\mathcal {T}}_{\chi _k}$, where $\chi _k$ is the criticality level of job $j_i$. Since jobs to the right of $j_i$ are shifted up to their finishing time in table ${\mathcal {T}}_{\chi _k}$, the back up copy of $C_i({\mathrm {LO}})$ units of execution time of job $j_i$ may miss its finishing time in table ${\mathcal {T}}_{\chi _k}$. In that case, our algorithm declares failure.

In the second part, from line 10 to line 18, a LO-criticality and HI-criticality time-triggered fault-tolerant scheduling table for HI-criticality job is constructed. In line 13, table ${\mathcal {S}}_{\mathrm {HI}}^i$ is constructed from table ${\mathcal {S}}_{\mathrm {LO}}^i$. This is the same process as the TT-Merge algorithm. Once table ${\mathcal {S}}_{\mathrm {HI}}^i$ is constructed, the algorithm allocates the backup time of $C_i({\mathrm {HI}})-C_i({\mathrm {LO}})$ units of execution time for the HI-criticality jobs in table ${\mathcal {S}}_{\mathrm {HI}}^i$. This is done in the same process as in Line 4. If job $j_i$ misses its finishing time in table ${\mathcal {T}}_{\mathrm {HI}}$, then our algorithm declares failure. Now we explain the proposed algorithm with an illustrative example.

Example 2

Consider the MC task set of 4 tasks given in Table 2.

The TT-Merge algorithm constructs table ${\mathcal {T}}_{\mathrm {LO}}$, ${\mathcal {T}}_{\mathrm {HI}}$, ${\mathcal {S}}_{\mathrm {LO}}$ and ${\mathcal {S}}_{\mathrm {HI}}$ as given in Fig. 3.

Now we apply our algorithm to the tables ${\mathcal {S}}_{\mathrm {LO}}$ and ${\mathcal {S}}_{\mathrm {HI}}$. We scan the table ${\mathcal {S}}_{\mathrm {LO}}$ from the right and the first job found in table ${\mathcal {S}}_{\mathrm {LO}}$ is $j_1$. So we need to construct table ${\mathcal {S}}_{\mathrm {LO}}^i$ which will be the fault-tolerant table for job $j_1$. To construct table ${\mathcal {S}}_{\mathrm {LO}}^1$, we copy the table ${\mathcal {S}}_{\mathrm {LO}}$ to ${\mathcal {S}}_{\mathrm {LO}}^1$. Then we allocate $C_1(\mathrm {LO})$ units of backup execution time immediately after $C_1(\mathrm {LO})$ units of primary execution time. To allocate the backup execution time we need to push all other jobs $j_k$ to their right till their finishing time in table ${\mathcal {T}}_{\chi _k}$. The resulting table is given in Fig. 4.

In the same process, we construct tables for ${\mathcal {S}}_{\mathrm {LO}}^2$, ${\mathcal {S}}_{\mathrm {LO}}^3$ and ${\mathcal {S}}_{\mathrm {LO}}^4$ as given in Fig. 5.

Since job $j_1$ and $j_3$ are LO-criticality jobs, they do not need backup time in the HI-criticality scenario. So the HI-criticality tables ${\mathcal {S}}_{\mathrm {HI}}^1$ and ${\mathcal {S}}_{\mathrm {HI}}^3$ can be constructed in the same way as the table ${\mathcal {S}}_{\mathrm {HI}}$. The resulting table is given in Fig. 6.

We construct tables ${\mathcal {S}}_{\mathrm {HI}}^2$ and ${\mathcal {S}}_{\mathrm {HI}}^4$ from tables ${\mathcal {S}}_{\mathrm {LO}}^2$ and ${\mathcal {S}}_{\mathrm {LO}}^4$, respectively. Here we need to take care of the backup execution time of each job $j_i$ for its $C_i({\mathrm {HI}})-C_i({\mathrm {LO}})$ units of execution time in table ${\mathcal {S}}_{\mathrm {HI}}^i$. As per the algorithm, we assign the $C_i({\mathrm {HI}})-C_i({\mathrm {LO}})$ units of backup execution time after the $C_i({\mathrm {HI}})-C_i({\mathrm {LO}})$ units of primary execution time. The resulting tables ${\mathcal {S}}_{\mathrm {HI}}^2$ and ${\mathcal {S}}_{\mathrm {HI}}^4$ are given in Fig. 7. From Fig. 7, it is clear that job $j_4$ is shifted to its right and 1 unit of extra backup execution time is assigned for job $j_2$ in the interval [9, 10].

Table 2 Instance for Example 2

Fig. 3

Tables constructed by the TT-Merge algorithm

Fig. 4

Table ${\mathcal {S}}_{\mathrm {LO}}^1$

Fig. 5

Table ${\mathcal {S}}_{\mathrm {LO}}$ for jobs $j_2$, $j_3$ and $j_4$

Fig. 6

Table ${\mathcal {S}}_{\mathrm {HI}}$ for jobs $j_1$ and $j_3$

Fig. 7

Table ${\mathcal {S}}_{\mathrm {HI}}$ for jobs $j_2$ and $j_4$

3.1 Correctness proof

For correctness, we need to show that if the FF-TT-MERGE algorithm finds the required scheduling tables ${\mathcal {S}}_{\mathrm {LO}}^i$ and ${\mathcal {S}}_{\mathrm {HI}}^i$ for each job $j_i$, then the jobs which are dispatched according to these tables will give a correct scheduling strategy. We start with the proof of some properties of the schedule. Since the TT-Merge algorithm is already proven, we focus on the function Faulttolerant(I,${\mathscr {T}}_{\mathrm {LO}}$,${\mathscr {T}}_{\mathrm {HI}}$,${\mathcal {S}}_{\mathrm {LO}}$,${\mathcal {S}}_{\mathrm {HI}}$).

Lemma 1

If Algorithm 4 does not declare failure, then (a) each job $j_k$ receives $C_k(\mathrm {LO})$ units of execution and a job $j_i$ receives twice the amount of $C_i(\mathrm {LO})$ units of execution in table ${\mathcal {S}}_{\mathrm {LO}}^i$ and (b) each HI-criticality job $j_k$ receives $C_k(\mathrm {HI})$ units of execution and a job $j_i$ receives twice the amount of $C_i(\mathrm {HI})$ units of execution in table ${\mathcal {S}}_{\mathrm {HI}}^i$ by its deadline.

Proof

First, we show that each job $j_k$ receives $C_k(\mathrm {LO})$ units of execution and a job $j_i$ receives twice the amount of $C_i(\mathrm {LO})$ units of execution in table ${\mathcal {S}}_{\mathrm {LO}}^i$. We construct table ${\mathcal {S}}_{\mathrm {LO}}^i$ from the table ${\mathcal {S}}_{\mathrm {LO}}$. We know that all the jobs $j_k$ as well as job $j_i$ got their stipulated $C_i(\mathrm {LO})$ units of execution in table ${\mathcal {S}}_{\mathrm {LO}}$. In Line 4 of the function Faulttolerant(I,${\mathscr {T}}_{\mathrm {LO}}$,${\mathscr {T}}_{\mathrm {HI}}$,${\mathcal {S}}_{\mathrm {LO}}$,${\mathcal {S}}_{\mathrm {HI}}$), we assign $C_i(\mathrm {LO})$ units of execution immediately after the right most segment of job $j_i$ in table ${\mathcal {S}}_{\mathrm {LO}}^i$ by pushing all the jobs to their right. In this process, no job can be pushed beyond its deadline and the extra $C_i(\mathrm {LO})$ units of execution must be scheduled in between the finishing time of the last segment and the finishing time of job $j_i$ in table ${\mathcal {T}}_{\chi _i}$. Hence if our algorithm does not declare failure, then our algorithm will assign $C_k(\mathrm {LO})$ units of execution for each job $j_k$ and twice the amount of $C_i(\mathrm {LO})$ units of execution in table ${\mathcal {S}}_{\mathrm {LO}}^i$.

Second, we show that each job $j_k$ receives $C_k(\mathrm {HI})$ units of execution and a job $j_i$ receives twice the amount of $C_i(\mathrm {HI})$ units of execution in table ${\mathcal {S}}_{\mathrm {HI}}^i$. The proof of this part is the same as the proof of the first part of this lemma. $\square$

Lemma 2

At any time t, if a job $j_i$ is present in ${\mathcal {S}}_{\mathrm {HI}}^i$ but not in ${\mathcal {S}}_{\mathrm {LO}}^i$, then the job $j_i$ has finished its LO-criticality execution before time t in ${\mathcal {S}}_{\mathrm {LO}}$.

Proof

Here we follow the same order of jobs in ${\mathcal {S}}_{\mathrm {LO}}^i$ to construct ${\mathcal {S}}_{\mathrm {HI}}^i$. Initially we allocate $C_i(\mathrm {LO})$ units of execution time of a HI-criticality job in table ${\mathcal {S}}_{\mathrm {HI}}$, then the remaining execution time, i.e., $C_i(\mathrm {HI})-C_i(\mathrm {LO})$ units of execution is allocated ${\mathcal {S}}_{\mathrm {HI}}$. We know that the HI-criticality jobs are preferred over the LO-criticality jobs in ${\mathcal {S}}_{\mathrm {HI}}^i$, i.e., a HI-criticality job is chosen to be allocated in table ${\mathcal {S}}_{\mathrm {HI}}^i$ if a LO-criticality job is found in ${\mathcal {S}}_{\mathrm {LO}}^i$ while allocating $C_i(\mathrm {HI})-C_i(\mathrm {LO})$ units of execution in table ${\mathcal {S}}_{\mathrm {HI}}^i$. This means each of the job segments present in table ${\mathcal {S}}_{\mathrm {HI}}^i$ is either at the same position in ${\mathcal {S}}_{\mathrm {LO}}^i$ or to the right of it. When a job $j_i$ is present in ${\mathcal {S}}_{\mathrm {HI}}^i$ and not in ${\mathcal {S}}_{\mathrm {LO}}^i$ at time t, it means this has already completed its LO-criticality execution in ${\mathcal {S}}_{\mathrm {LO}}^i$. $\square$

Lemma 3

At any time t, when a scenario change occurs, each HI-criticality job still has $C_i(\mathrm {HI}) - c_i$ units of execution in ${\mathcal {S}}_{\mathrm {HI}}^i$ after time t to complete its execution, if a fault has already occurred and twice of $C_i(\mathrm {HI})$ units of execution in ${\mathcal {S}}_{\mathrm {HI}}^i$ after time t to complete its execution, if a fault has not occurred, where $c_i$ is the execution time already completed by job $j_i$ before time t in ${\mathcal {S}}_{\mathrm {LO}}$.

Proof

Suppose a scenario change occurs at time t. This means all the HI-criticality jobs scheduled before time t have either signaled their completion or the current HI-criticality job is the first one to complete its $C_i(\mathrm {LO})$ units of execution without signaling its completion. We know that all the HI-criticality jobs are allocated their $C_i(\mathrm {HI})-C_i(\mathrm {LO})$ units of execution in ${\mathcal {S}}_{\mathrm {HI}}^i$ after the completion of their $C_i(\mathrm {LO})$ units of execution in both ${\mathcal {S}}_{\mathrm {LO}}^i$ and ${\mathcal {S}}_{\mathrm {HI}}^i$. At time t, there can be two possibilities, i.e., a fault has already occurred and no fault has occurred.

(a) If a fault has already occurred, then the job $j_i$ has already executed twice of $C_i(\mathrm {LO})$ units of execution in ${\mathcal {S}}_{\mathrm {LO}}^i$. Hence it requires $C_i(\mathrm {HI})-C_i(\mathrm {LO})$ units of time to be completed in ${\mathcal {S}}_{\mathrm {HI}}^i$. Because the system can tolerate at most one fault which has already occurred. When job $j_i$ initiates the scenario change, this is the first job which doesn’t signal its completion after completing its $C_i(\mathrm {LO})$ units of execution. Before time t, the scheduler uses the table ${\mathcal {S}}_{\mathrm {LO}}^i$ to schedule the jobs, while subsequently the scheduler uses table ${\mathcal {S}}_{\mathrm {HI}}^i$ due to the scenario change. If a job $j_i$ has already executed its $c_i$ units of execution in ${\mathcal {S}}_{\mathrm {LO}}^i$, then it requires $C_i(\mathrm {HI})-c_i$ units of time to be completed in ${\mathcal {S}}_{\mathrm {HI}}^i$ its execution which is less than or equal to $C_i(\mathrm {HI})-C_i(\mathrm {LO})$ units of time. We know that the tables ${\mathcal {S}}_{\mathrm {HI}}^i$ and ${\mathcal {S}}_{\mathrm {LO}}^i$ have the same order and according to Lemmas 1 and 2, each job will get sufficient time to complete its $C_i(\mathrm {HI})$ units of execution. Hence, each HI-criticality job will get $C_i(\mathrm {HI}) - c_i$ units of time in ${\mathcal {S}}_{\mathrm {HI}}^i$ to complete its execution after the scenario change at time t.

(b) If a fault has not occurred till time t, then the job $j_i$ has already executed its $C_i(\mathrm {LO})$ units of execution in ${\mathcal {S}}_{\mathrm {LO}}^i$. Hence it requires twice of $C_i(\mathrm {HI})$ units of time to be completed in ${\mathcal {S}}_{\mathrm {HI}}^i$. We know that the system can tolerate at most one fault. Hence all other HI-criticality jobs which have not completed their execution need to complete their $C_i(\mathrm {HI})$ units of execution only. From Lemmas 1 and and 2, we know that each job will get sufficient time to complete its $C_i(\mathrm {HI})$ units of execution. Hence, each HI-criticality job will get twice of $C_i(\mathrm {HI})$ units of time in ${\mathcal {S}}_{\mathrm {HI}}^i$ to complete its execution after the scenario change at time t. $\square$

Lemma 4

If a fault occurs for the job $j_i$ in table ${\mathcal {S}}_{\chi }$ at any time t, then each job $j_i$ still has $C_i(\chi )-c_i$ units of execution in ${\mathcal {S}}_{\chi }^i$ to complete its execution, where $c_i$ is the execution time already completed by job $j_i$ before time t in ${\mathcal {S}}_{\chi }$. Note that LO-criticality jobs may not execute in HI-criticality tables.

Proof

This proof follows from Lemmas 1 and 2. $\square$

Theorem 2

If the scheduler dispatches the jobs according to ${\mathcal {S}}_{\mathrm {LO}}^i$ and ${\mathcal {S}}_{\mathrm {HI}}^i$, then it will be a correct scheduling strategy in the presence of a fault.

Proof

We have already shown that all the jobs can be correctly scheduled in a LO-criticality scenario with the presence of at most one fault. We use the table ${\mathcal {S}}_{\mathrm {LO}}$ to schedule the jobs as proved in Lemma 1. Again in Lemma 1, we prove that all the HI-criticality jobs get sufficient units of execution time in table ${\mathcal {S}}_{\mathrm {HI}}$ to complete their execution with the presence of at most one fault. In Lemma 3, we have proved that when the scenario change occurs at time t, all the HI-criticality jobs can be scheduled without missing their deadline. In Lemma 4, we show that the table change occur due to the occurrence of a fault will be executed successfully. So from Lemmas 1, 3 and 4, it is clear that if the scheduler uses the tables ${\mathcal {S}}_{\mathrm {LO}}^i$ and ${\mathcal {S}}_{\mathrm {HI}}^i$ to dispatch the jobs then it will be a correct scheduling strategy. $\square$

Theorem 3

The proposed time-triggered fault-tolerant algorithm for mixed-criticality systems under the TT-Merge algorithm dominates all the existing time-triggered scheduling algorithms for mixed-criticality systems.

Proof

We know that the TT-Merge algorithm dominates all the existing time-triggered scheduling algorithms for mixed-criticality systems in terms of scheduling number of instances. In other words, any instance which can be scheduled by the existing time-triggered scheduling algorithm for mixed-criticality systems is also scheduled by the TT-Merge algorithm. Apart from this, TT-Merge also schedules some instances which are not scheduled by the existing algorithms. From the above facts, we infer that any fault-tolerant algorithm based on a time-triggered scheduling algorithm for mixed-criticality systems other than TT-Merge will schedule less number of instances than the proposed fault-tolerant algorithm based on TT-Merge. Hence the theorem is proved. $\square$

4 Results and discussion

Here we present the experiments conducted to evaluate our algorithm. The experiments show the impact of our algorithm in various settings. The comparison is done over a large number of instances with randomly generated parameters. The job generation policy may have significant effect on the experiments. The details of the job generation policy are as follows.

• The utilization ($u_i$) of the jobs of instance I are generated according to the UUniFast algorithm [8].

• We use the exponential distribution proposed by Davis et al [12] to generate the deadline ($d_i$) of the jobs of instance I.

• The $C_i(\mathrm {LO})$ units of execution time of the jobs are calculated as $u_i \times d_i$.

• The $C_i(\mathrm {HI})$ units of execution time of the jobs are calculated as $C_i(\mathrm {HI}) = \mathrm {CF} \times C_i(\mathrm {LO})$ where $\mathrm {CF}$ is the criticality factor which varies between 2 and 6 for each HI-criticality job $j_i$.

• Each instance I contains at least one HI-criticality job and one LO-criticality job.

• For each point on the X-axis, we have plotted the average result of 10,000 runs.

Since the proposed algorithm is the first time-triggered fault-tolerant algorithm of mixed-criticality systems, we compared the proposed algorithm with the existing time-triggered algorithms applying the same technique as the proposed algorithm.

For the first experiment, we fix the utilization at LO-criticality level of each instance at 0.9 and let the deadline of the jobs vary between 1 and 2000. Apart from this, the percentage of HI-criticality jobs in an instance is fixed to 60% and the number of jobs in each instance is set to 10.

Fig. 8

Comparison of number of fault-tolerant MC-schedulable instances at an utilization of 0.9

From the graph in Fig. 8, it is clear that the proposed algorithm schedules more instances successfully than both the OCBP-based algorithm and the MCEDF algorithm using the same techniques as the proposed algorithm. It can be seen from Fig. 8 for utilization of 0.9, about 400 instances out of 1000 instances can tolerate at most one fault over the hyper-period and successfully scheduled by our algorithm, which is four times more than the OCBP-based algorithm and 1.5 times more than the MCEDF algorithm. As the number of instances increases, the success ratio is more or less stable.

For the next experiment, we fix the number of jobs per instance at 10 and let the deadline of the jobs vary between 1 and 2000. Apart from this, the percentage of HI-criticality jobs in an instance is fixed to 60%. The graph in Fig. 9 shows the comparison between the number of schedulable instances those tolerate at most one fault over the hyperperiod from the randomly generated instances where the utilization at LO-criticality level of each instance is varied between 0.5 and 0.9.

Fig. 9

Comparison of number of fault-tolerant MC-schedulable instances with different utilizations

From the graph in Fig. 9, we can conclude that the success rate for all the algorithms is decreasing with the increase in LO-criticality level utilization. The graph in Fig. 9 shows the comparison between the number of schedulable instances that tolerate at most one fault over the hyper-period from the randomly generated instances. In Fig. 9, we can easily verify that the proposed algorithm schedules almost 750 instances out of 1000 instances when the utilization of an instance is 0.5. On the other hand, The OCBP-based time-triggered scheduling algorithm and MCEDF schedule 600 and 400 instances, respectively. As the utilization of instances increases, the number of successful fault-tolerant MC-schedulable instances decreases. This happens because the load in a hyper-period and the reservation time for the HI-criticality jobs increases with the increase in the utilization of an instance. Apart from this, the number of successful instances decreases due to the availability of less time to tolerate at most one fault over the hyper-period for each instance. It can be easily verified that the proposed algorithm dominates the existing algorithms in the above settings where our algorithm schedules more number of instances those can tolerate at most one fault than the existing algorithms.

Now we fix the utilization at the LO-criticality level of each instance to 0.9 and the deadline of each job in the instance is varied between 1 and 2000. Apart from this, the percentage of HI-criticality jobs in an instance is fixed to 60%. The graph in Fig. 10 shows the comparison between the number of schedulable instances those can tolerate at most one fault over the hyperperiod from the randomly generated instances where the number of jobs per instance is varied between 10 and 100.

Fig. 10

Comparison of number of fault-tolerant MC-schedulable instances with different number of jobs per instance

From the graph in Fig. 10, we clearly see that the success rate for all the algorithms is marginally decreasing with the increase in the number of jobs per instance. More utilization means more execution time of the jobs. That means there is significantly less time to re-execute a job in the hyper-period. Apart from this, the reservation time to schedule the HI-criticality jobs is more as the number of HI-criticality jobs in an instance is fixed to 60%. In Fig. 10, it is clear that our algorithm schedules significantly more (by a factor of 4) instances successfully those can tolerate at most one fault over the hyper-period than the OCBP-based algorithm and also schedules 1.3 times more instances than the MCEDF algorithm.

For the next experiment, we fix the number of jobs per instance at 10 and let the deadline of the jobs vary between 1 and 2000. Apart from this, the utilization at the LO-criticality level of an instance is fixed to 0.9. The graph in Fig. 11 shows the comparison between the number of schedulable instances those tolerate at most one fault over the hyperperiod from the randomly generated instances where the HI-criticality jobs in each instance is varied between 50% and 90%.

Fig. 11

Comparison of number of fault-tolerant MC-schedulable instances at different percentages of HI-criticality jobs in an instance

In Fig. 11 it is clear that our algorithm successfully schedules significantly more (by a factor of 1.5) instances that can tolerate at most one fault over the hyper-period than the OCBP-based algorithm and also schedules more instances than the MCEDF algorithm. Also, we infer that the success rate of all the algorithms gradually decreases with the increase in the number of HI-criticality jobs in an instance. This is because of the reserve time requirements for the HI-criticality jobs.

5 Conclusion

This paper discusses the general mixed-criticality scheduling problem and its importance in great detail with respect to various aspects like fault tolerance. Then we have done an extensive literature survey for the work done in fault-tolerant scheduling theory concerning the mixed-criticality systems. We discover a new problem in the scheduling theory of mixed-criticality systems with respect to fault-tolerance and time-triggered systems. We propose a new fault-tolerant algorithm for the time-triggered scheduling of mixed-criticality systems, which can tolerate at most one fault over the hyper-period, where the HI-criticality jobs must meet their deadlines. We also justify the above assumption. We proved that our fault-tolerant algorithm based on TT-Merge would schedule a bigger set of instances than the existing algorithms. We have also validated the proposed facts using extensive experiments on the randomly generated instances. We plan to extend this algorithm for multiprocessor systems and dependent job instances as a part of future work. We also plan to the fault-tolerant aspect in the presence of resource sharing among jobs in an instance.