Node-to-set disjoint paths problem in cross-cubes

Abstract

Hypercubes are popular topologies of massive multiprocessor systems due to their super properties. Cross-cubes are significant variations of hypercubes and they have smaller diameters and higher fault-tolerant capability than hypercubes at the same dimensions. In this paper, we construct node-to-set disjoint paths of an n-dimensional cross-cube, $C_{n}$, whose maximum length is limited by $2n-3$. Furthermore, we propose an $O(N \text {log}^{2}N)$ algorithm with a view to finding node-to-set disjoint paths of $C_{n}$, where N is the node number of $C_n$. And we also present the simulation results for the maximal length of disjoint paths obtained by our algorithm.

1 Introduction

Huge multiprocessor systems are solutions to large-scale computing problems such as weather forecasting, scientific research, intelligence agencies, and data mining [1]. Hypercubes are widely used in interconnection networks of massively multiprocessor systems due to their excellent properties, including regularity, symmetry, and small link complexity [2]. Based on the constructive method of hypercubes, many variants of hypercubes were proposed [3,4,5,6]. The n-dimensional cross-cube, $C_n$, has smaller diameter and higher fault-tolerant capability than the n-dimensional hypercube, $Q_n$. Moreover, a cycle of odd length and a complete binary tree of height n can be embedded into $C_n$, while $Q_n$ does not have these properties [3].

The disjoint path problems are substantial in the design and implementation of interconnection networks [7,8,9]. The node-to-set disjoint paths problem is one of the disjoint path problems: Given a single source node s and a set $D = \{d_1,d_2,\ldots ,d_k\}$ of k destination nodes with $s \notin D$ in a k-connected graph $G = (V(G),E(G))$, construct k paths from s to $d_i$ which are node-disjoint except for s for all $1 \le i \le k$. As the number of nodes in interconnection networks increases, node failure seems to become the norm rather than exception. Therefore, constructing disjoint paths increases the probability of finding fault-free communication route in interconnection networks. So far, problems of finding node-to-set disjoint paths on some classes of graphs have been studied, such as hypercubes [10], Möbius cubes [11], star graphs [12], pancake graphs [13], burnt pancake graphs [14], hierarchical cubic networks [15], perfect hierarchical hypercubes [16, 17], and biswapped networks [18].

In general, the node-to-set disjoint path problems can be obtained from the polynomial-order of |V(G)| by applying the maximum flow algorithm. However, the complexity of the algorithm is not eligible for an n-dimensional cross-cube $C_n$ because the number of nodes in $C_n$ is $2^n$. Bossard and Kaneko proposed an $O(\text {log}^{2}N)$ algorithm to find node-to-set disjoint paths in an n-dimensional hypercube $Q_n$, where their longest length is no more than $n+1$ and N is the node number of $Q_n$ [10]. Unfortunately, this algorithm is not appropriate for cross-cubes directly because they do not exist some properties that hold in hypercubes. Therefore, it is necessary to design an applicable algorithm by studying properties of a $C_n$. In this paper, we propose an $O(N \text {log}^{2}N)$ algorithm for constructing $n+1$ node-to-set disjoint paths in $C_n$, where $n+1$ is equivalent to the connectivity of $C_n$’s and N is the node number of $C_n$. Moreover, we prove that the length of the longest path of the $n+1$ disjoint paths constructed by our algorithm is no more than $2n-3$. We also show the experiments of $C_n$ to evaluate the performance of the algorithm we have proposed.

The remainder of this paper is organized as follows. Section 2 provides relevant preliminary knowledge. In Sect. 3, the construction of node-to-set disjoint paths in cross-cubes is studied. Conclusions of this paper and suggestions on future work are given in Sect. 4.

2 Preliminaries

For terminology and notation not defined here, we follow [19]. Given a simple graph $G=G(V(G),E(G))$ to represent an interconnection network, where V(G) and E(G) denote the node set and edge set, respectively. A path in a graph is a sequence of nodes, $P = (u_1, u_2, \ldots , u_j,\ldots ,u_{n-1}, u_{n})$, in which no node is repeated and $u_j, u_{j+1}$ are adjacent for any integer $1 \le j < n$. The length of a path P, l(P), is the number of edges in P, and we use V(P) to represent the node set in P. We also write the path $(u_1, u_2, \ldots , u_k)$ as $(u_1,Q, u_i, u_{i+1}, \ldots , u_k)$, where Q is the path $(u_2, u_3, \ldots , u_{i-1})$. If u and v are nodes on a path P, we write Path(P, u, v) to denote the sub-path of P from u to v. Furthermore, we use P[i] to denote the node $u_i$ for $P = (u_1, u_2, \ldots , u_{n})$ for any integer $1 \le i \le n$ and use $P[-1]$ to denote the last node in P.

For $U \subseteq V(G)$, we use $G[U]=(U,E')$ to denote the subgraph induced by U in G where $E'=\{(u,v)\in E(G)|u,v \in U\}$. Given two distinct nodes u and v of G, the distance between u and v is defined as the length of the shortest path between u and v in G, denoted by dist(G, u, v). The diameter of G is defined as d(G) = max(dist$(G,u,v)| u,v \in V(G), u \ne v$). A graph is connected when there is a path between every pair of nodes. In a connected graph, there are no unreachable nodes. A graph that is not connected is called to be disconnected. The connectivity $\kappa (G)$ of a connected graph G (other than a complete graph) is the minimum number of nodes whose removal disconnects G. We say u is a neighbor of v or u is adjacent to v if $(u, v) \in E(G)$. Then, we use $N_G(u)$ to denote neighbors of u in graph G.

A binary string u with length n can be written as $u_{n-1}u_{n-2} \ldots u_0$ and $u[i] = u_i \in \{0,1\}$ is denoted by the i-th bit of u for any integer i with $0 \le i \le n - 1$. The complement of $u_i$ is denoted by $\bar{u_i}$ or $1 - u_i$.

The n-dimensional cross-cube, $C_n$, has $2^n$ nodes and $(n+1)2^{n-1}$ edges. Each node of $C_n$ is represented by a unique binary string from 0 to $2^n-1$ of length n, called the address of the node. For $i \in \{0,1\}$, let $C^i_{n-1}$ denote the graph obtained by prefixing the address of each node of $C_{n-1}$ with i. Obviously, $C_{n-1}^i$ is isomorphic to $C_{n-1}$ with $i \in \{0,1\}$. In this paper, we would not make a distinction between nodes of $C_n$ and their addresses. We adopt the recursively definitions of $C_n$ from [3] as follows.

Definition 1

$C_2$ is a complete graph on four nodes whose addresses are 00, 01, 10, and 11. For $n \ge 3$, $C_n$ consists of $C^0_{n-1}$ and $C^1_{n-1}$. The nodes $u = u_{n-1}u_{n-2} \ldots u_0 \in V(C^0_{n-1})$ and $v = v_{n-1}v_{n-2} \ldots v_0 \in V(C^1_{n-1})$ are joined by an edge in $C_n$ if and only if $u_{n-2}u_{n-3} \ldots u_0 = v_{n-2}v_{n-3} \ldots v_0$.

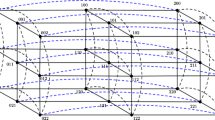
Figure 1 depicts several cross-cubes such as $C_{2}$, $C_{3}$, and $C_4$. For $n \ge 3$, let $u = u_{n-1}u_{n-2} \ldots u_1 u_0 \in V(C_n)$. Then, let $(u)^2 = \{u_{n-1}u_{n-2} \ldots u_2 \alpha | \alpha \in \{00,01,10,11\}$ and $\alpha \ne u_1 u_0\}$ be 2-neighbors of u and $(u)^i = u_{n-1}u_{n-2} \ldots (1-u_{i-1}) \ldots u_1 u_0$ be i-neighbor of u for $3 \le i \le n$.

Fig. 1

The structure of a two-dimensional cross-cube $C_2$, b three-dimensional cross-cube $C_3$, and c four-dimensional cross-cube $C_4$, respectively

Lemma 2

An n-dimensional cross-cube $C_{n}$ has the following combinatorial properties [3].

• 1. $C_{n}$ is $(n+1)$-regular;

• 2. The diameter of $C_{n}$ is $d(C_{n}) = n-1$;

• 3. The connectivity of $C_{n}$ is $\kappa (C_{n}) = n+1$.

Definition 3

The node-to-set disjoint paths problem in an n-dimensional cross-cube is to construct $n+1$ paths from a single source node s to each node in a destination nodes set $D = \{d_1,d_2,\ldots ,d_{n+1}\}$ which are node-disjoint except for s.

3 Main results

In this section, we construct $n+1$ node-to-set disjoint paths in $C_{n}$ in Theorem 10. Then, we propose an $O(N \text {log}^{2}N)$ algorithm for finding $n+1$ node-to-set disjoint paths in $C_{n}$, where N is the node number of $C_n$. Furthermore, we show simulations and experiments of $C_{n}$ to evaluate the performance of our algorithm proposed in cross-cubes.

3.1 Node-to-set disjoint paths in cross-cubes

In this subsection, one of main results is Theorem 10, in which the one-to-set disjoint paths of $C_{n}$ are constructed for any integer $n \ge 2$, using mathematical induction on $n$. For this purpose, Lemmas 4–9 are presented for the following construction schemes.

In [20], Wang, He, and Zhang proposed an O(n) algorithm to find a shortest path between any two distinct nodes u and v in $C_n$, which is called CRouting$(C_n,u,v$) algorithm. By Definition 1 and Lemma 2, the following lemma holds.

Lemma 4

l(CRouting$(C_n,u,v)) \le d(C_n)= n-1$.

Lemma 5

For any integer $n \in \{2,3\}$, choose a source node s and an arbitrary node set $D=\{d_1, d_2, \ldots , d_{n+1}\}$ in a $C_{n}$ with $s \notin D$, there exist $n+1$ node-disjoint paths (except for s) from s to nodes of D, whose maximum length is limited by $2n-3$.

Proof

First of all, we show that the lemma holds for $n=2$ since $C_{2}$ is a complete graph with 4 nodes [19]. Secondly, the lemma is verified by a computer program when $n=3$. For example, the four paths $P_{1}^1,P_{1}^2,P_{1}^3,P_{1}^4$ (resp. $P_{2}^1,P_{2}^2,P_{2}^3,P_{2}^4$; $P_{3}^1,P_{3}^2,P_{3}^3,P_{3}^4$; $\ldots$; $P_{35}^1,P_{35}^2,P_{35}^3,P_{35}^4$) from $s = 000$ to nodes of $D = \{010,011,001,111\}$ (resp. $\{010, 011, 001, 110\}$, $\{010, 011, 001, 100\}$, $\{010, 011, 001, 101\}$, $\{010, 011, 111, 110\}$, $\{010, 011, 111, 100\}$, $\{010, 011, 111, 101\}$, $\{010, 011, 110, 100\}$, $\{010, 011, 110, 101\}$, $\{010, 011, 100, 101\}$, $\{010, 001, 111, 110\}$, $\{010, 001, 111, 100\}$, $\{010, 001, 111, 101\}$, $\{010, 001, 110, 100\}$, $\{010, 001, 110, 101\}$, $\{010, 001, 100, 101\}$, $\{010, 111, 110, 100\}$, $\{010, 111, 110, 101\}$, $\{010, 111, 100, 101\}$, $\{010, 110, 100, 101\}$, $\{011, 001, 111, 110\}$, $\{011, 001, 111, 100\}$, $\{011, 001, 111, 101\}$, $\{011, 001, 110, 100\}$, $\{011, 001, 110, 101\}$, $\{011, 001, 100, 101\}$, $\{011, 111, 110, 100\}$, $\{011, 111, 110, 101\}$, $\{011, 111, 100, 101\}$, $\{011, 110, 100, 101\}$, $\{001, 111, 110, 100\}$, $\{001, 111, 110, 101\}$, $\{001, 111, 100, 101\}$, $\{001, 110, 100, 101\}$, $\{111, 110, 100, 101\}$) are node-disjoint (except for s), whose maximum length is limited by 3, are listed in Table 1. $\square$

Table 1 Four node-disjoint paths from 000 to nodes of D in $C_{3}$

Lemma 6

For any integer $n \ge 3$, $i \in \{0,1\}$, and any node $u \in V(C_{n-1}^i)$, let $u' = (u)^n$ and $x_1,x_2,\ldots ,x_{n}$ be the n neighbors of u in $C_{n-1}^{i}$. Furthermore, let $x'_j = (x_j)^n$ for all $j \in \{1,2,\ldots ,n\}$. Then, $P_1 =(u,x_1,x'_1)$, $P_2 =(u,x_2,x'_2)$, $\ldots$, $P_n =(u,x_n,x'_n)$, $P_{n+1} =(u,u')$ are $n+1$ node-disjoint paths (except for u) from u into $C_{n-1}^{1-i}$.

Proof

By Definition 1, for any integers j and k with $1 \le j,k \le n$ and $j \ne k$, we have $x_j \ne x_k$ and hence $x'_j \ne x'_k$. Then, since $u \ne x_j$ for any integer j with $1 \le j \le n$, so $u' \ne x'_j$. Accordingly, $P_1 =(u,x_1,x'_1)$, $P_2 =(u,x_2,x'_2)$, $\ldots$, $P_n =(u,x_n,x'_n)$, $P_{n+1} =(u,u')$ are $n+1$ node-disjoint paths (except for u) from u into $C_{n-1}^{1-i}$ (refer to Fig. 2). $\square$

Fig. 2

$n+1$ node-disjoint paths (except for u) from u into $C_{n-1}^{1-i}$

Lemma 7

For any integer $n \ge 3$, $i \in \{0,1\}$, and any node $u \in V(C_{n-1}^i)$, let $u' = (u)^n$. For any integer k with $1 \le k \le n-1$, let $T = \{u', y_1,y_2,\ldots ,y_k, y'_1,y'_2,\ldots ,y'_k\}$ with $u \notin T$, $y_1,y_2,\ldots ,y_k \in V(C_{n-1}^{i})$, and $y'_1,y'_2,\ldots ,y'_k \in V(C_{n-1}^{1-i})$ such that $y'_j = (y_j)^n$ for all $j \in \{1,2,\ldots ,k\}$. Then, there exists a path $P =(u,x,x')$ such that $(u,x) \in E(C_{n-1}^i)$, $x' = (x)^n$, and $V(P) \cap T = \emptyset$.

Proof

Let $x_1,x_2,\ldots ,x_{n}$ be the n neighbors of u in $C_{n-1}^{i}$. Furthermore, let $x'_j = (x_j)^n$ for all $j \in \{1,2,\ldots ,n\}$. By Lemma 6, these exist $n+1$ node-disjoint paths (except for u) $P_1 =(u,x_1,x'_1)$, $P_2 =(u,x_2,x'_2)$, $\ldots$, $P_n =(u,x_n,x'_n)$, $P_{n+1} =(u,u')$ from u into $C_{n-1}^{1-i}$. Accordingly, we have $V(P_{n+1}) \cap T = \{u'\}$. Since $k \le n-1$, there exists a node $x \in \{x_1, x_2, \ldots , x_n\}$ such that $x \notin \{y_1,y_2,\ldots ,y_k\}$ and $(u,x) \in E(C_{n-1}^i)$. Let $x' = (x)^n$ and $P =(u,x,x')$ (refer to Fig. 3). By Definition 1, we can verify that $x \notin T$ and $x' \notin \{y'_1,y'_2,\ldots ,y'_k, u'\}$. Hence, we have $V(P) \cap T = \emptyset$. $\square$

Fig. 3

Example of $P =(u,x,x')$ with $V(P) \cap T = \emptyset$

Lemma 8

For any integer $n \ge 3$, $i \in \{0,1\}$, and $u_1,u_2,\ldots ,u_r \in V(C_{n-1}^i)$ with $1 \le r \le \lceil \frac{n-1}{2} \rceil$, let $u_j' = (u_j)^n$ for $j \in \{1,2,\ldots ,r\}$. For any integer k with $1 \le k \le n - 2r + 1$, let $T = \{u_1',u_2',\ldots ,u_r', y_1,y_2,\ldots ,y_k, y'_1,y'_2,\ldots ,y'_k\}$ with $\{u_1,u_2,\ldots ,u_r\} \cap T = \emptyset$ such that $y_j \in V(C_{n-1}^{i})$, $y'_j\in V(C_{n-1}^{1-i})$, and $y'_j = (y_j)^n$ for $j \in \{1,2,\ldots ,k\}$. Then,

• (1) if $r = 1$, there exists a path $P =(u_1,x_{1},z_{1})$ such that $(u_1,x_{1}) \in E(C_{n-1}^i)$, $z_{1} = (x_{1})^n$, and $V(P) \cap T = \emptyset$.

• (2) if $2 \le r \le \lceil \frac{n-1}{2} \rceil$, there exist r node-disjoint paths $P_1 =(u_1,x_{1},z_{1})$, $P_2 =(u_2,x_{2},z_{2})$, $\ldots$, $P_r =(u_r,x_{r},z_{r})$ such that $(u_j,x_{j}) \in E(C_{n-1}^i)$, $z_{j} = (x_{j})^n$, and $V(P_j) \cap T = \emptyset$ for $j \in \{1,2,\ldots ,r\}$.

Proof

If $n = 3$, we have $r = 1$ and thus the lemma holds based on Lemma 7. In what follows, we will prove that the lemma holds for $n \ge 4$ by induction on r. By Lemma 7, the lemma holds for $r = 1$. We assume that the lemma holds for $r = \tau$ when $1 \le \tau \le \lceil \frac{n-1}{2} \rceil - 1$.

Then, we consider $r = \tau + 1$. Note that, we have $2 \le r = \tau + 1 \le \lceil \frac{n-1}{2} \rceil$. For any integer m with $1 \le m \le n - 2(\tau +1) + 1 < n - 2\tau + 1$, without loss of generality, denote $T' = \{u_1',u_2',\ldots ,u_\tau ', y_1,y_2,\ldots ,y_m, y'_1,y'_2,\ldots ,y'_m\}$. Clearly, we have $T' \subseteq T$ and $\{u_1,u_2,\ldots ,u_\tau \} \cap T' = \emptyset$. Accordingly, we have $V(P_j) \cap T' = \emptyset$ for $j \in \{1,2,\ldots ,\tau \}$.

Choose a node $u_{\tau +1} \in V(C_{n-1}^i)$ such that $u_{\tau +1} \notin \{u_1,u_2,\ldots ,u_\tau \}$ and $u_{\tau +1} \notin T'$. Let $u_{\tau +1}' = (u_{\tau +1})^n$ and $T''= T' \cup \{u_{\tau +1}'\} = \{u_1',u_2',\ldots ,u_\tau ', u_{\tau +1}', y_1,y_2,\ldots ,y_m, y'_1,y'_2,\ldots ,y'_m\}$. By Definition 1, it is easy to verify that $\{u_1,u_2,\ldots ,u_\tau , u_{\tau +1}\} \cap T'' = \emptyset$ and $u_{\tau +1}' \notin \{z_{1},z_{2},\ldots , z_{\tau }\}$. Thus, we have $V(P_j) \cap T'' = \emptyset$ for $j \in \{1,2,\ldots ,\tau \}$.

Denote $D = \{u_1,u_2,\ldots ,u_\tau \} \cup \{x_{1},x_{2},\ldots ,x_{\tau }\} \cup \{y_1,y_2,\ldots ,y_m\}$. Then, we have

$$\begin{aligned} \begin{aligned} |D| = \tau + \tau + m \le 2 \tau + n - 2(\tau +1) + 1 = n-1 < n. \end{aligned} \end{aligned}$$

Let $x_{\tau +1}^1,x_{\tau +1}^2,\ldots ,x_{\tau +1}^{n}$ be the n neighbors of $u_{\tau +1}$ in $C_{n-1}^{i}$. Since $|D| < n$, there exists a node $x_{\tau +1} \in \{x_{\tau +1}^1,x_{\tau +1}^2,\ldots ,x_{\tau +1}^{n}\}$ such that $x_{\tau +1} \notin D$ and $(u_{\tau +1}, x_{\tau +1}) \in E(C_{n-1}^{i})$. Let $z_{\tau +1} = (x_{\tau +1})^n$ and $P_{\tau +1} =(u_r,x_{\tau +1},z_{\tau +1})$. By Definition 1, we have $x_{\tau +1},z_{\tau +1} \notin T''$ and $x_{\tau +1},z_{\tau +1} \notin V(P_j)$ for $j \in \{1,2,\ldots ,\tau \}$.

Hence, $P_1 =(u_1,x_{1},z_{1})$, $P_2 =(u_2,x_{2},z_{2})$, $\ldots$, $P_\tau =(u_\tau ,x_{\tau },z_{\tau })$, $P_{\tau +1} =(u_{\tau +1},x_{\tau +1},z_{\tau +1})$ are $\tau + 1$ node-disjoint paths such that $V(P_j) \cap T'' = \emptyset$ for $j \in \{1,2,\ldots ,\tau +1\}$ (refer to Fig. 4).

From the above discussion, we claim that the lemma holds. $\square$

Fig. 4

$\tau +1$ node-disjoint paths $P_1, P_2, \ldots , P_\tau , P_{\tau +1}$ in $C_{n}$ with $V(P_j) \cap T'' = \emptyset$ for $j \in \{1,2,\ldots ,\tau +1\}$

Lemma 9

For any integer $n \ge 3$, choose an arbitrary source node s and an arbitrary node set $D=\{d_1, d_2, \ldots , d_{n+1}\}$ in a $C_{n}$ with $s \notin D$, there exist $n+1$ node-disjoint paths (except for s) from s to nodes of D, whose maximum length is limited by $2n-3$.

Proof

The lemma is proved by induction on n, which is the dimension of $C_{n}$. By Lemma 5, the lemma holds for $n = 3$. We assume that the lemma holds for $n = \tau -1$ when $\tau \ge 4$. Then, we can obtain the following statement based on the induction hypothesis: for a node s and a node set $D' = \{d_1,d_2,\ldots ,d_{\tau }\}$ in a $C_{\tau -1}$ with $s \notin D'$ and $\tau \ge 4$, there exist $\tau$ node-disjoint paths (except for s) from s to nodes of $D'$, whose maximum length is limited by $2(\tau -1)-3 = 2\tau -5$. In what follows, by choosing an arbitrary source node s and an arbitrary node set $D = \{d_1,d_2,\ldots ,d_{\tau +1}\}$ in a $C_{\tau }$ with $s \notin D$, we will prove that the lemma holds for $n = \tau$ when $\tau \ge 4$.

Choose an integer i with $i \in \{0,1\}$. Let $D_1 = D \cap V(C^{i}_{\tau -1})$, $D_2 = D \cap V(C^{1-i}_{\tau -1})$, $D_3 = \{u | u \in D_{1} \ \text {and} \ (u)^\tau \in D\}$, $D_4 = \{u | u \in D_{2} \ \text {and} \ (u)^\tau \in D\}$, $\alpha = |D_1|$, $\beta = |D_{2}|$, $\gamma = |D_3| = |D_4|$, and $s' = (s)^{\tau }$. Without loss of generality, suppose that $s \in V(C_{\tau -1}^i)$. Then, we can claim the following three cases with respect to $\alpha$.

Case 1. $\alpha = \tau + 1$.

Let $D'' = \{d_2,d_3,\ldots ,d_{\tau +1}\}$ and $\phi = 0$. According to induction hypothesis, there exist $\tau$ paths node-disjoint paths $Q_1,Q_2,\ldots ,Q_{\tau }$ (except for s) from s to nodes of $D'$, whose maximum length is limited by $2\tau -5$. Choose $\phi \in \{1,2,\ldots ,\tau \}$ such that $d_{\tau +1} \in V(Q_\phi )$. We further obtain the following two subcases with respect to $\phi$.

Case 1.1 $\phi \notin \{1,2,\ldots ,\tau \}$.

Let $d_{\tau +1}' = (d_{\tau +1})^{\tau }$ and $Q' = \text {CRouting}(C^{1-i}_{\tau -1}, s', d_{\tau +1}')$. For any integer $1 \le j \le \tau +1$, if $1 \le j \le \tau$, let $P_{j} = Q_j$; otherwise, let $P_{j} = ( s, Q', d_{\tau +1} )$ (refer to Fig. 5a).

Fig. 5

Illustrations for a Case 1.1 and b Case 1.2 in Lemma 9, respectively

By the induction hypothesis, $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, we can verify that $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{2\tau -5, \tau - 2 +2\} \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Subcase 1.2 $\phi \in \{1,2,\ldots ,\tau \}$.

Without loss of generality, denote $\phi = 1$. Let $d_{1}' = (d_{1})^{\tau }$ and $Q' = \text {CRouting}(C^{1-i}_{\tau -1}, s', d_{1}')$. For any integer $1 \le j \le \tau +1$, let

$$\begin{aligned} P_{j} = {\left\{ \begin{array}{ll} ( s,Q', d_{1} ) &{} \text {if} \ j = 1,\\ Q_j &{} \text {if} \ 2 \le j \le \tau ,\\ \text {Path}(Q_{1}, s, d_{\tau +1}) &{} \text {if} \ j = \tau +1. \end{array}\right. } \end{aligned}$$

Accordingly, all the $\tau +1$ needed paths connecting s and nodes of $D=\{d_1, d_2, \ldots , d_{\tau +1}\}$ of $C_{\tau }$ are constructed above (refer to Fig. 5b). By the induction hypothesis, $P_2,P_3,\ldots ,P_{\tau +1}$ are node-disjoint expect for s. In addition, we can verify that $V(P_1) \cap V(P_k) = \{s\}$ for all $2 \le k \le \tau +1$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{\tau - 2 +2, 2\tau -5, (2\tau -5) - 1\} \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Case 2. $\alpha = 0$.

For any integer j with $1 \le j \le \tau +1$, let $d'_j = (d_j)^{\tau }$. Let $D'' = \{d'_1,d'_2,\ldots ,d'_{\tau }\}$. We further deal with the following two subcases with respect to $s'$.

Subcase 2.1. $s' \in D$.

Without loss of generality, let $d_{\tau +1} = s'$. By the induction hypothesis, there are $\tau$ node-disjoint paths $Q_1,Q_2,\ldots ,Q_{\tau }$ (except for s) joining s and nodes of $D''$ in $C^{i}_{\tau -1}$ such that $d'_k \in V(Q_k)$ for $1 \le k \le \tau$, whose maximum length is limited by $2\tau -5$. For any integer $1 \le j \le \tau +1$, if $1 \le j \le \tau$, let $P_{j} = ( Q_j, d_j )$; otherwise, let $P_{j} = ( s, d_{\tau +1} )$ (refer to Fig. 6a).

Fig. 6

Illustrations for a Case 2.1 and b Case 2.2 in Lemma 9, respectively

By the induction hypothesis and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, we have $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By the induction hypothesis, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{1, (2\tau -5) + 1\} = 2\tau -4 \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Subcase 2.2. $s' \notin D$.

Let $D''' = \{d_2,d_3,\ldots ,d_{\tau +1}\}$. By the induction hypothesis, there exist $\tau$ node-disjoint paths $Q_2,Q_3,\ldots ,Q_{\tau +1}$ (except for $s'$) joining $s'$ and nodes of $D'''$ in $C^{1-i}_{\tau -1}$ such that $d_k \in V(Q_k)$ for $2 \le k \le \tau +1$, whose maximum length is limited by $2\tau -5$. Choose $\phi \in \{2,3,\ldots ,\tau +1\}$ with $d_{1} \notin V(Q_\phi )$. Without loss of generality, let $\phi = \tau +1$. By the induction hypothesis, there exist $\tau$ node-disjoint paths $S_1,S_2,\ldots ,S_{\tau }$ (except for s) joining s and nodes of $D''$ in $C^{i}_{\tau -1}$ such that $d_k \in V(S_k)$ for $1 \le k \le \tau$, whose maximum length is limited by $2\tau -5$. For any integer $1 \le j \le \tau +1$, let if $1 \le j \le \tau$, let $P_{j} = ( S_j, d_j )$; otherwise, let $P_{j} = ( s, Q_{\tau +1} )$ (refer to Fig. 6b).

By the induction hypothesis and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, we have $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By the induction hypothesis, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{(2\tau -5) + 1, (2\tau -5) + 1\} = 2\tau -4 \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Case 3. $1 \le \alpha \le \tau$.

Without loss of generality, denote $D_1 = \{d_1, d_2, \ldots , d_\alpha \}$, $D_2 = \{d_{\alpha +1}, d_{\alpha +2}, \ldots , d_{\tau +1}\}$, $D_3 = \{d_1, d_2, \ldots , d_\gamma \}$ and $D_4 = \{d_{\alpha +1}, d_{\alpha +2}, \ldots , d_{\alpha +\gamma }\}$ if $\beta \ge 1$ and $\gamma \ge 1$. Clearly, we have $\gamma \le \alpha$, $\gamma \le \beta$, and $\alpha + \beta = \tau +1$. For any integer j with $\alpha +1 \le j \le \tau + 1$, let $d'_j = (d_j)^{\tau }$. We further have the following four subcases with respect to $\gamma$ and $s'$.

Subcase 3.1. $\gamma = 0$ and $s' \in D$.

Without loss of generality, let $s' = d_{\tau +1}$. Then, let

$$\begin{aligned} D'' = {\left\{ \begin{array}{ll} \{d_1,d_2,\ldots ,d_{\alpha }\} &{} \text {if} \ \beta = 1,\\ \{d_1,d_2,\ldots ,d_{\alpha },d'_{\alpha +1},d'_{\alpha +2},\ldots ,d'_{\tau }\} &{} \text {if} \ \beta > 1. \end{array}\right. } \end{aligned}$$

By the induction hypothesis, there exist $\tau$ node-disjoint paths (except for s) $Q_1,Q_2,\ldots ,Q_{\tau }$ joining s and nodes of $D''$ in $C^{i}_{\tau -1}$ such that $d_k \in V(Q_k)$ for all $1 \le k \le \alpha$ and $d'_k \in V(Q_k)$ for all $\alpha +1 \le k \le \tau$ if $\beta > 1$, whose maximum length is limited by $2\tau -5$. For any integer $1 \le j \le \tau +1$, let

$$\begin{aligned} P_{j} = {\left\{ \begin{array}{ll} Q_j &{} \text {if} \ 1 \le j \le \alpha ,\\ ( Q_j, d_j ) &{} \text {if} \ \alpha +1 \le j \le \tau \ \text {and} \ \beta > 1,\\ ( s, d_{\tau +1} ) &{} \text {if} \ j = \tau +1. \end{array}\right. } \end{aligned}$$

Accordingly, all the $\tau +1$ needed paths connecting s and nodes of $D=\{d_1, d_2, \ldots , d_{\tau +1}\}$ of $C_{\tau }$ are constructed above (refer to Figure 7a, b). By the induction hypothesis and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, we can verify that $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{2\tau -5, (2\tau -5)+1, 1\} \le 2\tau -4 \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Fig. 7

Illustrations for a $\beta = 1$ and b $\beta > 1$ of Case 3.1 in Lemma 9, respectively

Subcase 3.2. $\gamma \le 1$ and $s' \notin D$.

Without loss of generality, let $d_{\tau +1} \in D_4$ if $\gamma = 1$. Let

$$\begin{aligned} D'' = {\left\{ \begin{array}{ll} \{d_1,d_2,\ldots ,d_{\alpha }\} &{} \text {if} \ \beta = 1,\\ \{d_1,d_2,\ldots ,d_{\alpha },d'_{\alpha +1},d'_{\alpha +2},\ldots ,d'_{\tau }\} &{} \text {if} \ \beta > 1. \end{array}\right. } \end{aligned}$$

Then, by the induction hypothesis, there exist $\tau$ node-disjoint paths (except for s) $Q_1,Q_2,\ldots ,Q_{\tau }$ joining s and nodes of $D''$ in $C^{i}_{\tau -1}$ such that $d_k \in V(Q_k)$ for all $1 \le k \le \alpha$ and $d'_k \in V(Q_k)$ for all $\alpha +1 \le k \le \tau$ if $\beta > 1$, whose maximum length is limited by $2\tau -5$.

If $\beta > 1$. Choose $\alpha -1$ distinct nodes (resp. node) $x_2,x_3,\ldots ,x_\alpha$ in $C^{1-i}_{\tau -1}$ such that $\{x_2,x_3,\ldots ,x_\alpha \} \cap \{s',d_{\alpha +1}, d_{\alpha +2}, \ldots , d_{\tau +1}\} = \emptyset$ when $\alpha > 1$. Then, let

$$\begin{aligned} D''' = {\left\{ \begin{array}{ll} \{d_{2}, d_{3}, \ldots , d_{\tau +1}\} &{} \text {if} \ \alpha = 1,\\ \{x_2,x_3,\ldots ,x_\alpha ,d_{\alpha +1}, d_{\alpha +2}, \ldots , d_{\tau +1}\} &{} \text {if} \ \alpha > 1. \end{array}\right. } \end{aligned}$$

By the induction hypothesis, there exist $\tau$ node-disjoint paths (except for $s'$) $S_2,S_3,\ldots ,S_{\tau +1}$ joining $s'$ and nodes of $D'''$ in $C^{1-i}_{\tau -1}$ such that $x_k \in V(S_k)$ for $2 \le k \le \alpha$ if $\alpha > 1$ and $d_k \in V(S_k)$ for $\alpha +1 \le k \le \tau +1$, whose maximum length is limited by $2\tau -5$.

For any integer $1 \le j \le \tau +1$, let

$$\begin{aligned} P_{j} = {\left\{ \begin{array}{ll} Q_j &{} \text {if} \ 1 \le j \le \alpha ,\\ ( Q_j, d_j ) &{} \text {if} \ \alpha +1 \le j \le \tau \ \text {and} \ \beta> 1,\\ ( s, S_{\tau +1} ) &{} \text {if} \ j = \tau +1 \ \text {and} \ \beta > 1,\\ ( s, \text {CRouting}(C^{1-i}_{\tau -1}, s', d_{\tau +1}) ) &{} \text {if} \ j = \tau +1 \ \text {and} \ \beta = 1. \end{array}\right. } \end{aligned}$$

Furthermore, all the $\tau +1$ needed paths connecting s and nodes of $D=\{d_1, d_2, \ldots , d_{\tau +1}\}$ of $C_{\tau }$ are constructed above (refer to Fig. 8a–c). By the induction hypothesis and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, by the induction hypothesis, we can verify that $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{2\tau -5, (2\tau -5)+1, (2\tau -5)+1, \tau - 2 +1\} \le 2\tau -4 < 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Fig. 8

Illustrations for a $\beta = 1$, b $\beta > 1$ and $\alpha = 1$, and c $\beta > 1$ and $\alpha > 1$ of Case 3.2 in Lemma 9, respectively

Subcase 3.3. $\gamma \ge 1$ and $s' \in D$.

Without loss of generality, let $s' = d_{\tau +1}$ and $d_{j} = (d_{\alpha +j})^{\tau }$ for $j \in \{1,2,\ldots ,\gamma \}$. For any integer j with $\gamma + 1 \le j \le \alpha$ and $\alpha + \gamma + 1 \le j \le \tau$, let $d'_{j} = (d_{j})^{\tau }$. Denote

$$\begin{aligned} T = {\left\{ \begin{array}{ll} \{d_{1},d_{2}, \ldots ,d_{\alpha },s, s', d'_{\gamma + 1},d'_{\gamma + 2},\ldots ,d'_{\alpha }\} &{} \text {if} \ \gamma = \beta -1,\\ \{d_{1},d_{2}, \ldots ,d_{\alpha },s, s', d'_{\gamma + 1},d'_{\gamma + 2},\ldots ,d'_{\alpha }, d_{\alpha + \gamma + 1}, d_{\alpha + \gamma + 2},\ldots ,d_{\tau }, d'_{\alpha + \gamma + 1}, d'_{\alpha + \gamma + 2},\ldots ,d'_{\tau } \} &{} \text {if} \ \gamma < \beta -1. \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} k = {\left\{ \begin{array}{ll} \alpha - \gamma + 1 &{} \text {if} \ \gamma = \beta -1,\\ \alpha - \gamma + 1 + \tau - (\alpha + \gamma ) &{} \text {if} \ \gamma < \beta -1. \end{array}\right. } \end{aligned}$$

Since $\alpha + \beta = \tau +1$, $\beta \ge \gamma + 1$, and $\alpha \ge \gamma$, we have $\gamma \le \frac{\tau }{2} = \lceil \frac{\tau -1}{2}\rceil$ and

$$\begin{aligned} k = {\left\{ \begin{array}{ll} \tau + 1 - \beta - \gamma + 1 = \tau - 2 \gamma + 1 &{} \text {if} \ \gamma = \beta -1,\\ \alpha - \gamma + 1 + \tau - (\alpha + \gamma ) = \tau - 2 \gamma + 1 &{} \text {if} \ \gamma < \beta -1. \end{array}\right. } \end{aligned}$$

If $\gamma = 1$, by Lemma 8, there exists a path $S_{\alpha +1} =(d_{\alpha +1},x_{\alpha +1},d'_{\alpha +1})$ such that $(d_{\alpha +1},x_{\alpha +1}) \in E(C_{\tau -1}^{1-i})$, $d'_{\alpha +1} = (x_{\alpha +1})^\tau$, and $V(S_{\alpha +1}) \cap T = \emptyset$; If $\gamma > 1$, by Lemma 8, there exist $\gamma$ node-disjoint paths $S_{\alpha +1} =(d_{\alpha +1},x_{\alpha +1},d'_{\alpha +1})$, $S_{\alpha +2} =(d_{\alpha +2},x_{\alpha +2},d'_{\alpha +2})$, $\ldots$, $S_{\alpha +\gamma } =(d_{\alpha +\gamma },x_{\alpha +\gamma },d'_{\alpha +\gamma })$ such that $(d_j,x_{j}) \in E(C_{\tau -1}^{1-i})$, $d'_{j} = (x_{j})^\tau$, and $V(S_j) \cap T = \emptyset$ for $j \in \{\alpha +1,\alpha +2,\ldots ,\alpha +\gamma \}$.

Furthermore, let $D'' = \{d_{1},d_{2},\ldots ,d_{\alpha }, d'_{\alpha +1},d'_{\alpha +2},\ldots ,d'_{\tau }\}$. Hence, we can verify that $D'' \cap \{s\} = \emptyset$ and $|D''| = \tau$. By the induction hypothesis, there exist $\tau$ node-disjoint paths (except for s) $Q_1,Q_2,\ldots ,Q_{\tau }$ joining s and nodes of $D''$ in $C^{i}_{\tau -1}$ such that $d_k \in V(Q_k)$ for $1 \le k \le \alpha$ and $d'_k \in V(Q_k)$ for $\alpha +1 \le k \le \tau$, whose maximum length is limited by $2\tau -5$. For any integer $1 \le j \le \tau +1$, let

$$\begin{aligned} P_{j} = {\left\{ \begin{array}{ll} Q_j &{} \text {if} \ 1 \le j \le \alpha ,\\ ( Q_j, x_{j}, d_{j} ) &{} \text {if} \ \alpha +1 \le j \le \alpha +\gamma ,\\ ( Q_j, d_j ) &{} \text {if} \ \alpha +\gamma +1 \le j \le \tau \ \text {and} \ \gamma <\beta -1,\\ ( s, d_{\tau +1} ) &{} \text {if} \ j = \tau +1. \end{array}\right. } \end{aligned}$$

Accordingly, all the $\tau +1$ needed paths connecting s and nodes of $D=\{d_1, d_2, \ldots , d_{\tau +1}\}$ of $C_{\tau }$ are constructed above (refer to Fig. 9a, b). By the induction hypothesis, Lemma 8, and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, by the induction hypothesis, we can verify that $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{2\tau -5, (2\tau -5)+1+1,(2\tau -5)+1, 1\} \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Fig. 9

Illustrations for a $\gamma =\beta -1$ and b $\gamma <\beta -1$ of Case 3.3 in Lemma 9, respectively

Subcase 3.4. $\gamma \ge 2$ and $s' \notin D$.

Without loss of generality, let $d_{j} = (d_{\alpha +j})^{\tau }$ for $j \in \{1,2,\ldots ,\gamma \}$. For any integer j with $\gamma + 1 \le j \le \alpha$ and $\alpha + \gamma + 1 \le j \le \tau +1$, let $d'_{j} = (d_{j})^{\tau }$. Denote $\phi =\gamma -1$, $k = 2 + (\beta - \gamma )$, and

$$\begin{aligned} T = {\left\{ \begin{array}{ll} \{d_{1},d_{2}, \ldots ,d_{\alpha },s, s', d_{\tau +1}\} &{} \text {if} \ \gamma = \beta ,\\ \{d_{1},d_{2}, \ldots ,d_{\alpha },s, s', d_{\alpha + \gamma },d_{\alpha + \gamma + 1}, \ldots ,d_{\tau +1}, d'_{\alpha + \gamma + 1},d'_{\alpha + \gamma + 2}, \ldots ,d'_{\tau +1}\} &{} \text {if} \ \gamma < \beta . \end{array}\right. } \end{aligned}$$

Since $\alpha + \beta = \tau +1$, $\gamma \le \beta$, and $\alpha \ge \gamma$, we have

$$\begin{aligned} \begin{aligned} 1 \le \phi = \gamma - 1 \le \frac{\tau +1}{2} - 1 \le \lceil \frac{\tau -1}{2}\rceil \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} k = 2 + (\beta - \gamma ) = \tau +1 - (\alpha + \gamma ) + 2 \le \tau - 2 (\gamma - 1) + 1 = \tau - 2 \phi + 1. \end{aligned} \end{aligned}$$

If $\phi = 1$, by Lemma 8, there exists a path $Q'_{\alpha +1} =(d_{\alpha +1},x_{\alpha +1},d'_{\alpha +1})$ such that $(d_{\alpha +1},x_{\alpha +1}) \in E(C_{\tau -1}^{1-i})$, $d'_{\alpha +1} = (x_{\alpha +1})^\tau$, and $V(Q'_{\alpha +1}) \cap T = \emptyset$; If $\phi > 1$, by Lemma 8, there exist $\phi$ node-disjoint paths $Q'_{\alpha +1} =(d_{\alpha +1},x_{\alpha +1},d'_{\alpha +1})$, $Q'_{\alpha +2} =(d_{\alpha +2},x_{\alpha +2},d'_{\alpha +2})$, $\ldots$, $Q'_{\alpha +\phi } =(d_{\alpha +\phi },x_{\alpha +\phi },d'_{\alpha +\phi })$ such that $(d_j,x_{j}) \in E(C_{\tau -1}^{1-i})$, $d'_{j} = (x_{j})^\tau$, and $V(Q'_j) \cap T = \emptyset$ for $j \in \{\alpha +1,\alpha +2,\ldots ,\alpha +\phi \}$.

Let $\varphi = \tau - 2\phi - (\beta - \phi )$. Accordingly, we have

$$\begin{aligned} \begin{aligned} \varphi = \tau - 2\phi - (\beta - \phi ) = \alpha + \beta - 1 - \phi - \beta = \alpha - (\phi +1) = \alpha - \gamma \end{aligned} \end{aligned}$$

and thus we have $0 \le \varphi < \alpha$. If $\varphi \ge 0$, we have $\alpha = \gamma$. If $\varphi \ge 1$, choose $\varphi$ distinct nodes (resp. node) $x_1,x_2,\ldots ,x_\varphi$ in $C^{1-i}_{\tau -1}$ such that $\{x_1,x_2,\ldots ,x_\varphi \} \cap \{s',d_{\alpha +1}, d_{\alpha +2}, \ldots , d_{\tau +1}, x_{\alpha +1},x_{\alpha +2},\ldots ,x_{\alpha +\phi }\} = \emptyset$. Furthermore, let

$$\begin{aligned} D'' = {\left\{ \begin{array}{ll} \{d_{\alpha +1},d_{\alpha +2},\ldots ,d_{\tau +1},x_{\alpha +1},x_{\alpha +2},\ldots ,x_{\alpha +\phi }\} &{} \text {if} \ \varphi = 0,\\ \{d_{\alpha +1},d_{\alpha +2},\ldots ,d_{\tau +1},x_1,x_2,\ldots ,x_\varphi , x_{\alpha +1},x_{\alpha +2},\ldots ,x_{\alpha +\phi }\} &{} \text {if} \ \varphi \ge 1. \end{array}\right. } \end{aligned}$$

and $D''' = \{d_{1},d_{2},\ldots ,d_{\alpha }, d'_{\alpha +1},d'_{\alpha +2},\ldots ,d'_{\alpha +\phi },d'_{\alpha +\gamma +1},d'_{\alpha +\gamma +2},\ldots ,d'_{\tau +1}\}$. Hence, we can verify that $D'' \cap \{s'\} = \emptyset$, $D''' \cap \{s\} = \emptyset$, $|D'''| = \beta + \alpha - 1 = \tau$, and

$$\begin{aligned} |D''| = {\left\{ \begin{array}{ll} \beta + \phi = \beta + \alpha - 1 = \tau &{} \text {if} \ \varphi = 0,\\ \beta + \phi + \varphi = \beta + \gamma - 1 + \alpha - \gamma = \beta + \alpha - 1 = \tau &{} \text {if} \ \varphi \ge 1. \end{array}\right. } \end{aligned}$$

By the induction hypothesis, there exist $\tau$ node-disjoint paths (except for $s'$) $Q_2,Q_3,\ldots ,Q_{\tau +1}$ joining $s'$ and nodes of $D''$ in $C^{1-i}_{\tau -1}$ such that $d_k \in V(Q_k)$ for all $\alpha +1 \le k \le \tau +1$, $x_{k+\phi } \in V(Q_k)$ for all $\alpha -\phi +1 \le k \le \alpha$, and $x_{k-1} \in V(Q_k)$ for all $2 \le k \le \alpha -\phi$ if $\varphi \ge 1$, whose maximum length is limited by $2\tau -5$. Moreover, by the induction hypothesis, there exist $\tau$ node-disjoint paths (except for s) $S_1,S_2,\ldots ,S_{\alpha +\phi },S_{\alpha +\gamma +1},$ $S_{\alpha +\gamma +2},\ldots ,S_{\tau +1}$ joining s and nodes of $D'''$ in $C^{i}_{\tau -1}$ such that $d_k \in V(S_k)$ for $1 \le k \le \alpha$ and $d'_k \in V(S_k)$ for $\alpha +1 \le k \le \alpha + \phi$ and $\alpha +\gamma +1 \le k \le \tau +1$, whose maximum length is limited by $2\tau -5$. For any integer $1 \le j \le \tau +1$, let

$$\begin{aligned} P_{j} = {\left\{ \begin{array}{ll} S_j &{} \text {if} \ 1 \le j \le \alpha ,\\ ( S_j, x_{j}, d_{j} ) &{} \text {if} \ \alpha +1 \le j \le \alpha +\phi ,\\ ( s, Q_{j} ) &{} \text {if} \ j = \alpha +\gamma ,\\ ( S_j, d_j ) &{} \text {if} \ \alpha +\gamma +1 \le j \le \tau + 1. \end{array}\right. } \end{aligned}$$

Accordingly, all the $\tau +1$ needed paths connecting s and nodes of $D=\{d_1, d_2, \ldots , d_{\tau +1}\}$ of $C_{\tau }$ are constructed above (refer to Fig. 10a–d). By the induction hypothesis, Lemma 8, and Definition 1, we can verify that the $\tau$ paths $P_1,P_2,\ldots ,P_{\tau }$ are node-disjoint expect for s. In addition, by the induction hypothesis, we can verify that $V(P_{\tau +1}) \cap V(P_k) = \{s\}$ for all $1 \le k \le \tau$. Therefore, we state that $P_1, P_{2}, \ldots , P_{\tau +1}$ are node-disjoint expect for s. By Lemma 4, we have

$$\begin{aligned} \begin{aligned} |P_j| \le \text {max}\{2\tau -5, (2\tau -5)+1+1,(2\tau -5)+1, (2\tau -5)+1\} \le 2\tau -3 \end{aligned} \end{aligned}$$

for $j \in \{1,2,\ldots ,\tau +1\}$ with $\tau \ge 4$. From these discussions, $\tau +1$ paths $P_1,P_2,\ldots ,P_{\tau +1}$ joining s and nodes of D in $C_{\tau }$ are node-disjoint expect for s, which is consistent with our assumptions.

Fig. 10

Illustrations for a $\gamma = \beta$ and $\varphi = 0$, b $\gamma = \beta$ and $\varphi \ge 1$, c $\gamma \le \beta -1$ and $\varphi = 0$, and d $\gamma \le \beta -1$ and $\varphi \ge 1$ of Case 3.4 in Lemma 9, respectively

In summary, the lemma holds for $n = \tau$. $\square$

By Lemma 5 and 9, the following theorem holds.

Theorem 10

For any integer $n \ge 2$, choose an arbitrary source node s and an arbitrary node set $D=\{d_1, d_2, \ldots , d_{n+1}\}$ in a $C_{n}$ with $s \notin D$, there exist $n+1$ node-disjoint paths (except for s) from s to nodes of D, whose maximum length is limited by $2n-3$.

Fig. 11

Six node-disjoint paths from $s = 00000$ to nodes of $D = \{01001, 01010, 01111, 11001, 11010, 11111\}$ in $C_5$ are constructed according to Theorem 10

Consider two nodes $s = 00000$ and $D = \{01001, 01010, 01111, 11001, 11010, 11111\}$ in $C_5$. The construction of the six node-disjoint paths falls into Lemma 9. The following six paths (refer to Figure 11) are constructed according to Lemma 9, respectively.

• $P_1 = ( 00000, 00001, 01001 )$,

• $P_2 = ( 00000, 00010, 01010 )$,

• $P_3 = ( 00000, 01000, 01011, 01111 )$,

• $P_4 = ( 00000, 10000, 11000, 11001 )$,

• $P_5 = ( 00000, 00011, 00111, 00110, 01110, 11110, 11010 )$, and

• $P_6 = ( 00000, 00100, 01100, 11100, 11111 )$.

The maximum length of the six node-disjoint paths is computed as 6. Actually, Theorem 10 took with the worst-case consideration of the maximal length of $n+1$ node-disjoint paths between node s and nodes of D in $C_{n}$.

3.2 A Constructive Node-to-set Algorithm of Cross-cubes

In this subsection, we give an efficient algorithm, Algorithm N2SMain, to find $n+1$ node-to-set disjoint paths in $C_{n}$ if $n \ge 2$. Then, we analyze the time complexity of the Algorithm N2SMain.

Theorem 11

For any integer $n \ge 2$, given any arbitrary source node s and an arbitrary node set $D=\{d_1, d_2, \ldots , d_{n+1}\}$ in a $C_{n}$ with $s \notin D$, there exist an $O(N \text {log}^{2}N)$ algorithm for finding $n+1$ node-disjoint paths (except for s) from s to nodes of D of $C_n$, where N is the node number of $C_n$.

Proof

Considering node-to-set disjoint paths for the given node u and set D in $C_{n}$ with $s \notin D$, we propose an efficient algorithm, Algorithm N2SMain. To simplify the presentation of the proposed routing algorithm, we first introduce two algorithms, namely CProute and CSet, that will be the two core components of the proposed algorithm.

In order to compactly express the algorithm, we need some notations. We use a dictionary as a data structure that represents a collection of keys and values pair of data. Let T be a dictionary, we use $T = [\ ]$ to denote a empty dictionary which contains zero element. Then, let $a,b \in V(G)$ be two nodes of G, we use $T(a)=b$ to set b as a value of key a and T(a) to return the item of b with key a in T, respectively. Let S be a set with m elements, we use |S| to denote the number of elements in a set S such that $|S|=m$. Furthermore, we use S.add(a) to add element a to the set S, S.remove(a) to remove element a from the set S, and $S = \emptyset$ to denote a empty set with $|S| = 0$ , respectively. $\square$

We first study the Algorithm CProute. In line 3, it takes O(1) time to get the last node from the path $Q_i$ with $i \in \{1,2,\ldots ,n\}$. In lines 5 and 7, we assume, in our time analysis, that $(x)^n$ can be computed in constant time, which is the case when using the connection rule given in Definition 1. In line 7, it takes O(1) time to compute T[x]. In line 5, it takes constant time to construct $P_i$ by joining path $Q_i$ and node $(x)^n$. In line 7, it takes O(1) time to construct $P_i$ by joining path $Q_i$ and nodes $(x)^n$, T[x]. In line 12, it takes constant time to return n paths $\{P_1,P_2,\ldots ,P_{n}\}$. Accordingly, we can verify that the time complexity of function CProute1 in Algorithm CProute is O(n). In lines 16 and 23, it takes O(1) time to compute $V(Q_i)$. In lines 16 and 23, it takes O(n) time to compute $D \cap V(Q_i)$. In lines 17 and 24, it takes constant time to return a path $Q_i$ with $i \in \{1,2,\ldots ,n\}$. Thus, we can verify that the time complexity of function CProute2 and CProute3 in Algorithm CProute is $O(n^2)$.

In addition, we propose Algorithm CSet. In lines 4 and 6, we assume, in our time analysis, that $(x)^n$ and $N_{G}(u)$ can be computed in constant time, which is the case when using the connection rule given in Definition 1. In lines 2 and 6 of Algorithm CSet, it takes constant time to compute H (resp. S, T, H.add(x), S.add(v), T[v], and M.remove(v)). Accordingly, we can verify that the time complexity of function CSet1 in Algorithm CSet is $O(n^2)$. In line 18, it takes O(n) time to choose $\phi$ distinct nodes $x_1,x_2,\ldots ,x_{\phi }$ from a node set D. Thus, we can verify that the time complexity of function CSet2 in Algorithm CSet is O(n).

Accordingly, we propose our main algorithm, Algorithm N2SMain. Given a node s and a node set $D = \{d_1, d_2, \ldots , d_{n+1} \}$ in $C_{n}$ where $s \notin D$, we construct $n+1$ node-disjoint paths except for s in $C_{n}$ joining s and D. Suppose that a path in algorithm N2SMain is saved by a doubly linked circular list whose head u and tail v are pointed by two pointers. Furthermore, each node is stored by a tuple.

In what follows, we will analyze the time complexity of Algorithm N2SMain as follows. In lines $1\sim 3$ of Algorithm N2SMain, it takes constant time to construct the required node-disjoint paths. In lines $4 \sim 5$ of Algorithm N2SMain, it takes O(1) time to compute i (resp. $\alpha$, $\beta$, $\gamma$, and $s'$). In lines 9, 12, and 33 of Algorithm N2SMain, it takes O(n) time to construct the required path from u to v using the $\texttt {CRouting}(C_n,u,v)$ function in $C_n$ [20]. In lines 4, 11, 16, 19, 28, 35, 41, 45, and 49 of Algorithm N2SMain, it takes O(n) time to compute $D_1$ (resp. $D_2$, $D_3$, $D_4$, $\phi$, $D_5$, and $D'$).

We use U(s, D, n) to denote the time of finding $n+1$ node-to-set disjoint paths between s and D in $C_n$. Furthermore, we assume that n is sufficiently large. Let

$$\begin{aligned} \begin{aligned} T(n) = \text {max}\{U(s,D,n)|\{s\},D \subset V(C_n) \ \text {and} \ s \notin D \}. \end{aligned} \end{aligned}$$

(3.1)

Accordingly, we have $T(2) = O(1)$. We can claim the following discussions with respect to n for $n \ge 3$. In lines $7 \sim 13$, $16 \sim 17$, $25 \sim 30$, and $32 \sim 33$ of Algorithm N2SMain, we have

$$\begin{aligned} \begin{aligned} T(n) \le T(n-1) + O(n). \end{aligned} \end{aligned}$$

(3.2)

In lines $45\sim 47$ of Algorithm N2SMain, we have

$$\begin{aligned} \begin{aligned} T(n) \le T(n-1) + O(n^2). \end{aligned} \end{aligned}$$

(3.3)

In lines $19\sim 20$, $35\sim 42$, and $49 \sim 52$ of Algorithm N2SMain, we have

$$\begin{aligned} \begin{aligned} T(n) \le 2 T(n-1) + O(n^2). \end{aligned} \end{aligned}$$

(3.4)

Thus, based on Eqs. (3.1)$\sim$(3.4) and Definition 1, we have

$$\begin{aligned} \begin{aligned} T(n)&\le \text {max} \{2 T(n-1) + O(n^2),T(n-1) + O(n^2), T(n-1) + O(n) \}\\&\le \text {max} \{O(n^2 2^n ), O(n^3), O(n^2)\}\\&\le O(n^2 2^n)\\&= O(N \text {log}^{2}N). \end{aligned} \end{aligned}$$

(3.5)

where $N=2^n$. Therefore, according to Eq. (3.5), under the worst case, the time complexity of algorithm N2SMain is $T(n) \le O(N \text {log}^{2}N)$, where $n \le 2$ and $N=2^n$ is the node number of $C_n$.

3.3 Evaluation of algorithm N2SMain

In this subsection, we use simulations to evaluate the performance of Algorithm N2SMain. The Algorithm N2SMain was implemented by using the programming language Python under version 3.8.1 with libraries include Networkx, Matplotlib, NumPy, Cython, etc. The program was run on a Lenovo notebook computer with Intel 1.61GHz CPU, 16GB DRAM, and 512GB hard disk.

In our simulations, A set of $n+1$ destination nodes $D=\{d_1, d_2, \ldots , d_{n+1}\}$ are selected randomly. Then, a source node s randomly was selected with $s \notin D$. Furthermore, we applied Algorithm N2SMain and measured the execution time and the path length. The results were obtained by at least 10000 simulation runs.

Given a n-dimensional cross-cube, $C_{n}$, we use M(n) and D(n) to denote the maximal length of disjoint paths constructed by Algorithm N2SMain and diameter of $C_n$, respectively. In the following, a comparison of M(n) and D(n) is shown in Fig. 12. In the experiment, we can find that the maximal length of node-to-set disjoint paths gotten by our algorithm is much closer to the diameter of $C_{n}$.

Fig. 12

A comparison of M(n) and D(n) in $C_{n}$

4 Conclusions

Cross-cubes have been proposed as significant variations of hypercubes, which have higher fault-tolerant capability and smaller diameter than hypercubes at the same dimension. In this paper, we construct node-to-set disjoint paths of an n-dimensional cross-cube, $C_{n}$, whose maximum length is limited by $2n-3$. Furthermore, we propose an $O(N \text {log}^{2}N)$ algorithm for finding node-to-set disjoint paths of $C_{n}$, where N is the node number of $C_n$. Then, we give the simulation results of the maximal length of disjoint paths obtained by our algorithm. Last but not least, as approaching to the end of this paper, further research issues on the cross-cubes are suggested. Some of them are fairly intriguing and still open for cross-cubes, e.g., set-to-set disjoint paths [21, 22], disjoint path covers [23, 24], completely independent spanning trees [25], and fault-tolerant routing [26].