Paired many-to-many two-disjoint path cover of balanced hypercubes with faulty edges

Abstract

As a variant of the well-known hypercube, the balanced hypercube $BH_n$ was proposed as a desired interconnection network topology for parallel computing. It is known that $BH_n$ is bipartite. Assume that $S=\{s_1,s_2\}$ and $T=\{t_1,t_2\}$ are any two sets of vertices in different partite sets of $BH_n$ ($n\ge 1$). It has been proved that there exist two vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path of $BH_n$ covering all vertices of $BH_n$. In this paper, we prove that there always exist two vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path covering all vertices of $BH_n$ ($n\ge 2$) with at most $2n-3$ faulty edges. The upper bound $2n-3$ of edge faults can be tolerated is optimal.

1 Introduction

The interconnection network (network for short) plays a crucial role in massively parallel systems [21]. It is impossible to design a network which is optimum in all aspects of performance; accordingly, many networks have been proposed. Linear arrays and rings are two fundamental networks. Since some parallel applications such as those in image and signal processing are originally designated on an array architecture, it is important to have effective path embedding in a network [1,2,3,4, 6, 7, 33].

In path embedding problems, to find parallel paths among vertices in networks is one of the most central issues concerned with efficient data transmission [5, 21]. Parallel paths in networks are usually studied with regard to disjoint paths in graphs. Since algorithms designed on linear arrays or rings can be efficiently simulated in a topology containing Hamiltonian paths or cycles, Hamiltonian path and cycle embedding property of graphs has been widely studied [9,10,11, 14,15,16, 31, 35, 36].

In disjoint path cover problems, the many-to-many disjoint path cover problem is the most generalized one [28]. Assume that $S=\{s_1, s_2,\ldots , s_k\}$ and $T=\{t_1, t_2,\ldots , t_k\}$ are two sets of k sources and k sinks in a graph G, respectively; the paired many-to-many k-disjoint path cover (paired k-DPC for short) problem is to determine whether there exist k-disjoint paths $P_1,P_2,\ldots ,P_k$ in G such that $P_i$ joins $s_i$ to $t_i$ for each $i\in \{1,2,\ldots ,k\}$ and $V(P_1)\cup \cdots \cup V(P_k)=V(G)$. Moreover, the DPC problem has a close relationship with Hamiltonian path problem in graphs. In fact, a 1-DPC of a network is indeed a Hamiltonian path between any two vertices.

Failure is inevitable when a massive system is put in use, so it is of great practical importance to consider the fault-tolerant capacity of a network. Hamiltonicity and k-DPC problems of various networks with faulty elements were investigated in the literature, for example, k-ary n-cubes [11, 32], recursive circulants [20, 30], hypercubes [19, 29, 31] and hypercube-like graphs [13, 27].

The balanced hypercube, proposed by Wu and Huang [34], is one of the most popular networks. It has many excellent topological properties, such as high symmetry, low-latency, regularity, strong connectivity. The special property of the balanced hypercube is that each processor has a backup processor that shares the same neighborhood. Thus, tasks running on a faulty processor can be shifted to its backup one [34]. With such novel properties above, different aspects of the balanced hypercube were studied extensively, including Hamiltonian embedding issues [17, 22, 24, 35, 37, 40], connectivity issues [25, 39], matching preclusion and extendability [23, 26], and symmetric properties [41, 42] and some other topics [18, 38]. Recently, Cheng el al. [12] have proved that the balanced hypercube $BH_n$ with $n\ge 1$ has a paired 2-DPC, which is a generalization of Hamiltonian laceability of the balanced hypercube [35]. To the best of our knowledge, there is no literature on k-DPC in the balanced hypercube when $k\ge 3$. In this paper, we will consider the problem of paired 2-DPC of the balanced hypercube with faulty edges.

The rest of this paper is organized as follows. In Sect. 2, some definitions and lemmas are presented. The main result of this paper is shown in Sect. 3. Conclusions are given in Sect. 4.

2 Preliminaries and some lemmas

Throughout this paper, a network is represented by a simple undirected graph, where vertices represent processors and edges represent links between processors. Let $G=(V(G),E(G))$ be a graph, where V(G) and E(G) are its vertex set and edge set, respectively. The number of vertices of G is denoted by |V(G)|. The set of vertices adjacent to a vertex v is called the neighborhood of v, denoted by $N_G(v)$. We will use N(v) to replace $N_G(v)$ when the context is clear. A path P in G is a sequence of distinct vertices so that there is an edge joining each pair of consecutive vertices, and the length of P is the number of edges, denoted by l(P). For simplicity, a path $P=\langle x_0,x_1,\ldots , x_k\rangle$ can also be denoted by $\langle x_0,P,x_k\rangle$. A u, v-path is a path whose end vertices are u and v. If a path $C=\langle x_0,x_1,\ldots , x_k\rangle$ is such that $k\ge 3$, $x_0=x_k$, then C is said to be a cycle, and the length of C is the number of edges. The distance between two vertices u and v, denoted by d(u, v), is the length of a shortest path of G joining u and v. A path (resp. cycle) containing all vertices of a graph G is called a Hamiltonian path (resp. cycle). A bipartite graph G is bipanconnected if, for two arbitrary vertices u and v of G with distance d(u, v), there exists a path of length l between u and v for every integer l with $d(u,v)\le l\le |V(G)|-1$ and $l\equiv d(u,v)($mod 2). For other standard graph notations not defined here, please refer to [8].

The definitions of the balanced hypercube are given as follows.

Definition 1

[34] An n-dimension balanced hypercube $BH_{n}$ contains $4^{n}$ vertices $(a_{0},$$\ldots ,a_{i-1},$$a_{i},a_{i+1},\ldots ,a_{n-1})$, where $a_{i}\in \{0,1,2,3\},$$0\le i\le n-1$. Any vertex $v=(a_{0},\ldots ,a_{i-1},$$a_{i},a_{i+1},\ldots ,a_{n-1})$ in $BH_{n}$ has the following 2n neighbors:

• (1) $((a_{0}+1)$ mod $4,a_{1},\ldots ,a_{i-1},a_{i},a_{i+1},\ldots ,a_{n-1})$,

  $((a_{0}-1)$ mod $4,a_{1},\ldots ,a_{i-1},a_{i},a_{i+1},\ldots ,a_{n-1})$, and

• (2) $((a_{0}+1)$ mod $4,a_{1},\ldots ,a_{i-1},(a_{i}+(-1)^{a_{0}})$ mod $4,a_{i+1},\ldots ,a_{n-1})$,

  $((a_{0}-1)$ mod $4,a_{1},\ldots ,a_{i-1},(a_{i}+(-1)^{a_{0}})$ mod $4,a_{i+1},\ldots ,a_{n-1})$.

The first coordinate $a_{0}$ of the vertex $(a_{0},\ldots ,a_{i},\ldots ,a_{n-1})$ in $BH_{n}$ is defined as the inner index, and other coordinates $a_{i}$$(1\le i\le n-1)$ are outer indices.

The recursive structure of the balanced hypercube is presented as follows.

Definition 2

[34]

• (1) $BH_{1}$ is a 4-cycle, whose vertices are labeled by 0, 1, 2, 3 clockwise.

• (2) $BH_{k+1}$ is constructed from 4 $BH_{k}$s, which are labeled by $BH^{0}_{k}$, $BH^{1}_{k}$, $BH^{2}_{k}$, $BH^{3}_{k}$. For any vertex in $BH_{k}^{i}(0\le i\le 3)$, its new labeling in $BH_{k+1}$ is $(a_{0},a_{1},\ldots ,a_{k-1},i)$, and it has two new neighbors:

  • (a) $BH^{i+1}_{k}{:}\,((a_{0}+1)$ mod $4,a_{1},\ldots ,a_{k-1},(i+1)$ mod 4) and

    $((a_{0}-1)$ mod $4,a_{1},\ldots ,a_{k-1},(i+1)$ mod 4) if $a_{0}$ is even.

  • (b) $BH^{i-1}_{k}{:}\,((a_{0}+1)$ mod $4,a_{1},\ldots ,a_{k-1},(i-1)$ mod 4) and

    $((a_{0}-1)$ mod $4,a_{1},\ldots ,a_{k-1},(i-1)$ mod 4) if $a_{0}$ is odd.

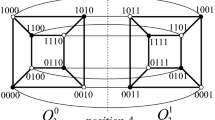
$BH_{1}$ is shown in Fig. 1a. One layout of $BH_{2}$ is shown in Fig. 1b, and the other one is shown in Fig. 1c, which reveals a ring-like structure of $BH_2$. Obviously, $BH_{2}$ can be also regarded as identifying diagonal vertices of eight twisted 4-cycles end-to-end.

The following basic properties of the balanced hypercube will be applied in the main result of this paper.

Lemma 1

[34] $BH_{n}$isbipartite.

By the above lemma, we give a bipartition $V_0$ and $V_1$ of $BH_{n}$, where $V_0=\{(a_0,\ldots ,a_{n-1})|(a_0,\ldots ,a_{n-1})\in V(BH_n)$ and $a_0$ is even$\}$ and $V_1=\{(b_0,\ldots ,b_{n-1})|$$(b_0,\ldots ,b_{n-1})\in V(BH_n)$ and $b_0$ is odd$\}$.

Lemma 2

[34, 40] $BH_{n}$ is vertex-transitive and edge-transitive.

Lemma 3

[34] Vertices $u=(a_{0},a_{1},\ldots ,a_{n-1})$and$v=((a_{0}+2)$ mod 4,$a_{1},\ldots ,a_{n-1})$in$BH_{n}$ have the same neighborhood.

Fig. 1

$BH_{1}$ and $BH_{2}$

For convenience, let p(u) be the vertex having the same neighborhood of u. It is obvious that u and p(u) differ only from the inner index.

Assume that u is a neighbor of v in $BH_n$. If u and v differ only from the inner index, then uv is called a 0-dimension edge, and u and v are mutually called 0-dimension neighbors. Similarly, if u and v differ from the j-th outer index ($1\le j\le n-1$), uv is called a j-dimension edge, and u and v are mutually called j-dimension neighbors. The set of all k-dimension edges of $BH_n$ is denoted by $E_k$ for each $k\in \{0,\ldots ,n-1\}$, and the subgraph of $BH_{n}$ obtained by deleting $E_{n-1}$ is written by $B^{i}$, where $0\le i \le 3$. Obviously, each of $B^{i}$ is isomorphic to $BH_{n-1}$. Let $u_i,v_i,w_i\in V_0$ (resp. $a_i,b_i,c_i\in V_1$) be vertices in $B^i$. For convenience, let $E_{i,i+1}$ be the edge set containing all edges between $B^{i}$ and $B^{i+1}$ ($0\le i\le 3$), where “+” is under modulo four. For any vertex v of $BH_n$, let e(v) be the set of edges incident to v. In particular, the two k-dimension edges incident to v is denoted by $e_k(v)$, where $0\le k\le n-1$. Let F be a set of edges in $BH_n$, we denote $F^i=F\cap E(B^i)$.

We will give some lemmas in the following, which will be used later.

Lemma 4

[38] Letubean arbitrary vertex of$BH_n$for$n\ge 1$. Then, for an arbitrary vertexvof$BH_n$, either u andvhave 0, 2, or 2ncommon neighbors. Furthermore, there is exactly one vertexwsuch thatuandwhave 2ncommon neighbors.

Lemma 5

[37] The balanced hypercube$BH_{n}$ is bipanconnected for all$n\ge 1$.

Lemma 6

[39] Assume that$n\ge 2$. There exist$4^{n-1}$edges between$B^i$and$B^{i+1}$for each$0\le i\le 3$.

Lemma 7

[35] Let uvbe an edge of$BH_{n}$. Thenuvis contained in a cycleC of length 8 in$BH_{n}$such that$|E(C)\cap E(B^i)|=1$for each$i=0,1,2,3$.

Lemma 8

[12] Let$u,x\in V_{0}$ and$v,y\in V_{1}$. Then there exist two vertex-disjoint paths P andQ such that: (1) Pconnects u to v, (2) Qconnectsx to y, (3) $V(P)\cup V(Q)=V(BH_{n})$.

Lemma 9

[40] Let F be a set of faulty edges of $BH_n$with$|F|\le 2n-2$for$n\ge 2$and letxandybe two vertices in different partite sets of$BH_n$. Then there exists a Hamiltonian path of$BH_n-F$ from x toy.

3 Paired two-disjoint path cover of faulty balanced hypercube

Because of the recursive structure of the balanced hypercube, induction is used to prove the main result. Before we present the main result, we need several lemmas. We start with the following useful definition, which we will apply later.

Let P and Q be two 2-paths with central vertices u and v, respectively. A tenon chain$T_m(u;\,v)$ from u to v is defined to be an m ($m\ge 1$) twisted 4-cycle chain with P and Q joining to its two ends, respectively. Additionally, let $P'$ and $Q'$ be two 2-paths with central vertices x and y, respectively. $P'$ and $Q'$ are joined to two ends of $T_m(u;\,v)$ the same way as P and Q do, we denote the graph obtained above by $T_m(u,x;\,v,y)$. In other words, $T_m(u,x;\,v,y)$ is an $m+2$ ($m\ge 1$) twisted 4-cycles chain with u and x being degree 2 vertices at one end and v and y being degree 2 vertices at the other end. By above, if $1\le m\le 6$, $T_m(u;\,v)$ and $T_m(u,x;\,v,y)$ are both subgraphs of $BH_2$. For convenience, we refer $T_m(u;\,v)$ and $T_m(u,x;\,v,y)$ ($1\le m\le 6$) to the subgraph of $BH_2$ (ring-like layout) from u to v clockwise. $T_3((1,0), (0,1))$ and $T_3((1,0),(3,0);\,(0,1),(2,1))$ are illustrated as heavy lines in Fig. 2a, b, respectively. Note that if u and v are in different partite sets of $BH_2$ then m is odd, otherwise, m is even.

Fig. 2

T((1, 0); (0, 1)) and T((1, 0), (3, 0); (0, 1), (3, 1))

To verify the base case of the main result, we present the following two lemmas.

Lemma 10

Given$T_m(x,y)$with mbeing odd. Iffis an arbitrary edge of $T_m(x,y)$, then there exists a Hamiltonian path of$T_m(x,y)-f$fromxtoy.

Proof

Since m is odd, x and y are in different partite sets. Either f is an edge incident to x or y, or f is an edge of any twisted 4-cycle, it is easy to obtain a Hamiltonian path of $T_m(x,y)$ from x to y avoiding f. The lemma holds. $\square$

It follows from Lemma 10 that there exists a Hamiltonian path of $T_m(x,y)$ from x to y when at most one edge fault occurs, so we also use $T_m(x,y)$ to denote a fault-free Hamiltonian path of $T_m(x,y)$ from x to y when there is no ambiguity.

Lemma 11

Given$T_m(u,x;\,v,y)$withmbeing odd. Leteandfbe two edges of$T_m(u,x;\,v,y)$such thateandfare not contained in the same twisted 4-cycle. Then there exist vertex-disjointu, v-path andx, y-path of$T_m(u,x;\,v,y)-\{e,f\}$ that cover all vertices of it.

Proof

Since m is odd, u and x are in one partite set, and v and y are in the other partite set of $T_m(u,x;\,v,y)$. To obtain the desired u, v-path and x, y-path, one has to go through all twisted 4-cycles of $T_m(u,x;\,v,y)$ and never go back. Accordingly, u, v-path and x, y-path contain the same number of vertices. Fault-free u, v-path and x, y-path of $T_m(u,x;\,v,y)-\{e,f\}$ can be constructed according to the following two rules:

• (1) If e (or f) is incident to one of u, x, v and y, say u, we then choose the other edge incident to u in u, v-path.

• (2) If $e=ab$ (or $f=ab$) is contained in a twisted 4-cycle $C=\langle a,b,c,d,a\rangle$, then ad (resp. bc) must be contained in exact one of u, v-path and x, y-path.

Hence, the lemma holds. $\square$

Based on the above two lemmas, the base case of the main result is presented as follows.

Lemma 12

Let$\{s_1,s_2\}$and$\{t_1,t_2\}$be two sets of vertices in different partite sets of$BH_{2}$ and let$F=\{e,f\}$ be an edge subset of$BH_2$ with$e\in E_0$and$f\in E_1$. Then there exist vertex-disjoint$s_1,t_1$-path and$s_2,t_2$-path of$BH_{2}-F$that cover all vertices of it unless there exists a common neighbor of$s_1$ and$s_2$ (or$t_1$and$t_2$), sayx, such that$F=e(x){\setminus} \{s_1x,s_2x\}$ (or$F=e(x){\setminus} \{t_1x,t_2x\}$).

Proof

Suppose without loss of generality that x is a common neighbor of $s_1$ and $s_2$, if $F=e(x){\setminus} \{s_1x,s_2x\}$, that is, $\{s_1x,s_2x\}\cap F=\emptyset$, which yields a 2-path starting from $s_1$ to $s_2$. Accordingly, it is impossible to obtain vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path that cover all vertices of $BH_2$. If $d(s_1,s_2)=2$, $F\ne e(x){\setminus} \{s_1x,s_2x\}$ is a necessary condition to guarantee that there exist vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path that cover all vertices of $BH_{2}-F$.

On the other hand, noting $e\in E_0$ and $f\in E_1$, each twisted 4-cycle of $BH_{2}$ (ring-like layout) contains at most one of e and f. By vertex-transitivity of $BH_2$, we may assume that $s_1=(0,0)$. According to all possible relative positions of $s_1,s_2,t_1$ and $t_2$ in $BH_2$, there are 15 essentially different distributions to be considered. In each case, we have verified that there always exist vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path of $BH_{2}-F$ that cover all vertices of $BH_{2}$ (by making use of Lemmas 10 and 11 to reduce the number of cases to be considered). Since the proof is tedious and rather long, we only list all different distributions of $s_1,s_2,t_1$ and $t_2$ in $BH_2$ as follows.

• (1) $s_2=(2,0), t_1=(1,0), t_2=(3,0)$;

• (2) $s_2=(2,0), t_1=(1,0), t_2=(3,3)$;

• (3) $s_2=(2,0), t_1=(1,0), t_2=(3,2)$;

• (4) $s_2=(2,0), t_1=(1,0), t_2=(3,1)$;

• (5) $s_2=(2,3), t_1=(1,0), t_2=(3,3)$;

• (6) $s_2=(2,3), t_1=(1,0), t_2=(3,2)$;

• (7) $s_2=(2,3), t_1=(1,0), t_2=(3,1)$;

• (8) $s_2=(2,2), t_1=(1,0), t_2=(3,3)$;

• (9) $s_2=(2,2), t_1=(1,0), t_2=(3,2)$;

• (10) $s_2=(2,1), t_1=(1,0), t_2=(3,3)$;

• (11) $s_2=(2,0), t_1=(1,3), t_2=(3,3)$;

• (12) $s_2=(2,0), t_1=(1,3), t_2=(3,2)$;

• (13) $s_2=(2,3), t_1=(1,3), t_2=(3,2)$;

• (14) $s_2=(2,3), t_1=(1,3), t_2=(3,1)$;

• (15) $s_2=(2,2), t_1=(1,3), t_2=(3,1)$.

$\square$

The following corollary is straightforward.

Corollary 13

Let$\{s_1,s_2\}$and$\{t_1,t_2\}$be any two sets of vertices in different partite sets of$BH_{2}$and letebe any edge of$BH_2$. Then there exist vertex-disjoint$s_1,t_1$-path and$s_2,t_2$-path of$BH_{2}-e$that cover all vertices of it.

Remark

Our aim is to guarantee that there exists a dimension $d\in \{0,1,2\}$ such that by dividing $BH_3$ into $B^i$ along dimension d we can use Lemma 12 and Corollary 13 as the induction basis of the main result. Let $F=\{f_0,f_1,f_2\}$ be a set of edges of $BH_3$ and let $\{s_1,s_2\}$ and $\{t_1,t_2\}$ be any two sets of vertices in different partite sets of $BH_{3}$. If there exists a dimension $d\in \{0,1,2\}$ such that $|E_d\cap F|\ge 2$, then $BH_3$ can be divided into $B^i$ ($0\le i\le 3$) along dimension d such that $|E(B^i)\cap F|\le 1$ for each $i\in \{0,1,2,3\}$. So we assume that $E_j\cap F=\{f_j\}$ for each $j=0,1,2$. By Lemma 4, $s_1$ and $s_2$ (or $t_1$ and $t_2$) have 0, 2 or 2n common neighbors.

If $s_1$ and $s_2$ (or $t_1$ and $t_2$) have no common neighbors, then we can safely divide $BH_3$ into $B^i$ ($0\le i\le 3$) along any dimension $d\in \{0,1,2\}$.

If $s_1$ and $s_2$ (or $t_1$ and $t_2$) have at least two common neighbors, we may assume that x is one of the common neighbors of $s_1$ and $s_2$. If we divide $BH_3$ into $B^i$ ($0\le i\le 3$) along some dimension $d\in \{0,1,2\}$ such that $s_1$, $s_2$, $t_1$ and $t_2$ are in the same $B^i$, say $B^0$, and $F=F'$, where $F'$ is the set of edges incident to x in $B^0$ (except $s_1x$ and $s_2x$). Furthermore, if $s_1$ and $s_2$ (or $t_1$ and $t_2$) have exact 2 common neighbors, then $s_1x$ and $s_2x$ are edges of different dimensions, then we can choose a dimension $d'\in \{0,1,2\}{\setminus} \{d\}$ such that by dividing $BH_3$ into $B^i$ ($0\le i\le 3$) along dimension $d'$, $s_1$ and $s_2$ (or $t_1$ and $t_2$) are not in the same $B^i$. Thus, the condition of Lemma 12 is satisfied. If $s_1$ and $s_2$ have 6 common neighbors, then $s_1x$ and $s_2x$ are edges of the same dimension, so we can divide $BH_3$ into $B^i$ ($0\le i\le 3$) along the dimension of the edges in $F'$. Thus, the condition of Lemma 12 is also satisfied. $\square$

We need three more technical results regarding the proof of some special cases of the main result.

Lemma 14

LetFbe a set of edges of$BH_n$ ($n\ge 3$) with$|F|=2n-3$. Given a dimensionkof$BH_n$such that$|E_k\cap F|=\max \{|E_j\cap F||0\le j\le n-1\}$. Let$B^i$, $0\le i\le 3$, be subgraphs of$BH_n$obtained by splitting$BH_n$along dimensionk. Then there exists four vertices$a,c\in V_0$ and$b,d\in V_1$ of$B^i$such that:

• (1) $a=p(c)$, $b=p(d)$, and a, b, canddform a 4-cycle in$B^i$;

• (2) there exists ak-dimension neighbor$a_{i+1}$of a and csuch that$e_k(a_{i+1})\cap F=\emptyset$;

• (3) there exist twok-dimension neighbors$u_{i-1}$ and$v_{i-1}$of b and dsuch that$e_k(b)\cap F=\emptyset , |e_k(d)\cap F|<2$and$cd\not \in F$;

• (4) there exists a neighboru ($u\ne a,c$) of b andd in$B^i$such that$|e_{j_1}(u)\cap F|<2$for each$j_1\in \{0,1,\ldots ,n-1\}$;

• (5) there exists a longest pathP from utoacovering all vertices of$B^i-F$ butb, candd.

Proof

We proceed the proof by induction on n. By the choice of k, we have $|E_k\cap F|=1$ or $|E_k\cap F|\ge 2$ when $n=3$. It is easy to verify that conditions (1)–(5) hold after splitting $BH_3$ by dimension k. Thus, the induction basis holds. So we assume that the lemma is true for all integers m with $3\le m\le n-1$. Next we consider $BH_n$.

Note that $|E_k\cap F|\ge 2$ whenever $n\ge 4$, suppose without loss of generality that $i=3$ and $k=n-1$. Since $|E_{n-1}\cap F|\ge 2$, $|F\cap E(B^i)|\le 2n-5$, $0\le i\le 3$. For each pair of vertices $u_0,u_0'\in V_0$ with $u_0=p(u_0')$ in $B^0$, there exist $2n-2$ common neighbors of them in $B^0$. Let $a_0$ and $a_0'$ be any two neighbors of $u_0$ and $u_0'$ with $a_0=p(a_0')$ in $B^0$. In addition, let $u_3$ and $u_3'$ be two ($n-1$)-dimension neighbors of $a_0$ and $a_0'$ and let $a_3,a_3'$ be two $k_1$-dimension neighbors of $u_3$ and $u_3'$ in $B^3$ for a given $k_1\in \{0,1,\ldots ,n-2\}$. Accordingly, let $u_2$ and $u_2'$ be two ($n-1$)-dimension neighbors of $a_3$ and $a_3'$ and let $a_2$ and $a_2'$ be two $k_1$-dimension neighbors of $u_2$ and $u_2'$ in $B^2$. Thus, the subgraph induced by $\{a_0,a_0',u_3,u_3',a_3,a_3',u_2,u_2',a_2,a_2'\}$ is a twisted 4-cycle chain. If there exist at least two edges of F in one of $\langle a_0',u_3,a_0,u_3',a_0'\rangle$, $\langle a_3',u_2,a_3,u_2',a_3'\rangle$ and $\langle a_2',u_2,a_2,u_2',a_2'\rangle$, then it may eliminate the choice of $a_3,a_3',u_3$ and $u_3'$ as a, b, c and d to satisfy conditions (1), (2) and (3) (see Fig. 3). By arbitrary choice of $a_0$ and $a_0'$, if there exist no such a, b, c and d satisfying conditions (1), (2) and (3) for given $u_0$ and $u_0'$, we have $|F|=2\times (n-1)=2n-2>2n-3$, a contradiction.

Fig. 3

Existence of a, b, c and d satisfying required conditions in Lemma 14

On the other hand, b and d have $2n-4$ common neighbors (except a and c) in $B^3$. Since $2\times (2n-4)>2n-3$ whenever $n\ge 4$, there must exist a common neighbor u of b and d satisfying condition (4). It remains to show that condition (5) holds.

By our assumption, $u,a,b,c,d\in V(B^3)$. Note that we have $|E(B^3)\cap F|\le 2n-5$, our aim is to show that there exists a longest path P from u to a covering all vertices of $B^3-F$ but b, c and d. Let $k_2\in \{0,1,\ldots ,n-2\}$ such that $|E_{k_2}\cap E(B^3)\cap F|\ge |E_{j}\cap E(B^3)\cap F|$ for each $j\in \{0,1,\ldots ,n-2\}{\setminus} \{k_2\}$. We further divide each $B^i$ into $B_{n-2}^{i_1,i}$, $0\le i_1\le 3$, along dimension $k_2$. That is, $B_{n-2}^{i_1,i}\cong BH_{n-2}$ for each $i_1$ and i. Assume without loss of generality that $a,b,c,d\in V(B_{n-2}^{0,3})$. By Definition 1, the graph induced by $V(B_{n-2}^{0,0})$, $V(B_{n-2}^{0,1})$, $V(B_{n-2}^{0,2})$ and $V(B_{n-2}^{0,3})$ is isomorphic to $BH_{n-1}$, for convenience, we denote it by H. Since u is a neighbor of b and d in $B^3$, we assume without loss of generality that $u\in V(B_{n-2}^{0,3})$.

Fig. 4

Longest path from u to a covering all vertices of $B^3-F$ but b, c and d

By induction hypothesis, there exists a longest path $P_0$ from u to a covering all vertices of $B_{n-2}^{0,3}-F$ but b, c and d. Since $l(P_0)=4^{n-2}-4$ and $(4^{n-2}-4)/2>2n-5$ whenever $n\ge 4$ (any vertex v on $P_0$ with $|e_{k_2}(v)\cap F|=2$ will eliminate the choice of two edges incident to v on $P_0$), we can choose an edge $u_0a_0\in E(P_0)$ such that there exist two edges $u_0a_1,u_3a_0\not \in F$, where $a_1\in V(B_{n-2}^{1,3})$ and $u_3\in V(B_{n-2}^{3,3})$. Deleting $u_0a_0$ from $P_0$ will generate two vertex-disjoint paths $P_{01}$ and $P_{02}$, where $P_{01}$ connects u to $a_0$ and $P_{02}$ connects $u_0$ to a. Let $u_1a_2$ and $u_2a_3$ be two fault-free $k_2$-dimension edges. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B_{n-2}^{1,3}$ from $u_1$ to $a_1$, a fault-free Hamiltonian path $P_2$ of $B_{n-2}^{2,3}$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B_{n-2}^{3,3}$ from $u_3$ to $a_3$. Hence, $\langle u,P_{01},a_0,u_3,P_3,a_3,u_2,P_2,a_2,u_1,P_1,a_1,u_0,P_{02},a\rangle$ is the path required (see Fig. 4).

This completes the proof. $\square$

Lemma 15

Let$F=\{e,f\}$be any two edges of$BH_2$with$e\in E_0$and$f\in E_1$. In addition, let$t_1,t_2\in V_1$be two arbitrary vertices. Then there exist two pairs of vertices in$V_0$differing only from the inner index, respectively, suppose without loss of generality thataandcis such a pair with$a=p(c)$, such that: (1) there exists a vertex$u\in V_0$of$BH_2$with$u\ne a,c$; (2) there exist two vertex-disjoint pathsP andQ of$BH_2-F$covering all vertices of it, wherePconnectsuto$t_2$, andQconnectscto$t_1$and$\langle c,b,a\rangle$is a subpath ofQ.

Proof

By vertex-transitivity of $BH_2$, we may assume that $t_1=(1,0)$. Since $e\in E_0$ and $f\in E_1$, e and f lie in different twisted 4-cycles of $BH_2$. Our aim is to find two pairs of vertices differing only from inner index, respectively, and satisfying conditions (1) and (2). There are three essentially different positions of $t_2$.

Case 1.$t_2=(3,0)$. We further deal with the following cases.

Case 1.1.e and f lie in consecutive twisted 4-cycles.

Case 1.1.1.e and f are nonadjacent. We may assume that $e=(0,0)(1,0)$ and $f=(2,0)(3,1)$. If $a=(2,0)$, $c=(0,0)$ and $u=(2,1)$, then $P^{-1}=\langle T_3((3,0);(0,1)),(3,1),(2,1)\rangle$ and $Q=\langle (0,0),(1,1),(2,0),(1,0)\rangle$ are the paths required.

If $a=(0,1)$, $c=(2,1)$ and $u=(2,2)$, then $P=\langle$(2, 2), (3, 2), (0, 2), (1, 3), (0, 3), (3, 3), (2, 3), (3, 0)$\rangle$ and $Q=\langle (2,1),(1,2),(0,1),(3,1)$, $(0,0),(1,1),(2,0),(1,0)\rangle$ are the paths required.

Case 1.1.2.e and f are adjacent. There are two relative positions of e and f, and we further deal with the following cases.

Case 1.1.2.1.$e=(0,0)(1,0)$ and $f=(0,0)(1,1)$. We can choose $a=(0,3)$, $c=(2,3)$ and $u=(0,2)$, or $a=(0,2)$, $c=(2,2)$ and $u=(0,1)$. The proof is similar to that of Case 1.1.1.

Case 1.1.2.2.$e=(0,0)(1,1)$ and $f=(1,1)(0,1)$. If $a=(2,1)$, $c=(0,1)$ and $u=(2,2)$, then $P=\langle$(2, 2), (3, 2), (0, 2), (1, 3), (0, 3), (3, 3), (2, 3), (3, 0)$\rangle$ and $Q=\langle (0,1),(1,2),(2,1),(1,1)$, $(2,0),(3,1),(0,0),(1,0)\rangle$ are the paths required.

If $a=(0,2)$, $c=(2,2)$ and $u=(2,3)$, then $P=\langle (2,3),(1,3),(0,3),(3,0)\rangle$ and $Q=\langle (2,2),(3,3),(0,2),(1,2)$, $(0,1),(3,2),(2,1),(1,1),(2,0),(3,1),(0,0),(1,0)\rangle$ are the paths required.

Case 1.2.e and f lie in inconsecutive twisted 4-cycles. Obviously, $BH_2$ can be decomposed into four edge-disjoint 4-cycles according to ring-like layout. By Lemma 11, each pair of vertices in $V_0$ differing only from the inner index can be chosen as a and c such that there exist two vertex-disjoint paths P and Q of $BH_2-F$ covering all vertices of it, where P connects u to $t_2$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q.

Case 2.$t_2=(3,3)$. We further deal with the following cases.

Case 2.1.$|F\cap T_0(t_1,(3,0);(1,3),t_2)|=2$. By Lemma 11, there exist two vertex-disjoint 2-paths $P_1$ and $Q_1$ covering all vertices of $T_0(t_1,(3,0);(1,3),t_2)$, where $P_1$ connects (3,0) to $t_2$ and $Q_1$ connects (1,3) to $t_1$. There are two pairs of vertices can be chosen as a and c: (1) $a=(0,2)$ and $c=(2,2)$; (2) $a=(0,1)$ and $c=(2,1)$.

If $a=(0,2)$ and $c=(2,2)$, let $u=(2,1)$, then $P=\langle (2,1),(1,2),(0,1),(3,1)$, $(0,0),(1,1),(2,0),(3,0),P_1,(3,3)\rangle$ and $Q=\langle (2,2),(3,2),(0,2),(1,3),Q_1,(1,0)\rangle$ are the paths required.

If $a=(0,1)$ and $c=(2,1)$, let $u=(2,0)$, then $P=\langle (2,0),(3,1)$, $(0,0),(3,0),P_1$, (3,3)$\rangle$ and $Q=\langle (2,1),(1,1),(0,1),(1,2),(0,2),(3,2),(2,2),(1,3)$, $Q_1,(1,0)\rangle$ are the paths required.

Case 2.2.$|F\cap T_0(t_1,(3,0);(1,3),t_2)|=1$ or $|F\cap T_0(t_1,(3,0);(1,3),t_2)|=0$. The proof is similar to that of Case 2.1, we omit it.

Case 3.$t_2=(3,2)$. The proof is similar to that of Case 2, we omit it. $\square$

Lemma 16

LetFbe a set of edges of$BH_n$with$|F|=2n-3$ ($n\ge 3$). Given a dimensionkof$BH_n$such that$|E_k\cap F|\ge |E_j\cap F|$for each$j\in \{0,1,\ldots ,n-1\}{\setminus} \{k\}$. Let$B^i$, $0\le i\le 3$, be subgraphs of$BH_n$obtained by splitting$BH_n$along dimensionk. In addition, let$t_1,t_2\in V_1$be two arbitrary vertices in$B^i$such that$t_1\ne t_2$. Then, there exist four vertices$u,a,c\in V_0$and$b\in V_1$of$B^i$with$a=p(c)$such that:

• (1) there exists ak-dimension neighbor$a_{i+1}$ofaandcsuch that$e_k(a_{i+1})\cap F=\emptyset$and there exists ak-dimension neighbor$u_{i-1}$ ofbsuch that$|e_k(b)\cap F|<2$, where b ($b\ne t_1,t_2$) is a common neighbor ofa and c;

• (2) for each$j_1\in \{0,1,\ldots ,n-1\}$, $|e_{j_1}(u)\cap F|<2$;

• (3) there exist two vertex-disjoint pathsPandQ of$B^i-F$ covering all vertices of it, wherePconnectsuto$t_2$, andQconnects c to $t_1$ and$\langle c,b,a\rangle$ is a subpath ofQ.

Proof

We proceed the proof by induction on n. Firstly, we shall show that the lemma is true when $n=3$. Suppose without loss of generality that $i=3$ and $k=2$, that is, $t_1,t_2\in V(B^3)$. Since $|E_{2}\cap F|\ge 1$, $|F\cap E(B^i)|\le 2$ for $0\le i\le 3$. It follows from Lemma 15 that the lemma is true when $n=3$. Thus, the induction basis holds. So we assume that the lemma is true for all integers m with $3\le m\le n-1$. Next we consider $BH_n$.

Obviously, we have $|E_{k}\cap F|\ge 2$ whenever $n\ge 4$. We may assume that $i=3$ and $k=n-1$. So we obtain four subgraphs $B^i$, $0\le i\le 3$, by splitting $BH_n$ along dimension $n-1$. Accordingly, by our assumption, $t_1,t_2\in V(B^3)$. Thus, we have $|E(B^3)\cap F|\le 2n-5$. Our aim is to show that there exist four vertices $u,a,c\in V_0$ and $b\in V_1$ of $B^3$ with $a=p(c)$ satisfying conditions (1)-(3). Let $k_1\in \{0,1,\ldots ,n-2\}$ such that $|E_{k_1}\cap E(B^3)\cap F|\ge |E_{j}\cap E(B^3)\cap F|$ for each $j\in \{0,1,\ldots ,n-2\}{\setminus} \{k_1\}$. We further divide each $B^i$ into $B_{n-2}^{i_1,i}$, $0\le i_1\le 3$, along dimension $k_1$. That is, $B_{n-2}^{i_1,i}\cong BH_{n-2}$ for each $i_1$. Assume without loss of generality that $t_1\in V(B_{n-2}^{0,3})$. By Definition 1, the graph induced by $V(B_{n-2}^{0,0})$, $V(B_{n-2}^{0,1})$, $V(B_{n-2}^{0,2})$ and $V(B_{n-2}^{0,3})$ is isomorphic to $BH_{n-1}$, for convenience, we denote it by H. There are four relative positions of $t_2$ in $B^3$, so we consider the following conditions.

If $t_2\in V(B_{n-2}^{0,3})$. By the induction hypothesis, there exist four vertices $u,a,c\in V_0$ and $b\in V_1$ of $B_{n-2}^{0,3}$ with $a=p(c)$ satisfying conditions (1) and (2) in H. Moreover, there exist two vertex-disjoint paths $P_0$ and Q of $B_{n-2}^{0,3}-F$ covering all vertices of it, where $P_0$ connects u to $t_2$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q. Since $l(P_0)+l(Q)=4^{n-2}-2$, it is obvious that there exists an edge on $P_0$ or Q, say $u_0a_0\in E(P_0)$, such that $u_0a_1,u_3a_0\not \in F$, where $u_0a_1$ and $u_3a_0$ are $k_1$-dimension edges. Thus, deleting $u_0a_0$ from $P_0$ will generate two vertex-disjoint paths $P_{01}$ and $P_{02}$, where $P_{01}$ connects u to $a_0$ and $P_{02}$ connects $u_0$ to $t_2$. By Lemma 6, there must exist two $k_1$-dimension fault-free edges $u_1a_2$ and $u_2a_3$, where $u_1\in V(B_{n-2}^{1,3})$, $u_2,a_2\in V(B_{n-2}^{2,3})$ and $a_3\in V(B_{n-2}^{3,3})$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B_{n-2}^{1,3}-F$ from $u_1$ to $a_1$, a fault-free Hamiltonian path $P_2$ of $B_{n-2}^{2,3}-F$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B_{n-2}^{3,3}-F$ from $u_3$ to $a_3$. Hence, $P=\langle u,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{1},a_1,u_0,P_{02},t_2\rangle$ and Q are paths satisfying condition (3) in $BH_n$.

If $t_2\in V(B_{n-2}^{1,3})$. Obviously, there exists a vertex $u\in V(B_{n-2}^{1,3})$ such that $|e_{j_1}(u)\cap F|<2$ for each $j_1\in \{0,1,\ldots ,n-1\}$. By Lemma 9, there exists a fault-free Hamiltonian path $P_1$ of $B_{n-2}^{1,3}-F$ from u to $t_2$. Since $l(P_1)=4^{n-2}-1$, there must exist an edge $u_1a_1\in E(P_1)$ such that $|e_{k_1}(u_1)\cap F|<2$ and $|e_{k_1}(a_1)\cap F|<2$. So let $u_1a_2$ and $u'a_1$ be two fault-free $k_1$-dimension edges. Additionally, deleting $u_1a_1$ from $P_1$ will generate two vertex-disjoint paths $P_{11}$ and $P_{12}$, where $P_{11}$ connects u to $a_1$ and $P_{12}$ connects $u_1$ to $t_2$. By the induction hypothesis, there exists four vertices $a,c\in V_0$ and $a_0,b\in V_1$ of $B_{n-2}^{0,3}$ with $a=p(c)$ such that: a, b and c satisfy condition (1) and $a_0$ satisfies condition (2) in H. Moreover, there exist two vertex-disjoint paths $P_0$ and Q of $B_{n-2}^{0,3}-F$ covering all vertices of it, where $P_0$ connects $u'$ to $a_0$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q. Obviously, there exist two $k_1$-dimension fault-free edges $u_2a_3$ and $u_3a_0$, where $u_2\in V(B_{n-2}^{2,3})$ and $u_3,a_3\in V(B_{n-2}^{3,3})$. By Lemma 9, there exist a fault-free Hamiltonian path $P_2$ of $B_{n-2}^{2,3}-F$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B_{n-2}^{3,3}-F$ from $u_3$ to $a_3$. Hence, $P=\langle u,P_{11},a_1,u',P_0,a_0,u_3,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{12},t_2\rangle$ and Q are paths satisfying condition (3) in $BH_n$.

If $t_2\in V(B_{n-2}^{2,3})$. Obviously, there exists a vertex $u\in V_0$ in $B_{n-2}^{2,3}$ such that $|e_{j_1}(u)\cap F|<2$ for each $j_1\in \{0,1,\ldots ,n-1\}$. By Lemma 9, there exists a fault-free Hamiltonian path $P_2$ of $B_{n-2}^{2,3}-F$ from u to $t_2$. Similarly, there must exist an edge $u_2a_2\in E(P_2)$ such that $|e_{k_1}(u_2)\cap F|<2$ and $|e_{k_1}(a_2)\cap F|<2$. So let $u_1a_2$ and $u_2a_3$ be two fault-free $k_1$-dimension edges. Additionally, deleting $u_2a_2$ from $P_2$ will generate two vertex-disjoint paths $P_{21}$ and $P_{22}$, where $P_{21}$ connects u to $a_2$ and $P_{22}$ connects $u_2$ to $t_2$. Let $a_0\in V(B_{n-2}^{0,3})$ be a vertex such that $|e_{k_1}(a_0)\cap F|<2$. By the induction hypothesis, there exist four vertices $u_0,a,c\in V_0$ and $b\in V_1$ of $B_{n-2}^{0,3}$ with $a=p(c)$ such that: a, b and c satisfy condition (1) and $u_0$ satisfies condition (2) in H. Moreover, there exist two vertex-disjoint paths $P_0$ and Q of $B_{n-2}^{0,3}-F$ covering all vertices of it, where $P_0$ connects $u_0$ to $a_0$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q. Obviously, there exist two fault-free $k_1$-dimension edges $u_0a_1$ and $u_3a_0$, where $u_3\in V(B_{n-2}^{3,3})$ and $a_1\in V(B_{n-2}^{1,3})$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B_{n-2}^{1,3}-F$ from $u_1$ to $a_1$, and a fault-free Hamiltonian path $P_3$ of $B_{n-2}^{3,3}-F$ from $u_3$ to $a_3$. Hence, $P=\langle u,P_{21},a_2,u_1,P_1,a_1,u_0,P_{0},a_0,u_3,P_{3},a_3,u_2,P_{22},t_2\rangle$ and Q are paths satisfying condition (3) in $BH_n$.

If $t_2\in V(B_{n-2}^{3,3})$. Similarly, there exists a vertex $u\in V(B_{n-2}^{2,3})$ such that $|e_{j_1}(u)\cap F|<2$ for each $j_1\in \{0,1,\ldots ,n-1\}$. Let $a_0\in V(B_{n-2}^{0,3})$ be a vertex such that $|e_{k_1}(a_0)\cap F|<2$. By the induction hypothesis, there exists four vertices $u_0,a,c\in V_0$ and $b\in V_1$ of $B_{n-2}^{0,3}$ with $a=p(c)$ such that: a, b and c satisfy condition (1) and $u_0$ satisfies condition (2) in H. Moreover, there exist two vertex-disjoint paths $P_0$ and Q of $B_{n-2}^{0,3}-F$ covering all vertices of it, where $P_0$ connects $u_0$ to $a_0$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q. So there exist three fault-free $k_1$-dimension edges $u_0a_1$, $u_1a_2$ and $u_3a_0$, where $u_1,a_1\in V(B_{n-2}^{1,3})$, $a_2\in V(B_{n-2}^{2,3})$ and $u_3\in V(B_{n-2}^{3,3})$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B_{n-2}^{1,3}-F$ from $u_1$ to $a_1$, a fault-free Hamiltonian path $P_2$ of $B_{n-2}^{2,3}-F$ from u to $a_2$ and a fault-free Hamiltonian path $P_3$ of $B_{n-2}^{3,3}-F$ from $u_3$ to $t_2$. Hence, $P=\langle u,P_{2},a_2,u_1,P_1,a_1,u_0,P_{0},a_0,u_3,P_{3},t_2\rangle$ and Q are paths satisfying condition (3) in $BH_n$.

This completes the proof. $\square$

Now we are ready to state the main result of this paper.

Theorem 17

Let F be a set of edges with $|F|\le 2n-3$ and let $\{s_1,s_2\}$ and $\{t_1,t_2\}$ be two sets of vertices in different partite sets of $BH_{n}$ for $n\ge 2$ . Then $BH_{n}-F$ contains vertex-disjoint $s_1,t_1$ -path and $s_2,t_2$ -path that cover all vertices of it. Furthermore, the upper bound $2n-3$ of faulty edges can be tolerated is optimal.

Proof

We proceed the proof by induction on n. By Lemma 13, the statement is true for $BH_2$. For $n=3$, we have characterized how to divide $BH_3$ by some dimension $d\in \{0,1,2\}$ in the Remark. Assume that the statement holds for $BH_{n-1}$ with $n\ge 3$. Next we consider $BH_n$. Since $|F|\le 2n-3$, by Pigeonhole Principle, there must exist a dimension $d\in \{0,1,\ldots ,n-1\}$ such that $|E_d\cap F|\ge 2$ whenever $n\ge 4$. Thus, $|E(B^i)\cap F|\le 2n-5$, $i\in \{0,1,2,3\}$. (We can also use Lemma 12 as induction basis when $n=3$.) Suppose without loss of generality that $d=n-1$. So we divide $BH_n$ into four subcubes $B^{i}$ ($i\in \{0,1,2,3\}$) by deleting $E_{n-1}$. By Lemma 2, $BH_n$ is vertex-transitive, we may assume that $s_1\in V(B^0)$ and $|V(B^0)\cap \{s_1,s_2,t_1,t_2\}|\ge |V(B^j)\cap \{s_2,t_1,t_2\}|$ for each $j\in \{1,2,3\}$. We consider the following cases.

Case 1.$|V(B^0)\cap \{s_2,t_1,t_2\}|=0$. We further deal with the following cases.

Case 1.1.$s_2\in V(B^1)$, $t_1\in V(B^2)$ and $t_2\in V(B^3)$. Since $4^{n-1}\ge 2n-3$ whenever $n\ge 3$, there always exists a fault-free edge $u_3a_0\in E_{3,0}$. In addition, there exists a fault-free edge $v_3b_0\in E_{3,0}$ such that $u_3\ne v_3$ and $b_0\ne a_0$. Similarly, there exist two fault-free edges $u_0a_1\in E_{0,1}$ and $u_2a_3\in E_{2,3}$ such that $u_0\ne s_1$ and $a_3\ne t_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $s_2$ to $a_1$, and a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $t_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $u_0$ to $a_0$ and $P_{02}$ connects $s_1$ to $b_0$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $u_3$ to $t_2$ and $P_{32}$ connects $v_3$ to $a_3$. Hence, $\langle s_1,P_{02},b_0,v_3,P_{32},a_3,u_2,P_2,t_1\rangle$ and $\langle s_2,P_1,a_1, u_0,P_{01},a_0,u_3,P_{31},t_2\rangle$ are two vertex-disjoint paths required (see Fig. 5).

Fig. 5

Illustration of Cases 1.1

Fig. 6

Illustration of Case 2.1.2

Case 1.2.$s_2\in V(B^1)$, $t_1\in V(B^3)$ and $t_2\in V(B^2)$. There always exist two edges $u_3a_0,v_3b_0\in E_{3,0}$ such that $u_3\ne v_3$ and $a_0\ne b_0$. Similarly, there exist an edge $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$, and an edge $u_2a_3\in E_{2,3}$ such that $a_3\ne t_1$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $s_2$ to $a_1$, and a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $v_3$ to $t_1$ and $P_{32}$ connects $u_3$ to $a_3$; there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $u_0$ to $a_0$ and $P_{02}$ connects $s_1$ to $b_0$. Hence, $\langle s_1,P_{02},b_0,v_3,P_{31},t_1\rangle$ and $\langle s_2,P_1,a_1, u_0,P_{01},a_0,u_3,P_{32},a_3,u_2,P_{2},t_2\rangle$ are two vertex-disjoint paths required.

Case 1.3.$s_2\in V(B^2)$, $t_1\in V(B^1)$ and $t_2\in V(B^3)$. There always exist two edges $u_3a_0,v_3b_0\in E_{3,0}$ such that $u_3\ne v_3$ and $a_0\ne b_0$, and two edges $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$. Similarly, there exist an edge $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$ and $a_1\ne t_1$, and an edge $u_2a_3\in E_{2,3}$ such that $u_2\ne s_2$ and $a_3\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $u_0$ to $a_0$ and $P_{02}$ connects $s_1$ to $b_0$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $v_1$ to $t_1$ and $P_{12}$ connects $u_1$ to $a_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $b_2$ and $P_{22}$ connects $s_2$ to $a_2$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $v_3$ to $a_3$ and $P_{32}$ connects $u_3$ to $t_2$. Hence, $\langle s_1,P_{02},b_0,v_3,P_{31},a_3,u_2,P_{21},b_2,v_1,P_{11},t_1\rangle$ and $\langle s_2,P_{22},a_2,u_1,P_{12},a_1,u_0,P_{01},a_0,u_3,P_{32},t_2\rangle$ are two vertex-disjoint paths required.

Case 1.4.$s_2\in V(B^2)$, $t_1\in V(B^3)$ and $t_2\in V(B^1)$. Obviously, there exist two non-faulty edges $u_3a_0\in E_{3,0}$ and $u_1a_2\in E_{1,2}$. By Lemma 9, there exist a fault-free Hamiltonian path $P_0$ of $B^0-F$ from $s_1$ to $a_0$, a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $u_1$ to $t_2$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $s_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $t_1$. Hence, $\langle s_1,P_{0},a_0,u_3,P_{3},t_1\rangle$ and $\langle s_2,P_{2},a_2,u_1,P_{1},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.$|V(B^0)\cap \{s_2,t_1,t_2\}|=1$. We further deal with the following cases.

Case 2.1. For some $j\in \{1,2,3\}$, $|V(B^j)\cap \{s_2,t_1,t_2\}|=2$.

Case 2.1.1.$t_1\in V(B^0)$ and $s_2,t_2\in V(B^1)$. By Lemma 9, there exists a fault-free Hamiltonian path $P_0$ of $B^0-F$ from $s_1$ to $t_1$. Since $4^{n-1}-3\ge 2(2n-3)$ whenever $n\ge 3$ and any vertex incident to two faulty $(n-1)$-dimension edges will eliminate the choice of two edges on $P_0$, we can choose an edge $u_0a_0\in E(P_0)$ such that there exist two non-faulty edges $u_0a_1\in E_{0,1}$ and $u_3a_0\in E_{3,0}$. Deleting $u_0a_0$ from $P_0$ will give rise to two disjoint paths $P_{01}$ and $P_{02}$, where $P_{01}$ connects $s_1$ to $u_0$ and $P_{02}$ connects $a_0$ to $t_1$. Additionally, there exist a fault-free edge $u_1a_2\in E_{1,2}$ such that $u_1\ne s_2$, and an edge $u_2a_3\in E_{2,3}$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $a_1$ to $u_1$ and $P_{12}$ connects $s_2$ to $t_2$. Moreover, there exist a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $a_2$ to $u_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $a_3$ to $u_3$. Hence, $\langle s_1,P_{01},u_0,a_1,P_{11},u_1,a_2,P_{2},u_2,a_3,P_3,u_3,a_0,P_{02},t_1\rangle$ and $\langle s_2,P_{12},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.1.2.$t_2\in V(B^0)$ and $s_2,t_1\in V(B^1)$. There exist fault-free edges $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$ and $a_1\ne t_1$, $u_1a_2\in E_{1,2}$ such that $u_1\ne s_2$, $u_2a_3\in E_{2,3}$ and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $u_0$ to $t_2$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{12}$ connects $u_1$ to $t_1$ and $P_{11}$ connects $s_2$ to $a_1$. By Lemma 9, there exist a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{12},t_1\rangle$ and $\langle s_2,P_{11},a_1,u_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required (see Fig. 6).

Case 2.1.3.$t_1\in V(B^0)$ and $s_2,t_2\in V(B^2)$. By Lemma 9, there exists a fault-free Hamiltonian path $P_0$ of $B^0-F$ from $s_1$ to $t_1$. We can choose an edge $u_0a_0\in E(P_0)$ such that there exist two fault-free edges $u_0a_1\in E_{0,1}$ and $u_3a_0\in E_{3,0}$. Deleting $u_0a_0$ from $P_0$ will give rise to two disjoint paths $P_{01}$ and $P_{02}$, where $P_{01}$ connects $s_1$ to $u_0$ and $P_{02}$ connects $a_0$ to $t_1$. There exist a fault-free edge $u_1a_2\in E_{1,2}$ such that $a_2\ne t_2$, and a fault-free edge $u_2a_3\in E_{2,3}$ such that $u_2\ne s_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $a_2$ to $u_2$ and $P_{22}$ connects $s_2$ to $t_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $a_1$ to $u_1$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $a_3$ to $u_3$. Hence, $\langle s_1,P_{01},u_0,a_1,P_{1},u_1,a_2,P_{21},u_2,a_3,P_{3},u_3,a_0,P_{02},t_1\rangle$ and $\langle s_2,P_{22},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.1.4.$t_2\in V(B^0)$ and $s_2,t_1\in V(B^2)$. There exist fault-free edges $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$, $u_1a_2\in E_{1,2}$ such that $a_2\ne t_1$, $u_2a_3\in E_{2,3}$ such that $u_2\ne s_2$ and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $u_0$ to $t_2$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $t_1$ and $P_{22}$ connects $s_2$ to $a_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $u_1$ to $a_1$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{21},t_1\rangle$ and $\langle s_2,P_{22},a_2,u_1,P_{1},a_1,u_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.1.5.$s_2\in V(B^0)$ and $t_1,t_2\in V(B^1)$. There always exist two fault-free edges $u_3a_0,v_3b_0\in E_{3,0}$ such that $u_3\ne v_3$ and $a_0\ne b_0$, two fault-free edges $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$, and two fault-free edges $u_2a_3,v_2b_3\in E_{2,3}$ such that $u_2\ne v_2$ and $a_3\ne b_3$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $s_2$ to $b_0$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $t_1$ and $P_{12}$ connects $v_1$ to $t_2$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $v_2$ to $b_2$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $u_3$ to $a_3$ and $P_{32}$ connects $v_3$ to $b_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{31},a_3,u_2,P_{21},a_2,u_1,P_{11},t_1\rangle$ and $\langle s_2,P_{02},b_0,v_3,P_{32},b_3,v_2,P_{22},b_2,v_1,P_{12},t_1\rangle$ are two vertex-disjoint paths required.

Case 2.1.6.$s_2\in V(B^0)$ and $t_1,t_2\in V(B^2)$. By Lemma 14, there exist four vertices $a,c\in V_0$ and $b,d\in V_1$ of $B^3$ such that:

• (1) $a=p(c)$, $b=p(d)$ and a, b, c and d form a 4-cycle in $B^3$;

• (2) there exists an $(n-1)$-dimension neighbor $a_{0}$ of a and c such that $a_{0}a,a_0c\not \in F$;

• (3) there exist two $(n-1)$-dimension neighbors $u_{2}$ and $v_{2}$ of b and d such that $u_2b,u_2d,v_2b\not \in F$ and $cd\not \in F$;

• (4) there exists a neighbor u of b and d in $B^3$ such that $ub_0\not \in F$ is an $(n-1)$-dimension edge;

• (5) there exists a longest path $P_3$ from u to a covering all vertices of $B^3-F$ but b, c and d.

It is obvious that $a_0\ne p(b_0)$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $s_2$ to $b_0$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $t_1$ and $P_{22}$ connects $v_2$ to $t_2$. Let $u_0$ (resp. $a_2$) be the neighbor of $a_0$ (resp. $u_2$) on $P_{01}$ (resp. $P_{21}$). For convenience, we denote $P_{01}-a_0$ by $P_{03}$, that is, $P_{03}$ is a path from $s_1$ to $u_0$. Similarly, we denote $P_{21}-u_2$ by $P_{23}$, that is, $P_{23}$ is a path from $a_2$ to $t_1$. If $|e_{n-1}(u_0)\cap F|=2$ or $|e_{n-1}(a_2)\cap F|=2$, say $|e_{n-1}(u_0)\cap F|=2$, let $u_0'\in V(B^0)$ such that $u_0'=p(u_0)$. Moreover, if $u_0'a_0\not \in F$, we can replace $u_0$ by $u_0'$ on $P_{03}$. Otherwise, we have at least three fault edges incident to $u_0$ and $u_0'$. Since there are $2n-2$ common neighbors of $u_0$ and $u_0'$ in $B^0$, fault edges incident to $u_0$ and $u_0'$ may affect $2n-2$ vertices as the choice of $a_0$. Since $3\times ((4^{n-1}-2)/2)/(2n-2)> 2n-3$ whenever $n\ge 3$, we can always choose such $u_0\in V(B^0)$ and $a_2\in V(B^2)$ that there exist two fault-free $(n-1)$-dimension edges $u_0a_1\in E_{0,1}$ and $u_1a_2\in E_{1,2}$. Then there exists a fault-free Hamiltonian path $P_{1}$ of $B^1-F$ from $a_1$ to $u_1$. Hence, $\langle s_1,P_{03},u_0,a_1,P_{1},u_1,a_2,P_{23},t_1\rangle$ and $\langle s_2,P_{02},b_0,u,P_{3},a,a_0,c,d,u_2,b,v_2,P_{22},t_2\rangle$ are two vertex-disjoint paths required (see Fig. 7).

Fig. 7

Illustration of Cases 2.1.6

Fig. 8

Illustration of Case 2.1.7

Case 2.1.7.$s_2\in V(B^0)$ and $t_1,t_2\in V(B^3)$. By Lemma 16, there exist four vertices $u,a,c\in V_0$ and $b\in V_1$ of $B^3$ with $a=p(c)$ such that:

• (1) there exists an $(n-1)$-dimension neighbor $a_{0}$ of a and c such that $a_{0}a,a_{0}c\not \in F$ and there exists an $(n-1)$-dimension neighbor $u_{2}$ of b such that $u_2b\not \in F$, where b ($b\ne t_1,t_2$) is a common neighbor of a and c;

• (2) there exists an $(n-1)$-dimension neighbor $b_0$ of u such that $ub_{0}\not \in F$;

• (3) there exist two vertex-disjoint paths $P_{31}$ and Q of $B^3-F$ covering all vertices of it, where $P_{31}$ connects u to $t_2$, and Q connects c to $t_1$ and $\langle c,b,a\rangle$ is a subpath of Q.

Deleting ab from Q will generate two vertex-disjoint paths bc and $P_{32}$, where $P_{32}$ connects a to $t_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $s_2$ to $b_0$. Similar to the proof of Case 2.1.6, let $u_0$ be the neighbor of $a_0$ on $P_{01}$ such that $u_0a_1\in E_{0,1}$ is a fault-free edge. For convenience, we denote $P_{01}-a_0$ by $P_{03}$, that is, $P_{03}$ is a path from $s_1$ to $u_0$. By Lemma 6, there must exist a fault-free edge $u_1a_2\in E_{1,2}$. Additionally, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $a_1$ to $u_1$, and a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $a_2$ to $u_2$. Hence, $\langle s_1,P_{03},u_0,a_1,P_{1},u_1,a_2,P_{2},u_2,b,c,a_0,a,P_{32},t_1\rangle$ and $\langle s_2,P_{02},b_0,u,P_{31},t_2\rangle$ are two vertex-disjoint paths required (see Fig. 8).

Case 2.2. For all $j\in \{1,2,3\}$, $|V(B^j)\cap \{s_2,t_1,t_2\}|\le 1$.

Case 2.2.1.$t_1\in V(B^0)$.

Case 2.2.1.1.$t_2\in V(B^1)$ and $s_2\in V(B^2)$. There exist fault-free edges $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$ and $a_1\ne t_2$, $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$, $u_2a_3\in E_{2,3}$ such that $u_2\ne s_2$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $u_0$ to $t_1$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $a_1$ and $P_{12}$ connects $v_1$ to $t_2$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $s_2$ to $b_2$. By Lemma 9, there exists a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{21},a_2,u_1,P_{11},a_1,u_0,P_{02},t_1\rangle$ and $\langle s_2,P_{22},b_2,v_1,P_{12},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.1.2.$t_2\in V(B^1)$ and $s_2\in V(B^3)$. There exist two non-faulty edges $u_1a_2\in E_{1,2}$ and $u_2a_3\in E_{2,3}$. By Lemma 9, there exist a fault-free Hamiltonian path $P_0$ of $B^0-F$ from $s_1$ to $t_1$, a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $u_1$ to $t_2$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $s_2$ to $a_3$. Hence, $\langle s_1,P_{1},t_1\rangle$ and $\langle s_2,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{1},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.1.3.$t_2\in V(B^2)$ and $s_2\in V(B^3)$. There exist fault-free edges $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$, $u_1a_2\in E_{1,2}$ such that $a_2\ne t_2$, $u_2a_3,v_2b_3\in E_{2,3}$ such that $a_3\ne b_3$ and $u_2\ne v_2$, and $u_3a_0\in E_{3,0}$ such that $u_3\ne s_2$ and $a_0\ne t_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $u_0$ to $t_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $v_2$ to $t_2$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $u_3$ to $a_3$ and $P_{32}$ connects $s_2$ to $b_3$. By Lemma 9, there exists a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $u_1$ to $a_1$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{31},a_3,u_2,P_{21},a_2,u_1,P_{1},a_1,u_0,P_{02},t_1\rangle$ and $\langle s_2,P_{32},b_3,v_2,P_{22},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.1.4.$t_2\in V(B^2)$ and $s_2\in V(B^1)$. There exist fault-free edges $u_0a_1\in E_{0,1}$ such that $u_0\ne s_1$, $v_1b_2\in E_{1,2}$ such that $v_1\ne s_2$ and $b_2\ne t_2$, $u_2a_3,v_2b_3\in E_{2,3}$ such that $a_3\ne b_3$ and $u_2\ne v_2$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $u_0$ to $a_0$ and $P_{02}$ connects $s_1$ to $t_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $v_2$ to $b_2$ and $P_{22}$ connects $u_2$ to $t_2$. Moreover, there must exist an edge $v_0b_0$ on $P_{01}$ or $P_{02}$, say $P_{02}$ such that there exist two fault-free $(n-1)$-dimension edges $v_0b_1\in E_{0,1}$ and $v_3b_0\in E_{3,0}$, where $v_3\ne u_3$ and $b_1\ne a_1$. Deleting $v_0b_0$ from $P_{02}$ will generate two vertex-disjoint paths $P_{03}$ and $P_{04}$, where $P_{03}$ connects $s_1$ to $b_0$ and $P_{04}$ connects $v_0$ to $t_1$. Analogously, there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $v_1$ to $b_1$ and $P_{12}$ connects $s_2$ to $a_1$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $v_3$ to $b_3$ and $P_{32}$ connects $u_3$ to $a_3$. Hence, $\langle s_1,P_{03},b_0,v_3,P_{31},b_3,v_2,P_{21},b_2,v_1,P_{11},b_1,v_0,P_{04},t_1\rangle$ and $\langle s_2,P_{12},a_1,u_0,P_{01},a_0,u_3,P_{32},a_3,u_2,P_{22},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.1.5.$t_2\in V(B^3)$ and $s_2\in V(B^1)$. The proof is quite analogous to that of Case 2.2.1.4, we omit it.

Case 2.2.1.6.$t_2\in V(B^3)$ and $s_2\in V(B^2)$. The proof is quite analogous to that of Case 2.2.1.4, we omit it.

Case 2.2.2.$t_2\in V(B^0)$.

Case 2.2.2.1.$t_1\in V(B^1)$ and $s_2\in V(B^2)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$ and $b_1\ne t_1$, $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$, $u_2a_3\in E_{2,3}$ such that $u_2\ne s_2$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $v_0$ to $t_2$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $t_1$ and $P_{12}$ connects $v_1$ to $b_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $s_2$ to $b_2$. By Lemma 9, there exists a Hamiltonian path $P_{3}$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{21},a_2,u_1,P_{11},t_1\rangle$ and $\langle s_2,P_{22},b_2,v_1,P_{12},b_1,v_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.2.2.$t_1\in V(B^1)$ and $s_2\in V(B^3)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$ and $b_1\ne t_1$, $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$, $u_2a_3,v_2b_3\in E_{2,3}$ such that $u_2\ne v_2$ and $a_3\ne b_3$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$ and $u_3\ne s_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $v_0$ to $t_2$; there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $t_1$ and $P_{12}$ connects $v_1$ to $b_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $v_2$ to $b_2$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $u_3$ to $a_3$ and $P_{32}$ connects $s_2$ to $b_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{31},a_3,u_2,P_{21},a_2,u_1,P_{11},t_1\rangle$ and $\langle s_2,P_{32},b_3,v_2,P_{22},b_2,v_1,P_{12},b_1,v_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.2.3.$t_1\in V(B^2)$ and $s_2\in V(B^1)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$, $u_2a_3\in E_{2,3}$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $v_0$ to $t_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $s_2$ to $b_1$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $t_1$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},a_3,u_2,P_{2},t_1\rangle$ and $\langle s_2,P_{1},b_1,v_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.2.4.$t_1\in V(B^2)$ and $s_2\in V(B^3)$. The proof is quite analogous to that of Case 2.2.2.1, we omit it.

Case 2.2.2.5.$t_1\in V(B^3)$ and $s_2\in V(B^1)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$, $u_1a_2\in E_{1,2}$ such that $u_1\ne s_2$, $u_2a_3\in E_{2,3}$ such that $a_3\ne t_1$, and $v_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $v_0$ to $t_2$ and $P_{02}$ connects $s_1$ to $a_0$. Moreover, there must exist an edge $u_0b_0$ on $P_{01}$ or $P_{02}$, say $P_{02}$ such that there exist two fault-free $(n-1)$-dimension edges $u_0a_1\in E_{0,1}$ and $u_3b_0\in E_{3,0}$, where $u_3\ne v_3$ and $a_1\ne b_1$. Deleting $u_0b_0$ from $P_{02}$ will generate two vertex-disjoint paths $P_{03}$ and $P_{04}$, where $P_{03}$ connects $s_1$ to $b_0$ and $P_{04}$ connects $u_0$ to $a_0$. Analogously, there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $a_1$ and $P_{12}$ connects $s_2$ to $b_1$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $v_3$ to $t_1$ and $P_{32}$ connects $u_3$ to $a_3$. By Lemma 9, there exists a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $a_2$. Hence, $\langle s_1,P_{03},b_0,u_3,P_{32},a_3,u_2,P_{2},a_2,u_1,P_{11},a_1,u_0,P_{04},a_0,v_3,P_{31},t_1\rangle$ and $\langle s_2,P_{12},b_1,v_0,P_{01},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.2.6.$t_1\in V(B^3)$ and $s_2\in V(B^2)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$, $v_1b_2\in E_{1,2}$, and $u_3a_0\in E_{3,0}$ such that $a_0\ne t_2$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $v_0$ to $t_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $v_1$ to $b_1$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $s_2$ to $b_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $t_1$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{3},t_1\rangle$ and $\langle s_2,P_{2},b_2,v_1,P_{1},b_1,v_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.3.$s_2\in V(B^0)$.

Case 2.2.3.1.$t_1\in V(B^1)$ and $t_2\in V(B^2)$. There exist fault-free edges $u_1a_2\in E_{1,2}$ such that $a_2\ne t_2$, $u_2a_3,v_2b_3\in E_{2,3}$ such that $u_2\ne v_2$ and $a_3\ne b_3$, and $u_3a_0,v_3b_0\in E_{3,0}$ such that $u_3\ne v_3$ and $a_0\ne b_0$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $a_0$ and $P_{02}$ connects $s_2$ to $b_0$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $v_2$ to $t_2$; there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $u_3$ to $a_3$ and $P_{32}$ connects $v_3$ to $b_3$. By Lemma 9, there exists a fault-free Hamiltonian path $P_{1}$ of $B^1-F$ from $u_1$ to $t_1$. Hence, $\langle s_1,P_{01},a_0,u_3,P_{31},a_3,u_2,P_{21},a_2,u_1,P_{1},t_1\rangle$ and $\langle s_2,P_{02},b_0,v_3,P_{32},b_3,v_2,P_{22},t_2\rangle$ are two vertex-disjoint paths required.

Case 2.2.3.2.$t_1\in V(B^1)$ and $t_2\in V(B^3)$. The proof is quite analogous to that of Case 2.2.3.1, we omit it.

Case 2.2.3.3.$t_1\in V(B^2)$ and $t_2\in V(B^3)$. By Lemma 16, there exist four vertices $u,a,c\in V_1$ and $b\in V_0$ of $B^0-F$ with $a=p(c)$ such that:

• (1) there exists an $(n-1)$-dimension neighbor $u_{3}$ of a and c such that $u_{3}a,u_{3}c\not \in F$ and there exists an $(n-1)$-dimension neighbor $a_{1}$ of b such that $a_1b\not \in F$, where b ($b\ne s_1,s_2$) is a common neighbor of a and c;

• (2) there exists an $(n-1)$-dimension neighbor $v_3$ of u such that $uv_{3}\not \in F$;

• (3) there exist two vertex-disjoint paths $P_{01}$ and Q of $B^0-F$ covering all vertices of it, where $P_{01}$ connects $s_2$ to u, and Q connects $s_1$ to c and $\langle c,b,a\rangle$ is a subpath of Q.

Deleting ab from Q will generate two vertex-disjoint paths $P_{02}$ and bc, where $P_{02}$ connects $s_1$ to a and bc is an edge. Let $a_3\in V_1$ be a vertex in $B^3$ such that $a_3\ne t_2$ and $u_2a_3\in E_{2,3}$ is a fault-free edge. In addition, there exist two vertex-disjoint paths $P_{31}$ and $P_{32}$ covering all vertices of $B^3-F$, where $P_{31}$ connects $v_3$ to $t_2$ and $P_{32}$ connects $u_3$ to $a_3$. Similar to the proof of Case 2.1.6, let $b_3$ be the neighbor of $u_3$ on $P_{32}$ such that $v_2b_3\in E_{2,3}$ is a fault-free edge. For convenience, we denote $P_{32}-u_3$ by $P_{33}$, that is, $P_{33}$ is a path from $b_3$ to $a_3$. By Lemma 6, there must exist a fault-free edge $u_1a_2\in E_{1,2}$ such that $a_2\ne t_1$. Thus, there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $t_1$ and $P_{22}$ connects $a_2$ to $v_2$. Additionally, there exists a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $a_1$ to $u_1$. Hence, $\langle s_1,P_{02},a,u_3,c,b,a_1,P_{1},u_1,a_2,P_{22},v_2,b_3,P_{33},a_3,u_2,P_{21},t_1\rangle$ and $\langle s_2,P_{01},u,v_3,P_{31},t_2\rangle$ are two vertex-disjoint paths required.

Case 3.$|V(B^0)\cap \{s_2,t_1,t_2\}|=2$.

Case 3.1.$t_1,t_2\in V(B^0)$ and $s_2\in V(B^1)$. There exist a fault-free edge $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $v_0$ to $t_2$ and $P_{02}$ connects $s_1$ to $t_1$. Moreover, there must exist an edge $u_0a_0$ on $P_{01}$ or $P_{02}$, say $P_{02}$ such that there exist two fault-free $(n-1)$-dimension edges $u_0a_1\in E_{0,1}$ and $u_3a_0\in E_{3,0}$, where $a_1\ne b_1$. Deleting $u_0a_0$ from $P_{02}$ will generate two vertex-disjoint paths $P_{03}$ and $P_{04}$, where $P_{03}$ connects $s_1$ to $a_0$ and $P_{04}$ connects $u_0$ to $t_1$. In addition, there exist two fault-free edges $u_1a_2\in E_{1,2}$ and $u_2a_3\in E_{2,3}$, where $u_1\ne s_2$ . Analogously, there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $a_1$ and $P_{12}$ connects $s_2$ to $b_1$. Moreover, by Lemma 9, there exist a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $a_2$ and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{03},a_0,u_3,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{11},a_1,u_0,P_{04},t_1\rangle$ and $\langle s_2,P_{12},b_1,v_0,P_{01},t_2\rangle$ are two vertex-disjoint paths required.

Case 3.2.$t_1,t_2\in V(B^0)$ and $s_2\in V(B^2)$. There exist a fault-free edge $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $v_0$ to $t_2$ and $P_{02}$ connects $s_1$ to $t_1$. Moreover, there must exist an edge $u_0a_0$ on $P_{01}$ or $P_{02}$, say $P_{02}$ such that there exist two fault-free $(n-1)$-dimension edges $u_0a_1\in E_{0,1}$ and $u_3a_0\in E_{3,0}$, where $a_1\ne b_1$. Deleting $u_0a_0$ from $P_{02}$ will generate two vertex-disjoint paths $P_{03}$ and $P_{04}$, where $P_{03}$ connects $s_1$ to $a_0$ and $P_{04}$ connects $u_0$ to $t_1$. In addition, there exist fault-free edges $u_1a_2,v_1b_2\in E_{1,2}$ such that $u_1\ne v_1$ and $a_2\ne b_2$, and $u_2a_3\in E_{2,3}$. Analogously, there exist two vertex-disjoint paths $P_{11}$ and $P_{12}$ covering all vertices of $B^1-F$, where $P_{11}$ connects $u_1$ to $a_1$ and $P_{12}$ connects $v_1$ to $b_1$; there exist two vertex-disjoint paths $P_{21}$ and $P_{22}$ covering all vertices of $B^2-F$, where $P_{21}$ connects $u_2$ to $a_2$ and $P_{22}$ connects $s_2$ to $b_2$. Moreover, by Lemma 9, there exists a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{03},a_0,u_3,P_{3},a_3,u_2,P_{21},a_2,u_1,P_{11},a_1,u_0,P_{04},t_1\rangle$ and $\langle s_2,P_{22},b_2,v_1,P_{12},b_1,v_0,P_{01},t_2\rangle$ are two vertex-disjoint paths required.

Case 3.3.$t_1,t_2\in V(B^0)$ and $s_2\in V(B^3)$. There exist fault-free edges $v_0b_1\in E_{0,1}$ such that $v_0\ne s_1$, $v_1b_2\in E_{1,2}$, and $v_2b_3\in E_{2,3}$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $t_1$ and $P_{02}$ connects $v_0$ to $t_2$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $v_1$ to $b_1$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $v_2$ to $b_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $s_2$ to $b_3$. Hence, $\langle s_1,P_{01},t_1\rangle$ and $\langle s_2,P_{3},b_3,v_2,P_{2},b_2,v_1,P_{1},b_1,v_0,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

Case 4.$s_2,t_1,t_2\in V(B^0)$. By the induction hypothesis, there exist two vertex-disjoint paths $P_{01}$ and $P_{02}$ covering all vertices of $B^0-F$, where $P_{01}$ connects $s_1$ to $t_1$ and $P_{02}$ connects $s_2$ to $t_2$. Since $l(P_{01})+l(P_{02})=4^{n-1}-2$ and any vertex has two $(n-1)$-dimension neighbors, there must exist an edge $u_0a_0$ on $P_{01}$ or $P_{02}$, say $P_{01}$ such that there exist two non-faulty edges $u_0a_1\in E_{0,1}$ and $u_3a_0\in E_{3,0}$. Thus, deleting $u_0a_0$ from $P_{01}$ will generate two vertex-disjoint paths $P_{03}$ and $P_{04}$, where $P_{03}$ connects $s_1$ to $a_0$ and $P_{04}$ connects $u_0$ to $t_1$. In addition, there exist non-faulty edges $u_1a_2\in E_{1,2}$ and $u_2a_3\in E_{2,3}$. By Lemma 9, there exist a fault-free Hamiltonian path $P_1$ of $B^1-F$ from $u_1$ to $a_1$, a fault-free Hamiltonian path $P_2$ of $B^2-F$ from $u_2$ to $a_2$, and a fault-free Hamiltonian path $P_3$ of $B^3-F$ from $u_3$ to $a_3$. Hence, $\langle s_1,P_{03},a_0,u_3,P_{3},a_3,u_2,P_{2},a_2,u_1,P_{1},a_1,u_0,P_{04},t_1\rangle$ and $\langle s_2,P_{02},t_2\rangle$ are two vertex-disjoint paths required.

By above, we have shown that for an edge subset F of $BH_n$ with $|F|\le 2n-3$, there always exists paired two-disjoint path cover of $BH_n-F$. We shall show that there exists an edge subset F of $BH_n$ with $|F|=2n-2$ such that there may not exist paired two-disjoint path cover of $BH_n-F$, which implies the optimality of the upper bound $2n-3$.

Let $s_1,s_2\in V_0$ and $t_1,t_2\in V_1$ be four vertices in $BH_n$. There exists a balanced hypercube $BH_n$ with $2n-2$ edge faults containing no vertex-disjoint paths $P_i$, $i=1,2$, that cover all vertices of it, where $P_i$ connects $s_i$ to $t_i$ and $V(P_1)\cup V(P_2)=V(BH_n)$. For example, let $s_1$ and $s_2$ be two vertices differing only from the inner index and let w be any common neighbor of $s_1$ and $s_2$. One can consider that the $2n-2$ edges incident to w (except $s_1w$ and $s_2w$) are all faulty (see Fig. 9). Obviously, w has exactly two fault-free edges incident to it. Therefore, it is impossible to have vertex-disjoint $s_1,t_1$-path and $s_2,t_2$-path that cover all vertices of $BH_n$. Hence, our result is optimal.

Fig. 9

$BH_n$ has no paired two-disjoint path cover with $2n-2$ faulty edges

Thus, this completes the proof. $\square$

4 Conclusions

In this paper, paired many-to-many two-disjoint path cover of the balanced hypercube with faulty edges is considered. We use induction to prove that the balanced hypercube $BH_n$, $n\ge 2$, is paired many-to-many two-disjoint path coverable when at most $2n-3$ edge faults occur. The upper bound $2n-3$ of edge faults tolerated is optimal. It is meaningful to explore algorithms to obtain 2-DPC in the (faulty) balanced hypercube. Moreover, the problem of the paired k-DPC with $k\ge 3$ of the (faulty) balanced hypercube is of interest and should be further investigated.