1 Introduction

The fast multipole method (FMM) is recognized as one of the top 10 algorithms of the twentieth Century [1]. Its multilevel version is developed later in computational electromagnetics and has been one of the most powerful numerical methods for computing electromagnetic scattering by electrical large objects with complex geometry due to its \(O(N\log N)\) complexity [2, 3], where N is the number of spatial degrees of freedom. Over the past two decades, researchers in computational electromagnetics (CEMS) have achieved a significant progress in the parallelization of the multilevel fast multipole algorithm (MLFMA) on homogeneous designed parallel computing architectures, for example the Intel multi-core system via the message passing interface (MPI) or OpenMP multithread programming [5,6,7,8,9,10], thereby increasing the problem size from tens of millions to billions.

Although the capability of the MLFMA is significantly improved, the actual electromagnetic engineering problem always puts a higher demand on the computing power toward real-time design. However, due to power consumption, network scalability and overheating problem, the increasing of the core CPU frequency has slowed down, and the heterogeneous many-core systems with both CPU resources and many-core accelerator resources have been recognized as a developing trend in the high-performance computing (HPC) area, the CPU and graphics processing unit (GPU) [11, 12], the CPU and Intel Xeon Phi Coprocessors (MIC) [13,14,15], the homegrown many-core processor Sunway SW26010 of China [16, 17], etc. The parallelization of MLFMA on a heterogeneous many-core system is a challenging task, not only due to the heterogeneity of the computer system, which may introduce non-uniformity in collaborative computing and bring difficulties in making full use of many-core capability, but also due to the complicated design of MLFMA itself.

Among various heterogeneous many-core supercomputer systems, the Sunway Taihulight, which took the top spot of the TOP500 list in 2016 and 2017 with a peak performance of 125 PFlops, is very special. Not only the computing performance, its power efficiency is also among the top in 2016. Its computing performance and power efficiency are outstanding when compared with existing GPU and MIC chips, but the on-chip buffer size and the memory bandwidth are relatively limited, which brings more difficulties in many-core parallel programming. Therefore, compared with those intensive researches dedicated to developing a variety of GPU parallelized algorithms of MLFMA [18,19,20,21,22], there is no successful many-core implementation of the MLFMA in computational electromagnetics (CEM) community on the SW26010 CPU to date.

Since the MPI-based parallelization of MLFMA was extensively studied in the past decade, the key of designing an efficient heterogeneous parallel implementation approach of MLFMA is how to explore capacity of the many-core fully. In this paper, an efficient many-core parallel implementation of the MLFMA based on the Athread parallel programming model on the SW26010, denoted as SW-MLFMA, is presented. A double buffering scheme is specially designed to make communication between master and slave cores overlapped with slave core computation. The arrays to be sent to slave cores are collated following the interface of structure of array (SoA) instead of array of structure (AoS) for optimum data transmission performance therefore improves data access efficiency. To ensure full utilization of computing capability, the adaptive workload distribution strategies are adopted, including pre-statistics of transmission volume and proper setting of block size of plane waves in different levels. This algorithm is shown to have a very high efficiency when solving large electromagnetic scattering problems. Numerical results show the speedup of the coefficient matrix assembly and the iterative solution is about 15 times and 5 times compared with which running on the CPU master core, respectively.

The remainder of the paper is organized as follows: In Sect. 2, the basic idea of MLFMA is outlined, followed by an introduction to the many-core programming model and architecture of SW26010 in Sect. 3. In Sect. 4, the parallelization of the SW-MLFMA is discussed in detail. Numerical analysis is presented in Sect. 5, and the conclusion is drawn in Sect. 6.

2 The formulation and implementation of the MLFMA

To present the implementation strategy of the SW-MLFMA clearly, a brief review of the MLFMA formulation and its numerical implementation is given here. Consider the scattering by a 3D object of arbitrary shape, when it is irradiated by an incident field \(({{\varvec{E}}^i},{{\varvec{H}}^i})\), the electric field integral equation (EFIE) and the magnetic field integral equation (MFIE) on the outer surface of the object are given by

$$\begin{aligned}&[{{\varvec{E}}^i} + Z{\varvec{L}}({\varvec{J}})]{|_t} = 0 \end{aligned}$$
(1)
$$\begin{aligned}&\varvec{J} - \varvec{n} \times \varvec{K}(\varvec{J}) = \varvec{n} \times {\varvec{H}^i} \end{aligned}$$
(2)

respectively, where \(|_t\) denotes the tangential components, \(\varvec{J}\) is the unknown surface current density, \(Z = \sqrt{\mu /\varepsilon }\) is the wave impedance in vacuum, \(\varvec{n}\) is the unit vector of surface outward norm. The integral operators \(\varvec{L}\) and \(\varvec{K}\) are defined as

$$\begin{aligned} \varvec{L}(\varvec{X})= & {} - jk\int {[\varvec{X} + \frac{1}{{{k^2}}}\nabla (\nabla '\varvec{X})]} G\mathrm{d}\tau ' \end{aligned}$$
(3)
$$\begin{aligned} \varvec{K}(\varvec{X})= & {} - \int \limits _{} {\varvec{X} \times \nabla \frac{{{e^{ - jkR}}}}{{4\pi R}}\mathrm{d}\tau '} \end{aligned}$$
(4)

where \(k=\omega \sqrt{\mu \varepsilon }\) is the free space wave number and \(R = \left| {\varvec{r} - \varvec{r}'} \right| \) denotes the distance between the field and source points.

To get rid of interior resonance, we can combine EFIE and MFIE together to form the combined field integral equation (CFIE) as follows:

$$\begin{aligned} \alpha \cdot Z\varvec{L}(\varvec{J}) + (1 - \alpha ) \cdot Z\left( {\varvec{J} - {\hat{\mathbf{n}}} \times \varvec{K}(\varvec{J})} \right) = \alpha \cdot \left( { - {\hat{\mathbf{n}}} \times ( {\hat{\mathbf{n}}} \times {\varvec{E}^i})} \right) + (1 - \alpha ) \cdot Z\left( { {\hat{\mathbf{n}}} \times {\varvec{H}^i}} \right) \end{aligned}$$
(5)

where \(\alpha \) is the combination parameter and is usually set to be 0.5.

Equation (5) can be discretized by following the procedure of method of moment (MoM). We first expand the unknown current density with the Rao–Wilton–Glisson (RWG) vector basis function [23] as

$$\begin{aligned} \varvec{J} = \sum \limits _{j = 1}^{{N_S}} {{\varvec{J}_j}{\mathbf{g}_j}} \end{aligned}$$
(6)

where \({N_S}\) denotes the total number of edges on S and \({\mathbf{g}_j}\) is the RWG basis function. In implementation, the surface of the particle is modeled by using small triangular patches and the RWG basis functions are associated with the edges of the triangular patches. By applying \(\mathbf{g}_i\) as the trial functions, a full matrix equation system can be obtained

$$\begin{aligned} {\varvec{Z}}\varvec{J} = \varvec{f} \end{aligned}$$
(7)

with

$$\begin{aligned} \varvec{Z}[i,j]= & {} \alpha \int _S {{\mathbf{g}_i} \cdot \varvec{L}({\mathbf{g}_j})\mathrm{d}{} \mathbf{r}} + (1 - \alpha )\int _S {(\hat{\mathbf{n}} \times {\mathbf{g}_i}) \cdot \varvec{K}({\mathbf{g}_j})\mathrm{d}{} \mathbf{r}} \end{aligned}$$
(8)
$$\begin{aligned} \varvec{f}[i]= & {} - \alpha (1/Z)\int _S {{\mathbf{g}_i} \cdot {\varvec{E}^i}(\mathbf{r})\mathrm{d}{} \mathbf{r}} - (1 - \alpha )\int _S {(\hat{\mathbf{n}} \times {\mathbf{g}_i}) \cdot {\varvec{H}^i}(\mathbf{r})\mathrm{d}{} \mathbf{r}} \end{aligned}$$
(9)

This matrix equation system can be solved efficiently via a Krylov subspace algorithm, in which the MLFMA is utilized to accelerate matrix vector multiplication. In MLFMA, the matrix vector multiplication is split into the near-field and the far-field interaction parts. The near-field interactions are calculated as in the conventional MoM, and the corresponding matrix entries are assembled and stored as a sparse matrix. The far-field interactions are calculated in a more complicated manner via a group approach in which aggregation, translation and disaggregation are performed level by level [3]. Both the operators \(\varvec{L}\) and \(\varvec{K}\) are involved in the matrix equation of CFIE; therefore, we need to solve two types of multiplication which can be expressed in terms of the multipole expansion as follows: [2, 3]:

$$\begin{aligned}&\int _S {{\mathbf{g}_i} \cdot {\varvec{L}}({\mathbf{g}_j})\mathrm{d}{} \mathbf{r}} = - {k^{ - 2}}{(4\pi )^{ - 2}}\int {{{\varvec{V}}_{1s}}(\hat{\mathbf{k}}) \cdot T(\hat{\mathbf{k}} \cdot \hat{\mathbf{r}}){{\varvec{V}}_f}(\hat{\mathbf{k}}){d^2}\hat{\mathbf{k}}} \end{aligned}$$
(10)
$$\begin{aligned}&\int _S {(\hat{\mathbf{n}} \times {\mathbf{g}_i}) \cdot {\varvec{K}}({\mathbf{g}_j})\mathrm{d}{} \mathbf{r}} = {k^{ - 2}}{(4\pi )^{ - 2}}\int {{{\varvec{V}}_{2s}}(\hat{\mathbf{k}}) \cdot T(\hat{\mathbf{k}} \cdot \hat{\mathbf{r}}){{\varvec{V}}_f}(\hat{\mathbf{k}}){d^2}\hat{\mathbf{k}}} \end{aligned}$$
(11)

where the aggregation terms \({\varvec{V}}_{1s}\) and \({\varvec{V}}_{2s}\), the disaggregation term \({\varvec{V}}_f\) and the translation term T are explicitly expressed as:

$$\begin{aligned} \begin{aligned} {\varvec{V}}_{1s}&= \int _S {e^{-j\mathbf{k} \cdot {\mathbf{r}}_{im}} ({\mathop {I}\limits ^{\leftrightarrow }} - {\hat{\mathbf{k}}}{\hat{\mathbf{k}}}) \cdot {\mathbf{g}}_i \mathrm{d}S} \\ {\varvec{V}}_{2s}&= \int _S {e^{-j{\mathbf{k}} \cdot {\mathbf{r}}_{im}} ({\hat{\mathbf{k}}} \times {\hat{\mathbf{n}}} \times {\mathbf{g}}_i) \mathrm{d}S} \\ {\varvec{V}}_f&= \int _{S'} {e^{-j{\mathbf{k}} \cdot {\mathbf{r}}_{jm'}} {\mathbf{g}}_j \mathrm{d}S'} \\ T&= \sum \limits _{n = 0}^L { (- j)^{n} (2n + 1)h_{n}^{(2)} (kr_{mm'})P_{n} ({\hat{\mathbf{k}}} \cdot \hat{\mathbf{r}}_{mm'})} \\ \end{aligned} \end{aligned}$$
(12)

where \({\mathop {I}\limits ^{\leftrightarrow }}\) denotes the \(3\times 3\) unit dyad and the integral is evaluated on the unit sphere, \(\mathbf{k}=k\hat{\mathbf{k}}\). \(\mathbf{g}_i\) and \(\mathbf{g}_j\) are the basis functions at ith and j th edges which reside in the groups m or \(m'\) centered at \({\mathbf{r}}_m\) and \({\mathbf{r}}_{m'}\), respectively, and we note \({\mathbf{r}}_{im}={\mathbf{r}}_i-{\mathbf{r}}_m\), \({\mathbf{r}}_{jm'}={\mathbf{r}}_j-{\mathbf{r}}_{m'}\) and \({\mathbf{r}}_{mm'}={\mathbf{r}}_m-{\mathbf{r}}_{m'}\). \(h_{n}^{(2)}\) denotes the spherical Hankel function of the second kind, \(P_{n}\) the Legendre polynomial of degree n and L the truncation number of multipole expansion terms.

In implementation, an octree is constructed by placing the object in a cubic box and bisecting each dimension of the cubic box recursively to generated at most eight boxes. This procedure is continued until the box size on the lowest tree level is in a specified size range. For a surface mesh of general 3D object, the number of boxes increases approximately fourfold, while the number of plane waves in each box decrease twofold at approximately the same speed in the \(\theta \) and \(\phi \)-directions from the current level to the next lower level.

In MLFMA, aggregation is performed via post-order traversal of the MLFMA tree from the lowest to the second highest level. At the lowest level, the coefficients that are provided by the iterative solver are multiplied by the aggregation matrix \(\varvec{V}_s\). Then, the radiated plane waves of the boxes at higher levels are obtained via central shifting and combining all the radiated fields of child boxes at lower levels. This procedure continues until it reaches the second level of the MLFMA tree. Disaggregation is conducted via pre-order traversal of the MLFMA tree from the second level to the lowest level, which is opposite the traversal direction for aggregation. In the disaggregation phase, not only the disaggregation operations of the plane waves from parent boxes at the higher level, but also the translation operations of the plane waves at the same level are required. At the second level, the radiated plane waves are first translated to the receiving plane waves for each group, which is then anterpolated and shifted to the centers of child boxes at the lower level. At the same time, the radiated plane waves at the lower level are translated to the receiving plane waves at the same level. Then, the total receiving plane waves at the lower level can be achieved by summing up the above two receiving plane waves. After all the receiving plane waves are achieved, the next level’s disaggregation and translation can be processed. This procedure is executed recursively until it reaches the lowest level. Then, the final far interactions can be obtained by multiplying the receiving plane waves at each smallest box with the corresponding disaggregation matrix \(\varvec{V}_f\). Note that near-field matrix, the aggregation/disaggregation matrix at the lowest level, the interpolation/anterpolation and the translation matrix at each level are assembled and stored explicitly during the setup stage of MLFMA.

3 The SW26010 architecture and the Athread many-core parallel programming model

Before presenting details of the SW-MLFMA, the key features of the SW26010 architecture and the Athread many-core parallel programming model are reviewed in this section [24, 25].

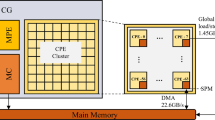
As shown in Fig. 1, the SW26010 processor is comprised of four core groups (CGs). Each CG has one management processing element (MPE), a protocol processing unit (PPU), a memory controller (MC) and 64 computing processing elements (CPEs). The MPE is like a CPU core, and the CPE cluster is like a many-core accelerator. From a micro-architecture perspective, two execution pipelines are embedded in each CPE. Both pipes can issue integer arithmetic instructions. But the Pipeline No.0 only supports floating-point operations, while the Pipeline No.1 only handles loading/storage and registering communication operations. Therefore, the computing capacity of a CPE is only about halved of that for an MPE.

There are two ways provided for accessing the main memory on SW26010: (1) transferring a chunk of data with direct memory access (DMA) or (2) using normal load/store instructions with global memory addresses (global load/store). The reading & writing bandwidth of DMA (about 22.6 GB/s) is almost an order of magnitude faster than global memory access (about 1.45 GB/s) [26]. The DMA operation is essentially asynchronous, which provides the possibility to implement hidden communication operations. Each CPE is equipped with a local 64 KB scratchpad memory (SPM). The SPM can be configured as either a fast buffer that supports precise user-controlled or a software-emulated cache that achieves automatic data caching. However, as the performance of the software-emulated cache is low, in practice we need a user-controlled buffering scheme to achieve good performance. Therefore, not only design of data transformation via DMA to reduce communication between master and slave cores, but also design of precise user-controlled SPM utilization to improve data caching is crucial to the SW26010 many-core parallel computation.

To make full use of the capacity of many-core, user-driven directive-based performance-portable parallel programming models, including OpenACC [27] and Athread [28], are specially designed for SW26010. These programming modes can help users port their codes to the SW26010 heterogeneous HPC hardware platform with significantly less programming effort. OpenACC is a user-driven directive-based performance-portable parallel programming model, which can quickly ramp-up application code in a simple way, but it can hardly achieve as high speedup as the Athread model for the parallelization of complicated algorithms such as the MLFMA. Therefore, the Athread programming model is used for the many-core implementation of MLFMA in this paper. The Athread programming model supports normal fork and join parallelism. Up to 64 threads, one thread per CPE can be started, and each thread executes the same code. It also provides a set of interfaces for DMA operations, which are asynchronous by default to facilitate overlap between computation and data communication. Details of the many-core parallelization of MLFMA with Athread are given in the following section.

Fig. 1
figure 1

Architecture of the SW26010 many-core processor

Full size image

4 The SW-MLFMA algorithm

The implementation of the SW-MLFMA algorithm contains two main parts: One is the setup stage, in which all the matrices to be used, including the near-field matrix, the aggregation/disaggregation matrix at the lowest level, the interpolation/anterpolation and the translation matrix at each level, are assembled and stored in the main memory. The other is the iterative solution stage, in which the evaluation of the far-field interaction \({\varvec{Z}_{far}}\varvec{J}\) and the near-field interaction \({\varvec{Z}_{near}}\varvec{J}\) are done repeatedly. To get a higher parallel efficiency, three main optimizations are employed.

The first optimization is the structure of array to improve data accessing efficiency. Take the mesh data to be used for filling matrices as an example. Conventionally, different types of mesh data are stored in sequence in different arrays by the global number, edge index, patch index, coordinate index, etc., which is essentially arranged based on array of structure. However, in MLFMA, when these arrays are used for filling matrices, they are extracted in the unit of a small box that was defined by the MLFMA tree, which are usually not continuous in memory, as illustrated in Fig. 2. Theoretically, each access operation to the main memory in DMA takes 278 clock cycles, while an SPM access by CPE only takes 4 clock cycles. The discontinuity of data will increase the number of times of DMA data transmission and reduce the computational efficiency. Therefore, in the process of data preprocessing, the original mesh data need to be reordered in the order of calculation, or in other words, based on the structure of array. Similar optimizations are also required for these arrays storing pre-calculated matrices to be used in the iterative solution stage. By using structure of array, total times of accessing global memory are significantly reduced, which in turn improves computation efficiency.

Fig. 2
figure 2

Illustration of data structure based on SoA

Full size image

The second optimization is the double buffering scheme to make data transition between main memory and the SPM overlapped CPE’s computation. Since the SPM of each CPE in SW26010 is very small, frequent data transferring is inevitable. If we use one buffer to receive data extracted from main memory to SPM through DMA, as shown in Fig. 3, too much time will be spent on waiting for finishing receiving data. In the double buffering scheme, as shown in Fig. 4, two individual buffers of the same size are used. In addition to the first and the last round, in each round of CPE calculation, one buffer (buffer A) is used for calculation and results storage, while the other (Buffer B) is used for receiving data only. Once the current round of calculation is finished, Buffer A sends the results back to the main memory; Buffer B is used for calculation and results storage. Such operations continue until each CPE finishes all the assigned computing tasks in this part. Obviously, with the double buffering scheme, the pipelining is implemented for each CPE. Therefore, its computation capacity is better explored; thereby, the efficiency is improved.

Fig. 3
figure 3

Illustration of processor work status with one buffering scheme

Full size image
Fig. 4
figure 4

Illustration of processor work status with double buffering scheme

Full size image
Fig. 5
figure 5

Local interpolation of a higher-level plane wave by lower-level waves

Full size image

The last optimization is the adaptive workload distribution strategy to balance computation and data communication of each CPE for the aggregation/disaggregation stage. In MLFMA, the number of plane waves in each box increases about fourfold from the current level to the next higher level. Since the size of SPM for each CPE is only 64KB, it is not sufficient for storing all plane waves in a box at higher levels, which brings great difficulties in performing interpolation/anterpolation operations. To solve such problem, on these levels, plane waves of each box are partitioned stripwise along the \(\theta \) direction. In MLFMA, the plane waves are uniformly sampled in \(\theta \) and \(\phi \), which yields a Cartesian grid of sampling points. When a local Lagrange interpolation is adopted, according to the bicubic interpolation schemes, for a given \(\theta \) direction higher-level plane waves, at most four sets of lower-level plane waves along \(\theta \) are required, irrespective of the \(\phi \)-values. Therefore, the interpolation of the higher-level plane wave (the red small cube) requires at most 16 lower-level plane waves (small circles enclosed by the red dashed line), as shown in Fig. 5. Hence, the interpolation matrix is highly sparse and has at most 16 nonzero entries per row. Then, we can estimate the total memory cost \(M_{total}^l\) per stripwise \(\theta \) range of the l level as:

$$\begin{aligned} M_{total}^l = M_{pw}^l + M_{pw}^{l +1} + M_{interpol}^{l} \end{aligned}$$
(13)

with \(M_{pw}^l \) and \(M_{pw}^{l + 1}\) denoting the memory cost for storing required plane waves on the current level and its lower level in single precision complex , \(M_{interpol}^{l}\) the memory cost for storing corresponding interpolation matrix part in single precision floating point. They can be evaluated as:

$$\begin{aligned} M_{pw}^l= \,& {} 2 \times {N_{R}^l} \times 2{L^l} \times 8 \end{aligned}$$
(14)
$$\begin{aligned} M_{pw}^{l + 1}=\, & {} 2 \times 4{N_{R^l}} \times 2{L^{(l+1)}} \times 8 \end{aligned}$$
(15)
$$\begin{aligned} M_{interpol}^{l}= \,& {} {N_{R}^l} \times 16 \times (4+4) \end{aligned}$$
(16)

where \(L_h\) and \(L_l\) are, respectively, truncation number of series for higher and lower MLFMA levels and \({N_{R}^l}\) the total plane waves per \(\theta \) strip. Taking into consideration that the \(M_{total}^l\) should be no greater than the size of SPM (64KB) and \(N_{R}^l\) should be as large as possible to reduce total number of DMA operations, an optimal value of \({N_{R}^l}\) can be getting. For a given 3D objects, \({N_{R}^l}\) varies of different levels. Since each box of the same level has the same number of planewaves, the \(N_{R}^l\) is predetermined automatically. Such procedure is done during the setup stage of MLFMA with neglectable time. Similar treatment is done for the anterpolation stage. Note the interpolation matrix and plane waves should be stored continuously by \(\phi \) per \(\theta \) to improve data accessing efficiency, which in fact follows the rule of structure of array.

5 Numerical results and analysis

In this section, a variety of numerical examples are presented to demonstrate the accuracy and efficiency of the SW-MLFMA. All the numerical examples are solved by the generalized minimum residual method (GMRES) with a targeted relative residual error of \(5 \times {10^{ - 3}}\). The single precision floating-point arithmetic is used. The CPU-MLFMA is executed on only one MPE. The SW-MLFMA is executed on a CPE Cluster equipped with 64 CPEs.

We first validate our code. The scattering by a conducting sphere with radius of 5m is simulated. The sphere is illuminated by a 0.3 GHz plane wave. Its surface is discretized into 80,000 triangular patches with 120,000 unknowns. The VV-polarized bistatic radar cross section (RCS) is computed in Fig. 6. Good agreement between the CPU-MLFMA, the SW-MLFMA and Mie series is observed. To show effectiveness of these optimization methods aforementioned, including SoA , double buffering scheme and adaptive workload distribution strategy, the running time for different parts is summarized in Table 1, in which \({\varvec{V}_{s}}\) and \({\varvec{V}_{f}}\) represent aggregation and disaggregation matrix assembly, \({\varvec{Z}_{near}}\) represents the near-field system matrix assembly and GMRES represents the iterative solution, respectively. Significant time reductions are obtained with these optimization methods.

Fig. 6
figure 6

Scattering analysis of a conducting sphere with 120,000 unknowns

Full size image
Table 1 Time reduction of optimization methods
Full size table

Next we investigate the data transfer overhead of the implementation. Wall clock time taken by different parts of the code is summarized in Table 2. As can be seen from this table, the data transfer overhead for the matrix assembly part can be nearly neglected. Hence, the matrix assembly part is computationally intensive and is easy to achieve a very high speedup. In contrast, the data transfer overhead plays an important role in the GMRES iterative solution procedure and therefore caused significant drawback on the overall speedup.

Table 2 Time of calculation and data transmission
Full size table

To study parallel computational efficiency of the SW-MLFMA, we consider the scattering by two larger conducting spheres with radius of 10 m and 14 m at 0.3 GHz, respectively. The former is discretized into 480,000 edges, and the latter is discretized into 904,800 edges. Tables 3 and 4 show details of the computation time for different parts for the two spheres. As we can see from this table, the speedup of near-field system matrix assembly part is over 15 times, which is significant because it is computation dense and gives full play to the CPE ability. Compared with near-field matrix assembly, far-field iteration takes up more time in data transmission; therefore, the speedup is not as large. The total speedup decreases as the number of unknowns increases, because the GMRES solution part plays a more important role than the matrix assembly part with increment of sphere size. However, the overall speedup achieved is still between 6.4 and 7.5 times, which is excellent.

Table 3 Speedup of a 10-m conducting sphere with 480,000 unknowns
Full size table
Table 4 Speedup of a 14-m conducting sphere with 940800 unknowns
Full size table

To further illustrate the capability and efficiency of the proposed method, an aerocraft model with 1209204 unknowns is considered (Fig. 7). The HH-polarized and VV-polarized bistatic RCSs for the aerocraft unknowns are shown in Fig. 8; details of the computation are listed in Table 5. We can see from this table similar speedups with those for the conducting sphere can be observed. The speedup for near-field system matrix assembly is over 21 times, the speedup of the GMRES iterative solution is 5 times, and the total speedup is 8 times. Comparing Table 3 and 4, it is easy to observe that for the problems with a similar number of unknowns, the speedup for each part is similar. Hence, the parallelization scheme is very robust and is insensitive to the geometrical shape of the object.

As can be seen from these numerical examples, excellent speedup is achieved in the matrix assembly, which increases as the number of unknowns grows. For different numbers of unknowns, the acceleration in the GMRES iterative solution remains almost the same because the data communications between the MPE and CPE take the majority of the time. The same phenomenon is observed for the GPU implementations given in references [19, 21, 22], where the speedup for the near-field system matrix filling is over 4 times of that for the iterative solution. This drawback is due to the design of MLFMA, independent of computer architecture.

Fig. 7
figure 7

Aerocraft with 1209204 unknowns

Full size image
Fig. 8
figure 8

Scattering analysis of an aerocraft with 1209204 unknowns

Full size image
Table 5 Speedup of an aerocraft with 1209204 unknowns
Full size table

6 Conclusion

In this paper, a many-core parallel implementation of the MLFMA on China’s homegrown SW26010 processor is presented for computing 3D electromagnetic scattering problems. The data structure of SoA is applied to reduce the number of data transmission times. The adaptive workload distribution strategies for different MLFMA tree levels are designed to ensure full utilization of CPE computing capability. A double buffering scheme is employed to make communication overlapped computation. Several examples are given to illustrate the effectiveness of the optimization method. The RCS from a practical aircraft model is also presented. Numerical results show the total speedup of the SW-MLFMA achieved is between 6.4 and 8.0 times compared with the CPU-MLFMA on the MPE, which can be quite important on heterogeneous supercomputers with many-core accelerators. Although the architecture of SW26010 is special, the basic idea of many-core parallel implementation of the MLFMA and optimizations presented in this paper are also very helpful for the case of other heterogeneous HPC hardware platforms, such as the CPU and GPU.