1 Introduction

The multilevel fast multipole algorithm (MLFMA) is a powerful and essential tool in computational electromagnetics (CEM), particularly for large-scale objects in stealth and anti-stealth design, as documented in various studies [1,2,3]. To extend the solvable problem scale of MLFMA, researchers have proposed several approaches for the distributed memory parallelization of MLFMA over the last few decades. These methods involve the utilization of message passing interface (MPI), hybrid MPI-OpenMP parallel implementations, the fast Fourier transform (FFT)-based method, etc. [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. With these efficient parallel implementations of MLFMA, problems with over ten billion unknowns can now be addressed [17].

To improve the computational capability of pure CPU systems, which is limited by the power and heat dissipation, heterogeneous multicore systems with many-core accelerator become popularized, the CPU and graphics processing unit (GPU), the CPU and Intel Xeon Phi Coprocessors (MIC), the homegrown many-core processor Sunway SW26010, etc. As the first supercomputer system with peak performance greater than 100P in the world, the computing performance and power efficiency of Sunway Taihulight are outstanding [20, 21]. Compared with MIC and GPU, the SW26010 processor of Sunway Taihulight also has several unique hardware features, such as the utilization of scratchpad memory (SPM) for each computing processing element (CPE), direct memory access (DMA) to transfer data between the main memory and the SPM and the design of register communication channels. Due to the challenges in many-core parallel programming on SW26010 processor brought by its special architecture, comparison with progresses on GPU accelerated parallel implementation of MLFMA has been made [22,23,24,25,26,27], and fewer successful many-core implementation of the MLFMA in CEM community has been proposed [28].

In this article, we extend our prior work in [28] to address electrically large-scale scattering problems through the development of a massively parallel, distributed memory, many-core accelerated parallel MLFMA algorithm on SW26010 processors, denoted as SW-PMLFMA. The proposed SW-PMLFMA algorithm partitions the MLFMA octree tree among processes using a ternary partitioning scheme [17]. Each MPI process’s computationally intensive components are then accelerated using the CPEs in the same core groups (CG). We employ a hierarchical parallelization strategy that simultaneously partitions both boxes and planewaves to ensure even workload distribution among all CPEs on higher MLFMA levels. We use the compressed sparse row (CSR) and compressed sparse column (CSC) sparse matrix storage formats for interpolation and anterpolation matrices, which are tailored to local Lagrange interpolation. To enhance data access efficiency in interpolation and anterpolation operations, we designed a hybrid dynamic and static buffer cache scheme. Further optimizations, such as the double buffering scheme and the structure of array (SoA) interface, are employed to improve the algorithm’s performance. We demonstrate the efficacy of the proposed SW-PMLFMA algorithm through various simulation results, which shows that it achieves high efficiency without sacrificing accuracy.

The structure of this article is as follows: Sect. 2 provides an overview of the MLFMA and its ternary parallelization approach, while Sect. 3 describes the architecture of the SW26010 many-core processor and the Athread programming model. Section 4 details the implementation of the SW-PMLFMA algorithm. In Sect. 5, we present the results of our numerical simulations, and Sect. 6 concludes the paper.

2 An outline of MLFMA for 3-D electromagnetic scattering and its ternary parallelization approach

The surface integral equation method and its multilevel fast multipole algorithm (MLFMA) acceleration are briefly reviewed in this section. For a general three-dimensional (3-D) object irradiated by an incident field\({\left( {{{{\textbf {E}}}_i},\;{{{\textbf {H}}}_i}} \right) }\), the combined field integral equation (CFIE) can be obtained as [3]:

$$\begin{aligned} \begin{aligned}&\alpha {\hat{{\textbf {n}}}} \times {\eta _0}\mathcal{L}({{\textbf {J}}}) \times {\hat{{\textbf {n}}}} + (1 - \alpha ){{\hat{{\textbf {n}}}}} \times {\eta _0}\left[ {\mathcal{K}({{\textbf {J}}}) + 0.5{{\hat{{\textbf {n}}}}} \times \mathcal{I}} \right] \\&\quad = - \alpha {{\hat{{\textbf {n}}}}} \times {{\textbf {{E}}}^{inc}} \times {{\hat{ {\textbf {n}}}}} - \left( {1 - \alpha } \right) {\eta _0}{{\hat{{\textbf {n}}}}} \times {{{\textbf {H}}}^{inc}} \end{aligned} \end{aligned}$$
(1)

where \(\alpha\) denotes the combined coefficient, \({{\hat{{\textbf {n}}}}}\) denotes the unit normal vector, \({\eta _0}\) is the impedance in free space. \(\mathcal{L}\) and \(\mathcal{K}\) are integral-differential operators defined by:

$$\begin{aligned} \mathcal{L}({{\textbf {J}}}):= & {} - j{k_0}\int _{S}^{\prime} {\left( {\mathcal{I} + \frac{1}{{k_0^2}}\nabla \nabla \cdot } \right) {{\textbf {J}}}(r)^{\prime}} G({{\textbf {r}}},{{\textbf {r}}}^{\prime})d{S^\prime } \end{aligned}$$
(2)
$$\begin{aligned} \mathcal{K}({{\textbf {J}}}):= & {} P.V.\int _{S}^{\prime} \nabla G({{\textbf {r}}},{{\textbf {r}}}^{\prime}) \times {{\textbf {J}}}({{\textbf {r}}}^{\prime})d{S^\prime } \end{aligned}$$
(3)

where \({G({{\textbf {r}}},{{\textbf {r}}}^{\prime}) = ({e^{ - j{k_0}R}}/4\pi R)}\) is the Green’s function in free space with \({R = |{r - r'} |}\), \({k_0} = {{2\pi } / {{\lambda _0}}}\). \(\mathcal{I}\) denotes the identity operator, \({{\textbf {J}}}\) represents the equivalent electric currents, and P.V. stands for the Cauchy principal value integration.

Following the procedure of method of moments (MoM), by using the Rao-Wilton-Glisson (RWG) functions as the basis functions, and applying the Galerkin’s method, a system of linear equations can be obtained:

$$\begin{aligned} \left[ {{Z_{mn}}} \right] \left\{ {{J_n}} \right\} = \left\{ {{f_m}} \right\} \end{aligned}$$
(4)

with

$$\begin{aligned} Z_{mn}^{}{} & {} = \alpha \int \limits _S {{{{\textbf {g}}}}_m} \cdot \left[ {\hat{{\textbf {n}}}} \times {\eta _0}\mathcal{L}({{{\textbf {g}}}_n}) \times {{\hat{{\textbf {n}}}}} \right] \text {d}S \nonumber \\{} & {} \quad + (1 - \alpha )\int \limits _S {{{{\textbf {g}}}_m} \cdot {{\hat{{\textbf {n}}}}} \times {\eta _0}\left[ {\mathcal{K}({{\textbf {J}}}) + 0.5{{\hat{{\textbf {n}}}}} \times \mathcal{I}} \right] \text {d}S} \end{aligned}$$
(5)
$$\begin{aligned} {f_m}{} & {} = \int \limits _S {{{{\textbf {g}}}_m} \cdot \left[ { - \alpha {{\hat{{\textbf {n}}}}} \times {{{\textbf {E}}}^{inc}} \times {{\hat{{\textbf {n}}}}} - \left( {1 - \alpha } \right) {\eta _0}{\hat{{\textbf {n}}}} \times {{{\textbf {H}}}^{inc}}} \right] \text {d}S} \end{aligned}$$
(6)

where g represents the RWG basis function. The full matrix equation system (4) can be solved iteratively by using Krylov subspace methods such as the generalized minimal residual method (GMRES), with MLFMA to accelerate the matrix–vector multiplication with a complexity of \(O(N\log N)\).

MLFMA can be employed to accelerate matrix–vector multiplications. The interaction can be separated into near-field and far-field interactions. The near field is calculated using conventional MoM, while the far field is computed in a group-wise manner by traversing the MLFMA octree level by level. The octree is constructed by recursively bisecting the dimensions of a cubic box until the size of the box on the lowest level is below a given threshold. The calculation of far-field interaction involves three operators: aggregation, translation and disaggregation. In contrast to FMM (fast multipole method) for Laplace equations, where the number of plane waves in a box remains constant, MLFMA for electromagnetic scattering problems solving Helmholtz equation has a twofold increase in the number of planewaves for a parent box at approximately the same rate in the \(\theta\)- and \(\varphi\)-directions as its child boxes. In the aggregation stage, plane waves from child boxes at the lower level are interpolated and centrally shifted to obtain higher-level plane waves of their parent boxes. In the disaggregation stage, incoming plane waves at the centers of boxes are anterpolated and shifted to the centers of their child boxes at the lower level. During disaggregation, translation operations of plane waves at the same level are required. The translation operators used here are diagonal in nature [2].

The key in designing a scalable parallelization approach of MLFMA is how to partitioning the weighted MLFMA tree among processes properly. In distributed memory parallelization of MLFMA, workload of each MLFMA level can be partitioned among MPI processes by boxes, by planewave directions, or both two simultaneously. The use of different partitioning strategies results in different parallelization approaches, the simple, the hybrid [4], the hierarchical [8] and the ternary [17]. The advantages of available partitioning strategies are integrated by the ternary parallelization approach, addressing the disadvantages presented by other methods. A parallel efficiency comparable to the hierarchical parallelization approach is achieved, and the restriction on the number of MPI processes utilized is substantially reduced.

In the ternary parallelization approach, several higher levels of the MLFMA tree are termed as plane wave partitioning (PWP) levels, on which each box partitions all its plane waves evenly on MPI processes along only the \({\theta }\)-direction. Lower levels are termed as box partitioning (BP) levels, and boxes of the same level are partitioned among MPI processes. The rest levels are hierarchical structure partitioning (HSP) levels, which switch the partitioning patterns of PWP and HSP by partitioning boxes into groups, and then partitioning planewaves in each box on a group of MPI processes along the \({\theta }\)-direction. Readers can refer to [17] for technical details of the ternary parallelization approach of MLFMA.

3 SW26010 many-core architecture and the Athread programming model

In this scholarly article, a comprehensive exposition of the SW26010 many-core architecture and the Athread programming model is presented by the authors, followed by a detailed exploration of the SW-PMLFMA.

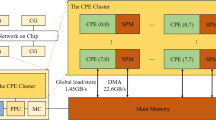
The SW26010 processor is characterized by its heterogeneity and is distinguished from prevailing pure CPU, CPU-MIC, and CPU-GPU architectures. It is composed of four CGs, within each of which one management processing element (MPE) and a CPE cluster of 64 CPEs are housed. As shown in Fig. 1, in a single SW26010 processor, four MPEs and 256 CPEs are encompassed.

The four CGs are interconnected by an on-chip network and typically used as four independent nodes. Additionally, each CPE has two execution pipelines, and its computational power is approximately half that of the MPE. Moreover, two types of memory spaces are featured in the SW26010 processor: an 8GB main memory assigned to each MPE, and a distinct local 64 KB SPM dedicated to each CPE.

The main memory can be accessed directly by all CPEs through global load/store with a bandwidth of 1.45GB/s. Data can also be transferred into the SPM of a CPE with a bandwidth of approximately 22.6GB/s via DMA channels. Additionally, the DMA operation is asynchronous, enabling users to implement hidden communication operations easily. Utilizing the SPM fully and reducing data communications are critical in SW26010 many-core acceleration computation.

Fig. 1
figure 1

SW26010 many-core architecture

Full size image

For SW26010, MPI and Athread parallel programming models are used for different aims. MPI is a widely-used, standardized, and portable message passing interface that facilitates the management of parallel computations across diverse computational grids. On the other hand, Athread is a directive-based, user-driven and performance-portable parallel programming model that leverages the parallelism of many-core processors. It enables the use of normal fork and join parallelism with up to 64 CPEs in the same CG, with one thread per CPE. In addition, it offers a set of DMA operation interfaces. The processing on the CPEs can be executed asynchronously to the MPE, and a hybrid MPI and Athread parallel programming model using the MPE and CPE asynchronous computing pattern is depicted in Fig. 2. The serial phase of the program on each MPI process is first executed on the MPE, followed by the parallel phase where CPEs in the same CG undertake a computation-intensive task. Upon completion of the parallel work by every CG, the MPE host process resumes runtime and executes instructions in the serial phase.

Fig. 2
figure 2

MPI and Athread parallel programming model

Full size image

4 Many-core acceleration implementation of the ternary PMLFMA

The MLFMA ternary parallelization approach involves a two-part computation process, namely the setup and the iteratively solution parts. During the setup stage, the near-field matrix, as well as the aggregation/disaggregation matrix at the lowest level, interpolation/anterpolation and translation matrix at each level, is explicitly distributed and stored. In the iteratively solution procedure, each matrix–vector multiplication (MVM) computation is further divided into near- and far-field interactions. The near-field interaction involves a sparse matrix–vector multiplication (SpMV), while the far-field interaction comprises three stages, namely the aggregation, the translation and the disaggregation. To accelerate the computation on SW26010 processors, we propose a many-core accelerated massively parallel MLFMA, which we abbreviate as SW-PMLFMA. This approach is implemented using a hybrid MPI and Athread programming model. The execution order of the different stages of the SW-PMLFMA is illustrated in Fig. 3. In the subsequent sections, we provide a detailed description of the primary stages of the proposed approach.

Fig. 3
figure 3

Specific implementation process of SW-PMLFMA

Full size image

4.1 Setup stage

At the very beginning of the program, preparation tasks include the auxiliary tree-based parallel mesh refinement, the constructing and partitioning of the MLFMA octree, which are executed by using only MPE. After the preparation tasks are completed, matrices filling is done with the aid of CPEs. Since the total number of CPEs in each CG is only 64, the idea of ‘one CPE per observer’ is used. The observer stands for a near box pair for near-field matrix filling, a box for the aggregation/disaggregation matrix filling, a box pair for the translation matrix filling, etc. Taking near-field matrix filling as an example, there are far more boxes than CPEs at all the lowest MLFMA level. Hence, when partitioning workload among CPEs during near-field matrix filling, computation associated with a box is assigned to a CPE. During execution, the required mesh data for RWG basis functions in a near box pair are fetched by each CPE, followed by the calculation of corresponding nonzero entries in the near-field matrix as dictated by the MoM procedure.

As studied in [28], the mesh data need to be preprocessed based on the structure of array to make the data in the order of calculation, which significantly reduces the total times of accessing global memory and in turn improves overall computation efficiency. The double buffering scheme proposed in [28] is also adopted to make data transition between main memory and the SPM overlapped CPE’s computation. Similar optimizations are also required for these arrays used for filling far-field matrices, the aggregation/disaggregation matrix, the interpolation/anterpolation matrix, the translation matrix, etc. In the study, the asynchronous features of SW26010’s MPE and CPE were leveraged. For instance, data requisite for double buffering was prepared by the MPE during the CPE’s near-field matrix population. Concurrently, while the CPE populated the far-field matrix and transfer matrix, the right-hand side was computed by the MPE, and other auxiliary arrays were filled.

Since the SPM of each CPE in SW26010 is very small, frequent data transferring is inevitable. The storage formats of different matrices should be carefully designed to improve data access efficiency in the iterative solution procedure through DMA. When local Lagrange interpolation is adopted to match different sampling rate of planewaves between successive levels, each target point in the fine grid has contributions from at most 16 neighboring points in the coarse grid, as shown in Fig. 4. The interpolation operation is in fact a SpMV products when local Lagrange interpolation is adopted, where the number of nonzero entries for each row of an interpolation matrix is no more than 16. The anterpolation matrix is the transpose of the interpolation matrix; therefore, the number of nonzero entries for each column of an anterpolation matrix is no more than 16. In coincidence with the special characteristic of local Lagrange interpolation, the CSR and the CSC sparse matrix storage format is used for storing interpolation and anterpolation matrices, respectively. To reduce the amount of storage that is required, the symmetry of the plane waves is used on the BP levels, which can significantly save the memory for storing lowest level aggregation/disaggregation matrix, the translation matrix and the interpolation/anterpolation matrix can be achieved.

Fig. 4
figure 4

Local interpolation of a higher-level plane wave by lower-level waves

Full size image

4.2 Iterative solution stage

After finishing the setup stage, the final matrix equation system is solved iteratively, with the aid of MLFMA to speed up MVM in each iteration. These coefficients are multiplied by the near-field matrix to evaluate the near interaction. The near interaction evaluation can be done with the aid of CPEs using the idea of ‘one CPE per box’. The acceleration of near interaction is simple and straightforward. Since the SPM is too small, matrix entries associated with a near box pair and the corresponding coefficients are transferred to SPM via DMA. After finishing computation, the resulting data are transferred back to the main memory, and then the next computation begins. The double buffering scheme is also used to make computation and data transformation overlapped. The far-field interaction calculation is far more complicated. At the very beginning, the coefficients provided by the iterative solver are multiplied by the aggregation matrix to obtain the radiation patterns. Since the number of edges and planewaves in a box is limited, the idea of ‘one CPE per box’ is used for aggregation on the lowest level. Each lowest level box is assigned to a CPE, and contributions from each edge source in the box to different direction planewaves is calculated in sequence. The contribution to a same plane wave from all edges in a box should be summarized to obtain the result. Then, the radiated plane waves of the child boxes at the lower level are interpolated and central shifted to obtain the radiation plane waves of boxes on the higher level. This process persists until the second level of the MLFMA tree is achieved. Different parallelization strategies are adopted for CPEs at different MLFMA tree levels. On these levels that the total number of boxes partitioned to the process is far greater than 64, the idea of ‘one CPE per box’ is used in the simple partitioning strategy. However, on the remaining high levels, for example the second highest level, the number of nonempty boxes is comparable or even smaller than the number of CPEs. If we still use the simple partitioning strategy, serious load unbalance occurs. To overcome this problem, the hierarchical partitioning strategy is selected, the idea of ‘one CPE group per box’ and ‘one CPE per planewave group’ is used. Firstly, 64 CPEs are divided into groups with the same number of CPEs, and then partitioning plane waves in a box is partitioned along the \({\theta }\)-direction on CPEs in the same CPE group. Being aware of that the number of plane waves in each box decreases twofold in the \({\theta }\)-direction from the current level to the next lower level, the number of CPE group should increase at the same speed, as shown in Fig. 5.

Fig. 5
figure 5

Illustration of hierarchical partitioning scheme for aggregation on high levels

Full size image

The interpolation operation between plane waves on two successive levels is in fact a SpMV products, in which the input and output vectors are plane waves of a child box and its parent, respectively. As discussed in the last section, when local Lagrange interpolation is adopted, nonzero entries of each row of the interpolation matrix which is stored in CSR format, is no greater than 16. Hence, in each interpolation operation of a child box, the rows of the interpolation matrix are partitioned into several subblocks. In each time, all nonzero entries of a subblock is transferred into SPM via DMA. On lower MLFMA levels, the box size is limited, plane waves in each child box can be cached in the SPM completely. However, on higher levels, the memory requirement for caching the whole plane waves of a box exceeds SPM size. If the input vector is stored in main memory, a notable computational deficiency is introduced due to the costly memory access latency from irregular access patterns to the input vector.

To solve the problem, a specially designed cache mechanism of hybrid dynamic and static buffers using the SPM is proposed in Fig. 6. In the proposed buffer scheme, a large fixed size static buffer and a small dynamic buffer are used. In each computation, the static buffer first caches a fixed length of continuous input vector entries in it, where the start row number equals to the column number of the first nonzero submatrix entry. During calculation, if row number of a required input vector entry is judged to be not cached in the static buffer, it will be searched in the dynamic buffer. If it still not founded in the dynamic buffer, a small length of row continuous input vector entries, with the not founded one as the first, will be fetched from the main memory into the dynamic buffer. Such procedure continues until the SpMV is finished. The result vector is stored continuously and finally transferred back to main memory and stored in the corresponding position.

Fig. 6
figure 6

Dynamic and static combination buffer

Full size image

The disaggregation is conducted oppositely the traversal direction for aggregation. The parallelization strategy used for disaggregation is similar to the aggregation stage. The anterpolation operation in disaggregation is also a SpMV, with the input and output vectors are plane waves of a parent box and its child, respectively. For the same two boxes, the anterpolation matrix is the transpose of the interpolation. When stored in CSC format, the nonzero entries of each column are stored continuously, with maximum number of nonzero entries no greater than 16. Different from the interpolation computation, the input vector entries are continuously cached into SPM, while the output vector entries are stored using the hybrid static and dynamic buffer scheme, where the dynamic buffer is used for writing data back to the main memory. The use of hybrid dynamic and static buffers scheme improves data access efficiency significantly, which in turn improves the computation efficiency. During disaggregation, translation operations of plane waves belonging to the second near boxes on the same level are done at the same time. The parallelization strategy used for disaggregation is also the same as that for the aggregation and disaggregation stages. At the lowest level, the incoming plane waves are multiplied by the disaggregation matrix and received by the testing functions. The final calculation results are then summed with the near interaction results to complete the matrix–vector multiplication.

5 Numerical results and analysis

This section presents a series of numerical experiments to assess the accuracy, efficiency and performance of SW-PMLFMA on the Sunway Taihulight supercomputer. The computational frequency of each MPE and CPE of an SW26010 CPU was 1.45GHz, with MLFMA being executed solely on MPEs, while SW-PMLFMA was executed with 64 CPEs to enhance the computation. The proposed approach was firstly validated by comparing the Radar Cross Sections (RCSs) of a conducting sphere with Mie series, where a 30 m diameter sphere was illuminated by a 0.6 GHz plane wave and discretized into 786,597 triangular patches with 2,312,652 unknowns. In total, 28 CGs were employed for the computation. The calculated results, together with Mie series and MLFMA, are presented in Fig. 7. According to this figure, the calculated results of the SW-PMLFMA well agree with the Mie series, with a root mean square (RMS) error of 0.2186 dB. The RMS error of RCS is defined as follows:

$$\begin{aligned} \text {RMS} = \sqrt{\frac{1}{{{N_s}}}\sum \limits _{i = 1}^{{N_s}} {{{\left| {{\sigma _{\text {ref}}} - {\sigma _{\text {cal}}}} \right| }^2}} } \end{aligned}$$
(7)
Fig. 7
figure 7

VV-polarized bistatic RCS of a sphere of diameter 30 m, where 0 and 180 correspond to the back-scattering and forward-scattering directions, respectively

Full size image

The computational statistics for the sphere with diameter 30 m were presented in Table 1, in which ‘MPE’ and ‘CPE’ represent the MLFMA and the SW-PMLFMA, respectively. \({V_s}\) and \(V_f\) denote aggregation and disaggregation matrix assembly on the lowest MLFMA level, and \({Z_{\text {near}}}\) denotes near-field matrix assembly. As the table shows, the speedup of near-field system matrix assembly part was over 14 times, which was significant because it was highly computational dense. However, the speedup achieved in the aggregation/disaggregation/translation process was not as pronounced, owing to the fact that the speedup of the far interaction was restricted not only by the data communications between the MPE and CPE but also by the MPI communications between MPEs. Nevertheless, the overall speedup achieved, which was almost 10 times, was a highly commendable result.

Table 1 Speedup of bistatic RCS calculation of a conductor sphere of diameter 30 m at 0.6 GHZ
Full size table

In order to demonstrate the efficiency of the parallel approach, scattering by a sphere was solved with varying numbers of CGs ranging from 4 to 40, using 1 MPI process and 64 CPEs per CG. The parallel efficiency is plotted against the number of CGs in Fig. 8. The parallel efficiency was defined as 100\(\%\) when 4 CGs were employed. It is worth noting that the parallel efficiency may occasionally exceed 100\(\%\) due to the limited number of levels in the MLFMA and the varying level sizes. As illustrated in the aforementioned figure, the parallel efficiency drops to 84.2\(\%\) when 60 CGs were employed. The decrement in computing efficacy can be attributed to the escalation in the number of CGs, resulting in a reduction of the computing time and a concomitant rise in the time taken for MPI communication.

Fig. 8
figure 8

Parallel efficiency for the solution of a sphere of diameter 30 m involving 2,312,652 unknowns

Full size image

To exemplify the efficiency and capability of the proposed method, a plane model as displayed in Fig. 9 was employed. The aircraft has a length of 38 ms and the incident plane wave frequency was set at 1.34 GHz. The calculation utilized a final mesh comprising of 1,873,675 triangular patches, resulting in a total of 5,473,044 unknowns. In the process, 80 MPEs and 5,120 CPEs were utilized, and simulation details are presented in Table 2. The near-field system matrix assembly part demonstrated a speedup of approximately 10 times, whereas the overall speedup achieved was nearly 9 times, indicating an exceptional performance of the proposed method.

Fig. 9
figure 9

Geometric illustration of an aircraft model

Full size image
Table 2 Speedup of bistatic RCS calculation of an aircraft at 1.34 GHZ
Full size table

In order to compare the method presented in this manuscript with the approach mentioned by the authors in [27], numerical experiment is conducted on both the GPU and the SW26010 platforms using the same example. For fairness, NVIDIA Tesla K80 GPU released at almost the same time as SW26010 was chosen. The chosen platform was equipped with an NVIDIA Tesla K80 GPU and two Intel E5-2640V4s, with a total power consumption of 480w. The power consumption of a single SW26010 chip has not been publicly disclosed. As reported in the Green 500 list, the total power consumption of the Sunway Taihulight supercomputer is approximately 15.3MW, with a Power Usage Effectiveness (PUE) of around 1.22, leading to a net computing power consumption of about 12.5MW. This supercomputer comprises 40,960 computing nodes, implying an average power consumption of 306w per node. A simulation was conducted on a metal sphere model using one node from the SW26010 platform and the GPU platform previously mentioned. Upon discretization, this model consisted of 197,192 triangles and 295,788 edges. The total computation time on the SW26010 platform was 41.4 s, whereas it was 45.49 s on the GPU platform. Detailed information can be found in Table 3. Taking into account the different power consumptions of the two platforms, the PMLFMA running on SW26010 was approximately 1.72 times faster than its GPU version, demonstrating the advantages and effectiveness of the proposed method and optimization measures.

Table 3 Comparison of calculation time for electromagnetic scattering of metal sphere in Tesla K80 and SW26010
Full size table

To compare the method presented in this article with the method presented in [28], we conducted numerical calculations using the same test cases. SW-MLFMA represents the MLFMA algorithm proposed in [28], while the SW-PMLFMA represents the method proposed in this article. The computations were performed on the SW26010 platform, employing the same computing resources, including 1 computing node consisting of 1 MPE and 64 CPE cores. A metal sphere model was computed after discretization, comprising 313,534 triangles and 470,301 edges. The detailed information of numerical calculation results is shown in Table 4. By utilizing the CSC/CSR sparse matrix storage format and implementing a hybrid dynamic and static buffer cache scheme, we effectively handled the challenges associated with large-scale matrix vector multiplication problems.

Table 4 Comparison of electromagnetic scattering time between SW-MLFMA and SW-PMLFMA for metal sphere
Full size table

To demonstrate the computational proficiency of the SW-PMLFMA approach, the frequency of the incident plane wave was raised to 15GHz. The aircraft model surface was discretized into 213,243,788 triangular patches, resulting in a total of 633,132,588 unknowns. In the computational procedure, a combination of 1,600 MPEs and 102,400 CPEs is utilized, leading to a peak memory usage of 2.50TB. After 63 iterations, a relative residual error of 0.005 was attained within a computation time of 103 min.

The calculated results of SW-PMLFMA and PMLFMA are presented in Fig. 10. According to this figure, the calculated results of the SW-PMLFMA well agree with the PMLFMA, with a RMS error of 0.0258 dB, while additional information regarding the simulations is tabulated in Table 5.

Fig. 10
figure 10

VV-polarized bistatic RCS of the aircraft model at 15 GHz. The target is illuminated by a plane wave that is propagating in the xy-plane at 30 degrees from the x-axis

Full size image
Table 5 Simulation details for an aircraft model
Full size table

6 Conclusions

This study introduces a hybrid approach to parallelizing the MLFMA on SW26010 processors to solve extremely large 3-D scattering problems. The approach utilizes a combination of MPI and Athread parallelization techniques, employing a flexible ternary partitioning scheme for MPI processes and a simple and hierarchical strategy for parallelization on the CPEs at various MLFMA tree levels to achieve a balanced workload. The interpolation and anterpolation matrices are stored in the CSR and CSC sparse matrix formats, respectively. To enhance data access efficiency, a hybrid dynamic and static buffer scheme is proposed. Numerical results demonstrate the effectiveness of the algorithm, with a total speedup of the SW-PMLFMA achieved between 8.8 and 9.6 times compared to the MLFMA on the MPEs. Furthermore, the study includes the results of a RCS analysis of an electrically large aircraft model, comprising over 600 million unknowns.