Optimal exact designs of experiments via Mixed Integer Nonlinear Programming

Abstract

Optimal exact designs are problematic to find and study because there is no unified theory for determining them and studying their properties. Each has its own challenges and when a method exists to confirm the design optimality, it is invariably applicable to the particular problem only. We propose a systematic approach to construct optimal exact designs by incorporating the Cholesky decomposition of the Fisher Information Matrix in a Mixed Integer Nonlinear Programming formulation. As examples, we apply the methodology to find D- and A-optimal exact designs for linear and nonlinear models using global or local optimizers. Our examples include design problems with constraints on the locations or the number of replicates at the optimal design points.

1 Motivation

Optimal design of experiments (DoE) is an old yet increasingly important subfield of statistics. Running experiments is costly, and users want to rein in cost without sacrificing statistical efficiency in their inference. Finding a formula or an analytic description of an optimal exact design for a nonlinear model is usually impossible due to technical difficulties. A practical approach is to develop efficient algorithms for finding optimal exact designs. In DoE, given a statistical model, a fixed total number of observations N and an optimality criterion, we seek the optimal number of design points, k, their locations from a pre-specified compact design space $\mathbf {X}$ and the number of replicates at each design point subject to the constraint that the number of replicates sum to N. Such an optimal design provides maximal precision for statistical inference at minimum cost (Fedorov and Leonov 2014).

There are two types of designs: large sample or approximate designs and small sample or exact designs. The former are essentially probability measures on the design space and are easier to find. In particular, when the optimality criterion is convex over the design space, we have a convex optimization problem (Kiefer 1974) and there are algorithms for searching the optimal approximate designs, including analytical tools for studying their properties and confirming optimality of the design. In practice, each of the weights at an optimal design point in an approximate design has to be multiplied by N and rounded to an integer such that they all sum to N before such an optimal approximate design can be implemented; Kiefer (1974), Pukelsheim (1993), Vandenberghe and Boyd (1999) provide details.

In optimal exact design problems, the numbers of observations at design points are integers and they sum to N. Consequently, we do not have a convex optimization problem in general and, so, finding optimal exact designs are computationally more challenging than finding approximate optimal designs (Boer and Hendrix 2000). Each optimal exact design problem has its own unique technical features that depend on the model, design criterion and N; analytic solutions are available only for some simple models, and there are no general algorithms for finding optimal exact designs (Gribik and Kortanek 1977). However, optimal exact designs are important in their own right because (i) simply rounding the approximate number of observations to take at each point from an optimal approximate design to obtain an optimal exact design may result in an inefficient design when N is small (Imhof et al. 2001); and (ii) even with a moderate sample size, a rounded optimal approximate design may not be implementable when some of the optimal proportions at some design points are very small.

There are various numerical algorithms for finding optimal exact designs based on exchange methods. They were initially proposed for the D-optimality criterion (Mitchell and Miller 1970; Wynn 1970; Fedorov 1972) and mainly for linear models. An appropriate starting design is required to initialize these algorithms and afterward, at each iteration, they delete points from the current design and add new points from a specified grid until a user specified stopping rule is met. The algorithms do not guarantee global optimality, and so they are run a few times using different starting designs to ascertain that they converge to the same optimal design. Refinements to these algorithms were continually made and include the DETMAX algorithm (Mitchell 1974), the modified Fedorov algorithm (Cook and Nachtsheim 1980) and the KL-exchange algorithm (Atkinson and Donev 1989). These are generally referred to as point-exchange algorithms, and they have been used to construct response surface designs involving random blocks (Goos and Vandebroek 2001; Goos and Donev 2006), D-optimal split-plot designs (Goos and Vandebroek 2003) or crossover designs (Donev 1998). The coordinate-exchange algorithm proposed by Meyer and Nachtsheim (1995) tackled some of the problems the point-exchange algorithms have by avoiding the explicit enumeration of candidate points where this problem occurred for both continuous and discrete and continuous factors. However, like other exchange algorithms, it still has the tendency that it gets trapped in a locally optimal design (Mandal et al. 2015; Palhazi Cuervo et al. 2016).

Mathematical programming methods provide alternative approaches to generate optimal exact designs and have been successfully applied to search for both approximate and factorial designs. Some examples for finding approximate designs include Linear Programming (Harman and Jurík 2008), Second-Order Cone Programming (Sagnol 2011), Semidefinite Programming (Vandenberghe and Boyd 1999; Duarte and Wong 2015), Semi-Infinite Programming (Duarte et al. 2015) and Nonlinear Programming (NLP) (Molchanov and Zuyev 2002). Recently, Mixed Integer Programming was also used to find mixed-level and two-level orthogonally blocked designs (Sartono et al. 2015b), orthogonal fractional factorial split-plot designs (Sartono et al. 2015a; Vo-Thanh et al. 2018) and trend robust run-order designs (Nuñez Ares and Goos 2008).

Applications of mathematical programming methods to find optimal exact designs in a general regression setting are less numerous due to the additional complexity. In Welch (1982), the design space is discretized and a convex optimization algorithm based on branch and bound is used to ensure that the optimal numbers of replicates of the D-optimal exact designs are integers. Similarly, Harman and Filová (2014) and Sagnol and Harman (2015) used, respectively, Mixed Integer Quadratic Programming (MIQP) and Mixed Integer Second-Order Cone Programming techniques (MISOCP) to find D-optimal exact designs. Both methods also require discretizing the design space, ensuring that the global optimal design is found on the discretized space. The resulting optimization problem can be solved efficiently using state-of-the-art solvers employing branch-and-bound techniques. Potential issues with the aforementioned methods include the exponential increase in the size of the optimization problem when the number of factors and the size of the candidate set of design points increase. Although coarser grids could reduce the size of the optimization problem, the resulting design may not be supported at the correct design points and can become inefficient.

Esteban-Bravo et al. (2017) showed that NLP formulations can be used to find unconstrained and constrained exact designs, and that Newton-based methods using Interior Point or Filter techniques performed well for the problem. Their formulation for finding optimal exact designs is that for finding approximate designs with the caveat that the weights are rational numbers so that all replicates are integers that sum to N, see also Leszkiewicz (2014). A general drawback of the NLP formulations is that the numerical calculation of the design criteria, such as those involving the determinant or trace of the inverse of a matrix, may suffer from numerical instabilities that result in multiple optima.

Our aim in this paper is to provide a general mathematical programming framework based on Mixed Integer Nonlinear Programming (MINLP) to find various types of optimal exact designs for a broad class of models. Some key advantages of our approach are: (i) unlike the MIQP and MISOCP formulations, our method does not require the design space to be discretized before optimization; (ii) the design points and the replicates are optimized simultaneously which leads to globally optimal designs in the original design space; and (iii) the method is flexible in that it can readily include additional user-defined constraints, such as restrictions on the distribution of the locations or the number of replicates at the design points. Moreover, the Cholesky decomposition to compute the determinant of the Fisher Information Matrix (FIM) is directly embedded into the optimization problem. From our knowledge, this is also new and, as it will be shown, improves the numerical stability and accuracy of the algorithm.

Section 2 presents the statistical background and reviews the general MINLP problem. In Sect. 3, we provide the formulations for D- and A-optimal exact design problems and extend them to find constrained optimal exact designs with various types of constraints. Section 4 implements the algorithm to generate optimal exact designs for linear models and locally optimal exact designs for several nonlinear models. Section 5 concludes with a summary.

2 Background

All our regression models addressed have a univariate response with $n_x$ independent variables ${\varvec{x}}\in \mathbf {X}\subset \mathbb {R}^{n_x}$, and the mean response at ${\varvec{x}}$ is

$$\begin{aligned} \mathbb {E}[y|\varvec{x},\varvec{p}]=f(\varvec{x},\varvec{p}). \end{aligned}$$

(1)

Here, $f(\varvec{x},\varvec{p})$ is a known differentiable function, apart from a vector of unknown model parameters $\varvec{p}\in \mathbf {P}\subset \mathbb {R}^{n_{\theta }}$ where $n_{\theta }$ is number of parameters in the model, and $\mathbb {E}[\bullet ]$ is the expectation operator with respect to the error distribution. The design space $\mathbf {X}$ is a known compact domain from which the design points are selected to observe the N outcomes.

Let $\xi$ be a k-point exact design supported at $\varvec{x}_1, \ldots , \varvec{x}_i, \ldots , \varvec{x}_k$ in $\mathbf {X}$ with $n_i$ replicates at $\varvec{x}_i$ subject to $\sum _{i=1}^k n_i=N$. Henceforth, we assume the number k of support points in the design sought is user specified, and an initial estimate for k is the number of parameters in the model, $n_{\theta }$. In what follows, let $\varvec{n}$ be the vector of all possible replicates at the design points, let $\varOmega _k^N=\{n_i:~0\le n_i < N, ~\sum _{i=1}^k n_i=N, ~1\le i \le k\}$ and let $\varXi _k^N\equiv \mathbf {X}^k \times \varOmega _k^N$ be the set of all k-point feasible designs on $\mathbf {X}$. We assume $k\ge n_{\theta }$; otherwise, there are not enough support points to estimate all the parameters in the model. The assumption that the number of support points is pre-specified by the user is a limitation, but it is sometimes not the case in practice. For instance, it can be expensive to take observations at a new design point and so it is desirable to limit the number of design points in the study; at other times, this fixed number of design points is naturally restricted. In biomedical studies, examples include the number of times blood samples can be drawn from an infant or an experimental drug is only available in a fixed number of dosages. Alternatively, since running the algorithm with various values of k presents no new technical difficulties, one may run the algorithm using different values of k and compare properties of the different optimal designs before implementation.

The quality of the design $\xi$ is measured by a convex function of its FIM, which is the matrix with elements equal to the negative of the expectation of the second-order derivatives of the log-likelihood of all observed data with respect to the parameters. When responses are independent, the global FIM of design $\xi$ is

$$\begin{aligned} \mathscr {M}(\xi ,\varvec{p})&= -\mathbb {E}\left[ \frac{\partial }{\partial \varvec{p}} \left( \frac{\partial {\mathscr {L}}(\xi ,\varvec{p})}{\partial \varvec{p}^{\text {T}}}\right) \right] = \sum _{i=1}^{k} \frac{n_i}{N} ~M(\delta _{\varvec{x}_i},\varvec{p})\nonumber \\&= \sum _{i=1}^{k} \frac{n_i}{N} \varvec{h}(\varvec{x}_i,\varvec{p}) \ \varvec{h}^{\intercal }(\varvec{x}_i,\varvec{p}) \end{aligned}$$

(2)

where $\mathscr {L}(\xi ,\varvec{p})$ is the log-likelihood function of the observed responses using design $\xi$, $\delta _{\varvec{x}}$ is the degenerate design that puts all its mass at $\varvec{x}$, $M(\delta _{\varvec{x}_i},\varvec{p})$ is the elemental FIM at $\varvec{x}_i$ and $\varvec{h}(\varvec{x}_i,\varvec{p})$ is the vector of first-order derivatives of the log-likelihood with respect to the parameters $\varvec{p}$ at $\varvec{x}_i$.

2.1 Optimality criteria

Here, we describe the design criteria and, when applicable, the theoretical tools to confirm the optimality of a design.

When errors are identically and normally distributed with independent errors, the volume of the confidence region for $\varvec{p}$ is inversely proportional to $\det [\mathscr {M}^{1/2}(\xi ,\varvec{p})]$. Consequently, minimizing the determinant of the inverse of the FIM by choice of a design leads to the most accurate estimates for the parameters. If the interest is in finding the best k-point D-optimal exact design, the optimization problem is

$$\begin{aligned} \xi _{D} = \arg \min _{\xi \in \varXi _k^N} \log \left\{ \det [\mathscr {M}(\xi ,\varvec{p})^{-1}]\right\} , \end{aligned}$$

(3)

which is equivalent to maximizing the determinant of the FIM,

$$\begin{aligned} \xi _{D} = \arg \max _{\xi \in \varXi _k^N} \log \left\{ \det [\mathscr {M}(\xi ,\varvec{p})]\right\} . \end{aligned}$$

(4)

Another common design criterion is A-optimality that minimizes the sum of the variances of all the estimated parameters in the mean function. Such a design $\xi _A$ satisfies

$$\begin{aligned} \xi _{A} = \arg \min _{\xi \in \varXi _k^N} \left\{ {\text {tr}}[ \mathscr {M}(\xi ,\varvec{p})^{-1}]\right\} . \end{aligned}$$

(5)

For a linear model, the FIM does not depend on the unknown parameters and so the optimal design does not depend on $\varvec{p}$. If it does, as when the model is nonlinear, nominal values based on experts’ opinion, previous or similar studies are used to replace $\varvec{p}$ before the criterion is optimized. The resulting design is called a locally optimal design because it depends on the nominal values (Chernoff 1953).

Approximate designs are similar to exact designs except that each $n_i$ is replaced by $w_i$, the proportion of observations to be taken at $\varvec{x}_i$. They are implemented by taking $N\times w_i$ observations at $\varvec{x}_i$ subject to each $N\times w_i$ is an integer, and they sum to N. When an optimal design is sought among all approximate designs on the design space and the design criterion is convex, the optimality of an approximate design $\xi$ can be verified using an equivalence theorem based on directional derivative considerations (Fedorov 1972; Kiefer 1974; Pukelsheim 1993). If we let $\delta _{\varvec{x}}$ be the degenerate design at the point $\varvec{x}\in \mathbf {X}$, the equivalence theorem says $\xi _D$ is a D-optimal approximate design among all designs on $\mathbf {X}$ if and only if

$$\begin{aligned} \varPsi (\varvec{x}|\xi _D,\varvec{p}) ={\text {tr}}\left\{ [\mathscr {M}(\xi _D, \varvec{p})]^{-1} \ M(\delta _{\varvec{x}},\varvec{p})\right\} \le n_{\theta }, \quad \forall \varvec{x}\in \mathbf {X}, \end{aligned}$$

(6)

with equality at every design point of $\xi _D$. The function $\varPsi (\varvec{x}|\xi ,\varvec{p})$ is the dispersion function of the design $\xi$. In Sect. 4.2, we display selected dispersion functions of the optimal exact designs we found and show that they are equivalent to optimal approximate designs when N is a multiple of $n_{\theta }$.

To compare two designs $\xi _1$ and $\xi _2$, we use their relative efficiencies. For the D-optimality criterion, the D-efficiency of $\xi _1$ relative to $\xi _2$ is defined by

$$\begin{aligned} \text {Eff}_D(\xi _1,\xi _2)= \left( \frac{\exp \left[ \log (\det [\mathscr {M}(\xi _1,\varvec{p})])\right] }{\exp \left[ \log (\det [\mathscr {M}(\xi _2,\varvec{p})])\right] }\right) ^{\frac{1}{n_{\theta }}}, \end{aligned}$$

(7)

and, similarly, for A-optimality criterion, the efficiency of $\xi _1$ relative to $\xi _2$ is defined by

$$\begin{aligned} \text {Eff}_A(\xi _1,\xi _2)= \frac{{\text {tr}}[\mathscr {M}^{-1}(\xi _2,\varvec{p})]}{{\text {tr}}[\mathscr {M}^{-1}(\xi _1,\varvec{p})]}. \end{aligned}$$

(8)

If $\xi _2$ is the optimal design sought, the above ratios become the D-efficiency and A-efficiency of $\xi _1$, respectively. The interpretation of an efficiency is that if a design has an efficiency of $50\%$, it needs to be replicated twice to do as well as the optimal design (Fedorov 1972; Pukelsheim 1993). In practice, designs with high efficiencies are desired.

2.2 Mixed Integer Nonlinear Programming

MINLP is a class of tools to optimize a nonlinear objective function $\psi (\varvec{x},\varvec{y})$ with possibly nonlinear constraints where some decision variables are integer. MINLPs arise in a wide range of applications, including chemical engineering, finance and management. If there are $n_x$ continuous variables and $n_y$ discrete variables to optimize, the general form of a MINLP is

$$\begin{aligned}&\min _{\varvec{x},\varvec{y}} \ \psi (\varvec{x},\varvec{y}) \end{aligned}$$

(9a)

$$\begin{aligned}&\text {s.t.} \ v_i(\varvec{x},\varvec{y}) =0, \quad \forall i\in \mathscr {E}\end{aligned}$$

(9b)

$$\begin{aligned}&\ g_i(\varvec{x},\varvec{y}) \le 0, \quad \forall i\in \mathscr {I} \end{aligned}$$

(9c)

$$\begin{aligned}&\ \varvec{x}\in \mathbf {X}, ~\varvec{y}\in \mathbf {Y}. \end{aligned}$$

(9d)

Here, the functions $v_i(\varvec{x},\varvec{y})$ and $g_i(\varvec{x},\varvec{y})$ map $\mathbb {R}^{n_x+n_y}$ to $\mathbb {R}$, $\mathscr {E}$ is the set of equality constraints, $\mathscr {I}$ the set of inequalities, $\mathbf {X}$ is a compact set containing continuous variables $\varvec{x}$, and $\mathbf {Y}$ is the set containing discrete variables $\varvec{y}$.

Some common algorithms to solve Mixed Integer Nonlinear Programs are the outer-approximation method (Duran and Grossmann 1986), the branch-and-bound method (Fletcher and Leyffer 1998) and the extended cutting plane method (Westerlund and Pettersson 1995). Floudas (2002) reviews the fundamentals of using MINLP to solve optimization problems and note that traditional MINLP algorithms guarantee the global optima under certain convexity assumptions.

Our design problems may have multiple local optima and to guarantee that a global optimum is found, a global solver must be employed. An example of a global solver is BARON. It implements deterministic global optimization algorithms that combine spatial branch-and-bound procedures and bound tightening methods via constraint propagation and interval analysis in a branch-and-reduce technique (Tawarlamani and Sahinidis 2002). Sahinidis (2014) showed that these techniques work quite well under fairly general assumptions. In our formulations, those assumptions are satisfied by construction as all decision variables are bounded. However, global optimization solvers still require a long computational time compared to local solvers (Lastusilta et al. 2007) and this may limit their utilization to small and average-sized problems.

A potential way to shorten the CPU time is to use a local MINLP solver, such as, SBB (GAMS Development Corporation 2013b), for handling several design problems addressed in the paper, see Sect. 4.2. In Sect. 4.1, we compare optimal designs obtained with local and global MINLP solvers, where BARON represents the latter class and SBB the former. Both MINLP tools use CONOPT as a NLP solver to handle the relaxed nonlinear programs (Drud 1985) and CPLEX to solve the Mixed Integer Linear Programs (GAMS Development Corporation 2013b).

3 Optimal design MINLP formulations

We introduce MINLP formulations for finding a k-point D- and A-optimal exact design in Sects. 3.1 and 3.2, respectively. We first focus on solving unconstrained optimal designs before we demonstrate how MINLP formulations can solve constrained optimization problems with user-selected restrictions. In Sect. 3.3, we review a common approach to initialize consistently the MINLP problems, tools for solving the optimization problems and discuss limitations of the formulations.

3.1 D-optimal designs

Given a statistical model and values for k and N, let $\mathscr {M}(\xi ,\varvec{p})$ be the FIM in (2). The formulation for finding a k-point D-optimal exact designs on $\varXi _k^N$ may be equivalently formulated as an optimization problem as follows:

$$\begin{aligned}&\max _{\xi \in \varXi _k^N} \ \log \left( \det [\mathscr {M}(\xi ,\varvec{p})]\right) \end{aligned}$$

(10a)

$$\begin{aligned}&\text {s.t.} \ \sum _{l=1}^kn_l=N \nonumber \\&\quad \ \varvec{x}\in \mathbf {X}, ~\varvec{n}\in \varOmega _k^N. \end{aligned}$$

(10b)

To maximize $\log \left( \det [\mathscr {M}(\xi ,\varvec{p})]\right)$, we apply the Cholesky decomposition to the FIM and write

$$\begin{aligned} \mathscr {M}(\xi ,\varvec{p})= \mathscr {U}^{\intercal }(\xi ,\varvec{p})~\mathscr {U}(\xi ,\varvec{p}) \end{aligned}$$

(11)

where $\mathscr {U}(\xi ,\varvec{p})$ is an upper triangular matrix and has positive diagonal elements $u_{i,i}$ when FIM is positive definite. It follows that

$$\begin{aligned} \det (\mathscr {M}(\xi ,\varvec{p}))=\prod _{i=1}^{n_{\theta }}u_{i,i}^2, \end{aligned}$$

(12)

$\log [\det (\mathscr {M}(\xi ,\varvec{p}))]=2\sum _{i=1}^{n_{\theta }} \log (u_{i,i})$ and maximizing $\det (\mathscr {M}(\xi ,\varvec{p}))$ is equivalent to maximizing the sum of the logarithm of the diagonal elements of $\mathscr {U}(\xi ,\varvec{p})$.

Hereafter, we write $i,j\in \llbracket n_{\theta }\rrbracket$ to represent indices i, j running from 1 to $n_{\theta }$. Similarly, the notation $i\in \llbracket n_{\theta }\rrbracket$ means the single index i runs from 1 to $n_{\theta }$. If $u_{i,j}$ is the $(i,j){\text {th}}$ element of $\mathscr {U}(\xi ,\varvec{p}), i,j\in \llbracket n_{\theta }\rrbracket$, our MINLP formulation for finding an D-optimal exact design is

$$\begin{aligned}&\max _{\varvec{x},\varvec{n}} \ \sum _{i=1}^{n_{\theta }} \log (u_{i,i}) \end{aligned}$$

(13a)

$$\begin{aligned}&\text {s.t.} \ m_{i,j}=\sum _{l=1}^k \frac{n_l}{N} h_{l,i}(\varvec{x},\varvec{p}) ~h_{l,j}(\varvec{x},\varvec{p}), ~\quad i,~j\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(13b)

$$\begin{aligned}&\ m_{i,j} = \sum _{l=1}^{k} u_{l,i} u_{l,j}, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\le j \end{aligned}$$

(13c)

$$\begin{aligned}&\ u_{i,i} \ge \epsilon , \quad i\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(13d)

$$\begin{aligned}&\ u_{i,j} =0, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\ge j+1 \end{aligned}$$

(13e)

$$\begin{aligned}&\ m_{i,i} \ge u_{i,j}^2, \quad i,j\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(13f)

$$\begin{aligned}&\ \sum _{l=1}^kn_l=N \nonumber \\&\ \varvec{x}\in \mathbf {X}, ~\varvec{n}\in \varOmega _k^N. \end{aligned}$$

(13g)

Here, $\epsilon$ is a small positive constant to ensure that the FIM is positive definite. For all examples in Sect. 4, $\epsilon = 1 \times 10^{-5}$. Equation (13b) follows from (2), (13c) represents the Cholesky decomposition, (13d) guarantees that all diagonal elements of $\mathscr {U}(\xi ,\varvec{p})$ are positive and (13e) assures that $\mathscr {U}(\xi ,\varvec{p})$ is upper triangular. Equation (13f) is a numerical stability condition imposed on the Cholesky factorization of positive semidefinite matrices (Golub and van Loan 2013, Theorem 4.2.8) and constraint (13g) restricts the total number of observations to be N and ensures that the design points belong to design space $\mathbf {X}$.

3.2 A-optimal design

A-optimal exact experimental plans may be formulated as follows:

$$\begin{aligned}&\min _{\xi \in \varXi _k^N} \ {\text {tr}}[\mathscr {M}^{-1}(\xi ,\varvec{p})] \end{aligned}$$

(14a)

$$\begin{aligned}&\text {s.t.} \ \sum _{l=1}^kn_l=N \nonumber \\&\quad \ \varvec{x}\in \mathbf {X}, ~\varvec{n}\in \varOmega _k^N. \end{aligned}$$

(14b)

The optimization problem (14) requires inverting $\mathscr {M}^{-1}(\xi ,\varvec{p})$ which is a potentially numerically unstable operation when the FIM is ill-conditioned. To avoid explicit computation of the inverse matrix, we apply the Cholesky decomposition to invert the resulting upper diagonal matrix $\mathscr {U}(\xi ,\varvec{p})$ that results from the decomposition of $\mathscr {M}(\xi ,\varvec{p})$; the rationale is that inverting an upper triangular matrix obtained by Cholesky factorization is numerically more stable than inverting the original matrix (Du Croz and Higham 1992). The procedure has three steps that are handled simultaneously within the optimization problem: (i) apply the Cholesky decomposition to the FIM, cf. Sect. 3.1; (ii) invert the upper triangular matrix $\mathscr {U}(\xi ,\varvec{p})$ using the relation $\mathscr {U}(\xi ,\varvec{p})~\mathscr {U}^{-1}(\xi ,\varvec{p})=I_{n_{\theta }}$, where $I_{n_{\theta }}$ is the $n_{\theta }$-dimensional identity matrix; and (iii) compute $\mathscr {M}^{-1}(\xi ,\varvec{p})$ via $\mathscr {U}^{-1}(\xi ,\varvec{p})$, i.e., $\mathscr {M}^{-1}(\xi ,\varvec{p})=\mathscr {U}^{-1}(\xi ,\varvec{p})\times [\mathscr {U}^{-1}(\xi ,\varvec{p})]^\intercal$ (Du Croz and Higham 1992), and, finally, compute ${\text {tr}}[\mathscr {M}^{-1}(\xi ,\varvec{p})]$.

Let $\overline{m}_{i,j}$ be the $(i,j){\text {th}}$ entry of $\mathscr {M}^{-1}(\xi ,\varvec{p})$ and $\overline{u}_{i,j}$ be the $(i,j){\text {th}}$ entry of $\mathscr {U}^{-1}(\xi ,\varvec{p})$ where $i,~j\in \llbracket n_{\theta }\rrbracket$. By construction, $\mathscr {U}(\xi ,\varvec{p})$ is positive definite and invertible if all the diagonal elements are positive. The same also holds for $\mathscr {U}^{-1}(\xi ,\varvec{p})$. Step (i) is the Cholesky decomposition of the FIM represented by (13c), and the second step corresponds to inverting $\mathscr {U}(\xi ,\varvec{p})$:

$$\begin{aligned}&{\left\{ \begin{array}{ll} \sum _{l=1}^{k} u_{i,l} \ \overline{u}_{l,j} =1 &{} \text {if}~ i=j \\ \sum _{l=1}^{k} u_{i,l} \ \overline{u}_{l,j} =0 &{} \text {if}~ i\not =j, \end{array}\right. } \end{aligned}$$

(15)

with step (iii) represented by

$$\begin{aligned} \overline{m}_{i,j} = \sum _{l=1}^{k} \overline{u}_{i,l} \overline{u}_{l,j}, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\le j. \end{aligned}$$

(16)

A-optimal designs minimize ${\text {tr}}(\mathscr {M}^{-1}(\xi ,\varvec{p}))$ or equivalently, minimizes the sum of all $\overline{m}_{i,i}, ~i\in \llbracket n_{\theta }\rrbracket$. The complete MINLP for computing the A-optimal designs is

$$\begin{aligned}&\min _{\varvec{x},\varvec{n}} \ \sum _{i=1}^{n_{\theta }} \overline{m}_{i,i} \end{aligned}$$

(17a)

$$\begin{aligned}&\text {s.t.} \ m_{i,j}=\sum _{l=1}^k \frac{n_l}{N} h_{l,i}(\varvec{x},\varvec{p}) ~h_{l,j}(\varvec{x},\varvec{p}), ~\quad i,~j\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(17b)

$$\begin{aligned}&\ m_{i,j} = \sum _{l=1}^{n_{\theta }} u_{l,i} u_{l,j}, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\le j \end{aligned}$$

(17c)

$$\begin{aligned}&\ \sum _{l=1}^{k} u_{l,i} \ \overline{u}_{l,j} =1, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i= j \end{aligned}$$

(17d)

$$\begin{aligned}&\ \sum _{l=1}^{k} u_{i,l} \ \overline{u}_{l,j} =0, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\not = j \end{aligned}$$

(17e)

$$\begin{aligned}&\ \overline{m}_{i,j} = \sum _{l=1}^{k} \overline{u}_{i,l} \overline{u}_{l,j}, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i\le j \end{aligned}$$

(17f)

$$\begin{aligned}&\ u_{i,i} \ge \epsilon , \quad i\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(17g)

$$\begin{aligned}&\ \overline{u}_{i,i} \ge \epsilon , \quad i\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(17h)

$$\begin{aligned}&\ u_{i,j} = 0, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i \ge j+1 \end{aligned}$$

(17i)

$$\begin{aligned}&\ \overline{u}_{i,j} = 0, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i \ge j+1 \end{aligned}$$

(17j)

$$\begin{aligned}&\ \overline{m}_{i,j} = \overline{m}_{j,i}, \quad i,~j\in \llbracket n_{\theta }\rrbracket , ~i \le j-1 \end{aligned}$$

(17k)

$$\begin{aligned}&\ m_{i,i} \ge u_{i,j}^2, \quad i,j\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(17l)

$$\begin{aligned}&\ \overline{m}_{i,i} \ge \overline{u}_{i,j}^2, \quad i,j\in \llbracket n_{\theta }\rrbracket \end{aligned}$$

(17m)

$$\begin{aligned}&\ \sum _{l=1}^kn_l=N \nonumber \\&\ \varvec{x}\in \mathbf {X}, ~\varvec{n}\in \varOmega _k^N. \end{aligned}$$

(17n)

Equations (17b, 17c, 17g, 17i, 17l) and (17n) are similar to those in the D-optimal design formulation. Equations (17d–17e) reflect relationship (15) and generate $\mathscr {U}^{-1}(\xi ,\varvec{p})$, equation (17k) captures constraint (16) to produce $\mathscr {M}^{-1}(\xi ,\varvec{p})$ and equations (17i) and (17j), respectively, impose the lower triangular structure of $\mathscr {U}(\xi ,\varvec{p})$ and $\mathscr {U}^{-1}(\xi ,\varvec{p})$. Equation (17k) imposes the symmetry on $\mathscr {M}^{-1}(\xi ,\varvec{p})$ and both equations (17g) and (17h) ensure that the diagonal elements of $\mathscr {U}^{-1}(\xi ,\varvec{p})$ and $\mathscr {M}^{-1}(\xi ,\varvec{p})$ are positive, respectively. Condition (17m) is the numerical stability insurance for the Cholesky factorization of $\mathscr {M}^{-1}(\xi ,\varvec{p})$. We impose the symmetry of $\mathscr {M}^{-1}(\xi ,\varvec{p})$ in Equation (17k) to reduce the feasibility region which may then help to improve the convergence rate of the solver. The symmetry of the FIM and its inverse are guaranteed by (17b) and (17k), respectively.

An advantage of our approach is that when there are additional constraints, such as restrictions on the number of replicates at each design point, they can be incorporated into our design formulation problem as linear or nonlinear inequalities or equalities. Specifically, we apply formulations (13) and (17) to search for k-point unconstrained optimal designs in $\varXi _k^N$, the set of feasible designs on $\mathbf {X}$. By including additional constraints in problems (13) and (17), our method can also find a constrained optimal exact designs from the set $\varXi _k^N\cap \{(\varvec{x},\varvec{n}): ~\gamma (\varvec{x},\varvec{n})\le \varvec{0}, ~ \phi (\varvec{x},\varvec{n})= \varvec{0}\}$. Here, $\gamma$ and $\phi$ are user-selected differentiable functions in the inequality and equality constraints, respectively, on the design space $\mathbf {X}$ or on the replicates space $\varOmega _k^N$, or both.

3.3 Initialization and limitations

To reduce CPU time, we provide consistent initial guesses to the MINLP solver. This means that the initial solution $\xi ^{(0)}$ has to be consistent and satisfy all constraints of the problem (Pantelides 1988). To construct $\xi ^{(0)}$, we first choose a point centrally located in $\mathbf {X}$ and then select the other grid points using the relation $\varvec{x}_i=\varvec{x}_{i-1}+\varDelta \varvec{x}$ where $\varDelta \varvec{x}=(\max \varvec{x}-\min \varvec{x})/(k-1)$ and k is the number of support points selected by the user. The replicates are then distributed so that the values of $n_i$ are equal while ensuring that their sum is N. Next, we compute the elemental and the global FIMs for $\xi ^{(0)}$, $\mathscr {U}^{\intercal }(\xi ^{(0)},\varvec{p})$ and $\mathscr {M}^{-1}(\xi ^{(0)},\varvec{p})$ and let the solver iterate until it converges to the optimum.

The formulations in Sect. 3 are coded in the GAMS environment (GAMS Development Corporation 2013a). GAMS is a general modeling system that supports mathematical programming applications in several areas. Upon execution, the code describing the mathematical program is automatically compiled, symbolically transcribed into a set of numerical structures, and all the information regarding the gradient and matrix Hessian is generated using the automatic differentiation tool and made available to the solver. We provide a sample of such a code in the Supplementary Material.

A drawback of the proposed formulations is their limited ability to find a global optimum in highly nonlinear problems, specifically. Typically, global optimizers can guarantee global optimality, but the computational burden required for finding optimal designs for models with several covariates can be massive or may not even converge within a realistic time frame. Using local optimizers lowers the computational effort but does not guarantee that the solution found is a global optimum. Therefore, the choice of using a global or a local optimizer involves a trade-off. One common strategy to further reduce the CPU time is to tighten the bounds for all the decision variables in the MINLP problem and provide an accurate initial solution. This is a particularly useful step when global optimizers are used.

Generally, our formulations (13) and (17) work well even when N or k are large unless the FIM becomes nearly singular and the model parameters have sensitivities [see Eq. (2)] of very different magnitude or the design space is multi-dimensional and the matrix inversion procedure becomes numerically unstable. However, even in these cases, we can scale properly the variables and equations to handle the problems. From our experiments in Sect. 4, the main limitations are related with the MINLP solvers currently available, and we were not able to identify a cutoff point, either on the size of the optimization problem or the FIM condition number, where the formulations fail. In this study, local solvers work surprisingly well to find a optimum for all problems addressed.

4 Numerical results

We now report D- and A-optimal exact designs for linear and nonlinear models found from our formulations. Some models were chosen for comparison with published results obtained using different numerical approaches. All computations were done using an Intel Core i7 machine running a 64 bits Windows 10 operating system with 2.80 GHz processor. In all problems, the relative and absolute tolerances used to solve the MINLP problems were set to $1 \times 10^{-5}$ and the absolute tolerance is set equal to $\epsilon$, the minimum value allowed for the diagonal entries in the FIM or its inverse so that they are positive definite matrices. The optima reported for each design in all the tables are for $\log [\det (\mathscr {U}(\xi ,\varvec{p}))]$ and ${\text {tr}}[\mathscr {M}^{-1}(\xi ^{(0)},\varvec{p})]$ for D- and A-optimality criteria, respectively (note the first is a maximizer and the last a minimizer). The efficiency of D-optimal designs is determined from (7) using the relation $\log [\det (\mathscr {M}(\xi ,\varvec{p}))]=2~\log [\det (\mathscr {U}(\xi ,\varvec{p}))]$.

We employ the formulations in Sect. 3 to find optimal designs for the models in Table 1. Models 1–2 are linear, and the design space is $\mathbf {X}=[-1,1]$ and $\mathbf {X}=[0.5,2.5]$, respectively. Some of the Models 3–8 have the same design spaces as in the original problems discussed in the literature, and the set of parameters used for constructing local designs was also preserved whenever possible. Models 3–8 are nonlinear, and we report locally optimal designs for the set of parameters listed below each model. The mean responses in Models 6 and 7 are structurally the same, except for the nominal value of the parameter m. Models 9–14 have multiple regressors and so they allow us to test our algorithm for multi-factor experiments. Model 14 is a four-factor second-order response surface model with pairwise interactions. We note that Gotwalt et al. (2009) obtained Bayesian optimal designs for models subsumed in Model 10. Specifically, they addressed optimal exact design problems by first setting $n_i=1, ~\forall i\in \llbracket N\rrbracket$, and allowing that, in result of the optimization, certain rows of the model matrix are identical. Consequently, here, the replication will become visible when multiple rows of the design are identical. Further, they set N but do not impose constraints on the number of distinct support points of the optimal design. Our framework is different as we set first set both N and the number of support points, k, and then optimize the design points and the replication, $n_i\in \varOmega _k^N, ~\forall i\in \llbracket k\rrbracket$. Rasch et al. (1997) found replication-free D-optimal designs for models 3–4, and we compare some of their optimal exact designs with ours.

We applied our algorithm to find optimal exact designs for a battery of models with one or more factors. We select these models to test our algorithms either because they are widely used in practice or their optimal designs have been analytically or numerically determined and available for comparison. Tables 7 and 8 show that models with more factors (i.e., higher dimension) may not necessarily pose additional numerical difficulty; the crucial issue usually lies in the nonlinearity of the MINLP problem. Smaller dimensional models such as Models 3 and 4 below can be more challenging for our methods to solve than models with more factors involving, for example, linear polynomial terms. That, combined with the existence of reference optimal designs, is the rationale for using Models 3–4 for comparison in next sections.

Table 1 Battery of statistical models used for testing the MINLP formulations

Table 2 D- and A-optimal exact designs for Models 3 and 4 in Table 1 obtained using a global MINLP solver

We first discuss minimally supported optimal designs where $k=n_{\theta }$ without constraints. Minimally supported designs are desirable when taking observations at a new location is expensive. Designs that have equal masses $n_{\theta }/N$ at every design point are called uniform designs (Pukelsheim 1993, Chap. 4). They are popular because of their simplicity and when appropriate, we compare our optimal designs with uniform designs. In Sect. 4.1, we first compare the optimal designs obtained with our formulations for Models 3 and 4 and use different N values to analyze the effect of different sample sizes on the design. We compare optimal designs obtained from a locally optimal MINLP solver (SBB) with those generated from a global optimization solver (BARON). In addition, we compare designs obtained from our algorithm with analytical solutions in the literature when the latter are available.

Section 4.2 presents unconstrained optimal designs obtained for the models in Table 1. Here, SBB was used to solve the MINLP optimization problems, where $N=3\times n_{\theta }$ for all cases. In Sect. 4.3, we find constrained optimal designs where the design space and/or the number of replicates are subject to restrictions. These constraints can be linear or nonlinear, and k is at least as large as $n_{\theta }$. For designs with $k>n_{\theta }$, we also set the value of k as in the minimally supported designs and then include an additional constraint in problems (13) and (17) imposing that all support points have at least one observation (i.e., $n_i\ge 1$). Practically, in our formulation these are constrained designs as they include additional constraints and will be addressed in Sect. 4.3. The D-optimal exact designs for most of the cases in Table 1 are new and so are all the A-optimal exact designs.

4.1 Comparison of results

In this subsection, we compare optimal exact designs found from our algorithm in a variety of ways: in Sect. 4.1.1, we study them using different sample sizes; in Sect. 4.1.2, we compare them with those found using a global optimal MINLP solver, and in Sect. 4.1.3, we compare them with analytical results when they are available.

4.1.1 Impact of the sample size

Table 2 presents optimal exact designs of different sizes for Models 3 and 4 found by BARON. For Model 3, $N=3\times n_{\theta }+q, ~q\in \{0,1,2\}$, and for Model 4, $N=4\times n_{\theta }+q, ~q\in \{0,1,2\}$. The generated optimal exact designs are presented as $2\times k$ matrices where the first line shows the design points and the second line shows their replicates.

The D-optimal exact designs found for $N=9$ and $N=15$ for Model 3 and 4 in Table 2, respectively, are similar to those of Rasch et al. (1997) found from an exchange algorithm. The exact D-optimal designs are uniform when N is a multiple of $n_{\theta }$, which is a general observation already made by others (Yang et al. 2012, 2016). When N is a multiple of $n_{\theta }$, the values of the optimum suggest that D-optimal designs are slightly more efficient than those found for other sample sizes. Both examples in Table 2 show that the optimum has slightly larger values of N that lead to exact designs equal to those obtained by rounding optimal approximate designs and the weights are equal for all support points. Practically, exact k-point optimal designs with unequal ratios $n_i/N$ can be slightly poorer than those where $n_i/N$ is equal $\forall i\in \llbracket n_{\theta }\rrbracket$. This finding is consistent with earlier observations for N-point D-optimal designs (Pukelsheim 1993, Chap. 4). Table 2 shows that changes in the support points of the D-optimal designs are marginal for small changes in the value of N.

The A-optimal exact designs are not uniform even when N is multiple of $n_{\theta }$ and so finding an optimal approximate design first and rounding it to obtain an exact design may result in a non-optimal exact design.

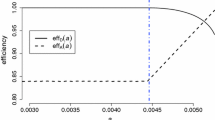
Figure 1 shows the plots of the dispersion functions of the D-optimal exact designs for Model 3 when $N=9,10,11$. It shows that the D-optimal exact design $\xi$ for $N=9$ has 3 support points and the function $\varPsi (\varvec{x}|\xi _D,\varvec{p})$ is bounded from above by $n_{\theta }$ with equality at the support points. The maxima of the dispersion functions for $N=10$ and $N=11$ are not $n_{\theta }$ implying that the D-optimal exact designs do not match the D-optimal approximate designs.

Fig. 1

Dispersion functions of the D-optimal designs for Model 3 in Table 2 when $k=n_{\theta }=3$ for different values of N

We report optimal design points to four decimal places for accuracy. In scenarios where the design variables cannot be controlled with this level of certainty, the optimal design will serve as a reference design for the implemented design, which will have a slightly lower efficiency.

4.1.2 Impact of the MINLP solver

In this section, we determine optimal designs for Models 3–4 using formulations in Sect. 3 with a local optimization MINLP solver (SBB). Table 3 displays the D- and A-optimal exact designs. When we compare them with the optimal exact designs in Table 2 found with a global optimization solver, we observe that (i) the CPU time required by the local optimization MINLP solver is on average 382 times shorter than that required by the global optimization MINLP solver; (ii) both solvers produce very similar A- and D-optimal exact designs with almost identical optimality values; (iii) both solvers produce D-optimal exact designs with replicates as equally distributed as possible and A-optimal exact designs with very different numbers of replicates at the design points; (iv) D- and A-optimal exact designs are supported at the extreme ends of the design space when the design space is small (e.g., Model 3), but this is no longer the case when the design space is large (Model 4); and (v) the largest support points of the A-optimal exact designs found by local and global optimization solvers are noticeably different.

We calculated the D- and A-efficiencies of the optimal exact designs obtained with the locally optimal MINLP solver relative to those obtained with the global optimization solver using Eqs. (7) and (8), and they are all close to 1.0000. That implies that for this set of problems, the local optimization solver is able to find designs very close to those obtained by a global optimization solver in a small fraction of time. We therefore use the local optimization MINLP solver SBB to generate all the optimal exact designs in the rest of our work. Typically, the optimal designs obtained with global optimizers are equally or more efficient than those obtained with local optimizers, an exception is the A-optimal design for Model 4 and $N=17$ in Table 3 where the design found by the global solver has an efficiency slightly below 100 %.

Table 3 D- and A-optimal exact designs for Models 3–4 in Table 1 obtained using a locally optimal MINLP solver

4.1.3 Models with analytically derived optimal designs

This section compares D-optimal designs obtained from our formulations with known D-optimal designs for some models, which are presented in Table 4. The first selected model with known D-optimal exact designs is the one with mean function equal to the first-order trigonometric regression model on a partial circle of different size and different values of N (Models 15–19 in Table 4). The D-optimal exact designs were reported in Chang et al. (2013, Theorem 4.1). Table 5 shows D-optimal exact designs found for Models 15–19 with formulation (13). Our results agree with the analytical D-optimal designs for the first-order trigonometric regression model. There are two optimal designs for Model 17, and our algorithm is able to find one of them. Further numerical experiences revealed that the other optimum can be obtained with a different starting point.

Table 4 Battery of statistical models with known D-optimal exact designs used for testing the MINLP formulations

The second selected model to compare optimal designs obtained from our algorithm and the theoretical designs is the one with a quadratic mean response function on $[-1,1]$ for $N=11,~12$ and $N=13$ (Models 20–22). The theoretical D-optimal exact designs were reported in Gaffke (1987). In particular, they showed that the D-optimal designs are all minimally supported with $k=3$. The D-optimal designs obtained by our algorithm for Models 20–22 in Table 5 agree with their theoretical results. Chang and Yeh (1998) and Imhof (1998) provided corresponding results for A-optimal exact designs, and we used them to verify the accuracy of the results from our formulations. Table 6 displays the A-optimal designs obtained from (17) for Models 20–22. Our A-optimal exact designs also agree with those obtained analytically by Chang and Yeh (1998, Theorem 2.1).

Table 5 D-optimal exact designs for Models 15–22 in Table 4 obtained using a locally optimal MINLP solver

Table 6 A-optimal exact designs for Models 19–21 in Table 4 obtained using a locally optimal MINLP solver

4.2 Unconstrained optimal exact designs

In this section, we determine minimally supported optimal designs for all the models in Table 1 assuming that $N=3\times n_{\theta }$. Other design setups are considered in Sect. 4.3.

Tables 7 and 8 list D- and A-optimal exact designs obtained from our algorithm, respectively. The D-optimal designs are uniform in all cases, and the CPU time required to solve the MINLP problems is generally short in part due to our initialization strategy, see Sect. 3.2, and because of the locally optimal MINLP solver. This shows that our formulation herein is effective for the problems we have tackled. We recall that Models 6 and 7 are structurally the same, except for the parameter value in the power exponent m, and the optimal designs obtained for both are equal. Our optimal designs for Model 9 are similar to those obtained using an exchange algorithm in Atkinson et al. (2007, Chap. 12). Unlike the D-optimal exact designs, our A-optimal designs are not uniform.

The designs obtained are in good agreement with the optimal approximate designs found in Duarte et al. (2018) using an adaptive semidefinite programming (ASP)-based algorithm. We observe that the exact designs are equally or slightly more efficient than those in Duarte et al. (2018) when $N=3\times n_{\theta }$ partly because they first discretized the design space and the optimum is found from this finite set of candidate points; in contrast, we work with continuous design spaces. In practice, the trend observed in Sect. 4.1.1 extends to models in Table 1 when different values of N are tested. The exact optimal designs for Model 14 were also determined by the global solver BARON, and the results obtained are similar to those in Table 7 and 8 (last line) except that the CPU time has increased to 3.12 s for D-optimal designs and to 138.35 s for A-optimal designs.

Table 7 D-optimal exact designs for Models 1–14 in Table 1 with $N=3\times n_{\theta }$

Table 8 A-optimal exact designs for Models 1–14 in Table 1 with $N=3\times n_{\theta }$

To further validate the formulations in Sect. 3, we compared the optimal designs found for surface response models, such as, Models 1, 9, 12 and 14 in Table 1 with those obtained from the commercial software $\texttt {JMP}^\circledR$ 14.0.0 (64 bit) (SAS Institute Inc. 2017). This software implements the coordinate-exchange algorithm (CEA) using an initial design to iterate from multiple initial points and keeping the best solution found. Tables S1 and S2 in the Supplementary Material report the D- and A-optimal designs obtained from CEA, respectively. They were obtained using $1 \times 10^{6}$ re-initializations of the algorithm, and we limit the analysis to linear (on covariates and parameters) surface response models and minimally supported designs so that they are equivalent to those found with MINLP formulations and can be compared. We note that CPU time required by $\texttt {JMP}^\circledR$ 14.0.0 (64 bit) for the examples addressed was of 8 min to 15 min and our formulations with a locally optimal solver require a few seconds. If a global optimizer were used with our formulations, we expect the CPU time would have increased 2 to 3 orders of magnitude even though in some cases the CPU times are still competitive.

Table 9 lists the D-optimal values found from the MINLP formulation and those found from the CEA along with the efficiencies of the latter relative to the former. We note that the optimal designs obtained with the formulations proposed herein have about the same efficiencies as those from the CEA. For a fair comparison between our algorithm and CEA, we set the number of re-initializations of the latest to $1 \times 10^{3}$ which allows reducing the CPU time needed to about 1 s for all the examples addressed. We note that the optimal designs obtained with CEA for this setup are close to the optimum having efficiencies higher than 0.94 (relative to optimal designs obtained with MINLP formulation).

4.3 Constrained optimal exact designs

Here, we test the algorithm to find D- and A-optimal designs when there are linear or nonlinear constraints compactly represented by inequalities $\varvec{\gamma }(\varvec{x},\varvec{n})\le \varvec{0}$ and equalities $\varvec{\phi }(\varvec{x},\varvec{n})=\varvec{0}$ where $\varvec{\gamma }\in \mathbb {R}^{n_i}$ and $\varvec{\phi }\in \mathbb {R}^{n_e}$, $n_i$ standing for the number inequality constraints and $n_e$ for the number of equality constraints. To fix ideas, in Sect. 4.3.1 we impose constraints only on the support points and search for optimal designs in the constrained space $\varXi _k^{N,x}\equiv \varXi _k^N\cap \{\varvec{x}: \varvec{\gamma }(\varvec{x})\le \varvec{0}, ~\varvec{\phi }(\varvec{x})=\varvec{0}\}$. In Sect. 4.3.2, we impose constraints only on the number of replicates and search for k-point optimal designs in the space $\varXi _k^{N,n}\equiv \varXi _k^N\cap \{\varvec{n}: \varvec{\gamma }(\varvec{n})\le \varvec{0}, ~\varvec{\phi }(\varvec{n})=\varvec{0}\}$. Finally, Sect. 4.3.3 allows constraints on both the support points and the number of replicates and we search for a k-point optimal design among the designs in space $\varXi _k^{N,n,x}\equiv \varXi _k^N\cap \{(\varvec{x},\varvec{n}): \varvec{\gamma }(\varvec{x},\varvec{n})\le \varvec{0}, ~\varvec{\phi }(\varvec{x},\varvec{n})=\varvec{0}\}$.

In this section, we apply the algorithm to find minimally supported A- and D-optimal exact designs for the Model 13 in Table 1 defined on the design space $\mathbf {X}=[0.5,2.0]\times [0.5,2.0]\times [0.5,2.0]$. We present results only for this model when $N=3\times n_{\theta }=27$ for space consideration and omit results for other models in Table 1. This model has 9 parameters and so $k=n_{\theta }=9$. For values of N not a multiple of $n_{\theta }$, we obtained optimal exact designs that exhibit a trend similar to that observed for Models 3–4 in Sect. 4.1.1.

Table 9 D-optimality values of the designs found with MINLP formulations and CEA for selected models

Table 10 Constrained D-optimal exact designs for Model 13 in Table 1 with $N=27$ and $k=9$

4.3.1 Constraints on the design space

We now test our algorithm when the design problem has equality or inequality constraints on the design space and the constraints are of linear or nonlinear kind.

Linear constraints arise naturally in some experimental design problems. For example, in mixture experiments, a support point represents the proportions from the various components in the study. Naturally, each support point has nonnegative components that add to unity, see for example, Atkinson et al. (2007, Chap.16). At other times, there are physical and linear constraints on the support points. As an illustration, suppose that we require that the sum of the components in each support point $\varvec{x}$ in the design is 1.0, i.e.,

$$\begin{aligned} \phi _1(\varvec{x}):=\sum _{j=1}^3x_{j,i} =1.0, \quad \forall i\in \llbracket k\rrbracket . \end{aligned}$$

(18)

The set of candidate designs are found from the given design space $\mathbf {X}=[0.05,1.0]\times [0.05,1.0]\times [0.0,1.0]$ that incorporates the additional constraints.

Nonlinear constraints on the design problem vary and occur frequently, depending on the problem at hand. For example, Berman’s model (Berman 1962) is typically defined on an arc in brain mapping studies; consequently, it is likely more appropriate that the design space is spherical in which case the support points are contained inside a sphere of radius r centered at $\varvec{x}=[c_1,c_2,c_3]^{\intercal }\in \mathbf {X}$, i.e.,

$$\begin{aligned} \gamma _1(\varvec{x}):=\sum _{j=1}^3(x_{j,i}-c_j)^2 \le r^2, \quad \forall i\in \llbracket k\rrbracket . \end{aligned}$$

(19)

Another example is requiring a minimum distance between the support points because it may not be practical or meaningful to take observations from locations too close together. Such a constraint may take the form

$$\begin{aligned} \gamma _1(\varvec{x}):=\delta ^2\le \sum _{j=1}^3(x_{j,i}-x_{j,l})^2, \quad \forall i,~l\in \llbracket k\rrbracket , ~l\ge i+1 \end{aligned}$$

(20)

where $\delta$ is the minimum distance allowed between any two support points. In our algorithm, we set $r=0.75$, $c_1=c_2=c_3=1.25$ in (19) and $\delta =0.2$ in (20).

Our last example has a discrete design space with three discrete factors $x_1, ~x_2$ and $x_3$, each with three levels and coded as 1,  2, and 3. Let $\varvec{y}$ be an integer variable containing the integer codes for $\varvec{x}$, and we want to find D- and A-optimal exact designs subject to the following constraints in problems (13) and (17), respectively.

$$\begin{aligned} \gamma _1(\varvec{x}):=&x_{j,i}=y_{j,i}+1, \quad \forall j\in \llbracket n_x\rrbracket , ~i \in \{1,2,3\} \end{aligned}$$

(21a)

$$\begin{aligned} \phi _1(\varvec{y}):=&y_{j,i} \le 2, \quad \forall j\in \llbracket n_x\rrbracket , ~i \in \{1,2,3\}, \quad y_{j,i}\in \mathbb {N}_0. \end{aligned}$$

(21b)

Each of the optimal designs is then obtained by finding the k most informative points from the 27 candidate design points. Tables 10 and 11 report the D- and A-optimal designs, respectively, obtained under constraints (18)–(21). The D-optimal designs are still uniform, and the CPU times required to solve the optimization problems are short for the various constraints. Table 11 shows that A-optimal designs require noticeably longer time to compute than D-optimal designs.

Table 11 Constrained A-optimal exact designs for Model 13 in Table 1 with $N=27$ and $k=9$

Table 12 Constrained D-optimal exact designs for Model 13 in Table 1 with $N=27$

Table 13 Constrained A-optimal exact designs for Model 13 in Table 1 with $N=27$

4.3.2 Constraints on the replicates

This section considers a design problem where the number of support points in the optimal design sought exceeds the number parameters in the model. As an example, suppose that we require 10 support points ($k=10$) and the optimal design must have at least two observations at each support point:

$$\begin{aligned} \gamma _1(\varvec{n}):=n_i \ge 2, \quad \forall i\in \llbracket k\rrbracket . \end{aligned}$$

(22)

Another setup is a problem where both spaces $\mathbf {X}$ and $\varOmega _k^N$ are constrained independently. Here, in addition to requiring having 10 support points and at least two replicates from each support point, a minimum distance between any two support points is required. The complete set of constraints is represented by (23), and each constraint depends on the number of replicates or the location of the support points. Assuming $k=10$, the 10-point optimal designs sought here satisfies

$$\begin{aligned} \gamma _1(\varvec{n}):=&n_i\ge 2, \quad \forall i\in \llbracket k\rrbracket \end{aligned}$$

(23a)

$$\begin{aligned} \gamma _2(\varvec{x}):=&\delta ^2\le \sum _{j=1}^3(x_{j,i}-x_{j,l})^2, \quad \forall i,~l\in \llbracket k\rrbracket , ~l \ge i+1 \end{aligned}$$

(23b)

where we set $\delta =0.2$. This design has k distinct support points, and the number of replicates at each support point is 2 or more subject to the constraint (23b) that assures a minimum distance between each pair of support points.

Tables 12 and 13 display the constrained optimal designs found from our algorithm and note that the designs obtained are not uniform due to the value of k.

4.3.3 Constraints on the design and replicates space

In practice, there may be constraints on both the design space and the number of replicates allowed at each point. For example, there are budget constraints to account for, the unitary cost of each factor is different and linearly proportional to the levels chosen in the experiment. An example is

$$\begin{aligned} \gamma _1(\varvec{x},\varvec{n}):=c_0+c_1~\sum _{i=1}^k n_i ~ x_{1i}+c_2~\sum _{i=1}^k n_i ~x_{2i}+c_3~\sum _{i=1}^k n_i ~x_{3i} \le b, \end{aligned}$$

(24)

where $c_0=15$ is the fixed experimental cost, $c_1=4$, $c_2=5$, $c_3=6$ are the variable experimental costs of each factor in the design, and $b=350$ is the budget available for the complete study. Here, we set $k=n_{\theta }$ as in the unconstrained design problem.

Tables 12 and 13 present D- and A-optimal exact designs found by our algorithm (third line) and subject to constraint (24). We notice the D-optimal exact design is not uniform in this case, and more replicates are allocated to treatment levels that combine lower levels of factors to satisfy the cost constraint. This trend is more evident for factors with higher cost in the experimental design. This example shows that D-optimal exact designs generated by our algorithm are not necessarily uniform if additional constraints are involved.

5 Summary

Our paper is the first to apply MINLP formulations to find D- and A-optimal exact designs for linear models and locally optimal designs for nonlinear models. We use algebra-based concepts to develop MINLP representations of the optimal exact design problems. The resulting problem may have multiple local optima, and we use global and local optimization MINLP solvers to determine the optimum. Our work suggests that there are numerical advantages of working with global optimization solvers for solving optimal exact design problems as they have the ability to assure that globally optimal designs are found. However, in our examples, local optimizers in most of the tests find optimal exact designs that coincide with those obtained using global solvers and in shorter time. Our general recommendation is to try both global and local solvers and compare results. Practically, one advantage of our formulations is that the structure of the optimization problems is transparent to the solver that, through matrix decomposition techniques, can efficiently solve it.

We tested our problem formulations and algorithm for finding A- and D-optimal exact designs for a range of linear and nonlinear models with one or more regressors, and they all performed well with a short CPU time. We recall that there is rarely a theoretical proof that an exact design is optimal for a nonlinear model and so, for comparison purposes, some of our models were chosen so that we can confirm our results with the few theoretical results reported in the literature.

The D-optimal exact designs coincide with optimal approximate designs when N is a multiple of the number of design points which is expected. We note that when the D-optimal exact designs are uniformly supported at their design points, but the same is not true for A-optimal exact designs. Using several examples, we also demonstrated that mathematical programming techniques can easily incorporate additional constraints in the design problems and as the number of constraints grow in complexity, the feasibility region shrinks and the optimum is easier to find, assuming it exists. However, the performance of the algorithm depends on the size of the problem and the constraints imposed on the design and replicates spaces.