V-optimality of designs in random effects Poisson regression models

Abstract

The knowledge of the Fisher information is a fundamental tool to judge the quality of an experiment. Unlike in linear and generalized linear models without random effects, there is no closed form for the Fisher information in the situation of generalized linear mixed models, in general. To circumvent this problem, we make use of the quasi-information in this paper as an approximation to the Fisher information. We derive optimal designs based on the V-criterion, which aims to minimize the average variance of prediction of the mean response. For this criterion, we obtain locally optimal designs in two specific cases of a Poisson straight line regression model with either random intercepts or random slopes.

1 Introduction

In a wide range of regression experiments, the response may be observed as count measurements which can be modeled by the Poisson distribution. An important application of the Poisson regression model is in cancer research. There, the clonogenic assay is a technique that is used to determine the effect of an anticancer drug on proliferating tumor cells. In these studies, a dose-response curve can be fitted to determine how much the dosage of a drug decreases the number of colony formations over different concentrations of the particular drug. Then, often the number of colonies is assumed to be Poisson distributed, and thus a Poisson regression model can be used to evaluate the results of the dose-response experiment (Minkin 1993).

The concept of generalized linear models (GLM; McCullagh and Nelder 1989) provides a fundamental idea to model such data. However, in statistical studies, the data set often reveals features that cause these models to be insufficient, in particular when observations are correlated that can be observed in clustered measurements (e.g., hierarchical data structures and longitudinal studies). To adjust for this clustering, generalized linear mixed models (GLMM; McCulloch and Searle 2001) can be used to generalize the GLMs by including random clusters and/or subject effects in the model equation to account for dependence in the data. In many applications, it is assumed that the random effects follow a normal distribution. In that case, it is well-known that, in general, the marginal likelihood of the GLMM cannot be expressed analytically in an explicit form. Hence, the maximum-likelihood (ML) estimation of the parameters has to be approximated numerically (Davidian and Giltinan 1995). Consequently, there is not sufficient knowledge about the statistical behavior of the ML estimators for GLMMs, which could serve as the basis for the design of experiments. Commonly the inverse of the Fisher information matrix is used to measure the performance of the ML estimator, at least in terms of its asymptotic properties. However, also the Fisher information cannot be expressed analytically in an explicit form. To resolve this, there are two different approaches to replacing the Fisher information matrix. One common approach is a direct approximation of the Fisher Information, for example, by linearization of the response function (see Mielke 2012). But Mielke and Schwabe (2010) showed that these Fisher information approximations might often be unreliable.

Another approach is to use alternative methods of estimation in GLMMs like Generalized Estimation Equations (GEE, see McCulloch and Searle 2001; Cameron and Trivedi 2013). In particular, the concept of quasi-likelihood can be identified as a GEE. It may serve as an attractive method to generate an efficient estimation of the parameters without using the full distributional assumptions. Niaparast (2009) used the quasi-likelihood method to obtain optimal designs in a Poisson regression model with random intercepts. There he employed results of Schmelter (2007) and proved for a range of criteria that an optimal design on an individual level is also optimal for the population parameters. Niaparast and Schwabe (2013) derived D-optimal designs for a Poisson regression model with random slope. In this article, we extend the results of Niaparast (2009) and Niaparast and Schwabe (2013) to obtain V-optimal designs in some Poisson regression models with random effects. The V-optimality criterion is a prediction-based optimality criterion that minimizes the average prediction variance of the estimated mean response. The V-optimality criterion is also often called I-optimality (Atkinson et al. 2007), Q-optimality (Bandemer 1977), or IMSE-optimality (Entholzner et al. 2005) in the literature.

As in all non-linear situations, there is a problem in finding optimal designs because of the dependence of the quasi-information matrix on unknown model parameters. Therefore, the local approach is adopted for which locally optimal designs are determined for prespecified nominal values of the parameters.

The structure of the paper is organized as follows: We first introduce the Poisson regression model with random effects in Sect. 2 and derive the quasi-information matrix for this model. The V-criterion is introduced in Sect. 3. In Sect. 4, we obtain V-optimal designs for two specific cases of straight line Poisson regression with either random intercepts or random slopes. Finally, the efficiency of a standard design is examined in a case study.

2 Model specification, information and design

In a Poisson regression model with random coefficients and log link, on the unit level it is assumed that the observation $Y_{ij}$ of unit i, $i=1,...,n$, at the jth replication, $j=1,...,m_i$, at the experimental setting $x_{ij}$ from the experimental region ${\mathcal {X}}$ is distributed according to a Poisson distribution with intensity $\lambda _{ij}=\exp (\varvec{f}^\textrm{T}(x_{ij}) \varvec{b}_i)$ where, in the linear component $\mathrm {\varvec{f}^T}(x_{ij}) \varvec{b}_i$, $\varvec{f}=(f_0,f_1,\cdots ,f_{p-1})^\textrm{T}$ and $\varvec{b}_i=(b_{0,i},\cdots , b_{p-1,i})^\textrm{T}$ are the p-dimensional vectors of known regression functions and individual coefficients, respectively. Conditional on the value of the individual coefficients, the observations $Y_{ij}$ are assumed to be independent.

On the population level, the individual coefficients $\varvec{b}_i$ are assumed to be random iid multivariate normal with population mean parameter $\varvec{\beta }=(\beta _0,\cdots , \beta _{p-1})^\textrm{T}$ and variance covariance matrix $\varvec{\Sigma }$ (see McCulloch and Searle 2001). For simplification, we further assume that $\varvec{\Sigma }$ is known. Then, the marginal mean of the observation $Y_{ij}$ is given by

$$\begin{aligned} \textrm{E}(Y_{ij})=\mu (x_{ij}) \end{aligned}$$

where $\mu (x)=\exp (\varvec{f}^\textrm{T} (x)\varvec{\beta }+\sigma (x, x)/2)$ is the mean function and $\sigma (x, x') = \varvec{f}^\textrm{T} (x) \varvec{\Sigma }\varvec{f} (x')$ is the dispersion function. Also, the marginal variance of the observation $Y_{ij}$ can be calculated as

$$\begin{aligned} \textrm{Var}(Y_{ij}) = \mu (x_{ij})+\mu (x_{ij})^2\textrm{c}(x_{ij},x_{ij}) \end{aligned}$$

where $\textrm{c}(x, x') =\exp (\sigma (x, x')) -1$ is the variance correction term.

Further the covariance of the observations within a unit is $\textrm{cov}(Y_{ij},Y_{ik})=\mu (x_{ij})\mu (x_{ik})\textrm{c}(x_{ij},x_{ik})$. Hence for the vector $\varvec{Y}_i = (Y_{i1},\cdots , Y_{im_i} )^\textrm{T}$, the mean and the variance covariance matrix of $\varvec{Y}_i$ are given by $\textrm{E}(\varvec{Y}_i)=(\mu (x_{i1}), \cdots , \mu (x_{im_i}))^\textrm{T}$ and

$$\begin{aligned} \textrm{Cov}(\varvec{Y}_i)=\varvec{A}_i +\varvec{A}_i \varvec{C}_i\varvec{A}_i, \end{aligned}$$

where $\varvec{A}_i= \textrm{diag}\{\mu (x_{ij})\}_{j=1,\cdots , m_i}$ is a $m_i \times m_i$ diagonal matrix with the observation means $\mu (x_{ij})$ as its non-zero, diagonal entries and $\varvec{C}_i = (c(x_{ij} , x_{ik}))_{j,k=1,\cdots ,m_i}$ is the $m_i \times m_i$ matrix of variance correction terms. As $\varvec{A}_i \varvec{C}_i \varvec{A}_i$ is the covariance matrix of the conditional expectation of $\varvec{Y}_i$ given $\varvec{b}_i$ and as $\varvec{A}_i$ is symmetric and non-singular, the matrix $\varvec{C}_i$ of variance correction terms is non-negative definite. The variance covariance matrix $\textrm{Cov}(\varvec{Y}_i)$ depends on the population location parameters $\varvec{\beta }$ only through the mean function.

Because of the integral in the marginal density with respect to the distribution of the random effects, it is not possible to derive a closed form for the likelihood function and the Fisher information. As an alternative approach, we will use the quasi-likelihood method.

By applying the quasi-likelihood approach, the amount of information contributed by the observations on the individual level can be described by the individual quasi-information matrix ${\mathfrak {M}}_{i,\varvec{\beta }}$,

$$\begin{aligned} {\mathfrak {M}}_{i,\varvec{\beta }} =\varvec{F}_i^\textrm{T} \left( \varvec{A}_{i}^{-1}+\varvec{C}_{i}\right) ^{-1} \varvec{F}_i, \end{aligned}$$

(1)

where $\varvec{ F}_i=\left( \varvec{f}(x_{i1}),\cdots ,\varvec{f}(x_{im_i})\right) ^\textrm{T}$ and, on the right hand side, only $\varvec{A}_{i}$ depends on $\varvec{\beta }$. Then on the population level, the quasi-information matrix is given by ${\mathfrak {M}}_{\varvec{\beta }}=\sum _{i=1}^n{\mathfrak {M}}_{i,\varvec{\beta }}$. For more details, see McCullagh and Nelder (1989, Chap. 9).

On the individual level, we define individual approximate designs $\xi _i$ as

$$\begin{aligned} \xi _i=\left\{ \begin{array}{ccc}x_{i1},\cdots ,x_{is_i}\\ w_{i1},\cdots ,w_{is_i}\end{array}\right\} \end{aligned}$$

where $x_{i1},\cdots ,x_{is_i}$ are mutually distinct experimental settings from the design region ${\mathcal {X}}$ and $w_{ij} = m_{ij}/m_i$ are the proportions of observations taken at $x_{ij}$ , $j=1,\cdots ,s_i$, $\sum _{j=1}^{s_i}w_{ij}=1$. Then, for the design $\xi _i$, the individual quasi-information matrix (1) can be represented as

$$\begin{aligned} {\mathfrak {M}}_{\varvec{\beta }}(\xi _i) =\varvec{F}_{\xi _i}^\textrm{T} \left( \varvec{A}_{\xi _i}^{-1}+\varvec{C}_{\xi _i}\right) ^{-1} \varvec{F}_{\xi _i}, \end{aligned}$$

(2)

where $\varvec{ F}_{\xi _i} = \left( \varvec{f}(x_{i1}),\cdots ,\varvec{f}(x_{is_i} )\right) ^\textrm{T}$, $\varvec{A}_{\xi _i} = \textrm{diag}(m_i w_{ij}\mu (x_{ij}))_{j=1,\cdots ,s_i}$ and $\varvec{C}_{\xi _i} = (\textrm{c}(x_{ij},x_{ik}))_{j,k=1,\cdots ,s_i}$ (see Niaparast and Schwabe 2013).

Similarly, we define population approximate designs $\zeta$ by

$$\begin{aligned} \zeta =\left\{ \begin{array}{ccc}\xi _{1},\cdots ,\xi _{q}\\ \nu _{1},\cdots ,\nu _{q}\end{array}\right\} , \end{aligned}$$

where $\xi _l$, $l=1,\cdots ,q$, are mutually distinct individual designs and $\nu _{l}>0$, $\sum _{l=1}^{q}\nu _{l}=1$, are the proportions of individuals that are observed under the corresponding individual designs. Based on the fact that $\varvec{C}_{\xi _i}$ is non-negative definite, Niaparast and Schwabe (2013) proved the convexity of the individual quasi-information. Following the argumentation in Schmelter (2007), it is sufficient to consider the class of single group designs, $\zeta =\left\{ \begin{array}{c}\xi \\ 1\end{array}\right\}$, where all individuals are observed under the same individual design, to obtain an optimal design in the class of all population designs, when for all units the same number $m_i=m$ of observations are taken. Hence, we have to optimize designs only on the individual level. To simplify notation, we may, thus, omit the index i in the individual design, $\xi =\left\{ \begin{array}{ccc}x_{1},\cdots ,x_{s}\\ w_{1},\cdots ,w_{s}\end{array}\right\}$ throughout the remainder of the text.

Our main interest in this paper is to find optimal designs for estimating the predicted response averaged over the design region with minimal variance. For the present model, the predictor ${\hat{\mu }}_x$ of the mean response at a given point x is given by

$$\begin{aligned} {\hat{\mu }}_x=\exp \left( \varvec{f}^\textrm{T}(x)\hat{\varvec{\beta }}+\sigma (x,x)/2\right) , \end{aligned}$$

where $\hat{\varvec{\beta }}$ is the quasi-likelihood estimator of $\varvec{\beta }$.

The mean response $\mu (x)$ and, hence, its predictor ${\hat{\mu }}_x$ does not have a linear structure. Therefore, the variance of the predictor has to reflect the non-linearity, and the asymptotic variance of the predictor has to be obtained by the delta method.

Lemma 1

The asymptotic variance $\textrm{Avar}({\hat{\mu }}_x)$ of the predictor ${\hat{\mu _x}}$ of the mean response $\mu (x)$ can be represented as

$$\begin{aligned} \textrm{Avar}({\hat{\mu }}_x) = \mu ^2(x)\varvec{f}^\textrm{T}(x){\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi )\varvec{f}(x) . \end{aligned}$$

Proof

According to McCullagh (1983), $\hat{\varvec{\beta }}$ is asymptotically normal with mean $\varvec{\beta }$ and asymptotic covariance matrix $\textrm{Avar}(\hat{\varvec{\beta }}) = {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi )$ equal to the inverse of the quasi-information matrix. Let $g(\varvec{\beta }) = \mu (x) = \exp \left( \varvec{f}^\textrm{T}(x)\varvec{\beta }+\sigma (x,x)/2\right)$. By the delta method, $g(\hat{\varvec{\beta }})$ is asymptotically normal with asymptotic variance $\nabla g(\varvec{\beta })^\textrm{T} \textrm{Avar}(\hat{\varvec{\beta }}) \nabla g(\varvec{\beta })$, where $\nabla g(\varvec{\beta }) = \exp \left( \varvec{f}^\textrm{T}(x)\varvec{\beta }+\sigma (x,x)/2\right) \varvec{f}(x) = \mu (x)\varvec{f}(x)$ is the the gradient vector of continuous partial derivatives of g. Hence, the statement of the lemma follows.

3 Optimality criterion and equivalence theorem

We consider the V-criterion

$$\begin{aligned} \phi (\xi )=\int \textrm{Avar}({\hat{\mu }}_x)\nu (\textrm{d}x), \end{aligned}$$

of the averaged asymptotic variance for the mean response with respect to a measure $\nu$ on the design region ${\mathcal {X}}$. Commonly this measure $\nu$ is chosen to be uniform on ${\mathcal {X}}$ (continuous or discrete depending on the structure of ${\mathcal {X}}$). For example, if x is a continuous variable and $\nu$ is uniform on the interval ${\mathcal {X}}=[a,b]$, then the V-criterion can be written as

$$\begin{aligned} \phi (\xi )=\int _a^b \textrm{Avar}({\hat{\mu }}_x)\textrm{d}x . \end{aligned}$$

More generally, the measure $\nu$ may be any (finite) measure on ${\mathcal {X}}$ or, in the case of extrapolation, it might be supported by an even larger set ${\mathcal {X}}^\prime$ of settings x for which the model equations are assumed to be valid. A design $\xi ^*$ will be called V-optimal if it minimizes the V-criterion $\phi (\xi )$. Note that here, as in all nonlinear models, the V-criterion depends on the nominal value of the parameter vector $\varvec{\beta }$ and, hence, the V-optimal design will be a local solution (at $\varvec{\beta }$). In the appendix, it is shown that the V-criterion is a convex function in $\xi$.

For the given model, the V-criterion can be represented as

$$\begin{aligned} \phi (\xi )= & {} \int \textrm{Avar}({\hat{\mu }}_x)\nu (\textrm{d}x) = \int \mu ^2(x)\varvec{f}^\textrm{T}(x){\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi )\varvec{f}(x) \nu (\textrm{d}x) \nonumber \\= & {} \int \textrm{tr}\left( {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ) \mu ^2(x)\varvec{f}(x)\varvec{f}^\textrm{T}(x)\right) \nu (\textrm{d}x) = \textrm{tr}\left( {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi )\varvec{B}\right) , \end{aligned}$$

(3)

where the matrix $\varvec{B}=\int \mu ^2(x)\varvec{f}(x)\varvec{f}^\textrm{T}(x)\nu (\textrm{d}x)$ does not depend on $\xi$.

The V-criterion and, hence, the V-optimal design depend on $\varvec{\beta }$ through the mean function $\mu (x)$. These designs will be called locally optimal (at $\varvec{\beta }$). Finding a V-optimal design requires knowledge of the values of the parameters. A common approach is to use an initial guess of the parameter values as nominal values which will be adopted here.

An important tool for checking the optimality of a design $\xi ^*$ for any convex and differentiable design criterion, is the equivalence theorem. This equivalence theorem has been originally proven by Kiefer and Wolfowitz (1960) for linear models in the case of D-optimality. The equivalence theorem has been extended to nonlinear models by White (1973) and to general convex criteria by Whittle (1973). A fundamental ingredient in the equivalence theorem is the sensitivity function, which constitutes the non-constant part of the directional derivative and plays a major role in optimal design theory (see Atkinson et al. 2007). The equivalence theorem for V-optimality in the given model is considered in the following theorem. For this we introduce the vector $\varvec{c}_{\xi ,x} = (\textrm{c}(x_j,x))_{j=1,...,s}$ of joint (correlation) correction terms for the settings $x_1,...,x_s$ of a design $\xi$ with a further setting x. This is part of the sensitivity function

$$\begin{aligned} d(x,\xi ) = m\mu (x) \left( \varvec{f}(x) - \varvec{F}^\textrm{T}_{\xi }\left( \varvec{A}^{-1}_{\xi }+\varvec{C}_{\xi }\right) ^{-1}\varvec{c}_{\xi ,x}\right) ^\textrm{T} {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ) \varvec{B} {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ) \\ \left( \varvec{f}(x) - \varvec{F}^\textrm{T}_{\xi }\left( \varvec{A}^{-1}_{\xi }+\varvec{C}_{\xi }\right) ^{-1}\varvec{c}_{\xi ,x}\right) . \end{aligned}$$

Theorem 1

$\xi ^*$ is V-optimal for the Poisson regression model with random effects if (and only if)

$$\begin{aligned} d(x, \xi ^*)\le & {} \textrm{tr}\left( {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ^* )\varvec{B}\right) \nonumber \\{} & {} - \textrm{tr}\left( {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ^*) {\varvec{F}}^\textrm{T}_{\xi ^*} \left( {\varvec{A}}^{-1}_{\xi ^*}+{\varvec{C}}_{\xi ^*}\right) ^{-1} {\varvec{C}}_{\xi ^*} \left( {\varvec{A}}^{-1}_{\xi ^*}+{\varvec{C}}_{\xi ^*}\right) ^{-1} {\varvec{F}}_{\xi ^*}{\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi ^*) \varvec{B}\right) ,\nonumber \\ \end{aligned}$$

(4)

for all $x\in {\mathcal {X}}$.

Moreover, if $\xi ^*$ is V-optimal, then equality holds in (4) for all support points x of $\xi ^*$.

The proof is given in the appendix.

4 Poisson regression with a single linear component

Often in dose-response experiments the mean response curve can be represented by a straight line relationship. In this case, a simple Poisson regression model with random effects may be fitted.

In this section, we are going to investigate two types of a straight line Poisson regression model with $p=2$ population parameters: The simple Poisson regression model with random intercepts and the simple Poisson regression model with random slopes. These models can be characterized by their intensities (mean response)

$$\begin{aligned} \lambda _{ij}=\exp (b_{0,i}+\beta _1x_{ij}) \end{aligned}$$

(5)

and

$$\begin{aligned} \lambda _{ij}=\exp (\beta _{0}+b_{1,i}x_{ij}) , \end{aligned}$$

(6)

respectively. In the former, the individual coefficients have only influence on the overall level of the response, and hence $b_{0,i}$ expresses as the random intercept with mean $\beta _0$ and the variance $\sigma ^2$. In the context of dose-response curves in cancer research, it is reasonable to assume that the slope $\beta _1$ is negative, because the purpose of using the drug is to eradicate the tumor cells. The dosage x will commonly measured on a standardized scale, $x\in [0,1]$ or $x\in \{0,1\}$, where $x=0$ indicates placebo or a control level.

It can be shown that in models with random intercepts the linear optimality criteria do not depend on the random variation of the intercept whereas this may be in challenge when the effect of the explanatory variable varies across individuals. The latter situation is described in (6) in which $b_{1,i}$ is the random slope effect with mean $\beta _1$ and variance $\sigma ^2$.

For these two models, the vector of regression functions is given by $\varvec{f}(x) = (1,x)^\textrm{T}$ and $\varvec{\beta } = (\beta _0,\beta _1)^T$. In this case the weighting matrix $\varvec{B}$ in the V-criterion can be written as $\varvec{B}=\begin{pmatrix} B_0 &{} B_1 \\ B_1 &{} B_2 \end{pmatrix}$, where $B_k = \int _{{\mathcal {X}}}x^k\mu ^2(x)\nu (\textrm{d}x)$ denotes the kth moment with respect to $\mu ^2(\cdot ) \textrm{d}\nu$, $k=0,1,2$.

4.1 Random intercepts

We first consider the Poisson model with random intercepts, where $b_{0,i}\sim N(\beta _0,\sigma ^2)$ and the slope $b_{1,i}=\beta _1$ for all units i is a fixed effect. This condition can be described formally by the dispersion matrix $\varvec{\Sigma }=\left( \begin{array}{cc}{\sigma ^2}&{}0\\ 0&{}0\end{array}\right)$. The dispersion function and the variance correction term are $\sigma (x, x') = \sigma ^2$ and $c(x, x') = \exp (\sigma ^2) -1$, respectively. In this case the functions $\sigma (x, x')$ and $c(x, x')$ are constant on x.

Theorem 2

For the Poisson regression with random intercept, the V-optimal design only depends on the slope $\beta _1$ and does not depend on the mean intercept $\beta _0$, the variance $\sigma ^2$ of the random intercept, and the number m of observations per unit.

Moreover, the V-optimal design for the random intercepts model coincides with that for the corresponding fixed effects model without random effects.

Proof

According to Niaparast (2010, Lemma 4.1.3), the information matrix can be represented as ${\mathfrak {M}}_{\varvec{\beta }}(\xi ) = \left( (\varvec{F}_{\xi }^\textrm{T}\varvec{A}_{\xi }\varvec{F}_{\xi })^{-1}+\varvec{U}\right) ^{-1}$, where $\varvec{U}=\begin{pmatrix} \exp (\sigma ^2)-1&{} 0 \\ 0 &{} 0 \end{pmatrix}$ does not depend on $\xi$. Then

$$\begin{aligned} \phi (\xi ) = \textrm{tr}\left( {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi )\varvec{B}\right) = \textrm{tr}\left( (\varvec{F}_{\xi }^\textrm{T}\varvec{A}_{\xi }\varvec{F}_{\xi })^{-1} \varvec{B}\right) + \textrm{tr}(\varvec{U}\varvec{B}) . \end{aligned}$$

The last expression does not depend on the design and can be ignored. Now let ${\check{\mu }}(x) =\exp (\beta _1x)$, $\check{\varvec{A}}_\xi = \textrm{diag}\{w_j{\check{\mu }}(x_j)\}_{j=1,\cdots , s}$, and $\check{\varvec{B}}=\begin{pmatrix} {\check{B}}_0&{} {\check{B}}_1\\ {\check{B}}_1&{}{\check{B}}_2 \end{pmatrix}$ with ${\check{B}}_k=\int x^k{\check{\mu }}^2(x)\nu (\textrm{d}x)$, $k=0,1,2$. Then,

$$\begin{aligned} \textrm{tr}\left( (\varvec{F}_{\xi }^\textrm{T}\varvec{A}_{\xi }\varvec{F}_{\xi })^{-1}\varvec{B}\right) = \frac{\exp (\beta _0+\sigma ^2/2)}{m} \textrm{tr}\left( (\varvec{F}_{\xi }^\textrm{T}\check{\varvec{A}}_{\xi }\varvec{F}_{\xi })^{-1}\check{\varvec{B}}\right) , \end{aligned}$$

and minimization of $\phi (\xi )$ is equivalent to minimization of ${\check{\phi }}(\xi ) = \textrm{tr}\left( (\varvec{F}_{\xi }^\textrm{T}\check{\varvec{A}}_{\xi }\varvec{F}_{\xi })^{-1}\check{\varvec{B}}\right)$ which does not depend on $\beta _0$, $\sigma ^2$ and m. Furthermore,

$$\begin{aligned} \phi (\xi )=a\phi _0(\xi )+c, \end{aligned}$$

(7)

where $a=\exp (\sigma ^2/2)$ and $c=\textrm{tr}(\varvec{U}\varvec{B})=\exp (2\beta _0+\sigma ^2)(\exp (\sigma ^2)-1){\check{B}}_0$. Obviously a and c do not depend on $\xi$ and $\phi _0(\xi )=\dfrac{\exp (\beta _0)}{m}{\check{\phi }}(\xi )$ can be identified as the V-criterion in the corresponding fixed effects model without random intercepts by formally letting $\sigma ^2=0$. This proves the theorem.

Example 1

(Binary regressor). We consider the simple Poisson regression model with random intercepts and binary predictor $x \in {\mathcal {X}}=\{0,1\}$, where $x=1$ denotes treatment and $x=0$ control. Here, the designs $\xi = \xi _w = \left\{ \begin{array}{cc}0 &{}1\\ 1-w&{}w\end{array}\right\}$ are uniquely characterized by the weight w allocated to $x=1$, $\varvec{F}_\xi =\left( \begin{array}{cc}1&{}0\\ 1&{}1\end{array}\right)$ is the same for all designs, and $\check{\varvec{A}}_\xi = \begin{pmatrix} 1 - w &{} 0 \\ 0 &{} w \exp (\beta _1) \\ \end{pmatrix}$ with the notation in the proof of Theorem 2. Note that, here, the uniform measure $\nu$ can be chosen as the counting measure on ${\mathcal {X}} = \{0,1\}$ which assigns weight 1 to each of the settings 0 and 1. Then $\check{\varvec{B}} = \begin{pmatrix} 1 + \exp (2\beta _1) &{} \exp (2\beta _1) \\ \exp (2\beta _1) &{} \exp (2\beta _1) \end{pmatrix}$, and we have to minimize

$$\begin{aligned} {\check{\phi }}(\xi ) = \frac{\exp (\beta _1)}{w} + \frac{1}{1-w} \end{aligned}$$

(8)

with respect to w. The derivative is $\textrm{d}{\check{\phi }}(\xi _w)/\textrm{d}w = - \left( \exp (\beta _1)/w^2\right) + \left( 1/(1-w)^2\right)$. Solving for a root satisfying $0\le w\le 1$ leads to the optimal weight $w^*= 1/\left( 1+\exp (-\beta _1/2)\right)$ at $x=1$.

The optimal weight $w^*$ is increasing in $\beta _1$, equal to 1/2 for $\beta _1 = 0$, and counter-symmetric with respect to sign change of $\beta _1$, i.e. if $w^*$ is optimal for $\beta _1$, then $1-w^*$ is optimal for $-\beta _1$. In accordance with the findings in Niaparast (2009), the V-optimal design does not depend on the variance $\sigma ^2$ of the random intercept and, hence, coincides with the V-optimal design in the corresponding fixed effects model without random effects. For example, if we assume a nominal value of $\beta _1 = -2$ for the slope, the optimal weight at $x = 1$ is $w^* = 0.269$.

Example 2

(Continuous regressor). Let ${\mathcal {X}}=[0,1]$ and $\nu$ uniform on ${\mathcal {X}}$. It can be shown that for the present model the V-optimal design is supported on two points $x_1^*$ and $x_2^*$ (see Schmidt 2019). Therefore, we search for the optimal design $\xi ^*$ among all two point designs for which $\xi ^*$ is of the form $\xi = \left\{ \begin{array}{cc}x_1 &{}x_2\\ 1-w&{}w\end{array}\right\}$ and $x_1<x_2$. According to the proof of Theorem 2, $\check{\varvec{A}}_\xi = \begin{pmatrix}(1-w)\exp (\beta _1x_1) &{} 0\\ 0 &{} w\exp (\beta _1x_2) \end{pmatrix}$ and $\check{\varvec{B}} = \begin{pmatrix} {\check{B}}_0&{} {\check{B}}_1 \\ {\check{B}}_1&{} {\check{B}}_2 \end{pmatrix}$ with ${\check{B}}_k = \int _0^1x^k{\check{\mu }}^2(x)\textrm{d}x$, $k=0,1,2$, such that

$$\begin{aligned} {\check{B}}_0= & {} \left( \exp (2\beta _1) - 1\right) /(2\beta _1), \\ {\check{B}}_1= & {} \left( (2\beta _1 -1)\exp (2\beta _1) + 1\right) /(2\beta _1)^2, \\ {\check{B}}_2= & {} \left( (4\beta _1^2 - 4\beta _1 + 2)\exp (2\beta _1) - 2\right) /(2\beta _1)^3. \end{aligned}$$

Solutions for the V-optimal designs are listed in Table 1 for different values of $\beta _1$, where $w^*$ denotes the optimal weight in $x_2^*$.

When $|\beta _1|$ is small, the support points will be the endpoints $x_1^*=0$ and $x_2^*=1$. For larger values $\vert \beta _1|$ of the slope, an internal support point $x^*$ will come in together with $x_2^*=1$ when $\beta _1$ is positive and $x_1^*=0$ when $\beta _1$ is negative. Hence, always the setting $x_1^*=0$ or $x_2^*=1$ is included in the optimal design which has highest intensity, respectively.

Table 1 Locally V-optimal settings $x_1^*$, $x_2^*$, and weights $w^*$ at $x_2^*$ for Example 2

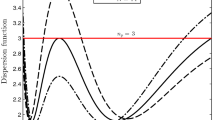
The conditions of Theorem 2 can be checked to confirm that the designs in Table 1 are V-optimal. For example, in the case of a nominal value $\beta _1 = -2$ for the slope, the optimal design is given by $\xi ^*=\left\{ \begin{array}{cc} 0.000 &{} 0.790 \\ 0.465 &{} 0.535 \end{array}\right\}$. Figure 1 shows that the sensitivity function of $\xi ^*$ attains its maximum at the support points $x^*_1= 0.000$ and $x^*_2 = 0.790$ of $\xi ^*$.

Fig. 1

Sensitivity function of $\xi ^*$ for $\beta _1=-2$ (Example 2)

Note that also here the optimal designs are counter-symmetric with respect to sign change of $\beta _1$, i.e. if the design $\left\{ \begin{array}{cc}x_1^*&{}x_2^*\\ 1-w^*&{}w^*\end{array}\right\}$ is optimal for $\beta _1$, then the design $\left\{ \begin{array}{cc}1-x_2^*&{}1-x_1^*\\ w^*&{}1-w^*\end{array}\right\}$ is optimal for $-\beta _1$. Further, the optimal designs can be transferred to arbitrary intervals ${\mathcal {X}}=[a,b]$ by means of the concept of equivariance (see Idais et al. 2021).

4.2 Random slopes

In the simple Poisson regression with random slopes, (6), the individual slope $b_{1,i}$ is assumed to be normally distributed with mean $\beta _1$ and variance $\sigma ^2$, and the intercept $b_{0,i}=\beta _0$ is constant across units. The covariance structure of the random effect $b_{i}=(\beta _0,b_{1,i})^\textrm{T}$ is $\varvec{\Sigma }=\left( \begin{array}{cc}0&{}0\\ 0&{}{\sigma ^2}\end{array}\right)$ which results in $\sigma (x,x') = \sigma ^2xx'$ for the dispersion function and $c(x, x') = \exp (\sigma ^2xx') - 1$ for the variance correction. For simplicity, as in Example 1 for the model with random intercepts, we consider also here the situation of a design region which is restricted two only two settings.

Example 3

(Binary regressor). As in Example 1 we treat the case of a design region ${\mathcal {X}}=\{0,1\}$ which only consists of two settings $x_1=0$ and $x_2=1$. Hence, again only designs $\xi$ of the form $\xi _w = \left\{ \begin{array}{cc}0 &{}1\\ 1-w&{}w\end{array}\right\}$ have to be considered, where w is the proportion of observations which are taken at $x_2=1$, $0<w<1$. To find the optimal design $\xi ^*$, it is sufficient to obtain the optimal weight $w^*$. In this situation $\varvec{F}_\xi =\left( \begin{array}{cc}1&{}0\\ 1&{}1\end{array}\right)$ is as defined in Example 1, $\varvec{A}_\xi = m \exp (\beta _0) \left( \begin{array}{cc}1-w&{}0\\ 0&{}w\exp (\beta _1+\sigma ^2/2)\end{array}\right)$, and $\varvec{C}_\xi =\left( \begin{array}{cc}0&{}0\\ 0&{}\exp (\sigma ^2)-1\end{array}\right)$. Here $\varvec{F}=\varvec{F}_\xi$ and $\varvec{C}=\varvec{C}_\xi$ do not depend on $\xi$, and the quasi-information matrix can be simplified as follows.

Lemma 2

Let ${\mathcal {X}}=\{0,1\}$. For the Poisson regression model with random slopes, the quasi-information matrix can be represented as

$$\begin{aligned} {\mathfrak {M}}_{\varvec{\beta }}(\xi )= \left( (\varvec{F}^\textrm{T}\varvec{A}_\xi \varvec{F})^{-1}+\varvec{C}\right) ^{-1}. \end{aligned}$$

Proof

Since $\varvec{C}=\varvec{F}^{-1}\varvec{C}\varvec{F}^\mathrm {{-T}}$, where $\varvec{F}^{-\textrm{T}}$denotes the inverse of $\varvec{F}^\textrm{T}$, we have

$$\begin{aligned} \varvec{F}^\textrm{T}(\varvec{A}_\xi ^{-1}+\varvec{C})^{-1} \varvec{F} = \left( \varvec{F}^{-1}\varvec{A}_\xi ^{-1}\varvec{F}^\mathrm {{-T}}+ \varvec{F}^{-1}\varvec{C}\varvec{F}^\mathrm {{-T}}\right) ^{-1} = \left( (\varvec{F}^\textrm{T}\varvec{A}_\xi \varvec{F})^{-1}+\varvec{C}\right) ^{-1} . \end{aligned}$$

Then the V-criterion can be simplified.

Theorem 3

Let ${\mathcal {X}}=\{0,1\}$. For the simple Poisson regression with random slopes, the V-optimal design does not depend on the mean intercept $\beta _0$ and the number m of observations per unit.

Proof

Using Lemma 2, we obtain

$$\begin{aligned} \phi (\xi ) = \textrm{tr}\left( {\mathfrak {M}}_{\varvec{\beta }}^{-1}(\xi )\varvec{B}\right) = \textrm{tr}\left( (\varvec{F}^\textrm{T}\varvec{A}_\xi \varvec{F})^{-1}\varvec{B}\right) +\textrm{tr}(\varvec{C}\varvec{B}). \end{aligned}$$

The last term of the above statement is independent of $\xi$ and can be disregarded for optimization. Define here ${\check{\mu }}(x) =\exp (\beta _1x+\sigma ^2x^2/2)$ and accordingly $\check{\varvec{A}}_\xi = \textrm{diag}\{w_j{\check{\mu }}(x_j)\}_{j=1,\cdots , s}$, $\check{\varvec{B}}=\left( \int x^{i+j-2}{\check{\mu }}^2(x)\nu (\textrm{d}x)\right) _{i=1,2}^{j=1,2}$, and ${\check{\phi }}(\xi ) = \textrm{tr}\left( (\varvec{F}^\textrm{T}\check{\varvec{A}}_\xi \varvec{F})^{-1} \check{\varvec{B}}\right)$. Then $\varvec{A} = m\exp (\beta _0)\check{\varvec{A}}$, $\varvec{B} = \exp (2\beta _0)\check{\varvec{B}}$, and $\textrm{tr}\left( (\varvec{F}^\textrm{T}\varvec{A}_\xi \varvec{F})^{-1}\varvec{B}\right) = \left( \exp (\beta _0)/m\right) {\check{\phi }}(\xi )$ . Hence, the minimization of $\phi (\xi )$ is the same as the minimization of ${\check{\phi }}(\xi )$. Obviously, ${\check{\phi }}(\xi )$ does neither depend on $\beta _0$ nor on m.

Inserting $\varvec{F}$, $\check{\varvec{A}}_\xi$ and $\check{\varvec{B}}$ in ${\check{\phi }}(\xi )$, we get

$$\begin{aligned} {\check{\phi }}(\xi ) = \frac{1}{1-w} + \frac{\exp (\beta _1+\sigma ^2/2)}{w} , \end{aligned}$$

(9)

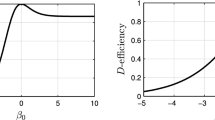
which is minimized at $w^* = 1/\left( 1+\exp (- \beta _1/2 - \sigma ^2/4)\right)$. For example, in the case of nominal values $\beta _1 = -2$ and $\sigma ^2 = 1$ for the mean slope, the optimal weight at $x=1$ is given by $w^*= 0.321$.

Note that when $\sigma ^2 = 0$ (no random effect), the optimal weight coincides with the fixed effects solution in Example 1. Figure 2 exhibits the optimal weights for different values of $\sigma ^2$ and $\beta _1$.

This figure shows that an increase of the mean slope $\beta _1$ or the variance $\sigma ^2$ of the random slopes leads to an increase in the optimal weight $w^*$ at $x=1$.

Fig. 2

Optimal weight $w^*$ at $x=1$ for the model with random slopes (Example 3)

5 Efficiency considerations

In many cases, it is prevalent that a standard design will be applied in the experiments. Therefore, we consider the uniform design $\xi _0 =\left( \begin{array}{cc}0 &{}1\\ 1/2&{}1/2\end{array}\right)$ on the endpoints of a standardized design region as a candidate.

To judge the gain of the design optimization, it is of interest to evaluate the efficiency of the design $\xi _0$ with respect to the V-optimal designs. In general, the V-efficiency of a design $\xi$ is defined by

$$\begin{aligned} \textrm{eff}(\xi )=\frac{\phi (\xi ^*)}{\phi (\xi )} \end{aligned}$$

(10)

relative to the V-optimal design $\xi ^*$. The efficiency of the design $\xi$ can be interpreted as the proportion of patients needed, when the V-optimal design $\xi ^*$ is used, to obtain the same value of the V-criterion as for the design $\xi$ under comparison. Note that the efficiency $\textrm{eff}(\xi )$ may depend on the parameters through both the non-linearity of the models as well as the presence of random effects.

5.1 Random intercepts

First, we consider the efficiency for models with random intercepts. The following theorem describes the dependence upon the parameters.

Theorem 4

For model (5), the efficiency depends on $\beta _1$ and on the remaining parameters only through $\gamma = m \exp (\beta _0 + \sigma ^2/2)\left( \exp (\sigma ^2) - 1\right) \ge 0$.

Proof

By (7), $\textrm{eff}(\xi )$ can be written as

$$\begin{aligned} \textrm{eff}(\xi ) = \textrm{eff}_0(\xi ) + \left( 1 - \textrm{eff}_0(\xi )\right) \frac{\gamma {\check{B}}_0}{{\check{\phi }}(\xi ) + \gamma {\check{B}}_0} , \end{aligned}$$

(11)

where $\textrm{eff}_0(\xi ) = \phi _0(\xi ^*) / \phi _0(\xi ) = {\check{\phi }}(\xi ^*) / {\check{\phi }}(\xi )$ is the efficiency in the corresponding fixed effects model. Since $\textrm{eff}_0(\xi )$, ${\check{\phi }}(\xi )$ and ${\check{B}}_0$ only vary in terms of $\beta _1$, the claim follows.

Equation (11) provides a lower bound $\textrm{eff}(\xi )\ge \textrm{eff}_0(\xi )$ for the efficiency $\textrm{eff}(\xi )$ in terms of its counterpart in the fixed effects model. This lower bound is attained only if either $\xi$ is optimal in the fixed effects model ($\textrm{eff}_0(\xi ) = 1$) or if there are no random effects ($\sigma ^2 = 0$).

Example 4

(Binary regressor). In the situation of Example 1 only two experimental settings $x = 0, 1$ are available. We assume $m = 100$, $\sigma ^2 = 1$ and nominal values $\beta _0 = -5$ and $\beta _1 = -2$ for the parameters resulting in $\gamma = 1.909$. For these values, the optimal weight at $x = 1$ is $w^* = 0.269$ (see Example 1), and the efficiency of $\xi _0$ amounts to $\textrm{eff}(\xi _0) = 0.905$ compared to its efficiency $\textrm{eff}_0(\xi _0) = 0.824$ in the fixed effects model. Although the optimal weight depends only on $\beta _1$, the efficiency is also affected by the other parameters through $\gamma$.

The efficiency $\textrm{eff}(\xi _0)$ of the standard design $\xi _0$ is exhibited in the two panels of Fig.  3 in dependence on $\beta _1$ and $\gamma$ while the other parameter is held fixed to its nominal value, respectively, together with $\textrm{eff}_0(\xi _0)$. For orientation, the nominal values are indicated there by vertical dotted lines in the corresponding panels.

Fig. 3

Efficiency of $\xi _0$ in dependence on $\beta _1$ (left panel) and $\gamma$ (right panel) in the random intercept (solid line) and the fixed effects (dashed line) model for a binary regressor (Example 4)

As can be seen from Fig.  3, the efficiency of $\xi _0$ increases in $\beta _1$ for negative values of $\beta _1$, attains its maximum 1 at $\beta _1 = 0$ where the design $\xi _0$ is (locally) V-optimal (see Example 1), and initially decreases for positive values of $\beta _1$. With respect to the other parameters $\beta _0$, $\sigma ^2$, and m, the efficiency is increasing through $\gamma$.

In the situation of Example 2 with a continuous regressor on ${\mathcal {X}} = [0,1]$, the behavior of the efficiency is qualitatively the same as in Example 4 and will, hence, not be reported in detail here.

5.2 Random slopes

For models with random slopes, we consider again a binary regressor as in Subsect. 4.2. Then the parameter dependence of the efficiency can be characterized as follows.

Theorem 5

Let ${\mathcal {X}}=\{0,1\}$. For model (6), the efficiency depends on $\beta _1$ and $\sigma ^2$ and on the remaining parameters only through $\gamma = m \exp (\beta _0) \ge 0$.

Proof

According to the proof of Theorem 3 and with the notation used there, the efficiency equals

$$\begin{aligned} \textrm{eff}(\xi )= & {} \frac{{\check{\phi }}(\xi ^*) + \gamma (\exp (\sigma ^2) - 1) {\check{B}}_2}{{\check{\phi }}(\xi ) + \gamma (\exp (\sigma ^2) - 1) {\check{B}}_2}\nonumber \\= & {} \check{\textrm{eff}}(\xi ) + \left( 1 - \check{\textrm{eff}}(\xi )\right) \frac{\gamma (\exp (\sigma ^2) - 1) {\check{B}}_2}{{\check{\phi }}(\xi ) + \gamma (\exp (\sigma ^2) - 1) {\check{B}}_2} \end{aligned}$$

(12)

where $\check{\textrm{eff}}(\xi ) = {\check{\phi }}(\xi ^*) / {\check{\phi }}(\xi )$ is a reduced version of the efficiency ignoring the additive term $\textrm{tr}(\varvec{C}\varvec{B})$ in the criterion $\phi$. Since $\check{\textrm{eff}}(\xi )$, ${\check{\phi }}(\xi )$ and ${\check{B}}_2$ only vary in terms of $\beta _1$ and $\sigma ^2$, the claim follows.

Example 5

(Binary regressor). For the situation of the random slopes model in Example 3, we assume $m = 100$, $\sigma ^2 = 1$ and nominal values $\beta _0 = -5$ and $\beta _1 = -2$ the parameters resulting in $\gamma = 0.674$ similar to Example 4. For these values, the optimal weight at $x = 1$ is $w^* = 0.321$ (see Example 3), and the efficiency of $\xi _0$ amounts to $\textrm{eff}(\xi _0) = 0.916$. Although the optimal weight depends only on $\beta _1$ and $\sigma ^2$, the efficiency is also affected by the other parameters through $\gamma$.

In Fig. 4 we present a graphical view of the efficiency $\textrm{eff}(\xi _0)$ for the standard design $\xi _0$ in dependence on $\beta _1$, $\sigma ^2$ and $\gamma$ while the other parameters are held fixed to their nominal values, respectively. As before, the corresponding nominal values are indicated in the panels by vertical dotted lines.

Fig. 4

Efficiency of $\xi _0$ in dependence on $\beta _1$ (top left panel), $\sigma ^2$ (top right panel) and $\gamma$ (bottom panel) in the random slope model for a binary regressor (Example 5)

In this figure, it can be seen that the efficiency of $\xi _0$ increases in $\beta _1$ up to $\beta _1 = -\sigma ^2/2$, where the efficiency attains its maximum value 1 because $\xi _0$ is (locally) V-optimal for this parameter combination (see Example 3). For larger values of $\beta _1$ the efficiency is initially decreasing. With respect to $\sigma ^2$, the efficiency is increasing up to $\sigma ^2 = -2\beta _1$, where again $\xi _0$ is (locally) V-optimal and the efficiency becomes 1. For larger values of $\sigma ^2$ the efficiency stays close to 1. Lastly, the efficiency is slightly increasing in m and $\beta _0$ through $\gamma$.

6 Discussion

The main purpose of this paper is to illustrate the problem of optimal design for prediction in the Poisson regression model with random effects using V-criterion. We apply the quasi-likelihood technique to derive the information matrix, which is applied to characterize V-criterion for this model. This criterion has been discussed in detail for the Poisson model with a single linear component on specific experimental regions, including binary and continuous. We also investigated the equivalence theorem to confirm the optimality of obtained designs. Besides, we discussed efficiency for the saturated standard design in terms of the different values of parameters.

Appendices

Appendix A Proof of the convexity of the V-criterion

Let $\xi _1$ and $\xi _2$ be two designs. For any $\alpha \in [0,1]$, Niaparast and Schwabe (2013) showed

$$\begin{aligned} {\mathfrak {M}}_{\varvec{\beta }}((1-\alpha )\xi _1+\alpha \xi _2)\ge (1-\alpha ){\mathfrak {M}}_{\varvec{\beta }}(\xi _1)+\alpha {\mathfrak {M}}_{\varvec{\beta }}(\xi _2) \end{aligned}$$

(B1)

in the sense of Loewner ordering of non-negative definiteness. This requires that the matrices $\varvec{C}_\xi$ of variance correction terms are non-negative definite which follows from the corresponding property of $\varvec{C}_i$ mentioned in Sect. 2.

By standard inversion formulas the convexity of the inverse follows,

$$\begin{aligned} {\mathfrak {M}}^{-1}_{\varvec{\beta }}((1-\alpha )\xi _1+\alpha \xi _2)\le (1-\alpha ){\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi _1)+\alpha {\mathfrak {M}}^{-1}_{\varvec{\beta }}(\xi _2) . \end{aligned}$$

Hence, because $\textrm{tr}(\varvec{A}\varvec{B})$ is linear in $\varvec{A}$, the V-criterion is a convex functional in $\xi$.

Appendix B Proof of Theorem 1

In order to obtain an equivalence theorem we consider the directional derivative of the trace $\phi (\xi )=\textrm{tr}({\mathfrak {M}}_{\varvec{\beta }}^{-1}(\xi )\varvec{B})$. The directional derivative of $\phi (\xi )$ in the direction of $\xi '$, $F_{\phi }(\xi ,\xi ')$ is

$$\begin{aligned} F_{\phi }(\xi ,\xi ')=\frac{\textrm{d}}{\textrm{d} \alpha }\textrm{tr}(({\mathfrak {M}}_{\varvec{\beta }}^{-1}((1-\alpha ){\xi }+\alpha {\xi '}))\varvec{B})|_{\alpha =0^+} \end{aligned}$$

(B1)

Since $(\varvec{A}^{-1}_{\xi }+\varvec{C}_{\xi })^{-1}=\varvec{A}_{\xi }-\varvec{A}_{\xi }(\varvec{I}+\varvec{C}_{\xi }\varvec{A}_{\xi })^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }$ where $\varvec{I}$ is the identity matrix, the quasi-information matrix in Eq. (2) can be represented as

$$\begin{aligned} {\mathfrak {M}}_{\varvec{\beta }}(\xi )=\varvec{F}^\textrm{T}_{\xi }\left( \varvec{A}_{\xi }-\varvec{A}_{\xi }(\varvec{I}+{\varvec{C}}_{\xi }\varvec{A}_{\xi })^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\right) \varvec{F}_{\xi }. \end{aligned}$$

(B2)

As in Niaparast and Schwabe (2013) we will derive a representation of the quasi-information matrix of the convex combination of $\xi$ and $\xi '$. For this we define the weighted joint intensity matrix $\varvec{A}_{\xi , \xi '}(\alpha )=\left( \begin{array}{cc}(1-\alpha )\varvec{A}_{\xi }&{}0\\ 0&{}\alpha \varvec{A}_{\xi '}\end{array}\right)$ for two designs $\xi$ and $\xi '$, $0 \le \alpha \le 1$, where $\varvec{A}_{\xi }$ and $\varvec{A}_{\xi '}$ are diagonal matrices with the weighted response means $(m_{j}\mu _{j})$ as diagonal elements corresponding to $\xi$ and $\xi '$ respectively, $\varvec{F}_{\xi ,\xi '}=\left( \begin{array}{cc}\varvec{F}^\textrm{T}_{\xi }&\varvec{F}^\textrm{T}_{\xi '}\end{array}\right) ^\textrm{T}$ the joint reduced design matrix for the designs $\xi$ and $\xi '$ and by $\varvec{C}_{\xi ,\xi '}=\left( \begin{array}{cc}\varvec{C}_{\xi }&{}\varvec{\Gamma }_{\xi ,\xi '}\\ \varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}&{}\varvec{C}_{\xi '} \end{array}\right)$ the combined correction matrix, which contains the mixed correction terms for $\xi$ and $\xi '$ in $\varvec{\Gamma }_{\xi ,\xi '}=(c(x,x'))$, where x and $x'$ are the support points of $\xi$ and $\xi '$, respectively.

Then regarding (B2), the quasi-information matrix of the convex combination of $\xi$ and $\xi '$ is as follow

$$\begin{aligned} \varvec{{\mathfrak {M}}}_{\varvec{\beta }}{((1-\alpha ){\xi }+\alpha {\xi '})}= & {} \varvec{F}^\textrm{T}_{\xi ,\xi '}[\varvec{A}_{\xi ,\xi '}(\alpha )\\{} & {} - \varvec{A}_{\xi ,\xi '}(\alpha )(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha )]{\varvec{F}_{\xi ,\xi '}}. \end{aligned}$$

Then,

$$\begin{aligned} F_{\phi }(\xi ,\xi ')= & {} \textrm{tr}(\frac{\textrm{d}}{\textrm{d}\alpha }(\varvec{F}^\textrm{T}_{\xi ,\xi '}[\varvec{A}_{\xi ,\xi '}(\alpha )-\varvec{A}_{\xi ,\xi '}(\alpha )(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1}\nonumber \\{} & {} \varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha )]\varvec{F}_{\xi ,\xi '})\varvec{B})|_{\alpha =0^+}\nonumber \\= & {} \textrm{tr}[-\varvec{{\mathfrak {M}}}_{\varvec{\beta }}^{-1}((1-\alpha ){\xi }+\alpha {\xi '})(\varvec{F}^\textrm{T}_{\xi ,\xi '}([\varvec{A}'_{\xi ,\xi '}(\alpha )-\varvec{A}'_{\xi ,\xi '}(0)\nonumber \\{} & {} (\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha )+\varvec{A}_{\xi ,\xi '}(\alpha )\nonumber \\{} & {} (\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1} \varvec{C}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(\alpha ) (\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1}\nonumber \\{} & {} \varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha )-\varvec{A}_{\xi ,\xi '}(\alpha )(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(\alpha ))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(\alpha )]\nonumber \\{} & {} \varvec{F}_{\xi ,\xi '})\varvec{{\mathfrak {M}}}_{\varvec{\beta }}^{-1}((1-\alpha ){\xi }+\alpha {\xi '})]\varvec{B})|_{\alpha =0^+}, \end{aligned}$$

(B3)

where $\varvec{A}'_{\xi ,\xi '}(\alpha )$ is the derivative of $\varvec{A}_{\xi ,\xi '}(\alpha )$ w.r.t. $\alpha$. We obtain for $\alpha =0$ that

$(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))= \left( \begin{array}{cc} \varvec{I}+\varvec{C}_{\xi }\varvec{A}_{\xi }&{}0\\ \varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi }&{}\varvec{I} \end{array}\right)$ is lower block triangular as well its inverse $(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))^{-1}=\left( \begin{array}{cc} (\varvec{I}+\varvec{C}_{\xi }\varvec{A}_{\xi })^{-1}&{}0\\ \varvec{-\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi }(\varvec{I}+\varvec{C}_{\xi }\varvec{A}_{\xi })^{-1}&{}\varvec{I }\end{array}\right)$.

We obtain by multiplication of the block matrix

$$\begin{aligned} \varvec{F}^\textrm{T}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(0)\varvec{F}_{\xi ,\xi '}= -\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }+\varvec{F}^\textrm{T}_{\xi '}\varvec{A}_{\xi '}\varvec{F}_{\xi '} \end{aligned}$$

and also we obtain

$\varvec{F}^\textrm{T}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(0)(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0)\varvec{F}_{\xi ,\xi '}$

$$\begin{aligned}= & {} -\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }-\varvec{F}^\textrm{T}_{\xi '}\varvec{A}_{\xi '}\varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }\\{} & {} \quad +\varvec{F}^\textrm{T}_{\xi '}\varvec{A}_{\xi '}\varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi '}\varvec{F}_{\xi }. \end{aligned}$$

By the same way we have

$\varvec{F}^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0)(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(0)(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0)\varvec{F}_{\xi ,\xi '}$

$$\begin{aligned}= & {} -\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }\\{} & {} -\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1} \varvec{\Gamma }_{\xi ,\xi '}\varvec{A}_{\xi '}\varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }\\{} & {} +\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{\Gamma }_{\xi ,\xi '}\varvec{A}_{\xi '}\varvec{\Gamma }^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi }\varvec{F}_{\xi }, \end{aligned}$$

and also

$\varvec{F}^\textrm{T}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0)(\varvec{I}+\varvec{C}_{\xi ,\xi '}\varvec{A}_{\xi ,\xi '}(0))^{-1}\varvec{C}_{\xi ,\xi '}\varvec{A}'_{\xi ,\xi '}(0)\varvec{F}_{\xi ,\xi '}$

$$\begin{aligned}= & {} -\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }\varvec{F}_{\xi }+\varvec{F}^\textrm{T}_{\xi }\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1} \varvec{\Gamma }_{\xi ,\xi '}\varvec{A}_{\xi '}\varvec{F}_{\xi '}. \end{aligned}$$

Inserting these results into (B3) we obtain

By $(\varvec{A}^{-1}_{\xi }+\varvec{C}_{\xi })^{-1}=\varvec{A}_{\xi }-\varvec{A}_{\xi }(\varvec{C}_{\xi }\varvec{A}_{\xi }+\varvec{I})^{-1}\varvec{C}_{\xi }\varvec{A}_{\xi }$, it follows that

The directional derivative ${F}_{\phi }(\xi ,\xi ')$ is linear in $\xi '$. Therefore, it suffices to consider one-point designs $\xi _x$ which assign all observations to a single setting x. For such one-point designs the directional derivative reduces to

According to the general equivalence theorem a design $\xi ^*$ is optimal, if and only if

$$\begin{aligned} F_{\phi }(\xi ^* ,\xi _x)\ge 0;~\forall x \in {\mathcal {X}} \end{aligned}$$

Hence, the result follows.