Practical computing for finite moment log-stable distributions to model financial risk

Abstract

This paper concentrates on the stable distributions which have maximum skewness to the left. The exponentials of such stable distributions are called finite moment log-stable distributions. They have the property that all moments are finite, and are of interest in financial options pricing as an alternative to log-normal distributions. Computation of density and distribution functions has been made faster by using interpolation formulae in two variables and made less error-prone by using computational objects to represent the distributions and performing computational procedures on those objects. Some computations using finite moment log-stable distributions for options pricing are illustrated. The most important qualitative difference from the Black–Scholes log-normal model for options pricing is that the log-stable model suggests that dynamic hedging will reduce portfolio risk by a much smaller amount than is suggested by the log-normal model. This suggests that finite moment log-stable distributions could be used to provide conservative assessments of portfolio risk.

1 Introduction

This work is motivated by the idea that it might be useful to assess the financial risk of a portfolio of options using finite moment log-stable distributions. The intuitive basis for this idea is that these distributions differ from the log-normal distributions which are commonly used for assessing the financial risk of options over assets in that they include the possibility of large decreases in asset values. However, this paper concentrates on some numerical analysis difficulties associated with use of log-stable distributions. The main development is a set of interpolation formulae described in Sect. 3.

The remainder of this section introduces the families of stable distributions and finite moment log-stable distributions, and outlines their computational difficulties. Section 2 gives technical details of how to achieve good precision when computing values of the distribution function or probability density by numerical integration. Section 3 discusses computing values of the distribution function or probability density by interpolation. Section 4 discusses the use of these basic methodologies for calculating option prices. An R package which implements these ideas allows reliable computations based on stable and log-stable distributions.

1.1 Stable distributions

Stable distributions were originally defined as the solution to a theoretical problem. They have the property that the sum of several independent and identically distributed random variables has the same distribution as the individual random variables, except that the location and scale parameters may be different. According to Feller (1966) page 169, Lèvy (1925) first found Fourier transforms of the family of stable distributions.

One parametrization of the characteristic function of a stable distribution, called the A parametrization by Zolotarev (1986) and called the S1 parametrization by Nolan (2013), is that if $Y$ has a stable distribution then

$$\begin{aligned}&\mathrm{E} [\exp (itY)]=\nonumber \\&\quad \left\{ \begin{array}{ll} \exp \left\{ -\sigma ^\alpha |t|^\alpha \left[ 1-i\beta \tan {{\scriptstyle \pi \alpha \over 2}} \mathrm{sign}(t)\right] +i\mu t\right\} &{} \mathrm{~~if~}\alpha \ne 1\\ \exp \left\{ -\sigma |t|\left[ 1+i\beta \frac{2}{\pi } \mathrm{sign}(t) \log |t| \right] +i\mu t\right\} &{} \mathrm{~~if~}\alpha =1. \end{array}\right. \end{aligned}$$

(1)

The distribution and density functions are not generally available in closed form, and are often computed by numerical integration using formulae given by Zolotarev (1986). He showed that the distributions are all unimodal and that the density functions are infinitely differentiable.

The family of stable distributions has four parameters: a location parameter denoted by $\mu$, a scale parameter denoted by $\sigma$, a skewness parameter denoted by $\beta$ and a parameter denoted by $\alpha$ which is called the characteristic exponent. If two independent random variables $X$ and $Y$ have identical stable probability distributions then the sum $X+Y$ has a stable probability distribution with a scale which is $2^{1/\alpha }$ times the scale of $X$.

One feature of stable distributions which has caused confusion is that there are many different parametrizations. See, for instance, Zolotarev (1986), Samorodnitsky and Taqqu (1994) or Nolan (2013). Different parametrizations are convenient for different purposes. Hall (1980) pointed out that mistakes concerning the direction of skewness of different parametrizations had been made by many people, including himself.

I wish to discourage readers from being distracted by the mathematical complexity of stable distributions. As described in Sect. 2.2 of this paper, I commenced by computational effort in this area my writing a computer program for calculating the density and distribution function for general stable distributions. However, maximally-skew stable distributions (ie, ones with $\beta =\pm 1$) can be regarded as more fundamental because Chambers et al. (1976) shows that all stable distributions can be expressed as mixtures of two maximally-skew stable distributions. Most of the work described in this paper is concerned only with the maximally-skew stable distributions.

1.2 Finite moment log-stable distributions

If $X$ has a maximally skew stable distribution which is skewed to the right (and $\beta$ must be either $+1$ or $-1$, possibly depending on the parametrization used) then $\exp (-X)$ can be said to have a log maximally skew stable distribution. This terminology is by analogy to the fact that if $X$ has a normal distribution then $\exp (X)$ is said to have a log-normal distribution. The log maximally skew stable distributions have also been called “finite moment log-stable distributions” by Carr and Wu (2003), highlighting their important property that all moments are finite. This makes them superficially attractive for modelling financial risk, following arguments including those by Mandelbrot (1963) and Fama (1965) that log-normal distributions are not adequate for modelling the prices of financial assets.

The family of finite moment log-stable distributions has three parameters. Relative to the four parameters for general stable distributions, this has two convenient consequences. Some of the complexity of the alternative parametrizations can be ignored; and interpolation for computing the density and distribution functions is much simpler.

Another difference from general stable distributions is that general stable distributions are not defined for $\alpha =0$, but limits of finite moment log-stable distributions as $\alpha \rightarrow 0$ are well-defined and useful. They are discrete distributions with atoms of probability at zero and at one other point. From the point of view of financial risk, the case $\alpha =0$ corresponds to the situation where the only risk is catastrophic: either the value will drop to precisely zero or the value will be some known positive value. In contrast, the case $\alpha =2$ corresponds to the case where risk is due to a large number of small effects each operating on a multiplicative scale: so the central limit theorem applies and the distribution of possible future values is log-normal.

1.3 Moments of finite moment log-stable distributions

The moment generating function for log maximally skew stable distributions is given by Samorodnitsky and Taqqu (1994) page 15, proposition 1.2.12. It can be found by taking the analytic continuation of the characteristic function given in Eq. (1) to values of $t$ on the imaginary axis. We will only deal with the case where $\alpha \ne 1$ for this parametrization because the limit as $\alpha \rightarrow 1$ will be dealt with later using the M parametrization. Using notation which reflects the fact that Eq. (1) uses what Zolotarev (1986) calls the A parametrization and Nolan (2013) calls the S1 parametrization, the moment generating function is

$$\begin{aligned} M_A(t)&= \mathrm{E}\left[ \exp \left( -t\left( \delta +\gamma X_A\right) \right) \right] \nonumber \\&= \exp \left( -\gamma ^\alpha t^\alpha / \cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) -\delta t\right) . \end{aligned}$$

(2)

The different ways of parametrizing general stable distributions do lead to different ways of parametrizing the log maximally skew stable distributions, but the translation between alternative parametrizations is much simpler because there is one parameter fewer.

For the maximally skew stable distributions, the parametrization which Zolotarev (1986) calls the M parametrization and Nolan (2013) calls the S0 parametrization differs from the A or S1 parametrization in that the location parameter differs by $\tan ({{\scriptstyle \pi \over 2}}\alpha )$. The moment generating function of the log maximally skew stable distributions in this parametrization is

$$\begin{aligned} M_M(t)=\exp \left( -\gamma ^\alpha t^\alpha /\cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) +t\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) -\delta t \right) , \end{aligned}$$

as can be seen by replacing $\delta$ by $\delta -\tan ({{\scriptstyle \pi \over 2}}\alpha )$ in Eq. (2). This parametrization has the desirable feature of being continuous around $\alpha =1$. If $\alpha$ is near to 1 then a computationally useful alternative expression in terms of $\varepsilon =\alpha -1$ is

$$\begin{aligned} M_M(t)= \exp \left\{ \frac{\gamma t}{\sin \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) } \left[ \mathrm{expm1}\left( \varepsilon \log (\gamma t)\right) +2\sin ^2\left( {{\scriptstyle \pi \over 4}}\varepsilon \right) \right] -\delta t \right\} . \end{aligned}$$

For $\alpha =1$, the moment generating function can be found as the limit of this expression as $\varepsilon \rightarrow 0$, namely $\exp ({{\scriptstyle 2\over \pi }}\gamma t\log (\gamma t))\exp (-\delta t)=(\gamma t)^{2t/\pi - \delta t}\exp (-\delta t)$.

For the maximally skew stable distributions, the parametrization which Zolotarev (1986) calls the C parametrization and which was used by Chambers et al. (1976) has a scale which is different by a factor of $\cos ^{1/\alpha }({{\scriptstyle \pi \over 2}}\alpha )$ from the A (or S1) parametrization but has the same origin for its location parameter. The moment generating function of the log maximally skew stable distributions in this parametrization is

$$\begin{aligned} M_{C}(t)= \exp \left( -(\gamma t)^\alpha -\delta t\right) . \end{aligned}$$

The mean and standard deviation of the finite moment log-stable distribution, which will be denoted by $\mu$ and $\sigma$, can be readily computed. For the M parametrization, the first moment is

$$\begin{aligned} \exp (-\delta )\exp \left( \frac{\gamma }{\sin ({{\scriptstyle \pi \over 2}}\varepsilon )} \left[ \gamma ^{\alpha -1}-\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) \right] \right) \end{aligned}$$

(3)

and the second moment is

$$\begin{aligned} \exp (-2\delta )\exp \left( \frac{2\gamma }{\sin ({{\scriptstyle \pi \over 2}}\varepsilon )} \left[ (2\gamma )^{\alpha -1}-\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) \right] \right) . \end{aligned}$$

(4)

For the C parametrization, the first moment is

$$\begin{aligned} \exp (-\delta )\exp \left( -\gamma ^\alpha \right) \end{aligned}$$

and the second moment is

$$\begin{aligned} \exp (-2\delta )\exp \left( -(2\gamma )^\alpha \right) . \end{aligned}$$

For both parametrizations, the ratio of the second moment to the square of the first moment (which ratio we will denote by $r$) is a function of $\gamma$ which does not involve $\delta$. So $r$ can be used to find the value for the parameter $\gamma$ for specified first moment, $\mu$, and second moment, $\mu ^2+\sigma ^2$. For the M parametrization, provided that $\alpha \ne 1$, the equation for $\gamma$ is of the form

$$\begin{aligned}&r = \exp \left( \frac{2\gamma }{\sin ({{\scriptstyle \pi \over 2}}\varepsilon )} \left[ (2\gamma )^{\alpha -1}+\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) \right] \right) \\&\div \exp \left( \frac{2\gamma }{\sin \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) } \left[ \gamma ^{\alpha -1}+\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) \right] \right) . \end{aligned}$$

Taking logarithms of both sides and simplifying:

$$\begin{aligned} \frac{2\gamma }{\sin ({{\scriptstyle \pi \over 2}}\varepsilon )}\left[ (2\gamma )^{\varepsilon }-\gamma ^{\varepsilon }\right] =\log (r). \end{aligned}$$

This is satisfied when

$$\begin{aligned} \gamma ^{\alpha }=\frac{\log (r)\sin ({{\scriptstyle \pi \over 2}}\varepsilon )}{2(2^{\varepsilon }-1)} =\frac{\log (r)\sin \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) }{2\,\mathrm{expm1}(\varepsilon \log 2)}. \end{aligned}$$

For the case $\alpha =1$ or $\varepsilon \rightarrow 0$, the corresponding equation is $\gamma =\pi \log (r)/(4\log 2).$ For the C parametrization, the equation for $\gamma$ is of the form

$$\begin{aligned} \exp \left( -(2\gamma )^{\alpha }\right) \div \exp \left( -2(\gamma )^{\alpha }\right) =r. \end{aligned}$$

This also has an explicit solution:

$$\begin{aligned} \gamma =\left[ \log (r)/(2-2^{\alpha })\right] ^{1/\alpha }. \end{aligned}$$

1.4 An easy-to-interpret parametrization

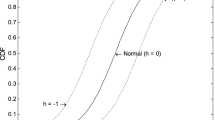
When working with finite moment log-stable distributions, I often use the mean and standard deviation, $\mu$ and $\sigma$ respectively, as parameters rather than the location and scale, $\delta$ and $\gamma$, of the corresponding stable distribution. It is easy to compute one set of parameters from another. The main advantage of the parameters $\mu$ and $\sigma$ is that they are easy to interpret.

Fig. 1

Distribution functions for various $\alpha$ for finite moment log-stable distributions which have mean 1 and standard deviation 1

The most obvious standard values for $\mu$ and $\sigma$ are both unity. Using the upper horizontal axis, Fig. 1 shows these standard log-stable distributions for a range of values of the parameter $\alpha$. The lower horizontal axis allows the corresponding stable distributions to be seen. The figure illustrates the following features.

• For $\alpha =2$ the stable variate has a normal distribution and the log-stable variate has a log-normal distribution.

• The left-hand tails of the stable distributions are lighter than the left-hand tail of the normal distribution which corresponds to $\alpha =2$. The right-hand tails of the stable distributions are heavier than the right-hand tail of the normal distribution which corresponds to $\alpha =2$.

• The limit as $\alpha \rightarrow 0$ for the log-stable variate has probability ${\scriptstyle 1\over 2}$ at $X=0$ and probability ${\scriptstyle 1\over 2}$ at $X=2$. The limit of the corresponding stable variates is not well-defined but essentially has probability ${\scriptstyle 1\over 2}$ at $X=-\log (2)$ and probability ${\scriptstyle 1\over 2}$ at $X=\infty$.

1.5 Computational difficulties

A major barrier to using these distributions is that dealing with stable and log-stable distributions is computationally difficult.

• The density and distribution functions are not available in closed form.

• Dealing with these distributions can often require use of numbers outside the ranges commonly used for storing real numbers on computers (eg, $4.9\times 10^{-324}$ to $1.8\times 10^{308}$). For instance, Fig. 2 shows a log-stable distribution with mean 1, standard deviation 2 and probability 0.7 of being larger than 0.00001. This might be suitable as a model for uncertainty about the economic value of a speculative venture at a future time when overall success or failure is likely to be known. The median of this distribution is $2.2\times 10^{-504}$ and the 10% quantile is approximately $10^{-2395993567}$.

• Standard mathematical parametrizations of the stable distributions all seem unsatisfactory in one of two ways. Either the distribution function is not continuous as a function of the parameters; or there are regions where the propagation of rounding errors from parameters to distribution function, its complement or the probability density is unsatisfactory. For instance for the S0 parametrization (which Nolan (2013) advocates so that the distribution function is continuous as a function of the parameters), the density for the maximally skew stable distribution with standard location and scale parameters is essentially a function of $x+\tan ({\scriptstyle 1\over 2}\pi \alpha )$. For $\alpha =0.01$ the density density is precisely zero for $x \le -\tan (0.005\pi )$ and reaches its peak when $x$ is approximately $5.706\times 10^{-201}$ larger than this critical value. Behaviour of the density in this region cannot readily be investigated using the S0 parametrization because the density is too sensitive to rounding errors in $x$. However the behaviour of the density can be investigated using other parametrizations for which the critical value for $x$ is zero.

Fig. 2

Distribution function for a finite moment log-stable distribution which has mean 1, standard deviation 2 and probability 0.7 of being larger than 0.00001

2 Accurate computations

My first step in developing fast and accurate computing procedures for dealing with finite moment log-stable distributions was to develop accurate computing procedures for general stable distributions. These distributions were later used as the basis for fast computing procedures based on interpolation. The main difficulty in this work was controlling rounding errors.

2.1 Propagation of rounding errors

It is well known in numerical analysis that mathematically equivalent formulae sometimes provide quite different computational accuracy. Computer systems generally provide facilities for computing common mathematical functions such as $\log$, $\exp$, $\sin$, $\arcsin$, $\cos$, $\arccos$, $\sinh$ and $\mathrm{asinh}$ to approximately the relative precision with which floating-point numbers are stored: about 1 part in $2^{52}$ or $2.2\times 10^{-16}$. The functions $\mathrm{log1p}$ and $\mathrm{expm1}$ are also available in most computer languages which are used for mathematical computing.

In some circumstances where the argument of the function might sensibly be specified as a deviation from a standard value or the quantity required is the function plus or minus a constant, we need to be very conscious of the precision that might be lost when numbers are subtracted. Some examples of this where $\delta$ denotes a small positive number such as $\delta = 1\times 10^{-13}$ known to good relative precision are that $\sin (\delta )$ is more accurate than $\sin (\pi -\delta )$, $\mathrm{expm1}(\delta )$ is more accurate than $\exp (\delta )-1$, $\mathrm{log1p}(\delta )$ is more accurate than $\log (1+\delta )$, $2\sin ^2(0.5\delta )$ is more accurate than $1-\cos (\delta )$, $2\arcsin (\sqrt{0.5\delta })$ is more accurate than $\arccos (1-\delta )$, $2\sinh ^2(0.5\delta )$ is more accurate than $\cosh (\delta )-1$, and $\mathrm{asinh}(\sqrt{\delta (2-\delta )})$ is more accurate than $\mathrm{acosh}(1+\delta )$.

One example of sensitivity to deviations from a standard value involving stable distributions is that the right-hand-tail probability for a maximally-skew stable distribution is asymptotically proportional to $2c_{\alpha }x^{-\alpha }$ where $c_{\alpha }=\Gamma (\alpha )\sin ({{\scriptstyle \pi \over 2}}\alpha )/\pi .$ Mathematically, $\sin ({{\scriptstyle \pi \over 2}}\alpha )$ is the same as $\sin ({{\scriptstyle \pi \over 2}}\delta )$ where $\delta = 2-\alpha$. However, if $\alpha$ is near to 2 and $\delta = 2-\alpha$ is known to good relative precision, then $c_{\alpha }$ can be computed more accurately using $c_{\alpha }=\Gamma (\alpha )\sin ({{\scriptstyle \pi \over 2}}\delta )/\pi .$

A second example is translating numerical values of parameters between different parametrizations for general stable distributions. The mathematical relationship between the $\beta$ parameters for the A and C parametrizations is usually written $\beta _C=\arctan (\beta _A\tan ({{\scriptstyle \pi \over 2}}\alpha ))/({{\scriptstyle \pi \over 2}}\alpha ).$ Better computational accuracy can be achieved using the following mathematically equivalent formulae in appropriate circumstances.

• If $\alpha$ is near unity and its difference from unity is known more accurately than $\alpha$ itself, compute $\tan ({{\scriptstyle \pi \over 2}}\alpha )$ as $1/\tan ({{\scriptstyle \pi \over 2}}(1-\alpha )).$

• If $\alpha$ is near two and its difference from two is known more accurately than $\alpha$ itself, compute $\tan ({{\scriptstyle \pi \over 2}}\alpha )$ as $-\tan ({{\scriptstyle \pi \over 2}}(2-\alpha )).$

• If $\beta _A$ is near unity and $1-\beta _A$ is known more accurately than $\beta _A$ then rather than computing $\beta _C=\arctan (\beta _A\tan ({{\scriptstyle \pi \over 2}}\alpha ))/({{\scriptstyle \pi \over 2}}\alpha )$ in the obvious way, first compute

  $$\begin{aligned} \tan \left( {{\scriptstyle \pi \over 2}}\alpha \left( 1-\beta _C\right) \right)&= \frac{\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) - \tan \left( {{\scriptstyle \pi \over 2}}\alpha \beta _C\right) }{1+\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) \tan \left( {{\scriptstyle \pi \over 2}}\alpha \beta _C\right) }\\&= \frac{\left( 1-\beta _A\right) \tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) }{1+\beta _A\tan ^2\left( {{\scriptstyle \pi \over 2}}\alpha \right) } \end{aligned}$$

  and then compute $1-\beta _C$ by taking the arctangent of this quantity. Similar computation of $1+\beta _C$ from $1+\beta _A$ can be done when $\beta _A$ is near $-1$.

Another circumstance where deviations from a standard value might matter is in numerical quadrature. Computing $W$ using Eq. (5) on page 5 is much more accurate in circumstances where $\theta -\phi _0$ and $1-\alpha$ are small in absolute value if they can somehow be obtained to good relative precision rather than being computed by subtraction from $\theta$ and $\alpha$.

Taking care to control the propagation of rounding errors has been a a dominant issue during the writing of the computer code described in this paper. It has frequently been necessary to use different computational algorithms in different regions in order to reduce the sizes of rounding errors.

2.2 Precise computation of density and distribution functions

I have written code in Fortran90 for computing the density and distribution function of stable distributions. The mathematical formulae behind this computation are variations of Zolotarev’s integral formulae, as used by Nolan (1997). These may be understood relative to the simulation method of Chambers et al. (1976) which uses the C parametrization. For $\alpha \ne 1$, the distribution function is

$$\begin{aligned} F_{\alpha }(x)=\int \exp (-W(\theta ,x))\,d\theta \end{aligned}$$

where

$$\begin{aligned} W&= \cos (\theta -\alpha (\theta -\phi _0)) \sin (\alpha (\theta -\phi _0))^{\frac{\alpha }{1-\alpha }}\nonumber \\&\quad \times \cos (\theta )^{-\frac{1}{1-\alpha }}x^{-\frac{\alpha }{1-\alpha }}. \end{aligned}$$

(5)

The integration limits are some combination of $-{{\scriptstyle \pi \over 2}}$, ${{\scriptstyle \pi \over 2}}$ and $\phi _0=-{{\scriptstyle \pi \over 2}}\beta k(\alpha ) /\alpha$ where $k(\alpha )=1-|1-\alpha |$, depending on the values of $\alpha$, $\beta$ and $x$. For $\alpha =1$, the distribution function is of the form

$$\begin{aligned} F_1(x)=\int \limits _{-{{\scriptstyle \pi \over 2}}}^{{{\scriptstyle \pi \over 2}}} \exp (-W(\theta ,x))\,d\theta \end{aligned}$$

where

$$\begin{aligned} W\!=\!{{\scriptstyle 2\over \pi }}\exp \left[ \left\{ \left( {{\scriptstyle \pi \over 2}}+\beta \theta \right) \tan \theta -{{\scriptstyle 2\over \pi }}x\right\} {\!\Big /\!}\beta \right] \left( {{\scriptstyle \pi \over 2}}+\beta \theta \right) \sec \theta . \end{aligned}$$

Formally differentiating these expressions with respect to $x$ gives the density as a one-dimensional definite integral.

The accuracy of this Fortran90 code was checked during its development by comparing results to values given by other people. The precision was checked by comparing both intermediate calculations and final results obtained using 64-bit and 128-bit precision for the floating point numbers. It was often found that rounding errors could be reduced by storing critical quantities relative to more than one origin so that the most appropriate could readily be used. For instance the values of $\alpha - 1$, $2-\alpha$, $\beta +1$ and $1-\beta$ were stored as well as $\alpha$ and $\beta$. For numerical integration with respect to $\theta$, the quantities $\theta \pm {{\scriptstyle \pi \over 2}}$, $\alpha (\theta -\phi _0) \pm \pi$ and $\theta - \alpha (\theta -\phi _0) \pm {{\scriptstyle \pi \over 2}}$ were also stored as well as $\theta$.

A simpler strategy for reducing rounding errors which is more compatible with existing software for automatic numerical integration was developed later. The variable of integration may be scaled to range from $-1$ to $+1$, so that even when the range of integration is halved up to 52 times there will be no rounding error in the computer representation of the endpoints of subintervals. Therefore the quantities $\theta$, $\theta \pm {{\scriptstyle \pi \over 2}}$, $\alpha (\theta -\phi _0) \pm \pi$ and $\theta - \alpha (\theta -\phi _0) \pm {{\scriptstyle \pi \over 2}}$ may be computed to high precision for the intermediate points from the values at endpoints of subintervals. Code for computing the distribution function of stable distributions using this strategy is included in the R package FMStable.

3 Interpolation of the distribution function and the probability density function

The main novel contribution of this paper is to show how the probability distribution function and probability density can be computed satisfactorily by interpolation. Concentration on the maximally skew stable distributions means that only two-dimensional interpolation is required.

In order to provide good approximations to the density, the distribution function and the right tail probability for all $\alpha$ and all $x$, it was found necessary to use different mathematical forms in each of several different regions. The regions where the various approximations have been used are indicated on Fig. 3. These regions were chosen by starting with various asymptotic approximations, investigating how many nodes needed to be included in order that interpolation formulae have relative precision of better than $10^{-14}$ over regions large enough to overlap, and finally fitting interpolation formulae over Region 4 (which is in the middle, so the approximations do not have to be compatible with any asymptotic approximations). Where there is overlap between adjacent regions of validity of interpolation formulae, an arbitrary decision is made as to which formula to use.

Fig. 3

Crude representation of regions where different approximations were used for the density and distribution function for log maximally-skew stable distributions. The boundaries between adjacent regions which are shown as horizontal lines are simply based on the value of $\alpha$. The boundaries which are shown as vertical lines are based on several different variables, considering Eq. (7), (11, (12) and (13). They are not based on a single $x$ variable. Adjacent regions generally overlap

Chebychev nodes have been used for interpolations over finite ranges. For a function $f(x)$ defined over the interval $(-1, +1)$, this means evaluating $f(x)$ at the $n$ points $x_i=\cos \left( (2i-1)\pi /(2n) \right)$ and using polynomial interpolation. For interpolation over the interval $(a,b)$, the function is evaluated at the points ${\scriptstyle 1\over 2}(a+b) + {\scriptstyle 1\over 2}(b-a)x_i$. Interpolation over two variables is done by interpolating over one variable for each of the nodes for the second variable, then interpolating over the second variable.

One-dimensional interpolation was always based on 16 nodes. If there are 8 nodes available on each side of a point for which an interpolated function value is required then the nearest 8 nodes on each side of that point are used. Otherwise, the nearest 16 nodes are used. This form of interpolation is moderately efficient and was used as a standard method in order to simplify the search for good methods of interpolation.

3.1 Region 1

From Holt and Crow (1973) Sect. 2.21 or Zolotarev (1986) Eqs. 2.4.3 and 2.4.8, the probability density at $x_C$ for the C parametrization is given by the convergent series

$$\begin{aligned} f_{\alpha }(x_C)=\frac{1}{\pi x_C}\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k!}\varGamma (\alpha k+1) x_C^{-\alpha k}\sin \left( {{\scriptstyle \pi \over 2}}k\alpha \right) . \end{aligned}$$

The probability in the right tail is

$$\begin{aligned} 1{\,-\,}F_{\alpha }(x_C){\,=\,} \frac{1}{\pi \alpha }\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k\times k!}\varGamma (\alpha k+1)x_C^{-\alpha k}\sin \left( {{\scriptstyle \pi \over 2}}k\alpha \right) .\!\!\!\!\nonumber \\ \end{aligned}$$

(6)

These series suggest that $x_Cf_\alpha (x_C)$ and $1-F_\alpha (x_C)$ can be interpolated as functions of $x_C^{-\alpha }$ and $\alpha$. Such interpolation was found to be reasonably accurate (ie, relative errors apparently less than $10^{-14}$) over the range $\alpha <0.5$ and $x_C>1$ in the C parametrization with 20 Chebyshev-spaced nodes in each of the variables. This is Region 1 on Fig. 3.

Using the first term of series (6) and taking $c_{\alpha }=\varGamma (\alpha )\sin ({{\scriptstyle \pi \over 2}}\alpha )/\pi$ gives the approximation

$$\begin{aligned} 1-F_{\alpha }(x_C) \approx 2c_{\alpha }x_C^{-\alpha }. \end{aligned}$$

This is useful as a first approximation when finding quantiles in this region.

3.2 Region 2

From Eq. (6), as $\alpha \rightarrow 0$ the probability in the right tail tends to

$$\begin{aligned}&\frac{1}{\pi \alpha }\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k\times k!} x_C^{-\alpha k}\left[ {{\scriptstyle \pi \over 2}}k\alpha \right] =\frac{1}{2}\sum _{k=1}^{\infty }\frac{(-1)^{k-1}}{k!} x_C^{-\alpha k}\\&\approx {\scriptstyle 1\over 2}\left( 1-\exp (-x_C^{-\alpha })\right) . \end{aligned}$$

In Region 2, interpolation was done using the variable $1-\exp (-x_C^{-\alpha })$, rather than $\exp (-x_C^{-\alpha })$ as in Region 1. Again, 20 Chebyshev-spaced nodes were used in each of the variables $\alpha$ and $1-\exp (-x_C^{-\alpha })$.

The approximation

$$\begin{aligned} F_{\alpha }(x_C) \approx 1 - 2c_{\alpha }x_C^{-\alpha }. \end{aligned}$$

was used as a first approximation when finding quantiles.

3.3 Region 3 and its dual

Zolotarev (1986) Eq. (2.5.17) tells us that when $\alpha <1$ the density of a maximally-skew stable variable for values of $x_C$ in the C parametrization near zero is approximately

$$\begin{aligned} \frac{\nu }{\sqrt{2\pi \alpha }}\xi ^{{{\scriptstyle 2-\alpha \over 2\alpha }}} \exp (-\xi ) \left\{ 1+\sum _{n=1}^{\infty }Q_n(\alpha )(\alpha \xi )^{-n}\right\} \end{aligned}$$

where

$$\begin{aligned} \xi =(1-\alpha )(x_C/\alpha )^{-\alpha /(1-\alpha )} \end{aligned}$$

(7)

and $\nu =(1-\alpha )^{-1/\alpha }$. The terms $Q_n(\alpha )$ are polynomials of degree $2n$.

Similarly, Zolotarev (1986) Eq. (2.5.20) tells us that the distribution function of a maximally-skew stable variable when $\alpha <1$ for values of $x_C$ in the C parametrization near zero is approximately

$$\begin{aligned} \frac{1}{\sqrt{2\pi \alpha \xi }}\exp (-\xi ) \left\{ 1+\sum _{n=1}^{\infty }\tilde{Q}_n(\alpha )(\alpha \xi )^{-n}\right\} \end{aligned}$$

(8)

where the polynomials $\tilde{Q}_n(\alpha )$ are not the same as $Q_n(\alpha )$.

We do not need to evaluate the polynomials $Q_n(\alpha )$ or $\tilde{Q}_n(\alpha )$. These formulae suggest that interpolation as functions of $\alpha$ and $(\alpha \xi )^{-1}$ can be used to approximate the expressions in large brackets, at least when $\alpha \xi$ is large. Calculations suggest that 20 Chebyshev-spaced nodes in $\alpha$ and 70 Chebyshev-spaced nodes in $(\alpha \xi )^{-1}$ were adequate to achieve good accuracy provided that $\alpha \xi < {{\scriptstyle 1\over 5}}.$

Zolotarev (1986) says that formula (8) also applies when $\alpha >1$ and $x_C \rightarrow \infty$ provided that $\alpha$ is replaced by $1/\alpha$ in the summation. This could also be shown by the principle of duality which is most simply stated in the C parametrization. See Zolotarev (1986) Sect. 2.3. The portions of maximally skew stable distributions for $\alpha >1$ for positive $x_C$ are related to portions of the maximally skew stable distributions for $\alpha <1$. Denoting the distribution function by $F_{\alpha }(x_C)$ and the density function by $f_{\alpha }(x_C)$: if $\alpha >1$ then

$$\begin{aligned} \alpha \left( 1-F_{\alpha }(x_C)\right) =F_{1/\alpha }(x_C^{-\alpha }) \end{aligned}$$

(9)

and

$$\begin{aligned} f_{\alpha }(x_C)=x_C^{-1-\alpha } f_{1/\alpha }(x_C^{-\alpha }). \end{aligned}$$

(10)

The values of $\xi$ are the same for points related by duality. For $\alpha >1$, it should be noted that $\xi$ as a function of $x_C$ in the complex domain has an essential singularity at $x_C=0$ except for the case when $\alpha =2$. Hence this approximation cannot be expected to be useful for negative $x_C$ or for $x_C$ near to zero.

Formulae (9) and (10) above are for the C parametrization. For the M (or S0) parametrization, $x_C$ needs to be replaced by

$$\begin{aligned} x_C=x_Ms \end{aligned}$$

(11)

where $s=(1+\tan ^2({{\scriptstyle \pi \over 2}}k))^{-1/(2\alpha )}$ in the formula for the distribution function. For the density, there needs to be a factor of $s$ as well as this replacement. When $\alpha <1$,

$$\begin{aligned} \xi =(1-\alpha )\left( \frac{x_M+\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) }{\alpha \cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) }\right) ^{-\alpha /(1-\alpha )} \end{aligned}$$

(12)

The inverse relationship for $x_M$ in terms of $\xi$ is

$$\begin{aligned} x_M=\alpha \left( \frac{1-\alpha }{\xi }\right) ^{(1-\alpha )/\alpha } \left( \cos ({{\scriptstyle \pi \over 2}}\alpha )\right) ^{-1/\alpha }-\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) . \end{aligned}$$

This relationship is not computationally practical for $\alpha$ near to 1. It can be rewritten as

$$\begin{aligned} x_M&= \frac{\alpha }{\cos ({{\scriptstyle \pi \over 2}}\alpha )}\mathrm{expm1}\left( \frac{1-\alpha }{\alpha }\log \frac{1-\alpha }{\xi \cos ({{\scriptstyle \pi \over 2}}\alpha )} \right) \\&\quad + \frac{\alpha }{\cos ({{\scriptstyle \pi \over 2}}\alpha )}-\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) . \end{aligned}$$

Computationally, this formula is handled by first calculating four quantities which are dependent only on $\alpha$ or on $\varepsilon =1-\alpha$. It turns out that these formulae work for $\alpha >1$ also, even though the earlier relationships would need to be modified by addition of some modulus signs and multiplication by $\mathrm{sign}(1-\alpha )$.

$$\begin{aligned} C_1&= \frac{\alpha }{\cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) } =\frac{\alpha }{\sin \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) }\\ C_2&= \frac{1-\alpha }{\alpha }=\frac{\varepsilon }{1-\varepsilon } \\ C_3&= \frac{1-\alpha }{\cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) } =\frac{\varepsilon }{\sin \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) } \\ C_4&= \frac{\alpha }{\cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) }-\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) =\frac{1-\varepsilon -\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) }{\cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) } \\&= \frac{2\sin ^2{{\scriptstyle \pi \over 4}}\varepsilon -\varepsilon }{\sin {{\scriptstyle \pi \over 2}}\varepsilon } \end{aligned}$$

Then translation between $x_M$ and $\xi$ for the M (or S0) parametrization can be handled using the equations

$$\begin{aligned}&x_M=C_1 \mathrm{expm1}\left( C_2\log (C_3/\xi )\right) +C_4\\&\xi =C_3/\exp \left( \mathrm{log1p}\left( \frac{x_M-C_4}{C_1}\right) \Big / C_2\right) . \end{aligned}$$

In these regions, an approximation to $\xi$ for given $F$ is found by approximately solving the equation

$$\begin{aligned} F = \frac{1}{\sqrt{2\pi \alpha \xi }}\exp (-\xi ). \end{aligned}$$

A first approximation is $\xi = -\log (F)$. This is refined using a single Newton-Raphson iteration.

3.4 Region 4

Because Region 4 is central, it is not necessary to match the method of interpolation with any asymptotic behaviour. The logarithm of the right hand tail probability and the logarithm of the probability density were interpolated as functions of $\alpha$ and $x_M$. Accuracy appeared to be satisfactory with 40 Chebyshev-spaced nodes over $\alpha$ and 60 Chebyshev-spaced nodes over $x_M$.

Approximate quantiles are found by using the approximation for Regions 3 and its dual if the left hand tail probability is the smaller, and by using the approximation for Regions 5 and 6 if the right hand tail probability is the smaller.

3.5 Regions 5 and 6

An approximation which is useful in these regions is given in Zolotarev (1986) Theorem (2.5.6). We compute

$$\begin{aligned} \eta =\tan \left( {{\scriptstyle \pi \alpha \over 2}}\right) \end{aligned}$$

and then compute $y$ using the implicit equation

$$\begin{aligned} x_M=y+\eta y^{1-\alpha }. \end{aligned}$$

(13)

The density and right hand tail probability at $x_M$ are approximately

$$\begin{aligned}&f_{\alpha }(x_M)\approx \frac{1}{\pi x_M}\sum _{n=1}^{\infty }A_n(\alpha )y^{-\alpha n}\nonumber \\&1-F_{\alpha }(x_M)\approx \frac{1}{\pi \alpha }\sum _{n=1}^{\infty } \frac{1}{n}\left( A_n(\alpha )+(1-\alpha )A_{n-1}(\alpha )\right) y^{-\alpha n}\nonumber \\ \end{aligned}$$

(14)

where $A_0=0$ and, using “Im” to stand for “imaginary part”,

$$\begin{aligned} A_n(\alpha )&= \mathrm{Im~}\left[ \sum _{k=1}^n \frac{\varGamma (\alpha k+n-k+1)}{\varGamma (k+1)\varGamma (n-k+1)}(-\eta )^{n-k}\right. \\&\quad \times \left. e^{i\pi \alpha k/2} (\eta e^{i\pi /2}-1)^k\right] . \end{aligned}$$

In particular,

$$\begin{aligned} A_1\left( \alpha \right)&= \mathrm{Im~}\frac{\varGamma \left( \alpha +1\right) }{\varGamma \left( 2\right) \varGamma \left( 1\right) } e^{i\pi \alpha /2}\left( \tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) e^{i\pi /2}-1\right) \nonumber \\&= \varGamma \left( \alpha +1\right) \mathrm{~Im~}\left\{ \cos \left( {{\scriptstyle \pi \over 2}}\alpha \right) - i\sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) \right\} \nonumber \\&\times \left\{ i\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) -1\right\} \nonumber \\&= 2\Gamma \left( \alpha +1\right) \sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) . \end{aligned}$$

(15)

For the purpose of interpolation, the density and the right tail probability at $x_M$ can be expressed as quantities which depend on $\alpha y^{-1-\alpha }$ times a polynomial in $y^{-\alpha }$ which may be taken to be unity at infinity (ie, $x_M=0$).

This for the A (or S1) parametrization. For the M (or S0) parametrization, the value of $x_M$ for given $y$ is

$$\begin{aligned} x_M&= y+\eta y^{1-\alpha }-\eta =y+\tan \left( {{\scriptstyle \pi \over 2}}\alpha \right) \left[ y^{1-\alpha }-1\right] \\&= y+\mathrm{expm1}\left( \varepsilon \log (y)\right) /\tan \left( {{\scriptstyle \pi \over 2}}\varepsilon \right) \end{aligned}$$

where $\varepsilon =1-\alpha$. The limit as $\varepsilon \rightarrow 0$ (ie, as $\alpha \rightarrow 1$) is $x_M=y+{{\scriptstyle 2\over \pi }}\log (y)$.

Zolotarev (1986) indicates that this approximation is intended to be applied when $\alpha <1$, so interpolation in terms of $\alpha$ and $y^{-1/\alpha }$ can be expected to be satisfactory. Numerical work has indicated that such interpolation also works well when $\alpha >1$.

Interpolation in Region 5 was done using 40 Chebyshev-spaced nodes over $\alpha$ and 20 Chebyshev-spaced nodes over $y^{-1/\alpha }$. Interpolation in Region 6 was done using 17 Chebyshev-spaced nodes over $\alpha$ and 20 Chebyshev-spaced nodes over values of $y^{-1/\alpha }$.

Approximations to quantiles can be found by truncating the series in Eq. (14) and using the known value for $A_1(\alpha )$.

$$\begin{aligned} 1-F_{\alpha }(x_M)\approx \frac{1}{\pi \alpha } 2\varGamma \left( \alpha +1\right) \sin \left( {{\scriptstyle \pi \over 2}}\alpha \right) y^{-\alpha }. \end{aligned}$$

Values for $y$ can be substituted into Eq. (13) to find values for $x_M$.

3.6 Region 7

As $\alpha \rightarrow 2$, it appears that

$$\begin{aligned} f'_{2}(x_M) = \lim _{\alpha \rightarrow 2} \frac{\partial f_{\alpha }(x_M)}{\partial \alpha } \end{aligned}$$

and

$$\begin{aligned} F'_{2}(x_M) = \lim _{\alpha \rightarrow 2} \frac{\partial F_{\alpha }(x_M)}{\partial \alpha } \end{aligned}$$

are bounded and are smooth functions of $x_M$. Interpolation in this region was done using 17 Chebyshev-spaced nodes over $2-\alpha$ and 100 Chebyshev-spaced nodes over $x_M$. This could probably be made computationally faster if good numerical approximations (such as continued fractions) were available for $f'_{2}(x_M)$ and $F'_{2}(x_M)$.

In this region, approximate quantiles were found using the fact that the limiting distribution for $\alpha =2$ is normal with variance 2.

4 Pricing financial options

Now we consider how the interpolation procedures for the density and distribution function of maximally skew stable distributions can be used for financial applications.

A financial derivative is a contract whose outcome depends on fluctuations in the price of an asset (such as 1000 shares in a company). “Call” and “put” options are financial derivatives whereby the purchaser acquires the right to buy or sell an asset for a specified price (referred to as the “strike”) prior to or on a specified date. The seller of the option (sometimes referred to at the “writer”) is required to assure that he/she will maintain the ability to uphold his end of the transaction and is paid a fee.

The simplest options are ones where the purchaser’s right may only be exercised at the specified date. They are referred to as “European” options. Options where the purchaser’s right may be exercised at any time prior to the specified are referred to as “American” options. And there are many more complicated styles of options which will not be of concern here. See, for instance, Hull (2003), for details and further information about options in finance.

One way of computing a fair price for a European option is based on the assumption that uncertainty about the future price of the asset may be described by a log-normal distribution. For instance, suppose that the logarithm of future price, $x=\log (P)$, is normally distributed with density function

$$\begin{aligned} \frac{1}{\sqrt{2\pi }\sigma } \exp \left[ -\frac{1}{2}\left( \frac{x-\mu }{\sigma }\right) ^2\right] . \end{aligned}$$

For the case of no interest and dividends, the value of a European call option with strike $S$ is the expectation of

$$\begin{aligned} (P-S)^+ = \left\{ \begin{array}{l@{\quad }l} (P-S) &{} \mathrm {~~if~} P-S \ge 0 \\ 0 &{} \mathrm {~~if~} P-S < 0. \end{array}\right. \end{aligned}$$

Using $Q(z)$ to denote the right hand tail probability for a standard normal distribution, this expectation is

$$\begin{aligned} \int \limits _{\log (S)} ^\infty \left( \exp (x)-S\right) \frac{1}{\sqrt{2\pi }\sigma } \exp \left[ -\frac{1}{2}\left( \frac{x-\mu }{\sigma }\right) ^2\right] \;dx \end{aligned}$$

which is $-S Q\left( \frac{\log (S) - \mu }{\sigma }\right)$ plus

$$\begin{aligned}&\!\!\!\int \limits _{\log (S)} ^\infty \frac{1}{\sqrt{2\pi }\sigma } \exp \left[ x-\frac{1}{2}\left( \frac{x-\mu }{\sigma }\right) ^2\right] \;dx\\&=\!\!\int \limits _{\log (S)} ^\infty \frac{1}{\sqrt{2\pi }\sigma } \exp \left[ \!-\frac{1}{2}\left( \frac{x-\mu -\sigma }{\sigma }\right) ^2 +{\scriptstyle 1\over 2}\sigma +\mu \!\right] \;dx\\&=\exp \left( {\scriptstyle 1\over 2}\sigma +\mu \right) Q\left( \frac{\log (S)-\mu -\sigma }{\sigma }\right) . \end{aligned}$$

This is equivalent to a particular case of what are known as the Black–Scholes formulas. Following Black and Scholes (1973), these formulas are usually derived from a differential equation which is based on a hedging argument. The above derivation based on calculating the expected payment to the purchaser of the option has the advantage that the same approach can easily be applied even if the form of the distribution used to describe the future value of the asset is something other than log-normal.

Option values are discussed in this section for the case of zero interest rate and zero holding cost. The values of options for non-zero interest rates and non-zero holding costs can be calculated by transforming the problem to one in which these are both zero, valuing the option for the standard case, then back-transforming the option value.

The parameter $\sigma$ in the log-normal model is generally referred to as the “volatility” in the financial options literature.

The log-normal model is not regarded as anywhere near perfect. One common way of discussing departures from it is to use the Black–Scholes formulas implicitly to calculate values for the volatility, $\sigma$, which give observed market prices for options. These values are called “implied volatilities”. It is commonly observed that the implied volatilities vary with the strike price and with the time-to-expiry of options.

4.1 Using log-stable distributions to price options

Carr and Wu (2003) argued that log-stable distributions are likely to be useful for modelling share-index options but not for modelling currency options, because the underlying stable distributions are not symmetric and this asymmetry persists as time-to-expiry increases. Vollert (2001) argued that log-stable distributions are a natural generalization of log-normal models for asset and index return distributions, with the substantial disadvantage that they are “computationally demanding”. Rachev et al. (1999) suggested that these distributions should be used more widely in econometrics.

For the case when the future value of an asset is assumed to come from a finite moment log-stable distribution, the values of options can be computed by numerical integration of the distribution function with respect to the asset price. This provides high precision and is sufficiently rapid for current purposes.

Figure 4 shows the values of options on scales which are often used by options traders. The horizontal axis gives the strike price on a logarithmic scale. The vertical axis gives the implied volatility. The non-bold continuous lines are for finite moment log-stable distributions with mean 1, standard deviation 0.18, and probabilities 0.01, 0.003, 0.001, 0.0003, 0.0001, 0.00003, 0.00001, 0.000003 and 0.000001 that the final asset price will be less than 0.01. The corresponding values for $\alpha$ are 0.687, 1.197, 1.527, 1.769, 1.897, 1.964, 1.9873, 1.99609 and 1.99869. The bold line gives the implied volatility for the distribution corresponding to $\alpha =0$, which is discrete with probability 0.03138 at zero and probability 0.96861 at 1.0324. The dotted line gives the implied volatility for the log-normal distribution corresponding to $\alpha =2$: It is 0.1786 and does not vary with the strike price.

Fig. 4

Implied volatility for option prices based on finite moment log-stable models with mean 1 and standard deviation 0.18 for several different values of the parameter $\alpha$

The lines for values of $\alpha$ greater than 1.0 have shapes consistent with what is sometimes called a “volatility smile”, a “volatility skew” or a “volatility smirk”. The implied volatility is higher for options with a strike price below the expected price than for options with a higher strike price. These graphs curve upwards like a cartoon of a smiley face, but are asymmetric. The left panel of Fig. 3 of Carr and Wu (2003) tells a similar story using $\alpha$ values of 1.2, 1.5, 1.8 and 2.

Other computational methods that might be useful for achieving greater speed are numerical inversion of Fourier transforms, finding three-parameter approximations for the most commonly-used regions of the parameter space (such as $\alpha$ near to 2 and coefficient of variation in the range 0.01 to 0.3), and finding interpolation formulae for the distribution functions of finite moment log-stable distributions that are able to be integrated in closed form term by term.

As an example of a three-parameter approximation, I have used non-linear optimization to fit models for the implied volatility of log-stable distributions with mean 1 as a ratio of polynomials in three variables, removing some terms which did not substantially affect the precision of the approximation. Denoting the scale parameter of the underlying stable distribution for the M parametrization by $\gamma$, denoting the standard deviation of the log-stable distribution by $\sigma$, denoting the standard deviation on the logarithmic scale of a log-normal variable which has the same mean and variance as the log-stable variable by $\sigma _{LN}$, and denoting the strike by $s$, the variables used in this curve-fitting exercise are $a = -(\log (2-\alpha ) + 3)/2$, $l = (\mathrm{\log (\gamma )} + 2.5)/1.5$ and $m = (\mathrm{\log (s)/\sigma _{LN}} + 1)/3$. The approximate implied volatility is

$$\begin{aligned} \sigma _{LN}\times \sum P(i,j,k)a^il^jm^k \Big / \sum Q(i,j,k)a^il^jm^k \end{aligned}$$

(16)

where the coefficients $P$ and $Q$ are given in Table 1. The largest relative error of this approximation when the absolute values of $a$, $l$ and $m$ are smaller than 1 is about 1%.

Table 1 Coefficients for approximation given in Eq. (16) for implied volatility

The relationship between $\gamma$ and $\sigma$ is that Eqs. (3) and (4) allow the variance $\sigma ^2$ to be computed from $\gamma$. The relationship between $\sigma$ and $\sigma _{LN}$ is

$$\begin{aligned} \sigma _{LN}=\sqrt{\mathrm{log1p}(\sigma ^2)} \end{aligned}$$

from the properties of a log-normal variable with unit mean. These relationships make the approximation given by Eq. (16) mathematically convoluted, but do not prevent it from being computationally practical.

4.2 Estimating the parameter $\alpha$

The location and scale parameters of finite moment log-stable distributions can be estimated quickly and accurately by maximum likelihood from data on daily or weekly returns, when interpolation is used to compute the probability density. However, estimation of the parameter $\alpha$ seems to be unreliable. A simulation study showed that if there are no large negative returns in the data then the estimate of $\alpha$ was often near two when the true value of $\alpha$ was 1.8. However, the lack of large negative returns in a set of historical data does not guarantee that there will not be large negative returns in the future.

One practical way to estimate $\alpha$ is to calculate the mean and standard deviation of daily or weekly returns, and to subjectively estimate the annual probability of bankruptcy or of some large drop in price, say 30 or 90%. The parameters of a finite moment log-stable distribution can then be fitted to these three pieces of information. (The estimated probability of bankruptcy must be interpreted as the probability of the price falling to a small but non-zero fraction such as 0.01 or 0.001 of the original price, because the finite moment log-stable model does not allow prices to drop to zero.)

A bank estimating the financial risk associated with its holding of options might adopt a conservative version of this approach whereby probabilities of large drops in prices were computed using a worst-case-scenario. For instance, these probabilities might be based on the observed frequencies of large drops in share prices during the global financial crisis or during major stock market crashes.

The influence of the probability $P_{0.01}$ of a fall to 0.01 of the original price on option values is illustrated in Tables 2 and 3. For the distributions in these tables the mean price is 1 and the inter-quartile range is 0.3. The values for the parameter $\alpha$ are given in the second column of Table 2.

Table 2 Put option values based on finite moment log-stable models with mean 1, inter-quartile range 0.3 and various probabilities $P_{0.01}$ of being less than 0.01. The second column gives values for the parameter $\alpha$

Table 3 Call option values based on finite moment log-stable models with mean 1, inter-quartile range 0.3 and various probabilities $P_{0.01}$ of being less than 0.01

The number $P_{0.01}$ may be interpreted as the probability of default or bankruptcy. The relationship between this number and the ratings quoted by ratings agencies such as Moody’s and Standard & Poor is not tightly defined. An approximate interpretation is that an asset with $P_{0.01}=0.1$ is speculative grade, $P_{0.01}=0.01$ is the high-risk limit of investment grade, $P_{0.01}=0.001$ is typical investment grade, and smaller numbers indicate blue chip grades.

We can see that the option prices deviatiate from the Black–Scholes option prices (which correspond to $\alpha =2$) as the probability of default increases, especially for out-of-the-money put options (such as the third column of Table 2). Note that all of these option values have been calculated ignoring the uncertainty about future volatility. This is quite unrealistic for distributions such as that for $P_{0.01}=0.1$ because there is generally great uncertainty about future volatility for speculative investments.

Another way to estimate $\alpha$ is to use data on the market prices for options, and to find the finite moment log-stable distribution which best fits those prices. This is complicated by the fact that option prices are strongly affected by the spot price of the underlying asset.

In order to check the computational feasibility of this approach, some data on prices for European options over BHP Billiton shares on the Australian Stock Exchange were used. These data were for the 18th December 2012 during which the spot price of BHP shares ranged from A$36.35 to A$36.73.

Data about all series of options over BHP shares were downloaded, but American options were ignored and only 268 European options trades were used. For each option trade, a spot price appropriate to the time when the option trade was made was computed using a Kalman filter fitted to the spot prices for all share trades. This gives approximately the average price of share trades over the two minutes before the option trade.

Considering a stockbroker’s predictions about likely future dividends and the likely taxation credits associated with those dividends, option prices were modelled as if dividends of A$0.60, A$0.66 and A$0.72 would be paid on 1 March 2013, 6 September 2013 and 1 March 2014, respectively.

An interest rate of 3% per annum was used. Log-stable distributions were fitted assuming that the expected share price increases at 3% per annum. The $\alpha$ and scale parameters were estimated by minimizing the weighted sum of squared deviations between modelled option prices and transaction prices, using weights proportional to the square root of the size of the transaction. This was done twice, with option prices which were more than 25 cents different from the modelled price being ignored for the second fitting of the model, in the hope that the fit might be more robust. (Prices for far-out-of-the-money options were seldom ignored. A tentative explanation for the prices that did not fit the model was that one party was not an experienced trader.) The best fit for the distribution describing the annual change in share price had a standard deviation of 0.1710159 and $\alpha =1.9256$. For this distribution, the probability of the share price falling to less than 0.01 of its initial value in a year is 0.000057. (For an investment grade asset like BHP shares, it is likely to be more satisfactory to estimate the probability of default using credit ratings or prices of 1 year Credit Default Swaps, because option values are not very sensitive to this parameter but they are sensitive to uncertainty about the volatility and this has not been considered here.)

This model-fitting was repeated using the approximate implied volatility model given in Eq. (16). Using the approximate methodology, the best fit for the distribution describing the annual change in share price had a standard deviation of 0.17266 and $\alpha =1.91354$. For this distribution, the probability of the share price falling to less than 0.01 of its initial value in a year is 0.000069.

Figure 5 shows the discrepancies between the two sets of fitted option prices. Only in two cases was the difference substantially greater than half a cent. The smallness of the discrepancies suggests that the approximate model is adequate for estimating the parameter $\alpha$ in this way.

Fig. 5

Approximation errors for European options over BHP shares on 18 December 2012

The accurate model-fitting procedure took about 7.2 seconds computer time on a personal computer. The approximate method took only 0.86 seconds. This comparison understates the computational speed advantage of using the approximate method because the fraction of the computation done using the interpreted R language (rather than using compiled C code) was greater for the approximate method.

These computation times are sufficiently short to suggest that log-stable distributions could be used in practice for assessing the financial risk of portfolios that included large numbers of options.

4.3 Hedging

One important aspect of the difference between finite moment log-stable models and log-normal models is that attempts to hedge risk are expected to be much less effective according to finite moment log-stable models with $\alpha$ substantially less than 2 than according to a log-normal model (which is a finite moment log-stable with $\alpha =2$).

Consider a portfolio which contains one share and has written some call options which are at-the-money (meaning that the strike price is equal to the current price) and have one year to expiry. The number of call options written is chosen so that the derivative of the value of the portfolio with respect to current share price is zero. In Table 4, the second row gives the partial derivative of the value of the call options with respect to current price. This partial derivative is referred to as $\Delta$. The number of call options in the portfolio is $1/\Delta$. It varies only a small amount with the parameter $\alpha$ over the range from $\alpha =1.5$ to $\alpha =2$ as shown in Table 4.

Table 4 Variances per unit time for portfolios which contains one share and has written $1/\varDelta$ at-the-money call options

The expected value of this portfolio is zero for any future time. This takes the reduction in the time-to-expiry of the options into account. However, the variance of the value of the portfolio increases with time into the future. This variance has been calculated by numerical integration of the probability density times the square of portfolio value over possible future asset prices. The numbers in the body of Table 4 are these variances divided by the length of the time period.

We can see that for the log-normal model ($\alpha =2$) the variance per unit time is much smaller for small time intervals than for large time intervals. The variance per unit time is approximately proportional to the length of the time interval. Therefore this model predicts that the risk of a portfolio can be substantially reduced by frequent adjustment of the hedging ratio (ie, adjusting the relative numbers of shares and options). The risk can be completely eliminated by continuous-time hedging according to the log-normal model. This apparent ability to reduce risk by dynamic hedging decreases as $\alpha$ is reduced from two. For instance, for $\alpha =1.9$ the minimum variance per unit time of the value of the portfolio per unit time is about 0.12. This is substantially smaller than the variance per unit time of 0.72 if the hedging ratio is not dynamically adjusted. It is also much larger than the variance per unit time over a period of 0.01 years according to the log-normal model. Intuitively, this may be interpreted as meaning that much of the risk of the portfolio can be reduced by dynamic hedging, but that a component of the risk cannot be eliminated.

5 Discussion

The main mathematical contribution of this paper is to show that use of finite moment log-stable distributions is computationally practical. The issues that have been most critical in making the computations fast are the concentration on maximally-skew stable distributions, so that only two-dimensional rather than three-dimensional interpolation is required, the use of different forms of interpolation in different parts of the parameter space, and the functional forms suggested by Zolotarev (1986). This is implemented in the R package FMStable which is about 1000 times faster than the alternative R package stabledist and is substantially more accurate, but stabledist has the advantage that it deals with stable distributions of arbitrary skewness.

The different parametrizations for stable distributions and the complication of using different algorithms for a single mathematical formula in different regions of the parameter space are handled by computer software, rather than requiring users to deal with this complexity. In the package FMStable such objects are of a class called stableParameters, but many other software solutions would be at least as effective. Users are encouraged to use commands which do not require explicit specification of parameters.

In my opinion, the main reason for encouraging use of finite moment log-stable distributions for modelling financial risk is that the reduction of risk achieved by hedging may be much less than when log-normal distributions are used. Methods based on finite moment log-stable distributions could be used for stress testing the portfolios of organizations with large, partly-hedged portfolios, such as banks, insurance companies and hedge funds. They could also be used by the regulators of those organizations.

Finite moment log-stable distributions can be regarded as a one-parameter extension of the log-normal model. It should be possible to consider variation in volatility varies due to changes in market sentiment and variations in the rate at which price-sensitive information is expected to arrive. This is beyond the scope of this paper, but would be expected to improve the ability of the log-stable model to fit observed market prices for options.

Possible future extensions to this work are making use of formulae for derivatives with respect to $\alpha$ at $\alpha =2$, extending the interpolation approach to three variables in order to deal with general stable distributions, developing interpolation formulae in three variables with a wider range than approximation (16). Perhaps the quantity tabulated might be the value of the put option divided by $xF(x)$ in the lower tail of the distribution, the value of the call option times $f(x)/F(x)^2$ in the upper tail, and the implied volatility in the middle of the distribution.