Predicting the Shape of Solar Cycle 25 Using a Similar-Cycle Method

Abstract

A similar-cycle method is applied in predicting the shape of Solar Cycle 25, through a more scientific definition to select similar cycles. Using the current solar minimum $R_{\mathrm{min}}(25)$ as a reference, the six most similar cycles to Solar Cycle 25 are found to be Cycles 24, 15, 12, 14, 17, and 10 (in that order). The monthly values of sunspot-number series for the whole of Cycle 25 are predicted by weighted averaging the corresponding ones in the six similar cycles. As a result, Solar Cycle 25 is predicted to peak around October 2024 with an amplitude of about $R_{\mathrm{m}}=137.8\pm 31.3$ and to end around September 2030. As a by-product, there might be a secondary peak eight months earlier. The similar-cycle method considers only the solar cycles with similar parameters rather than all ones as for regression methods. It has an advantage that it does not depend so much on the accuracy of the observation.

1 Introduction

Solar-cycle prediction is becoming an increasingly important topic in both solar and space-weather physics (Du, Li, and Wang, 2009; Du, 2020a). Spacecraft operators want to understand the strength and peak time of an ensuing solar cycle before or around its onset for planning future space missions. So far, numerous methods have been used to predict the maximum amplitude [$R_{ \mathrm{m}}$] of a sunspot cycle (Du, 2011a), of which some can be used before and some others can be used after the solar minimum [$R_{ \mathrm{min}}$].

At the time about two years after the solar minimum, one can use simple functions to describe the shape of the solar cycle (Stewart and Panofsky, 1938; Nordemann and Trivedi, 1992; Hathaway, Wilson, and Reichmann, 1994; Volobuev, 2009; Du, 2011b; Hathaway, 2015). At the early rising phase of the solar cycle, one can employ the growth rate to predict the following $R_{\mathrm{m}}$ (Thompson, 1988; Cameron and Schüssler, 2008; Du and Wang, 2012; Yoshida, 2014).

At the time around the solar minimum, the geomagnetic (Brown and Williams, 1969; Ohl and Ohl, 1979; Thompson, 1993; Kane, 2007; Du, Li, and Wang, 2009; Du, 2011a) and solar-precursor methods (Schatten et al., 1978; Schatten, 2005; Svalgaard, Cliver, and Kamide, 2005; Pesnell, 2008; Pesnell and Schatten, 2018) are two important ones to predict $R_{\mathrm{m}}$. Dynamo-based models (Babcock, 1961; Leighton, 1969) have been used to predict $R_{\mathrm{m}}$ only recently (Dikpati, de Toma, and Gilman, 2006; Choudhuri, Chatterjee, and Jiang, 2007; Labonville, Charbonneau, and Lemerle, 2019). Yoshida and Yamagishi (2010) pointed out that the decrease rate of the smoothed monthly mean sunspot number during the final three years of a solar cycle can be used as a precursor for the following amplitude (Han and Yin, 2019; Du, 2020b).

As the correlation between $R_{\mathrm{m}}$ and the preceding minimum [$R_{ \mathrm{min}}$] is not strong (Hathaway, Wilson, and Reichmann, 2002), the latter alone is seldom used to predict the former (Du and Wang, 2010; Ramesh and Lakshmi, 2012). Instead, one can predict $R_{\mathrm{m}}$ through combining $R_{\mathrm{min}}$ and the minimum aa geomagnetic index (Wilson, Hathaway, and Reichmann, 1998; Du and Wang, 2010), or combining $R_{\mathrm{min}}$ with the early rising rate of the solar cycle by a “similar cycle” method (Du and Wang, 2011).

Similar-cycle methods are based on the idea that solar cycles having approximatively the same strengths [$R_{\mathrm{m}}$] tend to have similar shapes (Gleissberg, 1971; Wang et al., 2002; Du and Wang, 2011). For example, Gleissberg (1971) estimated the length of Cycle 21 by averaging those of some similar cycles. Based on these methods, the amplitude (Wang and Han, 1997; Wang et al., 2009) and monthly values of the solar cycle (Han and Wang, 1999; Wang et al., 2002; Miao et al., 2008) can also be predicted. These authors adopted a simple average technique with equal weights. Du and Wang (2011) employed a weighted average technique with the weight given by the “degree of similarity” and predicted well the shape of Cycle 24.

In this work, a similar-cycle method is applied in predicting the monthly values of the upcoming Cycle 25. The data used in the current work are shown in Section 2. Section 3 is devoted to the results. The selection process of similar cycles and the concept of “degree of similarity” are introduced in Sections 3.1 and 3.2, respectively. In Section 3.3, the monthly values of sunspot-number series for Cycle 25 are predicted by weighted averaging the corresponding ones in the six similar cycles just obtained. The results using four compact similar cycles are shown in Section 3.4. Two examples using five and three similar cycles are analyzed in Section 3.5. Finally, the results are discussed in Section 4.

2 Data and Parameters

The smoothed monthly mean International Sunspot Number series [$R_{ \mathrm{I}}$] of the second version (Clette et al., 2016) is available at the Sunspot Index and Long-term Solar Observations (SILSO www.sidc.be/silso/datafiles). We employ the more reliable data since Cycle 8 (up to July 2020). The parameters used in this study are shown in Figure 1 and listed in Table 1, in which $R_{\mathrm{m}}$ (solid) and $R_{\mathrm{min}}$ (dotted) are the maximum and minimum amplitudes of the solar cycle, respectively, and $S$ (dashed) is the skewness of the cycle: a measure of symmetry about its maximum (Du and Wang, 2011). The current solar minimum is temporarily taken as $R_{\mathrm{min}}(25)=1.8$ (in December 2019).

Figure 1

Parameters of $R_{\mathrm{m}}$ (solid), $R_{\mathrm{min}}$ (dotted), and $S$ (dashed, using the right-hand ordinate axis).

Table 1 Parameters of the solar cycle.

3 Results

Similar cycles are those with approximatively the same $R_{\mathrm{m}}$, which tend to have similar shapes. This can be roughly indicated by the positive correlation coefficient between $R_{\mathrm{m}}$ and $S$ (representing the symmetry of the cycle), $r_{\mathrm{S}} = 0.51$ at the 96% confidence level. At the present time, as there is no other information about the ensuing cycle ($n_{ \mathrm{r}}=25$), we use the current solar minimum [$x_{\mathrm{r}}=R_{ \mathrm{min}}(25)=1.8$] as a reference to select several similar cycles of which the values of $x=R_{\mathrm{min}}$ are close to $R_{\mathrm{min}}(25)$.

3.1 Selection of Similar Cycles

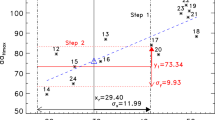
Figure 2 shows the scatter plot of $R_{\mathrm{m}}$ against $R_{\mathrm{min}}$ (triangles), which is used to describe the selection process of similar cycles, in which the cycle numbers are labeled.

Figure 2

$R_{\mathrm{m}}$ against $R_{\mathrm{min}}$ for selecting similar cycles.

Step 1. Initial selection by limiting $x$. First, we select the solar cycles whose $x$ are within $x_{\mathrm{r}}\pm \sigma _{\mathrm{x}}$,

$$ x_{\mathrm{r}}-\sigma _{\mathrm{x}}< x< x_{\mathrm{r}}+\sigma _{ \mathrm{x}}, $$

(1)

where $\sigma _{\mathrm{x}}=5.0$ is the standard deviation of $x=R_{\mathrm{min}}$ (over Cycles 8 – 24). These cycles are SC1 = [10, 12, 14, 15, 17, 19, 24], as indicated by the area to the left of the vertical dash-dotted line (1).

Step 2. Further selection by limiting $y$. Then we delete the cycles in SC1 whose $y$ are far from the range $[y_{1}-\sigma _{\mathrm{y}}, y_{1}+\sigma _{\mathrm{y}}]$ (enclosed by the red dotted lines $2'$ in Figure 2), here $\sigma _{\mathrm{y}}=50.9$ is the standard deviation of $y=R_{\mathrm{m}}$ (over Cycles 8 – 24) and $y_{1}=170.5$ (horizontal red solid line) is the average of $y$ over the cycles of SC1. For each time, we delete only the one whose $y$ is furthest from $y_{1}$ (Cycle 19 in this case), because the average [$y_{1}$] depends on the cycles involved. We use the new average of $y$ over the remaining cycles, $y_{2}=151.4$ (green solid line), to replace $y_{1}$, and we repeat this step until all the cycles selected satisfy

$$ y_{2}-\sigma _{\mathrm{y}}< y< y_{2}+\sigma _{\mathrm{y}} $$

(2)

(enclosed by the green dashed lines in Figure 2).

At this time, both conditions, Equations 1 – 2, are satisfied. The remaining six cycles, SC2 = [10, 12, 14, 15, 17, 24] are called the similar cycles of Solar Cycle 25 about $x$, which can be used to predict Cycle 25 (Section 3.3).

Step 3 (optional). Deep selection by further limiting $y$. If there are many similar cycles (more than six, for example), one can further select some compact cycles that behave slightly better,

$$ y_{2}-\sigma '_{\mathrm{y}}< y< y_{2}+\sigma '_{\mathrm{y}}, $$

(3)

where $\sigma '_{\mathrm{y}}=39.9$ is the standard deviation of $y$ over the Cycles of SC2. The remaining cycles after applying Equation 3 are now SC3 =[10, 12, 15, 24], enclosed by the blue dash-dotted lines (3) in Figure 2. These cycles are evaluated in Section 3.4.

3.2 Degree of Similarity

After selecting some (three to seven) similar cycles, most authors are satisfied to apply them in estimating the maximum amplitude (Wang and Han, 1997; Wang et al., 2009) or monthly values (Han and Wang, 1999; Wang et al., 2002; Miao et al., 2008) of the cycle to be predicted, through a simple average technique, e.g. $R_{\mathrm{m}}(25)=y_{2}= 151.4$ (Figure 2). However, the close proximities are different for different values of $R_{\mathrm{min}}(n)$ to the referenced $R_{\mathrm{min}}(25)$. We use the “degree of similarity” (Du and Wang, 2011) to represent the close proximities for the cycles relative to the referenced one (Figure 3a),

$$ \eta (n) = 1-\frac{1}{\sqrt{2\pi }}\left |\int _{E_{\mathrm{{r}}}}^{E_{\mathrm{{n}}}} {\mathrm{e}}^{-t^{2}/2} {\mathrm{d}}t\right |, $$

(4)

where

$$ E_{i} = \frac{\Delta x_{i}}{\sigma _{\mathrm{{x}}}}= \frac{x_{i}-\overline{x}}{\sigma _{\mathrm{{x}}}} $$

(5)

is the normalized deviation, and $\overline{x}$ and $\sigma _{\mathrm{{x}}}$ are the mean and standard deviation, respectively. The larger the value of $\eta (n)$, the more similar is Cycle $n$ to $n_{\mathrm{r}}$. A few cycles with larger $\eta (n)$ are called the similar cycles of $n_{\mathrm{{r}}}$ about $x$.

Figure 3

(a) Gaussian distribution. (b) $R_{\mathrm{min}}$ (solid) and $\eta _{\mathrm{}}$ (dotted, using the right-hand ordinate axis). The numbers indicate the orders of the six similar cycles.

3.3 Predicting the Monthly Values of Cycle 25 Using All the Six Similar Cycles

We use $x_{\mathrm{r}}=R_{\mathrm{min}}(25)=1.8$ as a reference to calculate the similarities [$\eta (n)$] by Equation 4 for all of the cycles $n=8,9,...,24$. Figure 3b shows the values of $R_{\mathrm{min}}$ (solid) and the values of $\eta$ (dotted) about the referenced one: $R_{\mathrm{min}}(25)$ (triangle). All of the six similar cycles selected in Step 2 (SC2 in Section 3.1) are used in this section, which are ordered as $n_{\mathrm{s}}=24, 15, 12, 14, 17$, and 10 according to $\eta$ (asterisks). This means that Cycle 24 is the (first) most similar cycle, Cycle 15 is the second, Cycle 12 is the third similar cycle of Cycle 25 about $R_{\mathrm{min}}$, and so on.

In similar-cycle methods, the predicted value of $R_{\mathrm{I}}$ for the $j$th month is the weighted average of the corresponding ones, $R_{\mathrm{I}}(j,n_{\mathrm{{s}}})$, over the similar cycles for the same month from the beginnings of the cycles with the weight given by the degree of similarity [$\eta$],

$$ R_{\mathrm{I}}(j) = \frac{ \sum _{i=1}^{6}R_{\mathrm{I}}(j,n_{\mathrm{{s}}}(i))w(i) }{ \sum _{i=1}^{6}w(i) }, $$

(6)

and the standard deviation,

$$ \sigma (j) = \sqrt{ \frac{ \sum _{i=1}^{6} (R_{\mathrm{I}}(j,n_{\mathrm{{s}}}(i))- \overline{R}_{\mathrm{I}}(j))^{2}w(i) }{ \sum _{i=1}^{6}w(i) } }, $$

(7)

is used as an uncertainty estimate for the value at this month, where $w(i) = \eta (n_{\mathrm{{s}}}(i))$ is the weight.

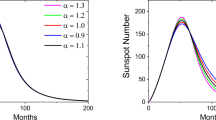
Figure 4a shows the monthly values of $R_{\mathrm{I}}$ for the similar cycles [$n_{\mathrm{{s}}}$] from the beginning. The results are shown in Figure 4b, from which we can calculate the peak value [$R_{ \mathrm{m}}=137.8\pm 31.3$], the rise time [$T_{\mathrm{a}}=58$ months], and the cycle length [$L_{\mathrm{c}}=129$ months]. If the end time of Cycle 24 is (temporarily) taken as December 2019 (the time of the current minimum), Cycle 25 is then predicted to peak around October 2024 with an amplitude of about $R_{\mathrm{m}}(25)=137.8\pm 31.3$ and to end around September 2030. It is interesting to note in Figure 4b that the shape of the cycle has a bimodal structure with the secondary peak [$p_{2}$] $R_{\mathrm{m2}}=137.2\pm 42.8$ around February 2024, eight months earlier than the main one.

Figure 4

(a) The values of $R_{\mathrm{I}}$ for six similar cycles $n_{s}=24, 15, 12, 14$, 17, and 10. (b) The predicted monthly values of $R_{\mathrm{I}}$ for Cycle 25 with uncertainties.

3.4 Predicting the Monthly Values of Cycle 25 Using Four Compact Similar Cycles

As mentioned in Section 3.1, the four similar cycles (SC3 in Step 3) are more compact in $y$-values. According to their similarities, $\eta (n)$ in Figure 3b, the four similar cycles are in the order of $n_{\mathrm{s}}=24, 15, 12$, and 10. The monthly values of $R_{\mathrm{I}}$ for these cycles are shown in Figure 5a and the predicted monthly values for Cycle 25 by Equation 6 are shown in Figure 5b.

Figure 5

(a) The values of $R_{\mathrm{I}}$ for four similar Cycles $n_{s}=24, 15, 12$, and 10. (b) The predicted monthly values of $R_{\mathrm{I}}$ for Cycle 25.

From Figure 5b, one obtains the peak value [$R_{\mathrm{m}}=136.6 \pm 26.7$], the rise time [$T_{\mathrm{a}}=58$ months], and the cycle length [$L_{\mathrm{c}}=134$ months]. So, Cycle 25 is predicted to peak around October 2024 with an amplitude of about $R_{\mathrm{m}}(25)=136.6\pm 26.7$ and to end around February 2031. There is also a secondary peak [$p_{2}$], $R_{\mathrm{m2}}=134.1\pm 44.1$ around February 2024, eight months earlier than the main one. These values are all close to the corresponding ones from six similar cycles in Figure 4b. The reason is that the difference of $R_{\mathrm{m}}$ from the average [$y_{2}$], $R_{\mathrm{m}}-y_{2}$, for Cycles 14 is close to that for Cycle 17 but in the opposite direction (Figure 2), and that Cycle 14 is a more similar one (to Cycle 25) and has a larger weight [$\eta$] than Cycle 17.

3.5 Predicting Cycle 25 Using Other Numbers of Similar Cycles

Figures 6 and 7 show the results for the five and three most similar cycles, $n_{\mathrm{s}}=24, 15, 12, 14$, and 17 and $n_{\mathrm{s}}=24, 15$, and 12, respectively, according to $\eta$ in Figure 3b. For the five (three) similar cycles, the peak time $t_{\mathrm{m}}=$ October 2024 (October 2024), end time $t_{\mathrm{end}}=$ February 2030 (January 2030), and the time of the secondary peak $t_{\mathrm{m2}}=$ January 2024 (January 2024) are all close to the corresponding ones from either six (Figure 4b) or four (Figure 5b) similar cycles.

Figure 6

(a) The values of $R_{\mathrm{I}}$ for five similar Cycles 24, 15, 12, 14, and 17. (b) The predicted monthly values of $R_{\mathrm{I}}$ for Cycle 25.

Figure 7

(a) The values of $R_{\mathrm{I}}$ for three similar Cycles $n_{s}=24, 15$, and 12. (b) The predicted monthly values of $R_{\mathrm{I}}$ for Cycle 25.

The predicted peak value of Cycle 25 from the five (three) similar cycles, $R_{\mathrm{m}}(25)=130.5\pm 28.1(124.6\pm 15.8)$, is slightly smaller than that ($137.8\pm 31.3$) from six similar cycles, because Cycle 10 (stronger than the average $y_{2}$) is missing in the similar cycles. The predicted value (124.6) of $R_{\mathrm{m}}(25)$ being smaller for three similar cycles than that (130.5) for five ones is due to the fact that the relative weight increases when the number of similar cycles decreases, which leads to more contributions of the weaker Cycles 12 and 24 (Figure 2).

4 Discussion and Conclusions

In an earlier article, Du and Wang (2011) predicted the monthly values of $R_{\mathrm{I}}$ for Cycle 24 based on a “similar cycle” method, employing $R_{\mathrm{min}}$ and the early rising rate of the cycle. The predicted amplitude ($R_{\mathrm{m}}=83.8\pm 16.6$) is close to the observed one (81.9, old version), the predicted peak time, September 2013 ± 8 (months), is in between the two observed ones (February 2012 and April 2014), and the predicted end time of Cycle 24, September 2019 ± 8 (months), is also close to the observed one (December 2019) in view of the current data. In addition, they also pointed out that there might be three peaks in Cycle 24 (Table 3 in the original work): apart from the later main one just mentioned, the first is in June 2012 (near the observed February 2012), and the middle is in January 2013 (which did not appear). Therefore, the similar-cycle method is effective in predicting the shape of the solar cycle.

In this study, we described the selection process of similar cycles (Section 3.1). Similar cycles are those satisfying both $|x-x_{\mathrm{r}}|<\sigma _{\mathrm{x}}$ and $|y-y_{2}|<\sigma _{\mathrm{y}}$, in which $x=R_{\mathrm{min}}$, $y=R_{\mathrm{m}}$, $\sigma _{\mathrm{x}} (\sigma _{\mathrm{y}})$ the standard deviation of $x(y)$, $x_{\mathrm{r}}=R_{\mathrm{min}}(25)=1.8$ a reference, and $y_{2}=\overline{y}(n_{\mathrm{s}})$ the average of $y$ over the similar cycles [$n_{\mathrm{s}}$]. According to this condition, the remaining six cycles are called similar cycles, $n_{\mathrm{s}}=24, 15, 12, 14, 17$, and 10, in the order of “degree of similarity” [$\eta$] in Figure 3b. It implies that the most similar cycle of Cycle 25 (about $x=R_{\mathrm{min}}$) is 24, the second one is 15, and so on. The monthly values of Cycle 25 are then predicted as the weighted averages of the corresponding ones over the similar cycles with the weight given by the degree of similarity [$\eta$]. As a result, Cycle 25 is predicted to peak around October 2024 with an amplitude of about $R_{\mathrm{m}}=137.8\pm 31.3$ and to end around September 2030. Besides, there might be a secondary peak eight months earlier than the main one, $R_{\mathrm{m2}} = 137.2\pm 42.8$ around February 2024.

If we further limit the similar cycles that satisfy Equation 3, the number of similar cycles will be reduced to four, $n_{\mathrm{s}}=24, 15, 12$, and 10 in the order of $\eta$. The characteristics of the predicted Cycle 25 (Figure 5b) are very close to those derived by six similar cycles (Figure 4b), such as the peak value, rise time, cycle length, and the secondary peak. If we only select the five (three) most similar cycles according to $\eta$ (Figure 3b), as shown in Figure 6(7), the rise time and cycle length of the predicted Cycle 25 are also very close to those derived by the six similar cycles, but the peak value, 130.5 (124.6), is slightly smaller than that (137.8) from by the six similar cycles. This is due to the fact that the stronger Cycle 10 (than the average $y_{2}$, Figure 2) does not contribute to the results. Based on the above analysis, there are not significant variations in the main characteristics predicted by this method for different numbers of similar cycles. Since we have no special reasons why Cycle 10 should be deleted from Figure 4 for the five similar cycles or from Figure 5 for the three similar cycles, we take the results from six similar cycles as those predicted for Cycle 25.

In the past, the number of similar cycles was usually (artificially) taken as three to seven (Wang et al., 2002, 2009) and the optimal number was believed to be five to six according to experience (Wang et al., 2002). If the number of similar cycles is too small, the characteristics of the predicted cycle will be close to those of the most similar cycle (if using only one similar cycle as an extreme example), and if the number is too large, the behavior of the predicted cycle will be close to the average behavior over all cycles (if using all cycles as another extreme example). In this study, we adopted a more scientific definition to (automatically) select the similar cycles (Equations 1 – 3).

At the current state, as there is no other information of the new cycle (25), we can only employ the current solar minimum $R_{\mathrm{min}}(25)=1.8$ to select the similar cycles. A few years after the solar minimum, similar cycles can be selected by supplementing new information about the solar cycle, such as the early rising rate (Du and Wang, 2011) or the duration of the rising phase (Wang et al., 2002). So, the prediction during the rising phase of the cycle should be more accurate than that at the solar minimum. However, the prediction is not ideal if selecting the similar cycles by other parameters, such as the amplitude or the duration of the descending phase (Wang et al., 2009), because the reference used to select similar cycles does not belong to the cycle to be predicted. If the amplitude of the previous cycle is directly used as a reference to select similar cycles, the amplitudes of these cycles and the predicted one will be close to the amplitude of the (preceding) referenced one. If the duration of the previous descending phase [$T_{\mathrm{d}}$] is used as a reference to select similar cycles, the prediction effect should not be good as the correlation between $T_{\mathrm{d}}$ and the amplitude [$R_{ \mathrm{m}}$] is too weak either for the same phase ($r=0.12$) or for the following $R_{\mathrm{m}}$ ($r=0.24$). Besides, the correlation between the adjacent amplitudes [$R_{\mathrm{m}}(n)$ and $R_{\mathrm{m}}(n-1)$] since Cycle 8 is also too weak ($r=0.17$). Therefore, adopting the previous amplitude and duration (Wang et al., 2009) is worse than adopting the solar minimum and rising rate (Du and Wang, 2011) as references to select similar cycles in predicting the solar cycle (24).

One advantage of the similar-cycle method is that it does not involve the details of a physical process, which may be rather complicated and may not be described by a simple relationship. Similar processes may likely occur if the initial levels of activity are similar. Certainly, even if the initial condition is identical, the final result may show some differences due to some extra occasional reasons (Figure 2). The similar-cycle method is in fact to average these processes so as to reduce the occasional factors. It considers only the similar processes rather than all events as is done by regression methods.

Regression methods tend to predict higher amplitudes than observations in the past (Hathaway, 2015; Pesnell and Schatten, 2018), similar to the case shown in Figure 2 ($y_{2}=151.4$). The main reason is that the peaks are considered to be aligned to the same time so that a higher value is naturally obtained by these methods. While, in this study, the monthly values of the predicted cycle are obtained from those of some similar cycles in which the peaks shift from each other in time, so that the peak value (137.8) inferred from these values is smaller than that (151.4) obtained directly by the amplitudes.

Another advantage of the similar-cycle method is that it does not depend so much on the accuracy of the observation. Even if the value of the referenced one is not observed accurately (due to observation conditions) or has not yet been finally determined (as is the case in the current work), the final results of this method change little. In fact, in the early preparation of this manuscript, we employed the data up to March 2020 and $R_{\mathrm{min}}(25)$ was taken as 3.1. The six similar cycles were the same as above, $n'_{\mathrm{{s}}}=15, 12, 24, 14, 17$, and 10, only the order of Cycle 24 being changed from the first to the third. The early results were almost the same as the above ones: $R'_{\mathrm{m}}=138.1\pm 31.4$, $T_{\mathrm{a}}=58$ (months), $L_{\mathrm{c}}=130$ (months). Certainly, if the end time of Cycle 24 is proved to shift a few months from that (December 2019) used in the current work, the peak time will also shift the same number of months, correspondingly.

Our main conclusions can be drawn as follows:

• i) A more scientific definition is proposed to (automatically) select similar cycles (Equations 1 – 3).

• ii) Using the current solar minimum $R_{\mathrm{min}}(25)$ as the reference, the six most similar cycles to Cycle 25 are $n_{\mathrm{s}}=24, 15, 12, 14, 17$ and 10 (in that order).

• iii) Based on the similar-cycle method, the monthly values of the sunspot-number series (shape) for Cycle 25 are predicted by weighted averaging the corresponding ones in the similar cycles.

• iv) As a result, Cycle 25 is predicted to peak around October 2024 with an amplitude of about $R_{\mathrm{m}}=137.8\pm 31.3$ and to end around September 2030. As a by-product, there might be a secondary peak eight months earlier.