1 Introduction

The key problem of space weather forecasting is the prediction of geoeffective transient solar wind streams that are capable of causing geomagnetic storms. One of the most geoeffective solar wind (SW) transients are interplanetary coronal mass ejections (ICMEs). They are considered as interplanetary manifestations of coronal mass ejections (CMEs) associated with solar activity eruptive processes. Observational criteria and properties of ICMEs and their specific types, such as magnetic clouds at 1 AU, can be found in many publications (e.g. Gosling, 1990; Bothmer and Schwenn, 1998; Zurbuchen and Richardson, 2006; Webb and Howard, 2012, and references therein).

For the earliest prediction of ICME arrival at Earth, one needs to understand the key factors that determine the formation of the transient plasma flows in the corona and their propagation in the heliosphere. From an observational point of view, a typical ICME develops in the corona in four main stages: (1) eruption of plasma with the formation and expansion of a flux rope in the corona that is observable by EUV telescopes up to a distance of \(1.3\,\mbox{--}\,1.7~\mbox{R}_{\odot}\) from the solar center, (2) appearance of a CME in the field of view of white-light coronagraphs above the limb at distances \({>}\,2~\mbox{R}_{\odot}\), (3) propagation of the CME in the heliosphere visible with wide-field coronagraphs or heliospheric imagers, (4) appearance in situ of the solar wind transient with signatures of ICME – significant deviations of the main parameters (\(V_{\mathrm{p}}\), \(n_{\mathrm{p}}\), \(T_{\mathrm{p}}\), and \(B\), which are the proton velocity, density, temperature, and the magnetic field, respectively) from the ambient values (Richardson and Cane, 2004, 2010). The tracking of a CME from the low corona to Earth using a qualitative morphological analysis of the pre-eruption structure and the subsequent events was presented by DeForest, Howard, and McComas (2013).

CMEs are the clearest evidence of ICME initiations. The source regions of CMEs in the solar corona can be identified and localized by their characteristic signatures: solar flares, flows, magnetic reconfiguration, EUV waves, jets, coronal dimmings or brightenings, filament eruptions, and post-flare loop arcades revealed by continuous monitoring of the solar corona by EUV imaging using well-developed methods of data processing. Cremades and Bothmer (2004) have studied 276 CMEs in the period 1997 – 2002 and concluded that the topology of these CMEs and their orientation were defined by the location and magnetic configuration of the sources, in particular, the position of the neutral line between two opposite magnetic polarities. This characteristic has been recognized in the solar event of 2 August 2011, which is considered below.

Prediction of ICME arrival in the Earth environment depends on the CME kinematics in the heliosphere. Solar wind models describe this propagation. The simplest one, the Archimedean spiral (or ballistic) model (ASM), is based on the assumption that the solar wind streams have constant velocity during the whole passage from the Sun to Earth (Nolte and Roelof, 1973; McNeice, Elliot, and Acebal, 2011). The ASM model does not take into consideration the evolution of the CME velocity in the heliosphere, so it can be used only for an approximate determination of the arrival time interval with an uncertainty of half a day. The improved drag-based model (DBM) assumes that the dynamics of CMEs is dominated by the magnetohydrodynamic (MHD) aerodynamic drag (Cargill et al., 1996; Vršnak, 2001; Owens and Cargill, 2004; Cargill, 2004; Vršnak et al., 2004, 2010; Vršnak and Žic, 2007; Vršnak, Vrbanec, and Čalogović, 2008; Borgazzi et al., 2009; Lara and Borgazzi, 2009), i.e. that above a distance of \(20~\mbox{R}_{\odot}\), CMEs faster than the ambient solar wind are decelerated, whereas those that are slower are accelerated by the ambient flow (Gopalswamy et al., 2000). A validation analysis shows that the mean uncertainty in predicting the arrival time of ICMEs by the DBM reaches from 12.9 hours, when the deviation of CMEs from the Sun–Earth line is larger than their half-width, to 6.8 hours when this deviation is smaller (Vršnak et al., 2013; Shi et al., 2015). Prediction of the arrival time by the kinematical models is based on the knowledge of the initial CME velocity at a distance of \({\sim}\,20~\mbox{R}_{\odot}\), which is subject to the projection effect, which in turn depends on the angle between the CME propagation direction and the Sun – Earth line. Colaninno and Vourlidas (2009) proposed a method to derive the propagation direction by comparing masses of the CME structure determined from the Thomson scattering intensities observed by the two Solar Terrestrial Relations Observatory (STEREO) spacecraft located in different angular positions. They found that the direction ambiguity becomes reasonably small (\({\leq}\,20^{\circ}\)) for angular separations between spacecraft \({>}\,50^{\circ}\). However, this method does not take into consideration the CME size and distribution of masses in the 3D CME structure, so it gives the center-of-mass velocity rather than the velocity of the leading edge that is commonly used in prediction.

The aforementioned estimations concern the propagation of single CMEs. In some cases, two or more successive CMEs propagate in the direction of Earth. As a result of interaction, these CMEs change their kinematic parameters. Temmer et al. (2012) described the case of 1 August 2010, when the interaction of two CMEs resulted in a strong deceleration of the overtaking second CME, followed by their merging and further propagation as a single structure. The authors succeeded to simulate the kinematical evolution of the second CME using the drag-based model (Vršnak et al., 2013) and varying the drag parameter, \(\Gamma\), value and the ambient solar wind speed from the region of interaction (\({\sim}\,35~\mbox{R}_{\odot}\)) to Earth. Other cases of interaction between CMEs and analyses of their kinematics by multipoint observations were described in Möstl et al. (2012), Lugaz et al. (2012), Colaninno and Vourlidas (2015), and in references therein.

Currently, several sophisticated physics-based models exist for solar wind forecasting near Earth and beyond with the use of the MHD approach: the Wang–Sheeley–Arge (WSA)-Enlil model, MHD-Around-a-Sphere (MAS)-Enlil model, Space Weather Modeling Framework (SWMF), and their combinations (Jian et al., 2015). These models structurally consist of two main parts: the solar coronal and heliospheric components. The coronal part of the WSA, MAS, and SWMF models approximates the outflow at the inner boundary of the heliosphere based on synoptic magnetograms constructed from daily full-disk photospheric magnetograms (Arge and Pizzo, 2000) using a semi-empirical model based on the potential magnetic field approximation. Then, the boundary outflow and magnetic field distributions are used as the initial data in MHD simulations, which describe the radial expansion and evolution of the solar wind plasma in the heliosphere.

The Enlil model is a 3D time-dependent heliospheric model based on ideal MHD equations (Odstrčil, 1994; Odstrčil, Dryer, and Smith, 1996; Odstrčil and Pizzo, 1999). The inner boundary of the Enlil model is placed at 21.5 or \(30~\mbox{R}_{\odot}\) beyond the outermost critical point and the outer boundary is taken from 2 to 5 or 10 AU. To predict the propagation of CMEs, the WSA-Enlil cone model additionally uses white-light images from the Large Angle and Spectrometric Coronagraph (LASCO: Brueckner et al. (1995)) and coronagraphs onboard STEREO (Howard et al., 2008). This model characterizes the basic properties of the CME, including velocity and size (Pizzo et al., 2011; Mays et al., 2015). It focuses mainly on the prediction of the arrival time of the CME without localizing its coronal origin. Mays et al. (2015) concluded in their statistical analysis of 35 CMEs between January 2013 and July 2014 that the mean estimated error of the CME arrival by the Enlil model was 12.3 hours. The inaccuracy of current models arises to a considerable degree from insufficient knowledge of the interaction of the CME plasma with the ambient solar wind and other wind components in the heliosphere. Information about these processes can be obtained from the fast-progressing heliospheric tomography that is based on the interplanetary scintillation (IPS) in radio waves (Manoharan, 2010).

Among other parameters of solar wind transients, the ion charge composition of the plasma is one of the important identifiers of their origin, whereas it depends on the parameters of the source and remains practically unchanged during the solar wind propagation in the heliosphere. Analysis of the ion charge state and mass composition of the solar wind plasma helps to separate its different components and to determine its source (Fisk, Schwadron, and Zurbuchen, 1998; Zhao, Zurbuchen, and Fisk, 2009; Zhao et al., 2014; Kilpua et al., 2014; Wang, 2012).

It is believed that the ion charge state of the solar wind, registered at Earth’s orbit, approximately corresponds to its state in the corona at the altitude where it is “frozen-in” (a transition to the limiting case, where the ionization and recombination times of the plasma in the corona are on the order of or longer that the time of the solar wind propagation in the heliosphere (Hundhausen, Gilbert, and Bame, 1968)). The frozen-in condition is valid at distances between 1.5 to \(4~\mbox{R}_{\odot}\), which depends on the type of ion and the level of activity (Feldman, Landi, and Schwadron, 2005).

The main factors that determine the ion composition of the CME plasma and its evolution in the corona are temperature, density, and mass velocity, which depend on the level of solar activity. At higher activity, plasma temperature and density in the source and average CME speed increase. During the expansion of the CME plasma from the origin to the frozen-in region, its ion composition evolves as a result of various processes, such as heating by an energy release from the flare site and cooling by heat conduction, radiation losses and adiabatic expansion. From in situ measurements it was established that the faster CMEs and ICMEs, as a rule, have higher ion charge states than the slower ones (Gopalswamy et al., 2013).

Gruesbeck et al. (2011) presented a procedure for deriving the ion composition of CMEs in the corona. To achieve this, they used in situ measurements of the ion charge states of C, O, Si, and Fe and interpreted them in the context of a model for the early evolution of the CME plasma. They obtained, in particular, a best fit for the data provided by an initial heating of the plasma, followed by a cooling expansion. Lepri et al. (2012) presented an analysis and comparison of the heavy ion composition, observed during the passage of an ICME at the Advanced Composition Explorer (ACE) and Ulysses. They compared the ion composition, obtained across the two different observation cuts through the ICME, with predictions for heating during the eruption, based on models of the time-dependent ionization balance throughout the event. The authors of these two articles based their considerations only on assumptions about conditions in the coronal sources without comparing them with measurements.

Lynch et al. (2011) and Reinard, Lynch, and Mulligan (2012) used large-scale non-ideal 2.5D MHD simulations of the solar wind and investigated the ion charge state composition during the CME propagation. They found only a qualitative matching between the observation and model in the charge state enhancements in the flux rope material and in its front because a 2.5D model is not suitable for the proper quantitative description of the ionization state of plasma elements. The 3D MHD model presented in this article (Pagano, Mackay, and Poedts, 2013b) certainly addresses these improvements, but the very different spatial domains of the two studies make direct comparison difficult. Pagano et al. (2008) have previously successfully derived the ion composition from the post-processing of MHD simulations. They explained several observational features of shocks connected to CMEs by reconstructing the out-of-equilibrium ionization state of O VI and Si XII, when an MHD shock undertakes the plasma.

In this article, we present a complex method to predict the ion composition of solar wind transients using both numerical simulations and direct observations of the CME initiation in the corona. This approach enables us to establish relations between parameters of the CME source in the corona and the resulting in situ parameters of the solar wind transients. We consider a case of three solar events: X-ray flares and CMEs that occurred on 2 – 4 August 2011, which led to significant disturbances of the solar wind near Earth on 4 – 7 August 2011 and produced a strong geomagnetic storm with a minimum value of \(\mathit {Dst}=-110~\mbox{nT}\) (Yiğit et al., 2016). In our work, we focus on the investigation of the solar part of this complex event under favorable conditions, when the associated coronal phenomena have arisen near the solar disk center and the resulting CMEs are observed in quadrature by the Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI: Howard et al., 2008) instruments onboard the STEREO-A and B spacecraft and the LASCO C2 coronagraph onboard SOHO.

The article consists of eight sections. This section presents a review of the methods for identification of ICMEs and their solar sources. In Section 2 we present a general description of three eruptions on 2 – 4 August 2011. Sections 3 – 6 contain a detailed analysis of the first event of 2 August 2011: the observational data, diagnostics of the CME plasma, description of the 3D MHD model of the flux rope ejection, comparison of the results of numerical simulations with observations, and analysis of the plasma ion composition in the solar source and its evolution in the corona. The final sections summarize the results of our study. A detailed study of the second and third events of 3 and 4 August, when two CMEs interacted in the heliosphere, will be presented in a next article.

In the analysis, we use the data from the Solar Dynamic Observatory (SDO): the solar EUV images from the Atmospheric Imaging Assembly telescope (AIA: Lemen et al., 2012), and the photospheric magnetic field maps from the Heliospheric and Magnetic Imager instrument (HMI: Schou et al., 2012). Diagnostics of flares in the coronal sources are fulfilled using the Geostationary Operational Environmental Satellite system (GOES) X-ray data, and temperature and density of the outflow plasma are defined by the differential emission measure (DEM) method using the AIA multi-wavelength EUV images. The solar wind data, including the ICME parameters and charge states of C, O, and Fe ions, are extracted from the ACE data (Stone et al., 1998).

2 The Solar Wind Transients of 4 – 7 August 2011 and Their Solar Sources

Figure 1 shows the level 2 one-hour averaged ACE solar wind data for the period 4 – 8 August 2011. The solar wind transients identified in these data were referenced in three databases related to the International Study of Earth-Affecting Solar Transients (ISEST).Footnote 1 The ICME and CME lists of the George Mason University (GMU)Footnote 2 and of the University of Science and Technology of China (USTC)Footnote 3 describe only one ICME of 6 August 2011, classified as the EJ+CIR+SH (ejecta + corotating interaction region + shock) event (GMU list) or SH+EJ (shock + ejecta) event (USTC list), which led to the geomagnetic storm of 6 August, 12:00 UT, with \(\mathit{Dst}=-110~\mbox{nT}\). The GMU list associates the ICME with the M9 flare and halo CME that occurred on 4 August 2011. The Richardson and Cane ICME list (hereafter RC list)Footnote 4 mentions two shocks and two ICMEs, indicated in Table 1 and marked in Figure 1. The shock times in the RC list correspond to the sudden commencement of the geomagnetic storms that accompanied the shocks when they reached the Earth’s magnetosphere (Richardson and Cane, 2010). The first ICME showed small enhancements of the magnetic field, proton density, and speed above the background level. The temperature-related ion ratios, \(\mbox{C}^{6+}/\mbox{C}^{5+}\), \(\mbox{O}^{7+}/\mbox{O}^{6+}\), and the mean charge of iron ions, \(Q_{\mathrm{Fe}}\), slightly exceeded the background. Only the structure-related Fe/O ratio showed a noticeable increase to the value of 0.55, which corresponds to a first ionization potential (FIP) bias of \({\sim}\,3\) and implies plasma from closed magnetic structures in the source region. The second ICME displayed a jump of the proton speed to \(610~\mbox{km}\,\mbox{s}^{-1}\) with moderate enhancements of the magnetic field magnitude and proton density. Thus, the typical ICME signatures (Zurbuchen and Richardson, 2006; Richardson and Cane, 2004), except for the decreased proton temperature and the ion composition, were shown weakly by both ICMEs. However, the identification of the second ICME in the RC list is rather ambiguous because other signatures such as an enhanced magnetic field and ion charge state did not appear. The negative values of the \(z\) component, \(B_{{z}}\), of the interplanetary magnetic field (IMF) (−5 and \(-17~\mbox{nT}\) in the geocentric solar magnetospheric (GSM) coordinate system) were registered in the sheaths that followed the shocks, being the most likely cause of the geomagnetic storm of 6 August 2011. The development of this storm was considered in detail by Yiğit et al. (2016).

Figure 1
figure 1

ACE solar wind data for 4 – 8 August 2011. The times of shocks, Sh1 and Sh2, that correspond to the geomagnetic storm sudden commencements (Richardson and Cane, 2010) are marked by the solid lines. The start and end of ICME1 and ICME2 are marked by the dot-dashed lines.

Full size image
Table 1 Characteristics of the ICMEs on 4 – 5 August 2011 presented in the ICME list of Richardson and Cane ( http://www.srl.caltech.edu/ACE/ASC/DATA/level3/icmetable2.htm ).
Full size table

An application of the ballistic propagation model (assuming that the ICME speed between the Sun and Earth is equal to its in situ value taken from the RC list) gives a preliminary time period for the solar events that probably produced these ICMEs from 31 July 2011, 18:00 UT to 4 August 2011, 13:00 UT. During this period, three flares and three CMEs, directed to Earth, occurred in active region (AR) 11261 (Table 2). To identify the solar sources of the solar wind transients, we used simulations of two heliospheric CME propagation models: the Advanced Drag Model (ADM) (Vršnak et al., 2013) and the WSA-Enlil Model (Pizzo et al., 2011). When we take an asymptotic solar wind speed of \(350~\mbox{km}\,\mbox{s}^{-1}\), the ADM gives transit times of 74.28, 84.48, and 51.08 hours with a mean uncertainty of \({\sim}\,10\) hours for the three CMEs listed in Table 2 (Shi et al., 2015). These transit times correspond to the time slots of the ICME arrival time (at Earth): 4 August 2011, 22:50 UT – 5 August 2011, 18:50 UT, 6 August 2011, 16:30 UT – 7 August 2011, 12:30 UT, and 5 August 2011, 21:20 UT – 6 August 2011, 17:20 UT (Figure 2). The slots associated with CME1 and CME2 agree well in time with the ICMEs in the RC list and enhancements in the ion charge state composition derived from ACE data. The slot associated with the fast CME3 coincides with the noticeable enhancements in the ion charge state and magnetic field magnitude, but was not identified as an ICME. It should be noted that the ADM time slots coincide with the ion charge state transients with a mean discrepancy of 5.6 hours. The minimum, maximum, and mean values of the ion composition parameters for these transients are given in Table 3.

Figure 2
figure 2

ACE \(Q_{\mathrm{Fe}}\) data. The solar wind transients identified by the \(Q_{\mathrm{Fe}}\) enhancements (solid lines with numbers) and their arrival time slots given by the Advanced Drag Model (the dash-dotted lines) are indicated. The numbers designate the association with the CMEs listed in Table 2.

Full size image
Table 2 Flares and CMEs that occurred on 2 – 4 August 2011 according to data from GOES, STEREO-A/COR2 (A) and SOHO/LASCO (L).
Full size table
Table 3 Ion composition parameters of the solar wind transients determined from the \(Q_{\mathrm{Fe}}\) enhancements (Figure 2).
Full size table

To understand the nature of the third transient, we consider the results of the simulation of this complex event by the WSA-Enlil model, presented in the Enlil solar wind prediction helioweather database.Footnote 5 It was found that CME3 (started on 4 August 2011) overtook CME2 because it was faster. CME2 started on 3 August 2011, at the distance of \({\sim}\,0.6~\mbox{AU}\), when CME1 had already reached Earth. In Figure 3 we present the map of the normalized plasma density in the ecliptic plane for 5 August 2011, 00:00 UT, and the J-map for the three solar wind transients from the helioweather database. As a result of the interaction between the second and third CMEs, the merged cloud reached Earth on 6 – 8 August 2011, producing the observed variation of the ion composition.

Figure 3
figure 3

(a) Normalized density map in the ecliptic plane. (b) The J-map for the three solar wind transients obtained with the WSA-Enlil model on 5 August 2011, 00:00 UT ( http://helioweather.net/archive/2011/08/ ).

Full size image

In Section 3 we consider in general the complex solar wind event of 4 – 7 August 2011, study its coronal sources, and examine in detail the formation of CME1, which originated on 2 August 2011. The features of the second and third CMEs and their solar origin will be studied in a following publication.

3 Formation of the CME of 2 August 2011 in the Corona

3.1 Kinematics

We study the formation of three CMEs on 2 – 4 August 2011 in the low corona using the SDO/AIA images in different wavelength channels. After preliminary processing of level 1 to level 1.5 data, we produce running-difference images to identify the moving coronal structures associated with a CME. These structures are seen as expanding loops, but in fact they represent projections of the expanding erupting shells integrated over their legs along the line of sight (LOS). In the studied events the largest contrast is seen in the 211 Å channel images.

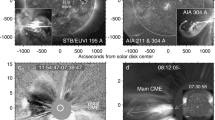
Figure 4a represents a group of expanding loop-like features in the 211 Å running-difference image at 05:58:02 UT, 2 August 2011, in the initial stage of CME1 formation (Table 1). These structures apparently represent projections of the eruption shell on the disk plane. They disappeared at \({\sim}\,06{:}00~\mbox{UT}\), probably as a result of the CME take-off or because of heating, as we show in Section 4. The distance-time graphs in Figure 4c show the height variation of the CME in the low corona, seen in EUV AIA images (channel 211 Å), and above the limb, seen by STEREO-A/EUVI in 171 Å (Figure 4b) and in the field of view of the LASCO C2 coronagraph. We associate the transverse distances from the LASCO data with height, assuming the self-similar expansion of the CME, when the vertical, \(d_{\mathrm{r}}\), and horizontal, \(d_{\mathrm{h}}\), displacements are in the same relation as the radial speed of the CME, \(v_{\mathrm{r}}\), measured by STEREO-A/COR2, and the transverse speed, \(v_{\mathrm{h}}\), measured by LASCO: \(d_{\mathrm{r}} / d_{\mathrm{h}} \simeq v_{\mathrm{r}} / v_{\mathrm{h}}= 1.09\). The acceleration phase of the CME corresponds to the second peak of the flare flux profile (bottom in Figure 4c).

Figure 4
figure 4

Formation of the CME on 2 August 2011. (a) The running-difference image (AIA, 211 Å) shows the erupted structures in projection on the disk at 05:58:02 UT. (b) The running-difference image of the CME seen by STEREO-A/EUVI in 171 Å at 06:02:15 UT. (c) The dotted line shows the dependence of the CME expansion height (the origin is marked by the cross in Figure 4a) on time. Crosses correspond to the brightest structure at the disk seen by AIA, triangles to the CME expansion above the limb seen by STEREO-A/EUVI, and the diamonds to the CME expansion seen by LASCO/C2. The solid line corresponds to the flux from GOES 1.0 – 8.0 Å in \(10^{-4}~\mbox{W}\,\mbox{m}^{-2}\) (the flare occurred on 2 August 2011). (d) Dependence of the CME speed on time seen by AIA, EUVI, and LASCO (symbols are the same as in (c)). The dotted line shows the fitting function (see text).

Full size image

Figure 4d shows the dependence of the CME speed on height, calculated from the data of different instruments. Projection effects are not important in our case. The WSA-ENLIL 3D simulations show that the leading edge of the CME structure in the ecliptic plane deviates from the Sun – Earth line westward by no more than \(10^{\circ}\), whereas the position angle of STEREO-A at that time was \(100.5^{\circ}\). Thus, the data in Figure 4d, obtained from observations by COR2 on STEREO-A, represent the real radial velocity of the CME. During the expansion, the CME speed increased from \(26~\mbox{km}\,\mbox{s}^{-1}\) at \(h_{\mathrm{r}}\simeq~0.06~\mbox{R}_{\odot}\) to \({\sim}\,800~\mbox{km}\,\mbox{s}^{-1}\) at \(5~\mbox{R}_{\odot}\).

3.2 Plasma Diagnostics

To derive the plasma parameters from the image data on 2 August 2011, we apply a plasma diagnostics method for the flare region and the moving coronal structure associated with the CME at five different times. We use the differential emission measure (DEM) analysis to evaluate averaged electron temperatures and densities of the plasma structures under consideration. The DEM analysis is carried out using intensities in six SDO/AIA EUV channels: 94 Å, 131 Å, 171 Å, 193 Å, 211 Å, and 335 Å. In all five positions along the direction of propagation, we build the light curves of the mean intensities in 4×4 arcsec boxes as a function of time and determine the fluxes in each spectral channel as the maximum value minus the mean background. The background corresponds to the quiet corona before the moving CME structure reaches it. The intensity flux \(F_{i}\) in the channel i can be written as

$$ F_{i} = \int _{\Delta T} G_{i}(T) \mathrm{DEM}(T) \,\mathrm{d}T , $$
(1)

where \(G_{i}(T)\) is the temperature response function of the passband i, and \(\mathrm{DEM}(T)\) is the DEM distribution of the plasma. To retrieve the function \(\mathrm {DEM}(T)\), we use a DEM technique that is based on the probabilistic approach to the inverse problem (see, e.g., Urnov et al., 2007; Goryaev et al., 2010; Urnov, Goryaev, and Oparin, 2012 for the details). The DEM temperature distribution for each plasma structure under consideration is then used to determine an effective temperature, \(T_{\mathrm{eff}}\), according to the formula

$$ T_{\mathrm{eff}} = \frac{\int_{\Delta T} T G(T) \mathrm{DEM}(T) \,\mathrm{d}T}{\int_{\Delta T} G(T) \mathrm{DEM}(T) \,\mathrm{d}T} , $$
(2)

where \(G(T)=\sum_{i} G_{i}(T)\) is the total temperature response for all channels. The averaged electron density in a given plasma structure is then estimated using the total emission measure (EM) and the plausible geometry of the corresponding plasma structure.

The averaged temperatures and densities for the flare on 2 August 2011 are given in Table 4. Furthermore, the plasma parameters for the moving CME structure on 2 August 2011 in the range \(0.1\,\mbox{--}\,0.15~\mbox{R}_{\odot}\) from the solar surface are presented in Figure 5. It is worth noting that the temperatures in the moving plasma structure are noticeably lower than in the corresponding flare.

Figure 5
figure 5

Electron temperature and density evolution for the expanding plasma structure determined by the DEM method from the AIA images on 2 August 2011.

Full size image
Table 4 Averaged values of the electron temperature and density in the flare on 2 August 2011 (the parameters are obtained in the region marked with a red cross in Figure 4a).
Full size table

4 Numerical Simulation of the Flux Rope Ejection

To model this specific flux rope ejection in the solar corona, we use an ideal 3D MHD simulation, coupled with a continuous time series evolution of the magnetic field through a series of quasi-static nonlinear force-free (NLFF) fields. The latter technique is used to produce a non-potential initial condition that is used in the ideal MHD simulation. This approach is a combination of the models presented in Pagano, Mackay, and Poedts (2013b) and Gibb et al. (2014), which have been specifically tuned for the present simulation.

The key idea is to describe the flux rope formation and the conditions before the onset of the ejection with the time series of NLFF fields, suited for a slow, quasi-static, and magnetically dominated evolution, and to adopt a full MHD description when the evolution of the system becomes fast, out of equilibrium, and in a multi-\(\beta\) regime, where \(\beta\) is the rate of the plasma pressure to the magnetic pressure.

4.1 NLFF Field Time Series

In order to describe the slow evolution of the region of interest, a continuous time series of NLFF fields are generated from the corresponding time series of magnetograms (Mackay, Green, and van Ballegooijen, 2011; Gibb et al., 2014). In the present application we use 50 magnetograms from 31 July 2011 at 05:00:41 UT to 2 August 2011 at 06:00:41 UT sampled every 60 minutes. The procedure and set of equations solved is the same as in Mackay, Green, and van Ballegooijen (2011).

The time series of NLFF fields is constructed assuming four closed boundaries at the sides for the 3D box. The bottom boundary, representing the solar surface, is forced to have magnetic flux balance and the top boundary is set to be open.

In Figure 6a – b we show the initial magnetograms on 31 July 2011 at 05:00:41 UT and the final magnetogram on 2 August 2011 at 06:00:41 UT with the final 3D magnetic configuration, shown by the green lines. The initial magnetic configuration is assumed to be potential, while the final stage is highly non-potential with a magnetic flux rope formed. Over the time series of NLFF fields, a magnetic flux rope forms as a consequence of the continuous motion and evolution of the magnetic field at the lower boundary. The flux rope forms along the polarity inversion line (PIL) and is about \(0.03~\mbox{R}_{\odot}\) long; its central point is located at the coordinates \(x = 0.0078~\mbox{R}_{\odot}\) and \(y = 0.018~\mbox{R}_{\odot}\), which in the MHD simulation domain correspond to the heliographic coordinates \(x= 181''\), \(y= 205''\) on 2 August 2011 at 06:00:41 UT. The flux rope covers only part of the PIL, whereas sheared magnetic field lines are present along the whole PIL, marking the non-potentiality of the final magnetic field configuration.

Figure 6
figure 6

Maps of the surface magnetic field measured on (a) 31 July 2011 at 05:00:41 UT (the heliographic coordinates of the center of the image are \(x = -252''\), \(y= 178''\)) and (b) on 2 August 2011 at 06:00:41 UT (the center of the image is at \(x = 174''\), \(y= 188''\)). In (b) we overplot some magnetic field lines from the 3D magnetic configuration, obtained with the NLFF time series. (c) Map of running-difference images from the AIA 211 Å filter with a Sobel filter applied (scale of difference in DN) on 2 August 2011 at 06:00:41 UT. Blue lines are representative of the flux rope.

Full size image

Figure 6c shows a running difference of AIA 211 Å passband image at the same time as the last magnetogram, where we apply the Sobel filter to highlight the coronal structures that are probably associated with the expanding flux rope. We find that the general topology of the loops is reproduced, where the magnetic field lines match the loop structures at the lower left corner of the image, and the system of loops departs in different directions from the enhanced emission region and many of the loops around the magnetic flux rope.

It is also crucial to point out that as a result of a slow variation of the magnetic field, the final magnetic configuration is not sensitive to time intervals of some minutes, which is different from the 60-minute sampling time of the HMI magnetograms. This means that the final configuration could represent any time within some minutes around the exact magnetogram.

4.2 MHD Model

The final 3D magnetic configuration from the NLFF field time series is then used as input for an ideal MHD simulation. This approach is an extension of the technique successfully adopted in Pagano, Mackay, and Poedts (2013a) and then further developed in Pagano, Mackay, and Poedts (2013b, 2014), where the magnetic configuration, obtained from a magneto-frictional nonlinear force-free model, is the input as an initial condition in an ideal MHD simulation.

To do so, we import the three components of the magnetic field from the NLFF time series grid to the grid of our 3D MHD model. Specifically, Pagano, Mackay, and Poedts (2013a, 2013b) described a number of thorough tests to show that this is possible to preserve the stability or instability of the configuration.

4.2.1 Interpolation of the Magnetic Configuration

In the present article we have simplified the way in which the 3D interpolation is performed and adopted a Cartesian grid. In Cartesian coordinates, let \(B(x,y,z)\) be the value that we wish to compute in the position \((x,y,z)\), which we know lies in the cell, defined by the indexes \([i:i+1,j:j+1,k:k+1]\), where the quantity \(b\) is defined. We compute

$$ B(x,y,z)=\sum_{i,j,k}^{i+1,j+1,k+1} b(i,j,k) V(i,j,k) / V , $$
(3)

where \(V(i,j,k)\) is the volume defined by the point \((x,y,z)\) and the cell corner opposite to the position \((i,j,k)\), and \(V\) is the sum of these volumes. This approach guarantees the continuity of the solution and its smoothness independently of the spatial resolution of the grid where \(B(x,y,z)\) is defined.

4.2.2 Plasma Distribution

As the time series of NLFF fields provides only the magnetic configuration, we need to adopt an initial distribution of plasma density, speed, and temperature in order to close a complete set of MHD variables. We aim at a realistic and general representation of the solar corona, so we seek to produce a distribution of plasma that takes the heterogeneity of the coronal plasma into account. In particular, we intend to describe the initial flux rope plasma as colder and denser than the plasma outside of the flux rope. Magnetic flux ropes are structures where the magnetic field is usually more intense than in their surroundings and where the magnetic field presents twist. Therefore, we define the following proxy function to link the plasma temperature and density to the magnetic field:

$$ \omega=\sqrt{\omega_{x}^{2}+ \omega_{y}^{2}+\omega_{z}^{2}} , $$
(4)

where

$$\begin{aligned} & \omega_{x}=\frac{ \vert {\boldsymbol {B}}\times \nabla B_{x} \vert }{ \vert \nabla B_{x} \vert }, \end{aligned}$$
(5)
$$\begin{aligned} & \omega_{y}=\frac{ \vert {\boldsymbol {B}}\times \nabla B_{y} \vert }{ \vert \nabla B_{y} \vert }, \end{aligned}$$
(6)
$$\begin{aligned} & \omega_{z}=\frac{ \vert {\boldsymbol {B}}\times \nabla B_{z} \vert }{ \vert \nabla B_{z} \vert } , \end{aligned}$$
(7)

where \({\boldsymbol {B}}=(B_{x},B_{y},B_{z})\) is the magnetic field, the Cartesian coordinates \(x\) and \(y\) are tangent to the solar surface, and \(z\) is perpendicular to the surface. The function \(\omega\) is positive definite and peaks where the magnetic field presents more twist and is more intense, e.g. near the center of the magnetic flux rope axis. As an example, at the flux rope axis, \(\nabla B_{z}\) is parallel to the solar surface along the direction connecting two opposite polarities and perpendicular to the magnetic field that is mostly parallel to the \(x\) – \(y\) plane. In this configuration, \(\omega_{z}\) is relatively high. Additionally, the value of \(\omega\) is proportional to the magnetic field intensity, which results in it being higher near the solar surface and lower at farther radial distances from the solar surface.

In order to effectively use \(\omega\) to model the solar atmosphere, we define the function

$$ \Omega=\arctan{\frac{\omega-\omega^{\star}}{\Delta\omega}}/\pi +0.5 , $$
(8)

where \(\omega^{\star}\) and \(\Delta\omega\) are two simulation parameters. \(\Omega\) is then bound between 0 and 1 and the temperature is defined by

$$ T=\Omega(T_{\mathrm{flux}\ \mathrm {rope}}-T_{\mathrm{corona}})+T_{\mathrm{corona}} , $$
(9)

where \(T_{\mathrm{flux}\ \mathrm{rope}}\) and \(T_{\mathrm{corona}}\) are two simulation parameters that represent the temperature in the flux rope and in the external corona. The thermal pressure is independently specified by the exponential solution for hydrostatic equilibrium with constant gravity with a uniform temperature set equal to \(T_{\mathrm{corona}}\):

$$ p=\frac{\rho_{0}}{\mu m_{\mathrm{p}}}k_{\mathrm{B}} T_{\mathrm{corona}} \exp{ \biggl(-z\frac{g \mu m_{\mathrm{p}}}{k_{\mathrm{B}} T_{\mathrm{corona}}} \biggr)} , $$
(10)

where \(p\) is the thermal pressure, \(\rho_{0}\) is a simulation parameter that sets the density at the solar surface, \(\mu=1.31\) is the average particle mass, \(m_{\mathrm{p}}\) is the proton mass, \(k_{\mathrm{B}}\) is the Boltzmann constant, and \(g\) is the solar gravitational acceleration at the solar surface. The density \(\rho\) is given by the equation of state:

$$ \rho=\frac{p}{T({\boldsymbol {B}})}\frac{\mu m_{\mathrm{p}}}{k_{\mathrm{B}}} , $$
(11)

where \(\rho\) is the density, and \(T\) is the temperature.

4.2.3 MHD Simulation

Based on the approach described in Section 4.2.2, and using the final 3D magnetic field configuration obtained from the NLFF time series as described in Section 4.1, we construct the initial condition for the MHD simulation. Table 5 shows the values used in our model for the relevant parameters.

Table 5 Values for the initial condition parameters of the ideal MHD simulation.
Full size table

We use the MPI-parallelized Adaptive-Mesh Refinement Versatile-Advection Code (MPI-AMRVAC) software (Porth et al., 2014) to solve the MHD equations, where external gravity is included as a source term,

$$\begin{aligned} & \frac{\partial\rho}{\partial t}+{\boldsymbol{\nabla}}\cdot(\rho{\boldsymbol {v}})=0, \end{aligned}$$
(12)
$$\begin{aligned} & \frac{\partial\rho{\boldsymbol {v}}}{\partial t}+{\boldsymbol{\nabla}}\cdot(\rho{\boldsymbol {v}}{\boldsymbol {v}}) +\nabla p-\frac{({\boldsymbol{\nabla}}\times{\boldsymbol {B}})\times {\boldsymbol {B}}}{4\pi} =\rho{\boldsymbol {g}}, \end{aligned}$$
(13)
$$\begin{aligned} & \frac{\partial{\boldsymbol {B}}}{\partial t}-{\boldsymbol{\nabla}}\times({\boldsymbol {v}}\times{\boldsymbol {B}})=0, \end{aligned}$$
(14)
$$\begin{aligned} & \frac{\partial e}{\partial t}+{\boldsymbol{\nabla}}\cdot\bigl[(e+p){\boldsymbol {v}}\bigr]=\rho {\boldsymbol {g}}\cdot{\boldsymbol {v}}, \end{aligned}$$
(15)

where \(t\) is time, \({\boldsymbol {v}}\) velocity, \({\boldsymbol {g}}\) is the vector of the solar gravitational acceleration, and the total energy density, \(e\), is given by

$$ e=\frac{p}{\gamma-1}+\frac{1}{2}\rho {\boldsymbol {v}}^{2}+ \frac{{\boldsymbol {B}}^{2}}{8\pi} , $$
(16)

where \(\gamma=5/3\) denotes the ratio of specific heats.

The computational domain is composed of \(256\times256\times248\) cells, distributed on a uniform grid. The simulation domain is similar to the one used in the time series of NLFF fields, and it extends over \(0.267~\mbox{R}_{\odot}\) in the \(x\) and \(y\) direction and over \(0.266~\mbox{R}_{\odot}\) in the \(z\) direction, starting from \(z = 0.0027~\mbox{R}_{\odot}\) above the photosphere. The boundary conditions are treated with a system of ghost cells. Two layers of cells between \(z= 0\) and \(z = 0.0021~\mbox{R}_{\odot}\) are used as fixed lower boundary conditions during the ideal MHD simulation. Open boundary conditions are imposed at the outer boundary, and finally, reflective boundary conditions are set at the \(x\) and \(y\) boundaries of the simulation box.

Figure 7 shows the values of the radial component of the Lorentz force at the lower boundary, the function \(\omega\), derived from the magnetic configuration, and the resulting distribution of the electron density \(n_{\mathrm{e}}\) and temperature \(T\). The Lorentz force is maximum at the location of the flux rope. The map of \(\omega\) follows the pattern we have prescribed, being higher around the region of the PIL and peaking where the flux rope is located. Consequently, the maps of \(n_{\mathrm{e}}\) and \(T\) show the regions with a higher twisted magnetic field. In particular, the position where the magnetic flux rope sits (compare with Figure 6) presents a density \({\sim}\,10\) times higher than its surroundings and a temperature value \({\sim}\,10\) times lower. It is also to be noted that in our model the location, where the flux rope is relatively cold is consistent with the observations of AIA in the 211 Å band (Figure 6c) as the location where the flux rope is not visible, since the filter is tuned to observe plasma at higher temperatures.

Figure 7
figure 7

Lower boundary of the initial condition of the ideal MHD simulation: (a) Lorentz force, (b) \(\omega\), (c) \(\log_{10}\) (\(\rho\) [\(\mbox{g}\,\mbox{cm}^{-3}\)]), and (d) \(\log _{10}\) (T [K]). The axes scales are in units of \(\mbox{R}_{\odot}\).

Full size image

The present initial condition is clearly out of equilibrium for a number of reasons. In our simulation the initial plasma \(\beta\) ranges between the two extrema of \(\beta\sim10^{-3}\) (at the flux rope) and \(\beta\sim10^{3}\) (in very confined regions where the magnetic field is less intense). Elsewhere it lies between \(10^{-2}\) and \(10^{-1}\). Therefore, the strongest unbalanced force in the initial condition is the Lorentz force in the magnetic flux rope, which is directed upward. At the same time, the radial profiles of density and pressure do not prescribe the balance between the thermal pressure gradient and the gravity force. However, as addressed in detail in Pagano, Mackay, and Poedts (2013a), this unbalance shows effects over timescales longer than the dynamics triggered by the Lorentz force, and these effects can therefore be neglected.

5 Results of the MHD Simulation and Comparison with Observations

We run the MHD simulation starting from the final magnetic configuration, obtained from the time series of NLFF fields, when the magnetic flux rope is fully formed, in order to describe the evolution of the ejection of the magnetic flux rope. The pre-eruptive initial magnetic configuration described in Section 4.1 is obtained from a long-term sequence of magnetograms with a cadence of one hour, and thus it cannot indicate the exact start time of the magnetic flux rope ejection. Therefore we present the MHD evolution in terms of the time elapsed from the initial condition, and we impose the time of the MHD simulation initial condition to match the observed CME initiation time. For this specific simulation, we report in Table 2 the onset of the eruption, i.e. the time of the initial condition, at 05:54:40 UT. The initial condition of the MHD simulation is out of equilibrium, and several plasma flows occur at the beginning.

However, the dominant evolution occurs where the flux rope plasma is pushed upward by the unbalanced Lorentz force and the flux rope starts erupting. In order to follow the evolution of the flux rope, we display the simulation from a line of sight parallel to the \(y\) axis. In Figure 8 we show the electron density, integrated along this line of sight, together with the temperature and velocity in the \(z\) direction, integrated along the line of sight and weighted over \(n_{\mathrm{e}}\). We use as characteristic stages in the evolution the times of \(t= 0~\mbox{min}\), \(t = 6.04~\mbox{min}\), and \(t = 14.51~\mbox{min}\) from the eruption onset. Additionally, by considering the evolution of \(v_{z}\) and \(\omega\), we manually track the directions of propagation of the magnetic flux rope and the position of its center along this direction at each snapshot of the simulation. This is possible because the cuts of both \(v_{z}\) and \(\omega\) along the direction of propagation of the flux rope show a local peak at the flux rope center. This direction is represented by the red line and the position of the red star in Figure 8.

Figure 8
figure 8

Panels showing the evolution of the MHD simulation. The upper row shows the integral of the electron density, the middle and lower row show the integrals of the \(z\) component of the velocity and temperature, respectively, averaged by the electron density. In the upper row some magnetic field lines (green lines) and flux rope field lines (blue lines) are overplotted. The left column shows quantities at the time in the simulation corresponding to \(t= 0~\mbox{min}\), the central column to \(t= 6.04~\mbox{min}\), and the right column to \(t= 14.51~\mbox{min}\) from the eruption onset. The red dashed line represents the direction of propagation of the magnetic flux rope and the red star is the position of the center of the flux rope at each time.

Full size image

The particle density maps show an expansion and an upward propagation of the structures that are initially lying low in the domain. The same motion is highlighted by the visible change in the magnetic field lines. In particular, the flux rope magnetic field lines (represented by the blue lines) show a distinctive motion, where the magnetic field lines are increasingly longer and less twisted in the course of the evolution.

The evolution of \(v_{z}\) describes this behavior well, where we see a region of the upward-directed velocity that is composed of an elongated region where the plasma speed is higher, and a bow-shaped region ahead that represents the front of the ejecta. In particular, the elongated region extends along the direction of propagation of the flux rope and dominates other motions that are present in the domain. The maximum of \(v_{z}\) reaches values greater than \(500~\mbox{km}\,\mbox{s}^{-1}\) at \(t = 11.5~\mbox{min}\) in the MHD simulation. It should be noted that some boundary effects are visible at the external boundary, where some moderate inflow develops over the course of the simulation. However, the low density of the inflowing plasma makes this effect negligible for the dynamics of the ejection. It is interesting to note that no shocks are formed ahead of the flux rope ejection. When we take the MHD simulation snapshot at 06:06:43 UT into consideration, we find that the plasma speed at the front of the ejection is \({\sim}\,130~\mbox{km}\,\mbox{s}^{-1}\), where the sound speed is \({\sim}\,300~\mbox{km}\,\mbox{s}^{-1}\). Only behind the propagation of the flux rope do we find regions with supersonic or super-Alfvénic velocities, where the Mach number is 1.5 or the Alfvénic Mach number is \({\sim}\,3\).

The evolution of the temperature is significantly complex because of the energetics of the flux rope ejection. As has been shown in similar simulations (Pagano, Mackay, and Poedts, 2014), the numerical resistivity plays a crucial role in heating the plasma, while expansion and decompression can lead to the cooling of the plasma in certain regions. As soon as the simulation starts, magnetic energy is converted into thermal energy, and this leads to an overall increase of the temperature. At the same time, this does not occur everywhere, but only where the magnetic field is initially more twisted, e.g. near the PIL. Subsequently, the temperature decreases in some regions, but overall stays above the initial one.

Although the detailed comparison between the final state of the MHD simulation and the corresponding state in the region under study poses major challenges, it is still interesting to carry out a qualitative comparison to gain a global understanding of the weaknesses and strengths of the model. Figure 9a shows a map of the temperature averaged for the electron density along the line of sight from the top view at \(t = 14.51~\mbox{min}\) in the MHD simulation. Figure 9b shows a difference image between the AIA 211 Å passband at 06:09:00.62 and 05:55:00.62 UT. The latter time is the closest AIA image to the assumed flux rope ejection time at 05:54:40 UT, the former time is 14.3 minutes later, which is approximately the duration of the MHD simulation. We find that the region in the center of the field of view, where the emission in the AIA 211 Å passband is enhanced, roughly corresponds to a region in the MHD simulation where the plasma is heated up on average (to about 4 MK) and that a nearby location where the emission diminishes corresponds to a relatively cold location in the MHD simulation. In general, the MHD simulation shows an increase in temperature, which is consistent with the generally enhanced emission in the 211 Å passband. The magnetic field lines displayed in Figure 9a also describe a topology with many similarities to the topology suggested by the structures in Figure 9b. Examples include the system of loops in the bottom left corner of the field of view and the expanding structures on the top right from the center of the image. They roughly correspond to the flux rope location at this time in the MHD simulation.

Figure 9
figure 9

(a) Temperature integrated along the \(z\) direction and averaged with the electron density at \(t = 14.51~\mbox{min}\) in the MHD simulation. Some magnetic field lines (green lines) and flux rope field lines (blue lines) are overplotted. (b) Difference in the AIA observations in the 211 Å passband between 06:09:00.62 and 05:55:00.62 UT (the scale is in DN).

Full size image

Additionally, we have carried out a simple visual comparison of the kinematics of the flux rope ejection with STEREO observations taken over a time span after the observed start of the flux rope ejection (at 05:54:40 UT), corresponding to the duration of the MHD simulation. The visual tracking of the CME in the STEREO images lets us follow the apex of the expanding loops that initiate the CME motion (cross points in Figure 10a). In Figure 10a, these radial distances are compared with the tracked radial distance of the center of the flux rope and the front that propagates from its ejection in the MHD simulation. We find a very good agreement of the locations identified in STEREO observations with the position of the flux rope front, showing that the apex of the loops probably represents their motion as a consequence of being pushed by the ongoing ejection and corresponds to the CME front. The same good agreement is found in Figure 10b, where we compare the speeds of propagation of the flux rope and the CME front with the speed inferred from STEREO observations. In the MHD simulation, the CME front accelerates from 100 \(\mbox{km}\,\mbox{s}^{-1}\) to about 200 \(\mbox{km}\,\mbox{s}^{-1}\), while the flux rope moves at 200 \(\mbox{km}\,\mbox{s}^{-1}\) until the end of the simulation, where it slows down to 100 \(\mbox{km}\,\mbox{s}^{-1}\). The points tracked in STEREO images always lie between 150 – 350 \(\mbox{km}\,\mbox{s}^{-1}\). As we cannot consider this analysis beyond a qualitative comparison, it is interesting to show that the speeds of the structures predicted by the MHD simulation are comparable to the speed at which they move in the STEREO observations. At the same time, it seems that the model underestimates the observed velocity for at least a fraction of the time of evolution around \(t = 200~\mbox{s}\). There, the observed speed is \({\sim}\,1.5\) higher than the speed of the flux rope center and the front of the ejecta in the MHD model. This difference would be enough to make the plasma flow overcome the sound speed, thus leading to a shock in the MHD model matching the observation. This may be a consequence of the differences between the real atmospheric profile of \(\rho\), \(T\) compared to the inferred and simulated profiles used here.

Figure 10
figure 10

(a) Comparison between the position of the center of the flux rope, the front of the ejection, and the position of the upward-expanding loops in STEREO images as a function of time. (b) Comparison between the speed of the center of the flux rope, the speed of the front of the ejection, and the apparent speed of the expanding loops in STEREO images as a function of time. Times are shown in minutes, where 0 is the starting time of the MHD simulation at 06:00:41 UT. Dashed lines represent the average speed of the expanding loops in STEREO observations with an error bar of \({\pm}\,65~\mbox{km}\,\mbox{s}^{-1}\).

Full size image

6 Ion Charge State Evolution of CMEs

The ion charge state of the CME plasma, as well as its evolution in the corona, depends mainly on the following factors: (i) the chemical element to which the considered ions belong, (ii) the plasma conditions (such as temperatures and electron densities), and (iii) the bulk velocities of the plasma in the corona. In the previous sections we derive parameters of the erupting plasma and of the emerging flux rope at distances of up to \(0.25~\mbox{R}_{\odot}\) from both direct EUV measurements and the MHD model. In this section, we investigate the ion charge state evolution of the plasma structures under study by considering the ratios of carbon, \(\mbox{C}^{6+}/\mbox{C}^{5+}\), and oxygen, \(\mbox{O}^{7+}/\mbox{O}^{6+}\), and the average charge of iron ions, \(Q_{\mathrm{Fe}}\), which were measured in situ with ACE. For this purpose, it is necessary to analyze how these parameters evolve during the plasma propagation in the corona at larger distances of several solar radii. We assume that in the whole space between the solar surface and the frozen-in region the expanding plasma is in a quasi-stationary state, i.e. the plasma ionization and recombination timescales are shorter than the expansion timescale of the plasma.

The evolution of the ion charge states in the corona can be described by the following system of continuity equations for a set of ions from the atomic species of interest in the rest frame of the expanding plasma structure (see, e.g. Ko et al., 1997):

$$ \frac{\partial y_{i}}{\partial t} = N_{\mathrm{e}} \bigl( y_{i-1}C_{i-1}(T_{\mathrm{e}}) - y_{i} \bigl( C_{i}(T_{\mathrm{e}}) + R_{i-1}(T_{\mathrm{e}}) \bigr) + y_{i+1}R_{i}(T_{\mathrm{e}}) \bigr) , $$
(17)

where \(y_{i} = n_{i} / \sum_{i=0}^{Z} n_{i}\) is the relative fraction of the ion with the number density \(n_{i}\) in the charge state \(i\), \(N_{\mathrm{e}}\) is the electron density, \(T_{\mathrm{e}}\) is the electron temperature, \(C_{i}\) is the ionization coefficient rate for the transition from charge state \(i\) to \(i+1\), and \(R_{i}\) is the total recombination rate (including both radiative and dielectronic recombination) from the charge state \(i+1\) to \(i\). To integrate the system of Equations (17), we use the recombination and ionization rate coefficients \(R_{i}\) and \(C_{i}\) from the CHIANTI database (an atomic database for emission lines) (Dere, 2007; Dere et al., 2009), where these data are given on the assumption that the electron speed distribution is Maxwellian.

In order to solve the system of equations, one needs to know the time evolution of the electron density and temperature, \(T_{\mathrm{e}}(t)\), \(N_{\mathrm{e}}(t)\), in the plasma structure under study as well as its bulk velocity, \(v(t)\). As the plasma parameters obtained from the EUV imaging and MHD modeling are known only in the low corona up to the distance \(r_{0}\approx0.25\) (in units of \(\mbox{R}_{\odot}\)) from the solar surface, we model the evolution of plasma conditions at larger distances, \(r > r_{0}\), analytically by taking the processes of cooling, heating, and expansion of the plasma into account, and we solve the system of equations (Equations (17)) for the chosen ion species. As the initial conditions, we used the plasma parameters derived from the MHD simulation. In our analysis we separate two specific regions: the hot flux rope structure (hereafter referred to as “flux rope”) and the colder CME leading edge or compression front (hereafter referred to as “CME LE”, see Figure 5 in Cheng et al., 2011) that surrounds the flux rope. The evolving profiles of electron temperatures and densities for the flux rope and the CME LE plasmas during the acceleration phase are presented in Figure 11.

Figure 11
figure 11

Evolution of electron temperature and density of the flux rope and CME LE plasmas derived from the MHD simulations.

Full size image

As seen in Figure 11, the temperature of the flux rope rises to 6 – 9 MK at the beginning of expansion and then drops as it moves away, whereas the CME LE temperature evolution has the reverse trend. This result is consistent with the recent studies where hot flux rope structures were observed before and during the eruptive flare and CME events using SDO/AIA data (see Cheng et al., 2011, 2012, 2013; Zhang, Cheng, and Ding, 2012). Nindos et al. (2015) reported that almost half of the investigated eruptive events contained a hot flux rope configuration. The high flux rope temperatures in Figure 11 are inconsistent with those of the moving CME structure in Figure 5 because the latter corresponds to the colder outer shell of the CME (see Figures 4a, 4b). At the same time, the hot flux rope is not visible in Figure 4a because the flare is brighter than its emission. This is in good agreement with the schematic model of the multi-temperature structure of the CME demonstrated by Cheng et al. (2011) in their Figure 5.

The electron density at distances \(r > r_{0}\) is taken to have a power-law form

$$ N_{\mathrm{e}}(r) = N_{\mathrm{e}}(r_{0}) \biggl( \frac{r_{0}}{r} \biggr)^{3} , $$
(18)

consistent with the flux rope evolution for expansion in both length and radius (see, e.g. Kumar and Rust, 1996; Lee et al., 2009). For the temperature profile we use a form similar to the adiabatic relation

$$ T_{\mathrm{e}}(r) = T_{\mathrm{e}}(r_{0}) \biggl( \frac{N_{\mathrm{e}}(r)}{N_{\mathrm{e}}(r_{0})} \biggr)^{\alpha}, $$
(19)

where the power index \(\alpha\) is chosen to be consistent with the in situ measured values of ion composition parameters. In the case of the adiabatic expansion, the factor \(\alpha= \gamma - 1\), where \(\gamma= 5/3\), is the adiabatic index. This simple form of the temperature profile is used to account for possible heating, which the ejected plasma usually undergoes long after the eruption (see, e.g. Akmal et al., 2001; Ciaravella et al., 2001). Lower values of the index \(\gamma\) are often used in coronal models to take phenomenologically into account mechanisms whose heating rates are unknown (see also Kumar and Rust, 1996; Lee et al., 2009).

Using Equations (17), we carried out calculations of the ion charge state evolution of C, O, and Fe ions for the event on 2 August, 2011. A relationship between cooling rates of plasma by different mechanisms, such as adiabatic expansion, thermal conductive cooling, and radiative losses, depends on the plasma parameters and configuration of the erupting structure and varies during the expansion in the corona. We analyze and estimate the cooling effectiveness of these three terms separately for our plasma conditions by considering the temperature evolution of the flux rope and the CME LE material. We find that the most effective cooling factor is an adiabatic expansion. For instance, at the distance \(r = 0.5\) the decrease in temperature for the adiabatic regime prevails over the decrease in radiative and conductive cooling by 3 – 5 times, and at \(r = 1\) it is up to one order of magnitude and higher. Thus, at distances \(r>0.25\), the adiabatic expansion is the clearly prevalent cooling process.

Assuming that the cooling is provided elsewhere only by adiabatic expansion, we obtain the following frozen-in ion composition parameters: \(\mbox{C}^{6+}/\mbox{C}^{5+}= 0.56\), \(\mbox{O}^{7+}/\mbox{O}^{6+}= 0.017\), and \(Q_{\mathrm{Fe}}= 7.4\) for the CME LE plasma, and \(\mbox{C}^{6+}/\mbox{C}^{5+}= 0.071\), \(\mbox{O}^{7+}/\mbox{O}^{6+}= 1.46 \times10^{-4}\), and \(Q_{\mathrm{Fe}}= 7.4\) for the flux rope structure. These values are too low in comparison with the in situ observations (see Table 3). If we then introduce a heating process in the region where the Fe ion state is frozen in by decreasing the index \(\alpha\) from the adiabatic value 2/3 to 0.1, the derived value of \(Q_{\mathrm{Fe}}\) increases to \({\sim}\,10\,\mbox{--}\,11\), which is in agreement with in situ observations. However, in this case, the frozen-in ratios \(\mbox{C}^{6+}/\mbox{C}^{5+}\) and \(\mbox{O}^{7+}/\mbox{O}^{6+}\) become noticeably higher by 2 – 3 times in comparison with the measurements.

In order to explain and to overcome this issue, we assume that the heating power depends on the height in the corona. First, our numerical analysis shows that the ion charge states of C and O ions reach the frozen-in conditions at distances of about \(1\,\mbox{--}\,2~\mbox{R}_{\odot}\), whereas the frozen-in region of Fe ions begins at distances of \({\approx}\,4\,\mbox{--}\,5~\mbox{R}_{\odot}\). The reason is that the recombination timescales of carbon and oxygen ions, \(\tau_{r} = 1/(N_{\mathrm{e}} R_{i})\), dominate those of the iron ions. Second, we consider separately two spatial intervals: the first is from \(r_{0}\) to \(r_{h} = 1.5\), where the frozen-in conditions begin to play a role only for C and O ions, and the second interval is from \(1.5~\mbox{R}_{\odot}\) for the Fe frozen-in region. We then calculate the evolution of the ion charge states of C and O ions by matching the parameter \(\alpha\) so that it agrees with the observational data in the first spatial interval. For the CME LE plasma we adopt the value \(\alpha=0.35\) and find frozen-in values \(\mbox{C}^{6+}/\mbox{C}^{5+} = 2.2\) and \(\mbox{O}^{7+}/\mbox{O}^{6+} = 0.32\). For the flux rope structure \(\alpha= 0.2\), and \(\mbox{C}^{6+}/\mbox{C}^{5+} = 1.77\) and \(\mbox{O}^{7+}/\mbox{O}^{6+}= 0.14\). At the same time, at \(1.5~\mbox{R}_{\odot}\) we obtain \(Q_{\mathrm{Fe}}\approx7\,\mbox{--}\,8\), which is noticeably lower than the measured in situ value.

Using the functional temperature difference between the proper adiabatic expansion and the fitted values of the index \(\alpha\) for the CME LE plasma and flux rope, we also estimate the heating power from the coronal source, which maintains this difference. We find that this source acts from \(r_{0}\) to \(r \approx0.5\) and its intensity sharply decreased with distance. The average heating power for the two plasma structures is \(Q_{\mathrm{CME}}\approx 5\times 10^{-3}~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\) for the CME LE plasma and \(Q_{\mathrm{FR}}\approx6\times 10^{-3}~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\) for the flux rope.

In order to match the value \(Q_{\mathrm{Fe}}\) with the in situ measurements, we assume that in the second interval \(r> 1.5~\mbox{R}_{\odot}\) the parameter \(Q_{\mathrm{Fe}}\) increases as a result of an additional heating power from the coronal source. We assume a temperature evolution at distances \(r_{h} \ge1.5\) as \(T_{\mathrm{e}}(r) = T_{h} (r/r_{h})^{\beta}\). Taking the index \(\beta= 0.75\), we obtain \(Q_{\mathrm{Fe}}\approx10\) for the CME LE plasma and \(Q_{\mathrm{Fe}}\approx11\) for the flux rope, which is compatible with the in situ observations. Our estimation of the heating power at the point \(r_{h} = 1.5\) gives \(Q_{h} \sim(1-2)\times 10^{-5}~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\).

7 Discussion

We propose a method to predict the ion charge state of the ICME, produced by the flare and CME solar event on 2 August 2011, using the SDO/AIA EUV observations, MHD numerical simulation of the flux rope formation, and the analytical description of the plasma ion charge state evolution in the corona up to the frozen-in region. We assume that the ion composition of the ICMEs does not vary during their propagation in the heliosphere because of the very long ionization and recombination relaxation times at low plasma density in comparison with the travel time. In order to obtain the values of the ion charge state ratios \(\mbox{C}^{6+}/\mbox{C}^{5+}\) and \(\mbox{O}^{7+}/\mbox{O}^{6+}\) and the average charge \(Q_{\mathrm {Fe}}\) close to those measured in situ, we introduce a heating process that has different rates at distances \(0.25\,\mbox{--}\,1.5~\mbox{R}_{\odot}\) and \(1.5\,\mbox{--}\,5~\mbox{R}_{\odot}\).

The results of plasma diagnostics (see Section 3.2) and MHD simulations suggest that the erupting plasma is heated far from the flare region. Figure 5 shows that the temperature drops to \({\approx}\,1.5~\mbox{MK}\) at the base of the ejected structure under consideration, whereas the MHD calculations exhibit noticeably higher temperatures for the hot flux rope and the colder CME LE plasmas. The assumption of a heating source above the flare region is of course debatable, but in a number of works the authors performed MHD simulations and discussed various heating mechanisms in the CME plasma (see, e.g. Lee et al., 2009; Lynch et al., 2011). At the same time, Zhang, Cheng, and Ding (2012) showed that in some cases, the heating of the flux rope can start simultaneously with the ejection, as they observed the appearance of hot channel signatures at the earliest stage of the slow rise of the ejection of a magnetic flux rope.

Reinard, Lynch, and Mulligan (2012) carried out a numerical simulation of ion composition for two ICMEs (magnetic clouds), detected by STEREO and ACE on 21 – 23 May 2007, using the Magnetohydrodynamics-on-A-Sphere (MAS) and ARC7 ideal 2.5D MHD models, described earlier by Lynch et al. (2011). Both models took field-aligned thermal conduction, radiative losses, and coronal heating from the flare site during the initiation and expansion of a flux rope in the corona up to distances of more than \(10~\mbox{R}_{\odot}\) into account. It follows from their results that the key question in predicting the ICME ion composition by numerical MHD modeling is a correct definition of the ratio between heating and cooling processes that act on the erupting plasma in the corona. In the two models described by Lynch et al. (2011), heating is introduced as the dominating factor that does not depend on real conditions in the source. Thus, they obtained that the slower CMEs became hotter than the faster CMEs, which contradicts the observations. In contrast, we use a 3D MHD model to determine the plasma parameters of the ejecta on the initial stage of the flux rope ejection and fit the results with the EUV measurements by selecting the initial parameters of the simulation.

Our consideration refers to the case when the ICME parameters correspond to the apex of the CME. In some cases, however, the nearby coronal holes (CHs) that produce high-speed streams can seriously influence the appearance and parameters of the ICME near Earth (Gopalswamy et al., 2009a,b, 2013; Mohamed et al., 2012; Mäkelä et al., 2013; Wood et al., 2012). An interaction of the CME with a high-speed stream from the nearby coronal hole can deflect the CME from its initial direction, which results in the shifting of the arrival time ahead or behind the time as predicted by the kinematic models and can change other solar wind parameters. We assume that the ion composition parameters in the collisionless heliosphere are not influenced by this interaction and can be used for the source identification, but these cases are worth a dedicated study.

It should be noted that our model is rather simplistic and idealized, as it does not reproduce some important details of the CME formation, such as laminar and turbulent features of the evolution visible in observations. Energy dissipation via electric resistivity, heat conduction, viscosity, and radiation should be especially taken into consideration during the early phase of the evolution in the dense corona. The ideal one-fluid MHD approach we use has a limited applicability in the case of the observed small-scale and fast variations. Moreover, the numerical ideal MHD modeling we conduct does not take into account the terms in the energy equation that play a role in the coronal dynamics. Thermal conduction can be responsible for diffusing heat in the domain, even though Pagano et al. (2007) and Pagano, Mackay, and Poedts (2014) showed that this is largely inhibited inside the flux rope during the CME propagation. Dimensionless scaling and the relative importance of corresponding terms in the energy balance equations are not quite clear and need more investigation to better understand the overall situation. Finally, a more accurate treatment of the effect of magnetic resistivity on the amount of magnetic energy that is converted into heating would require a much higher spatial resolution.

8 Summary and Conclusion

We present a complex study of a series of solar wind transients registered by ACE on 4 – 7 August 2011 and their solar sources, flares, and CMEs, which occurred on 2, 3 and 4 August 2011 in AR 11261. These events produced two shocks with sheaths and two ICMEs of the MC type, as identified by the RC list. The analysis of the ion charge state of the solar wind reveal three transients with enhanced temperature-dependent ratios \(\mbox{C}^{6+}/\mbox{C}^{5+}\), \(\mbox{O}^{7+}/\mbox{O}^{6+}\) and a mean charge of iron ions \(Q_{\mathrm{Fe}}\), which can be associated with hot plasma released in the coronal sources. The first transient, determined from the ion composition, coincided with the first ICME (Table 1), whereas the two others preceded the second ICME. The shift in time between transients 2, 3, and the second ICME might be caused by interaction between CMEs 2 and 3. Simulations with the WSA-Enlil cone model show that the third CME of 4 August surpassed the second CME of 3 August at a distance from the Sun of about 0.6 AU.

We study the formation of the first CME of 2 August in detail using the SDO/AIA images in 211 Å and numerical simulations using NLFF and MHD modeling. The images of the eruptive structures in different SDO/AIA spectral channels are used for diagnostics of the outflow plasma by means of the DEM analysis. From the observational data we find that in the event of 2 August, the temperature of the plasma during its visible expansion from 0.1 to \(0.13~\mbox{R}_{\odot}\) decreases from 2.7 to 1.7 MK and the density from \(1\times 10^{9}\) to \(5\times 10^{8}~\mbox{cm}^{-3}\). These values are lower than those obtained by modeling for the apex, and correspond to the legs of the eruption shell. This confirms that heating is more effective in the upper part of the expanding structure.

The initiation of the CME of 2 August 2011 is simulated numerically using a combination of the NLFF magnetic field extrapolation model with a 3D MHD model of the expanding flux rope, which is especially suited for the given case. The results of the simulation and comparison with the EUV measurements demonstrate that the general topology of the magnetic field matches the visible loop structure, whereas the flux rope is formed along the polarity inversion line and is pushed upward by the unbalanced Lorentz force. The maximum speed is below the sound speed of 300 \(\mbox{km}\,\mbox{s}^{-1}\), which means that the model does not predict the creation of a shock wave ahead of the flux rope ejection that was seen in the observations. The MHD simulation shows a temperature of \({\sim}\,4~\mbox{MK}\) in the CME apex, which coincides with an enhancement of radiation in the 211 Å channel. On the relative timescale starting at the moment of the flux rope increase, the simulated height-time dependence of the CME structure up to the heights of \(0.25~\mbox{R}_{\odot}\) agrees well with the observations of STEREO in 171 Å at the limb, the difference in speed is within the measurement errors \({\pm}\, 65~\mbox{km}\,\mbox{s}^{-1}\).

Based on the results of the observations and numerical simulation, the ion composition of CME1 in the frozen-in region in the event of 2 August 2011 is calculated with some assumptions about heating and cooling processes. The calculated values of the temperature-dependent ion ratios and the mean charge of iron agree with those measured in situ, under the assumption that the expanding plasma is heated by an additional source. The average heating power decreases with height from \({\sim}\,(5\,\mbox{--}\,6)\times 10^{-3}~\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}\) at \(r_{h} \approx0.5\,\mbox{--}\,1.5\) to \(\sim (1\,\mbox{--}\,2)\times 10^{-5}~[\mbox{erg}\,\mbox{cm}^{-3}\,\mbox{s}^{-1}]\) at \(r_{h} \approx1.5\,\mbox{--}\,5\).

In conclusion, our analysis of the ion composition of CMEs enables us to disclose a relationship between the parameters of solar wind transients and properties of their solar sources, which opens new possibilities of validating and improving solar wind forecasting models.

This work is a contribution to the International Study of Earth-affecting Solar Transients (ISEST) Minimax 24 project (the event of 4 August 2011 is included in the ISEST event list).Footnote 6