1 Introduction

It is well known that there exists generically an irreducible lower bound on the uncertainty with respect to the outcomes of simultaneous measurements of incompatible observables, i.e., the uncertainty principle originated from Heisenberg [1]. Initially, the Heisenberg uncertainty principle is inspired by an intriguing experiment for the measurements of the position and the momentum, and later was generalized by Kennard [2] and Robertson [3] to an arbitrary pair of observables A and B with a standard derivation

$$ {\Delta}_{\rho{{A}}}\cdot{\Delta}_{\rho{ B}}\geq\frac12|\langle[{ A},{ B}]\rangle| $$
(1)

for a given system ρ, where the variance \({\Delta }_{\rho } {{X}}=\sqrt {\langle {X}^{2}\rangle _{\rho }-\langle {X}\rangle ^{2}_{\rho }}\), and [A, B] = AB−BA stands for the commutator. However, the standard deviation in Robertson’s relation is not always a suitable measure for uncertainty. Specifically, Robertson relation is an ideal candidate for mapping the measurement of two incompatible observables, yet the right-hand side of Robertson’s relation depends on the systemic state ρ, which will provide a trivial bound if ρ is chosen to the zero expectation value of the commutator. In order to take out this defect and to acquire its physical nature, Deutsch [4] derived a novel result for the two-component measurement, so-called entropic uncertainty relation (EUR)

$$ S({ A})+S({ B})\geq \log_{2}{(\frac2{1+\sqrt{c}})^{2}} $$
(2)

for any pair of nondegenerate observables A and B associated with Shannon entropy. The parameter c quantifies the complementarity of A and B, where c = maxij|〈ψ i |φ j 〉|2 with |ψ〉 i and |φ〉 j being the eigenstates of A and B, respectively. Subsequently, Kraus [5] and Maassen [6] optimized Deutsch’s inequality and obtained a tighter uncertainty inequality

$$ S({ A})+S({ B})\geq \log_{2}\frac1c=S_{MU}, $$
(3)

in which the largest uncertainty can be obtained for observables being mutually unbiased.

As a matter of fact, the uncertainty principle is considerably important because it shows that the known quantum information stored in the quantum memory can reduce or eliminate the uncertainty about measurement outcomes of another particle that is entangled with the quantum memory, and is verified by several novel experiments [7, 8]. Moreover, EUR has burst out various remarkable applications including entanglement witness [9–13], the security analysis of quantum communication [9], analyzing entanglement dynamics [14, 15] and steering Bell inequality [16]. To be explicit, Coles et al. [9] have developed a more stringent formulation of both the uncertainty principle and the information exclusion principle to conduct the security analysis of quantum key distribution, entanglement estimation, and quantum communication. Hu et al. [13] investigated the relations between the quantum-memory-assisted EUR and entanglement witness in some structure reservoirs, and later reported a computable tight upper bound for quantum discord via the utilization of EUR [15]. Schneeloch et al. computed the inequalities witnessing Einstein-Podolsky-Rosen (EPR)-steering correlations by means of EUR.

However, the dissipation due to irreversible interactions with the extern environment will cause degradation of the systemic state and unavoidably affect the entropic uncertainty. Thus, investigating EUR under an open system is virtually important in the region of quantum information theory. By far, there have been a variety of investigations concerning EUR under a dissipative environment. Yao et al. [17] investigated the quantum-memory-assisted EUR for system of two qubits subjecting to several forms of independent quantum noise in both Markovian and non-Markovian regimes. Xu et al. [18] discussed quantum-memory-assisted EUR under local unital and non-unital noises, they proved that non-unital noises may reduce the amount of uncertainty in the long-time limit, the reduction effects cannot occur during the initial time. Therefore, overcoming decay is a necessary demand for practical realization of quantum information protocols. Various schemes for suppressing decoherence have been reported, such as the technique of dynamical decoupling, quantum Zeno effect, and so forth. Zou et al. [11, 12] have showed that increasing detuning in non-Markovian environment can reduce the lower bound of the entropic uncertainty. Zhang et al. [19] have derived tighter bounds on both entropic uncertainty relation and information exclusion relation for multiple measurements in the presence of quantum memory. Liu et al. [20] have explored the entropic uncertainty relations for multiple measurement settings which demonstrate the uncertainty principle of quantum mechanics, which are obtained with and without the presence of quantum memory. Zhang et al. [21] have investigated the dynamic features of the quantum-memory-assisted entropic uncertainty relation under a class of channels, i.e., amplitude damping. Zhang et al. [22] have put forward a proposal for increasing trapping of entanglement in the environment of a photonic bandgap material by use of combined weak measurement and quantum measurement reversals. Sun et al. [23] reported that the entanglement degradation of a bipartite state under amplitude damping noise can be suppressed via weak measurement to some extent and demonstrated a linear optics scheme upon its performance.

The aim of this work is to examine how the specific noises effect on the entropic uncertainty relations under dissipative environments. To do so, we will consider a two-level system with an arbitrary pure initial state, EUR under amplitude damping (AD) and depolarizing channels is investigated, respectively. Intuitively, thus, the entropic uncertainty ought to be increased, because the decay of the systemic states will lead to outflow of information inducing by the noisy environment. However, we have observed that the entropic uncertainty will be unnecessarily increased all the time, while decreased in a long-time regime. Particularly, we provide an effect strategy to decrease the amount of the uncertainty via a non-unitary operation–quantum weak measurement– (QWM) against the degradation of the qubit state. The paper is organized as follows. In Section 2, we derive the dynamics of EUR under AD channel, and present a strategy to reduce the uncertainty by the utilization of QWM. In Section 3, we numerically study the dynamics of EUR under depolarizing channel and the influence of QWM on the EUR in noisy environment. Finally, we end our paper with a brief summary in Section 4.

2 The Dynamics of EUR Under an Amplitude Damping Channel and Its Steering

Most often, due to interaction with the external environment, the decay of quantum state is inevitable. In the case of zero temperature, a type of decay can be modeled as the AD noise which is mathematically expressed by

$$ \rho(t)=\sum\limits_{i=0}^{1}\hat{ E}_{i}\rho(0) {\hat{ E}_{i}}^{\dagger} $$
(4)

with

$$ \hat{ E}_{0}= \left( \begin{array}{cc} 1 & 0 \\ 0 & \sqrt{1-p} \end{array} \right),\ \hat{ E}_{1}= \left( \begin{array}{cc} 0 & \sqrt p \\ 0 & 0 \end{array} \right), $$
(5)

where the decay strength p = 1−e −λt, ρ(0) is the initial systemic state and ρ(t) is the evolutionary state of the qubit system. Incidentally, λ is energy relaxation rate, and t is the storage period. And the experimental temperature of ∼50mK in this case corresponds to essentially the zero-temperature limit. This is exactly the regime, in which hω≫k B T is satisfied, where hw is the transition energy of quantum system, and K B is Boltzman constant. When the Kraus operators acting on the single qubit, it indicates that if an atom is in an excited state |1〉, it makes a transition to the ground state |0〉 with probability p, while the environment makes transition from the state |0〉 to state |1〉 with the same probability. Within the Weisskopf-Wigner approximation, the probability increases exponentially with time. Here we consider the case that the single-qubit system is initially in an arbitrary pure state of

$$ |{\Psi}(\theta,\phi)\rangle=cos \theta|0\rangle+e^{i\phi}sin\theta|1\rangle, $$
(6)

where \(\theta \in [0,\frac \pi 2]\) and ϕ∈[0, π], being coupled to one individual bath in the region of zero-temperature. Incidentally, the basis vector |0〉=(1,0)T corresponds to the ground state and |0〉=(0,1)T to the excited state. Thus, the qubit-systemic evolution density matrix has the form of

$$ {\rho(t)}=\left( \begin{array}{cc} \rho_{11}(t) & \rho_{12}(t) \\ \rho_{21}(t) & \rho_{22}(t) \end{array}\right) $$
(7)

with

$$\begin{array}{@{}rcl@{}} &\rho_{11}(t)=1-sin^{2}\theta\cdot e^{-\lambda t}, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} &\rho_{12}(t)=sin\theta cos\theta e^{(-i\phi-\lambda t/2)}, \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} &\rho_{21}(t)=\rho_{12}^{*}(t), \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} &\rho_{22}(t)=sin^{2}\theta\cdot e^{-\lambda t} \end{array} $$
(11)

after passing the AD channel. Here we employ two Pauli observables \(\mathbb {X}\) and \(\mathbb {Z}\) as the incompatibility. These matrices are traditionally used for describing the spin-1/2 observables. Each of the matrices has the eigenvalues ±1 with eigenstates \(|{\mathbb {X}}^{\pm }\rangle =\frac 1{\sqrt 2}(|0\rangle \pm |1\rangle )\) and \(|{\mathbb {Z}}^{\pm }\rangle =\{|0\rangle ,\ |1\rangle \}\), respectively.

2.1 The Dynamics of EUR Under Amplitude Damping Noise

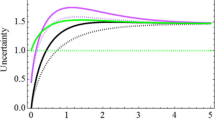
In the following, we numerically analyze the effects of AD noise on the dynamics of the systemic state and the amount of EUR. In Fig. 1, we choose the initial state with 𝜃 = π/2, π/5, 0.3383 and π/20, respectively. From the Figure, it has been shown that the quantity of states’s fidelity quantified by

$$ F={ Tr}\sqrt{{\rho(t)}^{1/2}\rho(0){\rho(t)}^{1/2}} $$
(12)

monotonously decreases over time due to the AD noise, where ρ(0)=|Ψ(𝜃, ϕ)〉〈Ψ(𝜃, ϕ)| is the initial state of the qubit system. From the Figure, one can readily see that the entropic uncertainty (EU) of observables \({\mathbb {X}}\) and \(\mathbb {Z}\) (\(S(\mathbb {X})+S(\mathbb {Z})\)) eventually decreases to an asymptotic value, which is the bound derived by Maassen and Uffink (MUB), due to the gradual decay of the fidelity of the system. Setting ratio of excited state and ground state β = tan(𝜃), we obtain a critical point 𝜃 = 0.3383. if β>0.0059, the entropic uncertainty will have smaller value at the beginning, and with the increasing of the decay time λt EU will firstly increase and then decrease to the asymptotic value when the value of 𝜃 is relatively large. By contrast, EU will always decrease to the asymptotic value when β≤0.0059. This reflects that the ratio of excited state and ground state affect the quantity EU drastically. As shown in Fig. 2, in the higher ratio, the excited state is dominated and will be influenced by the AD noise drastically; While the ground state is primary and will be weakly influenced by the noise under lower ratio. In this case, EU is mainly determined by the decay time λt and is monotonous.

Fig. 1
figure 1

The entropic uncertainty (EU) and fidelity (F) are as a function of the decay time λt with different decay strength p for the real ensembles’ states with φ = 0, respectively

Full size image
Fig. 2
figure 2

The entropic sum is state-of-dependent with different reversal strength λt for all pure ensembles’ states. Graph a p = 0; Graph b p = 0.1; Graph c p = 0.3; Graph d p = 0.5; Graph e p = 0.7; Graph f p = 0.9

Full size image

2.2 Reducing EUR in an AD Channel via QWM

Recently, a novel idea [24–26] has been proposed to protect quantum states and quantum entanglements from decoherence by using quantum partially collapsing measurement [27], i.e., quantum weak measurement (QWM). The result is limited to a special class of channel noise, which corresponds to the zero-temperature environmental noise. We say the temperature of the environment is zero when the condition hω≫k B T is satisfied. As a matter of fact, reducing entropic uncertainty is fundamental important to quantum precision measurement and ultralow noise quantum information. Enlighten by this, we present a interesting question whether the QWM can reduce the the amount of EUR in the AD channel. In the following, we introduce the posterior QWM procedure to observe its influence on EUR. For the single-qubit system, the map of QWM can be represented as

$$ \begin{array}{llll} &\rho_{11}\rightarrow \frac{1}{N}\rho_{11},\\ &\rho_{12}\rightarrow\frac{\sqrt{1-q}}{N}\rho_{12},\\ &\rho_{21}\rightarrow\frac{\sqrt{1-q}}{N}\rho_{21},\\ &\rho_{22}\rightarrow\frac{1-q}{N}\rho_{22}, \end{array} $$
(13)

where N = ρ 11+(1−q)ρ 22 is the normalized coefficient of the evolved state and also is the successful probability of the QWM. It is different from a typical AD, QWM essentially makes a postselection that removes the result of qubit transition |1〉→|0〉, which can be implemented by an ideal detector to monitor the environment. This is also called null-result QWM due to the detector does not signal. In a QWM, complete collapse to an eigenstate does not occur, and the qubits evolve still. But the decoherence can be largely suppressed by uncollapsing the quantum state towards the ground state after the AD. In Fig. 3, we have plotted the entropic sum as a function of the weak measurement strength q with different weak measurement strength p for the fixed real states, 𝜃 = π/10 in Fig. 3a, 𝜃 = π/8 in Fig. 3b, and 𝜃 = π/6 in Fig. 3c. The EU will decrease to an asymptotic value with the increase of weak measurement strength q, which is S MB . It is obvious that the stronger QWM can more effectively reduce the amount of the uncertainty. Of course, achieving strong measurement strength is at price of lower success probability.

Fig. 3
figure 3

The entropic sum is as a function of the weak measurement strength q with different weak measurement strength λt for the fixed real states. a 𝜃 = π/10; b 𝜃 = π/8; and c 𝜃 = π/6

Full size image

3 The Dynamics of EUR Under a Depolarizing Channel and Its Steering

3.1 The Dynamics of EUR in a Depolarizing Channel

We consider there is a system with an initial state of |Ψ(𝜃, ϕ)〉 as described by (6). Assume that the pure system is subjected to a canonical noise, depolarizing, and the process of the noise’s effect on the system can be mathematically expressed by

$$ \rho(t)=\sum\limits_{i=0}^{3}\hat{\mathcal{E}}_{i}\rho(0) {\hat{ \mathcal{E}}_{i}}^{\dagger} $$
(14)

with

$$ \hat{\mathcal{E}}_{0}=\sqrt{1-\gamma} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right),\ \hat{\mathcal{E}}_{1}=\sqrt{\frac{\gamma}{3}} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right),\ \hat{\mathcal{E}}_{2}=\sqrt{\frac{\gamma}{3}} \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right), \ \hat{\mathcal{E}}_{3}=\sqrt{\frac{\gamma}{3}} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right), $$
(15)

where γ is the decay strength, ρ(0) is the initial state of the qubit system, and ρ(t) is the evolutionary state. Thus, the evolutionary density matrix is given by

$$\begin{array}{@{}rcl@{}} \rho_{11}&=&(1-\frac2{3}\gamma)\cdot cos^{2}\theta+\frac23\gamma\cdot sin^{2}\theta, \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} \rho_{12}&=&(1-\frac43\gamma)sin^{2}\theta\cdot cos^{2}\theta\cdot e^{-i\phi}, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \rho_{21}&=&\rho_{12}^{*}(t), \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \rho_{22}&=&(1-\frac2{3}\gamma)\cdot sin^{2}\theta+\frac23\gamma\cdot cos^{2}\theta. \end{array} $$
(19)

Afterwards, we numerically analyze the effects of depolarizing noise on the EUR. In Fig. 4, we choose the initial state with 𝜃 = π/10, π/6, π/4, π/2 in the condition of ϕ = π/4, respectively. It shows that the states’s fidelity decreases linearly with the increase of the strength of the depolarizing noise. Similarly, we choose \(\mathbb {X}\) and \(\mathbb {Z}\) as a pair of non-commuting observables. As shown in Fig. 4, the entropic uncertainty (ES) of two observables firstly increases and then decreases due to system degradation induced by depolarizing noise. Generally speaking, the EU increases and will not return the initial outcome with the increase of the strength γ. In addition, we found that there exists a upper bound for EU, namely,

$$ S(\mathbb{X})+S(\mathbb{Z})\leq2 $$
(20)

in this case. Besides, we plotted the entropic sum as a function of initial states’ parameters ϕ and 𝜃 with different decay strength γ in Fig. 5. From the Figure, the uncertainty is symmetric around the axis of ϕ = π/2 for ∀𝜃. Thereby, depolarizing noise can lead to an increase of EU. Interestingly, we found that EU is not only bounded by the standard EUR as described as (3) but exists a fixed upper bound in depolarizing channel, which reads as

$$ \log_{2}\frac 1 c \leq S(\mathbb{X})+S(\mathbb{Z})\leq2. $$
(21)
Fig. 4
figure 4

The entropic uncertainty is as a function of γ with different real ensembles’ states. The maximal EU is 2 when γ = 0.75, the fidelity is independent of system states and the minimum of the fidelity is 1/3

Full size image
Fig. 5
figure 5

The entropic sum is as a function of initial states’ parameters ϕ and 𝜃 with different decay strength γ. The maximal EU is 2 when ϕ = π/2 and 𝜃 = π/4

Full size image

3.2 Reducing EUR in a Depolarizing Channel via QWM

In order to reduce the uncertainty for the qubit system affected by depolarizing, we introduce the posterior quantum weak measurement. For such a system, the map of QWM can be denoted as

$$ \begin{array}{lllll} &\rho_{11}\rightarrow \frac{1}{\widetilde{N}}\rho_{11},\\ &\rho_{12}\rightarrow\frac{\sqrt{1-m}}{\widetilde{N}}\rho_{12},\\ &\rho_{21}\rightarrow\frac{\sqrt{1-m}}{\widetilde{N}}\rho_{21},\\ &\rho_{22}\rightarrow\frac{1-m}{\widetilde{N}}\rho_{22}, \end{array} $$
(22)

where m is the weak measurement strength and \(\widetilde {N}=\rho _{11}+(1-m)\rho _{22}\) is the normalized coefficient of the evolved state, which quantifies the successful probability of QWM.

We have plotted the entropic uncertainty as a function of the measurement strength m for an initial state with 𝜃 = π/10 and ϕ = π/4 in Fig. 6. From the Figure, the QWM can efficiently decrease the uncertainty, and the reducing of EU is more intensive when the strength of the noise is stronger. Additionally, we have shown that EU is as a function of 𝜃 and ϕ for different measurement strength m with a fixed noisy strength γ = 0.5 in Fig. 7. From the Figure, one can easily the EU is quasi-symmetry at the point of 𝜃 = π/4 when there is no weak measurement, while the symmetry of EU is broken when the strength of QWM is non-zero. Besides, the maximum of EU will become smaller comparison to that without weak measurement. That is to say, weak measurement can not only reduce the uncertainty but also decrease the maximum of EU for all ensembles’ states.

Fig. 6
figure 6

the entropic uncertainty is as a function of the measurement strength m for an initial state with 𝜃 = π/10 and ϕ = π/4.

Full size image
Fig. 7
figure 7

The entropic uncertainty is as a function of 𝜃 and ϕ for different measurement strength m with γ = 0.5

Full size image

4 Conclusions

To summarize, we have derived the dynamic features of EUR under the dissipative environments. The initial state of the qubit system is assumed as an arbitrary pure state. In AD channels, generally speaking, the entropic uncertainty of two incompatible observables increases at first, and then decreases to an asymptotic value due to the gradual decay of the system when the amplitude angle is relatively large; yet the EU will always reduce to the asymptotic value S MU with the increase of the decay time, when the ratio of the excited state and the ground state is less than a threshold. This means the amplitude angle of the initial ensembles’ state can also affect the quantity of EU. Thus, we deduce that the uncertainty relation is state-dependent under such a noisy environment. For a depolarizing channel, the entropic uncertainty increases at first, and then decreases to an asymptotic value due to the decay of the system. Notably, there exists a fixed maximum of EU, which corresponds to the upper boundary of the entropic sum. To reduce the entropic uncertainty, we presented an efficient strategy by means of QWM. It has been proved that the QWM is able to effectively reduce the entropic uncertainty in the system suffering from either AD or depolarizing noises. Specifically, we numerically illuminated that the amount of EU can be reduced by QWM after the single-qubit system passes the AD channel and the depolarizing channel, respectively. Thereby, we claim that our investigation could be helpful for understanding the dynamics features of EUR and further achieving the steering for EUR in open systems.