Dynamics of field nonclassicality in the Jaynes–Cummings model

Abstract

Employing an informational quantifier for nonclassicality of bosonic field based on the Wigner–Yanase skew information, we investigate the dynamics of field nonclassicality in the Jaynes–Cummings model evolving from several typical initial atom–field states: coherent states, Fock states, and thermal states for the field, and ground state, excited state, symmetric superposition state, and maximally mixed state for the atom. We reveal some intriguing features of the field dynamics and their sensitivity on the initial states from an informational perspective. The results show that field nonclassicality can be generated in most cases and exhibits complex dynamic patterns involving collapses and revivals. A remarkable observation is that the initial coherent field states, assisted by the atom, can be converted to almost maximally nonclassical field states constrained by the average photon number, even though all coherent states are the most classical and possess the same minimal nonclassicality among pure states. The field dynamics may be exploited to estimate the initial atom as well as the field states, prepare desired evolving states and process quantum information.

1 Introduction

Radiation fields have played an instrumental and ubiquitous role in nature and science. While the classical field theory has been immensely successful in technologies, its quantum extension is necessary for the investigation of the microscopic world, as evidenced by the inception of quantum mechanics and quantum field theory. Nonclassicality of fields has become a fruitful subject with the rapid development of quantum optics and cavity quantum electrodynamics [1,2,3,4,5]. With the emergence of quantum information [6], nonclassicality of fields has attracted more attention and is playing an increasingly important role in quantum information processing [1,2,3,4,5,6].

Nonclassicality (with respect to coherent states) is a fundamental quantum feature with many theoretical implications and practical applications. In quantum optics, the coherent states and mixtures of them (i.e., states whose Glauber–Sudarshan distributions are genuine probability distributions) are customarily identified as classical states [7,8,9], while other states, including the non-vacuum Fock states, squeezed states, Schrödinger cat states, etc., are regarded as nonclassical ones [1,2,3]. In earlier days of quantum optics, these nonclassical states appear more as theoretical predictions than realities. However, with the advance of technologies, they have now been routinely realized and manipulated in laboratory experiments [10, 11] and have further been demonstrated to be indispensable for the successful implementation of many quantum tasks.

Motivated by both theoretical considerations and experimental needs, characterization and quantification of nonclassicality have been vigorously pursued in the last decades from many perspectives due to the richness of the concept. For example, various quantifiers for nonclassicality have been proposed, such as the Mandel Q factor [12, 13], various distance-based measures employing either different norms or entropic quantities [14,15,16,17,18,19,20,21,22], measures based on the algebraic (convex) structure of the states [23,24,25], the nonclassical depth [26,27,28,29,30], the negativity of the Wigner functions [31], the entanglement potentials [32], the Wehrl entropy difference [33], the operator ordering sensitivity [34], the generalized Wigner–Yanase skew information [35, 36], etc. Moreover, as a quantum feature, nonclassicality has been regarded as a kind of quantum resource [37], with the conversion between nonclassicality and other quantum features such as entanglement, quantum correlations, and metrological power being under active studies [32, 38,39,40,41,42,43,44,45,46,47].

In practice, when fields propagate in the medium, they inevitably interact with other systems such as the environment, which usually result in exchange of energy and information. A natural question arises in this context: How is the field nonclassicality influenced by its interaction with other systems and initial states? This issue, which is of importance in understanding the generation and evolution of nonclassicality, has been addressed extensively and intensively by many authors, in particular in the paradigm of the Jaynes–Cummings model [48], which accounts for the simplest atom–field interaction and yet exhibits rich dynamics [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82]. The dynamics of both the atom and the field in the Jaynes–Cummings model have attracted a lot of attention. It was shown that various nonclassical effects manifest. For the atom, most of the previous studies are about the collapses and revivals of several physical quantities, such as the excitation occupation probability and atomic inversion [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], while for the field, the Mandel Q factor, antibunching effect, squeezing, sub-Poissonian statistics, marginal entropy and quantum correlations have been investigated extensively [70,71,72,73,74,75,76,77,78,79,80,81,82]. However, none of the above quantities can characterize all aspects of field nonclassicality, and it is desirable to explore the field dynamics from as many perspectives as possible in order to gain a more complete picture of the dynamics. Here we pursue an informational approach to the dynamics of field nonclassicality in the Jaynes–Cummings model with the help of generalized Wigner–Yanase skew information.

The paper is organized as follows: In Sect. 2, we review the recently introduced nonclassicality quantifier of bosonic field states based on generalized Wigner–Yanase skew information [35]. In Sect. 3, we describe the Jaynes–Cummings model, analyze the dynamics of the field nonclassicality, and illustrate its various features. We further compare them with other quantities of the field dynamics such as the von Neumann entropy and fidelity. Finally, we conclude with a summary and discussion in Sect. 4. Some mathematical details for the derivation of the reduced field states of the Jaynes–Cummings model are presented in Appendix.

2 Quantifying field nonclassicality

The basic ingredients of a single-mode bosonic field consist of the annihilation operator a and its adjoint, the creation operator $a^{\dagger }$, which satisfy the canonical commutation relation $[a,a^\dagger ]=\mathbf{1}.$ Various features such as classicality and nonclassicality including squeezing, sub-Poissonian statistics and antibunching of bosonic field states have been extensively studied in quantum optics. Here we recall a recently introduced informational quantifier for nonclassicality of the bosonic field state $\rho$ based on generalized Wigner–Yanase skew information [35]:

$$\begin{aligned} N(\rho ) = \frac{1}{2}\mathrm{tr}([\sqrt{\rho },a][\sqrt{\rho },a]^{\dagger }), \end{aligned}$$

(1)

or more explicitly (noting that $[X,Y]=XY-YX$ denotes the commutator between operators),

$$\begin{aligned} N(\rho ) =\frac{1}{2} +\mathrm{tr}(\rho a^{\dagger }a)-\mathrm{tr}(\sqrt{\rho } a^{\dagger }\sqrt{\rho } a). \end{aligned}$$

(2)

Furthermore, simple manipulation shows that the nonclassicality can be equivalently expressed as

$$\begin{aligned} N(\rho )=\frac{1}{2}(I(\rho , Q)+I(\rho , P)), \end{aligned}$$

(3)

with

$$\begin{aligned} Q=\frac{a+a^\dagger }{\sqrt{2}}, \qquad P=\frac{a-a^\dagger }{i\sqrt{2}} \end{aligned}$$

being the conjugate quadratures and

$$\begin{aligned} I(\rho , X)=-\frac{1}{2} \mathrm{tr}([\sqrt{\rho }, X]^2) \end{aligned}$$

(4)

being the Wigner–Yanase skew information of the quantum state $\rho$ skew to the observable (Hermitian operator) X [83]. Since the Wigner–Yanase skew information is a kind of quantum Fisher information with many significant applications [83,84,85,86,87,88,89,90,91], the nonclassicality quantifier $N(\rho )$ is well motivated and has potential applications in quantum metrology [35].

By rewriting the Wigner–Yanase skew information, given by Eq. (4), as

$$\begin{aligned} I(\rho , X)=\frac{1}{2} \mathrm{tr}([\sqrt{\rho }, X][\sqrt{\rho }, X]^\dagger ) \end{aligned}$$

(5)

for Hermitian operator X, and comparing Eqs. (1) and (5), we see readily that the nonclassicality $N(\rho )$ is actually a natural generalization of the Wigner–Yanase skew information: One simply replaces the Hermitian operator X by the non-Hermitian annihilation operator a.

It has been shown that $N(\rho )$ has some nice and desirable properties required for nonclassicality [35], for example, it is nonnegative and convex with respect to quantum state, and invariant under the displacement or rotation in phase space in the sense that

$$\begin{aligned} N(U\rho U^\dag )=N(\rho ), \end{aligned}$$

(6)

where $U=e^{za^\dag -z^*a}$ or $e^{-i\theta a^\dag a},\ z\in C,\ \theta \in R.$ For pure quantum states, $N(\rho )\ge 1/2$ where the minimum value 1/2 is achieved if and only if $\rho$ is a coherent state $|\alpha \rangle$ (i.e., eigenstate of the annihilation operator, $a|\alpha \rangle =\alpha |\alpha \rangle$), while for any classical state $\rho$ which can be expressed as a probabilistic mixture of coherent states, $N(\rho )\le 1/2$. Thus if $N(\rho )>1/2$, we can conclude that $\rho$ is nonclassical. However, the converse is not true. In this sense, we use the term nonclassicality quantifier (rather than measure) for $N(\rho )$, which may be interpreted as a witness or probe for nonclassicality. Moreover, from the metrological point of view, as can be seen from Eq. (3), $N(\rho )$ is essentially a kind of total average quantum Fisher information, and can be further interpreted as quantum uncertainty and coherence [87, 88]. Put it succinctly, it quantifies quantumness in some sense and has direct physical and informational significance.

For most well known states, $N(\rho )$ can be easily calculated. For the coherent state $|\alpha \rangle$, its nonclassicality is $N(|\alpha \rangle )=1/2$, while for the squeezed coherent state $S_{\zeta }|\alpha \rangle$ with $S_{\zeta }=\exp (\zeta a^{\dagger 2}/2-\zeta ^{*} a^2/2)$, we have [35]

$$\begin{aligned} N(S_{\zeta }|\alpha \rangle )=\frac{1}{2}\cosh (2|\zeta |). \end{aligned}$$

It is clear that $N(S_{\zeta }|\alpha \rangle ) > 1/2$ for $\zeta \ne 0;$ therefore, the squeezed coherent state is nonclassical. Moreover, as $|\zeta |$ increases, $N(S_{\zeta }|\alpha \rangle )$ also increases: The more the squeezing, the more nonclassical the state is, which is consistent with physical intuition. For the Fock states $|n\rangle$ which are eigenstates of the number operator $N=a^{\dagger }a$, $N|n\rangle =n|n\rangle$, the nonclassicality is

$$\begin{aligned} N(|n\rangle )=n+\frac{1}{2}, \end{aligned}$$

which is neat and captures the physical essence of the Fock states. It is amusing here to note that even the vacuum state $|0\rangle$ has nonclassicality 1/2, which is reminiscent of (and well consistent with) the physics of vacuum fluctuations and zero-point energy in quantum field. Of course, this has the origin in the noncommutability between a and $a^\dagger$: $[a,a^\dagger ]=\mathbf{1}$. In this context, we emphasize that in quantum optics, although any coherent state (in particular the vacuum state) is regarded as classical, it is still a quantum state, fully obeys quantum mechanics laws, and possesses certain nonclassicality (quantumness). This is manifested by $N(\rho )=1/2$ for any coherent state $\rho$ [35]. In this sense, the classicality of coherent states seems a historically stuck misnomer, even though it is widely used.

From the expression of $N(\rho )$ given in Eq. (2), for an arbitrary quantum state $\rho$, we have

$$\begin{aligned} N(\rho )\le \frac{1}{2}+\mathrm{tr}\rho a^{\dagger }a, \end{aligned}$$

which implies that the Fock states achieve the maximal nonclassicality among the set of quantum states with fixed average photon number. This stands in sharp contrast to the coherent states, which achieves the minimal value 1/2 among all pure states. Indeed, the coherent states are the most classical pure states, while the Fock states are the most nonclassical: They stand on two opposite and extremal ends. Another important class of quantum states are the Fock-diagonal states

$$\begin{aligned} \rho _\mathrm{F}=\sum _{n=0}^{\infty }p_n|n\rangle \langle n|. \end{aligned}$$

From direct calculations, we have

$$\begin{aligned} N(\rho _\mathrm{F}) = \frac{1}{2} +\sum _{n=0}^{\infty } np_n-\sum _{n=0}^{\infty } (n+1)\sqrt{p_np_{n+1}}. \end{aligned}$$

(7)

3 Field nonclassicality in the Jaynes–Cummings model

Two of the most fundamental physical systems are the (discrete) qubit described by a two-level atom (with two energy eigenstates, the ground state $|g\rangle$ and excited state $|e\rangle$) and the (continuous) harmonic oscillator (described by a single-mode field with an infinitely many energy eigenstates $|n\rangle , n=0,1,2,\cdots$). In 1963, the same year when Wigner and Yanase introduced the celebrated notion of skew information [83], Jaynes and Cummings introduced a model now named after them to describe the interaction between a qubit (atom) and a harmonic oscillator (field) [48], as an idealization of the atom–field coupling in free space. Now this model, which constitutes the central paradigm of cavity quantum electrodynamics and quantum optics with rich characteristics and dynamics [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82], is widely used to describe the typical situation in cavity quantum electrodynamics where a single atom is coupled to a cavity mode, as well as in an ion trap where the internal ionic states are coupled, via laser beams, to the harmonic oscillator motional states of the ion in the trap [92]. In particular, the model is of both fundamental and practical importance for manipulating atoms with fields, or vice versa [10, 11].

The complete Hamiltonian of the Jaynes–Cummings model, in the rotating-wave approximation, reads

$$\begin{aligned} H=H_a\otimes \mathbf{1}+\mathbf{1}\otimes H_f+H_I, \end{aligned}$$

with the atom free evolution Hamiltonian $H_a=\omega \sigma _z/2,$ the field free evolution Hamiltonian $H_f= \mu a^{\dagger }a,$ and the atom–field interaction

$$\begin{aligned} H_I= \lambda (\sigma _+a+\sigma _-a^{\dagger }). \end{aligned}$$

Here $\mathbf{1}$ refers to the identity operator on the field space or the atom space, depending on the context. We have taken the Planck constant $\hbar$ to be 1, $\omega$ is the transition frequency of the two-level atom, $\mu$ is the frequency of the field, $\sigma _z=|e\rangle \langle e|-|g\rangle \langle g|$ is the third Pauli operator, $\sigma _+=|e\rangle \langle g|$ and $\sigma _-=|g\rangle \langle e|$ are atomic raising and lowering operators, respectively, and $\lambda$ is the interaction strength parameter. The difference $\omega -\mu$ is the detuning parameter. The model is pictorially depicted in Fig. 1.

Fig. 1

The Jaynes–Cummings model of atom–field coupling

Here we employ the nonclassicality quantifier $N(\cdot )$ given in Eq. (1) to study the field dynamics evolving from several typical initial atom–field states. For the resonant Jaynes–Cummings interaction with $\omega -\mu =0$, the unitary time-evolution operator at time t in the interaction picture can be expressed as [2]

$$\begin{aligned} e^{-itH_I}= & {} \cos (\lambda t\sqrt{N+1})|e\rangle \langle e|-i\frac{\sin (\lambda t\sqrt{N+1})}{\sqrt{N+1}}a|e\rangle \langle g|\\+ & {} \cos (\lambda t\sqrt{N})|g\rangle \langle g|-ia^{\dagger }\frac{\sin (\lambda t\sqrt{N+1})}{\sqrt{N+1}}|g\rangle \langle e| \end{aligned}$$

with $N=a^{\dagger }a$ being the field number operator. Since the nonclassicality quantifier $N(\cdot )$ is invariant under phase-space rotations [35], and the partial trace is invariant under local unitary transformations of the atom, we may consider the field state defined in Eq. (9) and calculate its nonclassicality by Eq. (2) without loss of generality. More precisely, due to the fact that (with proof given in Appendix)

$$\begin{aligned} N\Big (\mathrm{tr}_a \big (e^{-itH}(\rho _a\otimes \rho _f) e^{itH}\big )\Big )= & {} N\Big (\mathrm{tr}_a \big (e^{-itH_I}(\rho _a\otimes \rho _f) e^{itH_I}\big )\Big ), \end{aligned}$$

(8)

we may work in the interaction picture for evaluating nonclassicality of the evolved states. Evolving from the initial atom–field product state $\rho _a\otimes \rho _f$, the reduced field state at time t in the interaction picture can be calculated as

$$\begin{aligned} \rho _f (t)=\mathrm{tr}_a \big (e^{-itH_I}(\rho _a\otimes \rho _f ) e^{itH_I}\big ), \end{aligned}$$

(9)

where $\mathrm{tr}_a$ denotes the partial trace over the atom. For the initial field states $\rho _f,$ we distinguish four important and representative classes:

A. coherent states $|\alpha \rangle$ with $\alpha \ne 0,$

B. Fock states $|n\rangle$ with $n>0,$

C. thermal states

$$\begin{aligned} \rho _{\bar{n}}=\frac{1}{1+\bar{n}} \sum _{n=0}^\infty \Big (\frac{\bar{n}}{1+\bar{n}}\Big )^{n}|n\rangle \langle n| \end{aligned}$$

with $\bar{n}$ being the average photon numbers.

D. Vacuum state $|0\rangle .$

For the initial atomic states, we consider four typical cases: excited state $|e\rangle$, ground state $|g\rangle$, superposition state $(|e\rangle +|g\rangle )/\sqrt{2},$ and the maximally mixed state $(|e\rangle \langle e|+|g\rangle \langle g|)/2$, which is actually $\mathbf{1}/2$ (normalized identity operator).

The various combinations of the initial atomic and field states will induce rich dynamics of the Jaynes–Cummings model, in particular of the field, as illustrated below.

3.1 Field initially in coherent states

First, we consider the case when the field is initially prepared in the coherent state $\rho _f=|\alpha \rangle \langle \alpha |$ with the average photon number $\mathrm{tr}(|\alpha \rangle \langle \alpha |a^\dagger a)=|\alpha |^2$. For both pure and mixed initial atomic states $\rho _a$, the reduced field states $\rho _f (t)$ at time t can be obtained analytically through Eq. (9), and then by Eq. (2), the field nonclassicality $N(\rho _f (t))$ can be evaluated readily.

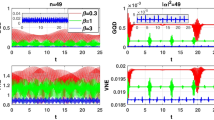
The field nonclassicality $N(\rho _f (t))$ versus the scaled time $\lambda t,$ evolving from various initial states $\rho _a\otimes |\alpha \rangle \langle \alpha |,$ is depicted in Fig. 2 for the initial field states to be the coherent states $|\alpha \rangle$ (with $|\alpha |^2=1,20)$ and the initial atomic states $\rho _a$ to be the excited state $|e\rangle ,$ the ground state $|g\rangle ,$ the superposition state $(|e\rangle +|g\rangle )/\sqrt{2},$ and the maximally mixed state $\mathbf{1}/2.$

Fig. 2

Field nonclassicality $N(\rho _f (t))$ versus $\lambda t,$ evolving from the initial atom–field states $\rho _a \otimes |\alpha \rangle \langle \alpha |$ with various initial atomic states $\rho _a=|e\rangle \langle e|, |g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2,$ and the initial coherent field states $|\alpha \rangle ,$ $|\alpha | ^2=1,20.$

From Fig. 2, we see that field nonclassicality can be generated as time goes, although initially the field is in (classical) coherent states. For example, considering the scenario of the field in coherent state $|\alpha \rangle$ with $|\alpha |^2=20,$ for both the initial excited and ground states of the atom, the evolved field nonclassicality periodically increases to the maximal value close to that allowed by the average photon number constraint and then decreases, and the pattern repeats in a slightly modified fashion.

For the initial superposition of the excited and ground states of the atom, the maximal value of the evolved field nonclassicality is only about one half of the case of excited or ground state and is actually similar to that evolved from the maximally mixed atomic state. Moreover, the maximal values for the latter two cases come much later and stay there approximately for much longer time (noting the different ranges of the scaled time $\lambda t$ between the top two frames and the other two frames in Fig. 2). We also see that the field nonclassicality dynamics are quite different for large and small amplitudes (or average photon numbers) of the initial coherent states. It is remarkable to observe that coherent state $|\alpha \rangle$ constitutes a kind of potential resources for nonclassicality, with large amplitude $|\alpha |$ (equivalently, average photon number $|\alpha |^2$) corresponding to large potentiality of nonclassicality, even though all coherent states are classical and possess the same amount of nonclassicality 1/2.

For comparison, we depict in Fig. 3 the corresponding marginal entropy $S(\rho _f(t))=-\mathrm{tr}(\rho _f(t)\mathrm{log}_2\rho _f(t))$ of the reduced field. We see that for the case of average photon number 20, when the nonclassicality is maximal, the corresponding von Neumann entropy is minimal, close to zero, indicating an almost pure field state at the instant. In this context, taking into account the fact that the nonclassicality at that instant is maximal, one may guess that the almost pure field state with the maximal nonclassicality (and minimal von Neumann entropy) is close to the maximally nonclassical Fock state $|20\rangle$ under the average photon number constraint. However, this is not the case, as can be seen from Fig. 4, in which the corresponding fidelity $F(\rho _f(t), |\bar{n}\rangle \langle \bar{n}|)=\langle \bar{n}|\rho _f(t)|\bar{n}\rangle ,$ for $\bar{n}=|\alpha |^2 =1 ,20,$ is depicted. It is also interesting to note that for the initial atomic states with the symmetric superposition state and the maximally mixed state, the evolved fidelities $F(\rho _f(t), |\bar{n}\rangle \langle \bar{n}|)$ turn out to be the same.

Fig. 3

Marginal entropy $S(\rho _f (t))$ of the reduced field versus $\lambda t,$ evolving from the initial atom–field states $\rho _a \otimes |\alpha \rangle \langle \alpha |$ with various initial atomic states $\rho _a=|e\rangle \langle e|, |g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2,$ and the initial coherent field states $|\alpha \rangle ,$ $|\alpha | ^2=1,20.$

Fig. 4

Fidelity $F(\rho _f(t), |\bar{n}\rangle \langle \bar{n}|)$ between the reduced field state $\rho _f(t)$ and the Fock state $|\bar{n}\rangle$ (for $\bar{n}=|\alpha |^2 =1,20$) versus $\lambda t,$ evolving from the initial atom–field states $\rho _a \otimes |\alpha \rangle \langle \alpha |$ with various initial atomic states $\rho _a=|e\rangle \langle e|, |g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2,$ and the initial coherent field states $|\alpha \rangle , |\alpha | ^2=1,20.$

3.2 Field initially in Fock states

Next, we consider the case when the field is initially prepared in the Fock state $|n\rangle$, which is the most nonclassical state for fixed average photon number n. From the derivations given in Appendix, the reduced field state at time t is

$$\begin{aligned} \rho _f (t)=\cos ^2(\lambda t \sqrt{n+1})|n\rangle \langle n|+\sin ^2(\lambda t \sqrt{n+1})|n+1\rangle \langle n+1| , \end{aligned}$$

and its nonclassicality is

$$\begin{aligned} N(\rho _f (t))=n-\cos ^2(\lambda t \sqrt{n+1})-\frac{n+1}{2}|\sin (2\lambda t \sqrt{n+1})|. \end{aligned}$$

We plot in Fig. 5 the field nonclassicality $N(\rho _f (t))$ versus the scaled time $\lambda t,$ evolving from various initial atom–field states $\rho _a\otimes |n \rangle \langle n |$ with the initial atomic states $\rho _a$ to be $|e\rangle , |g\rangle , (|e\rangle +|g\rangle )/\sqrt{2}, \mathbf{1}/2,$ and $n=1,20.$

Fig. 5

Field nonclassicality $N(\rho _f (t))$ versus $\lambda t,$ evolving from the initial atom–field states $\rho _a \otimes |n\rangle \langle n|$ with various initial atomic states $\rho _a=|e\rangle \langle e|, |g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2,$ and the initial Fock field states $|n \rangle , n=1,20.$

It is clear that the field nonclassicality $N(\rho _f (t))$ exhibits periodic yet different patterns for different initial atomic states. The collapses and revivals of nonclassicality are apparent and quite regular. The maximal value $n+1/2$ can be reached more periodically for the initial excited or ground state than for the superposition or the maximally mixed state. Comparing Figs. 2 and 5, we also see the sharp different dynamics caused by the initial coherent field states and the Fock states.

3.3 Field initially in thermal states

Now, we consider the case when the initial field state is the thermal state

$$\begin{aligned} \rho _{\bar{n}}=\sum _{n=0}^{\infty }\frac{\bar{n}^n}{(1+\bar{n})^{n+1}}|n\rangle \langle n|, \end{aligned}$$

which is a mixed classical state. We depict in Fig. 6 the field nonclassicality $N(\rho _f (t))$ versus the scaled time $\lambda t,$ evolving from various initial atom–field states $\rho _a\otimes \rho _{\bar{n}}$ with the initial atomic states $\rho _a$ to be $|e\rangle , |g\rangle , (|e\rangle +|g\rangle )/\sqrt{2}, \mathbf{1}/2,$ and $\bar{n}=1,20.$

Fig. 6

Field nonclassicality $N(\rho _f (t))$ versus $\lambda t,$ evolving from the initial combined states $\rho _a \otimes \rho _{\bar{n}}$ with various initial atomic states $\rho _a=|e\rangle \langle e|, |g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2,$ and the initial thermal field states $\rho _{\bar{n}} , \bar{n}=1,20.$

It can be seen that field nonclassicality is generated as long as the atom is not initially prepared in the maximally mixed state. Besides, $N(\rho _f (t))$ increases as $\bar{n}$ increases. Actually from the expression of $\rho _f (t)$ given in Appendix, for large $\bar{n}$, the weights of higher Fock states are enhanced, which contribute more to the nonclassicality. The oscillating nature of nonclassicality is apparent in all cases.

3.4 Field initially in the vacuum state

Finally, we consider the case when the field is initially prepared in the vacuum $|0\rangle ,$ which may be regarded simultaneously as a coherent, Fock and thermal state. This seemingly trivial initial state generates nontrivial dynamics. We depict in Fig. 7 the field nonclassicality $N(\rho _f (t))$ versus the scaled time $\lambda t,$ evolving from various initial combined states $\rho _a\otimes |0\rangle \langle 0|$ with the initial atomic states $\rho _a$ to be $|e\rangle , |g\rangle , (|e\rangle + |g\rangle )/\sqrt{2},\mathbf{1}/2.$

We have two interesting observations: First, the ground state and the excited state have radically different influences on the field dynamics: While the excited state leads to periodic oscillation of the field nonclassicality, the ground state leads to a constant and relatively low value. Actually the field state remains to be the vacuum state. Second, when the initial atomic state is the maximally mixed state, the resulting field nonclassicality is below 1/2 (the value taken by all coherent states) and oscillates, indicating quantum fluctuations from the vacuum.

Fig. 7

Field nonclassicality $N(\rho _f (t))$ versus $\lambda t,$ evolving from the initial combined states $\rho _a \otimes |0\rangle \langle 0|$ with the initial vacuum field states $|0 \rangle$ and various initial atomic states $\rho _a=|e\rangle \langle e|, (|g\rangle \langle g|, (|e\rangle +|g\rangle )(\langle e| +\langle g|)/2, \mathbf{1}/2.$

4 Conclusion

We have investigated the dynamics of field nonclassicality in the Jaynes–Cummings model by the nonclassicality quantifier $N(\rho )$, which is based on generalized Wigner–Yanase skew information. For several typical initial atomic and field states, we have illustrated the evolved field nonclassicality pictorially.

Our results show that field nonclassicality can be generated by the interaction between the atom and the field via the Jaynes–Cummings coupling. The dynamics of the field nonclassicality exhibits a complex pattern, reveals the interconversion between atomic coherence and field nonclassicality, and indicates high sensitivity to the initial states.

An interesting observation is that in the field dynamics, a coherent field state, assisted by the atom and via the Jaynes–Cummings coupling, can be converted to a nonclassical state whose nonclassicality achieves almost the maximal value allowed by the energy constraint specified by the coherent state amplitude. This is remarkable since all coherent states, irrespective of their average photon numbers, possess the same amount of nonclassicality. We have unveiled an intrinsic link between the average photon number (energy) and nonclassicality.

Our results shed informational insight on the atom–field interaction. The nonclassicality quantifier $N(\rho )$ is a general quantity with informational and metrological meaning, and it may be useful in characterizing nonclassicality in other physical models involving radiation fields and in quantifying quantum resources therein. Those topics will be worthy of further investigation.

Appendix

For the purpose of completeness and convenience of evaluating the field nonclassicality, we first prove Eq. (8) and then derive the standard results concerning the reduced field states of the Jaynes–Cummings model evolving from several typical initial atom–field states.

To establish Eq.(8), noting that $[H_a\otimes \mathbf{1}, \mathbf{1}\otimes H_f]=0,$ and

$$\begin{aligned} {[}\sigma _z\otimes \mathbf{1},\ H_I]= & {} \lambda (\sigma _z \sigma _+ - \sigma _+\sigma _z)\otimes a + \lambda (\sigma _z\sigma _--\sigma _-\sigma _z)\otimes a^\dag \\= & {} 2\lambda (\sigma _+\otimes a-\sigma _-\otimes a^\dag ),\\ {[}{} \mathbf{1}\otimes a^\dag a,\ H_I]= & {} \lambda \sigma _+ \otimes (a^\dag a^2-aa^\dag a) +\lambda \sigma _-\otimes (a^\dag aa^\dag -a^{\dag 2}a)\\= & {} \lambda (\sigma _-\otimes a^\dag -\sigma _+\otimes a). \end{aligned}$$

Therefore, if $\mu =\omega ,$ noting that $H_a=\omega \sigma _z/2$ and $H_f=\mu a^\dagger a,$ we have

$$\begin{aligned} {[}H_a\otimes \mathbf{1}+\mathbf{1}\otimes H_f, \ H_I]=0, \end{aligned}$$

from which we obtain

$$\begin{aligned} e^{-itH}= & {} e^{-it(H_a\otimes \mathbf{1}+\mathbf{1}\otimes H_f)}e^{-itH_I}=(e^{-itH_a}\otimes \mathbf{1})(\mathbf{1}\otimes e^{-itH_f})e^{-itH_I}. \end{aligned}$$

Consequently,

$$\begin{aligned}&\mathrm{tr}_a \big (e^{-itH}(\rho _a\otimes \rho _f) e^{itH}\big )\\&\quad =\mathrm{tr}_a \big ((e^{-itH_a}\otimes \mathbf{1})(\mathbf{1}\otimes e^{-itH_f})e^{-itH_I}(\rho _a\otimes \rho _f) e^{itH_I}(\mathbf{1}\otimes e^{itH_f})(e^{itH_a}\otimes \mathbf{1})\big )\\&\quad =e^{-itH_f} \mathrm{tr}_a\big (e^{-itH_I}(\rho _a\otimes \rho _f) e^{itH_I}\big )e^{itH_f}. \end{aligned}$$

By the phase-space rotation invariance of $N(\cdot )$ in Eq. (6), we obtain

$$\begin{aligned} N\Big (\mathrm{tr}_a \big (e^{-itH}(\rho _a\otimes \rho _f) e^{itH}\big )\Big )= & {} N\Big (\mathrm{tr}_a\big ( e^{-itH_I}(\rho _a\otimes \rho _f) e^{itH_I}\big )\Big ), \end{aligned}$$

which is the desired result.

Next, we derive reduced field states in the Jaynes–Cummings model. If the atom–field is initially in a pure product state $|\psi _a \rangle |\psi _f \rangle$ with the initial atomic state

$$\begin{aligned} |\psi _a\rangle =\sqrt{p}|e\rangle +\sqrt{1-p} |g\rangle , \qquad 0\le p\le 1 \end{aligned}$$

and the initial field

$$|\psi _f \rangle =\sum _{n=0}^\infty q_{n}|n\rangle ,$$

then the atom–field state at time t is

$$\begin{aligned} |\Psi (t)\rangle= & {} e^{-itH_I}(|\psi _a\rangle |\psi _f \rangle )\\= & {} \sum _{n=0}^\infty \big (a_{n}(t)|g\rangle |n\rangle +b_{n}(t)|e\rangle |n\rangle \big ) \end{aligned}$$

with

$$\begin{aligned} a_{n}(t)= & {} \sqrt{1-p}q_{n}\cos (\lambda t \sqrt{n})-i\sqrt{p}q_{n-1}\sin (\lambda t \sqrt{n}),\\ b_{n}(t)= & {} \sqrt{p}q_{n}\cos (\lambda t\sqrt{n+1})-i\sqrt{1-p}q_{n+1}\sin (\lambda t \sqrt{n+1}). \end{aligned}$$

The reduced field state can be expressed as

$$\begin{aligned} \rho _f (t)= & {} \mathrm{tr}_a |\Psi (t)\rangle \langle \Psi (t)|\\= & {} \sum _{m,n=0}^\infty \big (a_{n}(t)a_{m}^{*}(t)+b_{n}(t)b_{m}^{*}(t)\big )|n\rangle \langle m|. \end{aligned}$$

For the mixed initial atomic state

$$\begin{aligned} \rho _a=p_\mathrm{e}|e\rangle \langle e|+(1-p_\mathrm{e})|g\rangle \langle g|,\qquad 0\le p_\mathrm{e}\le 1 \end{aligned}$$

and mixed initial field state

$$\begin{aligned} \rho _f =\sum _{n=0}^\infty p_n|n\rangle \langle n|, \end{aligned}$$

the evolved state can be obtained by linear combinations and the reduced field state can be expressed as

$$\begin{aligned} \rho _f (t)= & {} \mathrm{tr}_\mathrm{a} \left( e^{-itH_I}(\rho _a\otimes \rho _f) e^{itH_I}\right) \\= & {} \sum _{n=0}^\infty c_n(t)|n\rangle \langle n|. \end{aligned}$$

which is a Fock-diagonal state with the coefficients

$$\begin{aligned} c_n(t)= & {} p_\mathrm{e}\left( p_n\mathrm{cos}^2(\lambda t\sqrt{n+1})+p_{n-1}\mathrm{sin}^2(\lambda t\sqrt{n}) \right) \\+ & {} (1-p_\mathrm{e})\left( p_n\mathrm{cos}^2(\lambda t\sqrt{n})+p_{n+1}\mathrm{sin}^2(\lambda t\sqrt{n+1}) \right) . \end{aligned}$$

In the following, we present the explicit expressions of $a_n(t),b_n(t)$ and $c_n(t)$ when the initial field states $\rho _f$ are the coherent states $|\alpha \rangle$, the Fock states $|n\rangle$ and the thermal states

$$\begin{aligned} \rho _{\bar{n}}=\frac{1}{1+\bar{n}} \sum _{n=0}^\infty \Big (\frac{\bar{n}}{1+\bar{n}}\Big )^{n}|n\rangle \langle n| \end{aligned}$$

with $\bar{n}$ being the average photon numbers.

A. Field initially in coherent states

Let the field be initially in the coherent state

$$\begin{aligned} |\psi _f \rangle =|\alpha \rangle =e^{-\frac{|\alpha |^{2}}{2}} \sum _{n=0}^\infty \frac{\alpha ^{n}}{\sqrt{n!}}|n\rangle , \end{aligned}$$

with the average photon number $\bar{n}=|\alpha |^{2}.$ For the initial state of the atom, we consider two cases:

(1) If the atom is initially in the superposition state $|\psi _a\rangle =\sqrt{p}|e\rangle +\sqrt{1-p} |g\rangle ,$ then the initial atom–field state is $|\psi _a \rangle \otimes |\alpha \rangle ,$ and the reduced field state at time t can be obtained as

$$\begin{aligned} \rho _f (t)=\sum _{m,n=0}^\infty \big (a_{n}(t)a_{m}^{*}(t)+b_{n}(t)b_{m}^{*}(t)\big )|n\rangle \langle m| \end{aligned}$$

with

$$\begin{aligned} a_{n}(t)= & {} \sqrt{1-p}e^{-\frac{|\alpha |^{2}}{2}}\frac{\alpha ^{n}}{\sqrt{n!}}\cos (\lambda t\sqrt{n})\\&-i\sqrt{p}e^{-\frac{|\alpha |^{2}}{2}}\frac{\alpha ^{n-1}}{\sqrt{(n-1)!}}\sin (\lambda t \sqrt{n}),\\ b_{n}(t)= & {} \sqrt{p}e^{-\frac{|\alpha |^{2}}{2}}\frac{\alpha ^{n}}{\sqrt{n!}}\cos (\lambda t\sqrt{n+1})\\&-i\sqrt{1-p}e^{-\frac{|\alpha |^{2}}{2}}\frac{\alpha ^{n+1}}{\sqrt{(n+1)!}}\sin (\lambda t\sqrt{n+1}). \end{aligned}$$

(2) If the atom is initially in the mixed state $\rho _a=p_\mathrm{e}|e\rangle \langle e|+(1-p_\mathrm{e})|g\rangle \langle g|,$ then the initial atom–field state is $\rho _a \otimes |\alpha \rangle \langle \alpha |,$ and the reduced field state at time t can be obtained from linear combinations as

$$\begin{aligned} \rho _f (t)= & {} e^{-|\alpha |^2}\sum _{m,n=0}^\infty \left( \frac{p_e\alpha ^{n-1}\alpha ^{*m-1}\sin (\lambda t\sqrt{n})\sin (\lambda t\sqrt{m})}{\sqrt{(n-1)!(m-1)!}}\right. \\+ & {} \frac{(1-p_e)\alpha ^{n+1}\alpha ^{*m+1}\sin (\lambda t\sqrt{n+1})\sin (\lambda t\sqrt{m+1})}{\sqrt{(n+1)!(m+1)!}}\\+ & {} \frac{p_e\alpha ^{n}\alpha ^{*m}\cos (\lambda t\sqrt{n+1})\cos (\lambda t\sqrt{m+1})}{\sqrt{n!m!}}\\+ & {} \left. \frac{(1-p_e)\alpha ^{n}\alpha ^{*m}\cos (\lambda t\sqrt{n})\cos (\lambda t\sqrt{m})}{\sqrt{n!m!}}\right) |n\rangle \langle m|. \end{aligned}$$

B. Field initially in Fock states

Next we consider the case when the field is initially in a Fock state $|\psi _f \rangle =|n\rangle .$ For the initial atomic state, we consider two cases:

(1) If the atom is initially in the superposition state $|\psi _a\rangle =\sqrt{p}|e\rangle +\sqrt{1-p} |g\rangle ,$ then the initial atom–field state is $|\psi _a\rangle \otimes |n\rangle ,$ and the reduced field state at time t is

$$\begin{aligned} \rho _f(t)= & {} \left( (1-p)\cos ^2(\lambda t\sqrt{n})+p\cos ^2(\lambda t\sqrt{n+1})\right) |n\rangle \langle n|\\&+p\sin ^2(\lambda t\sqrt{n+1})|n+1\rangle \langle n+1|\\&+(1-p)\sin ^2(\lambda t\sqrt{n})|n-1\rangle \langle n-1|\\&+i\sqrt{p(1-p)}\sin (\lambda t\sqrt{n+1})\cos (\lambda t\sqrt{n})|n\rangle \langle n+1|\\&-i\sqrt{p(1-p)}\sin (\lambda t\sqrt{n+1})\cos (\lambda t\sqrt{n})|n+1\rangle \langle n|\\&+i\sqrt{p(1-p)}\cos (\lambda t\sqrt{n+1})\sin (\lambda t\sqrt{n})|n\rangle \langle n-1|\\&-i\sqrt{p(1-p)}\cos (\lambda t\sqrt{n+1})\sin (\lambda t\sqrt{n})|n-1\rangle \langle n|. \end{aligned}$$

(2) If the atom is initially in a mixed state $\rho _a=p_\mathrm{e}|e\rangle \langle e|+(1-p_\mathrm{e})|g\rangle \langle g|,$ then the initial atom–field state is $\rho _a \otimes |n\rangle \langle n| ,$ and the reduced field state at time t is

$$\begin{aligned} \rho _f (t)= & {} (1-p_\mathrm{e})\mathrm{sin}^2(\lambda t\sqrt{n})|n-1\rangle \langle n-1|\\+ & {} p_\mathrm{e}\mathrm{sin}^2(\lambda t\sqrt{n+1}) |n+1\rangle \langle n+1|\\+ & {} \left( p_\mathrm{e}\mathrm{cos}^2(\lambda t \sqrt{n+1})+(1-p_\mathrm{e})\mathrm{cos}^2 (\lambda t\sqrt{n})\right) |n\rangle \langle n|. \end{aligned}$$

C. Field initially in thermal states

Finally we consider the case when the field is initially in the thermal state

$$ \rho _f =\rho _{\bar{n}}=\sum _{n=0}^\infty \frac{1}{1+\bar{n}}(\frac{\bar{n}}{1+\bar{n}})^{n}|n\rangle \langle n|.$$

For the initial atomic state, we also consider two cases:

(1) If the atom is initially in the pure state $|\psi _a\rangle =p|e\rangle +\sqrt{1-p^2} |g\rangle ,$ then the initial atom–field state is $|\psi _a\rangle \langle \psi _a|\otimes \rho _{\bar{n}},$ and by linear combination, the reduced field state at time t is

$$\begin{aligned} \rho _f (t)= & {} \sum _{n=0}^\infty \frac{1}{1+\bar{n}}(\frac{\bar{n}}{1+\bar{n}})^{n} \left[ \left( (1-p)\cos ^2(\lambda t\sqrt{n})\right. \right. \\&+\left. p\cos ^2(\lambda t\sqrt{n+1})\right) |n\rangle \langle n|\\&+p\sin ^2(\lambda t\sqrt{n+1})|n+1\rangle \langle n+1|\\&+(1-p)\sin ^2(\lambda t\sqrt{n})|n-1\rangle \langle n-1|\\&+i\sqrt{p(1-p)}\sin (\lambda t\sqrt{n+1})\cos (\lambda t\sqrt{n})|n\rangle \langle n+1|\\&-i\sqrt{p(1-p)}\sin (\lambda t\sqrt{n+1}) \cos (\lambda t\sqrt{n})|n+1\rangle \langle n|\\&+i\sqrt{p(1-p)}\cos (\lambda t\sqrt{n+1}) \sin (\lambda t\sqrt{n})|n\rangle \langle n-1|\\&-\left. ip\sqrt{1-p^2}\cos (\lambda t\sqrt{n+1}) \sin (\lambda t\sqrt{n})|n-1\rangle \langle n|\right] . \end{aligned}$$

(2) If the atom is initially in the mixed state $\rho _a=p_\mathrm{e}|e\rangle \langle e|+(1-p_\mathrm{e})|g\rangle \langle g|,$ then the initial atom–field state is $\rho _a \otimes \rho _{\bar{n}},$ and the reduced field state at time t is

$$\rho _f (t)=\sum _{n=0}^{\infty }c_n(t)|n\rangle \langle n|$$

with

$$\begin{aligned} c_n(t)= & {} \frac{{\bar{n}}^n}{(\bar{n}+1)^{n+1}}(p_\mathrm{e}u_n(t)+(1-p_\mathrm{e})v_n(t)) \end{aligned}$$

where

$$\begin{aligned} u_n(t)= & {} \mathrm{cos}^2(\lambda t\sqrt{n+1})+\frac{\bar{n}+1}{\bar{n}}\mathrm{sin}^2(\lambda t\sqrt{n}), \\ v_n(t)= & {} \mathrm{cos}^2(\lambda t\sqrt{n})+\frac{\bar{n}}{\bar{n}+1}\mathrm{sin}^2(\lambda t\sqrt{n+1}). \end{aligned}$$

D. Field initially in vacuum states

This is actually included in the above cases.