1 Introduction

As is well known, superposition of quantum states is recognized as one of the most fundamental features that mark the departure of quantum mechanics from the classical one [1]. In theory, QC arising from the superposition principle constitutes a powerful resource for quantum metrology [2, 3] and entanglement creation [4]. It is also at the root of fulfilling wide-ranging quantum information processing tasks, such as quantum optics [5, 6], quantum thermodynamics [7, 8], quantum information [9] and solid-state physics [10]. Recently, Baumgratz et al. [11] introduced a rigorous resource-theoretic framework for quantifying the QC. Based on it, they proposed two bona fide measures, i.e., \( l_{ 1} \) norm of coherence and relative entropy of coherence. Afterward, researches on the presence and functional roles of QC in various systems have attracted considerable interest [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. For example, Streltsov et al. [12] demonstrated that all measures of entanglement can be artfully used to define a family of valid measures for quantifying QC. Shao et al. [13] proved that the trace norm of coherence is a promising candidate for coherence monotone, while fidelity does not satisfy the monotonicity requirement as a measure of QC.

In the realistic quantum system, a long-standing and significant issue concerning quantum dynamics is the decoherence induced by the inevitable interaction between the quantum system and environment, so the quantum system is rarely isolated and should be regarded as open [31,32,33,34,35]. Based on Pollock’s theorem [36] that whether the future processes implemented on quantum system depend on the past controls, that is, whether these processes involve memory effects, one can divide the open dynamical process into two categories, i.e., Markovian and non-Markovian dynamical regimes [37, 38]. Moreover, coherence is an intrinsically fragile property which typically vanishes at macroscopic scales of space, time and temperature: the disappearance of coherence in quantum systems exposed to environmental noise is one of the major hindrances still threatening the scalability of most quantum machines. Therefore, it is extremely intriguing and important to probe the dynamical behaviors of QC when quantum system is coupled with environment [29, 30]. Yadin et al. [29] introduced QC as the speed of evolution of a system under decoherence and proven that coherence is the ability to estimate a dephasing channel, quantified by the quantum Fisher information. Despite all this, it recently has been found that the QC in open system can be frozen, and the conditions of sustaining long-lived QC were investigated [39,40,41,42,43,44]. Especially, Zhang [39] derived a criterion under which QC of two comoving atoms on a stationary trajectory is frozen to a nonzero value. Bromley et al. [40] found the freezing conditions in which the coherence remains unchanged during the entire evolution, whose prediction has been confirmed in a recent nuclear magnetic resonant experiment [44]. Naturally, a challenge for the study of QC is to explore the underlying mechanisms of interactions between the dynamics behaviors and environment.

Inspired by these works, we aim to investigate the open dynamics of QC from the geometric and entropic perspectives, respectively. When the Bell-diagonal state is coupled with Markovian channels, we analytically derive some dynamical conditions under which QC can be frozen and maintains in a nonzero value. The results indicate that the \( l_{ 1} \) norm of coherence exhibits freezing phenomena, whereas the relative entropy of coherence remains as a monotonically decreasing function of time. In this sense, the \( l_{1} \) norm of coherence is more robust against the decoherence than the relative entropy of coherence. In parallel, we demonstrate the damped revivals and oscillations of QC in the non-Markovian evolutions, which is contributed by memory effects involved in quantum processes. Moreover, we presented that the reservoir degree plays a positive role in these revivals, as it increasing the revival peak of coherence gradually increases, whereas it also prolongs the critical moment at when QC revealing. To address the physical mechanisms behind these dynamical behaviors of QC, we introduce the mixedness based on the normalized linear entropy which is an intuitive parameter to understand decoherence [45]. From the perspective of resource theory of purity, the mixedness can be obtained as a complementary quantity to global information [46, 47]. Our analysis shows that when quantum state is interacted with environment the degree of mixedness always is increased, while the state can hold on a fixed QC. Compared with the results given by Zhang who using system evolution to study coherent freezing conditions [39], we provide another way to explain the freezing QC from the perspective of entropy. In a word, progresses on this fundamental question lead to a more efficient exploitation of coherence to empower the performance of real-world quantum technology.

This paper is structured as follows. In Sect. 2, we firstly discuss the theory of QC from resource theory perspective and introduce two quantifiers, i.e., \( l_{ 1} \) norm of coherence and relative entropy of coherence. In Sect. 3, we investigate the dynamic behaviors of QC when Bell-diagonal state is coupled with Markovian and non-Markovian channels, respectively. We then analytically address the mechanisms behind these dynamical behaviors based on the trade-off relation between QC and mixedness in Sect. 4. Finally, conclusions are presented in Sect. 5.

2 Measures of quantifying QC

QC as a direct consequence of the quantum mechanical superposition principle is conventionally associated with the capability of a quantum state to exhibit interference phenomena. It is usually attributed to the size of the nonzero off-diagonal elements of density matrix with respect to a specific reference basis, whose choice is dictated by the physical scenario under consideration. Here, for a 2-qubit system in Hilbert space \( {\mathbb{C}}^{{2^{N} }} \), we fix the computational basis \( \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\}^{ \otimes 2} \) as the reference basis.

In the context of quantum information, coherence can be rigorously characterized in the context of quantum resource theory. Recently, Baumgratz et al. [11] formulated a set of physical requirements which should be satisfied by any valid measure of QC labeled by \( C \), which are as follows:

  1. A.

    A. \( C\left( \ell \right) = 0 \) for any incoherent state \( \ell \);

  2. B.

    Monotonicity under incoherent completely positive and trace-preserving (ICPTP) maps (\( \varLambda_{ICPTP} \)), \( C\left( {\varLambda_{ICPTP} \left( \rho \right)} \right) \le C\left( \rho \right) \);

  3. C.

    Monotonicity under selective measurements on average, \( C\left( \rho \right) \ge \sum\limits_{n} {p_{n} C\left( {\rho_{n} } \right)} \), where \( \rho_{n} = {{\left( {K_{n} \rho K_{n}^{\dag } } \right)} \mathord{\left/ {\vphantom {{\left( {K_{n} \rho K_{n}^{\dag } } \right)} {p_{n} }}} \right. \kern-0pt} {p_{n} }} \) and \( p_{n} = Tr\left( {K_{n} \rho K_{n}^{\dag } } \right) \), for any set of Kraus operators \( \left\{ {K_{n} } \right\} \) satisfying \( \sum\limits_{n} {K_{n} K_{n}^{\dag } } = I \) and \( K_{n} \ell K_{n}^{\dag } \in \ell \) for each \( n \);

  4. D.

    Convexity, \( C\left( {p\rho_{1} + \left( {1 - p} \right)\rho_{2} } \right) \le pC\left( {\rho_{1} } \right) + \left( {1 - p} \right)C\left( {\rho_{2} } \right) \) for any states \( \rho_{1} \) and \( \rho_{2} \) and \( p \in \left[ {0,1} \right] \).

Based on abovementioned criteria, two different types quantifier of coherence are introduced. The \( l_{ 1} \) norm of coherence is defined as

$$ C_{{l_{ 1} }} \left( \rho \right) = \sum\limits_{i,j,i \ne j} {\left| {\rho_{ij} } \right|} , $$
(1)

which is equal to a summation over the absolute values of all the off-diagonal elements \( \rho_{ij} \) of a given density matrix \( \rho \). Moreover, by virtue of the von Neumann entropy \( S\left( \rho \right) = - tr\left( {\rho \log \rho } \right) \), the relative entropy of coherence is formed as

$$ C_{\text{RE}} \left( \rho \right) = S\left( {\rho_{\text{diag}} } \right) - S\left( \rho \right), $$
(2)

where \( \rho_{\text{diag}} \) denotes the diagonal state obtained from state \( \rho \) by deleting all the off-diagonal elements. Methodologically, the \( l_{1} \) norm of coherence is an geometric measure, which can intuitively characterize the coherence by quantifying the minimal distance between quantum state and its nearest incoherent state, while the relative entropy of coherence is an entropic measure and has a clear physical interpretation, which equals the optimal rate of the distilled maximally coherent states by incoherent operations in the asymptotic limit of many copies of \( \rho \). On the other hand, when the initial state is either incoherent or maximally coherent, they can get same quantity [27, 30].

3 Dynamic behaviors of QC in decoherent reservoirs

Upon above definitions, we proceed by discussing the dynamic behaviors of QC when a two-qubit state is coupled with decoherent reservoirs. To this aim, we focus on the Bell-diagonal state because of its analytical simplicity in calculation and crucial roles in quantum tasks. In the Bloch representation, the initial state is expressed as [48]

$$ \rho^{AB} \left( 0 \right) = \frac{1}{4}\left[ {I^{A} \otimes I^{B} + \sum\nolimits_{i = 1}^{3} {c_{i} \left( 0 \right)\left( {\sigma_{i}^{A} \otimes \sigma_{i}^{B} } \right)} } \right], $$
(3)

which is identified by vector \( \vec{c}_{i} \left( 0 \right) = \left\{ {c_{1} \left( 0 \right),c_{2} \left( 0 \right),c_{3} \left( 0 \right)} \right\} \). Here, \( I^{A\left( B \right)} \) is the identity operator, and \( \left\{ {\sigma_{i = 1,2,3}^{A\left( B \right)} } \right\} \) denote the Pauli matrices. Following, we will consider two dynamic cases in which the initial state \( \rho^{AB} \left( 0 \right) \) is coupled with Markovian and non-Markovian reservoirs, respectively.

To delineate the state-reservoir dynamics, we use the operator-sum representation formalism to characterize the interaction. Based on the completely trace-preserving quantum operation \( \varepsilon \left( \cdot \right) \) in terms of Kraus operators, the reduced time-evolved system state is [34]

$$ \varepsilon \left( {\rho^{AB} } \right) = \sum\limits_{i,j} {\left( {K_{i}^{A} \otimes K_{j}^{B} } \right)\rho^{AB} \left( 0 \right)\left( {K_{i}^{A} \otimes K_{j}^{B} } \right)^{\dag } } , $$
(4)

where \( K_{i}^{A} \) and \( K_{j}^{B} \) are the Kraus operators associated with decoherent processes of subspaces \( A \) and \( B \), which satisfy the trace-preserving condition \( \sum\limits_{i,j} {K_{i,j}^{\dag } K_{i,j} } = I \).

3.1 Markovian reservoir

Some well-known channels such as bit flip and bit-phase flip channels are important for decoherent mechanisms in qubit system, and they are also the typical Markovian reservoirs. In the computational basis \( \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \), their Kraus operators are

$$ {\text{Bit}}\;{\text{flip}}\;{\text{channel:}}K_{0} = \sqrt {1 - {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}} I,\quad K_{1} = \sqrt {{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}} \sigma_{1} , $$
(5)
$$ {\text{Bit-phase}}\;{\text{flip}}\;{\text{channel:}}K_{0} = \sqrt {1 - {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}} I,\quad K_{1} = \sqrt {{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}} \sigma_{2} . $$
(6)

These Kraus operators acting on qubit are interpreted as probability \( 1 - {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2} \) of qubit remaining in the same, and probability \( {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2} \) of having an error.

Through the calculation, we show that both decoherent processes given in Eqs. (5) and (6) can fully preserve the Bell-diagonal form of the time-evolved state \( \varepsilon \left( {\rho^{AB} } \right) \). Under this constraint, the state \( \varepsilon \left( {\rho^{AB} } \right) \) is completely identified by the time-dependent vector \( \vec{c}_{i} \left( t \right) = \left\{ {c_{1} \left( t \right),c_{2} \left( t \right),c_{3} \left( t \right)} \right\} \), whose concrete expressions are

$$ {\text{Bit}}\;{\text{flip}}\;{\text{channel}}:\vec{c}_{i} \left( t \right) = \left\{ {c_{1} \left( 0 \right),c_{2} \left( 0 \right)\left( {1 - p} \right)^{2} ,\;c_{3} \left( 0 \right)\left( {1 - p} \right)^{2} } \right\}, $$
(7)
$$ {\text{Bit-phase}}\;{\text{flip}}\;{\text{channel}}:\vec{c}_{i} \left( t \right) = \left\{ {c_{1} \left( 0 \right)\left( {1 - p} \right)^{2} ,\;c_{2} \left( 0 \right),\;c_{3} \left( 0 \right)\left( {1 - p} \right)^{2} } \right\}. $$
(8)

From these time-dependent vectors, we clearly suggest that different initial conditions \( \vec{c}_{i} \left( 0 \right) \) lead to various dynamics of QC independently of the measure used to quantify coherence.

According to the definitions, the \( l_{1} \) norm of coherence for the time-evolved state \( \varepsilon \left( {\rho^{AB} } \right) \) is analytically derived as

$$ C_{{l_{1} }} \left( {\varepsilon \left( {\rho^{AB} } \right)} \right) = \frac{1}{2}\left( {\left| {c_{1} \left( t \right) - c_{2} \left( t \right)} \right| + \left| {c_{1} \left( t \right) + c_{2} \left( t \right)} \right|} \right) $$
(9)

and the relative entropy of coherence is

$$ C_{RE} \left( {\varepsilon \left( {\rho^{AB} } \right)} \right) = \sum\limits_{i = 1}^{4} {\lambda^{\prime}_{i} } \log_{2} \lambda^{\prime}_{i} - \frac{{1 \pm c_{3} \left( t \right)}}{2}\log_{2} \left( {1 \pm c_{3} \left( t \right)} \right) + 2 $$
(10)

with nonzero eigenvalues \( \lambda^{\prime}_{i} \left( {i = 1,2,3,4} \right) \) of state \( \varepsilon \left( {\rho^{AB} } \right) \).

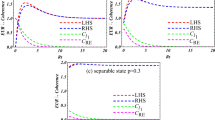
We take the case of the initial state interacted with bit flip channel as an illustration, which is mainly based on a fact that the results obtained in bit-phase flip channel are in good agreement with that behaved in the bit flip channel. In Fig. 1, we plot the variation of \( l_{1} \) norm of coherence and relative entropy of coherence under different initial correlation functions \( \vec{c}_{i} \left( 0 \right) \) as functions of the noise parameter \( p \). It is evident that both of them monotonously degrade at the beginning of the growth of parameter \( p \), meaning that the environment’s action of continuously affecting the system gradually causes a loss of information and therefore resulting in a decrease in QC. Afterward, the \( l_{1} \) norm of coherence is frozen when the noise intensity expands to the finite intensity, i.e., it becomes more robust as the noise increases. At the same time, the value of these inflection points at which QC become frozen are determined by the formulations of initial correlation function \( \vec{c}_{i} \left( 0 \right) \). On the contrary, the relative entropy of coherence remains as a monotonically decreasing function of time. In this sense, the \( l_{1} \) norm of coherence is more robust against the decoherent reservoir than the relative entropy of coherence.

Fig. 1
figure 1

Quantum coherence within bit flip channel as functions of the noise parameter \( p \). The initial state parameters are fixed as a \( \left| {c_{1} } \right| = {{\left| {c_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} } \right|} 2}} \right. \kern-0pt} 2} \), \( c_{2} = c_{3} \), b \( \left| {c_{1} } \right| = {{\left| {c_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} } \right|} 2}} \right. \kern-0pt} 2} \), \( c_{2} = - c_{3} \), c \( \left| {c_{1} } \right| = {{\left| {c_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} } \right|} 4}} \right. \kern-0pt} 4} \), \( c_{2} = c_{3} \) and d \( \left| {c_{1} } \right| = {{\left| {c_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} } \right|} 4}} \right. \kern-0pt} 4} \),\( c_{2} = - c_{3} \), respectively (Color online)

Full size image

In what follows, we aim to derive the dynamical conditions under which the QC is frozen. To do so, we differentiate the coherence with respect to the noise parameter \( p \), namely \( \partial_{p} C \), and then solve the equation of the differential which is equaled to zero. In this circumstances, the coherence will be unaffected during the evolution. Taking the \( p \) derivative of the \( l_{1} \) norm of coherence, we derive the dynamical conditions as shown in following inequation. For the bit flip channel, the conditions are

$$ \left| {c_{1} \left( 0 \right)} \right| < \left| {c_{2} \left( 0 \right)} \right|\quad{\text{with}}\;p > 1 - \sqrt {{{\left| {c_{1} \left( 0 \right)} \right|} \mathord{\left/ {\vphantom {{\left| {c_{1} \left( 0 \right)} \right|} {\left| {c_{2} \left( 0 \right)} \right|}}} \right. \kern-0pt} {\left| {c_{2} \left( 0 \right)} \right|}}}. $$
(11)

Similarly, for the bit-phase flip channel, they are

$$ \left| {c_{1} \left( 0 \right)} \right| > \left| {c_{2} \left( 0 \right)} \right|\quad {\text{with}}\; p > 1 - \sqrt {{{\left| {c_{2} \left( 0 \right)} \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} \left( 0 \right)} \right|} {\left| {c_{1} \left( 0 \right)} \right|}}} \right. \kern-0pt} {\left| {c_{1} \left( 0 \right)} \right|}}} . $$
(12)

These findings may provide some guidance in the preparation of robust quantum resource states for the practical quantum tasks.

3.2 Non-Markovian reservoir

We start by developing the single qubit non-Markovian dissipative dynamics, which is modeled by the Hamiltonian [37]

$$ H = \omega_{0} \sigma_{ + } \sigma_{ - } + \sum\limits_{k} {\omega_{k} b_{k}^{\dag } b_{k} } + \left( {\sigma_{ + } B + \sigma_{ - } B^{\dag } } \right), $$
(13)

where \( B = \sum\nolimits_{k} {g_{k} b_{k} } \) with \( g_{k} \) being coupling constant, \( \sigma_{ \pm } \) are the raising and lowering operators of qubit with a transition frequency \( \omega_{0} \). Moreover, the index \( k \) labels the field modes of reservoir with frequency \( \omega_{k} \), and \( b_{k}^{\dag } \left( {b_{k} } \right) \) is the creation (annihilation) operators. Particularly, Ref. [37] declared that the Hamiltonian given in Eq. (13) describes various systems such as a qubit formed by one exciton in a potential well reservoir that represents a quantum well. This reservoir is represented by a bath of harmonic oscillators, and the effective spectral density is [49]

$$ J\left( \omega \right) = \frac{1}{2\pi }\frac{{\gamma_{0} \lambda^{2} }}{{\left( {\omega_{0} - \omega } \right)^{2} + \lambda^{2} }}, $$
(14)

where \( \gamma_{0} \) is the system–reservoir coupling constant which is related to the decay rate of the system, and link with the inverse of the system relaxation time \( \tau_{R} \approx {1 \mathord{\left/ {\vphantom {1 {\gamma_{0} }}} \right. \kern-0pt} {\gamma_{0} }} \). \( \lambda \) is the spectral width of distribution, which is in turn the inverse of the reservoir correlation time \( \tau_{B} \approx {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda } \). We define the reservoir degree \( R = {{\gamma_{0} } \mathord{\left/ {\vphantom {{\gamma_{0} } \lambda }} \right. \kern-0pt} \lambda } \) in order to distinguish the strong coupling regime from the weak coupling regime. Strong coupling \( R > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2} \) corresponds to the non-Markovian regime and weak coupling \( R < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2} \) Markovian regime. Besides, the magnitude of reservoir degree can use to characterize the memory effects of environment. They are consistent, i.e., the lager reservoir degree the stronger memory effects. In the remainder of this work, we focus on the non-Markovian regime.

Based on the computational basis \( \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\} \), the dynamical map for single qubit interacted with the non-Markovian reservoir can be described by the reduced density matrix [37]

$$ \rho \left( t \right) = \left( {\begin{array}{*{20}c} {\rho_{00} \left( 0 \right)P_{t} } & {\rho_{01} \left( 0 \right)\sqrt {P_{t} } } \\ {\rho_{10} \left( 0 \right)\sqrt {P_{t} } } & {\rho_{11} \left( 0 \right) + \rho_{00} \left( 0 \right)\left( {1 - P_{t} } \right)} \\ \end{array} } \right), $$
(15)

where \( P_{t} \) is an oscillation term describing the decay of qubit’ excited state. It is induced by the interaction between the qubit system and the reservoir. For the effective spectral density \( J\left( \omega \right) \) as shown in Eq. (14), the oscillation term \( P_{t} \) is given by

$$ P_{t} = e^{ - \lambda t} \left[ {\cos \left( {\frac{dt}{2}} \right) + \frac{\lambda }{d}\sin \left( {\frac{dt}{2}} \right)} \right]^{2} $$
(16)

with \( d = \sqrt {2\gamma_{0} \lambda - \lambda^{2} } \). It will lead to a nonmonotonic dynamics behavior of the qubit system when the term \( P_{t} \) starts to oscillate. Then, using the reduced density matrix \( \rho \left( t \right) \) for the single qubit, we able to construct the reduced density matrix \( \rho^{AB} \left( t \right) \) of the two-qubit Bell-diagonal state interacted with non-Markovian reservoir. For the sake of simplicity, we here do not list its explicit form which has been detailed by Bellomo [37]. According to the definition, one can easier to obtain the explicit expression of \( l_{1} \) norm of coherence based on its calculable, which is

$$ C_{{l_{1} }} \left( {\rho^{AB} \left( t \right)} \right) = \frac{1}{2}\left[ {\left| {c_{1} \left( 0\right) - c_{2} \left( 0\right)} \right| + \left| {c_{1} \left( 0\right) + c_{2} \left( 0\right)} \right|} \right]\zeta \left( R \right) $$
(17)

\( {\text{with}}\;{\text{function}}\;\zeta \left( R \right) = e^{{ - \frac{{\gamma_{0} t}}{R}}} \left[ {\cos \left( {\frac{{\gamma_{0} t}}{2R}\sqrt {2R - 1} } \right) + \frac{1}{{\sqrt {2R - 1} }}\sin \left( {\frac{{\gamma_{0} t}}{2R}\sqrt {2R - 1} } \right)} \right]^{2} \).

In Fig. 2, we first display the dynamic behaviors of QC versus the scaled time \( \gamma_{0} t \) when different initial states are interacted with a specific environment with reservoir degree \( R = 10 \). One can clearly observe that both two QCs exhibit damped oscillations and suffer damped revivals during the evolution. This non-monotonicity appears in this non-Markovian reservoir because of the presence of memory effects involved in environment which can cause the back-flow of information from environment to system. In the asymptotic limitation of evolution, both two QCs eventually evolve to a stable value at last.

Fig. 2
figure 2

Quantum coherence within non-Markovian reservoir (reservoir degree is taken as \( R = 10 \)) as functions of the scaled time \( \gamma_{0} t \). The initial state parameters are fixed to same as what chosen in Fig. 1 (Color online)

Full size image

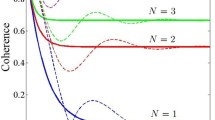
As a supplement, we explore the effects of reservoir degree \( R \) on the QC of a specific initial state (specified by the initial state parameters satisfying \( 2c_{1} = c_{ 2} { = }c_{ 3} \)) interacted with non-Markovian reservoir. In Fig. 3, we plot the dynamic behaviors verse the scaled time \( \gamma_{0} t \), which clearly suggests that the reservoir degree plays a positive role in the QC revivals. As the reservoir degree increasing, the revival peak gradually increases, meaning that the memory effects are enhanced and more information flow back from the environment to system. At the same time, the critical moment at which QC revealing is prolonged.

Fig. 3
figure 3

Quantum coherence as functions of the scaled time \( \gamma_{0} t \) when a specific initial state (\( 2c_{1} = c_{ 2} { = }c_{ 3} \)) coupled with the different degree non-Markovian reservoirs: the degrees are taken as a \( R = 2 \); b \( R = 5 \), c \( R = 10 \) and d \( R = 20 \) (Color online)

Full size image

4 Mechanisms underlying these dynamic phenomena of QC

To get a better understanding about the freezing and revivals of QC in the open systems, we will address the underlying physical mechanisms from the perspective of system entropy. From literatures [45,46,47], we find that coherence and mixedness of system always satisfy a dynamical trade-off relation, which derive the limits imposed by mixedness on the amount of coherence. In Ref. [47], the trade-off relation, for any arbitrary quantum system \( \rho \) in \( d \) dimensions, between coherence, as quantified by \( l_{1} \) norm, and mixedness in terms of the normalized linear entropy is

$$ \varOmega \left( \rho \right) = \frac{{C_{{l_{1} }}^{2} \left( \rho \right)}}{{\left( {d - 1} \right)^{2} }} + M_{l} \left( \rho \right) \le 1, $$
(18)

where \( M_{l} \left( \rho \right) = \frac{d}{d - 1}\left( {1 - Tr\rho^{2} } \right) \).

By approaching this dynamical relation, we try to give a physical representation about the freezing behaviors of QC. Taking the bit flip channel as an example, the mixedness of the time-evolved system is

$$ M_{l} \left( \rho \right) = 1 - \frac{1}{3}\left( {c_{1} \left( t \right)^{2} + c_{2} \left( t \right)^{2} + c_{3} \left( t \right)^{2} } \right). $$
(19)

To attain a better quantitative understanding of these freezing behaviors, we will study the derivatives of three quantities \( \frac{{{\text{d}}C_{{l_{1} }} \left( \rho \right)}}{{{\text{d}}p}} \), \( \frac{{{\text{d}}M_{l} \left( \rho \right)}}{{{\text{d}}p}} \) and \( \frac{{{\text{d}}\varOmega \left( \rho \right)}}{{{\text{d}}p}} \). Particularly, there are two consecutive time-intervals, namely \( T^{\left( 1 \right)} = \left[ {0,p^{*} } \right] \) and \( T^{\left( 2 \right)} = \left[ {p^{*} ,1} \right] \) with \( p^{*} \) being the critical time when the QC be frozen. In the time-interval \( T^{\left( 1 \right)} \), \( \frac{{{\text{d}}C_{l1} \left( \rho \right)}}{{{\text{d}}p}} = - 2\left| {c_{2} \left( 0 \right)} \right|\left( {1 - p} \right), \) and \( \frac{{{\text{d}}M_{l} \left( \rho \right)}}{{{\text{d}}p}} = \frac{2}{3}\left( {\left| {c_{2} \left( 0 \right)} \right| + \left| {c_{3} \left( 0 \right)} \right|} \right)\left( {1 - p} \right) \). During the second time-interval \( T^{\left( 2 \right)} \), \( \frac{{{\text{d}}C_{{l_{1} }} \left( \rho \right)}}{{{\text{d}}p}} = 0 \). To sum up, the results are

$$ \frac{{{\text{d}}\varOmega \left( \rho \right)}}{{{\text{d}}p}} = \left\{ {_{{\frac{2}{3}\left( {\left| {c_{2} \left( 0 \right)} \right| + \left| {c_{3} \left( 0 \right)} \right|} \right)\left( {1 - p} \right) ,\qquad\qquad\quad {\text{ p}} \in \left[ {1 - \sqrt {{{\left| {c_{1} \left( 0 \right)} \right|} \mathord{\left/ {\vphantom {{\left| {c_{1} \left( 0 \right)} \right|} {\left| {c_{2} \left( 0 \right)} \right|}}} \right. \kern-0pt} {\left| {c_{2} \left( 0 \right)} \right|}}} ,1} \right]}}^{{ - \frac{{4\left| {c_{2} \left( 0 \right)} \right|^{2} }}{9}\left( {1 - p} \right)^{3} + \frac{2}{3}\left( {\left| {c_{2} \left( 0 \right)} \right| + \left| {c_{3} \left( 0 \right)} \right|} \right)\left( {1 - p} \right),{\text{ p}} \in \left[ {0,1 - \sqrt {{{\left| {c_{1} \left( 0 \right)} \right|} \mathord{\left/ {\vphantom {{\left| {c_{1} \left( 0 \right)} \right|} {\left| {c_{2} \left( 0 \right)} \right|}}} \right. \kern-0pt} {\left| {c_{2} \left( 0 \right)} \right|}}} } \right]}} } \right.. $$
(20)

Therefore, QC can be frozen under environment when the initial state evolves during the second time-interval \( T^{\left( 2 \right)} \). At the same time, we illustrate the dynamic behaviors of \( \varOmega \left( \rho \right) \) and \( M_{l} \left( \rho \right) \) as a function of the noise parameter \( p \) in Fig. 4. It is shown that they first evolve in different trajectories, while always evolve parallel each other after the critical time \( p^{ * } \).

Fig. 4
figure 4

The dynamical behaviors of \( M_{l} \left( \rho \right) \) and \( \varOmega \left( \rho \right) \) versus parameter \( p \). Here, taking bit flip channel as example and the initial state is fixed at \( \left| {c_{1} } \right| = {{\left| {c_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {c_{2} } \right|} 2}} \right. \kern-0pt} 2} \), \( c_{2} = c_{3} \) (Color online)

Full size image

5 Conclusion

In conclusion, we have investigated the dynamic behaviors of QC witnessed by \( l_{1} \) norm of coherence and relative entropy of coherence when the Bell-diagonal state is coupled with Markovian and non-Markovian reservoirs, respectively. The results showed that the QC exists dynamical freezing and revival phenomena during their decoherent evolutions. Concretely, in the Markovian regime, we determined exact conditions such that the \( l_{1} \) norm of coherence is dynamically frozen when the qubits initialized in a particular class of states and undergone local dissipative flip channels. By contrast, the relative entropy of coherence remains as a monotonically decreasing function of time. In this sense, the \( l_{1} \) norm of coherence is more robust against the decoherent reservoir than the relative entropy of coherence. In the non-Markovian regime, both coherences exhibit damped oscillations and suffer damped revivals at critical time due to the memory effects involved in environment which can induce the back-flow of information from the environment to the quantum system. Moreover, we presented a detailed investigation of reservoir degree on the dynamics of QC and suggested that the reservoir degree plays a positive role in these revivals, as the reservoir degree increasing the revival peak gradually increases, whereas it prolongs the critical moment at when QC revealing. At last, we probed the physical mechanism underlying the freezing behaviors based on the trade-off relation between QC and mixedness. The degree of mixedness of system always increases, while quantum state can hold on a fixed coherence for finite evolution time. The results presented in our work show that the features of system–environment coupling can be utilized for the purpose of preserving coherence or invoking coherence back into the system. It also may provide impetus and alternative directions to study the effect of noise on quantum resources.