Quantum-Memory-Assisted Entropic Uncertainty Relation and Quantum Coherence in Structured Reservoir

Abstract

The uncertainty principle is regarded as one of basics in quantum mechanics, which sets up a strict lower bound to quantify the prediction on the outcome concerning a set of incompatible measurements. In this paper, we investigate the dynamic behaviors of quantum-memory-assisted entropic uncertainty relation (EUR), and quantum coherence in structured reservoir. The results shown that the EUR is smallest in the vanishing limit of noise regardless of the forms of the initial sate we considered, while the coherence keeps the maximal value. During the time-evolution process, the uncertainty bound is lifted and the coherence damps monotonously. Subsequently, the EUR converges to an asymptotic nonzero constant in the long-time limit, yet the coherence asymptotically decays to zero. Moreover, the initial state purity plays a deterministic role in the initial amounts of EUR and coherence, i.e. the larger purity the less EUR and larger coherence. As an application, we employ the EUR to witness the coherence, and prove that the corresponding witnessing efficiencies are only depended on the version of coherence, while are insensitive to the reservoir.

1 Introduction

Uncertainty principle, originally observed by Heisenberg [1], is one of the fundamental concepts in quantum theory, which able to clearly illustrate the divergence between the classical mechanics and quantum one [2, 3]. It sets a limit on the precise prediction of the outcomes concerning a set of incompatible quantum measurements. The first uncertainty relation was formulated for the case of position and momentum. Further, Robertson [4] and Schrödinger [5] generalized the uncertainty relation for an arbitrary pair of incompatible observables R and S. Based on the standard deviations, the Robertson uncertainty relation is formed as: $\varDelta R\cdot \varDelta S\ge \frac{1}{2}\left|\left\langle \left[R,S\right]\right\rangle \right|$. However, this Robertson uncertainty bound is state dependent and also trivial for finite-valued observables [6]. Hence, it is important to find an appropriate criterion to quantify the uncertainty relation.

In recent years, researchers have recast with the EUR because of its operational application for privacy issues in future quantum information processing tasks [7,8,9,10,11,12,13,14,15,16,17,18]. The original version was conjectured and put forth by Kraus [11], and then proved by Maassen and Uffink [12], which reads as

$$ H(R)+H(S)\ge 2{\log}_2\frac{1}{c}:\equiv {q}_{UM}, $$

(1)

where H(R) is the Shannon entropy of probability distribution of the outcomes when R is measured, and likewise for H(S). The term c ≡ max_{r, s}|〈ψ_r| φ_s〉| is the complementarity between observables R and S with |ψ_r〉 and |φ_s〉 being their eigenvectors, respectively. The relation (1) bounds the uncertainty in the case that there is no quantum memory, i.e. the observer can only access the classical information. If there is quantum entanglement, the bound q_UM may be violated. In this case, the quantum-memory-assisted entropic uncertainty principle was conjectured by Renes [13], and then strictly derived by Berta [14]. Mathematically, the quantum-memory-assisted EUR is

$$ S\left(R|B\right)+S\left(S|B\right)\ge 2{\log}_2\frac{1}{c}+S\left(A|B\right):\equiv {q}_B. $$

(2)

On the left-hand side (LHS) of eq. (2), S(X| B) is the conditional von Neumann entropy of the post-measurement state ${\rho}_{XB}=\sum \limits_r\left(\left|{\psi}_r\right\rangle \left\langle {\psi}_r\right|\otimes I\right){\rho}_{AB}\left(\left|{\psi}_r\right\rangle \left\langle {\psi}_r\right|\otimes I\right)$ after that subsystem A is measured by operators X with X ∈ (R, S), herein, {|ψ_r〉} are the eigenstates of X, and I is an identity operator. Moreover, we will pay attention to the extra term S(A| B) on the right-hand side (RHS) of eq. (2). The reason is that it can be used to witness whether quantum entanglement exists between the particle and memory [19,20,21]. This witness is based on a fact that if $S\left(P|B\right)+S\left(S|B\right)<2{\log}_2\left(1/c\right)$, then S(A| B) < 0, and hence ρ_AB is entangled [22, 23]. In the remainder of our work, we take Pauli observables σ_x and σ_z as the incompatible quantum measurements.

Actually, quantum system is inevitably suffered from surrounding environment, which will exponentially dampen its quantum traits, such as quantum entanglement and quantum coherence [24,25,26]. Quantum coherence, arising from the quantum state superposition principle, is a fundamental concept of quantum theory. Similar to the quantum entanglement, it is also regarded as an important physical resource for the astonishing quantum tasks. Hence, we here investigate the dynamics of EUR and quantum coherence under structured reservoir [27,28,29,30,31]. The results show that when the initial state is the Bell pure sate, LHS = RHS = 0 satisfies the EUR in the vanishing limit of noise, and the coherence keeps the maximal value 1. Then, the uncertainty bound is lifted and LHS > RHS is satisfied in the finite time limit. In the long-time limit, the EUR converges to an asymptotic nonzero constant, while the coherence asymptotically decays to zero. As an application, we utilize the EUR to witness the coherence, and prove that the witnessing efficiencies are only determined by the version of coherence, while are insensitive to the structured reservoir.

The outline of this paper is as follows. In Sect. 2, we give the definitions of two quantum coherence measures, i.e. geometric coherence and entropic coherence. In Sect. 3, we investigate the dynamics of EUR and coherence in structured reservoir within Markovian regime and non-Markovian regime, respectively. The application of EUR on witnessing coherence is discussed in Sect. 4, and the conclusion is given in Sect. 5.

2 Quantum Coherence Measures

Coherence properties of a quantum state are usually attributed to the off-diagonal elements of its density matrix with respect to a selected reference basis. Mathematically, the reasonable coherence quantification can be defined by measuring the distance between quantum state and its nearest incoherent state. In this vein, Baumgratz [24] presented two bona fide measures of quantum coherence from the geometric and entropy viewpoints, respectively. For a quantum state ρ in the fixed reference basis ${\left\{\left|i\right\rangle \right\}}_{i=1}^d$, the geometric coherence, i.e. l₁ norm of coherence ${C}_{l_1}\left(\rho \right)$, is

$$ {C}_{l_1}\left(\rho \right)=\sum \limits_{i,j,i\ne j}\left|{\rho}_{i,j}\right|, $$

(3)

and the entropy coherence, i.e. relative entropy of coherence C_RE(ρ) is

$$ {C}_{RE}\left(\rho \right)=S\left({\rho}_{diag}\right)-S\left(\rho \right), $$

(4)

where S(ρ) =  − tr(ρ log ρ) is the von Neumann entropy, and ρ_diag is the diagonal state by deleting all off-diagonal elements from the state ρ.

3 The Dynamics of EUR and Quantum Coherence in Structured Reservoir

We consider a bipartite quantum state formed by two noninteracting qubits A and B with each one locally interacted with its own reservoir labeled as a and b. The physical model and interaction Hamiltonian of the qubit+reservoir composite system are detailed in the Appendix. Concretely, the reservoir is initially in the vacuum state ${\left|\overline{0}\overline{0}\right\rangle}_{ab}$, and the qubits are prepared in the extended Werner-like (EWL) state [30].

$$ {\rho}_{AB}(0)=\frac{1-p}{4}I+p\left|\phi \right\rangle \left\langle \phi \right|, $$

(5)

where I is the identical identity matrix, α and β are state parameters specifying the Bell-like state |ϕ〉 = α|00〉 + β|11〉 with |α|² + |β|² = 1, and p indicates the purity of EWL state. When p = 0, the EWL state becomes completely mixed, while it reduces to the Bell-like pure state when p = 1. Besides, the EWL state is separable when p ≤ 1/(4αβ + 1). For the sake of simplicity, the time-evolution of qubit+reservoir composite system and the explicit forms of density matrixes ρ_ABab(t) as well as ρ_AB(t) are also detailed in the Appendix.

3.1 Markovian Dynamics

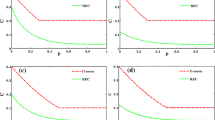
First, we focus on the dynamics of EUR and quantum coherence when the initial state is interacted with the Markovian reservoir Γ = 5R. We choose the state parameter as $\alpha =1/\sqrt{2}$, and plot their dynamic behaviors under different cases, i.e. Bell pure sate p = 1 in panel (a), mixed state p = 0.8 in panel (b), and separable state p = 0.3 in panel (c), as functions of dimensionless time Rt in Fig. 1.

Fig. 1

EUR and quantum coherence versus dimensionless time Rt within the Markovian regime Γ = 5R when the state parameter is $\alpha =1/\sqrt{2}$. Three types of initial state are explored, i.e. the Bell pure sate p = 1 in panel (a), the mixed state p = 0.8 in panel (b), and the separable state p = 0.3 in panel (c), respectively. The red dashing curve denotes LHS, blue dashing curve RHS, green dashing curve ${C}_{l_1}$, and purple dashing curve C_RE

When the initial state is prepared in the Bell pure sate (p = 1), we depict the dynamic behaviors of EUR and quantum coherence in Fig. 1(a). At the begin, LHS = RHS = 0 satisfy the EUR implying that the measuring outcomes can be accurately predicted. In the meantime, both quantum coherences keep their maximal values, ${C}_{l_1}={C}_{RE}=1$, meaning that two qubits A and B are initially entangled maximally. During the evolution process, the uncertainty bound is lifted and the inequality LHS > RHS is satisfied in the finite time limit. Soon afterwards, it converges to an asymptotic nonzero value in the long-time limit (Rt → ∞). However, both quantum coherences asymptotically decay to zero. In a word, when focusing on the qubit subsystem the variation of uncertainty is not fully synchronous with that of the quantum coherence. Physically, the intrinsic reasons behind this inconsistency can be presented as follows. If the qubit subsystem is interacted with the noisy environment, the information encoded in the qubit will flow into the reservoir, which inevitably increase the system mixedness [32,33,34]. At the same time, the enhancing mixedness do increase the uncertainty yet decrease the quantum coherence of the qubit system. When consider the mixed state (p = 0.8) and the separable state (p = 0.3), their dynamic behaviors are similar to the case of the Bell pure state. In addition, the state purity p plays a deterministic role in the initial values of EUR and coherence, i.e. the larger purity the less EUR and larger coherence. By the way, we verify that the geometric coherence is typically more robust against decoherence than the entropic version.

3.2 Non-Markovian Dynamics

In Fig. 2, we plot the dynamic behaviors of EUR and quantum coherence versus the dimensionless time Rt when the initial state ($\alpha =1/\sqrt{2}$) is coupled with the non-Markovian reservoir Γ = 0.1R. These figures are plotted with the same parameters as chosen in the Fig. 1. As shown in Fig. 2, the global evolution trends of both EUR and quantum coherence are coincide with that of in the Markovian regime. However, compared with thier Markovian dynamics the fundamental difference is that the non-Markovian dynamics exhibit quasi-periodic damped oscillations in finite time. From the physical viewpoint, these oscillation phenomena are induced by the memory effects of reservoir, which can induce the EUR and quantum coherence revival after a dark period time.

Fig. 2

EUR and quantum coherence versus the dimensionless time Rt under the non-Markovian regime Γ = 0.1R. These figures are plotted with the same parameters as chosen in the Fig. 1

4 Application: Quantum Coherence Witnessed by Uncertainty Relation

We continue by applying the EUR to witness the quantum coherence in structured reservoir. The theoretical basis is based on the fact that if $S\left(P|B\right)+S\left(S|B\right)<2{\log}_2\left(1/c\right)$, then S(A| B) < 0, and hence ρ_AB is entangled. Moreover, from the hierarchical relationship of entanglement and coherence, we know that entanglement is a sufficient condition for coherence. By illustrating the EUR and the quantum coherence of the Bell state ($\alpha =1/\sqrt{2}$ and p = 1) vs the dimensionless time Rt, we in Fig. 3 show the efficiencies of EUR on witnessing the geometric coherence and entropic coherence in the Markovian and non-Markovian reservoir, respectively. One can readily find that when Rt is smaller than a critical value Rt_c, no matter what versions of coherence can be witnessed by the EUR. Moreover, the witnessed regions of coherence do not explicitly depend on the reservoir, but the corresponding critical values Rt_c are different. As a consequence, we point out that the geometric coherence can be witnessed in region [0.8268, 1] and entropy coherence in [0.7753, 1], where the critical value Rt_c is of about 0.6977 in the Markovian limit and about 0.4589 in the non-Markovian limit. This means that, the coherence regions witnessed by the EUR are only determined by the version of coherence, while are regardless of the structured reservoir.

Fig. 3

Coherence witnessing by the EUR when the Bell state ($\alpha =1/\sqrt{2}$ and p = 1) is interacted with the Markovian regime Γ = 5R (left panel) and the non-Markovian regime Γ = 0.1R (right panel). The red, green, blue, cyan, and black lines from top to bottom represent the left-hand of EUR (2), the l₁ norm of coherence, the relative entropy of coherence, and the complementarity between two observers, respectively

5 Conclusion

In conclusion, we have investigated the dynamics of quantum-memory-assisted EUR, geometric coherence and entropic coherence in the structured reservoir. The physical model we focused on are consisting of two noninteracting qubits initially prepared in the EWL state and each locally coupling with its surrounding reservoir. Concretely, when the initial state is the Bell pure sate, the uncertainty satisfies LHS = RHS = 0 in the vanishing noise limit, and both coherences keep their maximal values, i.e. C_l1 = C_RE = 1. Subsequently, the uncertainty bound is lifted and the inequation LHS > RHS is satisfied in the finite time limit, and it converges to an asymptotic nonzero value in the long-time limit. However, both coherences asymptotically decay to zero with the growing dimensionless time. Moreover, the state purity plays a deterministic role in the initial values of EUR and coherence, i.e. the larger purity the less EUR and larger coherence. Furthermore, we have verified that the geometric coherence is typically more robust against decoherence than the entropic version. Compared with the Markovian dynamics, the non-Markovian dynamics exhibit quasi-periodic damped oscillations in the finite time. When the initial state is a mixed state or separable state, the dynamics evolutions of uncertainty and coherence are similar to that of the Bell pure state. In addition, we examined the efficiency of uncertainty relation on witnessing coherence. It turns out that if the dimensionless time is smaller than the critical Rt_c, both coherences can always be witnessed by the uncertainty relation no matter what regimes of the structured reservoir. As the quantum-memory-assisted EUR has been experimentally realized in decoherent environment, we expect that the results observed in this work may be certified in future experiments with currently available technologies.

Appendix

Here, we revisit the physical model with the interaction of single qubit+reservoir system and the global evolution of composite system. The physical model is that the single qubit is locally interacted with a multimode reservoir, and the corresponding Hamiltonian is (ℏ = 1) [27, 28].

$$ {H}_{Xx}={\omega}_0{\sigma}_{+}^X{\sigma}_{-}^X+\sum \limits_j{\omega}_j{x}_j^{\dagger }{x}_j+\sum \limits_j\left({g}_j{\sigma}_{+}^X{x}_j+{g}_j^{\ast }{\sigma}_{-}^X{x}_j^{\dagger}\right), $$

(6)

where g_j is coupling constant between the qubit and reservoir mode j, x^†(x) is the creation (annihilation) operator of the reservoir with frequency ω_j, ${\sigma}_{+}^X=\left|1\right\rangle \left\langle 0\right|$ and ${\sigma}_{-}^X=\left|0\right\rangle \left\langle 1\right|$ are the qubit rising operator and lowering operator acting on the Xth qubit with transition frequency ω₀ in the orthogonal computational basis {|0〉, |1〉}. The evolution of single qubit+reservoir subsystem depends on the choice of Lorentzian spectral density of the reservoir. To do it, the Lorentzian spectral distribution we taken is of the following form

$$ J\left(\omega \right)=\frac{R^2}{\pi}\frac{\varGamma }{{\left(\omega -{\omega}_c\right)}^2+{\varGamma}^2}. $$

(7)

The parameter R is connected to the qubit+cavity coupling strength and Γ denotes the half-width at half-maximum of the intracavity field spectrum profile. Moreover, their relative magnitudes determine the Markovian (Γ > 2R) and the non-Markovian (Γ < 2R) regimes, respectively.

In terms of the reservoir Hamiltonian (6) and Lorentzian spectral distribution (7), the interaction of single qubit+reservoir can be computationally formulated, which are

$$ {\left|0\right\rangle}_X{\left|\overline{0}\right\rangle}_x\to {\left|0\right\rangle}_X{\left|\overline{0}\right\rangle}_x, $$

(8)

$$ {\left|1\right\rangle}_X{\left|\overline{0}\right\rangle}_x\to \xi (t){\left|1\right\rangle}_X{\left|\overline{0}\right\rangle}_x+\sqrt{1-\xi {(t)}^2}{\left|0\right\rangle}_X{\left|\overline{1}\right\rangle}_x, $$

(9)

where $\xi (t)={e}^{-\varGamma t/2}\left[\cosh \left(\frac{dt}{2}\right)+\frac{\varGamma }{d}\sinh \left(\frac{dt}{2}\right)\right]$ with $d=\sqrt{\varGamma^2-4{R}^2}$. Here, we point out that form the independent qubit+reservoir system the analytical solutions of quantum states can be derived for arbitrary initial states.

When qubits A and B are initially prepared in the EWL state and reservoirs a and b are initially in the vacuum states ${\left|\overline{0}\overline{0}\right\rangle}_{ab}$, the initial density matrix of the total qubit+reservoir system thus reads

$$ {\rho}_{AB ab}(0)={\rho}_{AB}(0)\otimes {\left|\overline{0}\overline{0}\right\rangle}_{ab}\left\langle \overline{0}\overline{0}\right|, $$

(10)

which will evolve to

$$ {\rho}_{ABab}(t)=\frac{1-p}{16}{I}_{ABab}+p{\left|\phi (t)\right\rangle}_{ABab}\left\langle \phi (t)\right|, $$

(11)

with

$$ {\displaystyle \begin{array}{l}{\left|\phi (t)\right\rangle}_{ABab}=\alpha \left|00\overline{0}\overline{0}\right\rangle +\beta \left[{\left|{\xi}_0(t)\right|}^2\left|11\overline{0}\overline{0}\right\rangle +\left|{\xi}_0(t)\right|\left|{\xi}_1(t)\right|\left|10\overline{0}\overline{1}\right\rangle \right]\\ {}\kern3.75em +\beta \left[\left|{\xi}_0(t)\right|\left|{\xi}_1(t)\right|\left|01\overline{1}\overline{0}\right\rangle \left|11\overline{0}\overline{0}\right\rangle +{\left|{\xi}_1(t)\right|}^2\left|00\overline{1}\overline{1}\right\rangle \right]\end{array}} $$

(12)

where ξ₀(t) = ξ(t) and ${\xi}_1(t)=\sqrt{1-\xi {(t)}^2}$. By tracing over the reservoir freedom, we can obtain the reduced density matrix for the qubit subsystem ρ_AB(t), yielding

$$ {\displaystyle \begin{array}{l}{\rho}_{AB}(t)=\frac{1-p}{4}{I}_{AB}+p\left({\alpha}^2+{\beta}^2{\left|{\xi}_1(t)\right|}^4\right)\left|00\right\rangle \left\langle 00\right|\\ {}\kern2.5em +p{\beta}^2{\left|{\xi}_0(t)\right|}^2{\left|{\xi}_1(t)\right|}^2\left(\left|01\right\rangle \left\langle 01\right|+\left|10\right\rangle \left\langle 10\right|\right)\\ {}\kern2.5em +p{\beta}^2{\left|{\xi}_0(t)\right|}^4\left|11\right\rangle \left\langle 11\right|+ p\alpha \beta {\left|{\xi}_0(t)\right|}^2\left(\left|00\right\rangle \left\langle 11\right|+\left|11\right\rangle \left\langle 00\right|\right)\end{array}} $$

(13)