1 Introduction

Various quantum communication protocols, such as quantum key distribution(QKD) [1,2,3], measurement-device-independent QKD [4,5,6], controlled quantum teleportation [7,8,9,10,11,12], quantum secret sharing [13,14,15,16,17,18,19,20,21,22], controlled direct communication [23,24,25,26,27,28,29,30], remote state preparation [31,32,33], quantum private comparison [34], quantum steganography [35], and quantum key management [36] can be implemented on quantum networks [37,38,39,40,41,42,43,44,45,46]. All these protocols are based on an important assumption that a trusted third party is operating the quantum network. However, from the perspective of information security, a trusted third party does not exist, and there is a need for a quantum communication protocol that takes this into consideration. Furthermore, another topic of interest in the field of information security is the security of cloud services; thus, cloud services security is also being studied considering safety from third parties that provide such services. For example, in the case of a cloud service, user information is stored on a central server operated by a third party; therefore, the stored information can be leaked or altered by the third party. Blind quantum computation [47, 48] and homomorphic encryption [49, 50] are the methods used to prevent such leaks and alterations in cloud service.

In a previous study, we proposed a controlled mutual quantum entity authentication protocol [51] by which two communicators, referred to here as Alice and Bob, authenticate each other using entanglement swapping and under the control of a third party, Charlie, in a quantum network system established using a sequence of Greenberger–Horne–Zeilinger (GHZ)-like states. However, as mentioned previously, the assumption that Charlie is a trustworthy third party is not practical [52,53,54]. In this study, we present a method to ensure the security of our proposed protocol using an entanglement correlation check and random numbers to address the possibility that Charlie is an untrusted third party.

2 Brief review of controlled mutual quantum entity authentication

In this section, we outline our controlled mutual quantum entity authentication protocol [51]. Let us suppose that two communicators, Alice and Bob, want to authenticate each other in a quantum network created by the controller Charlie. This protocol consists of preparation, security checking, and entity authentication phases, which are discussed below.

2.1 Preparation phase

P1

Alice and Bob pre-share a secret key sequence \( K_{AB} = \left( {k_{1} , k_{2} , \ldots k_{N} } \right). \)The sequence \( K_{AB} = \left( {k_{1} , k_{2} , \ldots k_{N} } \right) \) is of 2N bits; the elements are defined as \( k_{i} \in \left\{ {00, 01, 10, 11} \right\} \), and secret key ki corresponds to the Pauli operator \( U_{{k_{i} }} \in \left\{ {I,\sigma_{x} ,i\sigma_{y} ,\sigma_{z} } \right\}. \) The subscript AB represents that Alice and Bob shared the key

P2

A third party, Charlie, prepares the qubit sequence \( (|\xi \rangle_{1} , |\xi \rangle_{2} , \ldots , |\xi \rangle_{N} ) \) consisting of N GHZ-like states as follows:

$$ \begin{aligned} \left| \xi \right\rangle_{{\left( {2i - 1} \right)123}} \otimes \left| \xi \right\rangle_{{\left( {2i} \right)123}} & = \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)12}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)3}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)12}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)3}} } \right) \\ & \quad \otimes \frac{1}{\sqrt 2 }\left( {\left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)12}} \left| 0 \right\rangle_{{\left( {2i} \right)3}} - \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)12}} \left| 1 \right\rangle_{{\left( {2i} \right)3}} } \right) \\ \end{aligned} $$
(1)

The subscripts (2i − 1) and (2i) refer to the odd-numbered qubits and even-numbered qubits, respectively, in the qubit sequence. In addition, the subscript 1, 2, or 3 indicates the order in the GHZ-like state.

P3

Charlie sends the first qubit to Alice, the second qubit to Bob, and retains the third qubit. He announces these facts to Alice and Bob. After Charlie’s actions, the qubits are given as follows:

$$ \begin{aligned} \left| \xi \right\rangle_{{\left( {2i - 1} \right)ABC}} \otimes \left| \xi \right\rangle_{{\left( {2i} \right)ABC}} & = \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)C}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)C}} } \right) \\ & \quad \otimes \frac{1}{\sqrt 2 }\left( {\left| {\Phi^{{ - }} } \right\rangle_{{\left( {2i} \right)AB}} \left| 0 \right\rangle_{{\left( {2i} \right)C}} { - }\left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} \left| 1 \right\rangle_{{\left( {2i} \right)C}} } \right) \\ \end{aligned} $$
(2)

The subscript A, B, or C represents the owner of a particular qubit. While transmitting N GHZ-like states to Alice and Bob, Charlie randomly inserts NC decoy qubits |x+〉, |x−〉 to detect eavesdropping [22, 34,35,36].

2.2 Security checking phase

S1

After confirming that Alice and Bob have safely received the qubit sequence, Charlie reveals the location of the decoy qubits [22, 34,35,36].

S2

Alice and Bob execute σx-basis measurements only on the decoy qubits received from Charlie and then report the results to Charlie. Charlie compares the initial states of the decoy qubits and the results reported by Alice and Bob. In effect, Charlie checks for eavesdropping [22, 34,35,36].

2.3 Entity authentication phase

E1

Charlie randomly selects one communication member, Alice or Bob, to apply the Pauli operation, which corresponds to the pre-shared key ki, for the qubit A(2i–1) or B(2i) in Eq. (2).

E2

Charlie executes the σz-basis measurement on the qubits {C(2i–1), C(2i)} in Eq. (11) in Ref. [51]. And his measurement outcomes are c2i–1c2i, where c2i–1c2i ∊ {00, 01, 10, 11}. After Charlie’s measurement, the GHZ-like states of Eq. (11) in Ref. [51] collapse into |Φ−〉(2i–1)AB|Φ−〉(2i)AB, |Φ−〉(2i–1)AB|Ψ+〉(2i)AB, |Ψ−〉(2i–1)AB|Φ−〉(2i)AB, or |Ψ−〉(2i–1)AB|Ψ+〉(2i)AB with a 25% probability, and Alice and Bob share one of the pairs of the entangled states.

E3

Alice and Bob execute the Bell-basis measurements on the qubits, \( \left\{ {A_{(2i - 1)} , A_{(2i)} } \right\}\,\,\,{\text{and}}\,\,\,\left\{ {B_{(2i - 1)} , B_{(2i)} } \right\}, \) respectively; this is called entanglement swapping [36, 55, 56]. Then, they exchange their measurement outcomes, \( a_{2i - 1} a_{2i} \,\,{\text{and}}\,\,b_{2i - 1} b_{2i} (a_{j} \,\,\,\& \,\,\,b_{j} \in \left\{ {0, 1} \right\},\,\,\,j = 2i - 1\,\,{\text{or}}\,\,2i). \)

E4

Charlie reveals the measurement outcomes of the classical bit c2i–1c2i acquired in phase E2. Then, both, Alice and Bob confirm whether their classical bits, a2i–1a2i and b2i–1b2i, correctly correspond to the revealed classical bit, c2i–1c2i, as shown in Table 4 in [51].

3 Cryptanalysis of controlled mutual quantum entity authentication

Cryptographically, schemes without a third party are ideal; however, the use of trusted third parties in various cryptographic schemes is unavoidable to ensure efficiency and security. Nevertheless, as Ingemarsson and Simmons indicate [53, 54], anyone involved in cryptographic communication in commercial or international applications cannot be trusted. This deduction also applies to quantum communication protocols, and there are a variety of related cases involving untrustworthy communication elements [22, 36]. In particular, Gao and Wang showed that a security loophole exists in this protocol when the controller Charlie cannot be trusted [52]; in addition, they described how an untrusted controller Charlie can obtain legitimate users’ authentication keys without introducing any errors in the protocol. Their procedure is described as follows.

  • Step 1 In phase P2, the controller Charlie executes sequential σz-basis measurements on qubits {3(2i–1), 3(2i)} of Eq. (1) and Bell-state measurements on qubits {1(2i–1), 1(2i)}and {2(2i–1), 2(2i)} of Eq. (1), instead of sharing the GHZ-like states \( |\xi \rangle_{{\left( {2i{-}1} \right)123}} \otimes |\xi \rangle_{{\left( {2i} \right)123}} \) of Eq. (1) with Alice and Bob. For example, when the σz-basis measurement outcomes are |0〉(2i–1)3 and |1〉(2i)3, the GHZ-like states of Eq. (1) collapse into |Ψ+〉(2i–1)12|Ψ+〉(2i)12, as follows:

    $$ \begin{aligned} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)12}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)12}} & = \frac{1}{2}\left(\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} + \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} \right. \\ & \left.\quad + \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} + \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} \right). \\ \end{aligned} $$
    (3)

    In addition, if Charlie performs Bell-state measurements on qubits {1(2i–1), 1(2i)}and {2(2i–1), 2(2i)} of Eq. (3), he can obtain measurement outcomes (12i–112i, 22i–122i) as:

    $$ \begin{aligned} (00,00):\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} , \hfill \\ (01,01):\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} , \hfill \\ (10,10):\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} , \hfill \\ {\text{or}}\,\,(11,11):\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)1\left( {2i} \right)1}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)2\left( {2i} \right)2}} . \hfill \\ \end{aligned} $$
    (4)

    Table 1 represents all the outcomes corresponding to these measurements by Charlie.

    Table 1 Measurement outcomes 3(2i–1)3(2i), 1(2i–1)1(2i), and 2(2i–1)2(2i) corresponding to the σz-basis and Bell-state measurements by Charlie
    Full size table

  • Step 2 Charlie transmits the Bell states that correspond to the outcomes of Bell-state measurements to Alice and Bob. Here, Alice and Bob cannot detect Charlie’s deception of using decoy qubits. Continuing with the example of Step 1, the Bell states that Alice and Bob receive from Charlie are given as follows:

    $$ \begin{aligned} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
    (5)

  • Step 3 Charlie requires Alice or Bob to apply the Pauli operator corresponding to the secret key ki. If the secret key ki is 01 and Charlie selects Alice, then Alice applies the Pauli operator iσy(= U10) to Bell states of Eq. (5), as follows:

    $$ \begin{aligned} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}}, \hfill \\ \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
    (6)

  • Step 4 Alice and Bob perform the Bell measurements on the Bell states of Eq. (6), and then they announce their measurement outcomes to Charlie. At this time, Charlie could identify the secret key ki by knowing only one measurement outcome from Alice or Bob. Continuing with the example of Step 3, the measurement outcomes (a2i–1a2i, b2i–1b2i) of Alice and Bob are

    $$ \begin{aligned} \left( {11,00} \right):\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left( {10,01} \right):\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left( {01,10} \right):\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}} \left( {00,11} \right):\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
    (7)

    Charlie can estimate that Alice’s operator is iσy(= U10) by comparing its measurement outcome 12i–112i with Alice’s measurement outcome a2i-1a2i. Based on this, Charlie can determine that the secret key is 10.

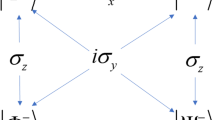
As a result, the controller Charlie can obtain the secret key shared between Alice and Bob using their measurement outcomes without disclosing his own measurement outcomes and without causing any errors. Figure 1 schematically illustrates the internal attack described above by the untrustworthy controller Charlie.

Fig. 1
figure 1

Schematic illustration of untrusted controller Charlie’s internal attack. a In phase P2, Charlie performs joint measurements and Bell-state measurements and then sends fake states |Ψ+〉A(2i–1)A(2i) and |Ψ+〉B(2i–1)B(2i) to Alice and Bob, respectively. b In phase E3, Charlie can estimate the secret key ki = 10 using Bell measurement results from Alice and Bob

Full size image

4 Security improvement of controlled mutual quantum entity authentication

4.1 Security improvement using entanglement correlation check

The security of various quantum communication protocols is ensured primarily by using decoy qubits [22, 34,35,36, 57,58,59] and entanglement correlation checking [34, 36, 60]. The insertion of decoy qubits is effective in detecting the involvement of malicious users in a quantum channel. Entanglement correlation checking is useful in determining whether quantum channel-based entangled states are well formed. In our controlled mutual quantum entity authentication protocol [51], we adopted decoy qubit insertion and entanglement correlation checking to ensure security. However, in this protocol, we did not consider the possibility of internal attack by a controller Charlie because we assumed that Charlie was a trustworthy third party. Therefore, we did not employ decoy qubit insertion or entanglement correlation checking to prevent an internal attack by Charlie. Gao et al. [52] indicated that, in real-world network communication, it is realistic to assume that the controller Charlie may be an untrustworthy third party. Therefore, an internal attack by the controller Charlie is possible because Alice and Bob do not check the correlation of the entangled state. To prevent this type of attack, we added a checking phase to confirm the correlation of the entangled state after phases S1 and S2. More specifically, Alice and Bob should select random states from among the sequence of N GHZ-like states \( |\xi \rangle_{{\left( {2i - 1} \right)ABC}} \otimes |\xi \rangle_{{\left( {2i} \right)ABC}} \) in Eq. (2) and perform σzor σx-basis measurements. For example, suppose Alice and Bob select the (2j − 1)th state:

$$ \begin{aligned} \left| \xi \right\rangle_{{ABC\left( {2j - 1} \right)}} & = \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2j - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2j - 1} \right)C}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2j - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2j - 1} \right)C}} } \right) \\ & \quad = \frac{1}{\sqrt 2 }\left( {\left| {x + } \right\rangle \left| {x + } \right\rangle \left| {x + } \right\rangle - \left| {x - } \right\rangle \left| {x - } \right\rangle \left| {x - } \right\rangle } \right)_{{\left( {2j - 1} \right)ABC}} \\ \end{aligned} $$
(8)

to perform σx-basis measurements. Then, Alice and Bob inform Charlie of the location of the (2j − 1)th state and the measurement basis σx. Charlie then performs the measurements in the same states as Alice and Bob and announces the measurement outcomes to them. Alice and Bob then announce their measurement outcomes to Charlie. In the case that Alice and Bob’s measurement outcomes \( a_{2j - 1} b_{2j - 1} \,\,\,\,{\text{are }} + + :|x + \rangle_{{\left( {2j - 1} \right)A}} |x + \rangle_{{\left( {2j{-}1} \right)B}} , \) then Charlie's measurement outcome c2j−1 would be \( + :|x + \rangle_{{\left( {2j - 1} \right)C}} . \) If Charlie normally transmits GHZ-like states to Alice and Bob, the outcomes of Alice, Bob, and Charlie should be correlated. Alice and Bob should recognize Charlie’s eavesdropping through the probability of \( D = 1 - (1 - d)^{{N_{d} }} , \) where d is the probability of detecting Charlie’s eavesdropping by checking one GHZ-like state and Nd is the number of GHZ-like states used to detect Charlie’s eavesdropping [61]. When Nd is sufficiently large, D approaches unity, and Alice and Bob can detect Charlie’s eavesdropping. Table 2 lists all the measurement outcomes that can be obtained during the entanglement correlation check of the (2j − 1)th state in Eq. (8).

Table 2 Measurement outcomes that can be caused by the entanglement correlation check of the (2j − 1)th state in Eq. (8)
Full size table

In the following lines, we provide a detailed explanation of how Alice and Bob can detect Charlie’s eavesdropping mentioned earlier using the entanglement correlation check. Suppose Alice and Bob received the Bell states of Eq. (5) from Charlie as shown in Step 2 of Sect. 3, as follows.

$$ \begin{aligned} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} \hfill \\ \end{aligned} $$
(9)

Then, if Alice and Bob perform σx-basis measurements on the Bell state {A(2i–1), B(2i–1)} of Eq. (9), they can obtain measurement outcomes (a2i–1b2i–1), as follows.

$$ \begin{aligned} ( + + ):\left| {x + } \right\rangle_{{\left( {2i - 1} \right)A}} \left| {x + } \right\rangle_{{\left( {2i - 1} \right)B}} \hfill \\ ( + - ):\left| {x + } \right\rangle_{{\left( {2i - 1} \right)A}} \left| {x - } \right\rangle_{{\left( {2i - 1} \right)B}} \hfill \\ ( - + ):\left| {x - } \right\rangle_{{\left( {2i - 1} \right)A}} \left| {x + } \right\rangle_{{\left( {2i - 1} \right)B}} \hfill \\ {\text{or}}\,( - - ):\left| {x - } \right\rangle_{{\left( {2i - 1} \right)A}} \left| {x - } \right\rangle_{{\left( {2i - 1} \right)B}} \hfill \\ \end{aligned} $$
(10)

Alice and Bob then inform Charlie of the (2i − 1)th states and the measurement basis σx. At this time, Charlie should disclose the measurement outcome as if it had normally shared the entanglement state to make its attack successful. According to Table 2, the measurement outcomes \( \left( { + - } \right):|x + \rangle_{{\left( {2i - 1} \right)A}} |x - \rangle_{{\left( {2i - 1} \right)B}} \) and \( ( - + ):|x - \rangle_{{\left( {2i - 1} \right)A}} |x + \rangle_{{\left( {2i - 1} \right)B}} \) of Eq. (10) are only obtained by Charlie’s attack. Furthermore, if the measurement outcome (a2i–1b2i–1) is \( \left( { + + } \right):|x + \rangle_{{\left( {2i - 1} \right)A}} |x + \rangle_{{\left( {2i - 1} \right)B}} , \) then Charlie must announce his measurement outcome + :|x + 〉(2i-1)C. In contrast, if the measurement outcome (a2i–1b2i–1) is \( \left( { - - } \right):|x - \rangle_{{\left( {2i - 1} \right)A}} |x - \rangle_{{\left( {2i - 1} \right)B}} , \) then Charlie must announce his measurement outcome \( - :|x - \rangle_{{\left( {2i - 1} \right)C}} . \) However, Charlie cannot predict Alice and Bob’s measurement outcomes (a2i–1b2i–1), and therefore, Charlie always reveals the measurement outcomes incorrectly with a 50% probability. As a result, the probability that Charlie succeeds in its attack in such a case is 25%. Moreover, if they perform σz-basis measurements on the Bell state {A(2i–1), B(2i–1)} in Eq. (9), they can obtain measurement outcomes (a2i–1b2i–1), as follows.

$$ \begin{aligned} \left( {00} \right):\left| 0 \right\rangle_{{\left( {2j - 1} \right)A}} \left| 0 \right\rangle_{{\left( {2j - 1} \right)B}} , \hfill \\ \left( {01} \right):\left| 0 \right\rangle_{{\left( {2j - 1} \right)A}} \left| 1 \right\rangle_{{\left( {2j - 1} \right)B}} , \hfill \\ \left( {10} \right):\left| 1 \right\rangle_{{\left( {2j - 1} \right)A}} \left| 0 \right\rangle_{{\left( {2j - 1} \right)B}} , \hfill \\ {\text{or}}\left( {11} \right):\left| 1 \right\rangle_{{\left( {2j - 1} \right)A}} \left| 1 \right\rangle_{{\left( {2j - 1} \right)B}} \hfill \\ \end{aligned} $$
(11)

Alice and Bob then inform Charlie of the (2i − 1)th states and the measurement basis σz. At this time, Charlie should disclose the measurement outcome as if it had normally shared the entanglement state to make his attack successful. According to Table 2, if the measurement outcome (a2i–1b2i–1) is \( \left( {01} \right):|0\rangle_{{\left( {2j - 1} \right)A}} |1\rangle_{{\left( {2j - 1} \right)B}} \,\,\,{\text{or}}\,\,\,\left( {10} \right):|1\rangle_{{\left( {2j - 1} \right)A}} |0\rangle_{{\left( {2j - 1} \right)B}} , \) Charlie must announce his measurement outcome as 0:|0〉(2j–1)A. In addition, if the measurement outcome (a2i–1b2i–1) is \( \left( {00} \right):|0\rangle_{{\left( {2j - 1} \right)A}} |0\rangle_{{\left( {2j - 1} \right)B}} or \, \left( {11} \right):|1\rangle_{{\left( {2j - 1} \right)A}} |1\rangle_{{\left( {2j - 1} \right)B}} , \) Charlie must announce his measurement outcome as 1:|1〉(2j–1)A. However, Charlie cannot predict Alice and Bob’s measurement outcomes (a2i–1b2i–1); thus, Charlie fails the attack with a 50% probability.

4.2 Security improvement using random numbers

As mentioned above, the controller Charlie can predict the secret key from the measurement outcomes of Alice and Bob, without sharing his measurement outcomes with them. Therefore, if there is a method that prevents the controller Charlie from guessing the secret key, the security of our proposed protocol is ensured. The proposed method involves using a random number; the protocol that modifies the entity authentication phase is described as follows.

E1. (a)

Alice and Bob prepare random numbers rA and rB, where \( r_{A} , r_{B} \in \left\{ {00,01, 10, 11} \right\}. \)

E1. (b)

Charlie randomly selects only one communication member, Alice or Bob. If Charlie selects Alice, Alice applies the Pauli operator corresponding to the classical information \( k_{i}^{{\prime }} \oplus r_{A} = k_{\left( i \right)A} \) to the qubit A(2i–1). If Charlie selects Bob, Bob applies the Pauli operator corresponding to the classical bit \( k_{i}^{{\prime }} \oplus r_{B} = k_{\left( i \right)B} \) to the qubit B(2i). Here, \( k'_{i} \left( { = k_{\left( i \right)A} \oplus r_{A} \,\,\,{\text{or}}\,\,\,k_{\left( i \right)B} \oplus r_{B} } \right) \) is a pre-shared secret key between Alice and Bob in the preparation phase, \( k_{i} \in \left\{ {00, 01, 10, 11} \right\}. \) For example, when \( k_{i}^{{\prime }} = 11 \) and rA = 01, Alice applies the Pauli operator \( i\sigma_{y} \left( { = U_{{k'_{i} \oplus r_{A} }} } \right) \) to the qubit A(2i–1); this is performed as follows:

$$ \begin{aligned} & \left( {i\sigma_{y} \otimes I \otimes I} \right)\left| \xi \right\rangle_{{\left( {2i - 1} \right)ABC}} \otimes \left| \xi \right\rangle_{{\left( {2i} \right)ABC}} \\ & = \frac{1}{\sqrt 2 }\left( {i\sigma_{y} \otimes I \otimes I} \right)\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)C}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)C}} } \right)\\&\quad \otimes \frac{1}{\sqrt 2 }\left( {\left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} \left| 0 \right\rangle_{{\left( {2i} \right)C}} - \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} \left| 1 \right\rangle_{{\left( {2i} \right)C}} } \right) \\ & = \frac{1}{\sqrt 2 }\left( {\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)C}} + \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)C}} } \right)\\&\quad \otimes \frac{1}{\sqrt 2 }\left( {\left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} \left| 0 \right\rangle_{{\left( {2i} \right)C}} - \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} \left| 1 \right\rangle_{{\left( {2i} \right)C}} } \right) \\ \end{aligned} $$
(12)

As another example, when \( k_{i}^{{\prime }} = 11 \)and rB = 10, Bob applies the Pauli operator \( \sigma_{x} \left( { = U_{{k'_{i} \oplus r_{B} }} } \right) \) to the qubit B(2i); this is performed as follows:

$$ \begin{aligned}& \left| \xi \right\rangle_{{\left( {2i - 1} \right)ABC}} \otimes \left( {I \otimes \sigma_{x} \otimes I} \right)\left| \xi \right\rangle_{{\left( {2i} \right)ABC}} \hfill \\& = \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)C}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)C}} } \right)\\&\quad \otimes \frac{1}{\sqrt 2 }\left( {I \otimes \sigma_{x} \otimes I} \right)\left( {\left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} \left| 0 \right\rangle_{{\left( {2i} \right)C}} - \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} \left| 1 \right\rangle_{{\left( {2i} \right)C}} } \right) \hfill \\ &= \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 0 \right\rangle_{{\left( {2i - 1} \right)C}} + \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| 1 \right\rangle_{{\left( {2i - 1} \right)C}} } \right)\\& \quad \otimes \frac{1}{\sqrt 2 }\left( {\left| {\Psi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} \left| 0 \right\rangle_{{\left( {2i} \right)C}} - \left| {\Phi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} \left| 1 \right\rangle_{{\left( {2i} \right)C}} } \right) \hfill \\ \end{aligned} $$
(13)

E2

Charlie executes the σz-basis measurement on the qubits {C(2i–1), C(2i)} in Eq. (12). And his measurement outcome is c2i–1c2i, where c2i–1c2i ∊ {00, 01, 10, 11}. After Charlie’s measurement, the GHZ-like states of Eq. (12) collapse into

$$ \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} ,\,\,\,\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} ,\,\,\,\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i} \right)AB}} ,\,\,\,{\text{or}}\,\,\,\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} $$
(14)

with a 25% probability, and Alice and Bob share one of the pairs of the entangled states. Continuing with the first example of E1. (b), when c2i–1c2i = 01, the GHZ-like states of Eq. (12) collapse into |Φ−〉(2i–1)AB|Ψ+〉(2i)AB:

$$ \begin{aligned} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} & = \frac{1}{2}\left(\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} + \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} \right.\\ &\left. \quad + \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} + \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} \right) \\ \end{aligned} $$
(15)

And, continuing with the second example of E1. (b), when c2i–1c2i = 01, the GHZ-like states of Eq. (13 collapse into |Ψ+〉(2i–1)AB|Φ+〉(2i)AB:

$$ \begin{aligned} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)AB}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i} \right)AB}} & = \frac{1}{2}\left(\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} + \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} \right.\\ & \left.\quad + \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} + \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A(2i)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} \right) \\ \end{aligned} $$
(16)

E3

Alice and Bob execute the Bell-basis measurements on the qubits {A(2i–1), A(2i)}and {B(2i–1), B(2i)} of Eq. (13), respectively. Then, they exchange their measurement outcomes, a2i–1a2i and b2i–1b2i (aj & bj ∊ {0, 1}, j = 2i − 1 or 2i). Continuing with the first example of E2, if Alice and Bob perform Bell-state measurement on {A(2i–1), A(2i)} and {B(2i–1), B(2i)} of Eq. (15), they can obtain measurement outcomes (a2i–1a2i, b2i–1b2i) as:

$$ \begin{aligned} (00,11):\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (01,10):\left| {\Phi^{{ - }} } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (01,10):\left| {\Psi^{{ - }} } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\,\,(11,00):\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
(17)

Then, they exchange their measurement outcomes (a2i–1a2i, b2i–1b2i) in Eq. (17). And continuing with the second example of E2, if Alice and Bob perform Bell-state measurement on {A(2i–1), A(2i)} and {B(2i–1), B(2i)} of Eq. (16), they can obtain measurement outcomes (a2i–1a2i, b2i–1b2i) as:

$$ \begin{aligned} (00,10):\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (01,11):\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (10,00):\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\,(11,01):\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
(18)

Then, they exchange their measurement outcomes (a2i–1a2i, b2i–1b2i) in Eq. (18).

E4. (a)

Charlie reveals the measurement outcomes c2i–1c2i acquired in Phase E2; then, Alice or Bob announces rA or rB to Charlie, respectively. Continuing with the first example of E3, Charlie and Alice announce c2i–1c2i = 01 and rA = 01 to each other in turn. And, continuing with the second example of E3, Charlie and Bob announce c2i-1c2i = 01 and rB = 01 to each other in turn.

E4. (b)

Alice and Bob confirm whether their classical bits, a2i–1a2i, b2i–1b2i, and c2i-1c2i, correspond correctly to the classical bit \( k_{\left( i \right)A} = k_{i}^{{\prime }} \oplus r_{A} \,\,\,{\text{or}}\,\,\,k_{\left( i \right)B} = k_{i}^{{\prime }} \oplus r_{B} , \) as presented in Table 4 in [51]. Continuing with the first example of E4. (a), if \( k_{i}^{{\prime }} = 11, \) a2i–1a2i = 11, b2i–1b2i = 00, and c2i-1c2i = 01. \( k_{\left( i \right)A} = k_{i}^{{\prime }} \oplus r_{A} \) must then be 10. And Continuing with the first example of E4. (1) \( k_{i}^{{\prime }} = 11, \) a2i–1a2i = 11, b2i–1b2i = 01, and c2i–1c2i = 01. \( k_{\left( i \right)B} = k_{i}^{{\prime }} \oplus r_{B} \) must then be 01.

Consequently, even if Charlie attempts an internal attack, he cannot estimate the pre-shared secret key ki without knowing the random numbers rA or rB. Suppose Alice and Bob received the Bell states in Eq. (5) from Charlie as shown in Step 2 of Sect. 3. When k’i = 11 and rA = 01, Alice applies the Pauli operator \( i\sigma_{y} \left( { = U_{{k'_{i} \oplus r_{A} }} } \right) \) to the qubit A(2i–1) of in Eq. (5):

$$ \begin{aligned} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\,\,\,\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} = \left[ {i\sigma_{y} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} } \right]\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
(19)

If Alice and Bob perform Bell-state measurement on {A(2i–1), A(2i)} and {B(2i–1), B(2i)} of Eq. (19), they can obtain measurement outcomes (a2i–1a2i, b2i–1b2i) as:

$$ \begin{aligned} (11,00):\left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (10,01):\left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ (01,10):\left| {\Phi^{ - } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ + } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} , \hfill \\ {\text{or}}\,(00,11):\left| {\Phi^{ + } } \right\rangle_{{\left( {2i - 1} \right)A\left( {2i} \right)A}} \left| {\Psi^{ - } } \right\rangle_{{\left( {2i - 1} \right)B\left( {2i} \right)B}} . \hfill \\ \end{aligned} $$
(20)

Later, if Alice and Bob release the Bell measurements a2i-1a2i = 11 and b2i-1b2i = 00, Charlie gets to know the \( k_{\left( i \right)A} = k_{i}^{{\prime }} \oplus r_{A} = 10. \) But Charlie cannot guess the secret key \( k_{\left( i \right)A} = k_{i}^{{\prime }} \oplus r_{A} = 11, \) because he does not know the random numbers rA = 01.

5 Conclusions

We proposed a secure controlled mutual quantum object authentication protocol that is viable even in an environment in which users cannot trust third party. Two schemes for ensuring the safety of the protocol are used: one is entanglement correlation checking, and the other is the use of random numbers. Entanglement correlation checking can be used to determine whether there is an abnormality in the quantum channel, while random numbers are used in the protocol to make it impossible for the untrusted controller to deduce the key directly. By applying these security protocols to a quantum network, we expect to prevent any malfeasance by an untrusted controller as well as an eavesdropper.