1 Introduction

As the major research of quantum information, quantum communication and quantum computation have attracted much attention of scholars over the past decades. With the ongoing development of quantum information theory and the advent of the relevant experiments [1–3], they have recently become important research topics, and some new research topic had been explained [4, 5]. As one kind of technique used to protect communication security, quantum information hiding can be known as the quantum counterpart of classical information hiding, and it utilizes the quantum mechanical effect to achieve the target of hiding information in process of quantum communication and quantum computation. Now, quantum information hiding has been a new research topic in quantum security communication.

As for quantum information hiding, the existing work mainly focus on two aspects: one is research about the quantum information hiding protocol based on characteristics of quantum mechanics; another is how to design novel quantum information hiding protocol with the aid of other quantum security communication. For the former, it was started with Therhal et al.’s [6] the work in 2001. They presented the first quantum data hiding protocol based on Bell states. In 2002, Eggeling and Werner [7] implemented LOCC (Local Operation and Classical Communication, LOCC) on multi-particle nonentangled states to extend Therhal et al.’s protocol. Later on, Guo et al. [8] used optical down converter to analyse the data hiding protocol based on Bell states, and presented an improved data hiding protocol. In 2005, Hayden et al. [9] proposed a quantum data hiding protocol with the aid of the threshold access structure, and their work laid the foundation for hiding the large capacity data. In 2007, Chattopadhyay et al. [10] presented a quantum multiparty data hiding protocol. The protocol utilized the characteristics that the reduced matrix of four orthogonal entangled states shared by even participants are the fully mixed states. In 2012, Fatahi and Naseri [11] proposed a quantum watermarking protocol. In the protocol, they used entanglement swapping to build up a hidden layer for secret messages. For the latter, researchers presented some quantum information hiding protocols based on other quantum security communication protocols. Worley [12] proposed the first quantum watermarking protocol in 2004. In the protocol, the secret message was embedded according to the error probability of measurement outcomes, and its idea is similar to Bennett and Brassard’s quantum key distribution protocol(BB84 protocol) [13]. Based on BB84 protocol, Martin [14] also proposed a novel protocol for quantum steganographic communication. The protocol hid a steganographic channel in BB84 protocol. In 2010, Z. G. Qu et al. [15] proposed a quantum steganography protocol. In order to transmit secret messages covertly, they used entanglement swapping of Bell states to build up a hidden channel based on the improved ping-pong protocol. In 2013, Xu et al. [16] also proposed a high-efficiency quantum steganography protocol. In the paper, they firstly proposed a hidden rule among the secure message. Under the control of the hidden rule, they proposed the quantum steganography protocol based on the tensor product of Bell states. The protocol established a hidden channel to transmit the secret message within any quantum secure direct communication(QSDC) scheme. Besides the forgoing two types, there are other types of quantum information hiding protocols. In 2002, Julio Gea-Banacloche [17] explored the possibility that encode a quantum state using quantum error-correcting code(QECC) to hide messages as errors in an arbitrary quantum data file, and he thought that the embedded secret message can act as watermarks to ensure authenticity and integrity of the data. Bilal A. Shaw and Todd A. Brun [18] also proposed two protocols for hiding quantum information based on QECC. Differ from the paper [17], this paper gave specific scheme for hiding information and a quantitative method for the secrecy of the protocol. G. Mogos [19] presented a novel quantum steganography protocol, which aimed to used qutrits (the three-orthogonal state system) to represent RGB(Red, Green, Blue) for hiding the secret message in digital color images. Moreover, the protocol expanded the field of applicability of the steganography from the classical informatics to the quantum one successfully. Takashi Mihara [20] proposed a new quantum steganography protocol. The protocol embedded the secret message into plain text without changing the content of the text, and had a good secrecy. In 2013, based on quantum Fourier transform, Zhang et al. [21] presented a quantum watermarking protocol. The protocol embedded the secret message in the coefficient of Fourier transform. However, the protocol did not consider the characteristics of quantum mechanics of quantum information, and used the classical computation in embedding procedure. In the same year, Yang et al. [22] showed the defect of Zhang’s protocol, and improved the protocol.

We can see that quantum steganography is a promising branch of quantum information hiding. It can be used to transmit classical or quantum messages covertly via quantum channels. The foregoing mentioned quantum steganography protocols support the development of quantum information hiding. However, there are some limitations in these protocols. The limitations can be briefly described as below. Firstly, some protocols mainly used the physical characteristic of quantum states, such as quantum entangled states. But the resource of the quantum states which meet the characteristics is restricted. In addition, these protocols need a lot of auxiliary resources. Therefore, these protocols are limited in applications. Secondly, most of other quantum steganography protocols were proposed based on other quantum security communication protocols. The security of these protocols need to rely on other protocols. Therefore, these protocols hardly can be used in general quantum communication, and hardly can apply in the future society of quantum information and quantum communication. Thirdly, quantum superposition states and entangled states tend to be easily disrupted by noise and interactions with their environment and decoherence [23, 24]. Therefore, it is very significant for quantum steganography protocols to transmit secret messages reliably in quantum noisy channels. Considering the further research for quantum steganography from the above aspects, this paper proposes a quantum steganography protocol for quantum noisy channels.

The paper firstly proved the protocol can be used in quantum communication via quantum noisy channels. Then, the detailed protocol is given. Our protocol aims to transmit n-qubit secret messages covertly in quantum noisy channels. Senders can embed the secret message into the cover data with the aid of positive operator valued measure(POVM) operators. Receivers can extract the secret message with a certain probability by using a set of appropriate projective measurement operators. Therefore, the extracting procedure does not need to publish the cover data. Without the cover data, it is impossible for illegal receivers to obtain any useful information about the secret message. This make the secret communication be imperceptible. Therefore, the protocol has good a secrecy. In addition, the security of our protocol does not rely on any other protocol, and the protocol can be widely applied in general quantum communication.

The rest of this paper is organized as below. Section 2 shows our protocol can be used in quantum communication via quantum noisy channels. The protocol are depicted in detail in Section 3. Section 4 analyzes the performance of the protocol in detail. Finally, the paper ends up with a conclusion in Section 5.

2 The Idea of Our Protocol Applying in the Communication via Quantum Noisy Channels

Indeed, any real-life device, which is used to accomplish the quantum communication, unavoidably interacts with its environment. This means that quantum superposition states and entangled states can be easily interfered with their environment. Therefore, it is necessary to make quantum steganography protocols apply to communications in quantum noisy channels. Reference [25] presented a quantum steganography protocol based on probability measurements. This paper extends the protocol. We simplify the method and prove that the method can be applied to quantum noisy channels.

In quantum noisy channels, quantum states can be described by mix states using its density matrix. We suppose that mixed states of two qubits(2-level quantum system) are:

$$ \rho_{1}=p_{0}|\varphi_{0}\rangle\langle\varphi_{0}|+p_{1}|\varphi_{1}\rangle\langle\varphi_{1}| $$
(1)
$$ \rho_{2}=r_{0}|\varphi_{0}\rangle\langle\varphi_{0}|+r_{1}|\varphi_{1}\rangle\langle\varphi_{1}| $$
(2)

where {p i ,|φ i 〉},{r i ,|φ i 〉},i=0,1 are ensembles of pure states, and {|φ i 〉,i=0,1} are mutually orthogonal. In order to meet T r(ρ 1)=T r(ρ 2)=1, there are p 0+p 1=1,r 0+r 1=1.

In order to encode the state of two qubits in one qutrit, we need to do purifications for ρ 1 and ρ 2 at first. Given the reference system B, then we will obtain pure states:

$$ |\phi_{1B}\rangle=\sqrt{p_{0}}|\varphi_{0}\rangle|\psi_{0}\rangle+\sqrt{p_{1}}|\varphi_{1}\rangle|\psi_{1}\rangle $$
(3)
$$ |\phi_{2B}\rangle=\sqrt{r_{0}}|\varphi_{0}\rangle|\psi_{0}\rangle+\sqrt{r_{1}}|\varphi_{1}\rangle|\psi_{1}\rangle $$
(4)

Where {ψ 0,ψ 1} is an orthogonal basis of B system. |ϕ 1B 〉,|ϕ 2B 〉 are pure states, and ρ 1=T r(|ϕ 1B 〉〈ϕ 1B |), ρ 2=T r(|ϕ 2B 〉〈ϕ 2B |).

Constructing a set of POVM measurement operators. It is listed in (5):

$$ \begin{array}{llll} M_{00}&=&\frac{1}{3}(|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|+|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|)\\ M_{01}&=&\frac{1}{3}(|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|+|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|)\\ M_{10}&=&\frac{1}{3}(|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|+|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|)\\ M_{11}&=&\frac{1}{3}(|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|+|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|+|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|) \end{array} $$
(5)

Where \({\sum }_{i=00,01,10,11}M_{i}=I\).

We act the POVM measurement on |ϕ 1B 〉⊗|ϕ 2B 〉 with the operator {M 00⊗I⊗I,M 01⊗I⊗I,M 10⊗I⊗I,M 11⊗I⊗I}:

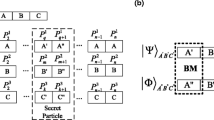
Due to Heisenberg’s uncertainty principle, the POVM measurement result is uncertainty. If the measurement result is 00, then the state |ϕ 1B 〉⊗|ϕ 2B 〉 is projected onto a three-dimensional subspace. The state is changed to be:

$$|\phi_{00}\rangle=N_{00}(\sqrt{p_{0}r_{0}}|\varphi_{0}\varphi_{0}\rangle|\psi_{0}\psi_{0}\rangle+\sqrt{p_{0}r_{1}}|\varphi_{0}\varphi_{1}\rangle|\psi_{0}\psi_{1}\rangle+ \sqrt{p_{1}r_{0}}|\varphi_{1}\varphi_{0}\rangle|\psi_{1}\psi_{0}\rangle) $$

where \(N_{00}=1/\sqrt {p_{0}r_{0}+p_{0}r_{1}+p_{1}r_{0}}\).

To recover the state of the first qubit, we perform the projective measurement on |ϕ 00〉. The used projective measurement operators are given as follows:

$$\begin{array}{@{}rcl@{}} \begin{array}{lllll} P_{1,s}=|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|; P_{1,f}=|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}| \end{array} \end{array} $$
(6)

If the measurement result is 1s, the state of the qutrit is projected onto a two-dimensional subspace. After the projective measurement, the state is changed to be (7):

$$ |\phi_{00}^{\prime}\rangle=\sqrt{p_{0}}|\varphi_{0}\varphi_{0}\rangle|\psi_{0}\psi_{0}\rangle +\sqrt{p_{1}}|\varphi_{1}\varphi_{0}\rangle|\psi_{1}\psi_{0}\rangle $$
(7)

By taking the partial trace to the second particle and its reference system B, we obtain |ϕ 1B 〉. Computing ρ 1=T r B (|ϕ 1B 〉〈ϕ 1B |), we recover the state of the first qubit successfully. If the obtaining result is 1f, the procedure of decoding fails. The probability of successful decoding the state of the first qubit is equal to \(\frac {2}{3}\). The probability is given in the reference [25] in detail.

Similar to the above procedure of decoding, we can use a set of projective measurement operators to recover the state of the second qubit. This measurement operators are listed as below:

$$ P_{2,s}=|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|; P_{2,f}=|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}| $$
(8)

The successful probability is also \(\frac {2}{3}\).

Similarly, if the POVM measurements result are 01,10,11, there are the corresponding encoding procedure and the corresponding decoding procedure by using appropriate quantum measurement operators. Figure 1 clearly gives a description about the encoding procedure and the decoding procedure.

Fig. 1
figure 1

The encoding and decoding workflow of mixed states of two qubits

Full size image

3 A Quantum Steganography Protocol for Quantum Noisy Channels

Based on the idea shown in the Section 2, this paper presents a quantum steganography protocol for quantum noisy channels. In our protocol, senders transmit 2n-qubit (n-qubit are the secret message, and the rest n-qubit are the cover data) to receivers in public quantum channels. Moreover, receivers can correctly extract the secret message with the probability of \(\frac {2}{3}\). Meanwhile, the cover data can normally be recovered with the same probability.

3.1 Embedding Procedure of the Secret Message

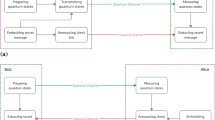
Suppose that Alice wants to covertly send n-qubit secret messages to Bob in public quantum channels. In order to make eavesdroppers be unaware of the existence of the secret message, Alice needs to use n-qubit cover data to conceal the secret message. The concrete embedding procedure is depicted as below:

  1. (1)

    Prior to embedding the secret message, Alice and Bob firstly share some information before their communications. Later on, the shared information is listed in Table 1 in detail.

    Table 1 The shared information between Alice and Bob
    Full size table
  2. (2)

    Alice prepares two n-qubit systems. These two n-qubit systems are the cover data and the secret message respectively. They can be written as follows:

    $$ \rho_{s}=\rho_{s,0}\otimes\rho_{s,1}\otimes\cdots\otimes\rho_{s,n-1} $$
    (9)
    $$ \rho_{c}=\rho_{c,0}\otimes\rho_{c,1}\otimes\cdots\otimes\rho_{c,n-1} $$
    (10)

    where ρ s,i =p 0,i |φ 0〉〈φ 0|+p 1,i |φ 1〉〈φ 1|,ρ c,i =r 0,i |φ 0〉〈φ 0|+r 1,i |φ 1〉〈φ 1|,i=0,1,⋯ ,n−1, and p 0,i +p 1,i =1,r 0,i +r 1,i =1.

  3. (3)

    Doing purifications for ρ s,i and ρ c,i ,i=0,1,⋯ ,n−1: Given the reference system D, we obtain |ϕ s D,i 〉 and |ϕ c D,i 〉,i=0,1,⋯ ,n−1. Then |ϕ s D,i 〉 and |ϕ c D,i 〉,i=0,1,⋯ ,n−1 are pure states, and ρ s,i =T r D (|ϕ s D,i 〉〈ϕ s D,i |) and ρ c,i =T r D (|ϕ c D,i 〉〈ϕ c D,i |).

  4. (4)

    Alice takes |ϕ s D,i 〉 and |ϕ c D,i 〉 (i=0,1,⋯ ,n−1) to make tensor products respectively, and obtains the sequence |ϕ s D,0〉⊗|ϕ c D,0〉,|ϕ s D,1〉⊗|ϕ c D,1〉,⋯ ,|ϕ s D,n−1〉⊗|ϕ c D,n−1〉.

  5. (5)

    Alice constructs n sets of POVM measurement operators, and each set of POVM measurement operators is given in (11).

    $$ \begin{array}{llll} M_{i}^{00}&=&\frac{1}{3}(|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|+|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|)\\ M_{i}^{01}&=&\frac{1}{3}(|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|+|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|)\\ M_{i}^{10}&=&\frac{1}{3}(|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|+|\varphi_{0}\varphi_{0}\rangle\langle\varphi_{0}\varphi_{0}|+|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|)\\ M_{i}^{11}&=&\frac{1}{3}(|\varphi_{1}\varphi_{1}\rangle\langle\varphi_{1}\varphi_{1}|+|\varphi_{1}\varphi_{0}\rangle\langle\varphi_{1}\varphi_{0}|+|\varphi_{0}\varphi_{1}\rangle\langle\varphi_{0}\varphi_{1}|) \end{array} $$
    (11)

    where \({\sum }_{j=00,01,10,11}{M_{i}^{j}}=I\)(i=0,1,⋯ ,n−1), and each set of POVM measurement operators can be written as \(M_{i}=\{M_{i}^{00},M_{i}^{01},M_{i}^{10},M_{i}^{11}\}\). Then, Alice acts the POVM measurement on |ϕ s D,i 〉⊗|ϕ c D,i 〉 (i=0,1,⋯ ,n−1) with the operators M i ⊗I⊗I respectively.

  6. (6)

    Alice does not publish the measurement result at once after acting the POVM measurements, but saves the measurement result. The result are written as k 0 k 1⋯k n−1. Meanwhile, |ϕ s D,i 〉⊗|ϕ c D,i 〉 collapse to be |ϕ i 〉,i=0,1,⋯ ,n−1, and Alice obtains the new sequence |ϕ 0〉,|ϕ 1〉,⋯ ,|ϕ n−1〉. The secret message and the cover data changed to be |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉.

  7. (7)

    Finally, in order to prevent from being attacked, we need to do attack-detection in the communication. Therefore, Alice prepares decoy state particles and inserts the particle into |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉 for doing attack-detection. Then, Alice sends |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉 with the decoy state particle to Bob.

In this way, the secret message are embedded into the cover data successfully.

3.2 Extracting Procedure of the Secret Message

After receiving the message from Alice, Bob wants to extract the secret message. Table 1 gives the shared information between Alice and Bob in detail. Without having influence on normally reading the cover data, Bob can extract the secret message with the probability of \(\frac {2}{3}\) using the information in Table 1.

In Table 1, k i ,i=0,1,⋯ ,n−1 is Alice’s feasible POVM measurement results. M s and M c are projective measurement operators. Table 1 shows the corresponding relationship between M s and k i . It also gives the corresponding relationship between M c and k i . M s and the corresponding relationship between M s and k i must be kept in secret and can be only known by Alice and Bob. While the corresponding relationship between M c and k i are public. Here, P s,s ,P s,f and P c,s ,P c,f are two sets of projective measurement basis, respectively.

To extract the secret message, Bob can perform the projective measurement on |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉 according to the shared information in Table 1. The extracting procedure can be depicted as below:

  1. (1)

    When Bob receives the message with decoy state particles from Alice, he will detect if there are eavesdrops using decoy state particles at first. Then Bob tells Alice whether there are eavesdrops or not, and removes the decoy state particles.

  2. (2)

    According to the result of attack-detection, Alice decide if she carry out the next step:

    • If there is no eavesdrop, Alice publishes her POVM measurement results k 0 k 1⋯k n−1, and Bob turns to the next step;

    • Otherwise, Alice does not publish the measurement results k 0 k 1⋯k n−1, and Bob does nothing. This communication is end.

  3. (3)

    According to the measurement result k 0 k 1⋯k n−1, Bob chooses a set of appropriate projective measurement operators {P s,s ,P s,f } of M s in the Table 1. With the chosen operators {P s,s ,P s,f }, Bob acts projective measurements on |ϕ i 〉,i=0,1,⋯ ,n−1, respectively. Then, |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉 collapses to be \(|\phi _{0}^{\prime }\rangle \otimes |\phi _{1}^{\prime }\rangle \otimes \cdots \otimes |\phi _{n-1}^{\prime }\rangle \).

  4. (4)

    Bob takes the partial trace to the second particle and its reference system D of \(|\phi _{i}^{\prime }\rangle ,i=0,1,\cdots ,n-1\) respectively, and obtains pure states |ϕ s D,i 〉,i=0,1,⋯ ,n−1.

  5. (5)

    Computing T r D (|ϕ s D,i 〉〈ϕ s D,i |) respectively, Bob can obtain the secret message ρ s,i ,i=0,1,⋯ ,n−1 with the probability of \(\frac {2}{3}\) successfully.

Likewise, we can read the cover data with the same probability by choosing an appropriate set of projective measurements operators {P c,s ,P c,f } of M c according to Table 1 to perform projective measurements on |ϕ 0〉⊗|ϕ 1〉⊗⋯⊗|ϕ n−1〉 respectively.

4 Performance Analysis

Similar to the classical steganography, security, secrecy and capacity are three factors to be considered when we analyze the performance of quantum steganogranphy protocols. We need to consider two aspects about the security of quantum steganography protocols: one is that the protocol must ensure that eavesdroppers cannot be aware of the existence of the secret message; Another is that the protocol can resist all kinds of eavesdropping attacks and insure that eavesdroppers cannot obtain the secret message exactly even if they have suspicioned the existence of the secret message. The former can also be considered as the secrecy. The two aspects can ensure the security of quantum steganography protocols. It is known that the secrecy is an important measure to evaluate the performance of quantum steganogranphy protocols. It makes secret communications be imperceptible. This means that eavesdroppers can hardly be ware that the secret communication has happened so as to prevent eavesdroppers from damaging the secret message.

In general, most of quantum steganography protocols need the key and the cover data to extract the secret message. The key, which is used to embed the secret message and is used to extract the secret message, must be shared in secure channels and can be only known by senders and legal recipients(Alice and Bob) in the communication. As for the cover data, they must be published in order to exactly extract the secret message. However, our protocol embeds the secret message into the cover data by a set of POVM measurement operators. The POVM measurement results k 0 k 1⋯k n−1, which are used to extract the secret message, can be published after confirming that there is no eavesdrops in the communication. For illegal recipients, they can normally read the cover data by performing the projective measurement on the message according to Alice’s POVM measurement results k 0 k 1⋯k n−1 and the public projective measurement operators M c in Table 1. Therefore, the existence of the secret message does not influence the cover data. Similarly, Bob can also extract the embedded secret message from Alice by performing the projective measurement on the message according to Alice’s POVM measurement results k 0 k 1⋯k n−1 and M s in Table 1. But the M s and the correspondence between k 0 k 1⋯k n−1 and M s are secret. In our protocol, Bob can exactly extract the secret message without the cover data. Alice does not need to publish the cover data for extracting the secret message in the communication. This means that eavesdroppers cannot obtain useful information about the cover data. The information that eavesdroppers can only obtain is |Ψ〉=|Φ〉=|ϕ 0〉⊗|ϕ 1〉,⋯ ,|ϕ n−1〉, so

$$ D({\Psi},{\Phi})=\frac{1}{2}|Tr(|{\Psi}\rangle\langle{\Psi}|-|{\Phi}\rangle\langle{\Phi}|)|=0 $$
(12)

In this situation, any eavesdropper cannot distinguish the secret message from the cover data. Thus, it is impossible for eavesdroppers to be aware that there is the embedded secret message in the communication. In other words, the protocol can meet the secrecy requirement of quantum steganography protocols.

Once eavesdroppers start to suspect the existence of the secret message, it is very important for quantum steganography protocols to be able to resist all kinds of eavesdropping attacks. In order to obtain the secret message, eavesdroppers attempt to adopt all kinds of attacks: such as the intercept-resend attack and the auxiliary particle attack. But no matter which attack they adopt, it is inevitable to introduce errors. Therefore, the attack can eventually be detected by Alice and Bob using attack-detection. Once Alice have known that there are eavesdrops in the communication, she will not publish the POVM measurement results k 0 k 1⋯k n−1. The POVM measurement results are completely random before being published by Alice. Therefore, eavesdroppers neither know k 0 k 1⋯k n−1 nor the shared information, and they only randomly speculate the measurement results and the shared information. Eavesdroppers can guess the correct information for a qubit secret message with the probability of \(\frac {1}{48}\). For n-qubit secret message, the probability is \(\frac {1}{48^{n}}\). Then, when n is large enough, our protocol meets the requirement of a 𝜖-security quantum steganography system. Moreover, all of the communication in our protocol except for the shared information can happen in the public quantum channel, and does not have special requests about the security of the quantum channel.

In general, our protocol can meet the secrecy and security requirement. In addition, we can see that the security of our protocol only relies on the uncertainty of quantum measurements, and does not rely on any other protocols. Therefore, our protocol can be used in general quantum communications. Using our protocol, we can utilize general quantum channels to covertly transmit the secret message. As for the physical implementation of our protocol, the problem faces two aspect: quantum purification and quantum state preparation. For common quantum states, purification and preparation of single-qubit states can be realized in cavity QED [26, 27]. The states, which are used in our protocol, are all common quantum states, and this make our protocol feasible in physical implementation.

For quantum steganography protocol, the capacity is an important measure. It is used to calculate that how many qubits(bits) secret message can be transmitted and how many qubits(bits) auxiliary information needs to be used in the communication for transmitting the secret message. Our protocol aims to transmit n-qubit secret message covertly. Our protocol needs not to expend a mass of the shared key and entangled states in the communication. With respect to the capacity, we give a calculation clearly about the consumption of our protocol: except for decoy state particles used in attack-detection, auxiliary resource used in our protocol includes n qubits and 2n bits message in order to transmit n-qubit secret message.

5 Conclusions

This paper presents a novel quantum steganography protocol for quantum noisy channels. The protocol is not affected by quantum noisy channels, and is able to transmit n qubits secret message covertly in public quantum channels. In our protocol, Bob can extract the secret message without publishing the cover data. The cover data can also be read normally by using the public projective measurement operator. Therefore, eavesdroppers can hardly be aware that the secret communication has taken place. Then, the protocol has a good secrecy. In addition, the security of our protocol relies on the uncertainty of quantum measurements rather than any other protocols. Due to owing the kind of security, our protocol can widely be used in the general quantum communication. Moreover, Bob can extract the secret message according to Alice’s POVM measurement results and the shared information in Table 1 in advance. The POVM measurement can be sent in public classical channels. This reduces the consumption of the communication. But because we used the POVM measurement operators in the embedding procedure and projective measurement operators in the extracting procedure respectively, the secret message can be only extracted with the probability of \(\frac {2}{3}\). We hope that the imperfect can be improve in future work.