1 Introduction

Discrete quantum Fourier transform (DQFT) [1], which is a linear transformation on qubits, can implement various quantum algorithms to solve problems like the factoring problem [2], the search problem [3], the phase estimation problem [4] and the hidden subgroup problem [5, 6]. Therefore, practical DQFT, which is experimentally implemented with current technology, is an important topic for quantum algorithms and computations. Many physical schemes have been proposed to realize DQFT based on cavity quantum electrodynamics [7–10], nuclear magnetic resonance [11, 12], ion trap systems [13–15], superconducting circuits [16], linear optical systems [17–20], and nonlinear optical systems [21–24].

In particular, optical nonlinearities can assist indirect interaction between photons for quantum information processing. Cross-Kerr nonlinearities (XKNLs) have been widely researched, both theoretically and experimentally, for feasible optical multi-qubit gates. After Nemoto and Munro [25] proposed a nearly deterministic controlled NOT gate using weak XKNLs, X-homodyne measurements, and linear optical elements, many researchers tried to increase the feasibility of quantum information processing schemes by suggesting various methods for optical multi-qubit gates (controlled gates). They include compositions of weak XKNLs, X-homodyne measurements [26–30], and weak XKNLs, coherent superposition states, P-homodyne measurements [31–33], and weak XKNLs, quantum bus beams, photon-number-resolving (PNR) measurements [34–42]. However, in practice, the decoherence effect of optical multi-qubit gates (by loss of photons) is unavoidable in optical fiber. Because the states of photons evolve into a mixed state after homodyne measurement [43–47], the fidelity of the optical multi-qubit gates will decrease. Fortunately, Jeong [44, 45] demonstrated that the decoherence effect can be made arbitrarily small simply by increasing the amplitude of the coherent state and by applying a displacement operator to the coherent state and the PNR measurements.

In this paper, we propose an optical DQFT scheme that can experimentally implement the operation of DQFT on qubits for quantum algorithms using nonlinearities. Our DQFT scheme is composed of the CPRkMP [controlled path-\(R_k \)(CPRk) + merging path (MP)] gates which are consecutively operated a controlled path-\(R_k \)(CPRk) gate and a merging path (MP) gate. Our CPRk and MP gates are based on a controlled path and a merging gates, which utilized weak XKNLs, and X-homodyne detections [26] or quantum bus beams and the PNR measurements [35–37]. However, the controlled path and merging gates in [26] are vulnerable (evolving the output state to mixed state) against decoherence effect due to the X-homodyne measurement [43–47]. Also, the controlled gates in Refs. [35–37] which used the quantum bus beams and the PNR measurements, for the reliable performance of the controlled path operation of the output state, the interactions of XKNL should be employed the maximum two times, compared with the scheme in [26], on account of the structure of the quantum bus beams. Thus, in the proposed DQFT scheme, we will design our CPRkMP (CPRk + MP) gate using weak XKNLs, the displacement operators and the PNR measurements [43–47], a single photon R-k \(\left( {U_{R_k } } \right) \) operator and linear optical operators, to acquire the advantages of the robustness against decoherence effect and less consumption of the interactions of XKNL, compared with the optical gates in Refs. [26, 35–37]. Then, we demonstrate that our CPRkMP gate, which is critical component in our DQFT scheme, can obtain the robustness against the decoherence effect by only using the strong amplitude of the coherent state, in accordance with the analysis and simulation from the master equation (describing open quantum system) [44, 45]. Further, this means that our DQFT scheme can be enhanced the feasibility under the decoherence effect compared with the existing DQTF scheme [24], which is constructed using controlled path, eraser and merging gates via XKNLs, when experimentally realized.

2 Discrete quantum Fourier transforms based on photon gates

2.1 Discrete quantum Fourier transform using qubit operations (controlled-\(R_k \) and swap)

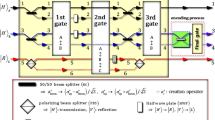
We introduce the DQFT operation, based on qubits, as described in Fig. 1 [1]. For a given state of n qubits\(\left| j \right\rangle =\left| {j_1 } \right\rangle \ldots \ldots ..\left| {j_n } \right\rangle \), where \(j_m \in \left\{ {0,1} \right\} \), it is transformed by the controlled-\(R_k \) and swap (CRkS) and Hadamard operations as follows:

$$\begin{aligned} \begin{array}{l} \left| j \right\rangle \Rightarrow \frac{1}{\sqrt{2^{n}}}\mathop {\sum }\limits _{k=0}^{2^{n}-1} {\mathrm{e}^{i2\pi jk/2^{n}}\left| k \right\rangle } =\frac{1}{\sqrt{2^{n}}}\left( {\left| 0 \right\rangle +\,\mathrm{e}^{i2\pi \left( {0.j_n } \right) }\left| 1 \right\rangle } \right) \otimes \left( \left| 0 \right\rangle \right. \\ \left. +\,\mathrm{e}^{i2\pi \left( {0.j_{n-1} j_n } \right) }\left| 1 \right\rangle \right) \otimes \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \otimes \left( {\left| 0 \right\rangle +\mathrm{e}^{i2\pi \left( {0.j_1 j_2 \cdot \cdot \cdot j_{n-1} j_n } \right) }\left| 1 \right\rangle } \right) , \\ \end{array} \end{aligned}$$
(1)

where \(0.j_1 j_2 \cdot \cdot \cdot \cdot j_{n-1} j_n =j_1 /2^{1}+j_2 /2^{2}+\cdot \cdot \cdot \cdot +j_{n-1} /2^{n-1}+j_n /2^{n}\).

Fig. 1
figure 1

The quantum circuit (on qubits) for implementation of the DQFT operation. This circuit is comprised of controlled-\(R_k \quad \left( {k=2\ldots ..n} \right) \) operations and Hadamard operations for DQFT of n qubits. The red box denotes the CRkS operation in which controlled-\(R_k \) and swap operations are consecutively performed (Color figure online)

Full size image

Then, an arbitrary quantum state \(\left| \varphi \right\rangle =\sum _{j=0}^{N-1} {\alpha _j } \left| j \right\rangle \) can be transformed to \(U_\mathrm{DQFT} \left| \varphi \right\rangle =\sum _{k=0}^{N-1} {\beta _k } \left| k \right\rangle \) via CRkS and Hadamard operations, where \(\beta _k =\left( {\sum _{j=0}^{N-1} {\alpha _j \mathrm{e}^{i2\pi jk/N}} } \right) /\sqrt{N}\). The critical element is CRkS operation \(U_\mathrm{CRkS} \), which is shown in Fig. 1, for DQFT of quantum states. Suppose that the initial state of two qubits is \(\left| \varphi \right\rangle _\mathrm{int} =x_0 \left| 0 \right\rangle _1 \left| 0 \right\rangle _2 +x_1 \left| 0 \right\rangle _1 \left| 1 \right\rangle _2 +x_2 \left| 1 \right\rangle _1 \left| 0 \right\rangle _2 +x_3 \left| 1 \right\rangle _1 \left| 1 \right\rangle _2 \). After state \(\left| \varphi \right\rangle _\mathrm{int} \) passes through the CRkS operation, \(U_\mathrm{CRkS} \), this state can be transformed to

$$\begin{aligned} \left| \varphi \right\rangle _{\hbox {fin}} =x_0 \left| 0 \right\rangle _1 \left| 0 \right\rangle _2 +x_1 \left| 1 \right\rangle _1 \left| 0 \right\rangle _2 +x_2 \left| 0 \right\rangle _1 \left| 1 \right\rangle _2 +x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle _1 \left| 1 \right\rangle _2 . \end{aligned}$$
(2)

The CRkS operation comprises consecutive a controlled-\(R_k \) operation with target qubit 1 and control qubit 2, swapping the two modes of the qubits. Because DQFT is based on the CRkS operation, it is important that the CRkS operation is experimentally implemented with nearly deterministic performance for DQFT having a probability of success and feasibility of realization.

2.2 Discrete quantum Fourier transform using optical gates (controlled path-\(R_k \) and merging path)

We propose a deterministic and experimentally feasible CPRkMP gate, an optical multi-photon gate, which can be directly implemented in the CRkS operation described in Sect. 2.1. This gate is composed of consecutive operations of a controlled path-\(R_k \)(CPRk) gate and a merging path (MP) gate, based on the controlled path gates and the merging gates in Refs. [26, 35–37], which employ the weak XKNLs, the displacement operators and the PNR measurements [43–47], and the linear optical operators (\(U_{R_k } \) and U: phase-flip). Let us consider two types of polarization: linear polarization (\(\left| H \right\rangle \) is horizontal, and \(\left| V \right\rangle \) is vertical) and circular polarization (\(\left| R \right\rangle \) is right- and \(\left| L \right\rangle \) is left-circular). The linearly polarized states and the circularly polarized states of a single photon correspond to the eigenstates of \(\sigma _Z :\left\{ {\left| H \right\rangle \equiv \left| 0 \right\rangle ,\left| V \right\rangle \equiv \left| 1 \right\rangle } \right\} \) and \(\sigma _X :\left\{ {\left| R \right\rangle \equiv \left| + \right\rangle ,\left| L \right\rangle \equiv \left| - \right\rangle } \right\} \).

Before explaining our CPRkMP gate, we introduce XKNL. The XKNL’s Hamiltonian is \(H_\mathrm{Kerr} =\hbar \chi N_1 N_2 \), where \(N_i \) is the photon number operator, and \(\chi \) is the strength of nonlinearity in the Kerr medium. Let us assume that \(\left| {n^{s}} \right\rangle _i \) represents a signal state of n photons and polarization s, and \(\left| \alpha \right\rangle _j \) is a coherent state (probe beam). After passing through the Kerr medium, the signal-probe system’s state is changed to \(U_\mathrm{Kerr} \left| {n^{s}} \right\rangle _1 \left| \alpha \right\rangle _2 =\mathrm{e}^{i\theta N_1 N_2 }\left| {n^{s}} \right\rangle _1 \left| \alpha \right\rangle _2 =\left| {n^{s}} \right\rangle _1 \left| {\alpha ^{in\theta }} \right\rangle _2 \), where \(\theta =\chi t\), and t is the interaction time.

Fig. 2
figure 2

The CPRkMP gate (red box) is comprised of the consecutive operation of a controlled path gate (blue box) and a merging path gate (black box) using XKNLs, the displacement operators, the PNR measurements, feed-forwards and a \(U_{R_k } \) operation (blue box). This CPRkMP gate experimentally implements the CRkS operation as described in Fig. 1 (Color figure online)

Full size image

Now, we propose a deterministic CPRkMP gate comprised of the consecutively performing a CPRk gate and a MP gate, which employ the weak XKNLs, the displacement operators and the PNR measurements, and the linear optical operators (\(U_{R_k } \), U) and the process of the crossing-path (swapping paths with each other). We assume that the initial state of two photons is \(\left| \phi \right\rangle _\mathrm{int} =x_0 \left| 0 \right\rangle ^{\hbox {a}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 0 \right\rangle ^{\hbox {a}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a}}\left| 0 \right\rangle ^{\hbox {b}}+x_3 \left| 1 \right\rangle ^{\hbox {a}}\left| 1 \right\rangle ^{\hbox {b}}\), where we denote \(\left\{ {\left| H \right\rangle ^{i},\left| V \right\rangle ^{i},\left| R \right\rangle ^{i},\left| L \right\rangle ^{i}} \right\} \equiv \left\{ {\left| 0 \right\rangle ^{i},\left| 1 \right\rangle ^{i},\left| + \right\rangle ^{i},\left| - \right\rangle ^{i}} \right\} \) and i represents a path of the photon, conventionally.

In the CPRk gate, first, as shown in Fig. 2, the initial state \(\left| \phi \right\rangle _\mathrm{int} \) of two photons passes through the Beam splitter (BS) on path \(\hbox {a}\) and the polarizing beam splitter (PBS) on path \(\hbox {b}\). Here, the action of a BS is described by \(a_{u}^+ \rightarrow \left( {a_{u}^+ +a_{d}^+ } \right) /\sqrt{2}\) and \(a_{d}^+ \rightarrow \left( {a_{u}^+ -a_{d}^+ } \right) /\sqrt{2}\) [48] where \(a_i^+ \) is the creation operator of a photon on path i (\(\hbox {u}\) is an up path and \(\hbox {d}\) is a down path). Also, when passing through the PBS, \(\left| H \right\rangle \equiv \left| 0 \right\rangle \) is transmitted and \(\left| V \right\rangle \equiv \left| 1 \right\rangle \) is reflected. Then, the phase shifts \(\theta \) and \(-\theta \), which are generated by two photons, are induced in the probe beam \(\left| \alpha \right\rangle _p \) in Kerr media (XKNLs). Then, displacement operation \(D\left( {-\alpha } \right) \) is performed on the probe beam. The transformed state \(\left| \phi \right\rangle _D \) of the signal-probe system is given by

$$\begin{aligned}&\left| \phi \right\rangle _D =\frac{1}{\sqrt{2}}\left[ \left( {x_0 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}} \right) \otimes \left| 0 \right\rangle _p +\left( x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}\right. \right. \nonumber \\&\quad \left. \left. +\,x_3 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}} \right) \otimes \left| 0 \right\rangle _p \right] \nonumber \\&\quad +\,\frac{\mathrm{e}^{-i\alpha ^{2}\sin \theta }}{\sqrt{2}}\left[ {\left( {x_0 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}} \right) \otimes \left| {\alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _p +} \right. \nonumber \\&\quad +\,\mathrm{e}^{2i\alpha ^{2}\sin \theta }\left. {\left( {x_1 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}}+x_3 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}}} \right) \otimes \left| {\alpha \left( {\mathrm{e}^{i\theta }-1} \right) } \right\rangle _p } \right] , \end{aligned}$$
(3)

where \(D\left( {-\alpha } \right) \left| {\alpha \mathrm{e}^{\pm i\theta }} \right\rangle =\mathrm{e}^{\pm i\alpha ^{2}\sin \theta }\left| {\alpha \left( {\mathrm{e}^{\pm i\theta }-1} \right) } \right\rangle \), and \(\left| {\alpha \left( {\mathrm{e}^{\pm i\theta }-1} \right) } \right\rangle =\mathrm{e}^{-\alpha ^{2}\left( {1-\cos \theta } \right) }\mathop {\sum }\limits _{n=0}^\infty {\frac{\alpha ^{n}\left( {\mathrm{e}^{\pm i\theta }-1} \right) ^{n}}{\sqrt{n!}}} \left| n \right\rangle \) for \(\alpha \in \mathbf{R}\). Subsequently, we utilize the measurement strategy of PNR detection (i.e., the converted voltage or current) on the probe beam. If the outcome of the measurement is \(\left| 0 \right\rangle _p \), then the output state \(\left| \phi \right\rangle _\mathrm{CP} \) is given by \(\left| \phi \right\rangle _\mathrm{CP} =x_0 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_3 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}\) in Eq. 3. Otherwise, the output state can be transformed into state \(\left| \phi \right\rangle _\mathrm{CP} \) by feed-forward operation of the linear phase shifter \(\Phi _n \) and path-switch S, according to the results \(\left| n \right\rangle _p \left( {n=1,2\ldots \ldots } \right) \) from the PNR measurement. Then, the state \(\left| \phi \right\rangle _\mathrm{CP} \) passes through a \(U_{R_k } \) operator on path \(\hbox {a.1}\). If the state of a photon is \(\left| 1 \right\rangle ^{\hbox {a.1}}\)(vertical polarization), the \(U_{R_k } \) operation is linearly shifted from the phase of state \(\left| 1 \right\rangle ^{\hbox {a.1}}\) to \(\mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.1}}\). Then, the output state of the CPRk gate is given by

$$\begin{aligned} \left| \phi \right\rangle _\mathrm{CPRk} =x_0 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}, \end{aligned}$$
(4)

where the path of first photon is divided into the two paths \(\hbox {a.0}\) and \(\hbox {a.1}\). So, we should use the MP gate to merge the split path of the first photon to a single path. The probability of error of the CPRk gate, \(P_\mathrm{err}^\mathrm{CPRk} \), which is the probability of detecting \(\left| 0 \right\rangle _p \) (no photon) in \(\left| {\alpha \left( {\mathrm{e}^{\pm i\theta }-1} \right) } \right\rangle _p \), in Eq. 3 is calculated as \(P_\mathrm{err}^\mathrm{CPRk} =\mathrm{e}^{-2\alpha ^{2}\left( {1-\cos \theta } \right) }/2\), where \(1-\cos \theta \approx \theta ^{2}/2\) for the weak XKNL (\(\theta<<1)\), and \(P_\mathrm{err}^\mathrm{CPRk} \) is approximated as \(\mathrm{e}^{-\alpha ^{2}\theta ^{2}}/2\). When \(\alpha \theta >\pi \), \(P_\mathrm{err}^\mathrm{CPRk} \) is smaller than \(10^{-4}\) that indicates that if we choose amplitude \(\alpha \) of the coherent state to be sufficiently large, the weak XKNL (\(\theta<<1)\) can be utilized for the CPRk gate. Thus, by using weak XKNLs, a displacement operator and PNR measurement with the condition \(\alpha \theta >\pi \), this CPRk gate is nearly deterministic with a certain probability of success (\(P_\mathrm{err}^\mathrm{CPRk} \rightarrow 1)\).

In the MP gate, second, as shown in Fig. 2, the output state of the CPRk gate, \(\left| \phi \right\rangle _\mathrm{CPRk} \), passes through the BS on between path \(\hbox {a.0}\) and \(\hbox {a.1}\) and the phase-flip operator \(\left( {U\equiv \left| H \right\rangle \left\langle H \right| -\left| V \right\rangle \left\langle V \right| =\left| 0 \right\rangle \left\langle 0 \right| -\left| 1 \right\rangle \left\langle 1 \right| } \right) \) on path \(\hbox {b}\). Then, the linear phase shift \(-\theta \) and the controlled phase shift \(\theta \) (XKNL), which is generated by one photon, are induced in the probe beam \(\left| \alpha \right\rangle _q \). And then, displacement operation \(D\left( {-\alpha } \right) \) is performed on the probe beam. The transformed state \(\left| \varphi \right\rangle _D \) of the signal-probe system is given by

$$\begin{aligned}&\left| \varphi \right\rangle _D =\frac{1}{\sqrt{2}}\left[ \left( x_0 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}\right. \right. \nonumber \\&\quad \left. \left. +\, \, x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}} \right) \otimes \left| 0 \right\rangle _q \right] \nonumber \\&\quad +\,\frac{\mathrm{e}^{-i\alpha ^{2}\sin \theta }}{\sqrt{2}}\left[ \left( x_0 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}-x_1 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}\right. \right. \nonumber \\&\quad \left. \left. -\,x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}} \right) \otimes \left| {\alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q \right] . \end{aligned}$$
(5)

Subsequently, we utilize the measurement strategy of PNR detection (i.e., the converted voltage or current) on the probe beam. If the outcome of the measurement is \(\left| 0 \right\rangle _q \), then the output state \(\left| \varphi \right\rangle _\mathrm{MP} \) is given by \(\left| \varphi \right\rangle _\mathrm{MP} =x_0 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}+x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}\) in Eq. 5. Otherwise, the output state can be transformed into state \(\left| \varphi \right\rangle _\mathrm{MP} \) by feed-forward operation of the path-switch S and the phase-flip U operator. The probability of error of the MP gate, \(P_\mathrm{err}^\mathrm{MP} \), which is the probability of detecting \(\left| 0 \right\rangle _q \) (no photon) in \(\left| {\alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q \), in Eq. 5 is calculated as \(P_\mathrm{err}^\mathrm{MP} =\mathrm{e}^{-2\alpha ^{2}\left( {1-\cos \theta } \right) }/2\). This error probability, \(P_\mathrm{err}^\mathrm{MP} \), is exactly same as \(P_\mathrm{err}^\mathrm{CPRk} =\mathrm{e}^{-\alpha ^{2}\theta ^{2}}/2\) of the CPRk gate for the weak XKNL (\(\theta<<1)\). So, this MP gate is also nearly deterministic with a certain probability of success (\(P_\mathrm{err}^\mathrm{MP} \rightarrow 1)\) because \(P_\mathrm{err}^\mathrm{MP} \) is smaller than \(10^{-4}\) when \(\alpha \theta >\pi \). Then, we finally cross the two paths of the state \(\left| \varphi \right\rangle _\mathrm{MP} \) (the crossing-path in Fig. 2). The output state, \(\left| \mathbf{\Phi } \right\rangle _{\hbox {fin}} \), of the CPRkMP gate is given by

$$\begin{aligned} \left| {\varvec{\Phi }} \right\rangle _{\hbox {fin}} =x_0 \left| 0 \right\rangle ^{\hbox {a}}\left| 0 \right\rangle ^{\hbox {b}}+x_1 \left| 1 \right\rangle ^{\hbox {a}}\left| 0 \right\rangle ^{\hbox {b}}+x_2 \left| 0 \right\rangle ^{\hbox {a}}\left| 1 \right\rangle ^{\hbox {b}}+x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a}}\left| 1 \right\rangle ^{\hbox {b}}, \end{aligned}$$
(6)

where the paths of two photons are swapped with each other. Consequently, this state \(\left| {\varvec{\Phi }} \right\rangle _{\hbox {fin}} \), in Eq. 6, which is transformed via the CPRkMP gate using the XKNLs, the displacement operators and the PNR measurement, is identical to the state \(\left| \varphi \right\rangle _{\hbox {fin}} \) in Eq. 2 by the CRkS operation (\(U_\mathrm{CRkS} )\) in Fig. 1.

Fig. 3
figure 3

The two-qubit DQFT using CR2S and two Hadamard operations is equivalent to two-photon DQFT, which is implemented by a CPR2MP gate and two HWPs. The Hadamard operation can be fulfilled with an HWP, which rotates the polarization of a photon

Full size image

For the simple example, we consider two-qubit DQFT, which employs a CR2S operation and two Hadamard operators. The two-qubit DQFT is deterministically realized using the proposed CPR2MP (CPR2 + MP) gate and two half-wave plates (HWPs), as described in Fig. 3. Furthermore, the construction of two-photon DQFT can be generalized to realize n-photon DQFT by the composition of the CPRkMP gates \(\left( {k=2,\ldots ..,n} \right) \) and HWPs.

Consequently, DQFT, in Fig. 1, based on the CRkS operations, is experimentally simulated by the CPRkMP gates in Fig. 2. Our CPRkMP gate is consisted of the consecutive operation of the CPRk gate and the MP gate. We utilize the weak XKNLs, the displacement operators and the PNR measurements for our optical gates. The fundamental concepts of our gates (CPRk and MP) are affected from the controlled path gates and the merging gates as described in Refs. [26, 35–37]. However, compared with the existed optical gates in Refs. [26, 35–37], we designed our gates using the displacement operators and the PNR measurements to consider of the experimentally implementation under the decoherence effect, and to prevent evolving to mixed state by the photon loss and the dephasing in the practical optical fiber [44, 45]. Thus, in the next section, we will show the detail analysis of our gate under the decoherence effect when implemented the CPRkMP gate in practice.

3 Controlled path-\(R_k \) gate and merging path gate using XKNLs under decoherence effect

In a practical implementation of the CPRk gate and the MP gate, the transformed states \(\left| \phi \right\rangle _D \), in Eq. 3, and \(\left| \varphi \right\rangle _D \), in Eq. 5, of the signal-probe system will be mixed states due to the decoherence effect in the nonlinear media (XKNLs: \(\theta \) and \(-\theta )\) of the CPRk gate and the MP gate. The important factor about decoherence in states \(\left| \phi \right\rangle _D \) and \(\left| \varphi \right\rangle _D \) is photon loss (energy decay) in the probe beam. We consider the decoherence effect in the Kerr medium. The decoherence effect of the state is described by solving the master equation [49]:

$$\begin{aligned} \frac{\partial \rho }{\partial t}=\hat{{J}}\rho +\hat{{L}}\rho ,\hat{{J}}\rho =\gamma a\rho a^{+},\hat{{L}}\rho =-\frac{\gamma }{2}\left( {a^{+}a\rho +\rho a^{+}a} \right) , \end{aligned}$$
(7)

where \(\gamma \) is the energy decay rate. The solution to Eq. 7 can be written as \(\rho \left( t \right) =\mathrm{e}^{\left[ {\left( {\hat{{J}}+\hat{{L}}} \right) t} \right] }\rho \left( 0 \right) \), where \(t\left( {=\theta /\chi } \right) \) is the interaction time. Thus, the probe beam \(\left| \alpha \right\rangle \) loses photons in the first nonlinear medium as \(\left| {\Lambda _t \alpha } \right\rangle \) where \(\Lambda _t =\mathrm{e}^{-\gamma t/2}\) (the photon decay rate). If the initial density operator is \(\left| \alpha \right\rangle \left\langle \beta \right| \), decoherence effect \(\tilde{D}_{\Delta t} \) can be described as \(\tilde{D}_{\Delta t} \left( {\left| \alpha \right\rangle \left\langle \beta \right| } \right) =\exp \left[ {-\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \left\{ {-\alpha \beta ^{{*}}+\left( {\left| \alpha \right| ^{2}+\left| \beta \right| ^{2}} \right) /2} \right\} } \right] \left| {\Lambda _{\Delta t} \alpha } \right\rangle \left\langle {\Lambda _{\Delta t} \beta } \right| \) for \(\Delta t\). Note that decoherence effect \(\tilde{D}_{\Delta t} \) simultaneously occurs with XKNL interaction \(\tilde{X}_{\Delta t} \) by the Hamiltonian \(H_\mathrm{Kerr} \) in the nonlinear medium. This process (decoherence + XKNL) can be modeled as follows [44, 45]:

$$\begin{aligned}&\left( {\tilde{D}_{\Delta t} \tilde{X}_{\Delta t} } \right) \left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| \alpha \right\rangle \left\langle \alpha \right| \nonumber \\&\quad =\hbox {exp}\left[ {-\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \left( {1-\mathrm{e}^{i\Delta \theta }} \right) } \right] \left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| {\Lambda _{\Delta t} \alpha \mathrm{e}^{i\Delta \theta }} \right\rangle \left\langle {\Lambda _{\Delta t} \alpha } \right| , \end{aligned}$$
(8)

where signal state \(\left| {1^{s}} \right\rangle \) (here, \(1^{s}\) means a single photon and the polarization s) is a control photon to drive the phase shift of the XKNL interaction, which can be described as \(\tilde{X}_{\Delta t} \left( {\left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| \alpha \right\rangle \left\langle \alpha \right| } \right) \rightarrow \left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| {\alpha \mathrm{e}^{i\Delta \theta }} \right\rangle \left\langle \alpha \right| \) where \(\Delta \theta =\chi \Delta t\) for \(\alpha \in \mathbf{R}\). Also, \(\hbox {exp}\left[ {-\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \left( {1-\mathrm{e}^{i\Delta \theta }} \right) } \right] \) is the coherent parameter to quantify the degree of dephasing by this process (decoherence + XKNL). We assume that interaction time \(\Delta t\) of \(\tilde{D}\) (decoherence) and \(\tilde{X}\) (XKNL) is arbitrarily small to obtain a good approximation of this process. In our analysis, as described in Jeong [44, 45], we chose \(N=10^{6}\) of time \(t\left( {=N\Delta t} \right) \) and \(\theta =\chi t=N\Delta \theta =\chi N\Delta t\) for this process. This value gives a good approximation against the induced coherent parameters in the CPRk gate and the MP gate of the proposed CPRkMP gate for the whole range (the amplitude of the probe beam) of \(\alpha \). For example, if the initial state \(\left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| \alpha \right\rangle \left\langle \alpha \right| \) of the signal-probe system, as in Eq. 8, evolves by this process for time \(t\left( {=N\Delta t} \right) \), it is given by

$$\begin{aligned}&\left( {\tilde{D}_{\Delta t} \tilde{X}_{\Delta t} } \right) ^{N}\left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| \alpha \right\rangle \left\langle \alpha \right| \nonumber \\&\quad =\hbox {exp}\left[ {-\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \sum _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{in\Delta \theta }} \right) } } \right] \left| {1^{s}} \right\rangle \left\langle 0 \right| \otimes \left| {\Lambda _t \alpha \mathrm{e}^{i\theta }} \right\rangle \left\langle {\Lambda _t \alpha } \right| ,\nonumber \\ \end{aligned}$$
(9)

where \(\Lambda _t =\mathrm{e}^{-\gamma t/2}\), \(\theta =N\Delta \theta \), and \(N=10^{6}\). We can quantify the degree of dephasing by the coherent parameter \(C\hbox { = exp}\left[ {-\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{in\Delta \theta }} \right) } } \right] \).

As we mentioned in Sect. 2.2, our gates employed the displacement operators and the PNR measurements to acquire the robustness against the decoherence effect. If the measurement strategy of the homodyne (X or P) is applied to the optical gates as describe in [26–30], the output states of the optical gates will be mixed states due to the photon loss and the dephasing, and then the fidelities of the optical multi-qubit gates will decrease [43–47] in practice. Therefore, we analyze our gates (CPRk, MP) using the simulation of the photon loss and the dephasing, which can be modeled as the process (decoherence + XKNLs) [44, 45] in Eqs. 8 and 9. And then, we demonstrate that the deterministic CPRk gate and MP gate, \(\left( {P_\mathrm{err}^\mathrm{CPRk} =P_\mathrm{err}^\mathrm{MP} \approx 10^{-4}} \right. \) for \(\left. {\alpha \theta =\pi } \right) \), which utilize the XKNLs, the displacement operators and PNR measurements as described in Sect. 2.2, can obtain to decrease the photon loss and the dephasing due to the decoherence effect by increasing the amplitude of the probe beam (\(\alpha )\) when experimentally implemented.

In a laboratory, when we realize the experimental implementation of our gates using the optical fiber and Kerr medium, it is known that an optical fiber of about 3000 km is needed for phase shift \(\theta =\pi \) of the XKNL [50, 51]. Thus, the amplitude (photons) will reduce at rate \(\mathrm{e}^{-\gamma t}\), while \(\theta =\pi \) is obtained for 3000 km, according to \(\chi /\gamma =0.0303\). This value (\(\chi /\gamma =0.0303)\) corresponds to the signal loss (\(0.15\,\hbox {dB/km})\), which is achieved using pure silica core fibers [52] in the current technology. When operating our CPRk gate and MP gate in practical terms, first we consider photon loss (without dephasing) of the decoherence effect for a fixed \(\alpha \theta =\pi \), as in Sect. 2.2. The resulting states \(\left| \phi \right\rangle _D \) of Eq. 3 and \(\left| \varphi \right\rangle _D \) of Eq. 5 should be modified to allow for photon loss (\(\Lambda _t =\mathrm{e}^{-\gamma t/2})\). The modified resulting state \(\left| {{\phi }'} \right\rangle _D \) of the CPRk gate is given by

$$\begin{aligned} \left| {{\phi }'} \right\rangle _D= & {} \frac{1}{\sqrt{2}}\left[ \left| A \right\rangle \left| 0 \right\rangle _p +\left| B \right\rangle \left| 0 \right\rangle _p +\mathrm{e}^{-i\Lambda _t^4 \alpha ^{2}\sin \theta }\left| C \right\rangle \left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _p \right. \nonumber \\&\left. +\,\mathrm{e}^{i\Lambda _t^4 \alpha ^{2}\sin \theta }\left| D \right\rangle \left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{i\theta }-1} \right) } \right\rangle _p \right] , \end{aligned}$$
(10)

where we denote \(\left| A \right\rangle \equiv x_0 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 0 \right\rangle ^{\hbox {b}}\), \(\left| B \right\rangle \equiv x_1 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}+x_3 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 1 \right\rangle ^{\hbox {b}}\), \(\left| C \right\rangle \equiv x_0 \left| 0 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle ^{\hbox {b}}\) and \(\left| D \right\rangle \equiv x_1 \left| 0 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}}+x_3 \left| 1 \right\rangle ^{\hbox {a.0}}\left| 1 \right\rangle ^{\hbox {b}}\), conventionally, in Eq. 3. Also, because of the photon loss by the decoherence effect, we should utilize the displacement operator \(D\left( {-\Lambda _t^2 \alpha } \right) \left| {\Lambda _t^2 \alpha \mathrm{e}^{\pm i\theta }} \right\rangle _p =\mathrm{e}^{\pm i\Lambda _t^4 \alpha ^{2}\sin \theta }\left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{\pm i\theta }-1} \right) } \right\rangle _p \) instead of \(D\left( {-\alpha } \right) \). And the modified result state \(\left| {{\varphi }'} \right\rangle _D \) of the MP gate is given by

$$\begin{aligned} \left| {{\varphi }'} \right\rangle _D =\frac{1}{\sqrt{2}}\left[ {\left| {M^{+}} \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle _q +\mathrm{e}^{-i\Lambda _t^2 \alpha ^{2}\sin \theta }\left| {M^{-}} \right\rangle ^{\hbox {a.0}}\left| {\Lambda _t^ \alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q } \right] , \end{aligned}$$
(11)

where we denote \(\left| {M^{\pm }} \right\rangle ^{\hbox {a.x}}\equiv x_0 \left| 0 \right\rangle ^{\hbox {a.x}}\left| 0 \right\rangle ^{\hbox {b}}\pm x_1 \left| 0 \right\rangle ^{\hbox {a.x}}\left| 1 \right\rangle ^{\hbox {b}}+x_2 \left| 1 \right\rangle ^{\hbox {a.x}}\left| 0 \right\rangle ^{\hbox {b}}\pm x_3 \mathrm{e}^{i2\pi /2^{k}}\left| 1 \right\rangle ^{\hbox {a.x}}\left| 1 \right\rangle ^{\hbox {b}}\), conventionally, in Eq. 5. And we should change the displacement operator \(D\left( {-\alpha } \right) \) to \(D\left( {-\Lambda _t \alpha } \right) \left| {\Lambda _t \alpha \mathrm{e}^{-i\theta }} \right\rangle _q =\mathrm{e}^{-i\Lambda _t^2 \alpha ^{2}\sin \theta }\left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q \) in Fig. 2. For the fixed \(\alpha \theta =\pi \) in the optical fiber having the signal loss (\(0.15\,\hbox {dB/km})\), we calculate the probabilities of success, \(P_\mathrm{succ}^\mathrm{CPRk} \) (in the CPRk gate) and \(P_\mathrm{succ}^\mathrm{MP} \) (in the MP gate), of the performance after taking the PNR measurement and the values of \(\Lambda _t^4 \) (in CPRk gate) and \(\Lambda _t^2 \) (in MP gate) due to photon loss \(\Lambda _t \), according to the increasing amplitude of the probe beam (\(\alpha )\), as shown in Fig. 4. The probabilities of success \(P_\mathrm{succ}^\mathrm{CPRk} \left( {=1-P_\mathrm{err}^\mathrm{CPRK} } \right) \) and \(P_\mathrm{succ}^\mathrm{MP} \left( {=1-P_\mathrm{err}^\mathrm{MP} } \right) \), which are obtained from probabilities of error \(P_\mathrm{err}^\mathrm{CPRK} \) to detect \(\left| 0 \right\rangle _p \) in \(\left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{\pm i\theta }-1} \right) } \right\rangle _p \) of Eq. 10 and \(P_\mathrm{err}^\mathrm{MP} \) to detect \(\left| 0 \right\rangle _q \) in \(\left| {\Lambda _t^ \alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q \) of Eq. 11, are given by

Fig. 4
figure 4

When only considering photon loss by the decoherence effect and the fixed value \(\alpha \theta =\pi \) via the optical fiber with \(\chi /\gamma =0.0303 \quad \left( {0.15\,\hbox {dB/km}} \right) \), the probabilities of success \(P_\mathrm{succ}^\mathrm{CPRk} \) (black dotted line) of the CPRk gate and \(P_\mathrm{succ}^\mathrm{MP} \) (black line) of the MP gate, and the rates of photon loss \(\Lambda _t^4 \) (red dotted line) and \(\Lambda _t^2 \) (red line) are plotted depending on the amplitude of the probe beam, \(\alpha \). For \(\alpha <500\), the plot shows \(P_\mathrm{err}^\mathrm{CPRk} \approx P_\mathrm{err}^\mathrm{MP} >10^{-3}\), and \(\Lambda _t^4 <0.66\) and \(\Lambda _t^2 <0.8\) (Color figure online)

Full size image
$$\begin{aligned} \begin{array}{l} P_\mathrm{err}^\mathrm{CPRK} =1-\exp [-\Lambda _t^4 \cdot \left( {\alpha \theta } \right) ^{2}]/2=1-\exp [-\mathrm{e}^{-2\pi /\left( {0.0303} \right) \cdot \alpha }\cdot \pi ^{2}]/2, \\ P_\mathrm{err}^\mathrm{MP} =1-\exp [-\Lambda _t^2 \cdot \left( {\alpha \theta } \right) ^{2}]/2=1-\exp [-\mathrm{e}^{-\pi /\left( {0.0303} \right) \cdot \alpha }\cdot \pi ^{2}]/2, \\ \end{array} \end{aligned}$$
(12)

for the fixed values \(\alpha \theta =\alpha \chi t=\pi \) and \(\chi /\gamma =0.0303\left( {0.15\,\hbox {dB/km}} \right) \) where \(\Lambda _t =\mathrm{e}^{-\gamma t/2}\) (the photon decay rate). This means that if the amplitude of the coherent state is \(\alpha <500\), the probabilities of error \(P_\mathrm{err}^\mathrm{CPRK} \), \(P_\mathrm{err}^\mathrm{MP} \) for our CPRk and MP gates are larger than \(10^{-3}\) because of the rapidly decreasing values of \(\Lambda _t^4 \) and \(\Lambda _t^2 \) (increasing the rate of photon decay). Thus, we can obtain the reliable CPRk and MP gates, against the photon loss, by increasing the amplitude of the probe beam.

Furthermore, in practical performance of the gate, we also have to consider that photon loss coincides with dephasing in our CPRkMP gate. This can be modeled as the process (decoherence + XKNLs) [44, 45] in Eqs. 8 and 9. Thus, the output state (Eq. 3) of the CPRk gate, which evolves by photon loss and dephasing, will be mixed state \(\rho _D^\mathrm{CPRk} \) (a density matrix) as follows:

$$\begin{aligned} \rho _D^\mathrm{CPRk} =\frac{1}{2}\left( {{\begin{array}{cccc} 1&{} {K^{*}\cdot C^{*}}&{} {L\cdot \mathrm{e}^{i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} {\mathrm{O}^{*}\cdot C^{*}\cdot \mathrm{e}^{-i\Lambda _t^4 \alpha ^{2}\sin \theta }} \\ {K\cdot C}&{} 1&{} {\mathrm{O}\cdot C\cdot \mathrm{e}^{i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} {L^{*}\cdot \mathrm{e}^{-i\Lambda _t^4 \alpha ^{2}\sin \theta }} \\ {L^{*}\cdot \mathrm{e}^{-i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} {\mathrm{O}^{*}\cdot C^{*}\cdot \mathrm{e}^{-i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} 1&{} {\mathrm{M}^{*}\cdot C^{*}\cdot \mathrm{e}^{-2i\Lambda _t^4 \alpha ^{2}\sin \theta }} \\ {\mathrm{O}\cdot C\cdot \mathrm{e}^{i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} {L\cdot \mathrm{e}^{i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} {\mathrm{M}\cdot C\cdot \mathrm{e}^{2i\Lambda _t^4 \alpha ^{2}\sin \theta }}&{} 1 \\ \end{array} }} \right) , \end{aligned}$$
(13)

where the basis states of the signal-probe system are \(\left| A \right\rangle \left| 0 \right\rangle _p \), \(\left| B \right\rangle \left| 0 \right\rangle _p \), \(\left| C \right\rangle \left| \Lambda _t^2 \alpha \right. .\left. . \left( {\mathrm{e}^{-i\theta }-1} \right) \right\rangle _p \)and \(\left| D \right\rangle \left| {\Lambda _t^2 \alpha \left( {\mathrm{e}^{i\theta }-1} \right) } \right\rangle _p \) from left to right and top to bottom. Also, \(C\hbox { = exp}\left[ {-\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{in\Delta \theta }} \right) } } \right] \) and the other coherent parameters (K, L, M and O) of the off-diagonal terms, which are calculated by the decoherence (\(\tilde{D}_t )\) and the XKNLs (\(\tilde{X}_t )\) [44, 45], are given by

$$\begin{aligned} K= & {} \hbox {exp}\left[ {-\alpha ^{2}\mathrm{e}^{-\gamma t}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{-i\cdot \left( {n\Delta \theta -\theta } \right) }} \right) } } \right] ,\nonumber \\ L= & {} \hbox {exp}\left[ {-\alpha ^{2}\mathrm{e}^{-\gamma t}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \cdot \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{in\Delta \theta }} \right) } } \right] \nonumber \\ M= & {} \hbox {exp}\left[ {-\alpha ^{2}\mathrm{e}^{-\gamma t}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{i\cdot \left( {n\Delta \theta +\theta } \right) }} \right) } } \right] ,\nonumber \\ O= & {} \hbox {exp}\left[ {-\alpha ^{2}\mathrm{e}^{-\gamma t}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \left( {1-\mathrm{e}^{i\theta }} \right) \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}} } \right] \end{aligned}$$
(14)

And the output state \(\rho _D^\mathrm{MP} \), which is evolved to a mixed state by the decoherence effect, of the MP gate is given by

$$\begin{aligned} \rho _D^\mathrm{MP} =\frac{1}{2}\left( {{\begin{array}{ccc} 1&{} {C^{*}\cdot \mathrm{e}^{i\Lambda _t^2 \alpha ^{2}\sin \theta }} \\ {C\cdot \mathrm{e}^{-i\Lambda _t^2 \alpha ^{2}\sin \theta }}&{} 1 \\ \end{array} }} \right) , \end{aligned}$$
(15)

where the basis states of the signal-probe system are \(\left| {M^{+}} \right\rangle ^{\hbox {a.1}}\left| 0 \right\rangle _q \) and \(\left| {M^{-}} \right\rangle ^{\hbox {a.0}}\left| {\Lambda _t^ \alpha \left( {\mathrm{e}^{-i\theta }-1} \right) } \right\rangle _q \) from left to right and top to bottom, and \(C\hbox { = exp}\left[ -\alpha ^{2}\left( {1-\mathrm{e}^{-\gamma \Delta t}} \right) \right. \left. \mathop {\sum }\limits _{n=1}^N {\mathrm{e}^{-\gamma \left( {n-1} \right) \Delta t}\left( {1-\mathrm{e}^{in\Delta \theta }} \right) } \right] \). From the coherent parameters (C, K, L, M and O, in Eq. 14), we can obtain a good approximation of the coherent parameters for \(t=N\Delta t\), \(\theta =N\Delta \theta \) and \(N=10^{6}\). And for the fixed \(\alpha \theta =\alpha \chi t=\pi \left( {P_\mathrm{err}^\mathrm{CPRk} =P_\mathrm{err}^\mathrm{MP} \approx 10^{-4}} \right) \), our CPRk and MP gates operate in optical fiber with signal loss \(0.15\,\hbox {dB/km }\left( {\chi /\gamma =0.0303} \right) \) [52]. If we use the strategy measurement of homodyne without the displacement operator in our gate, like as Ref. [26], the absolute values of coherent parameters rapidly decrease to zero [44, 45]. This means that the completely dephased states (the output states, \(\rho _D^\mathrm{CPRk} \) and \(\rho _D^\mathrm{MP} \), of the CPRk and MP gates) of the signal-probe system are no longer the pure quantum states; i.e., the DQFT gate completely fails.

Fig. 5
figure 5

When considering photon loss and dephasing by the decoherence effect, and XKNLs for the fixed values \(\alpha \theta =\pi \) and \(N=10^{6}\) via the optical fiber with \(\chi /\gamma =0.0303 \quad \left( {0.15\,\hbox {dB/km}} \right) \), the absolute values of coherent parameters in \(\rho _D^\mathrm{CPRk} \) and \(\rho _D^\mathrm{MP} \) are plotted depending on the increase in amplitude of the probe beam, \(\alpha \). This means that the increasing \(\alpha \) can converge coherent parameters at 1 in our CPRkMP under the decoherence effect (Color figure online)

Full size image
Fig. 6
figure 6

When the fixed \(\alpha \theta =\alpha \chi t=\pi \left( {P_\mathrm{err} \approx 10^{-4}} \right) \) and \(\chi /\gamma =0.0303\left( {0.15\,\hbox {dB/km}} \right) \), the absolute values of the coherent parameters in \(\rho _D^\mathrm{CPRk} \) (Eq. 13) and \(\rho _D^\mathrm{MP} \) (Eq. 15) are expressed for increasing the amplitude of the probe beam, \(\alpha \), in (1), (2), (a, b). Also, the fidelities \(F^\mathrm{C}\) of \(\rho _D^\mathrm{CPRk} \) (the output \(\left| {{\phi }'} \right\rangle _D \) in Eq. 10) and \(F^\mathrm{M}\) of \(\rho _D^\mathrm{MP} \) (the output \(\left| {{\varphi }'} \right\rangle _D \) in Eq. 11), according to amplitude\(\alpha \), are calculated by \(F^\mathrm{C}=\left| {\sqrt{\left\langle {{\phi }'} \right| \rho _D^\mathrm{CPRk} \left| {{\phi }'} \right\rangle _D }} \right| /2\) and \(F^\mathrm{M}=\left| {\sqrt{\left\langle {{\varphi }'} \right| \rho _D^\mathrm{MP} \left| {{\varphi }'} \right\rangle _D }} \right| \). For reliable performances of the CPRk and MP gates under the decoherence effect, the amplitude \(\alpha \) should be increased in accordance with fidelities (Color figure online)

Full size image

Figure 5 shows that our CPRkMP gate, which employs displacement operators, \(D\left( {-\Lambda _t^2 \alpha } \right) \) in the CPRk gate and \(D\left( {-\Lambda _t^ \alpha } \right) \) in the MP gate, and the PNR measurements, does not suffer the rapid dephasing of the off-diagonal terms in Eqs. 13 (\(\rho _D^\mathrm{CPRk} )\) and 15 (\(\rho _D^\mathrm{MP} )\). When increasing the amplitude of the probe beam, \(\alpha \), using optical fiber having signal loss \(0.15\,\hbox {dB/km }\left( {\chi /\gamma =0.0303} \right) \) [52] for a fixed \(\alpha \theta =\alpha \chi t=\pi \quad \left( {P_\mathrm{err}^\mathrm{CPRk} =P_\mathrm{err}^\mathrm{MP} \approx 10^{-4}} \right) \), the absolute values of coherent parameters can approach 1, where \(t=N\Delta t\), \(\theta =N\Delta \theta \), and \(N=10^{6}\). Thus, our gate, using the displacement operators and PNR measurements, prevents the decreasing degree of the dephasing coherent parameters by increasing amplitude of \(\alpha \) under the decoherence effect and XKNLs. Furthermore, the analysis of the performances of the CPRk and MP gates in the CPRkMP gate is important under the decoherence effect, because the proposed DQFT scheme is composed of our CPRkMP gates. When fixed \(\alpha \theta =\pi \) (\(P_\mathrm{err} \approx 10^{-4})\) in optical fiber has signal loss \(0.15\,\hbox {dB/km } \left( {\chi /\gamma =0.0303} \right) \) [52], Fig. 6 shows the needed \(\theta \) (phase shift: XKNL) and the length of the optical fiber in terms of the increasing amplitude of the probe beam, \(\alpha \). Also \(\left( 1 \right) \), \(\left( 2 \right) \), \(\left( \hbox {a} \right) \) and \(\left( \hbox {b} \right) \) represent the absolute values of coherent parameters in \(\rho _D^\mathrm{CPRk} \) (in Eq. 13) and \(\rho _D^\mathrm{MP} \) (in Eq. 15), depending on the amplitude of \(\alpha \). For experimentally reliable performances of the CPRk and MP gates, the output states should be the pure states, which has off-diagonal terms (coherent parameters) of 1, as \(\left| {{\phi }'} \right\rangle _D \) and \(\left| {{\varphi }'} \right\rangle _D \) in Eqs. 10 and 11. If the output states are mixed state \(\rho _D^\mathrm{CPRk} \) and \(\rho _D^\mathrm{MP} \) (the values of off-diagonal terms are not 1) by photon loss and dephasing, these can approach the pure states as \(\left| {{\phi }'} \right\rangle _D \) and \(\left| {{\varphi }'} \right\rangle _D \) (the off-diagonal terms of 1) by the increasing amplitude of the probe beam, \(\alpha \). For this and reliable performance of our CPRkMP gate, we can calculate the fidelities (\(F^\mathrm{C}\): CPRk gate, \(F^\mathrm{M}\): MP gate) that give a useful metric to quantitatively analyze the proposed gate. In Fig. 6, we prepare for the initial amplitude of the probe beam, \(\alpha \), to be larger, \(\alpha _{\left( {\hbox {1, a}} \right) } <\alpha _{\left( {\hbox {2, b}} \right) } =1\times 10^{6}\), and the output states \(\rho _D^\mathrm{CPRk} \) and \(\rho _D^\mathrm{MP} \) to be closer to the pure states \(\left| {{\phi }'} \right\rangle _D \) and \(\left| {{\varphi }'} \right\rangle _D \) for \(F_{\left( 1 \right) }^C <F_{\left( 2 \right) }^C \approx 0.999\) and \(F_{\left( \hbox {a} \right) }^M <F_{\left( \hbox {b} \right) }^M \approx 0.999\) where \(F^\mathrm{C}=\left| {\sqrt{\left\langle {{\phi }'} \right| \rho _D^\mathrm{CPRk} \left| {{\phi }'} \right\rangle _D }} \right| /2\) and \(F^\mathrm{M}=\left| {\sqrt{\left\langle {{\varphi }'} \right| \rho _D^\mathrm{MP} \left| {{\varphi }'} \right\rangle _D }} \right| \). When a fixed \(\alpha \theta =\pi \) (\(P_\mathrm{err} \approx 10^{-4})\) in the optical fiber has a \(0.15\,\hbox {dB/km}\) signal loss (\(\chi /\gamma =0.0303)\), our CPRk and MP gates can attain reliable performance (\(F^\mathrm{C}, F^\mathrm{M}\rightarrow 1)\) by the increasing amplitude of \(\alpha \) with the displacement operators and PNR measurements under the decoherence effect.

Consequently, our CPRkMP (CPRk + MP) gate is based on the controlled path and merging gates in [26, 35–37]. But our gate employed the displacement operators and the PNR measurements, unlike [26, 35–37], to decrease the decoherence effect. Compared with the existing gates in [26, 35–37], in our gate, we considered of the photon loss and the decreasing coherent parameters (dephasing) due to the decoherence effect, and simulated to analyze the performance of our gate using the model of the process (decoherence + XKNL) as [44, 45] in practice. By the increasing amplitude of \(\alpha \) with the displacement operators and PNR measurements, instead of the homodyne detection [26], our gate has the reliable performance (the high fidelity of gate in the optical fiber) against the decoherence effect. Also, the number of the interaction of XKNLs in our CPRk gate (two times) is identical with the controlled path gate in Ref. [26] in comparison with the number of the interaction of XKNLs in the controlled path gates (four times, due to the structure of quantum bus beams) of Refs. [35–37]. It shows that our gate enhances the efficiency in terms of the interaction of XKNLs with the robustness against the decoherence effect. Furthermore, our gate can decrease the magnitudes of the phase shifts (\(\theta \) and \(-\theta )\) by XKNL because of the increasing amplitude of \(\alpha \) for decreasing the decoherence effect, as shown in Fig. 6. Therefore, compared with the existing DQFT schemes [21–24] using nonlinearities, our DQFT scheme based on the proposed CPRkMP gate is experimentally implemented with feasibility.

4 Conclusion

So far, we have proposed an optical DQFT scheme that can experimentally implement the operation of DQFT on qubits for quantum algorithms and quantum computations [4–6]. This DQFT scheme is composed of CPRkMP gates, which utilize weak XKNLs (nonlinearities) and HWPs described in Sect. 2.2. Compared with linear optical systems [17–20], the nonlinear optics system (XKNL) can implement some tasks of quantum information processing, including DQFT, [21–47] to assist indirect interactions between photons. Also, by using only the linear optical model, the probability of success for quantum information processing schemes [53–55] is less than unity, in theory. Thus, we utilized XKNLs in our CPRkMP gate, which can realize the optical DQFT scheme, to be nearly deterministic with a certain probability of success (\(P_\mathrm{succ}^\mathrm{CPRk+MP} \rightarrow 1)\). Furthermore, we employed the displacement operators and the PNR measurements to design a CPRkMP gate robust against the decoherence effect. In practice (in optical fiber), there is photon loss and dephasing by the decoherence effect in the performance of our CPRkMP gate. It inevitably leads to decreasing fidelity of the CPRkMP gate, and then our DQFT gate will totally fail. For analysis of the decoherence effect, we simulated photon loss and dephasing, which occurred in our gate, using the master equation [44, 45]. Subsequently, we showed that the efficiency (decreasing the magnitudes of the phase shifts) in terms of the interaction of XKNLs with the robustness (decreasing the dephasing coherent parameters) against the decoherence effect in our optical gate can be enhanced via increasing amplitude of \(\alpha \) with the displacement operators and the PNR measurements through the analysis as described in Sect. 3. Thus, our CPRkMP (CPRk + MP) gate can experimentally realize CRkS operation and augment the robustness with respect to decoherence by using the proposed techniques (the strong coherent state, the displacement operator, and PNR measurement).

In this paper, the basic structure of our gate (CPRk + MP) bases on the controlled path and the merging gates, which used the homodyne measurements or quantum bus beams and the PNR measurements, as described in Refs. [26, 35–37]. However, as the above-mentioned statements, we utilized the weak XKNLs, the displacement operators and the PNR measurements in the CPRk and MP (CPRkMP) gate to obtain the robustness against the decoherence effect by increasing amplitude of \(\alpha \). Compared with the optical gates in [26, 35–37] and the proposed CPRkMP gate, first, the strategy measurement of homodyne in the optical gate [26] cannot prevent evolving the output state to a mixed state by the decoherence effect [43–47]. Second, other optical gates in [35–37], which employed the quantum bus beams and the PNR measurements for the controlled operation of the output state, required four the interactions of XKNL (due to the structure of quantum bus beams) to avoid the induced \(-\theta \) phase shift (not easy realization according to [56]). Here, the advantages of the CPRkMP gate are as follows:

  1. 1.

    We designed our gate to enhance the robustness against the decoherence effect using the displacement operators and the PNR measurements, unlike the gate in [26]. So, our gate will be more feasible and robust, using the strong amplitude of \(\alpha \), than the optical gates in [26] under the decoherence effect.

  2. 2.

    According to Sect. 3 (the analysis, in Eqs. 8 and 9, of the photon loss and the dephasing), if the number of the interaction XKNLs increases (two times \(\rightarrow \) four times), the probabilities of success of the optical gates decrease and the output state rapidly evolves from the pure state to the mixed state. Namely, the simulation by the master equation (as Eqs. 8 and 9) shows that the number of the coherent parameters will rise by two times when increased the interactions (XKNLs), as the optical gates in Refs. [35–37], and then the absolute values of coherent parameters (the off-diagonal terms in density matrices of the output states of the optical gates in [35–37]) rapidly decrease to zero more than the output state of our CPRk gate. Therefore, we constructed the CPRk gate to minimize the number of the interactions of XKNL (two times: \(\theta \) and \(-\theta )\) using the displacement operator and the PNR measurements without quantum bus beams, unlike the controlled path gate (four the interactions of XKNL) in [35–37]. Unfortunately, Kok [56] has shown that it is generally not possible to change the sign of the conditional phase shift (\(-\theta )\). However, in the CPRk gate, to decrease the decoherence effect, we should increase the amplitude of \(\alpha \). And as a result, we can extremely reduce the magnitudes of the phase shifts (including the minus phase shift) as illustrated in Sect. 3, i.e., \(\theta =3.14\times 10^{-6}\) when \(\alpha =1\times 10^{6}\), as shown in Fig. 6. Although our CPRk gate needs the minus phase shift, the magnitude of the phase shift will be small by the increasing amplitude of \(\alpha \) to reduce the decoherence effect. And we expect this advantage (small phase shift) of our CPRk gate to contribute the near future development for the implementation of the minus phase shift.

In conclusion, our DQFT scheme based on CPRkMP gates, which have the advantages as above, is experimentally applicable with a certain probability of success under the decoherence effect beside previous DQFT schemes [21–24] via nonlinearity optical systems.