1 Introduction

Quantum teleportation and superdense coding are two intriguing tasks in quantum information processing [1, 2]. In quantum teleportation, one can “teleport ”an intact unknown state from one place to another by using a pre-shared bipartite entangled state, the so-called EPR pair, and sending two bits of classical information [1]. A pre-shared EPR pair also enables superdense coding, which can double the classical capacity of a communication channel [2]. Besides the recent physical realization schemes [3–5], there appear many new theoretical advances too [6–9], and the main focus of these new advances is to generalize the original bipartite teleportation and superdense coding schemes to the multi-party cases. However, due to the inevitable environmental effects, a maximal EPR pair cannot be always available and it was shown that non-maximal EPR pairs cannot enable perfect quantum teleportation [10, 11] and perfect superdense coding [12–14]. As the number of entangled particles increases, interesting states arise, which cannot be transformed into each other by stochastic local operations and classical communications (SLOCC) in general [15] with the exceptions of tripartite states in the asymptotic regime [16, 17]. Multipartite entangled states can be used as resource for various quantum information and communication tasks, and there are tasks that can be achieved with only a specific state [18]. Therefore, preparation of different kinds of multi-particle entangled states is of great importance. Preparing multi-particle entangled states by fusing states with fewer particles has been extensively studied, and progress in this direction has been made both theoretically and experimentally [19–31]. Among these multi-particle states, W states [32] form an important class of multipartite entangled states, with a robust structure against particle losses [33]. Therefore, in contrast to GHZ states [34], W states can still be used as a resource even after the loss of particles. Recently, the preparation schemes and applications of maximally entangled W states have attracted considerable attentions [19, 20, 35–46].

Besides bipartite entangled states, multipartite entangled states can be used for quantum teleportation and superdense coding too. What is more, being much more complicated than bipartite entanglement, multipartite entanglement introduces more diversity into the teleportation and superdense coding schemes. Maximally entangled W states have been used in quantum teleportation protocols [47, 48], but one needs to perform non-local operations to recover the unknown state [47]. That is to say, this limitation restrains the possibility to recover the unknown state using maximally entangled W states, i.e., the so-called prototype W states, resulting in only imperfect teleportation schemes [48]. Similar limitations arise for superdense coding with maximally entangled W states [49]. Because of these imperfections with W states, an intense effort has been devoted to finding a special class of W states which can enable perfect teleportation and superdense coding. Gorbachev et al. [50] proposed a detailed scheme for teleporting entangled states via the W-class state quantum channel. Agrawal et al. showed that there exists a special class of three-qubit W states that can be used for perfect teleportation and superdense coding [49], and then, Li et al. [51] generalized these schemes to the cases with W-class states in higher-dimension systems. This special class of W-like states (denoted by \(|\mathcal {W}\rangle _N\) in this paper) can be used for perfect teleportation and superdense coding, so it is of great importance to generate \(|\mathcal {W}\rangle _N\) states.

In this paper, we propose a scheme to prepare \(|\mathcal {W}\rangle _N\) states via a polarization-dependent beam splitter (PDBS)-based fusion or expansion mechanism for polarization encoded photons. As a by-product, a large-scale maximally entangled W state can be generated by fusing or expanding the \(|\mathcal {W}\rangle _N\) states too, and the results show that this scheme is more efficient than the one starting from maximally entangled W states [52]. This paper is organized as follows: In Sect. 2 , we introduce the PDBS and the fusion or expansion strategy for \(|\mathcal {W}\rangle _N\) states. The strategy for expending or fusing \(|\mathcal {W}\rangle _N\) states into large-scale maximally entangled W states is presented in Sect. 3. In Sect. 4, we discuss the resource cost of the fusion strategy for \(|\mathcal {W}\rangle _N\) states and the results are summarized in Sect. 5.

2 PDBS-based fusion and expansion strategies for \(|\mathcal {W}\rangle _N\) states

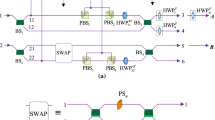
In this section, we show how to generate a large-scale \(|\mathcal {W}\rangle _N\) state by fusing or expanding small-size \(|\mathcal {W}\rangle _N\) states via a PDBS. A PDBS has polarization-dependent transmissivities: \(0<\mu <1\) for H polarization photons and \(0<\nu <1\) for V polarization photons. The function of the PDBS (as shown in red-dashed rectangle in Fig. 1) can be described by the following basic transformations [19],

$$\begin{aligned} |H\rangle _a|H\rangle _b\rightarrow & {} (2\mu -1)|H\rangle _ c|H\rangle _d + \sqrt{2\mu }\sqrt{1-\mu }|0\rangle _c|HH\rangle _d\nonumber \\&- \sqrt{2\mu }\sqrt{1-\mu }|HH\rangle _c|0\rangle _d, \end{aligned}$$
(1a)
$$\begin{aligned} |H\rangle _a|V\rangle _b\rightarrow & {} \sqrt{\mu }\sqrt{\nu }|H\rangle _c|V\rangle _d - \sqrt{1-\mu }\sqrt{1-\nu }|V\rangle _c|H\rangle _d \nonumber \\&+ \sqrt{1-\mu }\sqrt{\nu }|0\rangle _c|HV\rangle _d - \sqrt{\mu }\sqrt{1-\nu }|HV\rangle _c|0\rangle _d, \end{aligned}$$
(1b)
$$\begin{aligned} |V\rangle _a|H\rangle _b\rightarrow & {} \sqrt{\mu }\sqrt{\nu }|V\rangle _c|H\rangle _d - \sqrt{1-\mu }\sqrt{1-\nu }|H\rangle _c|V\rangle _d \nonumber \\&+ \sqrt{1-\mu }\sqrt{\nu }|0\rangle _c|VH\rangle _d - \sqrt{\mu }\sqrt{1-\nu }|VH\rangle _c|0\rangle _d, \end{aligned}$$
(1c)
$$\begin{aligned} |V\rangle _a|V\rangle _b\rightarrow & {} (2\nu -1)|V\rangle _ c|V\rangle _d + \sqrt{2\nu }\sqrt{1-\nu }|0\rangle _c|VV\rangle _d\nonumber \\&- \sqrt{2\nu }\sqrt{1-\nu }|VV\rangle _c|0\rangle _d. \end{aligned}$$
(1d)
Fig. 1
figure 1

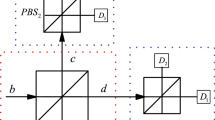
Fusion and detection mechanisms. The red-dashed rectangle represents the fusion mechanism, i.e., a PDBS. Two photons, one from \(|\mathcal {W}\rangle _A\) and the other from \(|\mathcal {W}\rangle _B\) are sent to the PDBS through input modes a and b, respectively. The corresponding output modes are labeled as c and d. The blue-dashed rectangles represent the detection mechanisms. The output photon from the mode c(d) is sent to the polarizing beam splitter (PBS), which reflects vertically (V)-polarized photons and transmits horizontally (H)-polarized photons, and the output modes of the PBSs are measured by detectors \(D_1\), \(D_2\), \(D_3\) and \(D_4\) (Color figure online)

Full size image

2.1 Creation of large-scale \(|\mathcal {W}\rangle \) states by fusing small-size \(|\mathcal {W}\rangle \) states

The special class of non-maximally entangled W states which can be used for perfect teleportation and superdense coding is found as [51]:

$$\begin{aligned} |\mathcal {W}\rangle _N= & {} \frac{1}{\sqrt{2}}[|HH\ldots HV\rangle _{1\ldots N}+\frac{1}{\sqrt{N-1}}(|HH\ldots VH\rangle _{1\ldots N}+\ldots +\nonumber \\&|VH\ldots HH\rangle _{1\ldots N})], (N\ge 2). \end{aligned}$$
(2)

To explain this class of W-like states, we first give the explicit expressions of the prototype W states [20], i.e., \(|W\rangle _n=\frac{1}{\sqrt{n}}[|({n-1})_H\rangle |1_V\rangle _1+\sqrt{n-1}|W_{n-1}\rangle |1_H\rangle _1]\). A tripartite W state is written as \(|W\rangle _3=\frac{1}{\sqrt{3}}(|HHV\rangle +|HVH\rangle +|VHH\rangle )=\frac{1}{\sqrt{3}}(|2_H\rangle |1_V\rangle _1+\sqrt{2}|W_2\rangle |1_H\rangle _1)\) with \(W_2\) being the W-type Bell pair, i.e., \(|W\rangle _2=\frac{1}{\sqrt{2}}(|HV\rangle +|VH\rangle )\) and obviously, a bipartite \(|\mathcal {W}\rangle \) state reduces to the \(|W\rangle _2\) state.

Firstly, let’s introduce the strategy for fusing a \(|\mathcal {W}\rangle _2\) and a \(|\mathcal {W}\rangle _3\) into a four-qubit \(|\mathcal {W}\rangle _4\) state. Two initial W-class states can be written as

$$\begin{aligned} |\mathcal {W}\rangle _2= & {} \frac{1}{\sqrt{2}}[|H\rangle |V\rangle _a+|V\rangle |H\rangle _a], \end{aligned}$$
(3a)
$$\begin{aligned} |\mathcal {W}\rangle _3= & {} \frac{1}{\sqrt{2}}[|HH\rangle |V\rangle _b+\frac{1}{\sqrt{2}}(|HV\rangle |H\rangle _b+|VH\rangle |H\rangle _b)]. \end{aligned}$$
(3b)

In the fusion strategy, we only have access to one photon of each W-class state, i.e., photons a, b. Photon a is from \(|\mathcal {W}\rangle _2\) and b from \(|\mathcal {W}\rangle _3\), and they will be sent into the PDBS for completing the fusion process (as shown in Fig. 1). The remaining photons are kept intact at their sites. We are only interested in the case where a photon is present in each of the modes c and d. So the state after the PDBS can be written as

$$\begin{aligned}&\frac{1}{2}[(2\nu -1)|HHH\rangle |V\rangle _c|V\rangle _d-\frac{1}{\sqrt{2}}\sqrt{1-\mu }\sqrt{1-\nu }|HHV\rangle |H\rangle _c|V\rangle _d\nonumber \\&\quad +\frac{1}{\sqrt{2}}\sqrt{\mu }\sqrt{\nu }|HHV\rangle |V\rangle _c|H\rangle _d\nonumber \\&\quad -\frac{1}{\sqrt{2}}\sqrt{1-\mu }\sqrt{1-\nu }|HVH\rangle |H\rangle _c|V\rangle _d+\frac{1}{\sqrt{2}}\sqrt{\mu }\sqrt{\nu }|HVH\rangle |V\rangle _c|H\rangle _d\nonumber \\&\quad -\sqrt{1-\mu }\sqrt{1-\nu }|VHH\rangle |V\rangle _c|H\rangle _d+\sqrt{\mu }\sqrt{\nu }|VHH\rangle |H\rangle _c|V\rangle _d]. \end{aligned}$$
(4)

As shown in Fig. 1 (blue-dashed rectangles), the detection mechanisms are placed after the output modes c and d. It seems that the two photons are all detected during the fusion mechanism. Actually, only one photon detection is needed for the completion of the fusion process, and the other photon detection is only done for the verification of the event where a photon is present in each of the two output modes of the PDBS. As discussed in Ref. [53], the second photon detection can be replaced with a connection to a further optical circuit to complete further applications of the output \(|\mathcal {W}\rangle _N\) state. That is to say, the verification process of the event where a photon is present in each of the two output modes of the PDBS and the applications of the output state are realized simultaneously. If an V-polarized photon is detected in \(D_2\), a four-qubit W-like state will be generated as

$$\begin{aligned} \frac{1}{2}C_1[|HHH\rangle |V\rangle _c+C_2|HHV\rangle |H\rangle _c+C_3|HVH\rangle |H\rangle _c+C_4|VHH\rangle |H\rangle _c], \end{aligned}$$
(5)

with

$$\begin{aligned} C_1= & {} 2\nu -1\nonumber ,\\ C_2= & {} C_3=-\frac{1}{\sqrt{2}}\frac{\sqrt{1-\mu }\sqrt{1-\nu }}{2\nu -1}\nonumber ,\\ C_4= & {} \frac{\sqrt{\mu }\sqrt{\nu }}{2\nu -1}. \end{aligned}$$
(6)

Obviously, we can obtain a \(|\mathcal {W}\rangle _4\) with \(|C_2|=|C_3|=|C_4|=\frac{1}{\sqrt{3}}\), which means that the parameter \(\nu \) for the PDBS must satisfy \(4\nu ^{3}+3\nu ^{2}-6\nu +1=0\). So, we can get the corresponding values of \((\nu , \mu )\), and the success probability \(Ps(|\mathcal {W}\rangle _4)=(2\nu -1)^2/2\). It should be noted that \((\nu , \mu )\) are defined in the range (0, 1). Thus the values of (\(\nu \), \(\mu \)) are (0.7726, 0.1283) or (0.1890, 0.6823). As \(\nu \) has two possible values, so does the success probability \(Ps(|\mathcal {W}\rangle _4)\). Therefore, \(Ps(|\mathcal {W}\rangle _4)\) can be maximized by choosing one set (\(\nu \), \(\mu \)) from the two possible sets.

This scheme can be generalized to the case of fusing a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state into a \(|\mathcal {W}\rangle _{N+M-1}\) state \((N\ne M)\). The multi-qubit state \(|\mathcal {W}\rangle _N\) can be used as a shared resource for teleportation and superdense coding, which was detailed in Ref. [51]. Two initial states can be written as follows:

$$\begin{aligned} |\mathcal {W}\rangle _N= & {} \frac{1}{\sqrt{2}}[|HH\ldots HV\rangle _{1\ldots N}\nonumber \\&+\,\frac{1}{\sqrt{N-1}}(|HH\ldots VH\rangle _{1\ldots N} +\ldots +|VH\ldots HH\rangle _{1\ldots N})], \end{aligned}$$
(7a)
$$\begin{aligned} |\mathcal {W}\rangle _M= & {} \frac{1}{\sqrt{2}}[|HH\ldots HV\rangle _{1\ldots M} +\frac{1}{\sqrt{M-1}}(|HH\ldots VH\rangle _{1\ldots M}+\ldots \nonumber \\&+\,|VH\ldots HH\rangle _{1\ldots M})]. \end{aligned}$$
(7b)

Two photons coming from these two initial states (say Nth and Mth photons), respectively, will be sent into the input modes a and b of the PDBS. Similarly, we are only interested in the case where a photon is present in each of the modes c and d, and the conditions the parameters \(\mu , \nu \) must satisfy can be written as

$$\begin{aligned}&4(N-M)\nu ^{3}+(-9N+3M+6)\nu ^{2}+(6N-6)\nu -(N-1)=0, \end{aligned}$$
(8a)
$$\begin{aligned}&\frac{\sqrt{\mu \nu }}{\sqrt{N-1}}=\frac{\sqrt{(1-\mu )(1-\nu )}}{\sqrt{M-1}}. \end{aligned}$$
(8b)

By fixing N and M, one can get the corresponding values of \(\mu \) and \(\nu \) by solving the two equations above. However, with the increase of the size of the output state \(|\mathcal {W}\rangle _k (k\ge 5)\), there are more and more solutions. For example, a \(|\mathcal {W}\rangle _5\) state can be generated by fusing two \(|\mathcal {W}\rangle _3\) states or a \(|\mathcal {W}\rangle _2\) and a \(|\mathcal {W}\rangle _4\) state. But according to the discussions in Ref. [20], there is such a conclusion that the closer the sizes of the two resource states are, the lower the cost is, i.e., it is optimal to generate \(|\mathcal {W}\rangle _N\) states by fusing two resource states of similar sizes. Following this approach, in Table.1, we give a list of the values for \(N, M, \mu , \nu \) and \(Ps(|\mathcal {W}\rangle _{N+M-1})\) for some optimal fusion strategies. \(Ps(|\mathcal {W}\rangle _{N+M-1})\) is the corresponding maximum success probability (\((2\nu -1)^2/2\)) for the combinations \((\nu , \mu )\). Moreover, it should be emphasized that the values of (\(\nu \), \(\mu \)) do not depend on the sizes of the input states when the sizes of the input states are equal, i.e., when fusing two identical \(|\mathcal {W}\rangle _N\) states, the values of (\(\nu \), \(\mu \)) are fixed \(\mu =(3\pm \sqrt{3})/6, \nu =(3\mp \sqrt{3})/6\).

By using this scheme, a \(|\mathcal {W}\rangle _3\) state can be prepared by fusing two \(|\mathcal {W}\rangle _2\) states, and notice that the \(|\mathcal {W}\rangle _2\) state is a maximally entangled Bell state. So if we take the Bell state as the initial resource, arbitrary-size \(|\mathcal {W}\rangle _N\) states can be generated via the fusion strategy above.

In addition, if an H-polarized photon is detected in \(D_1\), the fusion process fails in general (\(N >2,M > 2\)). In particular, when \(N=M=2\) , a \(|\mathcal {W}\rangle _3\) state will be generated if an V-polarized photon( H-polarized photon) is detected in \(D_2\) (\(D_1\)). It is worth mentioning that the Bell state can also be generated from two single-photon states by this fusion strategy too [52].

Table 1 List of the values of \(N, M, \mu , \nu \) and \(Ps(|\mathcal {W}\rangle _{N+M-1})\)
Full size table

2.2 Creation of large-scale \(|\mathcal {W}\rangle \) states by expanding small-size \(|\mathcal {W}\rangle \) states

Here, we propose a simple scheme for expanding a polarization-entangled \(|\mathcal {W}\rangle _N\) state by adding an H-polarized ancilla photon. With the help of a PDBS, one of the photons in the \(|\mathcal {W}\rangle _N\) state will interfere with an H-polarized photon, and after post-selection a \(|\mathcal {W}\rangle _{N+1}\) state can be generated. As depicted in Fig. 1 one (say the Nth) of the photons in the \(|\mathcal {W}\rangle _N\) state is inputted in mode a, and the H-polarized auxiliary photon is added in mode b. Here, we only select those events where there is only one photon in each output mode. After the PDBS, the state of the photons can be written as

$$\begin{aligned}&\frac{1}{\sqrt{2}}[C_1|HH\ldots HVH\rangle _{1\ldots N (N+1)}+C_2|HH\ldots HHV\rangle _{1\ldots N (N+1)}\nonumber \\&\quad +\,C_3(|HH\ldots VHH\rangle _{1\ldots N (N+1)}+\ldots +|VH\ldots HHH\rangle _{1\ldots N (N+1)}], \end{aligned}$$
(9)

with

$$\begin{aligned} C_1= & {} \sqrt{\mu }\sqrt{\nu }\nonumber ,\\ C_2= & {} =-\sqrt{(1-\mu )(1-\nu )}\nonumber ,\\ C_3= & {} \frac{(2\mu -1)}{\sqrt{N-1}}. \end{aligned}$$
(10)

In addition, when \(|\frac{C_1}{C_2}|=|\frac{C_3}{C_2}|=\frac{1}{\sqrt{N}}\), a \(|\mathcal {W}\rangle _{N+1}\) state will be obtained with success probability \(Ps(|\mathcal {W}\rangle _{N+1}) = (1-\mu )(1-\nu )\), and the corresponding condition that \(\mu \) must satisfy is \(4(N-1)\mu ^3-(3N-7)\mu ^2-4\mu +1=0\). The values of \(\mu \) and \(\nu \) will be determined when N is given. For example, as \(N=2\), \(\mu \) and \(\nu \) have two possible combinations: \(\mu _1=0.2991\), \(\nu _1=0.5398\) and \(\mu _2=0.6799\), \(\nu _2=0.1904\). In this case, no photon detection is needed during the expansion process, and the verification process of the event where a photon is present in each of the two output modes of the PDBS and the applications of the output state are realized simultaneously.

3 Creation of large-size maximally entangled W states by fusing or expanding \(|\mathcal {W}\rangle \) states

In this section, we propose an effective scheme to prepare large-scale maximally entangled W states by fusing or expanding \(|\mathcal {W}\rangle _N\) states. Based on the selective transmission rates of the PDBS for different polarization states, a maximally entangled W state can be generated by selecting suitable parameters \((\mu ,\nu )\). Because the scheme can generate maximally entangled states in terms of non-maximally entangled states, it may play important roles in quantum communication.

3.1 Creation of large-scale \(|W\rangle \) states by fusing small-size \(|\mathcal {W}\rangle \) states

We will now demonstrate how a large-scale maximally entangled W state can be generated by fusing small-size \(|\mathcal {W}\rangle _N\) states. First, let’s consider the case of fusing two identical tri-photon W-class states into a five-photon maximally entangled W state. Two input states can be written as

$$\begin{aligned} |\mathcal {W}\rangle _3= & {} \frac{1}{\sqrt{2}}[|HHV\rangle _{123}+\frac{1}{\sqrt{2}}(|VHH\rangle _{123}+|HVH\rangle _{123})], \end{aligned}$$
(11a)
$$\begin{aligned} |\mathcal {W}\rangle _3= & {} \frac{1}{\sqrt{2}}[|HHV\rangle _{456}+\frac{1}{\sqrt{2}}(|VHH\rangle _{456}+|HVH\rangle _{456})]. \end{aligned}$$
(11b)

In this fusion process, two photons (say photons 3, 6), respectively, coming from these two \(|\mathcal {W}\rangle _3\) states will be sent into the input modes a and b of the PDBS. In the case where there is only one photon in each output mode, we can get a five-qubit W-like state:

$$\begin{aligned} |\widetilde{W}\rangle _5= & {} C_1|HHHH\rangle _{1245}|V\rangle _c+C_2|HHHV\rangle _{1245}|H\rangle _c+C_3|HHVH\rangle _{1245}|H\rangle _c\nonumber \\&+\,C_4|HVHH\rangle _{1245}|H\rangle _c+C_5|VHHH\rangle _{1245}|H\rangle _c, \end{aligned}$$
(12)

with

$$\begin{aligned} C_1= & {} \frac{1}{2}(2\nu -1)\nonumber , \\ C_2= & {} -\frac{1}{2\sqrt{2}}\sqrt{1-\mu }\sqrt{1-\nu }\nonumber , \\ C_3= & {} -\frac{1}{2\sqrt{2}}\sqrt{1-\mu }\sqrt{1-\nu }\nonumber , \\ C_4= & {} \frac{1}{2\sqrt{2}}\sqrt{\mu }\sqrt{\nu }\nonumber , \\ C_5= & {} \frac{1}{2\sqrt{2}}\sqrt{\mu }\sqrt{\nu }, \end{aligned}$$
(13)

when a V-polarized photon is detected in detector \(D_2\). If the parameters \((\mu , \nu )\) for the PDBS are chosen to be \(\mu =2/3, \nu =1/3\) or vice versa, \(C_1=C_2=C_3=C_4=C_5\), and thus the W-like state obtained here becomes a standard W state. Then a five-photon maximally entangled W state can be generated with success probability \(Ps(W_5)=5/36\).

This fusion scheme can be generalized to the case of generating a \((2N-1)\)-qubit maximally entangled W state by fusing two \(|\mathcal {W}\rangle _N\) states. To start this fusion strategy, one (say the Nth) photon from each \(|\mathcal {W}\rangle _N\) state will be sent into the PDBS and the parameters \((\mu , \nu )\) for the PDBS are chosen to be \(\mu =[(4N-3)+\sqrt{4N-3}]/2(4N-3), \nu =[(4N-3)-\sqrt{4N-3}]/2(4N-3)\) or vice versa. If we are only interested in the case where a photon is present in each of the output modes, a maximally entangled \(|W\rangle _{2N-1}\) state can be generated when an V-polarized photon is detected in \(D_2\):

$$\begin{aligned} |W\rangle _{2N-1}= & {} \frac{1}{\sqrt{2N-1}}[|HH\ldots HV\rangle _{12\ldots (2N-1)}+|HH\ldots VH\rangle _{12\ldots (2N-1)}+\ldots \nonumber \\&+\,|HV\ldots HH\rangle _{12\ldots (2N-1)}+|VH\ldots HH\rangle _{12\ldots (2N-1)}]. \end{aligned}$$
(14)

The fusion process is also applicable to fusing a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state (\(N\ne M\)) into a maximally entangled \(|W\rangle _{N+M-1}\) state. In such a situation, the values of \(\mu , \nu \) are dependent on N, M:

$$\begin{aligned}&4(N-M)\nu ^{3}+(4M-8N+3)\nu ^{2}+(5N-M-3)\nu -(N-1)=0, \end{aligned}$$
(15a)
$$\begin{aligned}&\frac{\sqrt{\mu \nu }}{\sqrt{N-1}}=\frac{\sqrt{(1-\mu )(1-\nu )}}{\sqrt{M-1}}. \end{aligned}$$
(15b)

When N, M are given, \(\mu \) and \(\nu \) can be determined. For example, when \(N=3\) and \( M=4\), \((\nu , \mu )\) have two possible combinations: (0.3448, 0.5589) or (0.6469, 0.2669). Here \((\nu , \mu )\) are defined in the range (0, 1) too, and the success probability is \(Ps(W_{N+M-1})=(2\nu -1)^2(N+M-1)/4\).

It should be emphasized that, although we only discussed the situation where only one photon is present in each of the modes c and d, we also explored the case where two photons are in the same output mode. As discussed in Ref. [51], there exists the recyclable case in our strategy, i.e., two maximally entangled W states \(|W\rangle _{n-1}\) and \(|W\rangle _{m-1}\) can be left if two H-polarized photons are detected in \(D_1\). According to Ref. [51], these two maximally entangled W states can serve as the initial resource for the further fusion.

3.2 Creation of large-scale \(|W\rangle \) states by expanding small-size \(|\mathcal {W}\rangle \) states

In this subsection, let’s introduce the strategy for expanding a \(|\mathcal {W}\rangle _N\) state into a maximally entangled \(|W\rangle _{N+1}\) state. The \(|\mathcal {W}\rangle _N\) state can be written as in Eq. (2). One of the photons (say the Nth) from the \(|\mathcal {W}\rangle _N\) state and an H-polarized auxiliary photon will be sent into the PDBS for completing the expansion process. If we are only interested in the case where a photon is present in each of the output modes of the PDBS, the following state can be generated:

$$\begin{aligned}&\frac{1}{\sqrt{2}}[C_1|HH\ldots HVH\rangle _{1\ldots N (N+1)}+C_2|HH\ldots HHV\rangle _{1\ldots N (N+1)}\nonumber \\&\quad +\,C_3(|HH\ldots VHH\rangle _{1\ldots N (N+1)}+\ldots +|VH\ldots HHH\rangle _{1\ldots N (N+1)})]. \end{aligned}$$
(16)

with

$$\begin{aligned} C_1= & {} \sqrt{\mu }\sqrt{\nu }\nonumber ,\\ C_2= & {} =-\sqrt{(1-\mu )(1-\nu )}\nonumber ,\\ C_3= & {} \frac{(2\mu -1)}{\sqrt{N-1}}. \end{aligned}$$
(17)

If the parameters \((\mu , \nu )\) for the PDBS are chosen to be \(\mu =[(N+3)\pm \sqrt{(N+3)(N-1)}]/2(N+3), \nu =[(N+3)\mp \sqrt{(N+3)(N-1)}]/2(N+3)\), \(|C_1|=|C_2|=|C_3|\) holds, which means that when the input state is known for us, a maximally entangled state can be generated with success probability \(Ps(W_{N+1})=\mu \nu (N+1)/2\) by adjusting the parameters \((\mu , \nu )\) of the PDBS.

4 Cost analysis and discussion

In this section, we briefly discuss the resource costs of our strategies for fusing small-size \(|\mathcal {W}\rangle _N\) states into larger-scale \(|\mathcal {W}\rangle _N\) states or W states. With the PDBS fusion mechanism, a large-scale maximally entangled W state can be generated by fusing small-size \(|\mathcal {W}\rangle _N\) states. In addition, one of our previous works shows that the PDBS fusion mechanism can be used to generate a large-scale maximally entangled W state by fusing small-size maximally entangled W states too [52]. So it is necessary to make a cost comparison analysis among these two strategies. Because the two fusion strategies both start from \(|W\rangle _2\) states, we can define the basic resource cost for preparing a \(|W\rangle _2\) state as the unit cost, i.e., \(R[W_2]=1\), and make a comparison of the optimal costs of these two strategies by numerical evaluations.

4.1 Cost of fusing small-size \(|\mathcal {W}\rangle _N\) states into larger-scale \(|\mathcal {W}\rangle _N\) states

In Ref. [20], the resource cost of preparing a \(|W\rangle _{m+n-1}\) state by fusing a \(|W\rangle _{m}\) state and a \(|W\rangle _{n}\) state is defined as follows:

$$\begin{aligned} R[W_{m+n-1}] = \frac{R[W_m]+R[W_n]}{P_s(W_m,W_n)}, \end{aligned}$$
(18)

where both \(W_m\) and \(W_n\) are maximally entangled W states, and \(P_s(W_m,W_n)\) is the success probability of the fusion process. Similarly, because our fusion strategy starts from the standard \(|W\rangle _2\) state, the resource cost of generating a \(|\mathcal {W}\rangle _{N+M-1}\) state by fusing a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state can also be calculated in the same way. The success probability of getting a \(|\mathcal {W}\rangle _{N+M-1}\) state is \(Ps(|\mathcal {W}\rangle _{N+M-1})= (2\nu -1)^2/2\), and thus the resource cost can be expressed as

$$\begin{aligned} R[\mathcal {W}_{N+M-1}]=\frac{(R[\mathcal {W}_N]+R[\mathcal {W}_M])}{Ps(\mathcal {W}_{N+M-1})}. \end{aligned}$$
(19)

The numerical results of the resource cost \(R[\mathcal {W}_{N+M-1}]\) are shown in Fig. 2 for the optimal fusion processes, where the sizes of the input states are similar and the parameters of the PDBS have been chosen to maximize the success probabilities.

Fig. 2
figure 2

Resource cost of fusing a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state into a \(|\mathcal {W}\rangle _{N+M-1}\) state. The basic resource is the maximally entangled \(|W\rangle _2\) state. The vertical axis is labeled as the resource cost and the horizontal axis is labeled as the size of the output \(|\mathcal {W}\rangle \) state (Color figure online)

Full size image

4.2 Cost comparison

Here, we compare the resource costs of two different strategies for generating a maximally entangled W state. In the first strategy, a large-scale maximally entangled W state can be generated by fusing two small-size maximally entangled W states (a \(|W\rangle _N\) state and a \(|W\rangle _M\) state) [52], and its resource cost is denoted by \(R[W_{M+N-1}]\). The second fusion strategy is the one we proposed in this paper, i.e., a large-scale maximally entangled \(|W\rangle _{M+N-1}\) state can be generated by fusing a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state, and its resource cost is denoted by \(R[W_{M+N-1}]^{\prime }\). Both \(R[W_{M+N-1}]\) and \(R[W_{M+N-1}]^{\prime }\) are calculated in terms of the unit cost \(R[W_2]=1\). Figure 3 shows that the resource cost \(R[W_{M+N-1}]^{\prime }\) of the second method (red) is lower than that of the first method (black). The fusion strategy starting from non-maximally entangled \(|\mathcal {W}\rangle \) states is more efficient than the one starting from maximally entangled W states.

Fig. 3
figure 3

Resource cost comparison: the fusion strategy of generating a \(|W\rangle _{N+M-1}\) state from a \(|W\rangle _N\) state and a \(|W\rangle _M\) state (black), and the fusion strategy of generating a \(|W\rangle _{N+M-1}\) state from a \(|\mathcal {W}\rangle _N\) state and a \(|\mathcal {W}\rangle _M\) state (red). The basic resource cost for preparing a maximally entangled \(|W\rangle _2\) state is defined as unit cost. The vertical axis is labeled as the resource cost and the horizontal axis is labeled as the size of the output W state (Color figure online)

Full size image

5 Conclusion

In conclusion, we have proposed a fusion strategy of generating large-scale \(|\mathcal {W}\rangle \) photonic states, which play an important role in perfect teleportation and superdense coding. Our fusion strategy can start from Bell states. The main fusion mechanism is implemented by a PDBS, and no controlled gate is needed. The fusion process can succeed by adjusting the parameters of the PDBS, which makes the current scheme simple and feasible. Furthermore, with this fusion mechanism, a large-scale maximally entangled W state can be generated by fusing small-size \(|\mathcal {W}\rangle \) states as well. The cost analysis shows that our fusion strategy is more efficient than the one starting from maximally entangled W states [52]. The possibilities of generating large-scale \(|\mathcal {W}\rangle \) states and \(|W\rangle \) states via expansion mechanism have also been studied.