Opportunistic quantum network coding based on quantum teleportation

Abstract

It seems impossible to endow opportunistic characteristic to quantum network on the basis that quantum channel cannot be overheard without disturbance. In this paper, we propose an opportunistic quantum network coding scheme by taking full advantage of channel characteristic of quantum teleportation. Concretely, it utilizes quantum channel for secure transmission of quantum states and can detect eavesdroppers by means of quantum channel verification. What is more, it utilizes classical channel for both opportunistic listening to neighbor states and opportunistic coding by broadcasting measurement outcome. Analysis results show that our scheme can reduce the times of transmissions over classical channels for relay nodes and can effectively defend against classical passive attack and quantum active attack.

1 Introduction

Network coding theory [1] greatly improves network throughput and also creates a huge milestone for information area. On account of the broadcasting nature of wireless medium, wireless network coding has attracted much attention from researchers. In order to maximize the gain from network coding, there have been two alternative approaches to developing interflow network coding protocols, based on either opportunistic coding or coordinated coding [2]. In deriving the upper bounds of coding gain, it is often necessary to make assumptions about a particular coding structure, such as coding opportunities at a hotspot. As a paradigm of wireless network coding protocol, “COPE” (complete opportunity encoding) [3] allows nodes to combine more than two packets together through opportunistic listening. Relay nodes can learn neighbor states through opportunistic listening so that they can make an optimal coding option to ensure more neighbors can decode encoded packets. However, opportunistic coding such as in COPE may miss several coding opportunities, depending on the order in which nodes in a neighborhood transmit packets. Then the use of coordinated network coding was proposed, in which transmissions of neighboring nodes are scheduled with the goal of maximizing the gain from network coding. These works provide the key idea is to strengthen the cooperation and maximize the gain from network coding.

With the development of quantum information, network coding has been gradually applied to quantum network. Quantum network coding (QNC) has gradually become a major research area by virtue of its capability to improve the security and efficiency of quantum communication. Several achievements have been made in theoretical research in recent years. In 2007, Hayashi et al. [4] proposed the first quantum network coding protocol “XQQ” (crossing two qubits), which showed that quantum network coding is possible in the butterfly network and can realize crossing transmission of two arbitrary quantum states. Since this protocol uses approximate cloning to copy quantum states, approximate cloning results in the distortion of original quantum states. For high fidelity, Hayashi [5] further designed a new quantum network coding scheme with prior entanglement between two senders by applying quantum teleportation. It can transmit two quantum states across and perfectly over the butterfly network. In quantum teleportation, prior entanglement enables the transmission of quantum states only by sending classical information. The achievable fidelity is 1, which is obviously better than XQQ. More precisely, an upper bound of average fidelity is given in the butterfly network when prior entanglement is not allowed. Then Kobayashi et al. [6–8] showed the potential of quantum teleportation technique by demonstrating how any classical network coding protocol gives rise to a quantum network coding protocol. For these classical quantum network coding schemes, Jain et al. [9] provided a quantum information-theoretic framework for analyzing quantum communication with fidelity 1 over networks. They showed that in the case of multiple unicast communication, quantum network coding in directed quantum networks can outperform routing. Entanglement support intrinsic to the network topology can enable such a coding protocol. Moreover, Satoh et al. [10] presented a quantum network coding scheme for quantum repeaters under weaker assumption that adjacent nodes initially share one Einstein–Podolsky–Rosen(EPR) pair but cannot add any quantum registers or send any quantum information. Shang et al. [11] presented a quantum network coding scheme for general repeater networks to realize long-distance quantum communication over quantum repeater networks with complex topology. Based on Hayashi’s work, Ma et al. [12] proposed a quantum network coding protocol which can transmit M-qudit across over the butterfly network by sharing non-maximally entangled states between senders. Leung et al. [13] studied the problem of k-pair communication(or multiple unicast problem) of quantum information in networks of quantum channels. From the viewpoint of secure communication, Shang et al. [14] further proposed quantum network coding schemes based on controlled teleportation to realize the control of decoding process of receivers. A sender will fail to transmit quantum information to a receiver without the participation of a controller. However, these existing schemes cannot provide opportunistic characteristic for quantum network like COPE. Recently, the achievement of air-to-ground quantum key distribution [15] represents a key milestone toward quantum communication in free space. Thus it is worth concerning whether quantum network coding with opportunistic characteristic is also feasible or not.

Our objective is to strengthen the cooperation by virtue of opportunistic characteristics and maximize the gain from network coding. From the viewpoint of motivation, an opportunistic quantum network coding scheme is considered to provide opportunistic characteristic for quantum network so as to improve network performance. Since the demand of channel listening has great conflicts with the fact that quantum channel cannot be overheard without disturbance, it is a key issue to provide a feasible approach to channel listening and distinguish between legal listening and illegal eavesdropping in quantum communication.

Inspired by the characteristic of mixed channels of quantum teleportation, we present an opportunistic quantum network coding scheme to solve above problem by utilizing quantum channel for secure transmission of quantum states and classical channel for both opportunistic listening to neighbor states and opportunistic coding by means of broadcasting measurement outcome.

The main contributions of our work are:

• 1. A quantum network coding scheme with opportunistic characteristic is first proposed by taking full advantage of channel characteristic of quantum teleportation. Based on the principle that the measurement outcome of quantum teleportation is transmitted over a classical channel, the scheme has two main opportunistic characteristics. One is opportunistic listening. A listener can tell when the quantum information transmission is occurring in the neighborhood so as to further obtain neighbor’s state. The other is opportunistic coding. A relay node can transmit multiple measurement outcomes simultaneously by broadcast. Such opportunistic characteristics can improve network throughput.

• 2. The problem of how to distinguish between legal listener and illegal eavesdropper is well solved. Quantum channel verification method for EPR pair is used to detect eavesdroppers, while auxiliary classical channels for quantum teleportation are delicately used to provide the opportunity of channel listening for the transmitted quantum states.

2 Related works

2.1 Opportunistic coding

COPE [3] is a practical forwarding architecture that substantially improves the throughput of wireless networks. It detects coding opportunities and exploits them to forward multiple packets in a single transmission. Especially, it relies heavily on opportunistic listening of all the transmissions in a node’s neighborhood, in order to identify coding opportunities.

COPE incorporates three main techniques as follows:

• 1. Opportunistic listening

  It sets the nodes to snoop on all communications over the wireless medium and store the overheard packets for a limited period. In addition, each node broadcasts reception reports to tell its neighbors which packets it has stored.

• 2. Opportunistic coding

  Packets from multiple unicast flows may have encoded together at some intermediate hops. The nodes that perform encoding should aim to maximize the number of native packets delivered in a single transmission, while ensuring that each intended nexthop has enough information to decode its native packet. This can be achieved using the following simple rule: to transmit n packets, ${P_1},\ldots ,{P_n}$, to n nexthops, ${r_1},\ldots ,{r_n}$ , a node can XOR(exclusive OR) the n packets together only if each nexthop ${r_i}$ has all $n-1$ packets ${P_j}$ for $j \ne i$ . Opportunistic coding is illustrated in Fig. 1. Relay node R has four packets ${P_1}$, ${P_2}$, ${P_3}$, and ${P_4}$. For each coding option for R, it turns out different results. R obtains the states of neighbors by listening to neighbors and would like to choose to broadcast the encoded packets ${P_1}$ $\oplus$ ${P_3}$ $\oplus$ ${P_4}$, which seems to be the best option for the reason that it allows all neighbors to decode native packet once.

• 3. Learning neighbor state

  As explained earlier, each node broadcasts reception reports to tell neighbors its packet state. When the network suffers from congestion, reception reports might arrive too late or even get lost. Therefore, a node can not only rely on reception reports, it needs to guess whether a neighbor has the packet.

Fig. 1

Opportunistic coding

In conclusion, COPE is executed by overhearing and broadcasting packets. The characteristic of overhearing generates coding opportunities that can benefit both encoding and decoding, and reduce the times of packet transmissions, thus improving network throughput.

2.2 Quantum teleportation

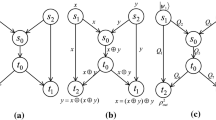
In 1993, Bennett et al. [16] first proposed the concept of quantum teleportation. Quantum teleportation provides a way for two parties to transmit an unknown qubit from one to the other, without transmitting the particle itself. As shown in Fig. 2, we assume that A and B are the two communication parties. The task of quantum teleportation is that A transmits an unknown quantum state to B. We denote the unknown quantum state by

$$\begin{aligned} {\left| \psi \right\rangle _C} = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle . \end{aligned}$$

(1)

Quantum teleportation includes a series of steps as follows:

Fig. 2

Quantum teleportation

Step 1 A and B share an entangled pair of particles.

$$\begin{aligned} \left| {{\phi ^ + }} \right\rangle = \frac{1}{{\sqrt{2} }}{\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right) _{AB}} \end{aligned}$$

(2)

Here the first member of the pair belongs to A and the second member of the pair belongs to B.

Step 2 A makes a Bell-state measurement on both qubits in its possession.

Step 3 A tells B the measurement outcome over a classical channel.

Let the classical bits correspond to the outcomes of Bell-state measurement as follows:

$$\begin{aligned} 00\rightarrow \left| {{\phi }^{+}} \right\rangle ,\quad 10\rightarrow \left| {{\phi }^{-}} \right\rangle ,\quad 01\rightarrow \left| {{\psi }^{+}} \right\rangle ,\quad 11\rightarrow \left| {{\psi }^{-}} \right\rangle . \end{aligned}$$

(3)

Step 4 When B receives the bits corresponding to measurement outcome, it can infer the state of its member of the EPR pair. Then B performs an appropriate quantum operator $U$ to his member. The appropriate operator will change its member to the unknown state ${\left| \psi \right\rangle _C}$, which is exactly the state that A wants to send to B.

So the quantum teleportation is completed.

2.3 Quantum channel verification

Quantum communication provides its unconditional security guaranteed by Heisenberg uncertainty principle and quantum no-cloning theory. Based on such quantum characteristic, quantum channel verification is used to detect the integrity of quantum channel and further judge whether there exists an attack. Many schemes such as quantum key distribution(QKD), quantum secure direct communication(QSDC) and quantum identity authentication(QIA) have adopted the related methods based on single particle, quantum teleportation, entanglement swapping, and so on. The first quantum key distribution protocol BB84 [17] uses a sequence of single photons and the bit information of measure bases to evaluate the quantum bit error rate(QBER). If QBER is larger than the threshold value, they abort the protocol. Otherwise, they proceed to the post-processing of classical data and generate a secure key. Considering the potential of quantum teleportation for network coding model, we focus on the quantum channel verification method for EPR pairs [18] as illustrated in Fig. 3.

Fig. 3

Quantum channel verification

The quantum channel verification method is described as follows:

Step 1 Communication parties A and B share a quantum channel which consists of n EPR pairs in advance. Each EPR pair can be expressed as

$$\begin{aligned} \left| {{\varPhi } _j^ + } \right\rangle = \frac{1}{{\sqrt{2} }}\left( {\left| {{0_{{a_j}}}{0_{{b_j}}}} \right\rangle + \left| {{1_{{a_j}}}{1_{{b_j}}}} \right\rangle } \right) ,\quad j = 1,\ldots ,n. \end{aligned}$$

(4)

where $a_j$ and $b_j$ represents the particles ${p_{{a_j}}}$ and ${p_{{b_j}}}$ owned by A and B, respectively.

Step 2 A prepares an arbitrary qubit ${p_{\mathrm {m}}}$ as measure particle.

$$\begin{aligned} \left| {{\psi _\mathrm{m}}} \right\rangle =\cos \theta \left| 0 \right\rangle +{e^{{-}i\varphi }}\sin \theta \left| 1 \right\rangle \end{aligned}$$

(5)

where $\theta$ and $\varphi$ are the secret parameters of A. Then A applies a C-Not gate on its particle ${p_{{a_1}}}$ and measure particle ${p_{\mathrm {m}}}$. This operation makes ${p_{\mathrm {m}}}$ entangled with an EPR pair ${p_{{a_1}}}{p_{{b_1}}}$.

$$\begin{aligned} \left| {{{\varPsi } ^c}} \right\rangle= & {} {{\mathrm {C}}_{a_1\mathrm{m}}}\left| {{\varPhi } _1^ + } \right\rangle \otimes \left| {{\psi _\mathrm{m}}} \right\rangle \nonumber \\= & {} \sum \limits _{i = 0,1} {{\gamma _i}\left( {\left| {{0_{{a_1}}}{0_{{b_1}}}{i_\mathrm{m}}} \right\rangle + \left| {{1_{{a_1}}}{1_{{b_1}}}\left( {i \oplus 1} \right) } \right\rangle } \right) } \nonumber \\= & {} \frac{1}{{\sqrt{2} }}\sum \limits _{i = 0}^1 {\left| {{i_{{a_1}}}{i_{{b_1}}}} \right\rangle } \otimes \left( {\mathrm{I}{\delta _{i,0}} + {{X}_\mathrm{m}}{\delta _{i,0}}} \right) \left| {{\psi _\mathrm{m}}} \right\rangle \end{aligned}$$

(6)

where ${\gamma _l} = \frac{1}{{\sqrt{2} }}(\cos \theta {\delta _{l,0}} + \sin \theta {e^{ - i\varphi }}{\delta _{l,1}})$, ${\delta _{i,j}}$ is Kronecker Delta function:

$$\begin{aligned} {\delta _{i,j}} = \left\{ { \begin{array}{ll} 1&{}\quad {i = j}\\ 0&{}\quad {i \ne j} \end{array}} \right. \end{aligned}$$

(7)

Then A sends the measure particle ${p_{\mathrm {m}}}$ to B.

Step 3 B receives ${p_{\mathrm {m}}}$ and applies a C-Not gate on ${p_{\mathrm {m}}}$ and ${p_{{b_1}}}$, which results in

$$\begin{aligned} {C_{b_1\mathrm{m}}}\left| {{{\varPsi } ^c}} \right\rangle =\left| {{\varPhi } _1^ + } \right\rangle \otimes \left| {{\psi _\mathrm{m}}} \right\rangle . \end{aligned}$$

(8)

The above equation shows that the state $\left| {{{\varPsi } _\mathrm{m}}} \right\rangle$ is disentangled from the combined state $\left| {{\varPhi } _1^ + } \right\rangle$, which means that the measure particle ${p_{\mathrm {m}}}$ is independent from the EPR pair ${p_{{a_1}}}{p_{{b_1}}}$.

Step 4 B makes ${p_{\mathrm {m}}}$ entangled with next EPR pair ${p_{{a_2}}}{p_{{b_2}}}$ by the same operation as Step 2 through a C-Not gate, and then B sends ${p_{\mathrm {m}}}$ back to A.

Step 5 A disentangles the entangled system to obtain independent ${p_{\mathrm {m}}}$. Then A measures the parameters $\theta$ and $\varphi$ of ${p_{\mathrm {m}}}$ and compares both the measurement outcome and original parameters. If they are consistent, the two EPR pairs ${p_{{a_1}}}{p_{{b_1}}}$ and ${p_{{a_2}}}{p_{{b_2}}}$ are integral. Otherwise, at least one EPR pair is disturbed.

Step 6 A and B choose a certain amount, $2h(h \in {N^ + }, h \le \frac{n}{2})$ EPR pairs for quantum channel verification. If error rate $\xi$ satisfies $\xi \le {{\Delta }\xi _0} + {\xi _0}$ ( here ${{\Delta }\xi _0}$ represents average influence of noise, while ${\xi _0}$ represents disturbance threshold value), disturbance is within normal range and the EPR pairs are secure. Otherwise, if error rate $\xi$ is beyond permission limit, it indicates that there exists an attack over quantum channels.

3 Opportunistic quantum network coding scheme

As we know, it is most difficult for opportunistic quantum network coding to realize opportunistic operation such as opportunistic listening and opportunistic coding in the three core parts of COPE due to the unconditional security of quantum communication. Thus we will focus on how to acquire coding opportunity from neighborhood and use the broadcasting characteristic of classical channels to reduce the times of transmissions.

3.1 Scheme

The main idea of our scheme is described as follows: quantum teleportation uses EPR pairs as quantum channel by sharing EPR pairs between communication parties, while it uses classical channel to transmit the measurement outcome. Assume there exists an eavesdropper during the transmission process. If it listens to quantum channel, quantum channel verification can help find the eavesdropper. If it listens to classical channel, the leakage of measurement outcome does not destroy the security of transmitted quantum states even though the eavesdropper cannot be found. Thus if channel listening was desired for normal acquisition information, only does it happen to classical channel. As a more meaningful approach, the transmission over classical channel can provide an immediate notification for neighboring nodes that a quantum information has just been transmitted from one communication party to another communication party, which is very important for opportunistic network coding to grasp opportunity to obtain neighbor’s states at the right time. Meanwhile, multiple measurement outcomes can be transmitted simultaneously by broadcast, which will reduce the times of transmissions.

A typical network model for opportunistic quantum network coding is constructed as shown in Fig. 4. In this scenario, L is a relay node which will try to overhear its neighbors and encode own packets, and A and B are L’s neighbors and can communicate with each other. E is an eavesdropper who may launch classical attacks or quantum attacks. Every two legal nodes share prior entangled EPR pairs, which are the foundation of quantum teleportation and quantum channel verification.

Fig. 4

Network model (Si denotes the step of the proposed scheme)

Assume A will transmit a packet to B, the proposed scheme is described as follows:

Step 1: Quantum channel verification Before communication, quantum channel verification is performed to verify the integrity of quantum channels (EPR pairs) and detect whether there exists an eavesdropper who launches quantum attacks. The procedure of quantum channel verification between A and B is described as follows:

(1.1) A and B share prior EPR pairs, and each EPR pair between A and B can be expressed as

$$\begin{aligned} \left| {{\varPhi } _j^ + } \right\rangle = \frac{1}{{\sqrt{2} }}\left( {\left| {{0_{{a_j}}}{0_{{b_j}}}} \right\rangle + \left| {{1_{{a_j}}}{1_{{b_j}}}} \right\rangle } \right) ,\quad j = 1,\ldots ,n. \end{aligned}$$

(9)

(1.2) A prepares an arbitrary qubit ${p_{\mathrm {m}}}$ as measure particle. Here $\theta$ and $\varphi$ are the secret parameters.

$$\begin{aligned} \left| {{{\varPsi } _\mathrm{m}}} \right\rangle =\cos \theta \left| 0 \right\rangle +{e^{{-}i\varphi }}\sin \theta \left| 1 \right\rangle \end{aligned}$$

(10)

Then A applies a C-Not gate on its particle ${p_{{a_1}}}$ and measure particle ${p_{\mathrm {m}}}$, which makes ${p_{\mathrm {m}}}$ entangled with an EPR pair ${p_{{a_1}}}{p_{{b_1}}}$.

$$\begin{aligned} \left| {{{\varPsi } ^c}} \right\rangle= & {} {{\mathrm {C}}_{a_1\mathrm{m}}}\left| {{\varPhi } _1^ + } \right\rangle \otimes \left| {{\psi _\mathrm{m}}} \right\rangle \nonumber \\= & {} \sum \limits _{i = 0,1} {{\gamma _i}\left( {\left| {{0_{{a_1}}}{0_{{b_1}}}{i_\mathrm{m}}} \right\rangle + \left| {{0_{{a_1}}}{0_{{b_1}}}\left( {i \oplus 1} \right) } \right\rangle } \right) } \nonumber \\= & {} \frac{1}{{\sqrt{2} }}\sum \limits _{i = 0}^1 {\left| {{i_{{a_1}}}{i_{{b_1}}}} \right\rangle } \otimes \left( {\mathrm{I}{\delta _{i,0}} + {\mathrm{X}_\mathrm{m}}{\delta _{i,0}}} \right) \left| {{\psi _\mathrm{m}}} \right\rangle \end{aligned}$$

(11)

Then A sends the measure particle ${p_{\mathrm {m}}}$ to B.

(1.3) B receives ${p_{\mathrm {m}}}$ and applies a C-Not gate on ${p_{\mathrm {m}}}$ and its particle ${p_{{b_1}}}$, which results in:

$$\begin{aligned} {C_{b_1\mathrm{m}}}\left| {{{\varPsi } ^c}} \right\rangle =\left| {{\varPhi } _1^ + } \right\rangle \otimes \left| {{{\varPsi } _\mathrm{m}}} \right\rangle . \end{aligned}$$

(12)

B makes ${p_{\mathrm {m}}}$ entangled with next EPR pair ${p_{{a_2}}}{p_{{b_2}}}$ by the same operation as Step 1.2, and then B sends ${p_{\mathrm {m}}}$ back to A.

(1.4) A disentangles the entangled system to obtain independent ${p_{\mathrm {m}}}$. Then A measures the parameters $\theta$ and $\varphi$ of ${p_{\mathrm {m}}}$ and compares both the measurement outcome and original parameters. If they are consistent, the two EPR pairs ${p_{{a_1}}}{p_{{b_1}}}$ and ${p_{{a_2}}}{p_{{b_2}}}$ are integral. Otherwise, at least one EPR pair is disturbed.

(1.5) A and B choose a certain amount, $2h (h \in {N^ + }, h \le \frac{n}{2})$ EPR pairs for quantum channel verification. If the EPR pairs are secure, they proceed. Otherwise, they abort communication.

Note that quantum channel verification can be performed by any two nodes. In consideration of EPR pair resource and communication efficiency, there is no need to implement quantum channel verification between every two nodes. It can be performed between a certain number of random node pairs, before the network runs or during a certain period of communication process, which needs to be designed and completed together by all nodes.

Step 2: Quantum information transmission When the quantum channel verification is completed, A intends to transmit a w-bit packet to B by quantum teleportation.

Based on the nature of quantum mechanics that orthogonal quantum states (such as $\left| {{{\varPsi } _0}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle + \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle$ and $\left| {{{\varPsi } _1}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle - \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle$) can be completely distinguished by measurement, A selects one pair of orthogonal bases $\left| {{{\varPsi } _0}} \right\rangle$ and $\left| {{{\varPsi } _1}} \right\rangle$ , which represent 0 and 1, respectively.

$$\begin{aligned} 0 \rightarrow \left| {{{\varPsi } _0}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle + \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle ,\quad 1 \rightarrow \left| {{{\varPsi } _1}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle - \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle \end{aligned}$$

(13)

(2.1) According to the w-bit packet and (13), A prepares w qubits.

Assume that A would like to transmit a qubit $p_i, i=1,\ldots ,w$, with state ${\left| {\varPsi } \right\rangle _{{p_i}}} = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle$(here ${\left| {\varPsi } \right\rangle _{{p_i}}}$ can be $\left| {{{\varPsi } _0}} \right\rangle$ or $\left| {{{\varPsi } _1}} \right\rangle$) to B, the overall state of three particles is

$$\begin{aligned} {\left| {\varPsi } \right\rangle _{p_ia_ib_i}}= & {} {\left| {\varPsi } \right\rangle _{p_i}} \otimes {\left| {{\phi ^ + }} \right\rangle _{a_ib_i}} \nonumber \\= & {} {(\alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle )_{p_i}} \otimes \frac{1}{{\sqrt{2} }}{(\left| {00} \right\rangle + \left| {11} \right\rangle )_{a_ib_i}}. \end{aligned}$$

(14)

(2.2) A makes a Bell-state measurement on both qubits ${p_ia_i}$ in its possession.

Note that the system state (14) can be rewritten as follows:

$$\begin{aligned} {\left| \psi \right\rangle _{{p_i}{a_i}{b_i}}} = {\left| \psi \right\rangle _{{p_i}}} \otimes {\left| {{\phi ^ + }} \right\rangle _{{a_i}{b_i}}}= & {} \frac{1}{{\sqrt{2} }}\Big [{\left| {{\phi ^ + }} \right\rangle _{{p_i}{a_i}}} \otimes {\left( \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle \right) _{{b_i}}}\nonumber \\&\ + \, {\left| {{\phi ^ - }} \right\rangle _{{p_i}{a_i}}} \otimes {\left( \alpha \left| 0 \right\rangle - \beta \left| 1 \right\rangle \right) _{{b_i}}}\nonumber \\&\ +\, {\left| {{\psi ^ + }} \right\rangle _{{p_i}{a_i}}} \otimes {\left( \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle \right) _{{b_i}}}\nonumber \\&\ +\,{\left| {{\psi ^ - }} \right\rangle _{{p_i}{a_i}}} \otimes {\left( \alpha \left| 0 \right\rangle - \beta \left| 1 \right\rangle \right) _{{b_i}}}\Big ] \end{aligned}$$

(15)

where $\left| {{\phi ^ \pm }} \right\rangle$ and $\left| {{\psi ^ \pm }} \right\rangle$ are Bell states, which are defined as follows:

$$\begin{aligned} \left| {{\phi }^{\pm }} \right\rangle =\frac{1}{\sqrt{2}}\left( \left| 00 \right\rangle \pm \left| 11 \right\rangle \right) ,\quad \left| {{\psi }^{\pm }} \right\rangle =\frac{1}{\sqrt{2}}\left( \left| 01 \right\rangle \pm \left| 10 \right\rangle \right) . \end{aligned}$$

(16)

According to (15), the measurement outcome must be one of the four Bell states in (16), with the same probability $\frac{1}{4}$.

(2.3) A tells B the measurement outcome over a classical channel.

Let the classical bits correspond to the outcomes of Bell-state measurement as follows:

$$\begin{aligned} 00\rightarrow \left| {{\phi }^{+}} \right\rangle ,\quad 10\rightarrow \left| {{\phi }^{-}} \right\rangle ,\quad 01\rightarrow \left| {{\psi }^{+}} \right\rangle ,\quad 11\rightarrow \left| {{\psi }^{-}} \right\rangle . \end{aligned}$$

(17)

(2.4) When B receives the bits corresponding to measurement outcome, he can infer the state of his member of EPR pair:

$$\begin{aligned}&{\left| {{\phi ^ + }} \right\rangle _{p_ia_i}} \rightarrow {(\alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle )_{{b_i}}}\nonumber \\&{\left| {{\phi ^ - }} \right\rangle _{p_ia_i}} \rightarrow {(\alpha \left| 0 \right\rangle - \beta \left| 1 \right\rangle )_{{b_i}}}\nonumber \\&{\left| {{\psi ^ + }} \right\rangle _{p_ia_i}} \rightarrow {(\alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle )_{{b_i}}}\nonumber \\&{\left| {{\psi ^ - }} \right\rangle _{p_ia_i}} \rightarrow {(\alpha \left| 0 \right\rangle - \beta \left| 1 \right\rangle )_{{b_i}}}. \end{aligned}$$

(18)

then B can apply an appropriate operator U to its particle $b_i$, which makes the state of $b_i$ turn out to be ${\left| {\varPhi } \right\rangle _{b_i}} = (\alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle )$. So the state of $p_i$ is finally transmitted and stored in the particle $b_i$.

Note that the sender A transforms classical bit into quantum state by (13), so the receiver B can easily transform the quantum state back into classical bit by measure. For example, B receives a qubit ${\left| {\varPhi } \right\rangle _{b_i}}$, then it measures the qubit with orthogonal bases $\left| {{{\varPsi } _0}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle + \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle$ and $\left| {{{\varPsi } _1}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle - \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle$ and transforms it back into classical bit:

$$\begin{aligned} \left| {{{\varPsi } _0}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle + \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle \rightarrow 0,\quad \left| {{{\varPsi } _1}} \right\rangle = \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle - \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle \rightarrow 1. \end{aligned}$$

(19)

Step 3: Opportunistic listening L overhears the classical bits during the communication between A and B. These classical bits are the outcomes of Bell-state measurement:

$$\begin{aligned} 00\rightarrow \left| {{\phi }^{+}} \right\rangle ,\quad 10\rightarrow \left| {{\phi }^{-}} \right\rangle ,\quad 01\rightarrow \left| {{\psi }^{+}} \right\rangle ,\quad 11\rightarrow \left| {{\psi }^{-}} \right\rangle . \end{aligned}$$

(20)

There will be 2w bits over a classical channel during communication when a w-bit classical packet is transmitted by quantum teleportation. By virtue of these classical bits, L can judge that a new transmission between A and B is occurring and desires the latest packet from A (or B), so L sends a request order to A (or B) to request the packet delivered just now which is denoted by ${P_r}$. Here the request order is one of defined orders in the form of classical bits, and it is used to request communication parties for latest packet, which is defined and listed in Table 1.

Table 1 Defined orders

Step 4: Neighbor state acquisition After receiving the request order from L, A(or B) will refer to its own transmission record and send a corresponding reply to L. As a result, L can acquire neighbor state by definite steps. Here the transmission record is stored locally so as to record which packets have been sent to each destination node. There are two cases for the corresponding reply of A (or B):

• (i) If transmission record indicates the packet ${P_r}$ was not transmitted to L before, namely L does not own the packet it requests for, A (or B) will send the packet ${P_r}$ to L by means of quantum channel verification and quantum teleportation as in Step 1 and Step 2.

• (ii) Otherwise, if transmission record indicates the ${P_r}$ has been transmitted to L before, namely L has owned the packet it requests for, then A (or B) will send a rejection order to L and let L know that ${P_r}$ is a packet it owns. Here the rejection order is also one of defined orders in the form of classical bits, and it is used to reject the requester for packet request and terminate the process of packet request, which is defined and listed in Table 1.

Note that although L can overhear the classical bits and judge that a new transmission is occurring between A and B, it does not know what is transmitting so that L may send multiple requests for same packets. For this reason, the above second case is used to avoid repetitive transmissions.

Step 5: Opportunistic coding L refers to its stored packets and makes an optimal coding decision for neighbors. An optimal coding is to ensure more neighbors can decode the encoded packet.

The procedure of opportunistic coding is illustrated in Fig. 5.

Fig. 5

Opportunistic coding

(5.1) For the purpose of allowing more neighbors to decode a new packet, L encodes a new packet $P_g$ for neighbors.

To ensure g neighbors ${R_1},{R_2},\ldots ,{R_g}$ can decode their needed packets $P_1,P_2,\ldots ,P_g$, L can XOR the g packets together when each neighbor ${R_i}$ owns all $g-1$ packets $P_j(j \ne i)$. The encoded packet can be generated by:

$$\begin{aligned} Pe = P_1 \oplus P_2 \oplus \cdots \oplus P_g \end{aligned}$$

(21)

Then L transmits the encoded packet to them by quantum teleportation, respectively. Since the operation on different EPR pairs occurs in local place, L can operate several EPR pairs at the same time as long as there are enough capacity of operation. Such encoding operation can reduce the requirement for quantum states in local preparation.

(5.2) When L completes the operation on its particles of EPR pairs, which is shared with g neighbors, respectively, L combines the measurement outcomes of g neighbors together and adds an l-bit notification bits to notify which nodes should operate their EPR pairs, because not every node is the desired receiver except the g neighbors. As shown in Fig. 6, the notification bits are set according to two simple rules as follows:

• (i) l denotes the total amount of nodes in a network, and each notification bit corresponds to a node.

• (ii) For a certain bit, the value of “1” means that the corresponding node is one of the desired receivers in this transmission, while the value of “0” means the corresponding node is not. That is to say, there will be g “1” in the notification bits if a node generates an encoded packet for g neighbors.

Fig. 6

Measurement outcomes and notification bits

Then L broadcasts one packet of the measurement outcomes and notification bits once.

(5.3) Each neighbor receives the broadcast packet from L and checks the notification bits. If it is a desired receiver in the notification bits, the node will apply transformation by its corresponding measurement outcomes, to its own particles in the EPR pairs with L. Thus it can get the w qubits and further the encoded packet. Otherwise, it is not a receiver, then it will do nothing.

We take an example to illuminate this scheme more clearly, which is shown in Fig. 7.

Fig. 7

Example of the proposed scheme

Example 1

In the scenario of Fig. 7, packet state is shown beneath a node. Assume A would like to send a w-bit packet ${P_1}$ to B. After quantum channel verification between A and B, A selects a pair of orthogonal bases and specifies the corresponding classical bits of 0 and 1 as follows:

$$\begin{aligned} 0 \rightarrow \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle + \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle ,\quad 1 \rightarrow \frac{{\sqrt{2} }}{2}\left| 0 \right\rangle - \frac{{\sqrt{2} }}{2}\left| 1 \right\rangle . \end{aligned}$$

(22)

A prepares w qubits according to the packet ${P_1}$ and the above rule, and then it transmits these w qubits to B by quantum teleportation over the shared EPR pairs. Then B measures the received qubits with orthogonal bases to get the packet ${P_1}$. Note that during the process of quantum teleportation, A sends 2w bits via classical channel. When L overhears these classical bits, it knows that data transmission is happening, so it sends a request order(11111) to A to request the latest packet ${P_1}$.

After receiving request order, A checks the packet states and knows that L does not own the packet ${P_1}$, so A sends ${P_1}$ to L by the same way as it sends ${P_1}$ to B.

After receiving the packet ${P_1}$, L tries to make an optimal coding decision for neighbors A, B, and C, by referring to neighbors’ packet states. L encodes a new packet ${P_e} = {P_1} \oplus {P_2} \oplus {P_4}$ for neighbors A, B, and C and prepares three copies of the same w qubits according to ${P_e}$, then it operates the particles in different EPR pairs with A, B, and C, respectively, to transmit the packet ${P_e}$. When the operation on EPR pairs is completed, L broadcasts a packet which includes all measurement outcomes and corresponding notification bits to the receivers A, B, and C as follows (Fig. 8):

Fig. 8

Example of measurement outcomes and notification bits

Each of A, B, and C gets its corresponding measurement outcomes in the broadcasted packet from L and applies corresponding transformation to the particles in EPR pairs with L, and thus all of them can get the w qubits and further the packet ${P_e}$ from one transmission of broadcast.

3.2 Property

Definition 1

Assume that there are l $\left( {l \ge 2} \right)$ neighbors around a relay node, and then the number of listeners who successfully obtain packets by opportunistic listening in unit time can be used to evaluate the extent of opportunistic characteristic. If all neighbors can successfully overhear the packet from the relay node, it is defined as completely opportunistic characteristic. If the number of successful listeners is $\le {l}$, it is defined as weakly opportunistic characteristic.

Property 1

Our scheme has weakly opportunistic characteristic compared with COPE which has completely opportunistic characteristic.

Proof

Because of the cooperation of classical channel and quantum channel in quantum teleportation, we can implement opportunistic listening in quantum communication, which seems to be impossible by using only quantum channel. However, the opportunistic characteristic in our scheme is weaker than COPE. $\square$

Fig. 9

Two types of opportunistic characteristic

Consider a common scenario in Fig. 9, there are $l\ (l=4)$ neighbors around two communication parties A and B. In COPE, all neighbors can overhear the encoded packet sent from A to B in unit time. Comparatively, in our scheme, all neighbors send request orders to A or B, but A and B can only transmit the packet to one neighbor, respectively, so the number of successful listeners is 2 and $2\le l$, where the equal sign makes sense only if there are merely 2 neighbors. So our scheme satisfies the condition of weakly opportunistic characteristic.

Table 2 Comparison between COPE and our scheme

Because of the cooperation of quantum channel for communication, and classical channel for listening in our scheme, the opportunistic characteristic of our scheme has some differences with COPE. A summary of comparison is shown in Table 2.

Property 2

Assume T(l) represents the delay of a packet obtained by l neighbors and T(l) in our scheme can achieve $O(\log _{2}l) \le T(l) \le O(l)$.

Proof

Assume that a packet ${P_r}$ is transmitted between A and B, and all l neighboring nodes can judge that a new transmission is occurring between A and B by opportunistic listening. We define a learned node as the node who owns the packet ${P_r}$, and then neighbors will send a request order to the learned node A or B, with the same probability $\frac{1}{2}$, to request for ${P_r}$. Restricted by quantum channel, A or B can only send the packet ${P_r}$ to one requester and other requesters will have to wait. $\square$

Fig. 10

Maximum delay in the worst case

T(l) represents the delay of a packet obtained by l neighbors during the process of opportunistic listening, which will decide the subsequent coding strategy of opportunistic coding so as to describe the transmission performance of a network. Fewer delay means higher flexibility and better performance. So the delay will be discussed in detail.

Firstly, we consider the worst case. If all neighbors send request orders to one node(e.g., A) as shown in Fig. 10a, A can only choose one requester(e.g., ${L_1}$) to transmit ${P_r}$. The rest of nodes has to wait, but they hear the transmission occurring between A and ${L_1}$, so they know that ${L_1}$ becomes a learned node. Then the rest of nodes will send request orders to three learned nodes A, B, ${L_1}$ with the same probability $\frac{1}{3}$. In the worst case, all nodes send request orders to the same node (just like A in Fig. 10b), regardless of how many leaned nodes there are. In this way, T(l) will reach maximum:

$$\begin{aligned} T(l) = O(l) \end{aligned}$$

(23)

Fig. 11

Minimum delay in the best case

Secondly, we consider the best case as shown in Fig. 11. In Fig. 11a, A and B both receive a request order and send ${P_r}$ to the requester ${L_1}$ and ${L_5}$, respectively. By opportunistic listening, neighbors know that ${L_1}$ and ${L_5}$ have received the packet from A and B, so there are ${2^2}=4$ learned nodes now. Next, the rest of nodes will send request orders again, but they have four choices this time, so they will send request order to A, B, ${L_1}$, ${L_5}$ with probability $\frac{1}{4}$, respectively. In the best case, four learned nodes will all receive request orders, and the number of learned nodes will be changed to ${2^3}=8$ after packet transmission. In this way, T(l) will reach minimum:

$$\begin{aligned} {2^1} + {2^2} + {2^3} +\cdots + {2^T} \ge l \end{aligned}$$

(24)

It can be rewritten as

$$\begin{aligned} T(l) = O({\log _2}l), \end{aligned}$$

(25)

So the delay T(l) of our scheme achieves $O(\log _{2}l) \le T(l) \le O(l)$.

4 Security analysis

4.1 Classical attack

Theorem 1

By only capturing classical bits, an attacker cannot get the transmitted packet in our scheme.

Proof

Assume that an attacker can capture classical bits without being discovered. In our scheme, the attacker may capture:

• (i) The classical bits between two communication parties. In quantum teleportation, these bits are the outcomes of Bell-state measurement as follows:

  $$\begin{aligned} 00\rightarrow \left| {{\phi }^{+}} \right\rangle ,\quad 10\rightarrow \left| {{\phi }^{-}} \right\rangle ,\quad 01\rightarrow \left| {{\psi }^{+}} \right\rangle ,\quad 11\rightarrow \left| {{\psi }^{-}} \right\rangle . \end{aligned}$$

  (26)

  According to the principle of quantum teleportation, they are used to tell the receiver which unitary operation should be performed on the particle of the shared EPR pair so as to “recover” the transmitted quantum state. So without the shared EPR pair, the measurement outcomes is meaningless for an attacker.

• (ii) The request order or rejection order between two communication parties. In our scheme, the request order is used to ask the receiver for latest packet, and the rejection order is used to refuse the packet request. Such orders are irrelevant to the content of a packet, so they are useless for attacker to get the transmitted packet.

• (iii) The broadcast packet from a relay node who encodes for neighbors. The broadcast packet from a relay node consists of measurement outcomes and notification bits. Measurement outcomes make no sense for an attacker, which is explained in the case of (i). The function of notification bits is to tell who are the desired receivers of measurement outcomes. It also makes no sense for an attacker unless what it wants to know is merely who the relay node sends the packet to, which is certainly not a secret for all nodes. $\square$

4.2 Quantum attack

There are two types of quantum channels in our scheme: One is the direct quantum channel used to transmit one measure particle $\textit{p}_\mathrm{m}$ during the process of quantum channel verification, and the other one is the latent channel between the shared EPR pairs. In order to obtain information, an attacker can disturb the above two types of quantum channels.

Fig. 12

Quantum attack

Theorem 2

Assume that an attacker replaces the measure particle ${p_{\mathrm {m}}}$ with another particle ${p'_\mathrm{m}}$, namely ${p_{\mathrm {m}}} \rightarrow {p'_\mathrm{m}}$, and it can be detected by quantum channel verification.

Proof

As shown in Fig. 12, any substitution of ${p_{\mathrm {m}}} \rightarrow {p'_\mathrm{m}}$ will cause that the state of quantum system changes, namely $\left| {{{\varPsi } ^c}} \right\rangle \rightarrow \left| {{{\varPsi } ^c}^\prime } \right\rangle$, and $\left| {{{\varPsi } ^c}^\prime } \right\rangle$ can be described as

$$\begin{aligned} \left| {{{\varPsi } ^c}^\prime } \right\rangle = \left| {{{\varPsi } ^c}} \right\rangle \otimes \left| {{A_\mathrm{m'}}} \right\rangle . \end{aligned}$$

(27)

When B receives the replaced ${p'_\mathrm{m}}$ and applies next operation:

$$\begin{aligned} {C_{b_j\mathrm{m}}}\left| {{{\varPsi } ^{c'}}} \right\rangle ={C_{b_j\mathrm{m}}}\left( \left| {{{\varPsi } ^c}} \right\rangle \otimes \left| {{A_\mathrm{m'}}} \right\rangle \right) \ne \left| {{{\varPhi } ^ + }} \right\rangle \otimes \left| {{{\varPsi } _\mathrm{m}}} \right\rangle . \end{aligned}$$

(28)

The above equation means that $\left| {{{\varPhi } ^ + }} \right\rangle$ and $\left| {{{\varPsi } _\mathrm{m}}} \right\rangle$ are not in product state, so the measure particle ${p_{\mathrm {m}}}$ cannot be separated from the entangled system. When the replaced particle ${p'_\mathrm{m}}$ is transmitted back to A, secret parameters $\theta$ and $\varphi$ are changed so that quantum channel verification will be failed. $\square$

Theorem 3

Any operation ${U_\varepsilon }$ that attackers perform on the shared EPR pair $\left| {{\varPhi } _j^ + } \right\rangle$ will destroy the integrity of quantum channel, which can be detected by quantum channel verification. $\square$

Proof

Assume that an attacker has the chance to disturb the EPR pairs, we denote his auxiliary quantum state by $\left| {{{\varPsi } _e}} \right\rangle$, and the entire state of the shared EPR pair and the auxiliary quantum state is

$$\begin{aligned} \left| {{{\varPsi } _{{a_j}{b_j}e}}} \right\rangle = \left| {{\varPhi } _j^ + } \right\rangle \otimes \left| {{{\varPsi } _e}} \right\rangle . \end{aligned}$$

(29)

where a, b represent two particles of the shared EPR pair, while e represents the particle corresponding to $\left| {{{\varPsi } _e}} \right\rangle$. The attacker applies a unitary operation ${U_\varepsilon }$ in $\left| {{{\varPsi } _{{a_j}{b_j}e}}} \right\rangle$, and the entire state of quantum system becomes

$$\begin{aligned} {U_\varepsilon }\left| {{\psi _{{a_j}{b_j}e}}} \right\rangle= & {} \left| {{0_{{a_j}}}{0_{{b_j}}}} \right\rangle \otimes \left| {{E_1}} \right\rangle + \left| {{0_{{a_j}}}{0_{{b_j}}}} \right\rangle \otimes \left| {{E_2}} \right\rangle \nonumber \\&+\, \left| {{1_{{a_j}}}{0_{{b_j}}}} \right\rangle \otimes \left| {{{{\tilde{E}}}_1}} \right\rangle + \left| {{1_{{a_j}}}{1_{{b_j}}}} \right\rangle \otimes \left| {{{{\tilde{E}}}_2}} \right\rangle . \end{aligned}$$

(30)

where $\left| {{E_1}} \right\rangle \bot \left| {{E_2}} \right\rangle$, $\left| {{{{\tilde{E}}}_1}} \right\rangle \bot \left| {{{{\tilde{E}}}_2}} \right\rangle$, and $\left\langle {{E_1}|{{{\tilde{E}}}_2}} \right\rangle + \left\langle {{E_2}|{{{\tilde{E}}}_1}} \right\rangle = 0$.

When A applies the C-NOT gate, (6) can be rewritten as follows

$$\begin{aligned} \left| {{\psi ^{c'}}} \right\rangle= & {} {C_{a\mathrm{m}}}\left( {{U_\varepsilon }\left| {{\psi _{{a_j}{b_j}e}}} \right\rangle } \right) \left| {{\psi _\mathrm{m}}} \right\rangle \nonumber \\= & {} \frac{1}{2}\Big [\left( \cos \theta \left| {{0_{{a_j}}}{0_{{b_j}}}{0_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{0_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes \left| {{E_2}} \right\rangle \nonumber \\&\ +\, \left( \cos \theta \left| {{1_{{a_j}}}{1_{{b_j}}}{1_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{1_{{a_j}}}{1_{{b_j}}}{0_\mathrm{m}}} \right\rangle \right) \otimes | {{{{\tilde{E}}}_2}} \rangle \nonumber \\&\ +\,\left( \cos \theta \left| {{0_{{a_j}}}{1_{{b_j}}}{0_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{0_{{a_j}}}{1_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes \left| {{E_1}} \right\rangle \nonumber \\&\ +\,\left( \cos \theta \left| {{1_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{1_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes | {{{{\tilde{E}}}_1}} \rangle \Big ]. \end{aligned}$$

(31)

The above equation shows the entire state after Step 2 in quantum channel verification under an attack’s disturbance. Then B performs some operations on $\left| {{\psi ^{c'}}} \right\rangle$ in Step 3 in quantum channel verification, the entire state (8) becomes

$$\begin{aligned} {C_{b\mathrm{m}}}\left| {{\psi ^{c'}}} \right\rangle= & {} \frac{1}{2} \Big [\left( \cos \theta \left| {{0_{{a_j}}}{0_{{b_j}}}{0_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{0_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes \left| {{E_2}} \right\rangle \nonumber \\&\ +\,\left( \cos \theta \left| {{1_{{a_j}}}{1_{{b_j}}}{0_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{1_{{a_j}}}{1_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes | {{{{\tilde{E}}}_2}} \rangle \nonumber \\&\ +\,\left( \cos \theta \left| {{0_{{a_j}}}{1_{{b_j}}}{1_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{0_{{a_j}}}{1_{{b_j}}}{0_\mathrm{m}}} \right\rangle \right) \otimes \left| {{E_1}} \right\rangle \nonumber \\&\ +\, \left( \cos \theta \left| {{1_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle + {e^{ - i\varphi }}\sin \theta \left| {{1_{{a_j}}}{0_{{b_j}}}{1_\mathrm{m}}} \right\rangle \right) \otimes | {{{{\tilde{E}}}_1}} \rangle \Big ]. \end{aligned}$$

(32)

It is obvious that ${C_{bm}}\left| {{\psi ^{c'}}} \right\rangle \ne \left| {{{\varPhi } ^ + }} \right\rangle \otimes \left| {{\psi _\mathrm{m}}} \right\rangle$, the measurement ${p_\mathrm{m}}$ cannot be separated correctly, and the paraments are changed, so the disturbance can be detected by quantum channel verification. $\square$

5 Performance analysis

5.1 Network throughput

Compared with conventional QNC schemes, our scheme realizes opportunistic characteristic by listening to classical channel. Furthermore, our scheme realizes opportunistic coding by broadcasting the measurement outcomes and notification bits, which allows more than one neighbor to receive the measurement outcome during one transmission and therefore improves network throughput.

Assume that a relay node L intends to send an encoded packet $P_g$ to g neighbors as shown in Fig. 5. For conventional quantum network without opportunistic characteristic, it can only transmit the packet $P_g$ to each neighbor, respectively, which results in a total number of ${N_v}=g$ for transmission. In contrast, our scheme takes full advantage of channel characteristic of quantum teleportation. For quantum teleportation, the operation on EPR pairs occurs at the local location of sender and receiver, as long as a relay node has enough capacity for operation, and it can operate several EPR pairs, which are shared with different nodes, at the same time. So the transmission time mainly depends on when the measurement outcomes arrive at receivers. In our scheme, a relay node operates different EPR pairs with g neighbors in its own place and then broadcasts the measurement outcomes and notification bits to notice the receivers, which helps each one of g neighbors get its needed measurement outcomes and further the encoded packet, during a number ${N_o}=1$ of transmission. Table 3 lists the comparison result.

In a word, compared with conventional unicast quantum communication, our scheme can improve network throughput by $\frac{{{N_v}}}{{{N_o}}} = g$, where g is the number of packet’s receivers.

Table 3 Performance comparison

5.2 Resource consumption

Since quantum communication is expensive, some extra resources, which may be less expensive than quantum communication, are considered in many quantum network coding schemes. Such representative resources include:

• (i) Classical communication;

• (ii) Pre-shared entanglement (such as EPR pairs).

The above two kinds of resources are both used in our scheme.

Our scheme is designed in the setting where every two nodes possess pre-shared entanglement(EPR pairs). For transmitting a w-bit-encoded packet to g neighbors, a relay node needs to apply quantum teleportation, and it consumes wg qubits, wg EPR pairs, 2wg bits, and another l bits for notification bits. For each time of quantum channel verification, it consumes h qubits and 2h EPR pairs to detect the integrity of EPR pairs. Meanwhile, some procedures consume only classical bits, such as sending request order or rejection order. Table 4 gives a summary of resource consumption in our scheme.

Table 4 Resource consumption

6 Conclusion

In this paper, we proposed an opportunistic quantum network coding scheme by taking full advantage of quantum teleportation. The proposed scheme has opportunistic characteristic by listening to classical channel and broadcasting measurement outcomes via classical channel, which generally cannot be achieved in conventional quantum network. Meanwhile, it can resist classical passive attack and quantum active attack. Furthermore, we will explore the usage of mixed channels of quantum teleportation. Classical channel can not only be used to broadcast measurement outcomes, but also be used to broadcast encoded packet directly on the premise of secure transmission. Moreover, some new quantum operations on qubit can be designed for the part of opportunistic coding, which will realize the improvement of transmission performance in quantum networks.