1 introduction

As an important resource, entanglement does not only play an important role in the field of quantum physics, but it also has wide applications in quantum information processing (QIP) tasks, for instance, in quantum computation [1], quantum teleportation [2,3,4], and quantum key distribution (QKD) [5]. Multipartite entangled states usually can be divided into many different classes: W states [6], GHZ states [7], cluster states [8], etc. These different classes of states cannot be converted into each other with stochastic local operations and classical communication (SLOCC) [9]. Because the special multiparticle entanglement is required for special quantum information processing tasks [8, 10,11,12], the simple and efficient schemes for preparing large-size multipartite entangled states become more and more important. Among the various multipartite entangled states, W state is a special class of multipartite entangled state, which possesses many particular properties. For instance, the W state has attracted more and more attention for its usefulness in QKD [13] and in quantum cloning machine [14]. Initially, the W state is applied to the quantum teleportation and quantum secret communication [13, 15,16,17,18,19]. Recently, the W state has a wide range of applications in other new fields, which plays an important role in the areas of the leader election problem in anonymous quantum networks [20], quantum Fisher information (QFI) of W state in the basic decoherence channels [21, 22], quantum thermalization of a single-mode cavity [23], etc. Therefore, it is a hot topic in the entanglement research to design an efficient scheme for preparing large-scale multipartite entangled W states.

In recent years, quantum state expansion and fusion techniques have been presented and experimentally confirmed as efficient methods for generating large-size multipartite entangled W states. With expansion technology, the number of qubits of the original entangled state is expanded by one or two each time [24,25,26,27,28,29], and one can get a larger entangled state from two or more multipartite entangled states by sending only one qubit of each seed entangled state to the fusion operation [30,31,32,33,34,35,36,37]. Compared to the expansion scheme, the creation of W states via the fusion process has attracted considerable attention as it is obviously more advantageous to prepare W states with larger number of particles. In 2011, Ozdemir et al. [31] first put forward an optical fusion gate, with which a \(W_{n+m-2}\) state can be generated from \(W_n\) and \(W_m\) \((n,m \ge 3)\) states [30], and many fusion schemes [32, 33] have been proposed to prepare the W states following some ideas as in Ref. [30]. However, in order to improve fusion efficiency, controlled quantum gates and ancilla qubits have been introduced in fusion mechanism of the previous works. But it is not an easy task to realize controlled quantum gates, which will increase the realization complexity of the fusion process. In addition, it is worth pointing out that there is qubit loss in most of the currently existing fusion schemes. This qubit loss will inevitably reduce the fusion efficiency as the number of the output entangled qubits is smaller than the sum of numbers of the input entangled qubits. In a repeated fusion operation, another very important question is the availability of quantum memories to store the throughput W states obtained at each fusion step. This requirement clearly adds complexity to the physical implementation. Because a qubit-loss-free fusion scheme reduces the number of the fusion steps for obtaining a W state of a target size considerably, the physical implementation process of it becomes much easier. Therefore, most of the recent works are mainly focusing on how to simplify fusion scheme without controlled quantum gates and reduce the loss of particles to improve the fusion efficiency.

In this paper, we propose a scheme to prepare W states via a polarization-dependent beam splitter (PDBS)-based fusion mechanism for polarization encoded photons. The \(W_{m+n}\) state can be generated from a n-qubit W state and a m-qubit W state without any qubit loss. The \(W_{m+n+t-1}\) can be generated from \(W_m\), \(W_n\) and \(W_t\) states which is a great progress in the loss of particle numbers in the fusion of three W states. In addition, our scheme is experimentally realizable because no controlled quantum gates operations and no ancillary qubits are required.

Fig. 1
figure 1

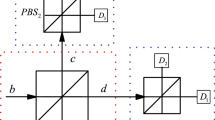
Fusion and detection mechanism of the PDBS. Two photons, from the \(|W\rangle _A\) and \(|W\rangle _B\), will be sent into the input modes of the fusion mechanism in the area of red dashed line. The output photons will be measured by detectors \(D_1\), \(D_2\), \(D_3\) and \(D_4\) in the area of blue dashed line. The function of the polarizing beam splitter (PBS) reflects vertically (V) polarized photons and transmits horizontally (H) polarized photons (Color figure online)

Full size image

This paper is organized as follows: In Sect. 2, we introduce the fusion and detection mechanism of the PDBS. The schemes for fusing two small-size maximally entangled W states into large-scale maximally entangled W states are presented in Sect. 3. The schemes for fusing three small-size maximally entangled W states are presented in Sect. 4. Section 5 is the conclusion section.

2 Fusion mechanism

The fusion schemes for fusing two or three maximally entangled W states will be presented in terms of the PDBS. The PDBS has independent polarization coefficients and different polarization-dependent transmissivities: \(0<\mu <1\) for horizontally (H) polarization photons and \(0<\nu <1\) for vertically (V) polarization photons, in which \(\mu , \nu \) are two independent parameters of the PDBS, a, b are the input modes, and c, d are the corresponding output modes. As shown in Fig. 1, two photons on the left of the arrow, from the \(|W\rangle _A\) and \(|W\rangle _B\), respectively, will be sent into the input modes a and b, and the right side are the output modes of the photons coupling after the PDBS. The function of the PDBS can be represented by the following four basic transformations [25]:

$$\begin{aligned} {|}H\rangle _a|H\rangle _b\rightarrow & {} (2\mu -1)|H\rangle _ d|H\rangle _c + \sqrt{2\mu }\sqrt{1-\mu }|0\rangle _c|HH\rangle _d\nonumber \\&- \sqrt{2\mu }\sqrt{1-\mu }|HH\rangle _c|0\rangle _d, \end{aligned}$$
(1a)
$$\begin{aligned} {|}H\rangle _a|V\rangle _b\rightarrow & {} \sqrt{\mu }\sqrt{\nu }|H\rangle _c|V\rangle _d - \sqrt{1-\mu }\sqrt{1-\nu }|V\rangle _c|H\rangle _d \nonumber \\&+ \sqrt{1-\mu }\sqrt{\nu }|0\rangle _c|HV\rangle _d - \sqrt{\mu }\sqrt{1-\nu }|HV\rangle _c|0\rangle _d, \end{aligned}$$
(1b)
$$\begin{aligned} {|}V\rangle _a|H\rangle _b\rightarrow & {} \sqrt{\mu }\sqrt{\nu }|V\rangle _c|H\rangle _d - \sqrt{1-\mu }\sqrt{1-\nu }|H\rangle _c|V\rangle _d \nonumber \\&+ \sqrt{1-\mu }\sqrt{\nu }|0\rangle _c|VH\rangle _d - \sqrt{\mu }\sqrt{1-\nu }|VH\rangle _c|0\rangle _d, \end{aligned}$$
(1c)
$$\begin{aligned} {|}V\rangle _a|V\rangle _b\rightarrow & {} (2\nu -1)|V\rangle _ d|V\rangle _c + \sqrt{2\nu }\sqrt{1-\nu }|0\rangle _c|VV\rangle _d \nonumber \\&- \sqrt{2\nu }\sqrt{1-\nu }|VV\rangle _c|0\rangle _d. \end{aligned}$$
(1d)

3 PDBS-based fusion scheme for two W states

In this section, it will be discussed that the n-qubit W state \(|W_n\rangle \) and the m-qubit W state \(|W_m\rangle \) \((n,m \ge 2)\) are fused into a \((n+m)\)-qubit W state with the help of a H-polarized ancilla photon. The maximally entangled W state \(|W_n\rangle \) can be written as [30]:

$$\begin{aligned} {|}W_n\rangle = \frac{1}{\sqrt{n}}\left[ |({n-1})_H\rangle |1_V\rangle _2 +\sqrt{n-1}|W_{n-1}\rangle |1_H\rangle _2\right] . \end{aligned}$$
(2)

Firstly, the strategy for fusing two \(|W\rangle _3\) states into a \(|W\rangle _6\) state with a H-polarized ancilla photon will be discussed as follows. As shown in Fig. 2, two initial W states can be written as:

$$\begin{aligned} |W_3\rangle _A= & {} \frac{1}{\sqrt{3}}(|HH\rangle |V\rangle _2 +|HV\rangle |H\rangle _2+|VH\rangle |H\rangle _2), \end{aligned}$$
(3a)
$$\begin{aligned} |W_3\rangle _B= & {} \frac{1}{\sqrt{3}}(|HH\rangle |V\rangle _3 +|HV\rangle |H\rangle _3+|VH\rangle |H\rangle _3). \end{aligned}$$
(3b)

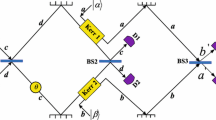
In the fusion strategy, only one photon of each W state (labeled as photons 2 and 3) has been accessed and is sent into a PDBS for completing the fusion process with one auxiliary photon. The remaining photons are kept intact at their sites. Our scheme is divided into two parts: One part is the first PDBS with the ancilla photon and the second photon comes from \(|W_3\rangle _A\) state, which is exactly what Tashima et al. [25] have done. Another part is one photon from the first PDBS which is input into the second PDBS with one photon from \(|W_3\rangle _B\) state. Considering the case where a photon is present in each of the modes, the state after the \(\hbox {PDBS}_1\) can be written as:

$$\begin{aligned} {\big |}\widetilde{W}\big \rangle _4= & {} \frac{1}{\sqrt{3}}\left[ \sqrt{\mu _1\nu _1} {|}HH\rangle |H\rangle _{1^{''}}|V\rangle _{2^{'}}+\sqrt{(1-\mu _1) (1-\nu _1)}|HH\rangle |V\rangle _{1^{''}}|H\rangle _{2^{'}}\right. \nonumber \\&\left. +\,(2\mu _{1}-1)|HV\rangle |H\rangle _{1^{''}}|H\rangle _{2^{'}} +(2\mu _{1}-1)|VH\rangle |H\rangle _{1^{''}}|H\rangle _{2^{'}}\right] . \end{aligned}$$
(4)

Obviously, the \(|W\rangle _4\) state will be generated with appropriately selected parameters \((\mu _1,\nu _1)\) for the \(\hbox {PDBS}_1\) \(\mu _1=(5+\sqrt{5})/10\) and \(\nu _1=(5-\sqrt{5})/10\) or vice versa. The first part is proposed by Tashima et al. that extending a W state by one photon. Then, one photon from this new W state is used to expand the second large-scale W state in the second step. These two photons extracted from two W states \(|W\rangle _4\) (labeled as photons \(1^{''}\)) and \(|W_3\rangle _B\) (labeled as photons 3), respectively, will be coupled on a \(\hbox {PDBS}_2\), whose output modes are labeled as \(1^{'}\) and \(3^{'}\). Similarly, in the case where there is only one photon in each output mode, the state after the \(\hbox {PDBS}_2\) can be written as:

$$\begin{aligned} {\big |}\widetilde{W}\big \rangle= & {} \frac{1}{3} \left\{ \sqrt{\mu _1\nu _1}\big [\sqrt{\mu _2\nu _2}|HHHH\rangle |V \rangle _{2^{'}}|V\rangle _{3^{'}}|H\rangle _{1^{'}}\right. \nonumber \\&+\,\sqrt{(1-\mu _2)(1-\nu _2)}|HHHH\rangle |V \rangle _{2^{'}}|H\rangle _{3^{'}}|V\rangle _{1^{'}}\nonumber \\&+\,(2\mu _{2}-1)|HHHV\rangle |V\rangle _{2^{'}}|H \rangle _{3^{'}}|H\rangle _{1^{'}}\nonumber \\&+\,(2\mu _{2}-1)|HHVH \rangle |V\rangle _{2^{'}}|H \rangle _{3^{'}}|H\rangle _{1^{'}}\big ] \nonumber \\&+\,\big (\sqrt{(1-\mu _1)(1-\nu _1)}\big )\big [(2\nu _{2}-1)|HHHH \rangle |H\rangle _{2^{'}}|V\rangle _{3^{'}}|V \rangle _{1^{'}}\nonumber \\&+\,\sqrt{\mu _2\nu _2}|HHHV\rangle |H \rangle _{2^{'}}|H\rangle _{3^{'}}|V\rangle _{1^{'}} \nonumber \\&+\,\sqrt{(1-\mu _2)(1-\nu _2)}|HHHV\rangle |H\rangle _{2^{'}}|V \rangle _{3^{'}}|H\rangle _{1^{'}}\nonumber \\&+\,\sqrt{\mu _2\nu _2}|HHVH \rangle |H\rangle _{2^{'}}|H \rangle _{3^{'}}|V\rangle _{1^{'}} \nonumber \\&+\,\sqrt{(1-\mu _2)(1-\nu _2)}|HHVH\rangle |H\rangle _{2^{'}}|V \rangle _{3^{'}}|H\rangle _{1^{'}}\big ]\nonumber \\&+\,(2\mu _{1}-1)\big [\sqrt{\mu _2\nu _2}|HVHH\rangle |H\rangle _{2^{'}}|V \rangle _{3^{'}}|H\rangle _{1^{'}}\nonumber \\&+\,\sqrt{(1-\mu _2)(1-\nu _2)}|HVHH \rangle |H\rangle _{2^{'}}|H\rangle _{3^{'}}|V\rangle _{1^{'}}\nonumber \\&+\,(2\mu _{2}-1)|HVHV\rangle |H\rangle _{2^{'}}|H\rangle _{3^{'}}|H \rangle _{1^{'}}\nonumber \\&+\,(2\mu _{2}-1)|HVVH\rangle |H\rangle _{2^{'}}|H \rangle _{3^{'}}|H\rangle _{1^{'}}\big ]\nonumber \\&+\,(2\mu _{1}-1)\big [\sqrt{\mu _2\nu _2}|VHHH\rangle |H\rangle _{2^{'}}|V \rangle _{3^{'}}|H\rangle _{1^{'}}\nonumber \\&+\,\sqrt{(1-\mu _2)(1-\nu _2)}|VHHH \rangle |H\rangle _{2^{'}}|H\rangle _{3^{'}}|V\rangle _{1^{'}}\nonumber \\&+\,(2\mu _{2}-1)|VHHV\rangle |H\rangle _{2^{'}}|H\rangle _{3^{'}}|H \rangle _{1^{'}}\nonumber \\&\left. +\,(2\mu _{2}-1)|VHHV\rangle |H\rangle _{2^{'}}|H \rangle _{3^{'}}|H\rangle _{1^{'}}\big ]\right\} . \end{aligned}$$
(5)

If the parameters of the PDBSs are set as \(\mu _1=(5\pm \sqrt{5})/10\), \(\nu _1=(5\mp \sqrt{5})/10\) and \(\mu _2=(5\pm \sqrt{5})/10\), \(\nu _2=(5\mp \sqrt{5})/10\), the maximally entangled \(W_6\) state will be generated when the V-polarized photon is detected in \(D_1\).

This fusion scheme can be generalized to the case of generating \(W_{m+n}\) state from a n-qubit W state and a m-qubit W state without any qubit loss. The two initial states n-qubit and m-qubit W state \((n,m \ge 2)\) can be written as:

$$\begin{aligned} {|}W_n\rangle= & {} \frac{1}{\sqrt{n}}\left[ |({n-1})_H\rangle |1_V\rangle _2 + \sqrt{n-1}|W_{n-1}\rangle |1_H\rangle _2\right] , \end{aligned}$$
(6a)
$$\begin{aligned} {|}W_m\rangle= & {} \frac{1}{\sqrt{m}}\left[ |({m-1})_H\rangle |1_V\rangle _3 + \sqrt{m-1}|W_{m-1}\rangle |1_H\rangle _3\right] . \end{aligned}$$
(6b)

Similarly, considering the case where a photon is present in each of the modes \(1^{\prime }\), \(2^{\prime }\) and \(3^{\prime }\), the state after the two PDBSs can be expressed as:

$$\begin{aligned} {\big |}\widetilde{W}\big \rangle= & {} \frac{\sqrt{m-1}}{\sqrt{mn}}\big [\sqrt{\mu _1 \nu _1}(2\mu _2-1)|({n-1})_H\rangle |W_{m-1}\rangle |V \rangle _{2^{\prime }}|H\rangle _{3^{\prime }}|H\rangle _{1^{\prime }}\nonumber \\&-\,\sqrt{(1-\mu _1)(1-\nu _1)}\sqrt{\mu _2\nu _2}|({n-1})_H \rangle |W_{m-1}\rangle |H\rangle _{2^{\prime }}|H\rangle _{3^{\prime }}|V \rangle _{1^{\prime }}\nonumber \\&+\,\sqrt{(1-\mu _1)(1-\nu _1)}\sqrt{(1-\mu _2)(1-\nu _2)}|({n-1})_H \rangle |W_{m-1}\rangle |H\rangle _{2^{\prime }}|V\rangle _{3^{\prime }}|H \rangle _{1^{\prime }}\big ]\nonumber \\&+\,\frac{1}{\sqrt{mn}}\big [\sqrt{\mu _1\nu _1}\sqrt{\mu _2\nu _2}|({n-1})_H \rangle |({m-1})_H\rangle |V\rangle _{2^{\prime }}|V\rangle _{3^{\prime }}|H \rangle _{1^{\prime }}\nonumber \\&-\,\sqrt{\mu _1\nu _1}\sqrt{(1-\mu _2)(1-\nu _2)}|({n-1})_H\rangle |({m-1})_H \rangle |V\rangle _{2^{\prime }}|H\rangle _{3^{\prime }}|V \rangle _{1^{\prime }}\nonumber \\&-\,\sqrt{(1-\mu _1)(1-\nu _1)}(2\nu _2-1)|({n-1})_H\rangle |({m-1})_H \rangle |H\rangle _{2^{\prime }}|V\rangle _{3^{\prime }}|V \rangle _{1^{\prime }}\big ]\nonumber \\&+\,\frac{\sqrt{{n-1}}}{\sqrt{mn}}\big [(2\mu _1-1)\sqrt{\mu _2\nu _2}|W_{n-1} \rangle |({m-1})_H\rangle |H\rangle _{2^{\prime }}|V\rangle _{3^{\prime }}|H \rangle _{1^{\prime }}\nonumber \\&-\,(2\mu _1-1)\sqrt{(1-\mu _2)(1-\nu _2)}|W_{n-1}\rangle |({m-1})_H \rangle |H\rangle _{2^{\prime }}|H\rangle _{3^{\prime }}|V \rangle _{1^{\prime }}\big ]\nonumber \\&+\,\frac{\sqrt{{m-1}}\sqrt{{n-1}}}{\sqrt{mn}}(2\mu _1-1) (2\mu _2-1)|W_{n-1}\rangle |W_{m-1}\rangle |H\rangle _{2^{\prime }}|H \rangle _{3^{\prime }}|H\rangle _{1^{\prime }}. \end{aligned}$$
(7)

At last, a \((n+m)\)-qubit W-class state will be generated if a V-polarized photon is detected in \(D_1\). That is

$$\begin{aligned} {\big |}\widehat{W}\big \rangle= & {} -\frac{\sqrt{m-1}}{\sqrt{mn}} \sqrt{(1-\mu _1)(1-\nu _1)}\sqrt{\mu _2\nu _2}|({n-1})_H \rangle |W_{m-1}\rangle |H\rangle _{2^{\prime }}|H \rangle _{3^{\prime }}\nonumber \\&-\,\frac{1}{\sqrt{mn}}\big [\sqrt{\mu _1\nu _1} \sqrt{(1-\mu _2)(1-\nu _2)}|({n-1})_H\rangle |({m-1})_H \rangle |V\rangle _{2^{\prime }}|H\rangle _{3^{\prime }}\nonumber \\&-\,\sqrt{(1-\mu _1)(1-\nu _1)}(2\nu _2-1)|({n-1})_H \rangle |({m-1})_H\rangle |H\rangle _{2^{\prime }}|V \rangle _{3^{\prime }}\big ]\nonumber \\&-\,\frac{\sqrt{{n-1}}}{\sqrt{mn}}(2\mu _1-1) \sqrt{(1-\mu _2)(1-\nu _2)}|W_{n-1}\rangle |({m-1})_H \rangle |H\rangle _{2^{\prime }}|H\rangle _{3^{\prime }}.\nonumber \\ \end{aligned}$$
(8)

With appropriately selected parameters \((\mu ,\nu )\) for the PDBS \(\mu _1=(5\pm \sqrt{5})/10\), \(\nu _1=(5\mp \sqrt{5})/10\) and \(\mu _2=(5\pm \sqrt{5})/10\), \(\nu _2=(5\mp \sqrt{5})/10\), a maximally entangled state \(|W_{n+m}\rangle \) will be generated, and the successful probability is \(P_s(W_m,W_n) = (m+n)/(25mn)\). It should be pointed out that the values of \((\mu ,\nu )\) do not depend on the sizes of the input states, which makes this fusion mechanism seem more universal. In addition, we need to have a discussion. As shown in Fig. 1, two detection mechanisms are placed at both the output modes c and d (blue dashed rectangles), which seems the two photons are all detected in the process of fusion. In fact, only one photon is detected during the whole process, and the other photon detection is simply to verify that there is one photon present in each of the two output modes (as shown in Fig. 2). As mentioned in Ref. [38], the verification process of the event where a photon is present in each of the two output modes of the PDBS and the applications of the output state are realized simultaneously. Furthermore, the fusion process fails if a H-polarized photon is detected in \(D_2\).

Fig. 2
figure 2

Fusion and detection mechanism for \(|W_n\rangle \), \(|W_m\rangle \) and a H-polarized ancilla photon \(|H\rangle _1\): Two photons (labeled as photons 2 and 3), from the \(|W_n\rangle \) and \(|W_m\rangle \), will be coupled with one ancilla photon \(|H\rangle _1\) in the PDBS1 and PDBS2. The corresponding output photons are labeled as \(1^{\prime }\), \(2^{\prime }\) and \(3^{\prime }\). One photon (\(1^{\prime }\)) of the three will be measured by detectors \(D_1\) and \(D_2\) in the polarizing beam splitter (PBS). It needs to be emphasized that we are only interested in the case where a photon is present in each of the out modes

Full size image

4 PDBS-based fusion scheme for three W states

In this section, the fusion scheme for fusing the \(|W\rangle _n\), the \(|W\rangle _m\) and the \(|W\rangle _t\) into a \(|W\rangle _{n+m+t-1}\) state will be introduced. In most of the currently existing design schemes, controlled quantum gates have been introduced to enhance the efficiency of the fusion mechanism. However, it is difficult to realize the controlled quantum gates, which will increase the realization complexity of the fusion process. Therefore, in this scheme, the PDBS-based schemes will be presented to prepare large-scale maximally entangled W states by fusing three small-size entangled W states with the help of a H-polarized ancilla photon. In the absence of any controlled quantum gate operation, the number of the output entangled qubits in the target W state are also increased. The schematic diagram of fusion scheme for fusing n-qubit, m-qubit and t-qubit polarization entangled W states is depicted in Fig. 3. The three initial W states can be written as:

$$\begin{aligned} {|}W_n\rangle= & {} \frac{1}{\sqrt{n}}\left[ |({n-1})_H\rangle |1_V\rangle _2 + \sqrt{n-1}|W_{n-1}\rangle |1_H\rangle _2\right] , \end{aligned}$$
(9a)
$$\begin{aligned} {|}W_m\rangle= & {} \frac{1}{\sqrt{m}}\left[ |({m-1})_H\rangle |1_V\rangle _3 + \sqrt{m-1}|W_{m-1}\rangle |1_H\rangle _3\right] , \end{aligned}$$
(9b)
$$\begin{aligned} {|}W_t\rangle= & {} \frac{1}{\sqrt{t}}\left[ |({t-1})_H\rangle |1_V\rangle _4 + \sqrt{t-1}|W_{t-1}\rangle |1_H\rangle _4\right] . \end{aligned}$$
(9c)
Fig. 3
figure 3

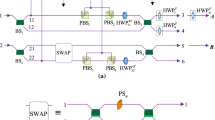
Fusion and detection mechanism for \(|W_n\rangle \), \(|W_m\rangle \), \(|W_t\rangle \) and a H-polarized ancilla photon \(|H\rangle _1\): Three photons (labeled as photons 2, 3 and 4), from the \(|W_n\rangle \), \(|W_m\rangle \), and \(|W_t\rangle \), will be coupled with one ancilla photon \(|H\rangle _1\) in the PDBS1, PDBS2 and PDBS3. \(1^{\prime }\), \(2^{\prime }\), \(3^{\prime }\) and \(4^{\prime }\) are output modes. Only two photons (\(3^{\prime }\) and \(4^{\prime }\)) will be measured by detectors \(D_1\), \(D_2\) and \(D_3\), \(D_4\) in the PBS (black dashed area). We are also interested in the case where a photon is presented in each of the output modes

Full size image

Similarly, only one photon of each W state has been accessed, i.e., three photons 1, 2, 3 extracted from \(|W_n\rangle \), \(|W_m\rangle \) and \(|W_t\rangle \), respectively, and with a H-polarized ancilla photon, will be coupled by the three PDBSs. The remaining photons are kept intact at their sites. For the expression describing the evolution of the total system is too long to be displayed here, all the possible inputs, outputs of the PDBS and the success and failure properties of the output states are listed in Table 1. Considering the case where a photon is presented in each of the modes \(1^{\prime }\), \(2^{\prime }\), \(3^{\prime }\) and \(4^{\prime }\), an \((n+m+t-1)\)-qubit W-class state can be generated when two V-polarized photons are detected in \(D_1\) and \(D_3\), respectively:

$$\begin{aligned} \big |\widetilde{W}_{n+m+t-1}\big \rangle= & {} C_1|(n-1)_H\rangle |W_{m-1} \rangle |(t-1)_H\rangle |H\rangle _{1^{'}}|H\rangle _{2^{'}}\nonumber \\&+\,C_2|(n-1)_H\rangle |(m-1)_H\rangle |W_{t-1}\rangle |H \rangle _{1^{'}}|H\rangle _{2^{'}}\nonumber \\&+\,C_3|W_{n-1}\rangle |(m-1)_H\rangle |(t-1)_H\rangle |H \rangle _{1^{'}}|H\rangle _{2^{'}}\nonumber \\&+\,C_4|(n-1)_H\rangle |( m-1)_H\rangle |(t-1)_H\rangle |H \rangle _{1^{'}}|V\rangle _{2^{'}}\nonumber \\&+\,C_5|(n-1)_H\rangle |( m-1)_H\rangle |(t-1)_H\rangle |V \rangle _{1^{'}}|H\rangle _{2^{'}}, \end{aligned}$$
(10)
Table 1 Truth table of the fusion scheme for fusing three W states: “Input” indicates the polarizations of the photons at the input of the PDBS; “Output” indicates the polarizations of photons after the PDBS; “Result” indicates the success (S), failure (F) properties of the output states of the fusion scheme
Full size table

where

$$\begin{aligned} C_1= & {} -\frac{\sqrt{m-1}}{\sqrt{mnt}}\sqrt{(1-\mu _1)(1-\nu _1)} \sqrt{(1-\mu _2)(1-\nu _2)}\sqrt{\mu _3\nu _3}, \nonumber \\ C_2= & {} \frac{\sqrt{t-1}}{\sqrt{mnt}}\sqrt{(1-\mu _1)(1-\nu _1)} (2\nu _2-1)\sqrt{(1-\mu _3)(1-\mu _3)},\nonumber \\ C_3= & {} \frac{\sqrt{n-1}}{\sqrt{mnt}}(2\mu _1-1)\sqrt{\mu _2\nu _2} \sqrt{\mu _3\nu _3},\nonumber \\ C_4= & {} \frac{1}{\sqrt{mnt}}\sqrt{\mu _1\nu _1}\sqrt{\mu _2\nu _2} \sqrt{\mu _3\nu _3},\nonumber \\ C_4= & {} \frac{1}{\sqrt{mnt}}\sqrt{(1-\mu _1) (1-\nu _1)}(2\nu _2-1)(2\nu _3-1). \end{aligned}$$
(11)

If the parameters \((\mu , \nu )\) for the PDBS are chosen to be \(\mu _1=(5\pm \sqrt{5})/10\), \(\nu _1=(5\mp \sqrt{5})/10\), \(\mu _2=(5\pm \sqrt{5})/10\), \(\nu _2=(5\mp \sqrt{5})/10\) and \(\mu _3=(5\pm \sqrt{5})/10\), \(\nu _3=(5\mp \sqrt{5})/10\), the maximally entangled state \(|W_{n+m+t-1}\rangle \) can be generated. On the other hand, if two H-polarized photons are detected, in \(D_2\) and \(D_4\), respectively, the fusion scheme fails.

Because the PDBS has selective transmission rates for different polarization states, our fusion has a distinct disadvantage, i.e., a certain attenuation of the input photon. Therefore, the probability of this fusion scheme is not very high. Nevertheless, in comparison with the complex controlled quantum gates existing in the current scheme, our scheme is relatively simple. Furthermore, in the previous scheme, one or more of the qubits entering the fusion mechanism must be measured so as to complete the whole fusion process. This qubit loss will inevitably lead to low efficiency and high realization complexity. Another important question in a repeated fusion process is the availability of quantum memories to store the throughput W states obtained at each fusion step. This requirement clearly increases the complexity of physical realization. Because there is qubit-loss-free in our fusion scheme for fusing two maximally entangled W states, which decreases the number of the fusion steps for obtaining a W state of a target size considerably, the physical realization of it would become much easier. Particularly, the number of particles that our scheme loses in the fusion of fusing three W states is smaller than all the current schemes, which effectively reduced the integration steps and complexity.

This fusion scheme can be generalized to the case of fusing k different W states of the same number of qubits, labeled as m. Only one H-polarized ancilla photon needed, but k PDBSs application in the scheme and more photons will be detected to choose the final large-scale W state. Let us make a simple statement why it is necessary to detect more photons. A maximally entangled \(|W_3\rangle \) state can be written as:

$$\begin{aligned} {|}W_3\rangle =\frac{1}{\sqrt{3}}(|HHV\rangle +|HVH\rangle +|VHH\rangle ). \end{aligned}$$
(12)

In the form of maximally entangled \(|W_3\rangle \) state, each term is made up of two H-polarized photons and one V-polarized photon. That is to say, for a n-qubit maximally entangled W state, every term in its expression must be a \((n-1)\)-qubit H-polarized photons and one V-polarized photon. However, suppose the fusion scheme of fusing two \(|W_3\rangle \) states is perfect and without any photons detected, there must be two V-polarized photons in each of its terms in the expression of the final large-scale W state [as shown in Eq. (5)]. Therefore, it is possible to generate a standard large-scale W state only by detecting a V-polarized photon. The auxiliary photon H added to the scheme is also designed to compensate for the detected V photon. Along the same line, when we increase the number of W states to be fused from two to three, there must be two V-polarized photons detected, and then the final state is \((n+m+t-1)\), which is one less than the total number of qubits in W states. Therefore, if the number of m-qubit W states entering the fusion process is k, a maximally entangled \(|W\rangle _{km-k+2}\) state can be generated when \((k-1)\) V-polarized photons are detected. The success probability is \(\mathrm{{Ps}}(W_{km-k+2})=(km-k+2)/5^{k}km\).

5 Conclusion

In conclusion, the PDBS-based fusion schemes were proposed for fusing two or three maximally entangled W states into large-scale maximally entangled states. The scheme is easy to be implemented in the experiment because it is not applied to controlled quantum gates operation. Because most of the currently existing fusion schemes are suffering from the qubit loss problem, the present scheme can generate \(W_{m+n}\) state from a n-qubit W state and a m-qubit W state without any qubit loss. This fusion mechanism greatly reduces the number of fusion steps as well as the requirement of quantum memories required to achieve a W state of a target size, which makes the physical implementation of it possible within the reach of current technology. The most distinct property of our schemes is that a \(W_{m+n+t-1}\) state can be generated by fusing \(W_m\), \(W_n\) and \(W_t\) states which is a great progress compared with the current scheme which has to lose at least two particles in the fusion of three W states.