1 Introduction

Entanglement is a special resource in quantum information processing, and one of the most astonishing applications is quantum teleportation [1]. Bennett et al. [1] demonstrated that an unknown quantum state can be teleported to a spatially separated place via Einstein–Podolsky–Rosen channels. If a quantum state is known to the sender, there is another way to transfer the quantum state without qubit transmission, which is known as remote state preparation (RSP) [2–4]. With shared quantum resource and additional classical information, RSP can be performed with simpler measurements and less classical communication costs than quantum teleportation. Since its first appearance, different kinds of RSP schemes have been proposed, such as oblivious RSP [5], continuous variable RSP [6], RSP in higher dimension space [7]. In recent years, RSP schemes that include many participants have also been proposed, like joint RSP (JRSP) [8–10] and controlled RSP (CRSP) [11, 12]. The difference between JRSP and CRSP is what the roles did the preparers played. In a JRSP scheme, each sender is a information carrier who holds partial information of a prepared state and all senders jointly prepare the state for a remote receiver. While in a CRSP scheme, there is a controller who does not know the information of the state, but the scheme will not be completed without the controller’s consent.

Besides, quantum entanglement has also been used to extend the scope of cryptograph. Applications like quantum key distribution [13], quantum data hiding [14–17] and quantum authentication [18, 19] have been proposed based on shared entanglement resource. Quantum secret sharing (QSS) [20] is another application of entanglement resource which enhances the secure level of classical secret sharing. The pioneering work of QSS was introduced by Hillery et al. [20] in 1999. After that, various QSS schemes have been proposed both theoretically [21–26] and experimentally [27–29]. According to the type of shared secret, QSS schemes can be divided into two classes, i.e., QSS of a classical secret and QSS of a quantum state. The latter one is also known as quantum state sharing (QSTS) named by Lance et al. in [30], where a secret state is shared among a set of agents, and only qualified agents groups can cooperate to reconstruct the state. QSTS has strong relationships with quantum teleportation and RSP. Many of the existing QSTS schemes can be regarded as quantum teleportation among multiparty who located at spatially separated places [20, 24, 31–34], where the secret state is unknown to the dealer. However, if the dealer already known the information of the secret state, the scheme can be performed in a simpler way. In 2014, we pointed out that the application of QSTS can also be achieved by using the idea of RSP [35].

Generally, most applications of entanglement were considered in an ideal condition; i.e., the entangled resources were perfectly generated and transmitted without any interaction with the outside environment. But in real world, a quantum system will unavoidably be affected by the environment. And these interactions are considered as noises. In recent years, some entanglement-based schemes with noisy environments have been studied. Adhikari et al. [36] proposed a QSS protocol of classical information with noisy channels. Xiang et al. [37] presented a RSP protocol for mixed state in depolarizing and dephasing channel. Chen et al. [38] investigated remote preparation of an entangled state through a mixed-state channel in nonideal conditions. Guan et al. [39] investigate the JRSP of an arbitrary two-qubit quantum state in noisy environments.

As is mentioned, we have shown that a QSTS scheme can be achieved by using the idea of RSP in Ref. [35], which is simpler and more efficient than by the idea of quantum teleportation. But like most of other QSTS schemes, our schemes were discussed with ideal environment and no outside noise was considered. One may ask how a QSTS scheme will be affected by the noise and how much information will be lost in the process? In this paper, we are going to discuss these problems. The organization of the paper is as follows. In Sect. 2, we present our multiparty QSTS scheme of an arbitrary known qubit state with ideal environment. Then, we investigate our QSTS scheme with the amplitude-damping noise and the phase-damping noise in Sects. 3 and  4, respectively. We discuss their security issues and their relationships with quantum teleportation and RSP in Sect. 5. The paper is concluded in Sect. 6.

2 State sharing scheme with ideal environment

To begin with, we are going to present a multiparty state sharing scheme of an arbitrary qubit state, which is a specific instance of our schemes in Ref. [35]. Let us suppose that Alice wants to distribute a secret state between two agents Bob and Charlie in such a way that only if two agents work together can they recover the state. Generally, an arbitrary single-qubit state has the form

$$\begin{aligned} {\left| \phi \right\rangle } = a_{0} e^{\text {i} \theta _{0}} {\left| 0 \right\rangle } + a_{1} e^{\text {i} \theta _{1}} {\left| 1 \right\rangle }, \end{aligned}$$
(1)

where \(a_{0}, a_{1} \in \mathcal {R}\), \(\theta _{0}, \theta _{1} \in [0, 2\pi ]\), with \(a_0^2 + a_1^2 = 1\). The parameters \(a_{0}, a_{1}, \theta _{0}\) and \(\theta _{1} \) of the secret state are known by Alice. She need not hold the state.

Our state sharing scheme of an arbitrary known qubit state in ideal environment can be described as follows.

  1. (1)

    Secret splitting phase

    1. (a)

      The dealer Alice prepares a GHZ state as shared quantum resource, which can be written as

      $$\begin{aligned} {\left| \varPhi \right\rangle } = \frac{1}{\sqrt{2}}({\left| 000 \right\rangle }+{\left| 111 \right\rangle })_{ABC}, \end{aligned}$$
      (2)

      where subscripts denote qubits of the state. Alice keeps qubit A in her laboratory. She sends qubit B to Bob and qubit C to Charlie through two ideal quantum channels, which means the outside environment will not affect qubits B and C. After qubits transmissions, Alice holds qubit A, Bob holds qubit B, and Charlie holds qubit C.

    2. (b)

      Alice prepares an ancilla state R in \({\left| 0 \right\rangle }\), and then, she performs a unitary operation U on qubits AR where

      $$\begin{aligned} U= \left( \begin{array}{cc} U_0 &{} 0 \\ 0 &{} U_1 \end{array}\right) ,\quad \text {with}~~ U_i= \left( \begin{array}{cc} a_i &{} \sqrt{1-a_i^2} \\ \sqrt{1-a_i^2} &{} -a_i \end{array}\right) ;\quad i = 0, 1. \end{aligned}$$
      (3)

      Then, the quantum system becomes

      $$\begin{aligned} \begin{aligned}&U_{AR}\otimes I_{BC} {\left| \varPhi \right\rangle }_{ABC} {\left| 0 \right\rangle }_{R} \\&\quad = \frac{1}{\sqrt{2}} (a_0 {\left| 000 \right\rangle }_{ABC} + a_1 {\left| 111 \right\rangle }_{ABC}) {\left| 0\right\rangle }_{R} \\&\qquad + \frac{1}{\sqrt{2}} \left( \sqrt{1-a_0^2}{\left| 000 \right\rangle }_{A BC} + \sqrt{1-a_1^2}{\left| 111 \right\rangle }_{A BC}\right) {\left| 1\right\rangle }_{R}. \end{aligned} \end{aligned}$$
      (4)
    3. (c)

      Alice measures qubit R in the computational basis. If she gets the result \({\left| 0 \right\rangle }\), the quantum system becomes

      $$\begin{aligned} a_0 {\left| 000 \right\rangle }_{ABC} + a_1 {\left| 111 \right\rangle }_{ABC}. \end{aligned}$$
      (5)

      While if Alice gets the result \({\left| 1 \right\rangle }\), she can use the recursive method proposed by Jiang et al. [40, 41] to get the above state.

    4. (d)

      Alice performs a projective measurement on qubit A under the basis \(\{ {\left| \Lambda _k \right\rangle }; k \in \{0, 1\} \}\) where

      $$\begin{aligned}&{\left| \Lambda _0 \right\rangle } =\frac{1}{\sqrt{2}} \left( e^{ -\text {i} \theta _{0} } {\left| 0 \right\rangle } + e^{ -\text {i} \theta _{1} } {\left| 1 \right\rangle } \right) , \end{aligned}$$
      (6)
      $$\begin{aligned}&{\left| \Lambda _1 \right\rangle } =\frac{1}{\sqrt{2}} \left( e^{ -\text {i} \theta _{0} } {\left| 0 \right\rangle } - e^{ -\text {i} \theta _{1} } {\left| 1 \right\rangle } \right) . \end{aligned}$$
      (7)

      Then, the quantum system can be rewritten as

      $$\begin{aligned} \begin{aligned}&a_0 {\left| 000 \right\rangle }_{A BC} + a_1 {\left| 111 \right\rangle }_{A BC} \\&\quad = \frac{1}{\sqrt{2}} \bigg [ {\left| \Lambda _0 \right\rangle }_{A} \left( a_0 e^{ \text {i} \theta _{0} } {\left| 00 \right\rangle } + a_1 e^{ \text {i} \theta _{1} } {\left| 11 \right\rangle }\right) _{BC} \\&\qquad + {\left| \Lambda _1 \right\rangle }_{A}\left( a_0 e^{ \text {i} \theta _{0} } {\left| 00 \right\rangle } -a_1 e^{ \text {i} \theta _{1} } {\left| 11 \right\rangle }\right) _{BC} \bigg ]. \end{aligned} \end{aligned}$$
      (8)
    5. (e)

      After the measurement of qubit A, the secret state is distributed between two agents. Here, Alice announces her measurement result \({\left| \Lambda _k \right\rangle }\) as k publicly.

  2. (2)

    Secret recovery phase

    1. (a)

      In the secret recovery phase, either Bob or Charlie can recover the shared secret state with the help of the other. As an example, suppose that Bob wants to help Charlie to recover the state. Here, Bob performs a single-qubit measurement on qubit B under the basis \(\{ {\left| \hat{0} \right\rangle }, {\left| \hat{1} \right\rangle }\}\) where \({\left| \hat{0} \right\rangle }=\frac{1}{\sqrt{2}} ( {\left| 0 \right\rangle }+{\left| 1 \right\rangle } )\), \({\left| \hat{1} \right\rangle }=\frac{1}{\sqrt{2}} ( {\left| 0 \right\rangle }-{\left| 1 \right\rangle } )\). Then, the resource shared among two agents becomes

      $$\begin{aligned} \begin{aligned}&a_0 e^{ \text {i} \theta _{0} } {\left| 00 \right\rangle }_{BC}+ (-1)^{k} a_1 e^{ \text {i} \theta _{1} } {\left| 11 \right\rangle }_{BC} \\&\quad = \frac{1}{\sqrt{2}} \sum _{k_1 = 0}^{1} { | \hat{k_1} \rangle } _{B} \left( a_0 e^{ \text {i} \theta _{0} } {\left| 0 \right\rangle } + (-1)^{ k + k_1} a_1 e^{ \text {i} \theta _{1} } {\left| 1 \right\rangle } \right) _{C}. \end{aligned} \end{aligned}$$
      (9)
    2. (b)

      For recovering the secret state, Bob sends his measurement result \({| \hat{k}_1 \rangle }\) as \(k_1\) to Charlie. After receiving \(k_1\), Charlie can recover the secret state \({\left| \phi \right\rangle }\) by performing the unitary operation \(\sigma _z^{k+ k_1 }\) on qubit C. Noted that Bob can also recover the secret state if Charlie agrees to help him, and each agent has the same power for recovering the secret state in the scheme, which means our scheme is symmetric.

3 State sharing scheme with amplitude-damping noisy environment

In the following, we are going to show our scheme with two specific noisy environments. And we start with the amplitude-damping noisy environment.

3.1 The amplitude-damping noise

The amplitude-damping noise is one of the most important decoherence noise which describes the energy-dissipation effects due to loss of energy from a quantum system. The action of amplitude-damping noise can be presented by a set of Kraus operators as follows [42]

$$\begin{aligned} E_0= \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} \sqrt{1-\lambda } \end{array}\right) , ~~~~ E_1= \left( \begin{array}{cc} 0 &{} \sqrt{\lambda } \\ 0 &{} 0 \end{array}\right) , \end{aligned}$$
(10)

where \(0 \le \lambda \le 1\) indicates the decoherence rate of the amplitude-damping noisy environment. When a quantum state passes through the noisy channel, there is a probability \(\lambda \) that the state will be affected.

3.2 The scheme with amplitude-damping noise

  1. (1)

    Secret splitting phase

    1. (a)

      Still, Alice prepares the GHZ state \( {\left| \varPhi \right\rangle }\) as shared quantum resource. The state can be represented in the form of density matrix as

      $$\begin{aligned} \rho _{ABC}={\left| \varPhi \right\rangle } {\left\langle \varPhi \right| }. \end{aligned}$$
      (11)

      Alice keeps qubit A and sends qubits B and C to Bob and Charlie through two identical amplitude-damping noisy channels, respectively. The effect of noisy environment can be described by operator sum representation. This process will convert the pure channel state into a mixed one. After qubits transmissions through amplitude-damping noisy channels, the quantum resource used for state sharing becomes

      $$\begin{aligned} \begin{aligned} \epsilon (\rho )&= \sum _{i,j=0,1}{E^B_i E^C_j } \rho (E^B_i)^{\dag } (E^C_j)^{\dag } \\&= \frac{1}{2} \left[ ( {\left| 000 \right\rangle } + (1-\lambda ) {\left| 111 \right\rangle } ) ({\left\langle 000 \right| } +(1-\lambda ){\left\langle 111 \right| } ) \right. \\&\quad \left. +\, (1-\lambda )\lambda {\left| 110 \right\rangle } {\left\langle 110 \right| } +(1-\lambda )\lambda {\left| 101 \right\rangle } {\left\langle 101 \right| }+\lambda ^2{\left| 100 \right\rangle } {\left\langle 100 \right| } \right] , \end{aligned} \end{aligned}$$
      (12)

      where superscripts B and C indicate that noise operators act on qubits B and C, respectively. And \(``{\dag }''\) means the conjugate transpose of a matrix.

    2. (b)

      Alice prepares an ancilla state R in \({\left| 0 \right\rangle }\), and she performs a unitary operation U on particles AR. Then, the quantum system becomes

      $$\begin{aligned} \begin{aligned} \rho _1&= U_{AR} \otimes I_{BC} \left\{ \epsilon (\rho )_{ABC} \otimes {\left| 0 \right\rangle } {\left\langle 0 \right| }_{R} \right\} U^{\dag }_{AR}\otimes I_{BC}, \\ \end{aligned} \end{aligned}$$
      (13)

      where each subscript indicates a qubit.

    3. (c)

      Alice measures qubit R in the computational basis. If she gets the result \({\left| 0 \right\rangle }\), the quantum system becomes

      $$\begin{aligned} \begin{aligned} \rho _2&= tr_R \left( \frac{M_0 \rho _1 M^{\dag }_0}{ tr(M_0 M^{\dag }_0 \rho _1)} \right) \\&= ( a_0 {\left| 000 \right\rangle } + a_1 (1-\lambda ) {\left| 111 \right\rangle } ) (a_0{\left\langle 000 \right| } +a_1 (1-\lambda ){\left\langle 111 \right| } ) \\&\quad + a_1^2 (1-\lambda ) \lambda {\left| 110 \right\rangle } {\left\langle 110 \right| } + a_1^2 (1-\lambda ) \lambda {\left| 101 \right\rangle } {\left\langle 101 \right| } + a_1^2\lambda ^2 {\left| 100 \right\rangle } {\left\langle 100 \right| }. \end{aligned} \end{aligned}$$
      (14)

      where \(M_0 ={\left| 0 \right\rangle } {\left\langle 0 \right| }\) is the measurement operator. While if Alice gets the result \({\left| 1 \right\rangle }\), she needs to use the recursive procedure.

    4. (d)

      Alice performs a projective measurement on qubit A under the basis \(\{ {\left| \Lambda _k \right\rangle }; k \in \{0, 1\} \}\). Suppose the measurement result is \({\left| \Lambda _k \right\rangle }\), the quantum system will be rewritten as

      $$\begin{aligned} \begin{aligned} \rho _3&= \frac{M_{\Lambda _k} \rho _2 M_{\Lambda _k}^{\dag }}{ tr (M_{\Lambda _k} M_{\Lambda _k}^{\dag } \rho _2)} \\&= \frac{1}{2} \left[ \left( a_0 {\left| 000 \right\rangle } \!+\! (-1)^k a_1 (1-\lambda ) e^{ \!-\!\text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left| 011 \right\rangle } + (-1)^k a_0 e^{ \text {i} \theta _{0} } e^{ -\text {i} \theta _{1} } {\left| 100 \right\rangle }\right. \right. \\&\quad \quad \left. +\,\, a_1 (1-\lambda ) {\left| 111 \right\rangle } \right) \times \left( a_0{\left\langle 000 \right| } + (-1)^k a_1 (1-\lambda ) e^{ \text {i} \theta _{0} } e^{ - \text {i} \theta _{1} } {\left\langle 011 \right| }\right. \\&\quad \quad \left. +\,\, (-1)^k a_0 e^{ -\text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left\langle 100 \right| } + a_1 (1-\lambda ){\left\langle 111 \right| } \right) \\&\quad \quad +\, a_1^2 (1-\lambda ) \lambda ( (-1)^k e^{- \text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left| 010 \right\rangle } + {\left| 110 \right\rangle })( (-1)^k e^{ \text {i} \theta _{0} } e^{ - \text {i} \theta _{1} } {\left\langle 010 \right| }\\&\quad \quad +\,{\left\langle 110 \right| } ) + a_1^2 (1-\lambda ) \lambda ( (-1)^k e^{- \text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left| 001 \right\rangle } + {\left| 101 \right\rangle } )( (-1)^k e^{ \text {i} \theta _{0} } e^{ - \text {i} \theta _{1} }\\&\quad \quad {\left\langle 001 \right| }+{\left\langle 101 \right| } ) +\, a_1^2\lambda ^2 ( (-1)^k e^{- \text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left| 000 \right\rangle }\\&\quad \quad \left. +\,\, {\left| 100 \right\rangle } )( (-1)^k e^{ \text {i} \theta _{0} } e^{ - \text {i} \theta _{1} } {\left\langle 000 \right| } +{\left\langle 100 \right| } ) \right] , \end{aligned} \end{aligned}$$
      (15)

      where \(M_{\Lambda _k} ={\left| \Lambda _k \right\rangle } {\left\langle \Lambda _k \right| } \) with \( k \in \{0, 1\}\) is the measurement operator, which means the quantum system of Bob and Charlie becomes

      $$\begin{aligned} \begin{aligned} \rho _4&= tr_A (\rho _3) \\&= a_0^2 {\left| 00 \right\rangle }{\left\langle 00 \right| } +(-1)^k a_0 e^{ \text {i} \theta _{0} } a_1 e^{ - \text {i} \theta _{1} } (1-\lambda ) {\left| 00 \right\rangle }{\left\langle 11 \right| } \\&\quad \quad +(-1)^k a_0 e^{- \text {i} \theta _{0} } a_1 e^{ \text {i} \theta _{1} } (1-\lambda ) {\left| 11 \right\rangle }{\left\langle 00 \right| } +a_1^2 (1-\lambda )^2 {\left| 11 \right\rangle }{\left\langle 11 \right| } \\&\quad \quad + a_1^2 (1-\lambda ) \lambda {\left| 01 \right\rangle }{\left\langle 01 \right| } + a_1^2 (1-\lambda ) \lambda {\left| 10 \right\rangle }{\left\langle 10 \right| } + a_1^2\lambda ^2 {\left| 00 \right\rangle }{\left\langle 00 \right| } . \end{aligned} \end{aligned}$$
      (16)
  2. (2)

    Secret recovery phase

    1. (a)

      In the beginning of this phase, Bob and Charlie’s quantum system is \(\rho _4\). Suppose that Bob agrees to help Charlie to recover the secret state. Here, Bob performs a single-qubit measurement under the basis \(\{ {\left| \hat{0} \right\rangle }, {\left| \hat{1} \right\rangle }\}\). Bob’s measurement result \({| \hat{k_1} \rangle }\) is represented as a cbit \(k_1\). Then, the state shared by Charlie becomes

      $$\begin{aligned} \begin{aligned} \rho _C&= tr_B \left( \frac{ M_{B_{k_1}} \rho _4 M_{B_{k_1}}^{\dag } }{ tr (M_{B_{k_1}} M_{B_{k_1}}^{\dag } \rho _4)} \right) \\&= (a_0^2 \!+\! a_1^2\lambda ) {\left| 0 \right\rangle }{\left\langle 0 \right| } \!+\! a_1^2 (1\!-\!\lambda ) {\left| 1 \right\rangle }{\left\langle 1 \right| } \!+\!(\!-\!1)^{k+k_1} a_0 e^{ \text {i} \theta _{0} } a_1 e^{ - \text {i} \theta _{1} } (1\!-\!\lambda ) {\left| 0 \right\rangle }{\left\langle 1 \right| } \\&\quad +(-1)^{k+k_1} a_0 e^{-\text {i} \theta _{0} } a_1 e^{ \text {i} \theta _{1} } (1-\lambda ) {\left| 1 \right\rangle }{\left\langle 0 \right| }, \end{aligned} \end{aligned}$$
      (17)

      where \(M_{B_{k_1}}={| \hat{k_1} \rangle } {\langle \hat{k_1} |} \) with \( k_1 \in \{0, 1\}\) is Bob’s measurement operator.

    2. (b)

      Bob sends his measurement result \(k_1\) to Charlie. Then, Charlie recover the secret state by performing \(\sigma _z^{k+ k_1}\) on qubit C. The recovery state has the form

      $$\begin{aligned} \begin{aligned} \rho _{out}&= \sigma _z^{k+ k_1} \rho _C (\sigma _z^{k+ k_1})^{\dag }\\&= (a_0^2 + a_1^2\lambda ) {\left| 0 \right\rangle }{\left\langle 0 \right| } + a_1^2 (1-\lambda ) {\left| 1 \right\rangle }{\left\langle 1 \right| } + a_0 e^{ \text {i} \theta _{0} } a_1 e^{ - \text {i} \theta _{1} } (1-\lambda ) {\left| 0 \right\rangle }{\left\langle 1 \right| } \\&\quad \quad + a_0 e^{- \text {i} \theta _{0} } a_1 e^{ \text {i} \theta _{1} } (1-\lambda ) {\left| 1 \right\rangle }{\left\langle 0 \right| }. \end{aligned} \end{aligned}$$
      (18)

3.3 Fidelity

Since the shared quantum resource has been affected by the noisy environment and become a mixed state in the secret splitting phase. The recovered state \(\rho _{out}\) will not be the same as \({\left| \phi \right\rangle }\). Generally, the difference between the two states can be measured by the fidelity as follows

$$\begin{aligned} \begin{aligned} F_{\mathrm{AD}}&= {\left\langle \phi \right| } \rho _{out} {\left| \phi \right\rangle }\\&= a_0^4+a_0^2 a_1^2(2-\lambda )+a_1^4(1-\lambda ). \end{aligned} \end{aligned}$$
(19)

As is shown in the above, the fidelity \(F_{\mathrm{AD}}\) for the amplitude-damping noise depends on the amplitude factors of the prepared state \(a_0, a_1\) and the decoherence rate \(\lambda \), but has nothing to do with the phase parameters \(\theta _0\) and \(\theta _1\). When \(F_{\mathrm{AD}}=1\), it is means that \(\rho _{out} ={\left| \phi \right\rangle } {\left\langle \phi \right| }\); i.e., the noise has no effect on the output shared state, and there is no information lost (in ideal condition that \(\lambda = 0\) or sharing a specific state \(e^{\text {i} \theta _0} {\left| 0 \right\rangle }\) where \(a_0=1\)). While if \(F_{\mathrm{AD}}<1\), it means that \(\rho _{out} \ne {\left| \phi \right\rangle } {\left\langle \phi \right| }\); i.e., some information has been lost since the affection of noise. The relationship among \(F_{\mathrm{AD}}\), \(\lambda \) and \(a_0\) is shown in Fig. 1 (noted that \(a_1^2 = 1-a_0^2\)).

Fig. 1
figure 1

Relationship among \(F_{\mathrm{AD}}\), \(\lambda \) and \(a_{0}\)

Full size image

4 State sharing scheme with phase-damping noisy environment

4.1 The phase-damping noise

The phase-damping noise is another important decoherence noise which describes the loss of quantum information without energy dissipation. The Kraus operators of a phase-damping noisy channel are [42]

$$\begin{aligned} E_0= \sqrt{1-\eta }I, ~~~~ E_1= \sqrt{\eta } \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array}\right) , ~~~~ E_2=\sqrt{\eta } \left( \begin{array}{cc} 0 &{} 0\\ 0 &{} 1 \end{array}\right) , \end{aligned}$$
(20)

where \(0 \le \eta \le 1\) is the error probability of the phase-damping noisy environment.

4.2 The scheme with phase-damping noise

  1. (1)

    Secret splitting phase

    1. (a)

      Alice prepares the GHZ state \(\rho ={\left| \varPhi \right\rangle } {\left\langle \varPhi \right| }\). She keeps particle A and sends particle B to Bob and particle C to Charlie through two phase-damping noisy channels. After interactions with the noises, the quantum system becomes

      $$\begin{aligned} \begin{aligned} \epsilon (\rho )&= \sum _{i,j=0}^{2}{E^B_i E^C_j } \rho (E^B_i)^{\dag } (E^C_j)^{\dag } \\&= \frac{1}{2} \left[ {\left| 000 \right\rangle } {\left\langle 000 \right| } +{\left| 111 \right\rangle } {\left\langle 111 \right| } + (1-\eta )^2 ({\left| 000 \right\rangle } {\left\langle 111 \right| } +{\left| 111 \right\rangle } {\left\langle 000 \right| } ) \right] . \end{aligned} \end{aligned}$$
      (21)
    2. (b)

      Alice prepares an ancilla state R in \({\left| 0 \right\rangle }\), and then, she performs a unitary operation U on particles AR. The quantum system becomes

      $$\begin{aligned} \begin{array}{lll} \rho _1= & {} U_{AR} \otimes I_{BC} \left\{ \epsilon (\rho )_{ABC} \otimes {\left| 0 \right\rangle } {\left\langle 0 \right| }_{R} \right\} U^{\dag }_{AR}\otimes I_{BC}. \end{array} \end{aligned}$$
      (22)
    3. (c)

      Alice measures qubit R in the computational basis. If she gets the result \({\left| 0 \right\rangle }\), the quantum system becomes

      $$\begin{aligned} \begin{aligned} \rho _2&= tr_R \left( \frac{M_0 \rho _1 M^{\dag }_0}{ tr(M_0 M^{\dag }_0 \rho _1)} \right) = \!\frac{1}{2} \left[ a_0^2 {\left| 000 \right\rangle } {\left\langle 000 \right| }\right. \\&\quad \left. +\,a_1^2 {\left| 111 \right\rangle } {\left\langle 111 \right| } \!+\!a_0 a_1 (1\!-\!\eta )^2 ({\left| 000 \right\rangle } {\left\langle 111 \right| }\! +\!{\left| 111 \right\rangle } {\left\langle 000 \right| } ) \right] . \end{aligned} \end{aligned}$$
      (23)

      While if Alice gets the result \({\left| 1 \right\rangle }\), she performs the recursive procedure.

    4. (d)

      Alice measures qubit A under the basis \(\{ {\left| \Lambda _k \right\rangle }; k \in \{0, 1\} \}\). Suppose the measurement result is \({\left| \Lambda _k \right\rangle }\), the quantum system can be rewritten as

      $$\begin{aligned} \begin{aligned} \rho _3&= \frac{M_{\Lambda _k} \rho _2 M_{\Lambda _k}^{\dag }}{ tr (M_{\Lambda _k} M_{\Lambda _k}^{\dag } \rho _2)} \\&= \frac{1}{2} \left[ a_0^2 \left( {\left| 000 \right\rangle } + (-1)^k e^{ \text {i} \theta _{0} } e^{ -\text {i} \theta _{1} } {\left| 100 \right\rangle }\right) \left( {\left\langle 000 \right| } + (-1)^k e^{ -\text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left\langle 100 \right| } \right) \right. \\&\quad \quad + a_1^2 \left( (-1)^k e^{ -\text {i}\theta _{0} } e^{ \text {i}\theta _{1}}{\left| 011 \right\rangle } + {\left| 111 \right\rangle } \right) \left( (-1)^k e^{ \text {i} \theta _{0} } e^{ -\text {i}\theta _{1} }{\left\langle 011 \right| }+{\left\langle 111 \right| } \right) \\&\quad \quad + a_0 a_1 (1-\eta )^2 \left( {\left| 000 \right\rangle } + (-1)^k e^{ \text {i} \theta _{0} } e^{ -\text {i} \theta _{1} } {\left| 100 \right\rangle }\right) \\&\qquad \times \left( (-1)^k e^{\text {i} \theta _{0} } e^{ -\text {i} \theta _{1} }{\left\langle 011 \right| }+{\left\langle 111 \right| }\right) \\&\quad \quad +\, a_0 a_1 (1-\eta )^2 \left( (-1)^k e^{ -\text {i} \theta _{0} } e^{\text {i} \theta _{1} }{\left| 011 \right\rangle }+{\left| 111 \right\rangle } \right) \\&\qquad \times \left. \left( {\left\langle 000 \right| } + (-1)^k e^{ -\text {i} \theta _{0} } e^{ \text {i} \theta _{1} } {\left\langle 100 \right| } \right) \right] . \end{aligned} \end{aligned}$$
      (24)

      And Bob and Charlie’s quantum system becomes

      $$\begin{aligned} \begin{aligned} \rho _4&= tr_A (\rho _3) \\&= a_0^2 {\left| 00 \right\rangle }{\left\langle 00 \right| } + a_1^2 {\left| 11 \right\rangle }{\left\langle 11 \right| } +(-1)^k a_0 e^{ \text {i} \theta _{0}} a_1 e^{ -\text {i} \theta _{1} } (1-\eta )^2 {\left| 00 \right\rangle }{\left\langle 11 \right| } \\&\quad \quad +(-1)^k a_0 e^{-\text {i} \theta _{0}} a_1 e^{ \text {i} \theta _{1} } (1-\eta )^2 {\left| 11 \right\rangle }{\left\langle 00 \right| }. \end{aligned} \end{aligned}$$
      (25)
  2. (2)

    Secret recovery phase

    1. (a)

      Here, Bob performs a single-qubit measurement under the basis \(\{ {\left| \hat{0} \right\rangle }, {\left| \hat{1} \right\rangle }\}\). Bob’s measurement result \({| \hat{k_1} \rangle }\) is represented as a cbit \(k_1\). Then, the resource hold by Charlie becomes

      $$\begin{aligned} \begin{aligned} \rho _C&= tr_B \left( \frac{ M_{B_{k_1}} \rho _4 M_{B_{k_1}}^{\dag } }{ tr (M_{B_{k_1}} M_{B_{k_1}}^{\dag } \rho _4)} \right) \\&= a_0^2 {\left| 0 \right\rangle }{\left\langle 0 \right| } +a_1^2 {\left| 1 \right\rangle }{\left\langle 1 \right| } +(-1)^{k+k_1} a_0 e^{ \text {i} \theta _{0} } a_1 e^{ -\text {i} \theta _{1} } (1-\eta )^2 {\left| 0 \right\rangle }{\left\langle 1 \right| }\\&\quad \,\, +(-1)^{k+k_1} a_0 e^{-\text {i} \theta _{0} } a_1 e^{ \text {i} \theta _{1} } (1-\eta )^2 {\left| 1 \right\rangle }{\left\langle 0 \right| }. \end{aligned} \end{aligned}$$
      (26)
    2. (b)

      Bob sends \(k_1\) to Charlie. After receiving \(k_1\), Charlie performs \(\sigma _z^{k+ k_1}\) on qubit C. Then, the secret state in Charlie’s side has the form

      $$\begin{aligned} \begin{aligned} \rho _{out}&= \sigma _z^{k+ k_1} \rho _C (\sigma _z^{k+ k_1})^{\dag }\\&= a_0^2 {\left| 0 \right\rangle }{\left\langle 0 \right| } +a_1^2 {\left| 1 \right\rangle }{\left\langle 1 \right| } + a_0 e^{ \text {i} \theta _{0} } a_1 e^{ -\text {i} \theta _{1} } (1-\eta )^2 {\left| 0 \right\rangle }{\left\langle 1 \right| }\\&\quad \quad + a_0 e^{-\text {i} \theta _{0} } a_1 e^{ \text {i} \theta _{1} } (1-\eta )^2 {\left| 1 \right\rangle }{\left\langle 0 \right| }. \end{aligned} \end{aligned}$$
      (27)

4.3 Fidelity

The fidelity of the output state can be calculated as

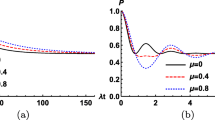
$$\begin{aligned} \begin{aligned} F_{PD}&= {\left\langle \phi \right| } \rho _{out} {\left| \phi \right\rangle }\\&=a_0^4+a_1^4 + 2 (1-\eta )^2 a_0^2 a_1^2. \end{aligned} \end{aligned}$$
(28)

As is shown in the above, the fidelity \(F_{PD}\) for phase-damping noise depends on the amplitude factors \(a_0, a_1\) and the decoherence rate \(\eta \), but has nothing to do with the phase parameters. The relationship among \(F_{PD}\), \(\lambda \) and \(a_0\) is shown in Fig. 2. As is shown, the Fidelity is 1 when \(\eta =0\) (no noise) or \(a_0 = 1, 0\) (sharing a specific state \(e^{\text {i} \theta _0} {\left| 0 \right\rangle }\) or \( e^{\text {i} \theta _1} {\left| 1 \right\rangle }\)). The minimum fidelity is \(F_{PD} = \frac{1}{2} \) when \(\eta =1\) and \(a_0 = \frac{1}{\sqrt{2}}\).

Fig. 2
figure 2

Relationship among \(F_{PD}\), \(\eta \) and \(a_0\)

Full size image

5 Discussions

5.1 Security

There are two kinds of threats in a QSS scheme. The first is that some dishonest agents may try to obtain the secret state without the cooperation of others from a qualified agents group, which is also called “participant attack.” The second is that an outside eavesdropper Eve may attempt to find the secret without being detected. Participant attack, firstly proposed by Gao et al [43], emphasizes that the attacks from dishonest users are generally more powerful since they can obtain more information than the eavesdropper Eve. This attack has attracted much attention in the cryptanalysis of quantum cryptography [44–46]. Qin and Gao [47] have pointed out that a QSS scheme is secure against the outside Eve if it is secure against inside dishonest agents, which means we only need to pay our attention to participant attack when studying the security of a QSS scheme.

A key security issue of our QSTS schemes is that the message carrier GHZ states have to be securely distributed among the dealer Alice and all the agents. The ways for sharing a sequence of GHZ states securely among remote players have been discussed in Refs. [20, 21, 26, 47, 48]. Alice can prepare the GHZ states and then use these methods to securely share the GHZ states with all the agents in the first step of the secret splitting phase. But noted that the error rate caused by the noise have to be lower than the detection probability, so that a malicious attack can be distinguished from noise. In other words, honest participants will not find the attack if the noise rate is too large since they cannot distinguish the attack from the noise; i.e., the attack is covered by the noise.

There is no qubit transmission in the recovery phase of our scheme. One may worry about that some dishonest agents may try to recover the secret state privately before the recovery phase. As is shown in Eq. (9), the system of Bob and Charlie has the form

$$\begin{aligned} a_0 e^{ \text {i} \theta _{0} } {\left| 00 \right\rangle }_{BC}+ (-1)^{k} a_1 e^{ \text {i} \theta _{1} } {\left| 11 \right\rangle }_{BC}, \end{aligned}$$
(29)

which means the partial trace of Bob has the form

$$\begin{aligned} \begin{aligned} tr_{C} ( a_0 e^{ \text {i} \theta _{0} } {\left| 00 \right\rangle } + (-1)^{k} a_1 e^{ \text {i} \theta _{1} } {\left| 11 \ldots 1 \right\rangle }) = a_0^2 {\left| 0 \right\rangle } {\left\langle 0 \right| }_{B} + a_1^2 {\left| 1 \right\rangle } {\left\langle 1 \right| }_{B}, \\ \end{aligned} \end{aligned}$$
(30)

while the partial trace of Charlie has the same form. From the above equation, we conclude that any unqualified agents group cannot recover the secret state by any general operations on their sides. Though they have the amplitude information, it is not sufficient since the phase information is not available. All in all, this QSTS scheme can be made to be secured.

5.2 State sharing of a known state

By a “known” quantum state, we mean that the information of the state is already known to the dealer. But noted that the secret information of the state is unknown to all the agents in the beginning of the schemes, which means our schemes meet the definition of the secret sharing. Each agent will get a share of the secret in the distribution phase, and authorized agents can cooperatively recover the secret state in the recovery phase. QSTS of a known qubit is similar to the QSS of classical bits. As is shown in Eq. (1), a general qubit \({\left| \phi \right\rangle }\) state has four parameters \(a_0, a_1, \theta _0\) and \(\theta _1\). The task of QSTS of \({\left| \phi \right\rangle }\) is to share these four parameters. Usually, a QSS of classical bits usually shares a real number secret, while our proposed protocols can share four real numbers each time, which means our quantum protocols have more information capacity.

It is interesting to discuss the relationships among QSTS, RSP and quantum teleportation. Firstly, QSTS is usually defined as sharing an unknown quantum state as a secret among a group of agents, which is similar to multiparty or controlled teleportation [49–51]. Secondly, RSP can be performed with simpler quantum operations and less classical communication costs than teleportation. Our QSTS schemes are similar to multiparty RSP (MRSP), and they have the same advantages as RSP to teleportation. Thirdly, there are two types of MRSP, which are JRSP [8–10, 52–54] and CRSP [11, 12, 55], and they have close relationships with our QSTS schemes. For one thing, JRSP is similar to the recovery phase of QSTS, where the secret share is already distributed in each of the agents and they can cooperate to reconstruct the secret state. For the other thing, CRSP can be regarded as a specific type of QSTS, i.e., secret sharing of a known state of the dealer. In secret splitting phase, all agents perform measurement or unitary operation on their side to get the classical share. While in recovery phase, authorized agents cooperate to recover the secret state.

6 Conclusions

In summary, we have studied a multiparty QSTS scheme of an arbitrary known qubit with two noisy environments. Starting with the scheme in an ideal condition, we investigated the QSTS scheme with the amplitude-damping noise and the phase-damping noise, respectively. The detailed process of each QSTS is presented. As is shown in our schemes, some information is lost through the noise channels. We use fidelity to describe how close is the final state to the original state, and how much information has been lost in the process. Our study indicates that the fidelity in both two schemes depends on the amplitude factor of the initial state and the decoherence rate, but is independent of the phase parameter.

Our QSTS scheme is symmetric since any agent is able to recover the state with the help of others. Different from a traditional QSTS scheme that shares an unknown quantum state among agents, our results showed that if a quantum state is already known to the dealer, it can be shared among agents in a simpler way by using the idea of RSP. We pointed out that the researches of quantum state sharing and remote state preparation have strong connection with each other.

In this paper, we have presented the impact of noise for the process of a QSTS scheme. To show our method, we consider the case that three participants share a qubit state. For multiparticipants that share a multiqubit or a multiqudit state, this method can also be used. But the calculation seems too tedious to present here. Besides the amplitude-damping noise and the phase-damping noise, it is also possible to consider other noises like depolarizing, bit-flip and bit-phase flip as noisy channels.