Structural stability of the quantum Fourier transform

Abstract

While it is important to investigate the negative effects of decoherence on the performance of quantum information processors, Landauer was one of the first to point out that an equally basic problem, i.e., the effects of unavoidable hardware flaws in the real-world implementations of quantum gates, needs to be investigated as well. Following Landauer’s suggestion, we investigated the structural stability of the quantum Fourier transform (QFT) via significantly changing the analytical form of its controlled rotation gates, thus modeling structural flaws in the Hamiltonian of the QFT. Three types of modified rotation gates were investigated, numerically and analytically, changing the exact QFT rotation angles $\pi /2^j$ to (1) $\pi /\alpha ^j$, (2) $\pi /2 j^{\beta }$, and (3) $\pi /\log _{\gamma }(j+1)$, where $\alpha$, $\beta$, and $\gamma$ are constants and $j$ is the integer distance between QFT qubits. Surprisingly good performance is observed in all the three cases for a wide range of $\alpha$, $\beta$, and $\gamma$. This demonstrates the structural stability of the QFT Hamiltonian. Our results also demonstrate that the precise implementation of QFT rotation angles is not critical as long as the angles (roughly) observe a monotonic decrease in $j$ (hierarchy). This result is important since it indicates that stringent tolerances do not need to be imposed in the actual manufacturing process of quantum information hardware components.

1 Introduction

There are many obstacles in the way of realizing a quantum computer. Prominent among them are gate defects [1, 2] and decoherence [1, 3, 4]. Much work has been focused on decoherence, culminating in methods of quantum error correction [3–8] that, at least in principle, are capable of controlling the detrimental effects of decoherence. However, the problem of decoherence notwithstanding, when it comes to an actual implementation of a physical quantum computer, the adverse effects of gate defects on the performance of the quantum computer need to be addressed first. This is so, because no matter how well we protect our quantum computer from its environment, even if we eliminate decoherence effects completely, if the performance of our quantum computer reacts sensitively to flaws in the implementation of its components, a working, physical quantum computer may never be realized. Given the fact that it is strictly impossible to execute a quantum gate with $100\,\%$ accuracy under any circumstances, we shall focus in this paper on the sensitivity of a quantum processor with respect to structural changes in its Hamiltonian.

As a testbed algorithm, we use the quantum Fourier transform (QFT) [3, 4]. This choice is justified since the QFT is one of the core ingredients of many important quantum algorithms, such as Shor’s algorithm [9]. Accordingly, there have already been a number of studies investigating the performance of the QFT under a variety of conditions [2, 10–15], and one of the findings is extraordinary robustness of the performance of the QFT with respect to static gate defects [15]. Adding to this result, we show in this paper that the QFT is also insensitive to structural changes in the actions of its phase rotation gates. Supporting the idea of the primary importance of the hierarchy, or the topology, of the QFT circuit [15], we confirm here that even maintaining only a rough hierarchy in the phase rotation gates of the QFT still allows us to find a hidden periodicity in a quantum input state with acceptable probability.

Several quantitative measures of phase angle hierarchy are proposed in this paper. First, we investigate an exponential hierarchy, i.e., the hierarchical type used in the exact QFT [3, 4]. This is followed by a study of a power-law hierarchy, which is fundamentally different from its exponential counterpart, since there is no scale factor in a power law. Structural insensitivity is found in both cases. Finally, further corroborating our results, we also present an inverse-log hierarchy and a random hierarchy, after which we discuss our results and conclude the paper.

We note that throughout this paper, we use the banded QFT [14], keeping only those phase rotation gates that are within $b$ nearest neighbors with respect to the control qubit, where $b$ is the bandwidth [14]. In particular, we use $b=8$. This choice is motivated by the fact that $b=8$ is sufficient for the practical use of the QFT in the period-finding part of Shor’s algorithm [11, 14]. The cases without banding, and how they relate to their banded counterparts, will be discussed briefly toward the end of this paper.

2 Numerical results

2.1 Exponential hierarchy

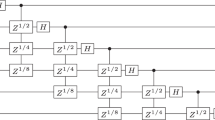
Operating between qubits number $k$ and $l$, we start by introducing the controlled phase rotation gate $\hat{\theta }_j$ (CROT) [3, 4] used in the QFT, where $j=|k-l|$ is the integer distance between qubits number $k$ and $l$. If qubit number $k$ acts as the control qubit $|c\rangle _k\in \{|0\rangle , |1\rangle \}$ and qubit number $l$ acts as the target qubit $|t\rangle _l\in \{|0\rangle , |1\rangle \}$, the CROT gate $\hat{\theta }_j$ is defined as

$$\begin{aligned} \hat{\theta }_j |c\rangle _k |t\rangle _l = {\left\{ \begin{array}{ll} |c\rangle _k \hbox {e}^{i\theta _j} |t\rangle _l, &{}\hbox {if}\,|c\rangle _k=|1\rangle =|t\rangle _l, \\ |c\rangle _k |t\rangle _l,&{}\,\hbox {otherwise,} \end{array}\right. } \end{aligned}$$

(1)

where, in the case of the exact QFT,

$$\begin{aligned} \theta _j = \frac{\pi }{2^j}. \end{aligned}$$

(2)

The relation (2) defines an exponential hierarchical structure of phase rotation angles, where the rotation angle of the target qubit decreases exponentially with its distance from the control qubit. The base 2 of the exponential in (2) is not an accident. It relates directly to the base-2 arithmetic used in transcribing the abstract QFT unitary transformation into a realization with qubits that have two possible states. Only in this way, because of number-theoretical relationships, will the qubit-based QFT perform perfectly, since desired amplitude cancellations and reinforcements (quantum interference) will happen exactly [3, 4]. One might think, then, that any change of the base 2 in (2), in conjunction with the continued use of qubits, will hopelessly muddle the inner workings of the QFT algorithm, effectively destroying its function. This seems especially critical in the case where the base 2 in (2) is changed to an irrational number, which does no longer correspond to a number system which is in a simple algebraic relationship to the base-2 number system induced by two-state qubits. However, in an actual, physical implementation of phase rotation gates, the precise base-2 relationship of the exponential hierarchy of phase rotations cannot be guaranteed. Therefore, still keeping the exponential nature of the hierarchy in (2), our first test case of a structural change in the QFT consists of replacing the exact rotation angles (2) with modified rotation angles according to

$$\begin{aligned} \theta _j \rightarrow \tilde{\theta }^{(\mathrm{E})}_j = \frac{\pi }{\alpha ^j}. \end{aligned}$$

(3)

As discussed above, this is a serious structural change in the QFT, since $\alpha$ is allowed to be any real number.

The exact $n$-qubit QFT $|s'\rangle$ of an $n$-qubit integer input state $|s\rangle$ is defined as the sum

$$\begin{aligned} |s'\rangle = \frac{1}{\sqrt{2^n}} \sum _{l=0}^{2^n-1} \varPhi (s,l) | l\rangle \end{aligned}$$

(4)

over all $n$-qubit integer output states $|l\rangle$, where

$$\begin{aligned} \varPhi (s,l) = \exp (2\pi i s l / 2^n). \end{aligned}$$

(5)

Defining $s_{[\nu ]}$ and $l_{[\mu ]}$ as the $\nu$th and $\mu$th binary digits of $s$ and $l$, respectively, we may alternatively write (5) in the form

$$\begin{aligned} \varPhi (s,l) = \prod _{l=0}^{n-1} \prod _{j=0}^{n-l-1} \exp \left( i\pi s_{[n-l-j-1]} l_{[l]} / 2^j \right) . \end{aligned}$$

(6)

Changing the base 2 in (6) to $\alpha$ according to (3), introducing the bandwidth $b$, and resumming, the phase (6) of the exact QFT is transformed into the phase of the general $n$-qubit exponentially hierarchical QFT according to

$$\begin{aligned} \varPhi ^{(\mathrm{E})}_b (s,l;\alpha ) = \exp \left[ i\varphi ^{(\mathrm{E})}_b (s,l;\alpha ) \right] , \end{aligned}$$

(7)

where

$$\begin{aligned} \varphi ^{(\mathrm{E})}_b (s,l;\alpha ) = \pi \left( \sum _{m'=0}^{n-1} s_{[m']}l_{[n-1-m']}+ \sum _{j=1}^{b} \frac{1}{\alpha ^j} \sum _{m=0}^{n-j-1} s_{[m]}l_{[n-j-1-m]}\right) . \end{aligned}$$

(8)

Using the most-prominent-peak criterion [13, 14], i.e., choosing the nearest integer peaks to the Fourier peaks of the QFT except for those trivial peaks that correspond to the powers-of-2 factor of a given periodicity [15] as our performance measure of the QFT (assumed here and throughout the paper), Fig. 1 shows the normalized performance $P$ of the banded ($b=8$), exponentially hierarchical QFT as a function of $\alpha$, where the normalization is performed with respect to the performance of the exact, exponentially hierarchical QFT with $\alpha = 2$ and $b=8$. For the input state $|s\rangle$, we used an $\omega$-periodic state, i.e., $\langle l+\omega |s\rangle = \langle l|s\rangle$, with periodicity $\omega = 30$.

Fig. 1

Normalized performance $P$ of the exponentially hierarchical, banded QFT with bandwidth $b=8$ as a function of the exponential hierarchy parameter $\alpha$. Shown are the cases with $n=12$ ($pluses$), $n=16$ ($squares$), and $n=20$ ($asterisks$) qubits

As expected, the best performance is achieved for $\alpha =2$, which corresponds to the exact QFT. However, as shown in Fig. 1, even for deviations of up to 5 % from $\alpha =2$, we still obtain better than 90 % performance for qubit numbers up to $n=20$ and better than 50 % performance for deviations up to 10 % from $\alpha =2$. This points to an extraordinary robustness of the QFT with respect to structural changes. However, we also observe a rapid decline in the performance for decreasing $\alpha$ (left wings of the performance curves in Fig. 1). A decreasing $\alpha$ flattens the hierarchy, i.e., for decreasing $\alpha$, $\pi /\alpha ^j$ takes longer to decline, erasing the hierarchy completely for $\alpha \rightarrow 1$, accompanied by zero performance. This shows that hierarchy in the rotation angles of the CROT gates is important. However, as the right wings of the performance curves in Fig. 1 show, it is not advisable to overemphasize the hierarchy. In fact, for $\alpha >2$, we also see a decline in the performance. The decline is not as fast as in the exponential case, since larger $\alpha$ effectively corresponds to cutting CROT gates, which corresponds to tighter banding [14]. This explains the slower decay of the performance for $\alpha >2$, since banding, in itself, is actually beneficial [14], but only to a certain extent. For $\alpha \gg 2$, too many CROT gates are effectively cut, again eliminating the hierarchy since for $\alpha \gg 2$, there are too few effective CROT gates left to define a hierarchy in the first place. In the limit $\alpha \rightarrow \infty$, this results in a QFT where the hierarchy is eliminated completely and only Hadamard gates remain. Therefore, the limiting performance for $\alpha \rightarrow \infty$ is expected to be the one of a QFT equipped with Hadamard gates only. This point will be discussed further in more quantitative detail below.

2.2 Power-law hierarchy

Next, we study a power-law hierarchy. Unlike in the exponential case, we can no longer vary a scale factor, since there is no scale factor in a power law. Instead, we characterize our power-law QFT in the following way:

$$\begin{aligned} \theta _j \rightarrow \tilde{\theta }^{(\mathrm{P})}_j = \frac{\pi }{2 j^{\beta }}, \end{aligned}$$

(9)

where the form (9) was chosen such that for $j=1$, both $\theta _j$ and $\tilde{\theta }^{(\mathrm{P})}_j$ are $\pi /2$. In this case, the phase of the $n$-qubit power-law QFT with input state $|s\rangle$ and output states $|l\rangle$ reads

$$\begin{aligned} \varPhi ^{(\mathrm{P})}_b (s,l;\beta ) = \exp \left[ i \varphi ^{(\mathrm{P})}_b (s,l;\beta ) \right] , \end{aligned}$$

(10)

where

$$\begin{aligned} \varphi ^{(\mathrm{P})}_b (s,l;\beta ) = \pi \left( \sum _{m'=0}^{n-1} s_{[m']}l_{[n-1-m']}+ \sum _{j=1}^{b} \frac{1}{2 j^{\beta }} \sum _{m=0}^{n-j-1} s_{[m]}l_{[n-j-1-m]}\right) . \end{aligned}$$

(11)

Again using the most-prominent-peak criterion and computing the performance of the QFT on the basis of (10), we plot, in Fig. 2, the resulting normalized performance $P$ of the banded ($b=8$), power-law hierarchical QFT for revealing the periodicity $\omega =30$ as a function of $\beta$. As before, the normalization is performed with respect to the absolute performance of the exact QFT with $\alpha =2$ and $b=8$.

Fig. 2

Normalized performance $P$ of the power-law hierarchical, banded QFT with bandwidth $b=8$ as a function of the power-law hierarchy parameter $\beta$. Shown are the cases with $n=12$ ($pluses$), $n=16$ ($squares$), and $n=20$ ($asterisks$)

As shown in Fig. 2, the performance of the power-law hierarchical QFT is qualitatively similar to the performance of the exponentially hierarchical QFT shown in Fig. 1. This time, however, we do not have an intuitive prediction for the location of the maximum of the performance, which occurs at $\beta _0\approx \,1.4$. Surprisingly, although the hierarchy is changed from exponential to power law, a significant qualitative change in the structure of CROT rotation angles, the peak performance of the power-law hierarchical QFT at $\beta _0$ is significantly larger than 90 %. Even for variations of the order of 10 % around $\beta _0$, we still obtain better than 90 % performance, which drops below 50 % only for deviations larger than 30 % from $\beta _0$. Arguments similar to the exponentially hierarchical case apply to explain, qualitatively, the behavior of the performance on the left and right wings of the performance curves in Fig. 2.

3 Analytical results

Analytical analysis of QFT performance on the basis of (7) or (10) is not straightforward. This is due to the intricate nature of the phases $\varPhi$ and to the fact that the $s$ values for a given $l$ value in the vicinity of the most prominent Fourier peaks tend to cluster in modulo $2\pi$ space. Still, we can extract some useful information regarding the shape and the location of the maxima of the curves shown in Figs. 1 and 2. Assuming that we obtain the best performance with the banded, otherwise exact QFT ($\alpha =2$), we see from the use of the phases $\varPhi ^{(\mathrm{E})}_b (\alpha )$ and $\varPhi ^{(\mathrm{P})}_b (\beta )$ in computing the respective E and P QFTs [the E and P analogs of (4)] that the performances of the exponentially and power-law hierarchical, banded QFTs may be estimated by quantifying the spreading of the phase angles $\varphi _b^{(\mathrm{E})}$ and $\varphi _b^{(\mathrm{P})}$ with respect to the values corresponding to the exact QFT as functions of $\alpha$ and $\beta$. This is so, since the tighter the distribution of phase angle differences, the closer the E and P QFTs are to the exact QFT, and, therefore, the better the performance of these QFTs. Choosing the variance as a representative measure of the spread, we expect the peaks of the curves to be located at those $\alpha _c$ and $\beta _c$, which minimize (a) $\langle \text{ var }[ \varphi _b^{(\mathrm{E})}(s,l;\alpha )-\varphi _b^{(\mathrm{E})}(s,l;\alpha =2) ]_{s}\rangle _{l^{(\mathrm np)}}$ and (b) $\langle \text{ var }[ \varphi _b^{(\mathrm{P})}(s,l;\beta )-\varphi _b^{(\mathrm{E})}(s,l;\alpha =2) ]_{s}\rangle _{l^{(\mathrm np)}}$, respectively. Here, $\text{ var }[\ldots ]_{s}$ denotes the variance in the argument $s$ and $\langle \ldots \rangle _{l^{(\mathrm{np})}}$ denotes averaging over $l^{(\mathrm{np})}$, the labels of those integer output states $| l^{(\mathrm{np})}\rangle$ that are closest to a Fourier peak. Minimizing (a) is straightforward and follows immediately from

$$\begin{aligned} \varphi _b^{(\mathrm{E})}(s,l;\alpha )-\varphi _b^{(\mathrm{E})}(s,l;\alpha =2) = \pi \sum _{j=1}^{b} \left( \frac{1}{\alpha ^j} - \frac{1}{2^j} \right) \sum _{m=0}^{n-j-1} s_{[m]} l_{[n-j-1-m]}, \end{aligned}$$

(12)

which shows that minimization is achieved for $\alpha =\alpha _c=2$, for which the variance is zero. This is consistent with the peak location of the curves in Fig. 1.

Minimizing (b) is not so straightforward, and a more sophisticated approach is required. Let us first state the argument of the variance that is to be minimized:

$$\begin{aligned} \varphi _b^{(\mathrm{P})}(s,l;\beta )-\varphi _b^{(\mathrm{E})}(s,l;\alpha =2) = \pi \sum _{j=1}^{b} \left( \frac{1}{2j^{\beta }}-\frac{1}{2^j}\right) \sum _{m=0}^{n-j-1} s_{[m]} l_{[n-j-1-m]}.\nonumber \\ \end{aligned}$$

(13)

Assuming (a) that the bits of the binary representations of both $s$ and $l^{(\mathrm{np})}$ are random, (b) that $s_{[m]}$ and $l_{[n-j-1-m]}$ are statistically independent, and (c) that the central limit theorem [16] is applicable, we may replace the $m$-sum in (13) with a Gaussian-distributed variable, whose variance is $3(n-j)/64$, centered around $(n-j)/4$. Assuming further that all $l^{(\mathrm{np})}$ respond to the change in hierarchy in unison in the statistical sense and since the variance of the sum of Gaussian-distributed variables is the sum of their variances [16], we obtain the minimum of the $l^{(\mathrm{np})}$-averaged variance of (13) for

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}\beta } \left[ \pi ^2 \sum _{j=1}^{b} \frac{3 (n-j)}{64} \left( \frac{1}{2^j} - \frac{1}{2j^{\beta }}\right) ^2\right] \Bigg |_{\beta =\beta _c} = 0. \end{aligned}$$

(14)

In the limit $n \gg b$, since $\min (n-j) = n-b \approx n$, (14) further simplifies to

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}\beta }\left[ \sum _{j=1}^{b} \left( \frac{1}{2^j} - \frac{1}{2j^{\beta }}\right) ^2\right] \Bigg |_{\beta =\beta _c} = 0. \end{aligned}$$

(15)

Solving (15) in the case $b=8$, we obtain $\beta =\beta _c = 1.364$, which is close to $\beta _0=1.4$, and therefore consistent with the peak locations of the curves in Fig. 2.

Along the lines of the discussion above, it is now straightforward to obtain the approximate shapes of the curves in Figs. 1 and 2. Since, to a good approximation, the $m$-sum in (12) and (13) is Gaussian distributed, together with the fact that the sum of Gaussian-distributed variables is yet another Gaussian-distributed variable [16], we expect the phase angles $\varphi _b^{(\mathrm{E})}(s,l;\alpha )$ and $\varphi _b^{(\mathrm{P})}(s,l;\beta )$ with respect to $\varphi _b^{(\mathrm{E})}(s,l;\alpha =2)$ to be Gaussian distributed. Now, in order to compute the normalized performance $P$ of the QFT, we first need to sum over the probabilities of obtaining any one of the most prominent peaks $l^{(\mathrm{np})}$ as a result of measurement after performing the QFT, which is computed by taking the absolute square of the sum of $\varPhi (s,l^{(\mathrm{np})})$, where $\varPhi (s,l^{(\mathrm{np})})$ may refer either to the exponential case or to the power-law case. Following this, we need to normalize these two results by the banded, otherwise exact, QFT. Denoting the absolute performance of the QFT by $\tilde{P}$, we obtain

$$\begin{aligned} P_b^{(\mathrm{E|P})} (\alpha |\beta ) = \frac{\tilde{P}^{(\mathrm{E|P})}_b(\alpha |\beta )}{\tilde{P}^{(\mathrm{E})}_b(\alpha =2)} = \frac{\sum _{l^{(\mathrm{np})}} \left| \sum _{s} \varPhi ^{(\mathrm{E|P})}_b (s,l^{(\mathrm{np})};\alpha |\beta )\right| ^2}{\sum _{l'^{(\mathrm{np})}} \left| \sum _{s'} \varPhi ^{(\mathrm{E})}_b (s',l'^{(\mathrm{np})};\alpha =2)\right| ^2}, \end{aligned}$$

(16)

where $\mathrm{E|P}$ and $\alpha |\beta$ refer to the exponential and power-law cases, respectively. Invoking the previous assumption that all $l^{(\mathrm{np})}$ respond in unison to a change in hierarchical structure in a statistical sense, we may approximate $P_b^{(\mathrm{E|P})}$ by dropping the sums over $l^{(\mathrm{np})}$ and $l'^{(\mathrm{np})}$ in (16). Writing $\varPhi ^{(\mathrm{E|P})}_b$ in the form

$$\begin{aligned} \varPhi ^{(\mathrm{E|P})}_b (\alpha |\beta ) = \exp \left[ i\varphi ^{(\mathrm{E})}_b(\alpha =2) \right] \exp \left\{ i \left[ \varphi ^{(\mathrm{E|P})}_b (\alpha |\beta )-\varphi ^{(\mathrm{E})}_b (\alpha =2) \right] \right\} , \end{aligned}$$

(17)

we find that the first exponential term on the right-hand side of (17) is a slowly varying function of $s$, while the second exponential term on the right-hand side of (17) is a rapidly fluctuating function of $s$. Therefore, assuming statistical independence of the slowly and rapidly fluctuating terms (separation ansatz), we may cancel the first term in (17) against the denominator in (16) to obtain

$$\begin{aligned} P_b^{(\mathrm{E|P})} (\alpha |\beta ) \approx \left| \frac{1}{\sqrt{K(s)}}\sum _{s} \exp \left\{ i \left[ \varphi ^{(\mathrm{E|P})}_b (\alpha |\beta )-\varphi ^{(\mathrm{E})}_b (\alpha =2) \right] \right\} \right| ^2, \end{aligned}$$

(18)

where $K(s)$ is the number of terms in the $s$-sum. At this point, we recall that the distribution function of the phase angles of the complex exponentials in (18) is Gaussian. Further approximating the $s$-sum with an integral and extending its limits to $\pm$ infinity, we obtain

$$\begin{aligned} P_b^{(\mathrm{E|P})} (\alpha |\beta ) \approx \left| \int _{-\infty }^{+\infty } \hbox {e}^{ix} G_{\sigma _b^{(\mathrm{E|P})}(\alpha |\beta )} \hbox {d}x \right| ^2, \end{aligned}$$

(19)

where $G_{\sigma _b^{(\mathrm{E|P})}(\alpha |\beta )}$ is a normalized Gaussian with standard deviation $\sigma _b^{(\mathrm{E|P})} (\alpha |\beta )$, and

$$\begin{aligned} x \equiv \varphi ^{(\mathrm{E|P})}_b (\alpha |\beta )-\varphi ^{(\mathrm{E})}_b (\alpha =2). \end{aligned}$$

(20)

Computing the integral in (19), we obtain

$$\begin{aligned} P_b^{(\mathrm{E|P})} (\alpha |\beta ) \approx \exp [-(\sigma _b^2)^{(\mathrm{E|P})}(\alpha |\beta )], \end{aligned}$$

(21)

where

$$\begin{aligned} (\sigma _b^2)^{(\mathrm{E})} = \pi ^2 \sum _{j=1}^{b} \frac{3(n-j)}{64} \left( \frac{1}{2^j} - \frac{1}{\alpha ^j} \right) ^2 \end{aligned}$$

(22)

and

$$\begin{aligned} (\sigma _b^2)^{(\mathrm{P})} = \pi ^2 \sum _{j=1}^{b} \frac{3(n-j)}{64} \left( \frac{1}{2^j} - \frac{1}{2j^{\beta }} \right) ^2. \end{aligned}$$

(23)

In Fig. 3a, b, together with the corresponding numerical data imported from Figs. 1 and 2, we plot (21) with (22) and (23) for the exponential and power-law cases, respectively. While the agreement between theory and numerical results is far from ideal, the analytical lines capture the scaling and the overall shape of the data to a good qualitative approximation. Apparently, away from the performance maxima, in the left and right wings of the performance curves, the analytical curves grossly overestimate the performance. This, however, is expected since (a) contrary to our simplifying assumptions, and strictly speaking, different $l^{(\mathrm{np})}$ respond (slightly) differently to alterations in the hierarchy, (b) the correlations between the two terms on the right-hand side of (17) were neglected (separation ansatz), and (c) the central limit theorem is only marginally applicable for $n \sim b$ [see (13) and (14)], which results in only a crude approximation of the distribution of $\varphi _b^{(\mathrm{E|P})} (\alpha |\beta ) - \varphi _b^{(\mathrm{E})}(\alpha =2)$ in (18) as a Gaussian. We note that for increasing $n$, as shown in Figs. 3a, b, the analytical lines become better approximations, since for increasing $n$ the statistics improves and the three limitations discussed above become less significant.

Fig. 3

Normalized performance $P$ of the a exponentially hierarchical and b power-law hierarchical, banded QFT with bandwidth $b=8$ as a function of the hierarchy parameters $\alpha$ and $\beta$. The $lines$ are the analytical results (21) with a $(\sigma ^2)^{(\mathrm{E})}$ defined in (22) and b $(\sigma ^2)^{(\mathrm{P})}$ defined in (23), for qubit numbers $n=12$ ($dashed line$), $n=16$ ($solid line$), and $n=20$ ($dash-dot line$). The numerical data in a and b, computed for $n=12$ ($pluses$), $n=16$ ($squares$), and $n=20$ ($asterisks$) are imported, unchanged, from Figs. 1 and 2, respectively

4 Discussion

Having explained the locations of peak performance and obtained a qualitative impression of the shape of the performance curves, let us now take a look at the limits $\alpha \rightarrow 1$ and $\beta \rightarrow 0$ in which the performances of both modified QFTs are zero (see Figs. 1, , 3). These are the two cases in which the rotation angles $\tilde{\theta }_j^{(\mathrm{E})}$ in (3) and $\tilde{\theta }_j^{(\mathrm{P})}$ in (9) of the associated CROT gates are constant as a function of $j$, the rotation angle hierarchy is completely wiped out, and zero performance is expected. Quantitatively, we show this in the following way. For $\alpha =1$, $\varphi ^{(\mathrm{E})}_b (s,l;\alpha =1)$ in (8) is equal to a multiple of $\pi$. As a consequence, the phases $\varPhi ^{(\mathrm{E})}_b (s,l;\alpha =1)$ in (7) take only two values, $-1$ and $1$. Assuming that both $s_{[m]}$ and $l_{[n-j-1-m]}$ assume the two values $0$ and 1 randomly as a function of their indices $m$ and $n-j-1-m$, respectively, we see that $\varPhi ^{(\mathrm{E})}_b (s,l;\alpha =1)$ assumes the values $-1$ and $1$ with equal probability. Therefore, the sum over $\varPhi ^{(\mathrm{E})}_b (s,l;\alpha =1)$ in (16) has expectation value zero, explaining the zero performance of the exponentially hierarchical QFT at $\alpha =1$. This explains our numerical results shown in Fig. 1.

Similar arguments hold for the power-law hierarchical case. Here, for $\beta =0$, the phase angles $\varphi ^{(\mathrm{P})}_b (s,l;\beta =0)$ in (11) are multiples of $\pi /2$. Again using the argument of randomness of the binary digits of $s$ and $l$, the sum over $\varPhi ^{(\mathrm{P})}_b (s,l;\beta =0)$ in (16) averages out, resulting in zero performance. This explains our numerical results shown in Fig. 2.

Now, let us take the other limit, i.e., $\alpha \rightarrow \infty$ and $\beta \rightarrow \infty$. In this case, $\tilde{\theta }_j^{(\mathrm{E})}$ in (3) and $\tilde{\theta }_j^{(\mathrm{P})}$ in (9) are both $0$, except for $\tilde{\theta }_1^{(\mathrm{P})}$, which is $\pi /2$. Hence, for the exponentially hierarchical, banded QFT, we expect, in the limit $\alpha \rightarrow \infty$, the performance corresponding to a pure Hadamard QFT ($b=0$), i.e., the case in which only Hadamard gates and no CROT gates are present. Also, since for the power-law hierarchical banded QFT the CROT gates with $j=1$ operate correctly, we expect the performance in this case to be that of the exact QFT with $b=1$. For $n=10, \ldots , 20$ we numerically confirm that this is indeed the case. All checks were performed for periodicity $\omega =30$.

So far in this paper, while varying the hierarchical structure, we have considered the banded QFT. As pointed out earlier, the bandwidth $b=8$ was chosen since according to [14], a QFT with $b=8$ is sufficient for its use in code-breaking. While it may be of limited value for practical applications, the exact QFT may still be studied by letting $b=n-1$ in the analytical results above. In this case, while the qualitative behavior of the performance as a function of $\alpha$ or $\beta$ should remain roughly the same for both the exponential and power-law cases, respectively, we expect a reduction in the peak performance in $\beta$, since the minimum of the variance at $\beta =\beta _c$ [see (14)] is an increasing function of $b$, hence $n$, for the non-banded QFT. Our numerical investigations confirm this expectation.

To further confirm the vital importance of the hierarchy in the QFT, we also investigated the logarithmically hierarchical QFT. Specifically, we chose

$$\begin{aligned} \theta _j \rightarrow \tilde{\theta }^{(\mathrm{L})}_j = \frac{\pi }{\log _{\gamma }(j+1)}, \end{aligned}$$

(24)

where $\gamma$ is a real number. As expected, in Fig. 4, a behavior similar to the one observed in Figs. 1 and 2 emerges when the normalized performance $P$ is plotted against the control parameter $\gamma$ that specifies the strength of the logarithmic hierarchy. Together with the exponential and power-law hierarchy results, this cements previous indications [15] that hierarchy is more important than the precise implementation of gates.

Fig. 4

Normalized performance $P$ of the power-law hierarchical, banded QFT with bandwidth $b=8$ as a function of the inverse-log hierarchy parameter $\gamma$. Shown are the cases with $n=12$ ($pluses$), $n=16$ ($squares$), and $n=20$ ($asterisks$)

Although our paper is theoretical in nature, it may have significant practical implications for the construction of quantum information processors. Currently, experimental implementations of the QFT are limited to fewer than five qubits [17], although no fundamental laws of physics forbid the scaling up of these quantum processors [18] to reach the number of qubits discussed in this paper. However, while many different physical realizations of the QFT may be envisioned, they all have one problem in common, i.e., how to implement, in a practical way, the phase rotation angles required to operate the QFT. Here our paper provides the insight that the precise implementation of the theoretically required exponential hierarchy may be unnecessary in practice for building a realistic QFT processor with acceptable performance. We illustrate this observation explicitly with two hierarchies (power-law and logarithmic) that are vastly different, qualitatively and quantitatively, from the exponential hierarchy, but still yield acceptable performance. It stands to reason, therefore, that many other types of hierarchies will achieve the same goal. To emphasize this point even further, we recently investigated yet another hierarchy, which we call the random hierarchy, which may have a real impact on facilitating actual hardware realizations of the QFT. We generated 100 random phase angles between 0 and $\pi$ and selected those eight phase angles that best matched the phase angles $\pi /2$, $\pi /4$, $\ldots$, $\pi /256$, required for a $b=8$ QFT. This method emulates a manufacturing process in which quantum gates are generated at random, selecting those that most closely match requirements. Although this process, for some gates, results in very large relative errors, this phase angle selection process yields astonishingly good performance, better than 90 %. This means that experimentalists and engineers do not have to produce or realize quantum gates with a targeted specification in mind, but may produce quantum gates at random, choosing the best matches, irrespective of relative error, according to a method of selection. To emphasize our point, we reduced the number of random rotation angles generated to 20 in the interval $[0,\pi ]$, which resulted in even larger individual phase angle errors, but still resulted in a performance of better than 80 %. More details of this method will be published elsewhere [19].

We also mention the fact that some quantum error correction schemes [3] require the resolution of rotation gates into a sequence of elementary, universal gates [20–25]. Realizing the exponential hierarchy with accuracy $\epsilon$ is expensive and requires gate sequences of length $\sim \log (1/\epsilon )$ [22]. However, our latest results on the random hierarchy teach us that it is not necessary to decompose each rotation gate to within a stringent $\epsilon$ requirement, but that the QFT still works using selected gates from a random set. This procedure may be re-interpreted as a much relaxed $\epsilon$, resulting in much shorter, decomposed realizations of quantum rotation gates that are much easier, and in particular cheaper, to implement.

Thus, based on the results in this paper, experimentalists and quantum engineers may take advantage of some significant quantum shortcuts resulting in tremendous anticipated savings in quantum resources. The best economy of resources is obtained as a result of a process that optimizes between target QFT performance and the optimal choice of hierarchy that best achieves the desired QFT accuracy with the minimal requirement of quantum resources.

5 Conclusion

This research was motivated by Landauer [1], who clearly separated the adverse effects experienced by a quantum processor into two logically and physically independent classes: decoherence and hardware flaws. While decoherence may be dealt with using quantum error correction [3–8], flaws in the hardware implementation of quantum gates are of a different nature. In fact, the effect of hardware flaws may be considered more fundamental than decoherence, since the issue of decoherence is a moot point if, for proper functioning of some quantum processor, the hardware tolerances can be proved to be too stringent to even consider practical implementation of the processor.

Since in the absence of decoherence any quantum processor may be interpreted as a unitary transformation of input states into output states governed by a quantum Hamiltonian, the effect of flaws in the hardware implementation of a quantum processor may be interpreted as a new quantum processor with an altered Hamiltonian, executing a different unitary transformation. Whether the new unitary transformation produces desirable results that are close to those produced by the original, intended Hamiltonian, depends on whether the original Hamiltonian governing the quantum processor is structurally stable. Structural stability is a term derived from dynamical systems theory [26] and refers to Hamiltonian systems in which small perturbations of the Hamiltonian lead to only small changes in the dynamics governed by the Hamiltonian. In this spirit, investigating the structural stability of the QFT, we changed the structural form of the phase rotation angles of the QFT’s CROT gates and computed the resulting change in performance of the QFT thus perturbed. The central result obtained is that even drastic alterations of the hierarchical structure of the QFT’s phase rotation angles do not significantly diminish the performance of the QFT. This result is astonishing since the altered QFT, from a number-theoretical point of view, is the QFT for a number system that is no longer binary, but rather a number system defined according to $\nu =\sum _j \phi _j x_j$, where $\phi _j$ is 0 or 1 and $x_j$ may be $1/x^j$, $1/j^x$, or $1/\log _{x}(j+1)$, or any other choice, if desired. As an example, let us look at the number system $\nu =\sum _j \phi _j (1/3)^j$. In this case, the set $\nu$ is isomorphic to the well-known middle-thirds Cantor fractal [26], which has measure zero in the set of real numbers. As a consequence, the numbers $\nu$ that are actually representable in this number system, although uncountable, are a vanishing fraction of all real numbers in the unit interval. This means that this “$1/3$ number system,” which in our context corresponds to $\alpha =3$, is vastly incomplete. Viewed in this light, it is even more astonishing that the corresponding QFT performs at all, and, in fact, operates with $>$10 % efficiency. Thus, our structural studies presented in this paper are fundamentally different from our studies of random, static gate defects [15], in which the binary number system, including its completeness, still holds. Thus, combined with our earlier results on the stability of the QFT with respect to static gate defects [15], the structural stability with respect to changes in the gate rotation angle hierarchy shows that the QFT is stable against all major flaws in potential future hardware implementations of the QFT and manufacturing tolerances may be relatively relaxed in the actual production of future quantum hardware.