1 Introduction

Quantum Fourier transform (QFT) is analogues to the discrete Fourier transform (DFT) and is one of the essential operations in quantum computing. The QFT is a linear transformation on quantum bits. The QFT is a basic part of many quantum algorithms, including the Shor’s algorithm for factoring, Deutsch and Simon algorithms, the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, algorithms for the hidden subgroup problem and others [1,2,3]. Additionally, the quantum QFT plays an essential role on the exponential speed-up over the best classical algorithms for integer factorization. The QFT also is considered in color image encryption, processing and representation of quantum images [4,5,6,7,8,9].

The r-qubit QFT can be completed resourcefully on a quantum computer, with

  • a certain decomposition into a product of sparse unitary and diagonal matrices.

  • a quantum circuit consisting of only \( O\left( {r^{2} } \right) \) Hadamard gates and controlled phase shift gates, where \( r \) is the number of input qubits.

The critical issue of the quantum information processing algorithm is to create algorithms that are far superior in asymptotic running time to any “classical” counterparts known to date which solve the same problems. Shor presented the QFT computation “mixed-radix” method [1]. Coppersmith showed that in the \( N = 2^{r} \) case, there exist quantum circuits performing the QFT with \( O\left( {r^{2} } \right) \) gates [10]. This complexity is small when comparing with \( O\left( {r2^{r} } \right) \) for the Cooley–Tukey fast Fourier transform (FFT) [11]. These circuits are based on a recursive description of the QFT that is analogous to the description of the DFT exploited by the fast transforms. Different FFT algorithms have their advantages and can lead to different effective circuits for the QFT. Practically, the QFT offers a different way to make arithmetic operations on a quantum computer. The QFT algorithm represents a significant perfection in the complexity of the commonly used FFT algorithm, from \( O\left( {N{ \log }_{2} N} \right) \) to \( O\left( {{ \log }_{2}^{2} N} \right) \) [10, 12]. The QFT can be implemented approximately by eliminating the rotation gates with smaller a certain threshold value angle. Recently, several approximate QFT computation algorithms have been developed [10, 13,14,15,16,17,18,19]. For example, Coppersmith presented an approximate QFT computation, with complexity \( O\left( {N{ \log }_{2} N} \right) \), where \( 1 \le m \le { \log }_{2} N \) is the parameter that defines a degree of approximation, usually taken as \( O\left( {{ \log }_{2} { \log }_{2} N} \right) \). Lately, an implementation of the QFT by using multiple-valued quantum gates (by replacing the Walsh–Hadamard gate with the so-called Chrestenson quantum gates) was proposed [20].

In this paper, we build quantum circuits for the \( r \)-qubit QFT from the \( N \)-point fast Fourier transform (FFT), when \( N = 2^{r} \). We describe and analyze signal-flow graphs of the paired FFT and circuits that can be implemented for calculating the discrete Fourier transform in a quantum computer. The method of paired transform is used [21,22,23]. This technique may provide insight into the development of new quantum algorithms. The quantum DFT for inputs being two, three and four qubits is described in detail. The resulting unitary matrices can be interpreted as quantum logic gates. The circuits for calculating the fast discrete Hadamard transform (DHT) are also considered. In paired representation, the DFT is reduced to the DHT, when omitting all twiddle factors [24, 25]. Therefore, for instance, the circuit for the 16-point DFT can easily be simplified for the 16-point DHT. The rest of the paper is organized in the following way. In Sect. 2, a brief background information related to the FFT and QFT is given. Section 3 introduces the concept of the discrete paired transform and its fast algorithm by the Hadamard gates. Examples with the 2-qubit DFT and DHT are described. Sections 4 and 5 present the 8- and 16-point paired FFTs and the corresponding circuits for the 3- and 4-qubit DFTs. The conclusion is given in Sect. 6.

2 Background

The concept of the discrete Fourier transform is used widely in different areas of signal processing and communication systems. Many fast algorithms were developed, which are called the fast Fourier transforms (FFT), and one of them is the split radix N-point FFT, when \( N = 2^{r} ,\; r > 1 \); it is the well-known decimation-in-frequency FFT (Cooley–Tukey 1965). This algorithm splits the transform by two length-N/2 transforms, and such process is continued for the N/2-point DFTs and so on. One of the first FFTs used for quantum circuits was the decimation-in-time algorithm, wherein N/2 butterflies over two N/2 DFTs define the values of the N-point DFT. We also mention the paired FFT, or the FFT by the paired transform (Grigoryan 1986) that splits recursively the transform by the N/2, N/4, N/8…, 4, 2, 1-point DFTs. This splitting requires \( m\left( N \right) = N/2\left( {r - 3} \right) + 2 \) operations of complex multiplication [21,22,23,24]. The concept of the DFT was also applied in quaternion and octonion arithmetic, fast algorithms were developed and applied for color image processing [26]. The DFT became important in quantum computing and used in many different algorithms [17, 27,28,29,30,31].

When comparing the quantum DFT and the classical FFT, it should be noted the following:

  1. 1.

    The concept of the N-point DFT was moved formally from the complex arithmetic to quantum computing. It is not a transform on N qubits; it is a transform of amplitudes of the N-dimensional state of r qubits. The classical DFT has a physical meaning; it is the spectral characteristic of the signal. As a system, this transform presents a beautiful and real process of rotation of data around circles in the complex plane. In general, the DFT exists with rotation around ellipses; we call such transforms the elliptic DFTs [24, 32]. The Fourier transform was originated from the concept of the Fourier series of discrete periodic signals. Does the concept of periodic discrete qubit signals exist in quantum computing? The geometric interpretation of the DFT in quantum computing is unclear. It is possible that the definition of the Fourier transform on qubits will be found and clearly justified in future.

  2. 2.

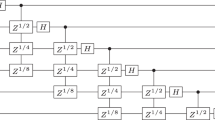
    All fast algorithms of the DFT were developed on real and complex inputs, as well as for quaternions and octonions [26, 33,34,35]. In matrix representation, any FFT algorithm presents a decomposition of the DFT matrix by simple and sparse unitary matrices plus a few diagonal matrices that contains a small number of twiddle factors. The first known circuit of the quantum r-qubit DFT, which is shown in Fig. 1 for the 3-qubit DFT [2], is not exception.

    Fig. 1
    figure 1

    The known circuit for the 3-qubit DFT

    Full size image
  3. 3.

    The analysis of the paired FFT shows that, with optimal organization and parallel computing, the splitting of the FFT in the classical computer can be performed for \( 2{ \log }_{2} \left( N \right) \) steps, including the reordering of the output. In quantum computing, the DFT can be accomplished by about \( \left({ \log }_{2} N \right)^{2} \) elements, or steps. For instance, the 3-qubit DFT, or the 8-point inverse DFT that is shown in Fig. 1 uses seven elements.

  4. 4.

    The FFT has been used in classical computers for many decades and applied in many areas of engineering, and the QFT exits only in the theory. To this day, the concept of the QFT is used as a theoretical tool for solving different tasks in quantum computing. There are no real practical examples of accomplishment of the QFT in the quantum computer.

  5. 5.

    Simplest gate on one qubit is called the Hadamard gate which is shown in Fig. 1 as the H gate.

3 Fast discrete paired transform

In this section, we briefly describe the concept of the paired representation of the signal and the splitting of the DFT. The discrete paired transform (DPT) is the frequency–time representation of the signal that corresponds to a special splitting of both discrete Fourier and Hadamard transforms. The Hadamard matrix is considered in the recursive form of Sylvester’s construction as

$$ \varvec{A}_{2} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} \\ 1 & 1 \\ \end{array} } \right], $$
(1)
$$ \varvec{A}_{4} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & { - \;1} & 1 \\ 1 & 1 & { - \;1} & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{A}_{2} } & { - \;\varvec{A}_{2} } \\ {\varvec{A}_{2} } & {\varvec{A}_{2} } \\ \end{array} } \right], $$
$$ \varvec{A}_{N} = \left[ {\begin{array}{*{20}c} {\varvec{A}_{N/2} } & { - \varvec{A}_{N/2} } \\ {\varvec{A}_{N/2} } & {\varvec{A}_{N/2} } \\ \end{array} } \right],\quad N = 2^{r} ,\; r > 2. $$
(2)

The basic 2 × 2 matrix \( \varvec{A}_{2} \) is considered without the normalized coefficient \( 1 /\sqrt 2 . \) The determinant of this matrix is 2, and the inverse matrix is

$$ \varvec{A}_{2}^{ - 1} = \frac{1}{2} \varvec{A}_{2}^{'} = \frac{1}{2}\left[ {\begin{array}{*{20}r} \hfill 1 & \hfill 1 \\ \hfill { - \;1} & \hfill 1 \\ \end{array} } \right]. $$

The normalized matrix \( 1 /\sqrt 2 \varvec{A}_{2} \) is unitary, which is important to mention since in quantum computing the operations on one qubit are described by only unitary transforms. The matrix \( \varvec{A}_{2} \) is similar to the Walsh–Hadamard matrix

$$ \varvec{H} = \left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & { - \;1} \\ \end{array} } \right], $$
(3)

with different order of rows. The matrix \( \varvec{A}_{2} \) can be described by the NOT gate X and gate H,

$$ \varvec{A}_{2} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} \\ 1 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & { - \;1} \\ \end{array} } \right] = \varvec{XH}. $$
(4)

Thus, the matrix \( \varvec{A}_{2} \) is the same Hadamard gate that is used in quantum computing (or the matrix \( \varvec{H} \) in Fig. 1), but with different order of output. In the graphs, this matrix will be shown by the following butterfly:

The normalized coefficient is omitted because the N-point DFT is defined in digital signal processing as

$$ F_{p} = \mathop \sum \limits_{n = 0}^{N - 1} f_{n} W_{N}^{np} = \mathop \sum \limits_{n = 0}^{N - 1} f_{n} {\text{e}}^{ - i2\pi np/N} ,\quad p = 0,1,2, \ldots , \left( {N - 1} \right). $$
(5)

The inverse transform is calculated by

$$ f_{n} = \frac{1}{N}\mathop \sum \limits_{p = 0}^{N - 1} F_{p} W_{N}^{ - np} = \frac{1}{N}\mathop \sum \limits_{p = 0}^{N - 1} F_{p} {\text{e}}^{i2\pi np/N} ,\quad n = 0,1,2, \ldots , \left( {N - 1} \right). $$
(6)

It should be noted that in many publications of quantum computing [2, 28], the discrete Fourier transform is defined in a different way, namely with clock-wise rotation of input data and normalized coefficient,

(7)

The paired FFT splits the transform of order \( N = 2^{r} , r > 1 \), by the set of \( \left( {r + 1} \right) \) DFTs of lengths \( N/2,N/4,N/8, \ldots , 2,1,1 \) [24, 36].

Example 1

The signal-flow graph of the 4-point DFT is shown in Fig. 2.

Fig. 2
figure 2

Signal-flow graph of the paired 4-point FFT

Full size image

The transform is split by the 4- and 2-point discrete paired transforms (DPT) with the matrices [24]

$$ \varvec{\chi}_{4}^{\prime } = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right]\quad {\text{and}}\quad\varvec{\chi}_{2}^{\prime } = \varvec{A}_{2} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} \\ 1 & 1 \\ \end{array} } \right] $$

as follows:

$$ \left[ {\begin{array}{*{20}c} {F_{3} } \\ {F_{1} } \\ {F_{2} } \\ {F_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & { - \;i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{0} } \\ {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ \end{array} } \right]. $$

The graph of the 4-point DFT given in Fig. 2 can be redrawn, as shown in Fig. 3. Therefore, the transform can be written as

$$ \left[ {\begin{array}{*{20}c} {F_{3} } \\ {F_{1} } \\ {F_{2} } \\ {F_{0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & { - \;1} \\ 0 & 0 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & { - \;i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {f_{0} } \\ {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ \end{array} } \right]. $$
Fig. 3
figure 3

Signal-flow graph of the 4-point DFT

Full size image

Considering the matrix of permutation of outputs

$$ \varvec{S}_{4} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right], $$

the matrix of the 4-point DFT can be presented as

$$ \varvec{F}_{4} = \varvec{S}_{4} \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & { - \;1} \\ 0 & 0 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & { - \;i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} } \right]. $$

Direct calculations show that

$$ \varvec{F}_{4} = \varvec{S}_{4} \left[ {\begin{array}{*{20}c} 1 & i & { - 1} & { - \;i} \\ 1 & { - \;i} & { - \;1} & i \\ 1 & { - 1} & 1 & { - 1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ 1 & { - \;i} & { - \;1} & i \\ 1 & { - 1} & 1 & { - \;1} \\ 1 & i & { - \;1} & { - \;i} \\ \end{array} } \right]. $$

Let \( \varvec{W}_{2} \) be the matrix of rotation

$$ \varvec{W}_{2} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & { - \;i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right], $$

and let \( \varvec{A}_{0,2;1,3} \) and \( \varvec{A}_{0,1;2,3} \) be, respectively, the matrices

$$ \varvec{A}_{0,2;1,3} = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} } \right] \quad {\text{and}}\quad \varvec{A}_{0,1;2,3} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & { - \;1} \\ 0 & 0 & 1 & 1 \\ \end{array} } \right]. $$

Each of these matrices is described by two Hadamard gates,

$$ \varvec{A}_{0,2;1,3} = \varvec{A}_{0,2} \varvec{A}_{1,3} = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & { - \;1} \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} } \right] $$
$$ \varvec{A}_{0,1;2,3} = \varvec{A}_{0,1} \varvec{A}_{2,3} = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & { - \;1} \\ 0 & 0 & 1 & 1 \\ \end{array} } \right]. $$

Here and hereinafter, we denote by \( \varvec{A}_{k,l} \) the identity matrix with two additional coefficients equal 1 and − 1 at positions \( \left( {k,l} \right) \) and \( \left( {l,k} \right), \) respectively, when \( k \ne l. \) This matrix describes the Hadamard gate with inputs being the \( k \) th and \( l \) th components of data.

Thus, the matrix of the 4-point DFT can be decomposed as

$$ \varvec{F}_{4} = \varvec{S}_{4} \varvec{A}_{0,1} \varvec{A}_{2,3} \varvec{W}_{2} \varvec{A}_{1,3} \varvec{A}_{0,2} , $$
(8)

or

$$ \varvec{F}_{4} = \varvec{S}_{4} \varvec{A}_{0,1} \varvec{W}_{2} \underbrace {{\varvec{A}_{2,3} \varvec{A}_{0,2} \varvec{A}_{1,3} }}_{{}}. $$
(9)

Here, the product of three matrices is the matrix of the 4-point paired transform, \( \chi_{4}^{\prime } \). Figure 4 shows the circuit of the 4-point DFT with four Hadamard gates and one trivial rotation matrix. Each Hadamard gates requires one addition and one subtraction.

Fig. 4
figure 4

Circuit for the 4-point DFT

Full size image

A two-qubit state is described by four complex or real numbers of four-dimensional vector

with the condition that \( |f_{00} |^{2} + |f_{01} |^{2} + |f_{10} |^{2} + |f_{11} |^{2} = 1. \) These numbers are called the amplitudes of the 2-qubit state. The two-qubit DFT state

is calculated by

$$ \begin{aligned} F_{00} & = f_{00} + f_{01} + f_{10} + f_{11} , \\ F_{01} & = f_{00} - if_{01} - f_{10} + if_{11} , \\ F_{10} & = f_{00} - f_{01} + f_{10} - f_{11} , \\ F_{11} & = f_{00} + if_{01} - f_{10} - if_{11} . \\ \end{aligned} $$

The circuit for calculating the 4-point DFT, or 2-qubit DFT by the paired transforms is shown in Fig. 5.

Fig. 5
figure 5

Circuit for the 2-qubit DFT with three stages

Full size image

In quantum computing, the states \( \left| {\left. {00} \right\rangle } \right., \left| {\left. {01} \right\rangle } \right.,\left| {\left. {10} \right\rangle } \right. \) and \( \left| {\left. {11} \right\rangle } \right. \) are numbered simply by 0, 1, 2, and 3, as these numbers presented in binary form. The 2-qubit state can be written as the vector , and the same for the Fourier transform, . Therefore, there is no difference between the circuits in Figs. 4 and 5, which are shown for the complex data and amplitudes of qubits, respectively.

Example 2

We consider the discrete Hadamard transform [37]. When omitting the diagonal matrix in this decomposition in Eq. 8, the transform becomes the 4-point discrete Hadamard transform (DHT), i.e.,

$$ \left[ {\begin{array}{*{20}c} 1 & { - \;1} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & { - \;1} & { - \;1} & 1 \\ 1 & 1 & { - \;1} & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 \\ \end{array} } \right]. $$

The circuit for the 4-point fast Hadamard transform (FHT), or the 2-qubit FHT, is shown in Fig. 6.

Fig. 6
figure 6

Circuit for the 2-qubit FHT with two stages

Full size image

When considering the 4-point DFT with the normalized coefficient,

$$ F_{p} = \frac{1}{2}\mathop \sum \limits_{n = 0}^{3} f_{n} W_{4}^{np} = \frac{1}{2}\mathop \sum \limits_{n = 0}^{3} f_{n} {\text{e}}^{ - i2\pi np/4} , \quad p = 0,1,2,3, $$

the above signal-flow graphs and circuits can be used with the normalized matrix, i.e., in the circuit we need make changes \( \varvec{A}_{2} \to \varvec{A}_{2} /\sqrt 2 . \)

4 Circuits for length-8 Fourier and Hadamard transforms

In general case of \( N = 2^{r} , \;r > 1 \), the discrete paired transform requires only \( 2\left( {N - 1} \right) \) operations of addition and subtraction [38]. The transform has a matrix with only 0 and ± 1 coefficients. For the \( N = 8 \) case, the matrix equals

$$ \left[ {\chi_{8}^{\prime } } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & { - \;1} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & { - \;1} & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & { - \;1} & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & { - \;1} \\ 1 & 0 & { - \;1} & 0 & 1 & 0 & { - \;1} & 0 \\ 0 & 1 & 0 & { - \;1} & 0 & 1 & 0 & { - \;1} \\ 1 & { - \;1} & 1 & { - \;1} & 1 & { - \;1} & 1 & { - \;1} \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]. $$
(10)

The rows of this matrix, or basic functions of the 8-point DPT, are not normalized. The normalization of the matrix is performed by multiplication with the diagonal matrix \( \varvec{D} = {\text{diag}}(1/\sqrt {2,} 1/\sqrt {2,} 1/\sqrt {2,} 1/\sqrt {2,} 1/2,1/2,1/\sqrt 8 ,1/\sqrt 8 \)). The matrix \( D\left[ {\chi_{8}^{\prime } } \right] \) has determinant 1 and is unitary, i.e., its inverse matrix equals the transpose matrix.

For \( N = 4 \) and 8, the signal-flow graphs of fast DPT are shown in Fig. 7. One can see that the transforms can be calculated by 7 and 3 butterflies.

Fig. 7
figure 7

Signal-flow graphs of the 4- and 8-point DPTs

Full size image

In the general case, the DPT can be calculated by \( \left( {N - 1} \right) \) butterflies or Hadamard matrices \( \varvec{A}_{2} \). The matrix of the high-order discrete paired transform can be defined in recursive form

$$ \left[ {\chi_{16}^{\prime } } \right] = \left[ {\begin{array}{*{20}c} {I_{8} } & { - \;I_{8} } \\ {\left[ {\chi_{8}^{\prime } } \right]} & {\left[ {\chi_{8}^{\prime } } \right]} \\ \end{array} } \right],\quad \left[ {\chi_{32}^{\prime } } \right] = \left[ {\begin{array}{*{20}c} {I_{16} } & { - \;I_{16} } \\ {\left[ {\chi_{16}^{\prime } } \right]} & {\left[ {\chi_{16}^{\prime } } \right]} \\ \end{array} } \right], \ldots , $$
(11)

where \( I_{M} \) denotes the identity matrix \( M \times M \).

Example 3

The signal-flow graph of the 8-point DFT by the paired transforms is shown in Fig. 8.

Fig. 8
figure 8

Signal-flow graph of the paired 8-point FFT

Full size image

Here, the twiddle factors are \( W^{1} = W_{8}^{1} = {\text{e}}^{ - i2\pi /8} = 0.7071\left( {1 - i} \right), \) and \( W^{3} = W_{8}^{3} = {\text{e}}^{ - i2\pi /8} = 0.7071\left( { - 1 - i} \right). \) According to this signal-flow graph, the matrix of the 8-point DFT can be written as [24, 36]

$$ \varvec{F}_{8} = \varvec{S}_{8} \left[ {\begin{array}{*{20}c} {\underbrace {{\left[ {\begin{array}{*{20}c} {\chi_{2}^{\prime } } & {} & {} \\ {} & 1 & {} \\ {} & {} & 1 \\ \end{array} } \right]{\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - i} \\ 1 \\ 1 \\ \end{array} } \right\}\chi_{4}^{\prime } }}_{{}}} & {} & {} & {} \\ {} & {\chi_{2}^{\prime } } & {} & {} \\ {} & {} & 1 & {} \\ {} & {} & {} & 1 \\ \end{array} } \right]{\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ { - i} \\ {W_{8}^{3} } \\ 1 \\ { - i} \\ 1 \\ 1 \\ \end{array} } \right\}\chi_{8}^{\prime } , $$
(12)

where the matrix \( \varvec{S}_{8} \): \( \left( {7,3,5,1,6,2,4,0} \right) \to \left( {0,1,2,3,4,5,6,7} \right) \) corresponds to the permutation of outputs. Using the full graphs of the 8- and 4-point DPTs, we can draw the signal-flow graph of the 8-point DFT, as shown in Fig. 9.

Fig. 9
figure 9

Signal-flow graph of the 8-point DFT

Full size image

By separating the multiplications by twiddle coefficients, we obtain the signal-flow graph that is shown in Fig. 10. Three stages in this graph correspond to the calculation of the different lengths of butterflies.

Fig. 10
figure 10

Signal-flow graph of the 8-point DFT with three groups of butterflies

Full size image

The matrix of the 8-point DFT can be written as

$$ \varvec{F}_{8} = \varvec{S}_{8} \varvec{A}_{\text{III}} \varvec{W}_{\text{II}} \varvec{A}_{\text{II}} \varvec{W}_{\text{I}} \varvec{A}_{\text{I}} . $$
(13)

The matrices in this decomposition are described as follows. The first stage of calculation can be written in matrix form as

$$ \varvec{A}_{\text{I}} = \varvec{A}_{2} \otimes \varvec{I}_{4} = \left[ {\begin{array}{*{20}c} {\varvec{I}_{4} } & { - \varvec{I}_{4} } \\ {\varvec{I}_{4} } & {\varvec{I}_{4} } \\ \end{array} } \right]. $$

Here, the operation \( \otimes \) denotes the Kronecker product of matrices from the right. The matrix \( \varvec{A}_{\text{I}} \) describes the operation with four butterflies, or Hadamard gates,

$$ \varvec{A}_{I} = \varvec{A}_{0,4;1,5;2,6;3,7} = \varvec{A}_{0,4} \varvec{A}_{1,5} \varvec{A}_{2,6} \varvec{A}_{3,7} . $$
(14)

On the second stage, the calculations are described by the matrix

$$ \varvec{A}_{\text{II}} = \varvec{I}_{2} \otimes \left( {\varvec{A}_{2} \otimes \varvec{I}_{2} } \right) = \left[ {\begin{array}{*{20}c} {\varvec{I}_{2} } & { - \;\varvec{I}_{2} } & {} & {} \\ {\varvec{I}_{2} } & {\varvec{I}_{2} } & {} & {} \\ {} & {} & {\varvec{I}_{2} } & { - \;\varvec{I}_{2} } \\ {} & {} & {\varvec{I}_{2} } & {\varvec{I}_{2} } \\ \end{array} } \right]. $$

This is another operation with four butterflies,

$$ \varvec{A}_{\text{II}} = \varvec{A}_{0,2;1,3;4,6;5,7} = \varvec{A}_{0,2} \varvec{A}_{1,3} \varvec{A}_{4,6} \varvec{A}_{5,7} . $$
(15)

On the last stage, we consider the matrix

$$ \varvec{A}_{\text{III}} = \varvec{I}_{4} \otimes \varvec{A}_{2} = \left[ {\begin{array}{*{20}c} {\varvec{A}_{2} } & {} & {} & {} \\ {} & {\varvec{A}_{2} } & {} & {} \\ {} & {} & {\varvec{A}_{2} } & {} \\ {} & {} & {} & {\varvec{A}_{2} } \\ \end{array} } \right] $$

that describes the performance of four butterflies

$$ \varvec{A}_{\text{III}} = \varvec{A}_{0,1;2,3;4,5;6,7} = \varvec{A}_{0,1} \varvec{A}_{2,3} \varvec{A}_{4,5} \varvec{A}_{6,7} . $$
(16)

Also, we introduce the diagonal matrices that describe the multiplications by twiddle factors \( W^{1} ,\;W^{2} = - \;i, \) and \( W^{3} \),

$$ \varvec{W}_{8}^{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {W_{8}^{1} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] = {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} } \right\}, $$
$$ \varvec{W}_{8}^{2} = {\text{diag}}\left\{ {1,1, - \;i,1,1,1,11} \right\},\quad \text{and} $$
$$ \varvec{W}_{8}^{3} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {W_{8}^{3} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] = {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ {W_{8}^{3} } \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} } \right\}, $$

These rotation matrices describe three multiplications by the twiddle factors between Stages I and II, and we denote by \( \varvec{W}_{\text{I}} \) the product

$$ \varvec{W}_{\text{I}} = \varvec{W}_{8}^{1} \varvec{W}_{8}^{2} \varvec{W}_{8}^{3} . $$

For two trivial multiplications by \( {-}\;i \) after Stage II, we introduce the following diagonal matrix:

$$ \varvec{W}_{\text{II}} = I_{2} \otimes \varvec{W}_{4}^{1} = I_{2} \otimes {\text{diag}}\left\{ {1, - \;i,1,1} \right\}. $$

All above matrices \( \varvec{W} \) are matrices of rotation. The last matrix we need is the matrix of the permutation

$$ S_{8} = \left( {\begin{array}{*{20}c} {01234567} \\ {73516240} \\ \end{array} } \right) = \left( {07} \right)\left( {13} \right)\left( {25} \right)\left( {46} \right). $$

The result of the above reasoning is shown in Fig. 11. It is the circuit for calculating the 8-point complex FFT that can be used in quantum computing with 12 Hadamard gates and five matrices of rotations (three of them are trivial). The 3-qubit state is described as

with condition \( |f_{0} |^{2} + |f_{1} |^{2} + \cdots + |f_{7} |^{2} = 1. \) We consider the new 3-qubit state

Fig. 11
figure 11

Circuit for the quantum 8-point complex FFT

Full size image

The components of this state, which is called the 3-qubit DFT, are calculated by

$$ F_{p} = \mathop \sum \limits_{n = 0}^{7} f_{n} W_{8}^{np} = \mathop \sum \limits_{n = 0}^{7} f_{n} {\text{e}}^{ - i2\pi np/8} ,\quad p = 0,1, \ldots ,7. $$
(17)

One can notice from this circuit, as well as from Eq. 13, that the 8-point FFT includes six stages of parallel computing \( f_{n} \to \varvec{S}_{8} \varvec{A}_{\text{III}} \varvec{W}_{\text{II}} \varvec{A}_{\text{II}} \varvec{W}_{\text{I}} \varvec{A}_{\text{I}} \left( {f_{n} } \right): \)

  1. 1 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{I}} \),

  2. 2 stage.

    Perform three multiplications by rotation matrices of \( \varvec{W}_{\text{I}} \),

  3. 3 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{II}} \),

  4. 4 stage.

    Perform two multiplications by rotation matrices of \( \varvec{W}_{\text{II}} \),

  5. 5 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{III}} \),

  6. 6 stage.

    Reorder the outputs in accordance with the matrix \( \varvec{S}_{8} \).

Thus, there is only six steps and \( 6 = 2{ \log }_{2} N = 2 \times 3. \)

Comments

The circuits for the quantum DFT are usually drawn with lines that denote the qubits, as shown in Fig. 1. The circuit in Fig. 11 is given in the traditional form with the input and output components, \( f_{n} \) and \( F_{p} \), respectively. Let us find out if the circuits in these two figures really differ. The matrix \( \varvec{A}_{\text{I}} \) with four Hadamard gates is

$$ \varvec{A}_{I} = \varvec{A}_{0,4;1,5;2,6;3,7} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & { - \;1} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & { - \;1} & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & { - \;1} & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & { - \;1} \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ \end{array} } \right] . $$
(18)

and it presents the block H, i.e., the Hadamard gate but on the 3rd qubit, not the 1st qubit in the circuit in Fig. 1. Only block H should be changed by the equivalent \( \varvec{A}_{2} \). Similarly, the matrix \( \varvec{A}_{\text{II}} \) with other four Hadamard gates

$$ \varvec{A}_{\text{II}} = \varvec{A}_{0,2;1,3;4,6;5,7} = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \;1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & { - \;1} & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & { - \;1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & { - \;1} \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ \end{array} } \right] $$
(19)

is similar to the second block H on the 2nd qubit, as in Fig. 1. Also, in the decomposition of the Fourier matrix in Eq. 13, the matrix \( \varvec{A}_{\text{III}} \) with four Hadamard gates describes the block \( \varvec{A}_{2} \) applied on the 1st qubit, and not on the last qubit, as shown in Fig. 1. The same correspondence has place for the rotation matrices in the figures. The diagonal matrix with the twiddle factors in the paired FFT is

$$ {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ { - \;i} \\ {W_{8}^{3} } \\ 1 \\ { - \;i} \\ 1 \\ 1 \\ \end{array} } \right\} = {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ { - \;i} \\ {W_{8}^{3} } \\ \end{array} } \right\} \oplus {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - \;i} \\ \end{array} } \right\} \oplus {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right\}. $$

Here, the first 4 × 4 diagonal sub-matrix describes the rotations (similar to blocks S and T in Fig. 1) over the 3rd qubit;

$$ {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ { - i} \\ {W_{8}^{3} } \\ \end{array} } \right\} = \varvec{T}_{1} \otimes \varvec{T}_{2} \triangleq {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - i} \\ \end{array} } \right\} \otimes {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ \end{array} } \right\}. $$

The difference between these diagonal matrices, \( \varvec{T}_{1} \) and \( \varvec{T}_{2} \), and matrices S and T in Fig. 1 is in the fact that \( - \;i \) is substituted by \( i \), since the circuit in Fig. 1 is for the inverse DFT not the direct DFT. Now, we consider the order of qubits in the input and output of the circuit for the 3-qubit DFT when splitting by the paired transform. The orders of amplitudes and qubits are shown in Fig. 12.

Fig. 12
figure 12

The order of amplitudes of the input and output in the paired 8-point FFT

Full size image

Here, to change the order of amplitudes in qubits, the quantum NOT gate can be used; \( \varvec{X} = \left[ {0 1;1 0} \right]. \) Fig. 13 shows the circuit of the paired algorithm for the 3-qubit DFT.

Fig. 13
figure 13

The circuit for the 3-qubit direct DFT by the paired splitting

Full size image

When comparing the circuits in Figs. 1 and 13, the following can be noted:

  1. 1.

    The qubits in inputs are given in reversal order;

  2. 2.

    The gates \( \varvec{A}_{2} \) are used in circuit of Fig. 13, instead of gates \( \varvec{H} \) in circuit of Fig. 1;

  3. 3.

    The same NOT gate is used for each qubit on the last stage of the circuit in Fig. 13. In the circuit of Fig. 1, the permutation \( \varvec{P} \) of amplitudes of the 8-dimensional vector of the 3-qubit state is used. The matrix of this permutation equals

    $$ \varvec{P} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]. $$

Since the \( \varvec{A}_{2} \) gate is the composition of two gates, \( \varvec{A}_{2} = \varvec{XH} \), we can change the last gate \( \varvec{A}_{2} \) with the gate \( \varvec{X} \) by one \( \varvec{H} \) gate or draw the above circuit with Walsh–Hadamard gates, as shown in Fig. 14. It is not difficult to notice, that the last operations on the 1st output qubit can be written as

$$ \varvec{XA}_{2} = \varvec{XXH} = \varvec{H}. $$
Fig. 14
figure 14

The circuit for the 3-qubit direct DFT by the paired splitting

Full size image

Example 4

When splitting by the paired transform, the matrix of the 8-point discrete Hadamard transform (DHT) is represented as [24, 39]

$$ \varvec{A}_{8} = \varvec{S}_{8} \left[ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\chi_{2}^{\prime } } & {} & {} \\ {} & 1 & {} \\ {} & {} & 1 \\ \end{array} } \right]\chi_{4}^{\prime } } & {} & {} & {} \\ {} & {\chi_{2}^{\prime } } & {} & {} \\ {} & {} & 1 & {} \\ {} & {} & {} & 1 \\ \end{array} } \right]\chi_{8}^{\prime } ,\quad \left( {\chi_{2}^{\prime } = \varvec{A}_{2} } \right). $$
(20)

Here, the matrix of the transformation is considered to be equal

The circuit in Fig. 11 with omitted all matrices of rotation is shown in Fig. 15. It is the circuit for calculating the 8-point discrete Hadamard transform.

Fig. 15
figure 15

The circuit for calculating the 8-point DHT with three stages

Full size image

Thus, there are only 4 stages in computing the 8-point DHT, \( f_{n} \to \varvec{S}_{8} \varvec{A}_{\text{III}} \varvec{A}_{\text{II}} \varvec{A}_{\text{I}} \left( {f_{n} } \right) \):

  1. 1 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{I}} \),

  2. 2 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{II}} \),

  3. 3 stage.

    Perform four Hadamard gates in \( \varvec{A}_{\text{III}} \),

  4. 4 stage.

    Reorder the outputs in accordance with matrix \( \varvec{S}_{8} \).

The circuit for this 3-qubit DHT is given in Fig. 16.

Fig. 16
figure 16

The circuit for the 3-qubit direct DHT by the paired splitting

Full size image

The same circuit but with Walsh–Hadamard gates \( \varvec{H} \) instead of \( \varvec{A}_{2} \) is shown in Fig. 17. Thus, we have two circuits for the same discrete Hadamard transform, one is written for calculation in the classical computer, and another for calculation in the quantum computer.

Fig. 17
figure 17

The circuit for the 3-qubit direct DHT by the paired splitting with Walsh–Hadamard gates

Full size image

5 Sixteen-point Fourier and Hadamard transforms

The circuit for calculating the DFT of high order can be described in a way similar to the above considered cases \( N = 4 \) and \( 8 \). The paired transform splits recursively the DFT into a minimum number of short transforms. It is difficult to expect a recursive calculation in a quantum computer. Therefore, all Hadamard gates in the paired transforms should be grouped by stages, as in the above case \( N = 8 \) (in Fig. 10). Figure 18 shows the splitting of the 16-point DFT by the paired transforms, namely by one 16- and 8-point DPTs, two 4-point DPTs, and four 2-point DPT which are the butterflies 2 × 2 [24, 36]. There are only 10 non-trivial twiddle coefficients; seven are trivial multiplications by \( {-}\;i \). Thus, only 17 rotation matrices are used in the circuit for the 16-point FFT. The number of Hadamard gates (\( 2 \times 2 \) butterflies) for each \( 2^{k} \)-point DPT equals \( (2^{k} - 1) \). Therefore, the total number of Hadamard gates in the \( N \)-point FFT equals \( N/2{ \log }_{2} N \), or 32 for the 16-point FFT.

Fig. 18
figure 18

Block-scheme of calculation of the 16-point paired FFT

Full size image

When opening this block-diagram in detail, by calculating the paired transforms by the Hadamard gates, we obtain the circuit that is shown in Fig. 19. It is not difficult to see that the calculation of the 16-point FFT includes only 8 stages of parallel computing, including the last operation of reordering the output.

Fig. 19
figure 19

Circuit for computing the 16-point FFT

Full size image

This is the circuit for the 16-point DFT for the classical computer. The same circuit for calculating the 4-qubit DFT in the quantum computer is given in Fig. 20. The performance of 32 operators \( \varvec{A}_{2} \) is equivalent to 4 gates \( \varvec{A}_{2} \) in the quantum circuit. As in the case of 3-qubit DFT, the permutations of outputs are performed inside each qubit by the NOT gate. It is considered that the diagonal matrix with the twiddle factors in the paired 16-point FFT is

$$ {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{16}^{1} } \\ {W_{16}^{2} } \\ {W_{16}^{3} } \\ { - \;i} \\ {W_{16}^{5} } \\ {W_{16}^{6} } \\ {W_{16}^{7} } \\ \end{array} } \right\} \oplus {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ { - \;i} \\ {W_{8}^{3} } \\ \end{array} } \right\} \oplus {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - \;i} \\ \end{array} } \right\} \oplus {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right\}. $$
Fig. 20
figure 20

The circuit for the 4-qubit direct DFT by the paired splitting

Full size image

Here, the first 8 × 8 diagonal sub-matrix can be written as

$$ {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - \;i} \\ \end{array} } \right\} \otimes {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{16}^{1} } \\ {W_{16}^{2} } \\ {W_{16}^{3} } \\ \end{array} } \right\} = \varvec{T}_{1} \otimes \varvec{T}_{2} \otimes \varvec{T}_{3} \triangleq {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ { - \;i} \\ \end{array} } \right\} \otimes {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{8}^{1} } \\ \end{array} } \right\} \otimes {\text{diag}}\left\{ {\begin{array}{*{20}c} 1 \\ {W_{16}^{1} } \\ \end{array} } \right\}. $$

As it was done for the \( N = 8 \) case, the circuit in Fig. 20 can be reduced to the circuit for calculating the 16-point Hadamard, by removing all multiplications by the twiddle factors. For that, the same circuit can also be used, when setting all rotations matrices \( \varvec{T}_{k} \) to the 2 × 2 identity matrix. Figure 21 shows this circuit for calculating the 4-qubit DHT.

Fig. 21
figure 21

The circuit for the 4-qubit direct DHT by the paired splitting

Full size image

The equivalent circuit in the classical computer for calculating the 16-point fast Hadamard Transform (FHT) is shown Fig. 22. For high length \( N = 2^{r} \), \( r > 4 \), the circuits for computing the \( N \)-point FFT and FHT by paired can be described in a similar way.

Fig. 22
figure 22

Circuit for computing the quantum 16-point FHT

Full size image

In the general case when \( N = 2^{r} \), \( r \ge 1 \), a \( r \)-qubit state as the \( N \)-dimensional vector of amplitudes is described as

(21)

with condition that \( |f_{0} |^{2} + |f_{1} |^{2} + |f_{2} |^{2} + \cdots + |f_{{2^{r - 1} }} |^{2} = 1 \). The components of the new state, which is called the r-qubit DFT,

(22)

are defined as

$$ F_{p} = \frac{1}{\sqrt N }\mathop \sum \limits_{n = 0}^{N - 1} f_{n} W_{N}^{np} = \frac{1}{\sqrt N }\mathop \sum \limits_{n = 0}^{N - 1} f_{n} {\text{e}}^{ - i2\pi np/N} ,\quad p = 0,1, \ldots ,\left( {N - 1} \right). $$
(23)

As stated in [16], the QFT performs the task different from the FFT that computes a new complex vector. The QFT changes the state of \( r \) qubits. If the result of measurement is \( \left| {\left. n \right\rangle } \right. \) with probability \( |f_{n} |^{2} \), the same value in the new state of the quantum DFT may occur, or can be measured with probability \( |F_{n} |^{2} \). In Eq. 23, the normalized coefficient 1/ \( \sqrt N \) is needed, in order to have the same condition \( |F_{0} |^{2} + |F_{1} |^{2} + \cdots + |F_{{2^{r - 1} }} |^{2} = 1 \) for the new state . Therefore, in all above circuits for calculating the \( r \)-qubit DFT and DHT, the matrix \( \varvec{A}_{2} \) should be considered with the normalized coefficient \( 1/\sqrt 2 \).

5.1 Brief comparison with quantum circuits

The above analysis of the method was described in detail and compared with the first quantum circuit for the QFT [2], which is given in Fig. 1 for three qubits. The main difference is in using the gate \( \varvec{A}_{2} \) instead of the Walsh–Hadamard gate \( \varvec{H} \), and also in a simple permutation of the output qubits, by using only NOT \( \varvec{X} \) gates. The paired transform splits the DFT by a set of short DFTs which are processed separately. In contrast to such a splitting, the above QFT is based on the frequency-in-time algorithm and uses a number of butterflies over the short DFTs, which requires the sequence of SWAP gates.

Similar to the known method of approximation of the QFT with a bounded error, which is performed by removing a few rotation gates from the circuit (Coppersmith 1994), the proposed circuit could be used in a similar way to approximate the transform. We also mention four quantum circuits for the QFT that are described in [28]. One of these quantum circuits is the quantum circuit for the QFT [2] (which we used above for comparison with the paired QFT), but completed with the bit-reversal circuit. Other three complete circuits are similar to the first one; all four circuits are based on the same iteration formula (Eq. 20 in [28]) of the FFT but with different implementations, wherein the permutation between components of qubits is performed in the beginning or between the intermediate stages. In our opinion, such permutations do not make the circuits more effective than the first circuit, and moreover, the proposed circuit.

6 Conclusion

In this paper, the circuits for computing the length \( N = 2^{r} \) fast Fourier and Hadamard transforms with splitting by the paired transform were described and analyzed in detail for the \( N = 4, 8 \), and \( 16 \) cases. It was shown that the signal-flow graphs of the paired algorithms can be used for calculating the quantum Fourier and Hadamard transforms with minimum number of stages. The calculation of all components of the transforms is performed by the Hadamard gates and matrices of rotations and all simple NOT gates for permutation of output qubits. The author hopes that this paper will be useful for the advance of new-paired transform-based resourceful quantum algorithms.