The wrong skewness problem in stochastic frontier analysis: a review

Abstract

We provide a review of the literature related to the “wrong skewness problem” in stochastic frontier analysis. We identify two distinct approaches, one treating the phenomenon as a signal from the data that the underlying structure has some special characteristics that allow inefficiency to co-exist with “wrong” skewness, the other treating it as a sample-failure problem. Each leads to different treatments, while siding with either raises certain methodological issues, and we explore them. We offer simulation evidence that the wrong skewness as a sample problem likely comes from how the noise component of the composite error term has been realized in the sample, which points towards a new way to handle the problem. We also investigate the issues that arise when attempting to use the unconstrained Normal-Half Normal (Skew Normal) likelihood.

1 Introduction

The production stochastic frontier model (SFM) is generically formulated (in logarithms) as

$$\begin{array}{ll} &y=m\left(x\right)+\varepsilon,\;\;\varepsilon=v-u,\\ &E\left(v\right)=0,\;\;E\left(v^3\right)=0,\;\;u\geq0,\;\; v {\perp\!\!\!\perp} u, \end{array}$$

(1)

where m(x) is the maximum production function. Its defining property is the composite regression error, ε = v − u, where the non-negative u component represents inefficiency measured in output units, the distance of actual production from its maximum given inputs, due to efficiency losses. The component v represents “noise" and is traditionally specified as being symmetric around zero. Given this, and combined with the fact that u is non-negative and enters with a minus sign, the presumption is that the composite error ε should exhibit negative skewness (or positive skewness, for the cost-frontier model, where u enters with a plus sign). We will discuss the topic based on the production SFM.

The “wrong skewness problem” is particular to estimation of the SFM and relates to the error term: it occurs when the skewness of the residuals has the opposite sign from what we expect from the model. It was first identified through simulations in Olson et al. (1980) as a “Type I failure”. The authors announced the issue in the context of discussing the Corrected OLS estimator (COLS) for the production SFM. They wrote, “A ‘Type I’ failure occurs if the third moment of the OLS residuals is positive”, and a few lines later, “(…) in every case of Type I failure we encountered, the maximum likelihood estimate of λ also turned out to equal zero. (This makes some sense, though we cannot prove analytically that it should happen.) As a result, Type I failures are not a serious problem.” The parameter λ = σ_u/σ_v is the ratio of the inefficiency scale parameter over the noise scale parameter.

But why “when the 3rd moment of OLS residuals is positive” do we have a “failure”? And what kind of failure? As regards the COLS estimator, it fails because it incorporates the assumption that the skewness should be non-positive (and would lead to a non-positive or even negative estimate for σ_u). As regards MLE, it fails because it too incorporates the assumption that the skewness should be negative, and as Waldman (1982) proved formally, the MLE for σ_u (${\widehat{\sigma }}_{u}$) is 0 when a “Type I failure” happens. But this is an artificial result, as we will explain in Section 5.¹

So before calling it a “failure”, first and foremost it represents a mismatch between our a priori assumptions as regards the population (negative skewness) and what the available sample indicates, assuming that the sample is “representative of the population”. Now the issue becomes: Is our a priori assumption of negative population skewness justified? Yes, under the standard additional assumptions that v is symmetric and independent of u, and that u is non-negative with monotonically declining density and hence positive skewness. It is under these three assumptions, that the population skewness of ε is (should be) negative, and so when the sample skewness is positive, it is viewed as having the wrong sign, hence the “wrong skewness problem”.

Since it is a “problem” only under these additional assumptions, the whole matter moves one level back: when we obtain positive skewness, should we re-examine the assumptions that led to it being labeled a “problem”, a case of a sample not representing faithfully the population in that respect? Is it not possible that our a priori assumptions on v and u are what is “wrong”?

And indeed, one strand of the literature on the wrong skewness problem has done just that: existing research has relaxed either the monotonically declining density/positive skewness assumption on u, the independence assumption between v and u, and/or the symmetry assumption on v. Not that these assumptions are unreasonable: The positive skewness assumption for u has an economic motivation: market forces make efficiency a factor of survival so more firms will tend to be closer to low levels of inefficiency. The independence and v-symmetry assumptions have more to do with modeling convenience but they may also represent true unanticipated shocks. But the relaxations that we will review are also supported by economic and structural reasoning—they are not mechanical alterations of mathematical/statistical assumptions. For these scholars, the positive skewness is not “wrong” but a population characteristic realized in the sample. We will review this literature first, in Section 2, because it is this strand of literature that clearly dispels a misconception about the relation between inefficiency and the sign of the error skewness: it shows that the existence of inefficiency is not equivalent to a particular sign of skewness in the population. It is not necessarily true that, as one scholar once put it, when we have a positive skewness in a production data sample,“the sample does not support an inefficiency story”. In a production SFM, we can have inefficiency and positive population skew. Correspondingly, in a cost SFM, we can have inefficiency and negative population skew. But if this is the case, then our a priori assumptions are not really sine qua non in order to obtain a model that can study what we want to study.²

Section 3 contains a methodological discussion on whether “taking clues from data” to re-specify the SF model as regards its distributional assumptions belongs to questionable practices of data-mining and the like, or not. But the data aren’t always right: the other strand of the literature on the wrong skewness problem stressed that it can indeed be “wrong” and not infrequently: it is visibly probable, and not just theoretically possible, to have a production population with negative skew and a sample from it with positive skew. To begin with, this may be a purely statistical matter. Simar and Wilson (2009, p. 71) show through simulations that, for example, when λ = 0.71 and the sample size is n = 1000, there is a 22% chance of obtaining a sample skewness with the wrong sign. But this statistical aspect may also have a structural foundation: it is more likely to appear when the “strength” of inefficiency u is relatively low, either in absolute terms, or relative to the noise error component v. This could reflect a distinctive structural characteristic of the market under study. We review this literature in Section 4.

Whatever the case may be, the conflict between our assumptions on v and u on the one hand, and the realities of the sample on the other, was dramatically showcased in what is still the largest in scope empirical SFA study, the book Industrial Efficiency in Six Nations by Caves (1992). In their Table 1.1, p. 8, we learn that in a very large collection of 1,318 industry-level samples from five countries (Australia, Japan, Korea, UK, USA), 27% of them had the “wrong skewness problem”. That is a very high percentage. Mester (1997) reported the wrong skewness problem for three of the twelve samples that she used (25%). But after that, the wrong skewness problem disappeared from published empirical work. Indicatively, Bravo-Ureta et al. (2007) in a meta-regression analysis of 117 published empirical production SF papers, found that all of them had negative sample skewness. To our knowledge, from the paper of Mester in 1997 to today, namely in 25 years, a quarter of a century of intense publication of empirical papers using the SFM, the only studies that reported a wrong skewness problem in an empirical setup are Parmeter and Racine (2012) and Haschka and Wied (2022).

So, either the wrong skewness problem was a short-lived socio-economic phenomenon, perhaps a fin-de-siècle/mal-du-siècle aberration that disappeared with the onset of the new millennium, or, applied researchers, instead of implementing the various approaches and solutions that theorists kept publishing on the matter, kept abandoning these samples, resulting in the phenomenon being exorcised from the published scientific record. Since samples with the wrong skewness have a tangible probability of appearing by the laws of chance alone, we believe it is the latter case.

After reviewing the literature on both fronts, we embark on certain explorations of our own: we provide simulation evidence that the sample skewness will be “wrong” mostly when the noise error component is realized skewed, even if it comes from a symmetric population. In such cases it would have merit to specify the, theoretically symmetric but asymmetric in the sample, error component as, exactly, asymmetric, attempting with this tactic to “follow the sample” and separate the chance skewness that comes from v from the skewness that comes from u (and relates to inefficiency).

In Section 5 we examine more closely the statistical foundation of the Normal-Half Normal SFM, the Skew Normal distribution. The wrong skewness as a sample problem emerges when the relative strength of the inefficiency component is low. This brings us close to the neighborhood of values where the MLE for the Skew Normal has singular Hessian, and hence a non-standard behavior. This casts doubt on whether it is advisable to keep the original parametrization of the model, and we discuss two (similar) re-parametrization schemes that have been proposed. Section 6 catalogs open theoretical issues related to the wrong skewness problem, and Section 7 concludes with empirical guidance.

2 "Wrong skewness” as a property of the population

2.1 Skewness of inefficiency

What if the “wrong skewness” is not wrong? What if our sample represents faithfully the population’s skewness, as regards its sign? Can we have real-world economic structures where a production-data population has inefficiency and positive skew? Can we have a cost-data population that has inefficiency and negative skew?

We can. Consider a market that, for whatever reason but most likely due to heavy regulation or rigid barriers to entry (e.g. “closed professions”), is characterized by many and seriously inefficient firms. Then, the distribution of the non-negative inefficiency component in a production setting will exhibit negative skew: few firms will hover near the origin (zero inefficiency), while the majority will sit comfortably near higher positive values of inefficiency, although eventually the probability mass for very inefficient firms will go to zero. This creates a long tail for lower inefficiency values towards zero, a mode at some higher inefficiency level, and a steeper tail as we move even further from the origin. We have a high concentration of values to the right of the graph of the distribution, with a longer tail to the left: the skew of this distribution is negative. But since the inefficiency component enters with a minus sign in the composite production error term, the skew of the composite error itself will be positive in the population, while representing high inefficiency.³

This situation, which should be disheartening for any economist but nevertheless is occasionally observed in the real world, is exactly what Carree (2002) explored. He pointed out that there exist well-known distributions that are bounded from below at zero, and can exhibit negative skew (hence positive after the minus sign in front): for example the Binomial and the Weibull. Carree examined the SFM with Binomial inefficiency, and Tsionas (2007) formulated a panel-data SFM with Weibull inefficiency and a Bayesian approach to inference.⁴

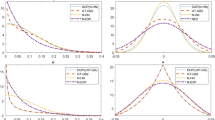
To visualize this, consider Fig. 1. In the left panel we plot the densities for the Half Normal (with parameter 1), Weibull, with shape parameter 5.5 and scale parameter 3, and a (scaled) Binomial with size 20 and probability 0.75.⁵ We see the classic positive skew for the Half Normal density but a negative skew for the specific parameterizations for the Binomial and the Weibull. It is clear for these two distributions that negative skew implies a large percentage of firms that are highly inefficient compared to those that are highly efficient (the opposite of the Half Normal implication).

Fig. 1

Density plots for u (left panel) and ε = v − u (right panel) for the Half Normal, Binomial and Weibull densities

The right panel of Fig. 1 displays the density of ε = v − u. Again, it is clear that the density of the convolution between v (here a Standard Normal) and u leads to densities that can have negative skew (Half Normal) or positive skew (Weibull/Binomial).

Carree (2002) mentioned that assuming a bounded support for a non-negative random variable (i.e. truncated also from above) can also lead to a distribution with a negative skewness, but he did not act on it. This happened some years later, when, towards the other market-structure extreme, Almanidis and Sickles (2011) and Almanidis et al. (2014) questioned the accuracy of using a distribution for the inefficiency component that has unbounded support to the right. They argued that inefficiencies which are too large will not be tolerated by the market and that the forces of competition will root out rather quickly grossly inefficient firms. Technically, this can be modeled if we truncate from above the distribution for the inefficiency component. Specifically, for technical inefficiency following the doubly-truncated Normal distribution, they showed that this may lead to negative skewness for u, and hence to a positive population skew for the composite production error.

We must note though, that, even under truncation, a negative skew of the inefficiency component reflects that inefficiencies tend towards the upper bound rather than zero. So while the “Bounded Inefficiency” approach with negative skew does not allow for long right tails and extreme inefficiencies, it shares with the previous approach the phenomenon of relatively high inefficiencies, which constitutes a conceptual internal conflict in the economic rationale and motivation of the model (that high inefficiency does not survive). It provides a picture of the market where highly inefficient firms may be non-existent, but the surviving ones tend towards the upper bound of “allowed” inefficiency. Although we should be realistically open to all sorts of situations in a market, it is perhaps more consistent to implement a Bounded Inefficiency model using distributions that retain a positive skew even under truncation, in which case, they stop being a structural rationalization of the wrong skewness problem.

2.2 Dependence and omitted variables

The approaches above proposed economic reasons why one of the standard assumptions of the SFM, positively skewed inefficiency, may not always be representative of the real world. Others questioned another standard assumption, again on economic grounds: that the components v and u of the composite error term are statistically independent. The earliest study to consider correlated error components is to our knowledge Pal and Sengupta (1999).⁶ Their economic motivation for the existence of intra-error dependence was the fact that “managerial decisions may be affected by natural factors such as climatic conditions which is a statistical noise”, but also misspecification in the form of omitted latent variables that may affect inefficiency (“personal bias, family norms and standards” as they write). These factors, being latent, are incorporated in the noise component v. They constructed a SFM where noise and efficiency followed jointly a bivariate correlated truncated Normal.

Smith (2008) also explored an SFM with intra-error dependence, mentioning the ever-present weather and seasonality in agriculture, but also the side-effects of a heavy-industry polluter on its own workforce due to uncontrolled spillage of hazardous materials, as a by-product of the production process. He employed a Copula to model dependence and join the marginal distributions, an approach that has also been adopted by, for example, El Mehdi and Hafner (2014), Bonanno et al. (2017), Sriboonchitta et al. (2017), as well as by Bonanno and Domma (2022). In the presence of dependence, the skewness of the composite error term can be either negative or positive, so again the “wrong” skewness may in reality be a population characteristic.

Papadopoulos (2021) returned to the omitted latent variables argument of Pal and Sengupta (1999) but now related directly to the sign of skewness, and for a more pressing issue: due usually to lack of data, we do not often include management as a distinct production factor (Alfred Marshall would frown disapprovingly, Paul Samuelson would sigh stoically). But management has a positive effect on output, and it may be stronger than the effect of the inefficiency component, resulting in positive skewness of the composite error term. The solution he proposes is to specify a two-tier stochastic frontier model for production, and treat management as a latent variable entering positively in the composite error. In this way, the composite error may have positive or negative population skewness, being the net result of the Tug-of-War between two opposing forces (management and inefficiency) that are estimated separately.

2.3 Asymmetry of the noise component

Bonanno et al. (2017) also innovated on another front: they relaxed the symmetry assumption of the noise component v. As economic motivation, they invoked a macroeconomic dynamic framework where macro-shocks affect the noise component of a production function, resulting in time-varying skewness. They implemented a statistical specification that allowed for either sign of skewness in the noise component, something that naturally allows for the composite error skewness to have any sign. Allowing the noise component to be skewed has also been recently explored by Badunenko and Henderson (2023) and Horrace et al. (2023) who develop SFMs where the noise component is, respectively Skew Normal and Asymmetric Laplace, while inefficiency is assumed to follow an Exponential distribution. Badunenko and Henderson (2023) mention many instances of economic activity where what is modeled as noise is expected and often found to be asymmetric: Asset pricing, risk management, banking, supply shocks, interest rate parity, education.⁷ We examine in more depth the issue of skewed noise in Section 4.

Based on all these structural explanations on why we may have inefficiency and “wrong” skewness, we cannot agree with Simar and Wilson (2009) when they write (p. 73), referring to the standard production SFM with pre-specified negative skewness, that “positively skewed residuals should not be taken as evidence that the model is misspecified.” They may very well be evidence of that, and it is the duty of the researcher to confront the matter. The critical and subtle issue is what kind of misspecification can we validly treat without inadvertently adopting methodologically questionable practices of “data mining”, and we turn next to this important issue.

3 Mine or mind the data? Navigating model specification

As we saw, there are many real-world economic situations that could lead to a population with both inefficiency and “wrong” skewness: high and widespread inefficiency, bounded inefficiency, heterogeneous inefficiency, intra-error dependence of noise and inefficiency, omitted positive forces, or even a causally skewed noise. It is difficult to argue then that the negative skewness for the production case (or the positive for the cost model case), should constitute the “anticipated” structural reality (and as we discussed earlier, the sample skewness in published SFA studies is rather unreliable as evidence). Even if it is eventually the case that statistically we observe more often negatively skewed production data (positively skewed cost data), nevertheless, if the obtained skewness is the “wrong” one, researchers should contemplate whether any or many of these situations may exist in their particular sample, making the sample skewness sign to match, after all, the population one. Only if they can argue against the structural plausibility of such occurrences (by knowing the particular market they are studying), it becomes valid to consider the obtained skewness sign as “wrong” and treat it as a sample problem. The simulations in Simar and Wilson (2009) indicating that there is a not-small probability that we may obtain the wrong skewness purely by the laws of chance, cannot be used as an argument to skip the structural discussion: if say, there is a 20% chance to get the wrong skewness by chance, this means that there is an 80% chance that the sign of the sample skewness is faithful to the population, a four-times-higher probability. The core arguments for treating the sample skewness as wrong should be economic, with the statistical laws being supportive to them, not the other way around.

But we could also realize that the population we examine through a sample may have the skewness sign that the sample says it does. In such a case, we could implement any of the models presented in the previous section.

In a conference presentation of this study, concerns were raised that such an approach, where we estimate through OLS the sample skewness and then we may change our intended model accordingly, is an instance of “data mining” and should be avoided.⁸ We have the following thoughts on the matter, drawing from Leamer (1974, 1978, 1983), Aris Spanos on data mining, Spanos (2000), and the still very stimulating (actual) conversation on econometric methodology between David Hendry and Edward Leamer, hosted by Dale Poirier, (Hendry et al.1990, HLP1990 thereafter).

Taking ideas from the data is the most natural thing to do in scientific exploration. Heckman and Singer (2017), in their advocacy for “abducting" empirical economic analysis, appear to have just encountered a wrong skewness case when they write, “Abduction is the process of generating and revising models, hypotheses, and data analyzed in response to surprising findings." (our emphasis) A wrong skewness sign in a stochastic frontier model is indeed a “surprise", given our predominant preconceptions. Exploring and responding to it is not at all equivalent to fiddling with data in order to extract support for a priori anticipations. As is the case with detected sample patterns, correlations and associations, so is with other sample characteristics, which may be detected but be spurious in the end (“fiction”, as Almanidis and Sickles 2011 put it). But as Spanos writes (p. 248), “any empirical regression that survives a thorough misspecification testing (…) is worth another theoretical look (is there a theory justification for such a correlation?) because it captures something that appears to persist and is invariant over the whole of the sample period.”

Building a model that aligns with the statistical aspects of the data can not be considered a questionable approach. Spanos states the obvious when he writes (p. 236), “If an estimated model is going to be used for any form of statistical inference, its statistical adequacy is what ensures the reliability of the overall inference”, where “statistical adequacy” is understood as (p. 262) “capturing all the statistical systematic information in the observed data.” Hardly an unimportant desideratum. As Hendry says (HLP1990, p. 193) “(…) there are instances where empirical work has changed how economists think about the world, and these are then built into later thinking. Inflation effects in the consumption function are a classic case in Britain, since once they were added to the large macro models, many of the multipliers changed sign, prompting theoretical rethinking as well as further empirical testing.” Ah, the issue of sign again…In pp. 210-211 of HLP1990, discussing Leamer’s three phases of empirical research, planning, criticism, revision, and what would constitute a “genuine criticism” (that would lead to a revision of the model), the following illuminating dialogue unfolds:

• Leamer: I think wrong signs can make you upset…

• Hendry: I can’t accept that phraseology. A “wrong sign” is a wrong notion. There we disagree. There are only wrong interpretations. The coefficient must have the sign it’s got: you are misinterpreting the sign.

• Leamer: I think of the plan as being contingent on the choice of the sampling distribution and the choice of prior. What you seem to be saying is that a wrong sign forces you to rethink your prior and thus to alter your plan.

• Hendry: No, I would say you are misinterpreting the sign.

• Leamer: “Misinterpreting” means that you had the wrong prior.

• Hendry: “Misinterpreting” means you have the wrong theory.

• Leamer: Then, I’m not sure I understand what you mean.

• Hendry: To form a theory of how the world works, a conjecture when you approach data, is something that all of us do. You can call it beliefs or you can call it priors etc., although I think there is a distinction between the theory one is using and a prior distribution over the parameters of that theory. We may have no idea whether an entity is going to be positive or negative, in which case there would be no misinterpretation.

Apart from detecting the usual semantic hurdles that people face when they try to understand each other, it is clear that both scholars consider the existence of a wrong sign as a serious matter that should be treated with the appropriate deliberation, and not as something that could be summarily dismissed as an unfortunate incident that has no true relation to the real-world phenomenon that we study. We note that this is the same Edward Leamer that has offered us the tour-de-force on the dangers and the consequences of data-mining, “Specification Searches: Ad Hoc Inference with Nonexperimental Data” (Leamer 1978), always a recommended reading. Our case would fall in the category of “data-instigated models” (his ch. 9, which is largely based on Leamer 1974). But there, Leamer is almost exclusively concerned with the selection of regressors. Adopting the Bayesian view of Leamer, we ask, why our priors include a negative error skewness in a production SFM? If they do because we have thought about the market we are studying, and we have excluded the structural possibilities presented in the previous section, then we are justified in treating a positive sample skewness as “wrong”, and decide our next steps based on that. But if the intention to specify a likelihood with negative skewness does not involve some conscious structural arguments from our part, then, it would appear, in reality we “have no idea whether an entity is going to be positive or negative” as Hendry put it, and so, in order to reflect our situation in our modeling we should specify a likelihood unconstrained as regards the direction of the skewness and let the data decide. Alternatively, running an initial OLS regression to obtain the sample skewness, is not done to dictate how we should proceed with our likelihood, but to inform us on what we are facing: to push this to the extreme, if in a production data set we obtain negative sample skewness, we should also worry if the population skew is positive (for any of the reasons presented in Section 2) and so have a “wrong skewness problem” in our hands, even if the sign of sample skewness is the “traditionally anticipated” one. Leamer (1983) himself expands his beloved “Sherlock Holmes” parable to present what the true dangers are. Quoting, (pp. 317-318).

In response to a question from Dr. Watson concerning the likely perpetrators of the crime, Sherlock Holmes replied “No data yet…It is a capital mistake to theorize before you have all the evidence. It biases the judgments”. Were Arthur Conan Doyle trained as a theoretical statistician, he might have had Watson poised to reveal various facts about the crime, with Holmes admonishing: “No theories yet…It is a capital mistake to view the facts before you have all the theories. It biases the judgments.”

Each of these quotations has a certain appeal. The first warns against placing excessive confidence in the completeness of any set of theories and suggests that over-confidence is a consequence of excessive theorizing before the facts are examined. The second quotation, on the other hand, points to the problem which data-instigated theories necessarily entail. Theories which are constructed to explain the given facts, cannot at the same time be said to be supported by these facts.

What we have tried to make clear earlier, is that we do not argue that our theory about what happens in the market we study should follow the data blindly, the sign of the sample skewness in our case. A positive skewness in a production data set should not automatically mean zero-inefficiency or a sample problem, but neither should it mean, automatically, that some idiosyncratic structural characteristic is present in the population that creates positive skewness in the presence of inefficiency. We do not construct a theory to explain the data, our case is not one of “double-duty” for the data or “observations in search of hypotheses”, as Leamer (1978, p. 285) puts it. We do not contemplate filtering out “nasty" observations, or changing regressors/controls, or the mathematical expression for the frontier function (from, say, Cobb-Douglas to Translog). What we desire is statistical adequacy of the model in the sense of Spanos. The model we started with is a regression equation estimated by ordinary least squares. No distributional assumptions are involved in obtaining the estimated skewness of the residuals. What we do is let the data have a say on the specific matter, not necessarily the final say.

The reason why we desire to have a statistically adequate model, is in order to arrive at a characterization of our sample as being representative of the population. Because, suppose now that we have obtained a sample skewness that we honestly consider wrong, after performing our due diligence. Then another hurdle is awaiting us: in what sense is it meaningful to proceed with the sample at hand, since we ourselves have concluded that it is not representative of the population in that respect?

In a series of papers, Kruskal and Mosteller (1979a, b, c, 1980) conducted a wide review of both the statistical and not-statistical scientific but also non-scientific literature, and identified no less than nine variants as regards the meaning of the concept “representative sampling”: in order of appearance in their papers they are, (1) generalized if unjustified acclaim for data, (2) absence of selective forces, (3) miniature of the population, (4) typical or ideal case or cases, (5) coverage of the population, (6) a vague term to be made precise, (7) representative sampling as a specific sampling method, (8) as permitting good estimation, or (9) good enough for a particular purpose.

It is difficult to include a sample having the sign of the empirical skewness opposite to the population’s in any of these categories, and so accept it as “representative". Note that the last category (Kruskal and Mosteller 1979c), “good enough for a particular purpose” refers to situations where the question to be answered by the data is things like mere existence, order-of-magnitude, ballpark estimates and the like, so perhaps a more accurate label would be “good enough for a not very ambitious or demanding purpose”. But asking that the sample gets the sign of skewness right cannot be considered as very demanding, especially since we are talking about the skew of OLS residuals: there is no distributional misspecification to contribute to the result and the residual is the linear projection error for the specific set of regressors used.

So, if we do think that the sign of the sample skewness is wrong, we must treat our sample as partly non-representative. Thankfully, scholars have come up with a menu of different ways to proceed with a sample that does indeed have the wrong skewness, and we now turn to present them. These are methods to conduct valid estimation and inference with a non-representative sample, something that should attract the attention of statisticians and econometricians in general, not just researchers in stochastic frontier analysis.

4 "Wrong skewness” as a property of the sample

There are constructs with plausible natural assumptions that lead to statistical distributions for the inefficiency term that have positive skewness (leading to negative skewness of the composite error term). Torii (1992) presents two such constructs. The first is based on “capital vintage”, and the inefficiency resulting from technological progress and non-immediate replacement of fixed assets inside each decision-making unit. The second construct assumes that inefficiency is due to the incompleteness of managerial control. Here the “management effort” to mitigate inefficiency will be distributed Half Normal or Exponential depending on whether this effort is statistically correlated with the level of inefficiency (leading to the Half Normal), or not. Correlation would indicate a more proactive management, while a less proactive management maps intuitively to the “absent-minded” Exponential distribution. Kuosmanen and Fosgerau (2009) present another managerial narrative that leads to a distribution of inefficiency with positive skewness.

So we do have economic arguments to support this approach, in which case, facing a sample that has the wrong skewness may indicate a non-representative composition, while it can also be helped by a population characteristic: low population inefficiency-low skewness combined with the laws of chance. The sample skew is a random variable and it can take negative and positive values, so there is always non-zero probability that it will fall on the wrong side of zero. And the closer to zero is the value of the population skew, the more probable this becomes.

There are different structural economic scenarios that may lead to low skewness. Consider for example an emerging market for a new product: inefficiency may still be high as firms are at the first stages of their learning curves, but noise and uncertainty are expected to also be high, in an unsettled market with consumers being also at the first stages of their learning curves. This may lead to a low signal-to-noise ratio (ratio of standard deviations between inefficiency and noise) and low skewness for the composite error. In a totally different setup, we may observe low skewness due to low inefficiency in mature markets with thin profit margins: here, efficiency is an acute matter of survival. This case has been formalized in the “zero-inefficiency” model of Kumbhakar et al. (2013), where a proportion of firms have “zero” (negligible) inefficiency, while the rest have low inefficiency. Nevertheless, this is not a model to handle a wrong skewness situation, since its likelihood pre-assigns a negative skew. But the wrong skewness can just be a chance event, as the simulations of Simar and Wilson (2009) indicated, for which we will provide further evidence in a while.

So we see that, as there are valid reasons to contemplate the case of the “wrong skewness” as actually being a population characteristic, there are also reasons that support the position that the sample skewness has the opposite sign of the population skewness. What we advocate here is that researchers should face the issue transparently and argue why they adopt one or the other interpretation.

4.1 Approaches to migrate from wrong skew

Simar and Wilson (2009), after showing that the sample skewness may have the wrong sign by chance alone, proposed three different ways to conduct valid inference in the presence of it: first, in order to construct prediction intervals, they propose a “bagging” procedure (bootstrapping and aggregating on predictors), or alternatively a method to obtain bootstrap-adjusted interval estimates. For confidence intervals they construct a parametric bootstrap algorithm. They present simulations that support the improved performance of their algorithms against conventional methodologies.

Hafner et al. (2018) proposed another approach, by extending the density of the model: they create the extension by mirroring the density onto the negative axis by reflecting it at zero, and they truncate and shift it so that it has a non-negative support (while also being bounded from above). The novelty here is that the manner in which the density is reflected is such that regardless of the sign of the skewness, the density has the same mean. Why does this matter? Given the focus on the Half-Normal distribution, being a single parameter density, the mean is itself enough to identify said parameter. This implies that the mirrored density can circumvent issues pertaining to the sign of the skewness in identifying the parameters of the inefficiency distribution.

The elegance of this approach is that it retains the standard distributional assumptions commonly invoked by applied researchers, but manipulates the density of inefficiency in such a way that guarantees that the sign of skewness no longer plays the key role in identifying the model. An unfortunate side-effect of this manipulation of the underlying density is that one can no longer use standard formulae and statistical software to estimate the model. The authors point out the similarities with Almanidis and Sickles (2011) and Almanidis et al. (2014). They establish the asymptotic properties of the corrected OLS and maximum likelihood estimators corresponding to this new density, and provide the expressions for predicting technical efficiency when inefficiency is distributed either Half Normal or Exponential. They also derive a likelihood-ratio test for the symmetry of the composite error term.

Cai et al. (2021) pushed the view that the wrong skewness is a finite sample problem to its logical decision-making consequences, in order to get the job done: if it is, then force the estimator to “ignore” it. They proposed estimating the stochastic frontier model by imposing a (linearized) inequality constraint on the skewness sign of the residuals (either in a COLS or an MLE framework), the forbidden sign depending on whether one estimates a production or a cost model. Such a constraint requires a numerical bound away from zero. Naturally the size of this bound will impact the estimator, for in any scenario where the wrong skew arises, the constrained MLE for the variance parameter of inefficiency will be set equal to this bound. An interesting feature of incorporation of the constraint is that it leads locally to the same behavior as found by Waldman (1982). That is, in an area of the parameter space near the OLS estimates, the constraint binds.

For maximum likelihood Cai et al. (2021) suggested using a Bayesian Information Criterion to optimally determine the bound’s value, while for COLS, a criterion based on the residual sum of squares (similar to Mallow’s C_p). Their simulations indicated that these criteria work well. However the bound is selected, the intuition is quite simple: when confronted with wrong skew and the belief that the empirical model is correctly specified, the researcher simply replaces the 0 estimate for the variance parameter from the Half Normal distribution with a small number. It is the selection of this small number where all the statistical interest lies, but the switch is what matters for practice. Our exposition here is a bit more simplified that what is proposed by the authors. This is because we do not keep all of the original maximum likelihood estimates (read OLS) and simply replace the 0 value with some other number. The constraint in some sense prevents the local (global?) optima that is OLS from being reached and so all of the parameter estimates are likely to differ to some extent.

An important feature of the constrained MLE/COLS approach adopted by Cai et al. (2021) is that the bound on the constraint is not an interesting model parameter. In fact, it is not a parameter at all. It is simply a device that allows one to circumvent wrong skewness when one believes that the model is correctly specified.

Zhao and Parmeter (2022) and Parmeter and Zhao (2023), in a similar fashion as both Hafner et al. (2018) and Cai et al. (2021), attempted to by-pass wrong skewness but do so using a slightly different approach that does not require modifications to the density or the selection of a lower bound on a constraint. The idea in both of their papers (one being MLE and the other COLS), is to solve the model (or place constraints on the model) based on the expected value of the absolute value of the composite error. That is, whereas Hafner et al. (2018) constructed a density that no longer requires skewness to identify key parameters and Cai et al. (2021) constrained the skewness, Zhao and Parmeter (2022) and Parmeter and Zhao (2023) used a different moment condition altogether. As it turns out, use of this moment condition, either in MLE or COLS, requires nonlinear techniques, but reduces quite dramatically the occurrence of “Type I failures” (but does not completely eliminate their occurrence). That is, the use of this moment, E[∣ε∣], does not guarantee that wrong skewness is eschewed as in Hafner et al. (2018), but it also does not require a fundamental change to the shape of the density while it drastically lessens the occurrence of the issue. In the MLE case, use of E[∣ε∣] as a constraint is independent of any tolerances (as in Cai et al. 2021) and again dramatically lowers the occurrence of wrong skewness (but does not completely eliminate it). The constraints that Zhao and Parmeter (2022) required are

$$E\left[| {\varepsilon }_{i}| \right]=\sigma \sqrt{2/\pi },\quad \frac{{\left(E\left[| {\varepsilon }_{i}| \right]\right)}^{2}}{Var\left({\varepsilon }_{i}\right)}=\frac{2(1+{\lambda }^{2})}{\pi +(\pi -2){\lambda }^{2}}.$$

(2)

These moment constraints are entirely consistent with the Normal-Half Normal distributional assumptions.⁹

4.2 Blame it on the noise

One thing these articles did not explore in detail is what must happen so that we obtain a sample that has the sign of the empirical skewness opposite to the population sign. In Table 1 we present the results from a simulation to indicate that perhaps “the noise is to blame”: that the noise component of the composite error term is realized skewed in the sample, not because it is skewed in the population, but because symmetry is a fragile property, and not easy to achieve in a finite sample.

Table 1 $\Pr \left[{\widehat{\gamma }}_{1}(v)\, >\, 0| {\widehat{\gamma }}_{1}(\varepsilon )\, >\, 0\right]$. σ_v = 1

We draw from a Normal-Half Normal distribution with negative skewness. The table shows the empirical probability of having a positively skewed realized sample of the Normal variate given that the sample skewness of the composite error term is estimated as positive. We see that there is a very high probability that the two will happen together. To connect with Simar and Wilson (2009) simulations, for λ² = 0.5 and n = 1000 the probability they report of obtaining by chance a sample skew with sign opposite to that of the population is 0.22. Our results say that in these 22 in 100 cases, 94% of the time the noise component has been realized as positively skewed. So we are bound to obtain a chance wrong skewness in our samples not infrequently.

This provides a motive to specify the noise component so as to allow for skewness, even if it is symmetric in the population: this is deliberate “misspecification” in order to “follow the sample” and be able to separate the chance skewness from the skewness coming from the inefficiency. We should implement a density that nests the symmetric case so that we do not create inconsistency. As already mentioned, Badunenko and Henderson (2023) and Horrace et al. (2023) explored models with Skew Normal and Asymmetric Laplace noise, respectively, and Exponential inefficiency. Tsionas (2020) built a model with Asymmetric Laplace noise and Half Normal inefficiency, although only in a Bayesian framework. Wei et al. (2021) proposed the Extended Skew Normal for the noise component, coupled with Half Normal inefficiency.¹⁰ Finally, Zhu et al. (2022) combined dependence and noise skewness, and proposed modeling the composite error term as a multivariate Skew Normal distribution, where noise and inefficiency are allowed to be dependent, and both are marginally Skew Normals.

We see that modeling the noise component as skewed can serve two masters, becoming an agnostic escape: whether we think the wrong skewness is a population characteristic or a sample failure, it can accommodate both situations. But the approach is not without dangers: in certain cases we may have complete loss of parameter identification, and also, statistical power may suffer.¹¹

Finally, it is conceivable that the wrong skewness emerged because the noise error component was realized as skewed in the sample, while at the same time inefficiency is “zero". Modeling the error term as skewed, this situation should be uncovered through a very low estimate for the mean/scale parameters of the inefficiency component.

5 Maximum likelihood with wrong or low skewness

We have mentioned in the beginning that Waldman (1982) proved that in the standard SFM production model with Normal noise and Half Normal inefficiency (and so a Skew Normal composite error with imposed negative skew), the maximum likelihood estimate of inefficiency will be the value zero when the skewness of the OLS residuals is positive. Some other papers explored this topic further. Rho and Schmidt (2015) found that this result also holds in the “zero-inefficiency” model of Kumbhakar et al. (2013) where a proportion of firms are fully efficient. Horrace and Wright (2020) showed that the result holds even more generally. Cho and Schmidt (2020) qualified the result, showing that when “environmental variables” are used to model the scale parameter of inefficiency, this stationary point is in general neither a minimum nor a maximum.

That the MLE formally estimates inefficiency as being zero when we have “wrong skewness”, does not make it a good estimate for what holds in the data. On the contrary this is an artificial result that comes about due to the constraint on the direction of skewness. Consider turning into a log-likelihood the unconstrained Skew Normal density

$${g}_{\varepsilon }(\varepsilon )=\frac{2}{\sigma }\phi (\varepsilon /\sigma ){{{\rm{{{\Phi }}}}}}(\lambda \varepsilon /\sigma ),\ \ \ \sigma \,>\, 0,\ \ \ \lambda \in {\mathbb{R}}.$$

(3)

Here, ϕ is the standard Normal density and Φ the corresponding distribution function.

The profile log-likelihood with respect to λ (with fixed sample and fixed σ) is unimodal, with the mode at the value that reflects the data at hand. So if the data dictates a positive value for λ, by disallowing these values, the part of the likelihood that remains is monotonic, and so has a maximum at the value λ = 0. We present such a case in Fig. 2. For simplicity, we have generated a sample of size n = 1000 from v + u, where v is zero-mean Normal with σ_v = 1 and u is Half-Normal with σ_u = 3. This behaves as a v − u convolution with u having negative skewness. We fixed σ, and used the sample to compute the average profile log-likelihood for different values of λ. By design this sample has positive skewness, so the mode lies on the dotted part of the graph. Suppose that it was presented to us as a production data sample. If we tried to fit a Skew Normal with imposed negative skewness, we would allow only the solid part of the graph of the profile likelihood, while the dotted part would not be permitted. Hence, the value λ = 0 becomes necessarily the maximum, since the log-likelihood is monotonic as it approaches the maximum that is consistent with the sample.

Fig. 2

Profile log-likelihood for skewness parameter λ

In light of these remarks another idea arises in order to deal with “wrong skewness” in the Normal-Half Normal (Skew Normal) SFM, when we do believe that it is wrong, an idea that is simpler to the approaches presented earlier: could we perhaps “follow the sample” just by specifying a Skew Normal likelihood with unconstrained skewness sign, and taking the obtained estimate while ignoring its sign? Note that this encompasses another possible idea, to specify a Skew Normal likelihood with imposed positive skewness, since this constraint will not be binding. There are three issues with this approach.

First, one cannot help but notice the very flat likelihood in Fig. 2. Although a mode does exist, locating it with accuracy is bound to be difficult (and this graph comes from a sample size of n = 1000). This weak identification issue is reminiscent of the findings in Canale (2011) for the Extended Skew Normal that we have mentioned earlier.

Second, if the sample skewness is wrong because the noise component v has been realized as skewed while it is symmetric in the population, then it will have a positive sample 3rd cumulant κ₃(v). Chiogna (2005) has shown that an approximate expression for the MLE of λ is

$$\widehat{\lambda }\approx {{{\rm{sgn}}}}\{{\kappa }_{3}(\varepsilon )\}\cdot \frac{{\left\vert {\kappa }_{3}(\varepsilon )\right\vert }^{1/3}}{{c}_{\lambda }\cdot \sqrt{{\kappa }_{2}(\varepsilon )}},\qquad {c}_{\lambda }\approx 0.6018.$$

(4)

In the production SFM and under independence of v and u, we have κ₃(ε) = κ₃(v) − κ₃(u). Under wrong skewness (“WS”), ${\kappa }_{3}^{{{{\rm{WS}}}}}(v)\, >\, {\kappa }_{3}(u)\, > \,0$, while if the sample is representative ("R") of the population in that respect, we expect ${\kappa }_{3}^{{{{\rm{R}}}}}(v)\approx 0$. Taking the ratio of the estimates in the two situations, we have (ignoring the sign and canceling out the denominators)

$$\frac{{\widehat{\lambda }}^{{{{\rm{WS}}}}}}{{\widehat{\lambda }}^{{{{\rm{R}}}}}}\approx {\left\vert \frac{{\kappa }_{3}^{{{{\rm{WS}}}}}(v)-{\kappa }_{3}(u)}{{\kappa }_{3}(u)}\right\vert }^{1/3}={\left\vert \frac{{\kappa }_{3}^{{{{\rm{WS}}}}}(v)}{{\kappa }_{3}(u)}-1\right\vert }^{1/3}.$$

(5)

From this we obtain

$$\begin{array}{ll}0 \,<\, {\kappa }_{3}(u) \,<\, {\kappa }_{3}^{{{{\rm{WS}}}}}(v)\, <\, 2{\kappa }_{3}(u)&\ \Rightarrow \ {\widehat{\lambda }}^{{{{\rm{WS}}}}}\, < \,{\widehat{\lambda }}^{{{{\rm{R}}}}}\\ 0 \,< \,2{\kappa }_{3}(u)\, < \,{\kappa }_{3}^{{{{\rm{WS}}}}}(v)&\ \Rightarrow \ {\widehat{\lambda }}^{{{{\rm{WS}}}}}\, > \,{\widehat{\lambda }}^{{{{\rm{R}}}}}.\end{array}$$

(6)

If the sample 3rd cumulant of the noise is smaller than double the 3rd cumulant of inefficiency, the MLE of λ will be smaller than what we would have obtained under correct skewness. If it is higher, we will get a larger estimate. This shows that the possible sign switch in the sample from the population is not accompanied by a full “mirroring” property: it is not like we have the mirror image of a sample that would be representative of the population. Therefore, “trusting the magnitude and ignoring the sign” is not justified.

A third danger when using the unconstrained Skew Normal log-likelihood is that it has a singular Hessian when λ = 0. This is an example of a more general result to be found in Catchpole and Morgan (1997), where an Exponential-family model is “parameter redundant” if the mean can be expressed using a reduced number of parameters –and then the information matrix becomes singular. This implies that we cannot just say “by specifying the Skew Normal we nest the zero-inefficiency case.” We do, as regards the mathematics, but as regards statistical inference we would have to deal with the rather complicated topic of maximum likelihood estimation under such a singularity.¹² But also, when λ = 0, the distribution of the MLE is bimodal, with one positive and one negative mode. This has been formally derived by Chiogna (2005),

$${n}^{1/6}\,\widehat{\lambda }{\to }_{d}{Z}^{1/3},\qquad Z \sim N(0,{\sigma }_{z}^{2}),$$

(7)

where ${\sigma }_{z}^{2}$ is some complicated expression (and irrelevant to our discussion here). It follows that the approximate distribution of $\widehat{\lambda }$ in finite samples has density

$${g}_{{\lambda },n}(\widehat{\lambda })\,=\,\frac{3{\widehat{\lambda }}^{2}}{\sqrt{(2\pi )({\sigma }_{z}^{2}/n)}}\exp \left\{-\frac{1}{2}\frac{{\widehat{\lambda }}^{6}}{({\sigma }_{z}^{2}/n)}\right\}.$$

(8)

This density is symmetric around zero and bimodal, the modes being located at

$${\widehat{\lambda }}^{* }=\pm {\left(\frac{2{\sigma }_{z}^{2}}{3n}\right)}^{1/6}.$$

(9)

Although the case λ = 0 should not be expected to hold in any real-world data (zero-inefficiency is a Platonic ideal), Azzalini and Capitanio (2014) have shown through indicative simulations (pp. 68-70) that due to the slow convergence rate, O(n^−1/6), of $\widehat{\lambda }$, this bimodality persists even when λ = 1.

A solution to these issues is to reparametrize the model. The reparametrization (“centred” as the authors called it) was already mentioned in Azzalini (1985), and formally derived in Azzalini and Capitanio (1999a) (see Azzalini and Capitanio (1999b) for the full version). The reparametrization amounts to centering the error term (making it zero-mean), and also, to estimate the skewness coefficient γ₁ instead of the skewness parameter λ. As the authors report, the reparametrization removes the singularity of the information matrix, lessens the correlation between the estimated parameters, and improves the curvature of the log-likelihood.¹³

Lee (1993) investigated a slightly different transformation specifically for the SFM, where the error term is again centered, but the skewness parameter λ is retained. That this simpler transformation works, shows (as was pointed out in Azzalini and Capitanio 2014, p. 59) that in a regression setup the practical cause of the singularity when λ = 0 is the existence of the constant term of the regression, since then the related elements of the gradient of the log-likelihood become linearly dependent. In order to obtain the full production frontier, centering should be reversed after estimation.

Finally, as reparametrizations go, we could invoke the invariance property of the MLE and estimate ξ ≡ λ³, writing the related part of the density as Φ(ξ^1/3ε/σ) which would result in a first-order condition with respect to ξ,

$$\frac{1}{{\xi }^{2/3}}\frac{1}{3\sigma }\mathop{\sum }\limits_{i=1}^{n}\frac{\phi \left({\xi }^{1/3}{\varepsilon }_{i}/\sigma \right)}{{{\Phi }}\left({\xi }^{1/3}{\varepsilon }_{i}/\sigma \right)}{\varepsilon }_{i}=0.$$

(10)

Looking at the asymptotic distribution of $\widehat{\lambda }$ in Equation (7), one would expect $\widehat{\xi }$ to have the usual convergence rate. Moreover, its presence in the denominator of the first-order condition for the log-likelihood would make the estimator more sensitive to values near zero.

6 Open theoretical issues

We have focused on examining the wrong skewness problem in relation to a production setting (essentially covering its dual partner, the cost framework, as well), which are the traditional topics of stochastic frontier analysis. But frontiers arise in other situations, and SF models have been applied to cases of “investment efficiency” where financing constraints operate as the inefficiency force (Wang 2003), inefficiency in energy use (Filippini and Hunt 2011), and entry deterrence due to regulation and the resulting inefficiency (Orea 2012). Thinking about how “wrong skewness” could arise in such situations as a population characteristic could reveal interesting structural aspects that do not coincide with those operating in production and cost matters.

Moving to the other line of thought, if one treats wrong skewness as a case of sample failure, the “zero-inefficiency” model of Kumbhakar et al. (2013) could possibly be used as a device to single out the observations that cause the problem. Here, the firms deemed to be fully efficient could be the culprits for the problem. Certainly, even if it could be shown to be a valid approach from a technical point of view, the question would remain: should we do something with the suspected observations, or would that be unacceptable data-tampering?

In a similar vein, treating wrong skewness as a sample failure, one could predict the noise error component following Papadopoulos (2023), and look at the observations with high positive predicted noise error component as those that drive the wrong skewness result (in a production setting). Or, using a result proven in Papadopoulos and Parmeter (2022), that a large composite error most likely has a high realization of the noise component and low inefficiency component, one could look at the OLS residuals and examine more closely what happens with those observations that have a high positive residual. These are possibly simple diagnostic methods, that nevertheless require proper examination and auditing before being proposed as applied tools.

One topic that could see further exploration is the impact that “determinants of inefficiency” have on the wrong skewness case. As Cho and Schmidt (2020) note, there is a wrong skewness type issue that arises when determinants of inefficiency are present, but it is different. In this case no identification issue may arise. And therein lies the rub. Part of the wrong skewness issue that has plagued researchers going back to the origins of SFA is that this is an exercise in deconvolution, and deconvolution is hard. When we add additional information, such as the presence of determinants, this helps to lessen the burden of deconvolution. These matters could be explored further.

Finally, recently there has been some interest in examining wrong skewness in more advanced stochastic frontier models (endogeneity, panel data, spatial error components). A common strategy has been to use one of the approaches discussed in Section 4 that help to mediate or circumvent the need for positive skewness to identify the model. However, these lines of research are still nascent. Whereas in the cross-sectional setting Waldman (1982) demonstrated precisely that OLS is MLE when the skewness of the OLS residuals is of the wrong sign, no such results exist in these more advanced settings. In Greene (2005)’s True Fixed Effects model, is LSDV equal to MLE when the skewness of the LSDV residuals is of the wrong sign? In Amsler et al. (2016)’s setting where there is endogeneity, is IV equal to MLE when the skewness of the IV residuals is of the wrong sign? The answers to these questions remain unknown at the moment and proposals advocating for some type of insulation to wrong skewness are solutions in search of an as yet unidentified problem.

7 Empirical guidance

Theoretical explorations aside, the main and forceful conclusion of this review for empirical research is that the existence of inefficiency is not equivalent to a specific sign of the population skewness. This has important consequences and we next list the resulting steps one should take in an empirical study:

• 1. Run an OLS regression and obtain the sign of the residual skewness.

• 2. If the sign is the opposite of your a priori expectations, contemplate on the market you are studying, its characteristics and possible peculiarities.

• 3. Based on 2., formulate your arguments and decide as to whether this “wrong skewness" is a population characteristic or indicates a failure of your sample to be representative of the population in that respect.

• 4. If you have concluded that the “wrong" sign in the OLS residuals has a valid structural/economic interpretation and so it is a population characteristic, proceed to adjust the statistical aspects of the econometric model in order for it to reflect the features of the data and become statistically adequate, applying one of the models presented in Section 2 (or any newer contribution that may appear).

• 5. If you have concluded that the wrong skewness sign is indeed wrong and a case of the sample failing to be representative, choose a method to do valid estimation and inference from those presented in Section 4 (or any newer approach that may appear).

• 6. Evidently, report all these in your study, laying down your arguments as to why you have chosen one or the other interpretation and the associated estimation model and method. Certainly do not just silently reject the sample and go hunting for another one, as it appears to have been the dominant choice up to now.