1 Introduction

The basic formulation of a production stochastic frontier (SF) modelFootnote 1 can be expressed as \(y = f\left( {x;\beta } \right){e^{\cal E}}\), where y is the firm production, x is a vector of inputs; β is vector of unknown parameters. The error term, \({\cal E} = V - U\), is assumed to be made of two statistically independent components, a positive random variable, denoted by U, and a symmetric random variable, denoted by V. U reflects the difference between the observed value of y and the frontier and can be interpreted as a measure of firms’ inefficiency, while V captures random shocks, measurement errors and other statistical noise.

One major difficulty analysts often face when estimating an SF model is related to the choice of the distributions of the random variables U and V. Different combinations have been proposed, including the normal—half-normal model (Aigner et al.1977; Battese and Corra1977), the normal—exponential model (Meeusen and van denBroek1977), the normal—truncated normal model (Stevenson 1980), and the normal—Gamma model (Greene 1990; Stevenson 1980). Perhaps the range of alternatives has been so far limited by computational challenges due to issues about the tractability of taking the convolution of the two error components. The choice of distributional specification is sometimes a matter of computational convenience.

The limited alternatives for the possible distributions also poses empirical challenges. For instance, several authors have addressed the problem related to the observed difference between the expected and the estimated sign of the asymmetry of the composite error. Specifically, for the standard SF model, the third central moment of \({\cal E}\) is

$$ E\{ [ {\cal E} - E( {\cal E} ) ]^3 \} = - E\{ [ U - E(U) ]^3\},$$
(1)

thereby meaning, for example, that a positive skewness for the inefficiency term U implies an expected negative skewness for the composite error \({\cal E}\). However, in many applications, the residuals yield the wrong sign. This is called in the literature the wrong skewness phenomenon in SF models, initially pointed out by Green and Mayes (1991). In SF models, this phenomenon is important because it implies that the estimated variance of the inefficiency component is zero with positive probability. This, in turn, causes the inefficiency scores to be zero.

To overcome this problem, several authors have proposed the use, for the inefficiency component, of distribution functions with negative asymmetry. In particular, Carree (2002) uses the binomial probability function, Tsionas (2007) suggests the Weibull distribution whilst Qian and Sickles (2009),Almanidis and Sickles (2011) and Almanidis et al. (2014) consider a double truncated normal distribution.

More recent attempts to obtain the desired direction of the residual skewness are Feng et al. (2015), where the authors propose a finite sample adjustment to the existing estimators, and Hafner et al. (2016), where the authors propose a new approach to the problem by generalizing the distribution used for the inefficiency variable.

In this paper we argue that the wrong skewness problem has been only partially addressed because the relation described by Eq. (1), and the consequent discussion of the wrong skewness anomaly, is a direct consequence of all the assumptions underlying the specification of the basic formulation of an SF model. In fact, in a more general framework, where we relax the hypothesis of symmetry for V, of positive skewness for U, and of independence between U and V, after simple but tedious algebra, the third central moment of the composite error turns out to beFootnote 2

$$E\{[{\cal E} - E( {\cal E} )]^3\} = - E\{ [ U - E( U ) ]^3 \} + E\{ [ V - E( V ) ]^3 \}\kern2pc \\ + 3Cov( {U^2},V ) - 3Cov( U,{V^2}) - 6[ E( U ) - E( V ) ]Cov( U,V). $$
(2)

From Eq. (2), it is clear that the sign of the asymmetry of U and V and the dependence between U and V both affect the expected sign of the asymmetry of the composite error.

In order to take into account the different sources affecting the asymmetry of the composite error, in this paper we propose a very flexible specification of the SF model, introducing skewness in the random error V through a distribution whose shape can be asymmetric negative, positive, or symmetrical, depending on the value of one of its parameters, and the dependence between the two error components U and V. The dependence structure is modeled with a copula function that allows us to specify the joint distribution with different marginal probability density functions. Moreover, we use a copula function able to model positive or negative dependence, and the special case of independence, depending on the value of a dependence parameter.

In some special cases, the convolution between the two error components admits a semi-closed expression also in cases of statistical dependence between U and V. An example is provided in Smith (2008), who uses FGM copulas to relax the assumption of the independence of the two error terms. In a basic economic setting and with simple marginal distribution, Smith (2008) points out that the introduction of a statistical dependence between the two error terms may have a substantial impact on the estimated efficiency level. The author obtains an expression for the density of the composite error in terms of hypergeometric functions for a model with an exponential distribution for the inefficiency error and a standard logistic distribution for the random error. We propose a first generalization of Smith (2008) by using a Type I Generalized Logistic (GL) distribution for the random error. This distribution describes situations of symmetry or asymmetry (positive or negative), depending on the value of one of its parameters. This allows us to analyze the statistical properties of a model which has both statistical dependence and possible asymmetry in the random error component. While Kumbhakar and Lovell (2000) attribute some well-known limitations of the SF approach to incorrect specifications of the frontiers, we point out that some of the anomalies observed in the empirical literature may come from an incorrect specification of the shape of the density function of the two error components.

A relevant point is the economic interpretation of our assumption about the dependence and asymmetry of the random error. As stressed by some authors, (Gómez-Déniz and Pérez-Rodriguez 2015; Pal and Sengupta 1999; Smith 2008), there are no statistical and economic reasons to assume the orthogonality of the errors. In particular, the independence of these error components in a productive industry is, in the opinion of Smith (2008), not obvious from either the economic or the statistical point of view. Pal and Sengupta (1999) argue that managerial efficiency may be affected by natural factors (representing statistical noise) in the agricultural sector. In addition, in a context in which current managerial decisions are influenced by past natural shocks (even in the short period), it easy to understand that the assumption of independence is too stringent. This holds particularly in agriculture, since a disturbance in one season will affect future decisions, thereby influencing the inefficiency component. Given that the same disturbance will affect the random error component, this could lead to the presence of a dependence between the random noise and the inefficiency. Also in this respect, Gómez-Déniz and Pérez-Rodriguez (2015) and Smith (2008) propose some examples of dependence in the agricultural sector. There are some good farmers who deal better with bad climatic conditions than do others. This will affect their efficiency when the weather is bad, meaning that a dependence among the error components cannot be excluded. A different interpretation is according to misspecification errors. In fact, there are some variables affecting the efficiency that cannot be included in the model because they are not well defined or not measurable (e.g., managerial ability, personal bias). Thus, they can flow into the statistical noise, given that it contains all things not included in the model, and this could lead to the presence of dependence (Pal and Sengupta 1999). In the manufacturing sector, unexpected events can occur in different phases of the productive process, influencing managerial decisions, e.g. damage to industrial machines, and defective products.

Regarding the asymmetry of the random error term, we depart from the huge literature which addresses this issue from a statistical point of view. In fact, some research deals with the normality of the residuals in different economic contexts (Azzalini 2005). From an economic perspective, unexpected shocks might affect the random error component, which does not necessarily follow a normal distribution. Normality seems to be a convenient assumption for mathematical computations. In several fields of research (economics, finance, sociology, engineering) error structures in regression models are not symmetric (Lewis and McDonald 2013; Lin et al.2013; Wu 2013). A more general example, in our opinion, would relate to a panel data context, thinking, for instance, macro-shocks affect the noise component of a production function. We expect that the skewness of this noise component could vary over time, following macro-cyclical patterns. For example, regarding our first empirical analysis of data from the NBER, we estimated production functions for different years and only in 19 years out of the 1958–2005 period were there cases of wrong skewness. We find that in one of these years (1979), the asymmetric random component contributes greatly to the decomposition of the third central moment. This dataset is a well known example of data evidencing wrong skewness (Bădin and Simar 2009; Hafner et al. 2016). The empirical results suggest that the dependence between the two error components is statistically rejected. Nonetheless, a strong positive asymmetry of the random error can be accepted. But, more importantly, our approach is able to estimate a non-zero inefficiency term, thus solving, at least in this dataset, the wrong skewness problem.

The second dataset has been chosen to test the class of models proposed in this paper when no wrong skewness is present in the data. In this empirical analysis, we find a strong non-linear dependence structure between the two sources of error. We show that this dependence structure has a significant impact on the observed Technical Efficiency (TE) scores.

Our model allows for statistical dependence through copulas in a straightforward manner. Thus, our paper is also related to the growing strand of the literature which uses copulas in stochastic frontiers. In particular, Amsler et al. (2014, 2016) introduce time dependence through copulas. Carta and Steel (2012) use copula functions to introduce a dependence between the outputs in a multi-output context. Lai and Huang (2013) propose a model taking into account the correlation among a set of individuals. Shi and Zhang (2011) use copulas for modeling the dependence in long-tail distributions. Tran and Tsionas (2015) model the dependence through a copula between endogenous regressors and the overall error term in a case in which external instruments are not available. We contribute to this literature by: (i) Giving a specification that generalizes Smith (2008); (ii) Indicating the exclusion of dependence as a possible cause of the wrong skewness phenomenon and the relative wrong skewnees problem; (iii) Suggesting that the presence of dependence between the two sources of error might considerably affect the estimation of TE scores.

This paper is organized as follows. In Section 2 we introduce the economic model and we list the steps required for the construction of the likelihood function and for the calculation of the TE. The new specification of the SF models is presented in Section 3, where a semi-closed expression for the probability density function of the model in terms of hypergeometric functions is derived. This allows us to discuss the statistical properties of the model in a rather transparent way. Section 4 reports the results of the two applications. In Section 5, we conclude. Then, Appendix 1 presents the proof of our Proposition 1. Despite the semi-closed formula for the composite error function, the estimation of our examples requires a numerical discretization of the density. In this paper we use Gaussian quadratures, and the entire procedure is described in Appendix 2. Finally, Appendix 3 presents the analytical derivation of the TE and Appendix 4 presents the statistical properties of the copulas used in the empirical applications.

2 Stochastic frontiers and copula functions

The generic model of a production function for a sample of N firms is described as follows:

$$\bar y = \bar x\beta + V - U$$
(3)

where \(\bar y\) is an (N × 1) vector of firms’ log-outputs; \(\bar x\) is an (N × K) matrix of log-inputs; β is a (K × 1) vector of unknown elasticities; V is an (N × 1) vector of random errors; U is an (N × 1) vector of random variables describing the inefficiencies associated to each firm (for a detailed discussion Kumbhakar and Lovell 2000).

To complete the description of the model, we need to specify the distributional properties of the random variables (U,V). The standard specification assumes independence between the random error and the inefficiency component, and a normal distribution for both random variables (although the inefficiency error must be truncated at zero to guarantee positiveness). We depart from this specification by considering a general joint probability density function f U,V (⋅, ⋅,Θ) for the couple (U,V), where Θ is the vector of parameters to be estimated, which includes β, the marginal and the dependence parameters. This density is defined on ℝ + × ℝ, since inefficiency needs to be non-negative. The probability density function (pdf) of the composite error \({\cal E}: = V - U\) is the convolution of two dependent random variables U and V, i.e.

$${f_{\cal E}}\left( \epsilon \right) = \mathop {\int}\limits_{{\Re ^ + }} {{f_{U,V}}\left( {u,\epsilon + u} \right)du} $$
(4)

where the joint probability density function, f U,V (u,v), is constructed using the properties of copula functions.

Copulas are widely appreciated tools used for the construction of joint distribution functions. To highlight the potential of this tool, it is sufficient to note that a copula function joins margins of any type (parametric, semi-parametric, and non-parametric distributions), not necessarily belonging to the same family, and captures various forms of dependence (linear, non-linear, tail dependence, etc.). A two-dimensional copula is a bivariate distribution function whose margins are uniform on (0,1). The importance of copulas stems from Sklar’s theorem, which states how copulas link joint distribution functions to their one-dimensional margins. Indeed, according to Sklar’s theorem, any bivariate distribution H(x,y) of the variables X and Y, with marginal distributions F(x) and G(y), can be written as H(x,y) = C(F(x),G(y)), where C(.,.) is a copula function. Thus any copula, together with any marginal distribution, allows us to construct a joint distribution.

For the sake of parsimony, in this paper we do not include the rigorous construction of the copula function (details are Nelsen 1999). Rather, we describe the procedure we use to embed the copula into the stochastic frontier model described above (see also Smith (2008)), through 5 steps:

  1. 1.

    The choice of marginal distributions for the inefficiency error and the random error. We denote by f U (⋅), g V (⋅) their pdfs, and by F U (⋅), G V (⋅) their distribution functions.

  2. 2.

    The selection of the copula function C θ (F U (⋅),G V (⋅)). This usually involves additional dependence parameters, denoted here by θ.

  3. 3.

    The joint distribution function f U,V (u,v) has the following standard representation:

    $${f_{U,V}}\left( {u,v} \right) = {f_U}\left( u \right){g_V}\left( v \right){c_\theta }\left( {{F_U}\left( u \right),{G_V}\left( v \right)} \right),$$
    (5)

    where \({c_\theta }\left( {{F_U}\left( u \right),{G_V}\left( v \right)} \right) = \frac{{{\partial ^2}{C_\theta }\left( {{F_U}\left( u \right),{G_V}\left( v \right)} \right)}}{{\partial {F_U}\left( u \right)\partial {G_V}\left( v \right)}}\) is the density copula.

  4. 4.

    The pdf of the composite error f ϵ(·;Θ) is the convolution of the joint density as in (4). Now, observing that \({\epsilon _i} = {{\bar y}_{i}} - {{\bar{\bf x}}_i}\beta \), the likelihood function is given by

    $$L = \mathop {\prod}\limits_{i = 1}^N {{f_{\cal E}}\left( {{{\bar y}_i} - {{\bar{\bf{x}}}_i}\beta ;\Theta } \right)} $$
    (6)

    where \({\bar{\bf x}_i}\) is the ith row of \(\bar{\bf x}\).

  5. 5.

    Finally, the technical efficiency (TE Θ ) is

$$ T{E_{{\Theta }}}\! =\! E\left[ {{e^{ - U}}\left| {\cal E} \right. = {\epsilon ^*}} \right]\! = \frac{1}{{{f_{\cal E}}\left( {{\epsilon ^*};{{\Theta }}} \right)}}\mathop {\int}\limits_{{\Re ^ + }} {{e^{ - u}}{f_{U,V}}\left( {u,\epsilon + u;{{\Theta }}} \right)du} .$$
(7)

The complexity of the procedure described above depends on the choice of the marginal distribution functions F U (⋅), G V (⋅) and the copula function C θ (⋅,⋅). It is equally obvious that the same choice influences the flexibility of the model. In the next section, we present a specification that represents a balanced trade-off between complexity and flexibility.

3 A new specification of SF models

In this section we propose a new specification for the composite error, which gives rise to a semi-closed expression for the composite error of a production stochastic frontier. The density functions and the distribution functions of our specification are presented in Table 1. We model the inefficiency component of the composite error through an exponential random variable. This is a natural choice for the distribution of the inefficiency term, and has been used in many empirical applications (see Greene 1990; Smith 2008 to mention only a few). To model the random component of the composite error, we use a slight modification of the Type I generalized logistic distribution. To this end, we assume that the random variable V′ is distributed as a Type I generalized logistic distribution with parameters (α v , δ v , λ v ) and distribution function \({G_{V\prime }}\left( {v\prime } \right) = {\left( {1 + {e^{ - \frac{{v' - {\lambda _v}}}{{{\delta _v}}}}}} \right)^{ - {\alpha _v}}}\), where α v is a shape parameter, δ v is a scale parameter, and λ v is a location parameter (see, for example, Johnson et al. (1995)), and with expected value and variance given by E[V′] = λ v  + δ v [Ψ(α v )−Ψ(1)] and Var(V′) = δ v [Ψ′(α v ) + Ψ′(1)], respectively.

Table 1 Marginal distribution functions and FGM copula
Full size table

In order to interpret V′ as a random error with zero mean, we consider the difference V = V′−E(V′). It is immediate to verify that the distribution function of V is \({G_V}\left( v \right) = {\left( {1 + {e^{ - \frac{{v + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}}}} \right)^{ - {\alpha _v}}}\), with E(V) = 0 and Var(V) = Var(V′).Footnote 3 Moreover, this choice makes our results directly comparable with those of Smith (2008), who uses a standard logistic distribution. Our results thus specialize to Smith (2008) when α v  = 1. This particular choice for the distribution of the random error is motivated by the need for flexibility. Indeed, as shown in Domma (2004) and in Domma and Perri (2009), such s distribution is capable of generating either symmetric or positively/negatively skewed distributions. However, despite this flexibility, its density function is simple enough to be handled with relative ease. The final ingredient of our specification is the FGM copula. This assumption is motivated by the need to obtain a semi-closed form solution for the density of the random component. We would like to emphasize that in empirical applications, this copula is likely to produce poor estimates because of its well-known limitations. However, while at this stage the tractability is a priority, we will perform our empirical analyses with different specifications of the copula to check the robustness of our empirical results.

The following proposition presents a semi-explicit formulation of the pdf of the composite error in terms of a linear combination of hypergeometric functions,Footnote 4 the expected value, the variance and the third central moment of the composite error.

Proposition 1

Assuming that \(U \sim Exp\left( {{\delta _u}} \right)\), \(V \sim GL ( {{\alpha _v},{\delta _v}}) \) and the dependence between U and V is modeled by an FGM copula. Let k 1(ϵ) be defined as \({k_1}\left( \epsilon \right) = exp\left\{ { - \frac{{\epsilon + {\delta _v}\left[ {\Psi \left( {{\alpha _v}} \right) - \Psi \left( 1 \right)} \right]}}{{{\delta _v}}}} \right\}\)

  1. 1.

    The density function of the composite error is

    $${f_{\cal E}}\left( {\epsilon ;{{\Theta }}} \right) = {w_1}{\left( \epsilon \right)_2}{F_1}\left( {{\alpha _v} + 1,\frac{{{\delta _v}}}{{{\delta _u}}} + 1;\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right) \\ \\ +{w_2}{\left( \epsilon \right)_2}{F_1}\left( {{\alpha _v} + 1,2\frac{{{\delta _v}}}{{{\delta _u}}} + 1;2\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right) \\ \\ + {w_3}{\left( \epsilon \right)_2}{F_1}\left( {2{\alpha _v} + 1,\frac{{{\delta _v}}}{{{\delta _u}}} + 1;\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right) \\ \\ + {w_4}{\left( \epsilon \right)_2}{F_1}\left( {2{\alpha _v} + 1,2\frac{{{\delta _v}}}{{{\delta _u}}} + 1;2\frac{{{\delta _v}}}{{{\delta _u}}} + 2; - {k_1}\left( \epsilon \right)} \right)\\ $$
    (8)

    where the functions w 1(.), w 2(.), w 3(.) and w 4(.) are defined by

    $$\begin{array}{*{20}{l}}\\ {{w_1}\left( \epsilon \right) = (1 - \theta )\frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{{\delta _v} + {\delta _u}}}} \hfill & {{w_2}\left( \epsilon \right) = 2\theta \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{2{\delta _v} + {\delta _u}}}} \hfill \\ \\ {{w_3}\left( \epsilon \right) = 2\theta \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{{\delta _v} + {\delta _u}}}} \hfill & {{w_4}\left( \epsilon \right) = - 4\theta \frac{{{\alpha _v}{k_1}\left( \epsilon \right)}}{{2{\delta _v} + {\delta _u}}}} \hfill \\ \end{array}$$
  2. 2.

    The expected value, the variance, and the third central moment of the composite error are

$$E\left[ {\cal E} \right] = - {\delta _u},$$
(9)
$$Var\left[ {\cal E} \right] = \delta _u^2 + \delta _v^2\left[ {\Psi \prime \left( {{\alpha _v}} \right) + \Psi \prime \left( 1 \right)} \right] - \frac{{\theta {\delta _u}{\delta _v}}}{2}\left[ {\Psi \left( {2{\alpha _v}} \right) - \Psi \left( {{\alpha _v}} \right)} \right]$$
(10)

and

$$ E\{ [ {\cal E} - E( {\cal E} ) ]^3 \} = - 2{\delta _u^3} + {\delta _v^3}[ \Psi \prime\prime ({\alpha _v}) - {\Psi \prime\prime} (1)]\\ \\ + \frac{3}{4}\theta {\delta _u}{\delta _v}\{ {\delta _u}[ \Psi (2{\alpha _v}) - \Psi ({\alpha _v})] \kern1.5pc \\ \\ +2{\delta _v}[{\Psi \prime} ({\alpha _v}) + {\Psi \prime} (1)]-{\delta _v}[\Psi (2{\alpha _v}) \\ \\ - \Psi ({\alpha _v})]^2 - {\delta _v}[{\Psi \prime} (2{\alpha _v} ) + {\Psi \prime} (1)]\}\kern0.5pc\\ $$
(11)

where Ψ( ⋅ ), Ψ′( ⋅ ) and Ψ′′( ⋅ ) are, respectively, the Digamma, Trigamma and Tetragamma functions.

Proof

See Appendix 1.

To appreciate the flexibility of our model, we point out that depending on the values of some parameters, we can specify the following four possible models:

  • for θ = 0 and α v  = 1, we get the model of independence and symmetry, denoted by (I,S);

  • for θ = 0 and α v  ≠ 1, we have the model of independence and asymmetry, denoted by (I,A);

  • for θ ≠ 0 and α v  = 1, we obtain the model of dependence and symmetry, denoted by (D,S);

  • for θ ≠ 0 and α v  ≠ 1, we have the model of dependence and asymmetry, denoted by (D,A)

In what follows, we will assess the impact of the asymmetry of the random error (via parameter α v ) and the effect of the dependence (via parameter θ) between U and V on the variance of the composite error. In particular, we compare four variances of the composite error, corresponding to the four models described above. First, we observe that for α v  = 1, given that \(\psi \prime \left( 1 \right) = \frac{{{\pi ^2}}}{6}\) and ψ(2)−ψ(1) = 1, and by Eq. (10), we obtain the special case

$$Var_{\cal E}^{\left( {D,S} \right)} = \delta _u^2 + \frac{{{\pi ^2}}}{3}\delta _v^2 - \frac{{\theta {\delta _u}{\delta _v}}}{2}$$
(12)

which overlaps Smith (2008) in the case of the symmetry of V and a dependence between U and V (this corresponds to a variance of \({\cal E}\) of the DS model). Moreover, to make the discussion simple, we highlight that the variance of the composite error in the cases of (a) independence and asymmetry and (b) independence and symmetry, are given, respectively, by \(Var_{\cal E}^{\left( {I,A} \right)} = \delta _u^2 + \delta _v^2\left[ {\psi \prime \left( {{\alpha _v}} \right) + \psi \prime \left( 1 \right)} \right]\) and \(Var_{\cal E}^{\left( {I,S} \right)} = \delta _u^2 + \frac{{{\pi ^2}}}{3}\delta _v^2\). Obviously, the variance of the composite error in the case of dependence and asymmetry is \(Var_{\cal E}^{\left( {D,A} \right)} = Var\left( {\cal E} \right)\) reported in Eq. (10).

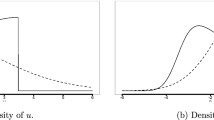
Figure 1 plots the variance of \({\cal E}\) as a function of α v . The three lines corresponds to different dependence structures (θ = −1, θ = 0 or θ = 1). In this figure, the effect of asymmetry on the variance of the composite error is particularly evident.

Fig. 1
figure 1

Plot of \(Var\left( {\cal E} \right)\) for a production frontier with θ = −1, θ = 0 and θ = 1 (α v ranges between 0 and 2)

Full size image

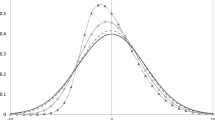
Next, we determine the effects of α v on the distribution function of \({\cal E}\).Footnote 5 In fact, Fig. 2 shows how the asymmetry of the random error affects the distribution of the composite error. Imposing a maximal positive dependence between U and V (θ = 1), we plot different pdfs for different values of α v and observe that α v affects not only the shape of the density, but also, and more importantly, the behavior of the distribution at the tails. The effect is more pronounced for negatively skewed distributions of the random error. This explains the impact on the variance observed above: negative skewness assigns much more probability mass to the extreme negative values of \({\cal E}\) than does positive skewness.

Fig. 2
figure 2

Density function of \({\cal E}\) of a production frontier with δ u  = δ v  = 1, α v  = 1 and θ = 1 (α v ranges between 0.25 and 3)

Full size image

The empirical literature often finds estimated skewed density functions of the composite error which contrast with the theoretical predictions of the model (the ‘wrong skewness’ anomaly). In this regard, there is no general consensus on the interpretation of this misalignment between the assumptions and the observed facts. For instance, Kumbhakar and Lovell (2000) ascribe the misalignment to economically significant model misspecifications, while Simar and Wilson (2010) and Simar and Wilson (2011) claim that it may be due to an unfortunate sampling from a correctly specified population. Smith (2008) argues that the observed skewness may arise from the dependence between the random error and the inefficiency. Here, we contribute to the debate by suggesting one more possible explanation: it could be the interaction between the dependence (as argued by Smith) and the fundamental asymmetry of the distribution of the random error.

4 Empirical examples of production frontiers

In this section we present two empirical applications.Footnote 6 We use two different data samples, one in which a case of wrong skewness occurs, and one in which it does not occur.

For each dataset, we estimate the classic SF model and different variations within our class of models. For the reader’s convenience, Table 2 presents the acronyms used to distinguish the models, together with their statistical properties. The acronyms have been chosen to mimic the statistical properties of the models analyzed, so that IS stands for Independence and Symmetry, IA for Independence and Asymmetry, and DA for Dependence and Asymmetry. IS is the most parsimonious, and is the specification closest to the classic SF. It cannot capture either asymmetries in the random component of the composite error or any dependence between the two error components.

Table 2 Summary of the statistical models
Full size table

In empirical applications, when selecting a copula function to capture some kind of dependence structure, one must take into account several factors, such as its tractability, the type of dependence (linear or non-linear), and the strength of the dependence. This last factor is usually measured with Kendall’s τ K (see Joe 1997; Nelsen 1999), which is defined as

$${\tau _K} = 4{\int} {\mathop {\int}\limits_{{I^2}} {C\left( {{F_u},{G_v}} \right)dC\left( {{F_u},{G_v}} \right)} } - 1$$

for two arbitrary marginal U and V with distribution functions F U and F V coupled with the density copula C(⋅, ⋅). We test three different specifications of the copula function. The FGM copula (Nelsen 1999) (models DS and DA) has the advantage of producing a quasi-closed form density function for the composite error, and this allows us to obtain the decomposition in Proposition 1. However, in our applications this copula may suffer from some limitations. In particular, it can describe only situations where the dependence structure is limited, since it can only capture situations where τ K ∈[−2/9, 2/9]. Stronger dependence structures need more sophisticated copulas. The bivariate Gaussian copula (included in DS Gauss and DA Gauss models) captures a linear dependence between two random variables. It is used mainly because it is easy to parametrize (Meyer 2013). It alleviates at least in part the limitations of the FGM, given that \({\tau _K} = \frac{2}{\pi }arcsin\left( \theta \right)\) where θ, in this case, is the correlation measure, but has the drawback of only being capable of capturing linear dependence. Lastly, the Frank copula (models DS Frank and DA Frank ) is capable of capturing a non-linear dependence structure. It belongs to the family of Archimedean copulas and has a Kendall’s \({\tau _k} = 1 - \frac{4}{\theta } + 4\frac{{{D_1}\left( \theta \right)}}{\theta }\), where \({D_1}\left( \theta \right) = \frac{1}{\theta }{\int_0^\theta} \frac{x}{{\exp^x} - 1}{\rm{d}}x\) (Huynh et al. 2014) and θ the association parameter. In Appendix 4, we present some of the mathematical characteristics of the Gaussian and Frank copula functions.

4.1 Wrong skewness in the data from the NBER database

We test our models in an SF production frontier using data from the NBER manufacturing productivity database (Bartelsman and Gray 1996). This archive is freely available online and contains annual information on US manufacturing industries from 1958 to the present.

In the underlying economic model, the variable ‘value added’ is our output, and total employment (lemp) and capital stock (lcap) are the input factors (all variables are in logarithms). The frontier assumes the Cobb-Douglas functional form.

We focus on the data for 1979 since we find the presence of a strong positive skewness in 1979, while negative skewness was expected from the traditional model (this was also shown in Hafner et al. (2016)). The wrong skewness phenomenon present in this data implies the wrong skewness problem in the sense that, according to the classical SF, the inefficiency hypothesis should be rejected.

4.1.1 Estimation

In this section we present the results in Tables 3 and 4, where significant coefficients are in bold (t-statistics are in parentheses).

Table 3 Estimations of production SF using US textile industry data (1979)
Full size table
Table 4 Estimations of models capturing dependence through Gaussian and Frank copulas. NBER dataset
Full size table

What we observe first is a significant and strong positive asymmetry of the random error that, following the reasoning of this paper, should be the unique cause of the wrong skewness phenomenon (and the relative problem) of the data at hand.

Second, we observe that the DS and DA models (Table 3) provide non-significant association measures. In any case, testing the hypothesis θ = 0 means testing whether there is independence between the inefficiency and the random component of the composite error. In this particular dataset, the data suggest that no dependence structure should be included.Footnote 7

The Akaike Information Criterion (AIC) does not give a strong indication of which model should be preferred, since for the IA model the AIC is equal to −22.45, followed by IS (−21.15), DA (−20.52) and DS (−19.19).Footnote 8 However, even if each of our four models may be indifferent to the others (Burnham and Anderson 2004), the association measures are not significant and, comparing IA with IS, the former is preferred. Thus, the better fit goes in the direction of preferring models capturing asymmetry of the random error and not involving dependence structure.

As a robustness check, and driven by the high but not significant association parameters of the FGM copula, we have run a set of estimations in order to test whether other copulas can capture different forms of dependence. In more detail, we estimate both the DS and DA models, in which the dependence is captured through both the Gaussian and the Frank copulas. We present the results in Table 4. The main findings are: (i) If we look at the significance test on each estimated θ, the results suggest again the absence of dependence; (ii) Comparison of all the estimated models suggests that the IA model remains the better fit, evidencing in a second way the absence of dependence in the NBER sample.

5 Asymmetry decomposition and technical efficiency

We now use the results of Proposition 1 to investigate the statistical aspects of the wrong skewness phenomenon and to decompose the asymmetry of the composite error.

Table 5 contains some descriptive statistics for the estimated parameters and the estimated composite error \(\hat \varepsilon \). Each column represents one model, whose statistical characteristics are in Table 2. It is worth noting that the true direction of asymmetry is measured by factoring the sum of the deviations from the median (Zenga 1985).Footnote 9 One element of this decomposition is \(E{\left[ {{\cal E} - E\left( {\cal E} \right)} \right]^3}\), which is the measure derived in Eq. (11). Table 5 presents the contributions of the single components to explain \(E{\left[ {{\cal E} - E\left( {\cal E} \right)} \right]^3}\) and \(E{\left[ {{\cal E} - Me\left( {\cal E} \right)} \right]^3}\).

Table 5 Summary measures and skewness of the composite error (data from NBER)
Full size table

We find a positive skewness of \({\cal E}\) in the IA and DA models, in which the v-component is strongly positive. The DS model also has a positive skewness due to the positive dependence-component. For the IS model, we can accept the symmetry of \({\cal E}\) (all the skewness measures are very close to 0). For the other specifications (IA, DS and DA) we have no wrong skewness anomaly. In fact, the signs of \(E{\left[ {{\cal E} - Me\left( {\cal E} \right)} \right]^3}\) and \({\sum} {\left[ {\hat \epsilon - Me\left( {\hat \epsilon } \right)} \right]^3}\) are the same. We remark that: (i) IS assumes a priori that the v-component and the dependence-component are equal to 0, as in the classic SF; (ii) the dependence-component is positive for both models with a dependence structure, DA and DS, but it is very small, and also (iii) dependence is statistically rejected in this data sample.

Table 6 presents some descriptive statistics for the estimated TE for each model.Footnote 10

Table 6 Some descriptive statistics of Technical Efficiency (data from NBER)
Full size table

The wrong skewness problem is evident in the classic SF and IS specifications. These models, indeed, present an industry where all manufacturers are perfectly efficient (the mean TE score is 1), and there is no variability (the variance of the efficiency score approaches zero). What we observe in our preferred model (IA) is that we can actually estimate a non-zero TE. In other words, the IA model has the ability to estimate the variability in the industry, thus solving, at least in this dataset, the wrong skewness problem.

5.1 Application to a sample of Italian manufacturing firms

We use data from AIDA (‘Analisi Informatizzata delle Aziende Italiane’), which is a database containing financial and accounting information of Italian firms. This dataset does not evidence wrong skewness. Nonetheless, we would like to determine the impact of our specification on the distribution of the efficiency scores. It turns out, indeed, that incorporating dependence between the two sources of error significantly affects the estimated TE.

We use again a Cobb-Douglas production function where the dependent variable is the value added, representing the firms’ output, while labor and capital are the traditional inputs. Moreover, we introduce ICT and R&D investments as additional inputs. All variables refer to the calendar year 2009 and are in logarithms.Footnote 11

5.1.1 Estimation

The results from Table 7 highlight the robustness of the estimates across our models and the significance of all fitted parameters (t-statistics are in brackets). Moreover, in terms of the AIC, the classic SF models are very far from the other specifications. The distance is much more than 10 points (Burnham and Anderson 2004). In particular, the more general DA model has the better fit (AIC 1042.26), but the AIC for the DS model is very close (1042.46). Hence, we reject the asymmetry of the random error for all the specifications. Thus, the results indicate the presence of a positive dependence and the symmetry of V in this data sample.

Table 7 Estimations of production SF for the Italian manufacturing firms using data from AIDA (2009)
Full size table

The estimated values for θ give reasons to further investigate the dependence, but even more, the calculated values of τ k convinced us to carry out a more in-depth analysis of the dependence (0.18 for the DS model and 0.22 for the DA model, considering that 0.22 is the maximum value for τ k with the FGM copula). Table 8 presents the estimations of the DS and DA models capturing the dependence through the Gaussian and Frank copulas. If we look at the AIC, we can say that the better model is DS Frank (1034.47), also with respect to the estimations in Table 7. This means a strong positive dependence between U and V, in fact τ k is equal to 0.48 (the maximum is 1).

Table 8 Estimations of models capturing dependence through Gaussian and Frank copulas. AIDA dataset
Full size table

5.1.2 Technical efficiency

In the previous subsection, we showed that from a purely statistical point of view, the dataset evidences a strong non-linear dependence between the inefficiency error and the random error. The questions are: Does this dependence affect the distribution of the efficiency scores? In which ways?

Table 9 displays the summary statistics of the efficiency scores for each of the 9 models under investigation (the classic SF as well as 8 models with different variants of our specification). We find significant differences in the observed distributions of the TE scores of the classic SF and our models. In particular, an inspection of Table 9 reveals that the left tails of the distributions are completely different. For instance, the classic SF gives a minimum efficiency level of 0.33, whereas the minimum level is 0.87 for DS Frank , which is the best model in terms of AIC. We also observe a pronounced difference in terms of the expected values and the variability in the industry. To better highlight the difference in the distribution of the efficiency scores, we plot in Fig. 3 the kernel densities of the distributions of the efficiency scores observed in the classic SF and DS Frank . The classic SF presents an industry where the efficiency is more variable among the firms than it is for DS Frank . A number of firms in the industry are very inefficient: only a few firms are very efficient. On the other hand, DS Frank presents a completely different picture of the industry. Here, a large number of firms are concentrated around the very high expected value, and only a few firms are moderately inefficient.

Table 9 Some descriptive statistics of technical efficiency (data from AIDA)
Full size table
Fig. 3
figure 3

Kernel density of efficiency scores for model classic SF and DS Frank

Full size image

The observed differences in the distribution of the efficiency scores raise the question of whether the underlying economic model is correctly specified.

A possible explanation of the remarkable difference in the distributions of the TE is due to misspecification errors of the underlying economic model. In fact, some variables affecting the efficiency cannot be included in the model because they are either not well defined or not measurable. Thus, the bias in the economic model can flow into the statistical noise, given that this noise contains everything not included in the model, and this might introduce a dependence between the two different sources of error (see Pal and Sengupta 1999). In such situations, not properly taking into account the dependence structure might produce an estimated TE producing a different picture of the industry.

6 Conclusions

In this paper, we have shown that the so-called ‘wrong skewness’ anomaly in stochastic frontiers is a direct consequence of the basic hypotheses, which appear to be overly restrictive. In fact, relaxing the hypotheses of the symmetry of the random error and the independence of the components of the composite error, we obtain a re-specification of the stochastic frontiers model that is sufficiently flexible. This allows us to explain the difference between the expected and the estimated signs of the asymmetry of the composite error that is found in various applications of the classic stochastic frontier model.

We have decomposed the third moment of the composite error into three components, namely: (i) the asymmetry of the inefficiency term; (ii) the asymmetry of the random error; and (iii) the dependence structure of the error components. This enables us to reinterpret the unusual asymmetry in the composite error by measuring the contribution of each component in the model. This has been shown in one of the two empirical examples, i.e. the data from the NBER archive, for which a case of wrong skewness has been reported when using the classic SF specification.

When wrong skewness occurs, estimations with classic SF correspond to OLS estimations, and the inefficiency scores are zero. This misleads one to the conclusion that there is no inefficiency. Our specification allows overcoming this difficulty, as witnessed in both empirical applications, where our estimates of the output elasticities with respect to the inputs are more robust than those involved in the standard SF specification and the estimated efficiency scores are lower than unity.