1 Introduction

Within the past few years, exact solutions of NPDEs have gained considerable attention. For this reason many distinct procedures have utilized by researchers. We can list some of them as follows. Wazwaz have derived periodic soliton solutions of the Dodd-Bullough-Mikhailov and the Tzitzeica-Dodd-Bullough equations by tanh technique Wazwaz (2005). Akbulut et al. employed the modified simple equation method to the the fifth-order KdV equation Akbulut et al. (2021a) and verified trivial conservation laws and solitary wave solutions for the fifth order Lax equation Akbulut et al. (2021b). Akinyemi et al. have implemented the improved Sardar sub-equation method to the perturbed nonlinear Schrödinger-Hirota equation with spatio-temporal dispersion Akinyemi et al. (2021). Aksoy et al. utilized the exponential rational function method for space–time fractional differential equations Aksoy et al. (2016). Ma et al. have considered the Hirota-Maccari system via the first integral procedure to extract bright, singular, and dark soliton solutions Ma et al. (2021). Sun et al. have utilized the Hirota bilinear technique to the (2+1)-dimensional B-Kadomtsev-Petviashvili equation to find M-lump solutions Sun et al. (2022). Durur et al. sub-equation procedure to the KdV6 equation Durur et al. (2020). Hosseini et al. have analyzed soliton solutions of the Hirota-Satsuma-Ito equation via the linear superposition principle Hosseini et al. (2021). Raza et al. have applied the Painleve approach to a nonlinear Kudryashov’s equation Raza et al. (2021). Kumar have founded travelling waves, kink waves, rational function, lump-type solitons, multi-solitons, hyperbolic function, and trigonometric solutions by generalised exponential rational function method Kumar (2021). Osman et al. verified some travelling wave solutions of the 2D-chiral nonlinear Schrodinger equation Osman et al. (2020). Inc et al. have founded exact analytic solutions for the (2+1)-dimensional Ito equation by using simplest equation technique Inc et al. (2021). Akbulut et al. obtained the conservation laws of time fractional modified Korteweg–de Vries (mkdv) equation Akbulut and Tascan (2017a), searched some soliton solutions for various equations Akbulut et al. (2022), and applied conservation theorem and modified extended tanh-function procedure to nonlinear coupled Klein–Gordon–Zakharov equation Akbulut and Tascan (2017b). Mirzazadeh et al. employed the improved F-expansion method to find different wave solutions Mirzazadeh et al. (2022). Hosseini et al. obtained conservation laws and kink solitons of the Sharma–Tasso–Olver–Burgers equation Hosseini et al. (2022). In this paper, to explain the propagation pulse in optical fiber, we are considering a new NPDE, in the following form

$$\begin{aligned} if_t+f_{xx} +\alpha _1 f|f|^{2m-2n} +\beta _1 f |f|^{2m-n}+\gamma _1 f |f|^{2m}+\delta _1 f |f|^{2m+n}+\lambda _1 f |f|^{2m+2n}=0. \end{aligned}$$
(1)

In Eq. (1), the complex function f(x, t) representing optical wave, where m and n are usually rational numbers (not necessarily integers) \(\alpha _1\) , \(\beta _1\) , \(\gamma _1\), and \(\lambda _1\) are the parameters. Equation (1) is the generalization of the well known nonlinear Schrödinger equation. At \(m=0\) Eq. (1) get the following form

$$\begin{aligned} if_t + f_{xx} +\alpha _1 f\left| f\right| ^{-2n} +\beta _1 f |f|^{-n}+\delta _1 f|f|^{n}+\lambda _1 f |f|^{2n}=0. \end{aligned}$$
(2)

The motivation of this paper is to study Eq. (1). For investigating Eq. (1), two partial differential equations have been obtained from Eq. (1) by taking \(m=n\) and \(m=2n\). Upon putting \(m=n\), Eq. (1) becomes

$$\begin{aligned} if_t + f_{xx} +\alpha _1 f +\beta _1 |f|^{n}f+\gamma _1|f|^{2n} f+ \delta _1|f|^{3n}f+\lambda _1 |f|^{4n}f=0, \end{aligned}$$
(3)

and when we consider \(m=2n\), we obtain the equation with polynomial nonlinearity in the following expression

$$\begin{aligned} if_t + f_{xx} +\alpha _1 |f|^{2n} f +\beta _1 |f|^{3n}f+\gamma _1|f|^{4n} f+ \delta _1 |f|^{5n}f+\lambda _1|f|^{4n}f=0. \end{aligned}$$
(4)

The paper consists of the following sections: We presented the mathematical analysis of the considered model in Sect. 2. Then, we gave a description of utilized techniques, respectively the SGE and the MAE techniques in Sect. 3. The extraction of soliton solutions for the proposed models was given in Sect. 4. Section 5 gives graphical illustrations of the obtained results. Finally, the conclusion of the whole research in Sect. 6.

2 The mathematical analysis

In order to find the exact soliton solution of Eqs. (3) and (4), the following traveling wave transformation is considered, as

$$\begin{aligned} f(x,t)=F(\Upsilon )e^{i (kx-wt)},\;\;\; \Upsilon =x-c t, \end{aligned}$$
(5)

where c is the speed and \(\Upsilon \) is the amplitude of traveling wave. Using the transformation Eq. (5), the real parts of Eqs. (3) and (4) have been transformed into following ODEs, respectively as,

$$\begin{aligned} F''-\left( w-k^2+\alpha _1\right) F+\beta _1 F^{n+1}+\gamma _{1}F^{2n+1}+\delta _{1}F^{3n+1}+2\lambda _{1}F^{4n+1}=0. \end{aligned}$$
(6)

and

$$\begin{aligned} F''-\left( w-k^2\right) F+\alpha _1 F^{2n+1}+\beta _1 F^{3n+1}+\gamma _{1}F^{4n+1}+\delta _{1}F^{5n+1}+2\lambda _{1}F^{6n+1}=0. \end{aligned}$$
(7)

The imaginary parts of Eqs. (3) and (4) gives the speed of traveling wave as

$$\begin{aligned} c=2k. \end{aligned}$$
(8)

In order to obtain the closed form solutions for Eq. (6), apply the following transformation

$$\begin{aligned} F=V^{\frac{1}{2n}} \end{aligned}$$
(9)

Eq. (6) takes the following form

$$\begin{aligned} \frac{1}{2n}\left( \frac{1}{2n}-1\right) (V')^{2}+\frac{1}{2n}V V''+(w-k^2+\alpha _1)V^2+\beta _1 V^{\frac{5}{2}}+\gamma _1 V^3+\delta _1 V^{\frac{7}{2}}+\lambda _1 V^4=0. \end{aligned}$$
(10)

For obtaining closed form solutions for Eq. (10), the constraint conditions \(\beta _1=\delta _1=0\) have been imposed. Equation (10) becomes

$$\begin{aligned} \frac{1}{2n}\left( \frac{1}{2n}-1\right) (V')^{2}+\frac{1}{2n}V V''+(w-k^2+\alpha _1)V^2+\gamma _1 V^3+\lambda _1 V^4=0. \end{aligned}$$
(11)

In order to obtain the closed form solutions for Eq. (7), apply the following transformation

$$\begin{aligned} F=V^{\frac{1}{3n}} \end{aligned}$$
(12)

Eq. (7) takes the following form

$$\begin{aligned} \frac{1}{3n}\left( \frac{1}{3n}-1\right) (V')^{2}+\frac{1}{3n}V V''+(w-k^2)V^2+\alpha _1 V^{\frac{8}{3}}+\beta _1 V^{3}+\gamma _1 V^{\frac{10}{3}}+\delta _1 V^{\frac{11}{3}}+\lambda _1 V^4=0. \end{aligned}$$
(13)

For obtaining closed form solutions for Eq. (13), the constraint conditions \(\alpha _1=\gamma _1=\delta _1=0\) have been imposed. Equation (13) becomes

$$\begin{aligned} \frac{1}{3n}\left( \frac{1}{3n}-1\right) (V')^{2}+\frac{1}{3n}V V''+(w-k^2)V^2+\beta _1 V^{3}+\lambda _1 V^4=0. \end{aligned}$$
(14)

3 Description of utilized techniques

In this section, we gave a description of utilized techniques, SGE Alquran and Krishnan (2016)- Inc et al. (2018) and MAE Khater et al. (2019) respectively.

3.1 The Sine-Gordon expansion method

We take into consideration:

$$\begin{aligned} f_{xx}-f_{tt}=a^{2}\sin f, \end{aligned}$$
(15)

where \(f=f(x,t)\) and \(a\ne 0\).

Then, we apply the traveling wave transformation Eqs. (5), (15) reduces to

$$\begin{aligned} F^{''}=\frac{a^{2}}{1-c^{2}}\sin F.\end{aligned}$$
(16)

Integrating the above equation gives,

$$\begin{aligned} \left[ \left( \frac{F}{2}\right) ^{'}\right] ^{2}=\frac{a^{2}}{1-c^{2}}\sin ^{2} \left( \frac{F}{2}\right) +X, \end{aligned}$$
(17)

Here X is an integration constant. If we set \(X=0\), \(\frac{F}{2}=\vartheta (\Upsilon )\) and \(h^{2}=\frac{a^{2}}{1-c^{2}}\), then Eq. (17) becomes

$$\begin{aligned} \vartheta ^{'}=h\sin ( \vartheta ). \end{aligned}$$
(18)

If we take \(h=1\) in Eq. (18), then we find

$$\begin{aligned} \vartheta ^{'}=\sin ( \vartheta ). \end{aligned}$$
(19)

Afterwards, we solve Eq. (19) to find

$$\begin{aligned}&\sin \vartheta =\sin ( \vartheta (\Upsilon ))=\frac{2 d e^{\Upsilon }}{d^{2}e^{2\Upsilon }+1}|_{d=1}={{\,\mathrm{sech}\,}}(\Upsilon ), \end{aligned}$$
(20)
$$\begin{aligned}&\cos \vartheta =\cos ( \vartheta (\Upsilon ))=\frac{d^{2} e^{2\Upsilon }-1}{d^{2}e^{2\Upsilon }+1}|_{d=1}=\tanh (\Upsilon ). \end{aligned}$$
(21)

We predict the solution as follows:

$$\begin{aligned} F(\Upsilon )=\displaystyle \sum _{i=1}^{N}\tanh ^{i-1}(\Upsilon )\left[ B_{i}sech(\Upsilon )+A_{i}\tanh (\Upsilon )\right] +A_{0}. \end{aligned}$$
(22)

Using Eqs. (20), (21), (22) becomes

$$\begin{aligned} F(\vartheta )=\displaystyle \sum _{i=1}^{N}\cos ^{i-1}(\vartheta )\left[ B_{i}\sin (\vartheta )+A_{i}\cos (\vartheta )\right] +A_{0}. \end{aligned}$$
(23)

Here N is the balancing number, which will be determined according to the homogenous balance technique. Then, we insert Eq. (23) into ODE to find an equation system for \(A_{0}\), \(A_{i}\), \(B_{i}\). This system is founded if we equate the coefficients of each power of \(\sin ^{p}(\vartheta ) \cos ^{q}(\vartheta )\) to zero. Solving the resulting system for \(A_{0}\), \(A_{i}\), \(B_{i}\).

3.2 Modified auxiliary equation (MAE) method

According to MAE method the solution of transformed ODE has the following form

$$\begin{aligned} F(\Upsilon )=p_{0}+\sum ^{N}_{k=1}\left[ q_{k}(w^{G})^{k}+r_{k}(w^{G})^{-k}\right] , \end{aligned}$$
(24)

\(p_0\), \(q_{k}\) and \(r_{k}\) are constants. \(G(\Upsilon )\) satisfies the differential equation

$$\begin{aligned} G^{'}(\Upsilon )=\frac{\beta +\alpha w^{-G}+\sigma w^{G}}{\ln w}, \end{aligned}$$
(25)

\(\beta \), \(\alpha \), \(\sigma \) are constants along with \(w>0\) and \(w\ne 1\). The differential equation (25) has three types of solutions which are given below

Type 1:

When \(\beta ^{2}-4\alpha \sigma <0\) and \(\sigma \ne 0\) then

$$\begin{aligned} w^{G(\xi )}=\frac{-\beta +\sqrt{4\alpha \sigma -\beta ^{2}}\tan \bigg (\frac{\sqrt{-\beta ^{2}+4\alpha \sigma }\Upsilon }{2}\bigg )}{2\sigma }. \end{aligned}$$

or

$$\begin{aligned} w^{G(\xi )}=-\frac{\beta +\sqrt{4\alpha \sigma -\beta ^{2}}\cot \bigg (\frac{\sqrt{-\beta ^{2}+4\alpha \sigma }\Upsilon }{2}\bigg )}{2\sigma }. \end{aligned}$$

Type 2:

When \(\beta ^{2}-4\alpha \sigma >0\) and \(\sigma \ne 0\) then

$$\begin{aligned} w^{G(\xi )}=-\frac{\beta +\sqrt{\beta ^{2}-4\alpha \sigma }\tanh \bigg (\frac{\sqrt{\beta ^{2}-4\alpha \sigma }\Upsilon }{2}\bigg )}{2\sigma }. \end{aligned}$$

or

$$\begin{aligned} w^{G(\xi )}=-\frac{\beta +\sqrt{\beta ^{2}-4\alpha \sigma }\coth \bigg (\frac{\sqrt{\beta ^{2}-4\alpha \sigma }\Upsilon }{2}\bigg )}{2\sigma }. \end{aligned}$$

Type 3:

When \(\beta ^{2}-4\alpha \sigma =0\) and \(\sigma \ne 0\) then

$$\begin{aligned} w^{G(\xi )}=-\frac{2+\beta \xi }{2\sigma \Upsilon }. \end{aligned}$$

4 Construction of solutions using proposed methods

This section gives the extraction of soliton solutions for the proposed models Eqs. (3) and (4) by employing the most efficient analytical procedures, SGE and the MAE techniques.

4.1 Method-I (SGE) method

In this subsection, we will obtain soliton solutions of Eqs. (3) and (4) via the SGE procedure. For this purpose, we balance \(V'^2\) with \(V^{4}\) in Eq. (11) and find \(N=1\). Therefore, the solution takes the form:

$$\begin{aligned} V(\Upsilon )=B_{1}{{\,\mathrm{sech}\,}}(\Upsilon )+A_{1}\tanh (\Upsilon )+A_{0}.\end{aligned}$$
(26)

Then, we use the solution procedure as explained earlier in Sect. 3. The values of unknowns \(A_{0}\), \(A_{1}\), \(B_{1}\) are calculated as:

SET 1:

$$\begin{aligned} A_{0}= & {} \frac{1+n}{4 n^2 \gamma _1},~~ A_{1}=\frac{1+n}{4n^2 \gamma _1},~~B_{1}=\frac{i(1+n)}{4 n^2 \gamma _1},~~\lambda _1=-\frac{n^2(1+2n)\gamma _1^2}{(1+n)^2},~~w=k^2-\frac{1}{4n^2}-\alpha _1. \end{aligned}$$

SET 2

$$\begin{aligned} A_{0}= & {} \frac{1+n}{ n^2 \gamma _1},~~ A_{1}=-\frac{1+n}{n^2 \gamma _1},~~B_{1}=0,~~\lambda _1=-\frac{n^2(1+2n)\gamma _1^2}{4(1+n)^2},~~w=k^2-\frac{1}{n^2}-\alpha _1. \end{aligned}$$

SET 3

$$\begin{aligned} A_{0}= & {} 0,~~ A_{1}=0,~~B_{1}=\pm \frac{\sqrt{1+2n}}{2 n \sqrt{\lambda _1}}, ~~w=k^2-\frac{1}{4n^2}-\alpha _1.\end{aligned}$$

Bright-dark soliton solutions can be founded for SET 1 as

$$\begin{aligned} f_{1}(x,t)=e^{i (kx-wt)}\left[ \left( \frac{\imath (1+n)}{4 n^2 \gamma _1}\right) {{\,\mathrm{sech}\,}}(\Upsilon )+\left( \frac{1+n}{4 n^2 \gamma _1}\right) \tanh (\Upsilon )+\frac{1+n}{4 n^2 \gamma _1}\right] ^{\frac{1}{2n}}. \end{aligned}$$
(27)

Bright soliton solutions can be founded for SET 2 as follows

$$\begin{aligned} f_{2}(x,t)=\pm e^{i (kx-wt)}\left[ \left( \frac{\sqrt{1+2n}}{2 n \sqrt{\lambda _1}}\right) {{\,\mathrm{sech}\,}}(\Upsilon )\right] ^{\frac{1}{2n}}.\end{aligned}$$
(28)

Dark soliton solutions are obtained for SET 3 as follows

$$\begin{aligned} f_{3}(x,t)=e^{i (kx-wt)}\left[ -\left( \frac{1+n}{n^2 \gamma _1}\right) \tanh (\Upsilon )+\frac{1+n}{ n^2 \gamma _1}\right] ^{\frac{1}{2n}}. \end{aligned}$$
(29)

Moreover, we will also find soliton solutions of Eq. (4) via SGE technique. If we balance \(V'^2\) with \(V^{4}\) in Eq. (14), we find as \(N=1\). The values of unknowns \(A_{0}\), \(A_{1}\), \(B_{1}\) are calculated as:

SET 1:

$$\begin{aligned} A_{0}= & {} \frac{4+6n}{9 n^2 \beta _1},~~ A_{1}=\pm \frac{4+6n}{9n^2 \beta _1},~~B_{1}=0,~~\lambda _1=-\frac{9n^2(1+3n)\beta _1^2}{4(2+3n)^2},~~w=k^2-\frac{4}{9n^2}. \end{aligned}$$

Dark soliton solutions can be founded for SET 1 as

$$\begin{aligned} f_{4}(x,t)=e^{i (kx-wt)}\left[ \pm \frac{4+6n}{9n^2 \beta _1}\tanh (\Upsilon )+\frac{4+6n}{9 n^2 \beta _1}\right] ^{\frac{1}{3n}}. \end{aligned}$$
(30)

4.2 Method-II (MAE) technique

In this subsection, we will find soliton solutions of Eq. (3) via MAE technique. Since N is founded as 1, Eq. (24) takes the following form

$$\begin{aligned} V(\Upsilon )=p_{0}+ q_{1}w^{G}+r_{1}w^{-G}, \end{aligned}$$
(31)

where \(p_0, q_1\) and \(r_1\) are constants to be determined by Inserting Eq. (31) in the Eq. (11). Then assemble all the coefficients of the powers of \(w^{G(\xi )}\) and put them equal to zero. This leads to construction of set of algebraic equations. Upon solving the obtained system gives the value of arbitrary parameters \(p_0, q_{1}\) and \(r_{1}\), which are summarized in the following sets of solutions as

SET 1:

$$\begin{aligned}&p_{0}=0,\quad q_{1}=\frac{\sigma }{(1-2n)\gamma _1},\quad r_1=0,\quad \alpha =0,\quad \beta =\frac{n}{2n-1},\\\nonumber&\lambda _1=-\frac{(1-2n)^2(1+2n)\gamma _1^2}{4n^2},\quad w=\frac{1+(4-8n)(k^2+\alpha _1)}{4-8n} \end{aligned}$$
(32)

SET 2:

$$\begin{aligned}&p_0=\frac{1+n}{2n^2\gamma _1},\quad q_1=\frac{(1+n)\sigma }{2n^2\gamma _1},\quad r_1= \frac{(1+n)\alpha }{2n^2\gamma _1},\quad \beta =1,\nonumber \\&\lambda _1=-\frac{n^2(1+2n)\gamma _1^2}{(1+n)^2},\quad w=k^2-\alpha _1+\frac{4\alpha \sigma -1}{4n^2}. \end{aligned}$$
(33)

The solutions corresponding to SET 1: are evaluated below.

Type 2:

When \(\beta ^{2}-4\alpha \sigma >0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{5}(x,t)=e^{i (kx-wt)}\left[ \frac{n(1+\tanh \left[ \frac{n\xi }{4n-2}\right] )}{2(1-2n)^2\gamma _1}\right] ^{\frac{1}{2n}} \end{aligned}$$
(34)

or

$$\begin{aligned} f_{6}(x,t)=e^{i (kx-wt)}\left[ \frac{n(1+\coth \left[ \frac{n\xi }{4n-2}\right] )}{2(1-2n)^2\gamma _1}\right] ^{\frac{1}{2n}} \end{aligned}$$
(35)

The solutions corresponding to SET 2: are evaluated below.

Type 1:

When \(\beta ^{2}-4\alpha \sigma <0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{7}(x,t)=e^{i (kx-wt)}\left[ \frac{(1+n)(-1+4\alpha \sigma )\sec \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] ^{2}}{4n^2\gamma _1\left( -1+\sqrt{-1+4\alpha \sigma }\tan \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{2n}} \end{aligned}$$
(36)

or

$$\begin{aligned} f_{8}(x,t)=e^{i (kx-wt)}\left[ -\frac{(1+n)(-1+4\alpha \sigma )\csc \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] ^{2}}{4n^2\gamma _1\left( 1+\sqrt{-1+4\alpha \sigma }\cot \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{2n}} \end{aligned}$$
(37)

Type 2:

When \(\beta ^{2}-4\alpha \sigma >0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{9}(x,t)=e^{i (kx-wt)}\left[ \frac{(1+n)(1-4\alpha \sigma ){{\,\mathrm{sech}\,}}\left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] ^{2}}{4n^2\gamma _1\left( 1+\sqrt{1-4\alpha \sigma }\tanh \left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{2n}} \end{aligned}$$
(38)

or

$$\begin{aligned} f_{10}(x,t)=e^{i (kx-wt)}\left[ -\frac{(1+n)(1-4\alpha \sigma ){{\,\mathrm{csch}\,}}\left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] ^{2}}{4n^2\gamma _1\left( 1+\sqrt{1-4\alpha \sigma }\coth \left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{2n}} \end{aligned}$$
(39)

We wil find soliton solutions of Eq. (4) via MAE procedure.

SET 1:

$$\begin{aligned}&p_{0}=0,\quad q_{1}=\frac{(3n+2\beta )\sigma }{9n^2\beta _1},\quad r_1=0,\quad \alpha =0,\quad \lambda _1=-\frac{9n^2(1+3n)\beta _1^2}{(3n+2\beta )^2},\nonumber \\&\quad w=\frac{9n^2k^2+3n(-1+\beta )\beta -\beta ^2}{9n^2} \end{aligned}$$
(40)

SET 2:

$$\begin{aligned}&p_0=\frac{2+3n}{9n^2\beta _1},\quad q_1=\frac{(2+3n)\sigma }{9n^2\beta _1},\quad r_1= \frac{(2+3n)\alpha }{9n^2\beta _1},\quad \beta =1,\nonumber \\&\lambda _1=-\frac{9n^2(1+3n)\beta _1^2}{(2+3n)^2},\quad w=\frac{-1+9n^2k^2+2\alpha \sigma }{9n^2}. \end{aligned}$$
(41)

The solutions corresponding to SET 1: are evaluated below.

Type 2:

When \(\beta ^{2}-4\alpha \sigma >0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{11}(x,t)=e^{i (kx-wt)}\left[ \frac{\beta (3n+2\beta )(1+\tanh \left[ \frac{\beta \xi }{2}\right] )}{18n^2\beta _1}\right] ^{\frac{1}{3n}} \end{aligned}$$
(42)

or

$$\begin{aligned} f_{12}(x,t)=e^{i (kx-wt)}\left[ \frac{\beta (3n+2\beta )(1+\coth \left[ \frac{\beta \xi }{2}\right] )}{18n^2\beta _1}\right] ^{\frac{1}{3n}} \end{aligned}$$
(43)

The solutions corresponding to SET 2: are evaluated below.

Type 1:

When \(\beta ^{2}-4\alpha \sigma <0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{13}(x,t)=e^{i (kx-wt)}\left[ \frac{(2+3n)(-1+4\alpha \sigma )\sec \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] ^{2}}{18n^2\beta _1\left( -1+\sqrt{-1+4\alpha \sigma }\tan \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{3n}} \end{aligned}$$
(44)

or

$$\begin{aligned} f_{14}(x,t)=e^{i (kx-wt)}\left[ -\frac{(2+3n)(-1+4\alpha \sigma )\csc \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] ^{2}}{18n^2\beta _1\left( 1+\sqrt{-1+4\alpha \sigma }\cot \left[ \frac{1}{2}\sqrt{-1+4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{3n}} \end{aligned}$$
(45)

Type 2:

When \(\beta ^{2}-4\alpha \sigma >0\) and \(\sigma \ne 0\) then

$$\begin{aligned} f_{15}(x,t)=e^{i (kx-wt)}\left[ \frac{(2+3n)(1-4\alpha \sigma ){{\,\mathrm{sech}\,}}\left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] ^{2}}{18n^2\beta _1\left( 1+\sqrt{1-4\alpha \sigma }\tanh \left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{3n}} \end{aligned}$$
(46)

or

$$\begin{aligned} f_{16}(x,t)=e^{i (kx-wt)}\left[ -\frac{(2+3n)(1-4\alpha \sigma ){{\,\mathrm{csch}\,}}\left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] ^{2}}{18n^2\beta _1\left( 1+\sqrt{1-4\alpha \sigma }\coth \left[ \frac{1}{2}\sqrt{1-4\alpha \sigma }\xi \right] \right) }\right] ^{\frac{1}{3n}} \end{aligned}$$
(47)

5 Graphical illustrations

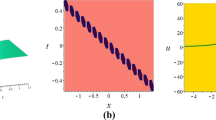
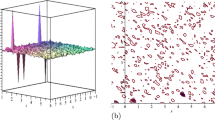
In this section, we provide the graphical illustrations of few of the determined solutions. It is important to mention here that explicit and consistent wave solutions are extracted by applying two different reliable schemes. Figures 1, 2, 3 and 4 represents the 3D and 2D plots of Eqs. (29), (30), (35) and (44) respectively by taking \(\gamma _1=2\), \(k=1\), \(w=2\), \(\alpha =1\), \(\sigma =1\) and \(\beta _1=2\).

Fig. 1
figure 1

a is 3D plot of Eq. (29) for \(n=2\), b is 2D line plots of Eq. (29) with respect x

Full size image
Fig. 2
figure 2

a is 3D plot of Eq. (30) for \(n=2\), b is 2D line plots of Eq. (30) with respect x

Full size image
Fig. 3
figure 3

a is 3D plot of Eq. (35) for \(n=2\), b is 2D line plots of Eq. (35) with respect x

Full size image
Fig. 4
figure 4

a is 3D plot of Eq. (44) for \(n=2\), b is 2D line plots of Eq. (44) with respect x

Full size image

6 Conclusion

In this work, the trigonometric function solutions, hyperbolic function solutions, and rational function solutions have been analyzed to investigate the propagation of pulses in optical fiber. These results are beneficial and useful in optical fibers and nonlinear wave phenomena. We have successfully implemented the SGE and the MAE technique with the help of computerized symbolic computation. The outcomes of the present manuscript affirmed the capacity of the schemes in handling a broad diverseness of NPDEs. Moreover, for future works, super nonlinear, quasi-periodic, chaotic, and solitonic waves can be founded.