Darboux transformation of a new generalized nonlinear Schrödinger equation: soliton solutions, breather solutions, and rogue wave solutions

Abstract

In this paper, a new generalized nonlinear Schrödinger (GNLS) equation is investigated by Darboux matrix method. Firstly, the n-fold Darboux transformation (DT) of the GNLS equation is constructed. Then, the soliton solutions, breather solutions, and rogue wave solutions of the GNLS equation are studied based on the DT by choosing different seed solutions. Furthermore, the dynamic features of these solutions are explicitly delineated through some figures with the help of Maple software.

1 Introduction

It is well known that the standard nonlinear Schrödinger (NLS) equation

$$\begin{aligned} iu_{t}+\gamma u_{xx}+\sigma u|u|^{2}=0\text {,} \ \ \sigma =\pm 1 \end{aligned}$$

(1.1)

is one of the most important integrable systems among many branches of applied mathematics and physics, especially in optics, water wave and so on [1,2,3]. In Eq. (1.1), $u=u(x,t)$ is a complex smooth function of x and t, the subscripts denote partial derivatives and the parameter $\gamma$ is real constant.

In 1995, Fokas [4] studied an integrable generalized nonlinear Schrödinger (GNLS) equation by means of bihamiltonian operators based on the NLS equation

$$\begin{aligned} iu_{t}-\nu u_{tx}+\gamma u_{xx}+\sigma |u|^{2}(u+i\nu u_{x})=0\text {,} \ \ \sigma =\pm 1, \end{aligned}$$

(1.2)

where $\gamma$ and $\nu$ are real constants. In fact, Eq. (1.2) can be transformed into Eq. (1.1) when the parameter $\nu =0$.

In 2010, Lenells [5] did further investigation to Eq. (1.2) by the dressing method, and Eq. (1.2) is transformed into a new form

$$\begin{aligned}&u_{tx}+\alpha \beta ^{2}u-2i\alpha \beta u_{x}-\alpha u_{xx} +\sigma i\alpha \beta ^{2}|u|^{2}u_{x}=0\text {,}\nonumber \\&\quad \sigma =\pm 1 \end{aligned}$$

(1.3)

under the transformation of

$$\begin{aligned} u\rightarrow \beta \sqrt{\alpha } e^{i\beta x}u \text {,} \ \ \sigma =-\sigma \text {,} \end{aligned}$$

where $\alpha =\frac{\gamma }{\nu }>0$, $\beta =\frac{1}{\nu }$.

There are many methods to get the exact solutions to the integrable equations, for instance, Darboux transformation method (DT) [6, 7], inverse scattering transformation [8], Hirota method [9], bilinear method [10] and so on. DT possesses a lot of advantages compared with other methods. It is a more valid and powerful tool to study the exact solutions of an integrable system from a seed solution. We can investigate solutions of different kinds when choosing different seed solution and analysis the relations among them. One can make the DT once again and get another set of new solutions if the obtained solutions are taken as the new starting point. Therefore, the high-order solutions can be constructed through iterations of the DT. In this paper, we construct the exact solutions of Eq. (1.3) by means of DT, including the soliton solutions, breather solutions, and rogue wave solutions.

Before discussing the DT, we shall briefly introduce the rogue waves. Rogue waves (RWs) appear in both the shallow water and deep ocean, which are notorious for causing a large number of disasters for people. As is known to all, storms and tsunamis associated with typhoon can be predicted hours in advance; however, the oceanic RWs suddenly appear from nowhere and disappear without a trace [11]. Consequently, RWs attract more and more attention to many scientists and have been studied extensively in a lot of other fields, such as in optics [12,13,14], physics (for example acoustic turbulence in He II) [15], femtosecond plus propagation [16, 17], hydromechanics [18], meteorology [19] and even finance [20]. Nowadays, it is widely accepted that the modulation instability (MI) is the fundamental mechanism for the generation of the rogue waves [3, 21]. The foremost description of a single rogue wave is the rational solution of the NLS equation which features a localized peak whose amplitude is three times larger than that of the average height [22]. The high-order rogue wave solutions of the NLS equation have been studied in [23, 24]. Gradually, the rogue wave has been found in many other systems (e.g., the Hirota equation [25], Boussinesq equation [26], Sasa-Satsuma equation [27], Fokas–Lenells equation [28], the Manakov system [29], coupled Hirota equations [30, 31], NLS–Maxwell–Bloch system [32] and Yajima–Oikawa system [33]). Moreover, it is confirmed that the high-order rogue waves have some interesting patterns [34, 35], for instance, fundamental pattern, ring structure, triangular structure and so on.

The rest of the paper is organized as follows. In Sect. 2, we give the Lax pair and construct the corresponding classical DT and generalized DT of Eq. (1.3). In Sect. 3, the multisoliton solutions, breather solutions, and rogue wave solutions are derived by making use of the DT with the help of Maple. In Sect. 4, conclusions are given.

2 Lax pair and Darboux transformation

2.1 Lax pair

Without losing generality, let $\sigma =-1$,then Eq. (1.3) will become the following form:

$$\begin{aligned} u_{tx}+\alpha \beta ^{2}u-2i\alpha \beta u_{x}-\alpha u_{xx}-i\alpha \beta ^{2}|u|^{2}u_{x}=0\text {,} \end{aligned}$$

(2.1)

and the Lax pair (i.e., linear spectral problem) [36] of Eq. (2.1) is

$$\begin{aligned} \left\{ \begin{array}{l} R_{x}=UR,\ \ R_{t}=VR\text {,}\\ U=\begin{pmatrix} -i\lambda ^{2} &{} \lambda u_{x}) \\ \lambda r_{x} &{} i\lambda ^{2} \end{pmatrix},\\ V=\begin{pmatrix} -\frac{i\alpha \beta ^{2}}{2}ur-i\eta ^{2} &{} \frac{i\alpha \beta ^2}{2\lambda }u+\alpha \lambda u_{x} \\ -\frac{i\alpha \beta ^2}{2\lambda }r+\alpha \lambda r_{x} &{} \frac{i\alpha \beta ^{2}}{2}ur+i\eta ^{2} \end{pmatrix}, \end{array} \right. \end{aligned}$$

(2.2)

where $\eta = \sqrt{\alpha }(\lambda - \frac{\beta }{2\lambda })$, $r=-u^{*}$, “$*$” denotes the complex conjugate and the vector $R=(f,g)^T$ is an eigenfunction associated with $\lambda$ and potential u, which consists of two complex functions $f=f(x,t)$ and $g=g(x,t)$.

Trough direct calculations, we can verify that the integrability condition $U_t-V_x+[U,V]=0$ exactly gives Eq. (2.1), where $[U,V]=UV-VU$.

2.2 The classical DT

The DT is an effective approach used to solve the soliton equations [37,38,39]. We can obtain the soliton solutions, breather solutions by the classical DT and get the rogue wave solutions by the generalized DT. In the following, we will construct the two DTs.

(1) One-fold classical DT

The DT is a special gauge transformation,

$$\begin{aligned} R{[1]}=T{[1]}R, \end{aligned}$$

(2.3)

with

$$\begin{aligned} T{[1]}=T{[1]}(\lambda )=A_1 \lambda ^{2}+B_1 \lambda +I, \end{aligned}$$

(2.4)

where I denotes the identity matrix, and $A_1=(a_{ij}{[0]})_{2\times 2}$, $B_1=(b_{ij}{[0]})_{2\times 2}$ are $2\times 2$ matrices. The DT (2.3) transforms the old Lax pair (2.2) into a new Lax pair

$$\begin{aligned} \left\{ \begin{array}{l} R{[1]}_{x}=U{[1]}R{[1]}, \\ R{[1]}_{t}=V{[1]}R{[1]}, \end{array} \right. \end{aligned}$$

(2.5)

where U[1], V[1] have the similar forms as U, V in Eq. (2.2) with u replaced by u[1], and U[1], V[1] satisfy

$$\begin{aligned} \left\{ \begin{array}{l} U{[1]}T{[1]}=T{[1]}_{x}+T{[1]}U,\\ V{[1]}T{[1]}=T{[1]}_{t}+T{[1]}V. \end{array} \right. \end{aligned}$$

(2.6)

Furthermore, by direct computations and comparing the coefficients of $\lambda ^{i}$ (i is the power of $\lambda$) based on Eq. (2.6) [40], we can obtain the forms of $A_1$ and $B_1$

$$\begin{aligned} A_1=\begin{pmatrix} a_{11}{[0]} &{} 0 \\ 0 &{} a_{22}{[0]} \end{pmatrix}, \ \ \ B_1=\begin{pmatrix} 0 &{} b_{12}{[0]} \\ b_{21}{[0]} &{} 0 \end{pmatrix},\nonumber \\ \end{aligned}$$

(2.7)

and get the relation between potential functions u[1] and u:

$$\begin{aligned} u{[1]}=u+b_{12}{[0]}. \end{aligned}$$

(2.8)

Next, in order to determine the exact form of T[1], we assume that $R_1=(f_1,g_1)^T$ is an eigenfunction of the Lax pair (2.2) at $\lambda =\lambda _1$ when $u=u[0]$ is the initial seed solution, and then, $R_1^{\prime }=(-g^{*}_{1},f^{*}_{1})^{T}$ is also an eigenfunction of the Lax pair (2.2) at $\lambda =\lambda ^{*}_{1}$ and u[0], and the two eigenfunctions all satisfy the following algebraic equations

$$\begin{aligned} \left\{ \begin{array}{l} T[1](\lambda )|_{\lambda =\lambda _1}R_1=0,\\ T[1](\lambda )|_{\lambda =\lambda _1^*}R_1^{'}=0. \end{array} \right. \end{aligned}$$

(2.9)

Solving Eq. (2.9), we can get

$$\begin{aligned} \begin{aligned} a_{11}{[0]}=&-\frac{|f_{1}|^2\lambda _{1}^*+|g_{1}|^2\lambda _{1}}{|\lambda _{1}|^2(|f_{1}|^2\lambda _{1}+|g_{1}|^2\lambda _{1}^*)},\\ a_{22}{[0]}=&-\frac{|f_{1}|^2\lambda _{1}+|g_{1}|^2\lambda _{1}^*}{|\lambda _{1}|^2(|f_{1}|^2\lambda _{1}^*+|g_{1}|^2\lambda _{1})},\\ b_{12}{[0]}=&\frac{f_{1}g_{1}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^2(|f_{1}|^2\lambda _{1}+|g_{1}|^2\lambda _{1}^*)},\\ b_{21}{[0]}=&\frac{g_{1}f_{1}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^2(|f_{1}|^2\lambda _{1}^*+|g_{1}|^2\lambda _{1})}. \end{aligned} \end{aligned}$$

So the one-fold classical DT of Eq. (2.1) is defined as

$$\begin{aligned} \left\{ \begin{array}{l} R{[1]}=T{[1]}R, \ \ u{[1]}=u[0]+b_{12}{[0]},\\ T{[1]}=\begin{pmatrix} a_{11}{[0]}\lambda ^{2}+1 &{} b_{12}{[0]}\lambda \\ b_{21}{[0]}\lambda &{} a_{22}{[0]}\lambda ^{2}+1 \end{pmatrix},\\ b_{12}{[0]}=\dfrac{f_{1}[0]g_{1}[0]^{*}(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}[0]|^{2}\lambda _{1}+|g_{1}[0]|^{2}\lambda ^{*}_{1})}, \end{array} \right. \end{aligned}$$

(2.10)

where we set $R_{1}[0]=(f_1[0],g_1[0])^T=(f_1,g_1)^T$ for the uniform symbol representation in later words.

(2) Two-fold classical DT

To do the second step of classical DT, we assume that $R_{2}=(f_{2},g_{2})^{T}$ is a solution of Eq. (2.2) at $\lambda _{2}$ and u[0], then we employ $R_{2}{[1]}$, which is mapped to

$$\begin{aligned} R_{2}{[1]}=(f_{2}{[1]},g_{2}{[1]})^{T}=T{[1]}(\lambda )|_{\lambda =\lambda _{2}}R_{2}, \end{aligned}$$

and $R_{2}{[1]}$ is the solution of Eq. (2.2) at $\lambda =\lambda _{2}$ and u[1], as well as $R_{2}{[1]}^{'}=(-g_{2}{[1]}^*,f_{2}{[1]}^*)^{T}$ is also the solution for Eq. (2.2) at $\lambda =\lambda _{2}^*$ and u[1] [6]. Next, by the similar process as the one-fold classical DT, we can construct the two-fold classical DT

$$\begin{aligned} \left\{ \begin{array}{l} R{[2]}=T{[2]}R{[1]}=T{[2]}T{[1]}R,\\ u{[2]}=u{[1]}+b_{12}{[1]}=u[0]+(b_{12}{[0]}+b_{12}{[1]}),\\ T{[2]}=\begin{pmatrix} a_{11}{[1]}\lambda ^{2}+1 &{} b_{12}{[1]}\lambda \\ b_{21}{[1]}\lambda &{} a_{22}{[1]}\lambda ^{2}+1 \end{pmatrix},\\ b_{12}{[1]}=\dfrac{f_{2}{[1]}g_{2}{[1]}^*(\lambda ^{2}_{2}-\lambda ^{*2}_{2})}{|\lambda _{2}|^{2}(|f_{2}{[1]}|^{2}\lambda _{2}+|g_{2}{[1]}|^{2}\lambda ^{*}_{2})}. \end{array} \right. \end{aligned}$$

(2.11)

(3) n-fold classical DT

If n distinct solutions $R_{j}=(f_{j},g_{j})^{T}$, $1\le j \le n$ of Eq. (2.2) are given, then the classical DT may be iterated. Continuing the above iteration process, we get the n-fold classical DT and have the following theorem.

Theorem 1

Let $R_{1}, R_{2}, \ldots , R_{n}$ be n distinct solutions of Eq. (2.2) at $\lambda _{1}, \lambda _{2}, \ldots , \lambda _{n}$, respectively. Then the n-fold classical DT for the GNLS equation (2.1) is defined as

$$\begin{aligned} \left\{ \begin{array}{l} R{[n]}=T{[n]}T{[n-1]}\ldots T{[1]}R,\\ u{[n]}=u[0]+\sum _{j=1}^{n} b_{12}{[j-1]},\\ T{[j]} =\begin{pmatrix} a_{11}{[j-1]}\lambda ^{2}+1 &{} b_{12}{[j-1]}\lambda \\ b_{21}{[j-1]}\lambda &{} a_{22}{[j-1]}\lambda ^{2}+1 \end{pmatrix}, \\ b_{12}{[j-1]}=\dfrac{f_{j}{[j-1]}g_{j}{[j-1]}^*(\lambda ^{2}_{j}-\lambda ^{*2}_{j})}{|\lambda _{j}|^{2}(|f_{j}{[j-1]}|^{2}\lambda _{j}+|g_{j}{[j-1]}|^{2}\lambda ^{*}_{j})}, \end{array} \right. \end{aligned}$$

(2.12)

and $R_{1}{[0]}=(f_{1}{[0]},g_{1}{[0]})^{T}=(f_1,g_1)^{T}$,

$$\begin{aligned} \begin{aligned} R_{j}{[j-1]}&=(f_{j}{[j-1]},g_{j}{[j-1]})^{T}\\&=(T{[j-1]}T{[j-2]} \ldots T{[1]})|_{\lambda =\lambda _{j}}R_{j}, \end{aligned} \end{aligned}$$

(2.13)

where u[0] is the initial seed solution of Eq. (2.2), and $R_{j}{[j-1]}$, $j=1, 2, 3, \ldots n$ is the solution of Eq. (2.2) at $\lambda =\lambda _{j}$ and $u{[j-1]}$.

Obviously, the iteration process of the DT can be simply described as

$$\begin{aligned} R \xrightarrow {T[1]} R[1] \xrightarrow {T[2]} R[2] \xrightarrow {T[3]} \dots R[n-1] \xrightarrow {T[n]} R[n], \end{aligned}$$

and then

$$\begin{aligned} u[0] \longrightarrow u[1] \longrightarrow u[2] \longrightarrow \dots u[n-1] \longrightarrow u[n]. \end{aligned}$$

2.3 The generalized DT

In the high-order iteration process of DT, the classical DT must be performed under the distinct eigenvalues $\lambda _j$ $(j=1,2,\dots ,n)$. However, for getting the high-order rogue wave solutions of the soliton equations, the iteration process of DT must be performed under the same eigenvalues, that is the generalized DT. Next, we manage to construct the generalized DT.

(1) One-fold generalized DT

Suppose that $R_1(\lambda _{1}+\delta )$ is a basic solution for Eq. (2.2) at $\lambda =\lambda _{1}+\delta$, and we can expand it at $\delta =0$, then we have form as follows:

$$\begin{aligned} R_1=R_1^{[0]}+R_1^{[1]}\delta +R_1^{[2]}\delta ^{2}+\cdots +R_1^{[n]}\delta ^{n}+\cdots ,\qquad \end{aligned}$$

(2.14)

where $\delta$ is a small parameter, $R_1^{[k]}=(f_1^{[k]},g_1^{[k]})^{T}$ $=\lim \limits _{\delta \rightarrow 0}{\frac{1}{k!}\frac{\partial ^{k}R_1}{\partial \delta ^{k}}}$ $(k=0, 1, 2, \ldots )$, and $R_1^{[0]}=(f_1^{[0]},g_1^{[0]})^{T}$ is a special solution of Eq. (2.2) at $\lambda =\lambda _{1}$ when the seed solution is $u=u[0]$. Thus, the first step of the generalized DT for Eq. (2.1) is the same as the one-fold classical DT, that is

$$\begin{aligned} \left\{ \begin{array}{l} R{[1]}=T{[1]}R,\ \ u{[1]}=u[0]+b_{12}{[0]},\\ T{[1]}=\begin{pmatrix} a_{11}{[0]}\lambda ^{2}+1 &{} b_{12}{[0]}\lambda \\ b_{21}{[0]}\lambda &{} a_{22}{[0]}\lambda ^{2}+1 \end{pmatrix},\\ b_{12}{[0]}=\frac{f_{1}{[0]}g_{1}{[0]}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}{[0]}|^{2}\lambda _{1}+|g_{1}{[0]}|^{2}\lambda ^{*}_{1})}, \end{array} \right. \end{aligned}$$

(2.15)

where $R_{1}{[0]}=(f_{1}{[0]},g_{1}{[0]})^{T}=(f_1^{[0]},g_1^{[0]})^{T}$.

(2) Two-fold generalized DT

Now we make the two-fold generalized DT through a limit process. After the transformation in Eq. (2.15), we know that $T{[1]}R_1$ is a solution of Eq. (2.2) at $\lambda =\lambda _{1}+\delta$ and u[1]. Thus, through the limit process

$$\begin{aligned} \begin{aligned} \lim _{\delta \rightarrow 0}\frac{T{[1]}|_{\lambda =\lambda _{1}+\delta }R_1}{\delta }&=\lim _{\delta \rightarrow 0}\frac{(T{[1]}|_{\lambda =\lambda _{1}}+C_{1}\delta +C_{2}\delta ^{2})R_1}{\delta }\\&=T{[1]}|_{\lambda =\lambda _{1}}R_1^{[1]}+C_{1}R_1^{[0]}\\&=R_{1}{[1]}, \end{aligned} \end{aligned}$$

(2.16)

with

$$\begin{aligned} \begin{aligned}&T{[1]}|_{\lambda =\lambda _{1}}R_1^{[0]}=0,\ \ C_{1}=\begin{pmatrix} 2a_{11}{[0]}\lambda _{1} &{} b_{12}{[0]} \\ b_{21}{[0]} &{} 2a_{22}{[0]}\lambda _{1} \end{pmatrix},\\&C_{2}=\begin{pmatrix} a_{11}{[0]} &{} 0 \\ 0 &{} a_{22}{[0]} \end{pmatrix}, \end{aligned} \end{aligned}$$

(2.17)

we can find that $R_{1}{[1]}=(f_1[1],g_1[1])^T$ is a solution of Eq. (2.2) at $\lambda =\lambda _{1}$ and u[1]. So the second step of the generalized DT of Eq. (2.1) is defined as

$$\begin{aligned} \left\{ \begin{array}{l} R{[2]}=T{[2]}R{[1]}=T{[2]}T{[1]}R,\\ u{[2]}=u{[1]}+b_{12}{[1]}=u[0]+(b_{12}{[0]}+b_{12}{[1]}),\\ T{[2]}=\begin{pmatrix} a_{11}{[1]}\lambda ^{2}+1 &{} b_{12}{[1]}\lambda \\ b_{21}{[1]}\lambda &{} a_{22}{[1]}\lambda ^{2}+1 \end{pmatrix},\\ b_{12}{[1]}=\frac{f_{1}{[1]}g_{1}{[1]}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}{[1]}|^{2}\lambda _{1}+|g_{1}{[1]}|^{2}\lambda ^{*}_{1})}. \end{array} \right. \end{aligned}$$

(2.18)

(3) Three-fold generalized DT

Similarly, we have the limit

$$\begin{aligned} \begin{aligned}&\lim _{\delta \rightarrow 0}\frac{(T{[2]} T{[1]})|_{\lambda =\lambda _{1}+\delta }R_1}{\delta ^{2}}\\&\quad = \lim _{\delta \rightarrow 0}\frac{1}{\delta ^{2}}\{(T{[2]}|_{\lambda =\lambda _{1}}+C_{3}\delta +C_{4}\delta ^{2})\cdot \\ {}&\quad \qquad (T{[1]}|_{\lambda =\lambda _{1}}+C_{1}\delta +C_{2}\delta ^{2})R_1\}\\&\quad =(T{[2]}T{[1]})|_{\lambda =\lambda _{1}}R_1^{[2]}\\&\qquad +(T{[2]}|_{\lambda =\lambda _{1}}C_{1}+C_{3}T{[1]}|_{\lambda =\lambda _{1}})R_1^{[1]}\\&\qquad +(C_{3}C_{1}+T{[2]}|_{\lambda =\lambda _{1}}C_{2}+C_{4}T{[1]}|_{\lambda =\lambda _{1}})R_1^{[0]}\\&\quad = R_{1}{[2]}, \end{aligned} \end{aligned}$$

(2.19)

with

$$\begin{aligned} \begin{aligned}&T{[1]}|_{\lambda =\lambda _{1}}R_1^{[0]}=0,\\&T{[2]}|_{\lambda =\lambda _{1}}(T{[1]}|_{\lambda =\lambda _{1}}R_1^{[1]}+C_{1}R_1^{[0]})=0,\\&C_{3}=\begin{pmatrix} 2a_{11}{[1]}\lambda _{1} &{} b_{12}{[1]} \\ b_{21}{[1]} &{} 2a_{22}{[1]}\lambda _{1} \end{pmatrix},\ \ C_{4}=\begin{pmatrix} a_{11}{[1]} &{} 0 \\ 0 &{} a_{22}{[1]} \end{pmatrix}. \end{aligned} \end{aligned}$$

(2.20)

And Eq. (2.19) provides a solution $R_1[2]=(f_1[2],g_1[2])^T$ for Eq. (2.2) at $\lambda =\lambda _{1}$ and u[2]. Thus, we may do the third-step iteration of the generalized DT as follows:

$$\begin{aligned} \left\{ \begin{array}{l} R{[3]}=T{[3]}R{[2]}=T{[3]}T{[2]}T{[1]}R,\\ u{[3]}=u{[2]}+b_{12}{[2]}=u[0]+\sum _{j=1}^{3} b_{12}{[j-1]},\\ T{[3]}=\begin{pmatrix} a_{11}{[2]}\lambda ^{2}+1 &{} b_{12}{[2]}\lambda \\ b_{21}{[2]}\lambda &{} a_{22}{[2]}\lambda ^{2}+1 \end{pmatrix}, \\ b_{12}{[2]}=\frac{f_{1}{[2]}g_{1}{[2]}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}{[2]}|^{2}\lambda _{1}+|g_{1}{[2]}|^{2}\lambda ^{*}_{1})}. \end{array} \right. \end{aligned}$$

(2.21)

(4) n-fold generalized DT

Continuing the above process and basing on the classical DT, the high-order generalized DT is constructed. Thus, we can obtain the n-fold generalized DT of Eq. (2.1):

$$\begin{aligned} \left\{ \begin{array}{l} R{[n]}=T{[n]}T{[n-1]}\ldots T{[1]}R,\\ u{[n]}=u[0]+\sum _{j=1}^{n} b_{12}{[j-1]},\\ T{[j]} =\begin{pmatrix} a_{11}{[j-1]}\lambda ^{2}+1 &{} b_{12}{[j-1]}\lambda \\ b_{21}{[j-1]}\lambda &{} a_{22}{[j-1]}\lambda ^{2}+1 \end{pmatrix}, \\ b_{12}{[j-1]}=\frac{f_{1}{[j-1]}g_{1}{[j-1]}^*(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}{[j-1]}|^{2}\lambda _{1}+|g_{1}{[j-1]}|^{2}\lambda ^{*}_{1})}, \end{array} \right. \end{aligned}$$

(2.22)

where $R_{1}{[0]}=(f_1{[0]},g_1{[0]})^{T}=(f_1^{[0]},g_1^{[0]})^{T}$,

$$\begin{aligned} \begin{aligned}&R_{1}{[j-1]}=(f_{1}{[j-1]},g_{1}{[j-1]})^{T}\\&\quad =\lim _{\delta \rightarrow 0}\frac{(T{[j-1]}T{[j-2]}\ldots T{[1]})|_{\lambda =\lambda _{1}+\delta }R_1}{\delta ^{j-1}}, \end{aligned} \end{aligned}$$

(2.23)

and $R_{1}{[j-1]}$, $(j=1, 2, 3, \ldots , n)$ is the solution of Eq. (2.2) at $\lambda =\lambda _{1}$ and $u{[j-1]}$.

Fig. 1

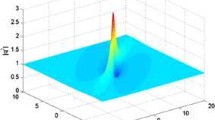
a Evolution of one-soliton solution $u_{s}{[1]}$ via Eq. (3.2) with parameter $\lambda _{1}=\frac{1}{4}+\frac{1}{4}i$, b corresponding density plot

3 Soliton solutions, breather solutions, and rogue wave solutions

3.1 Multisoliton solutions

In this subsection, we present the multisoliton solutions of Eq. (2.1) explicitly. Take $u=u[0]=0$, that is zero initial seed solution for Eq. (2.2) and let $\alpha = 1$, $\beta = -1$. Then solving Eq. (2.2) by the Maple, we can obtain the forms of eigenfunction with regard to $\lambda =\lambda _{j}$ $(j=1, 2,\ldots , n)$

$$\begin{aligned} \begin{aligned}&R_{j}=(f_{j},g_{j})^T,\\&f_{j}={e^{ - i\left( {\frac{{{{(2\lambda _j^2 + 1)}^2}}}{{4\lambda _j^2}}t + \lambda _j^2x} \right) }},\ \ g_{j}={e^{i\left( {\frac{{{{(2\lambda _j^2 + 1)}^2}}}{{4\lambda _j^2}}t + \lambda _j^2x} \right) }}. \end{aligned} \end{aligned}$$

(3.1)

(1) When $n=1$, after simple calculations in Eq. (2.10), we have

$$\begin{aligned} u_{s}{[1]}=4i\eta _{1}\xi _{1}\frac{e^{F_{s1}}}{(\lambda _{1}e^{D_{s1}}+ \lambda _{1}^{*})|\lambda _{1}|^{2}}, \end{aligned}$$

(3.2)

with

$$\begin{aligned} \begin{aligned}&\lambda _{1}=\xi _{1}+i\eta _{1},\ \ \lambda _{1}^{*}=\xi _{1}-i\eta _{1},\\&F_{s1}= \frac{{ - i}}{{2\lambda _1^2}}\left( {4\lambda _1^4(x + t) + (4\lambda _1^2 + 1)t} \right) ,\\&D_{s1}=2\xi _{1}\eta _{1}\frac{4|\lambda _{1}|^{4}(x+t)-t}{|\lambda _{1}|^{4}}. \end{aligned} \end{aligned}$$

$u_{s}{[1]}$ is the one-soliton solution of Eq. (2.1), and it represents a bright single soliton whose dynamic features are delineated in Fig. 1 when we take the parameter $\lambda _{1}=\frac{1}{4}+\frac{1}{4}i$.

(2) When $n=2$ in Theorem 1, we can obtain the following two-soliton solution of Eq. (2.1)

$$\begin{aligned} \begin{aligned} u_{s}{[2]}=&\frac{{{{60i}}{{{e}}^{ - 2it}}F_{s2}}}{{D_{s2} \cdot D_{s3}}}, \end{aligned} \end{aligned}$$

(3.3)

with

$$\begin{aligned} \begin{aligned} D_{s2}&= ( {{{1 + i}}} ){{{e}}^{{{ - }}\frac{{15}}{4}{{t + }}\frac{1}{4}{{x}}}}{{ + }}( {{{1 - i}}} ){{{e}}^{\frac{{15}}{4}{{t - }}\frac{1}{4}{{x}}}} ,\\ F_{s2}&= ( {1 + i} ) \left( 2{e^{\frac{1}{2}x + \frac{{15}}{2}t}}\right. \\&\quad \left. +\, 2{{{e}}^{\frac{3}{2}{{x - }}\frac{{15}}{2}{{t}}}}{{ - }}{{{e}}^{\frac{{15}}{4}{{t - }}\frac{1}{4}{{x}}}}{{ - }} {{{e}}^{{{ - }}\frac{{45}}{4}{{t + }}\frac{3}{4}{{x}}}} \right) \\&\quad +\, ( {1 - i} )\left( 2{e^{ - \frac{1}{2}x - \frac{{15}}{2}t}} + 2{e^{ - \frac{3}{2}x + \frac{{15}}{2}t}} \right. \\&\quad \left. - {{{e}}^{{{ - }}\frac{{15}}{4}{{t + }}\frac{1}{4}{{x}}}} - {e^{\frac{{45}}{4}t - \frac{3}{4}x}} \right) ,\\ D_{s3}&= ( {1 + i} )\left( 9{e^{\frac{3}{2}x - \frac{{15}}{2}t}} + 16{e^{ - x}} \right. \\&\quad \left. + 25{e^{\frac{1}{2}x + \frac{{15}}{2}t}} - 40{e^{\frac{{15}}{4}t - \frac{1}{4}x}} \right) \\&\quad +\, ( {1 - i} )\left( 9{e^{ - \frac{3}{2}x + \frac{{15}}{2}t}} + 16{e^x} \right. \\&\quad \left. +\, 25{e^{ - \frac{1}{2}x - \frac{{15}}{2}t}}{{ - 40}}{{{e}}^{{{ - }}\frac{{15}}{4}{{t + }}\frac{1}{4}{{x}}}} \right) , \end{aligned} \end{aligned}$$

when we take $\lambda _{1}=\frac{1}{4}+\frac{1}{4}i$, $\lambda _{2}=\frac{1}{2}+\frac{1}{2}i$.

The dynamic features of the two-soliton solution $u_{s}{[2]}$ are displayed in Fig. 2. We find that the two-soliton solution represents the elastic interaction between two bell-shaped bright solitons, and the solitonic shapes as well as amplitudes have not changed after the interaction.

(3) When $n=3$ in Theorem 1, similarly, we get the three-soliton solution of Eq. (2.1)

$$\begin{aligned} \begin{aligned} u_{s}{[3]}=u_{s}{[2]}+\frac{f_{3}{[2]}g_{3}{[2]}^*(\lambda ^{2}_{3}- \lambda ^{*2}_{3})}{|\lambda _{3}|^{2}(|f_{3}{[2]}|^{2}\lambda _{3}+|g_{3}{[2]}|^{2} \lambda ^{*}_{3})}, \end{aligned} \end{aligned}$$

(3.4)

where $u_{s}{[2]}$ is given in Eq. (3.3), and $R_3{[2]}=(f_{3}{[2]},g_{3}{[2]})^{T}=(T{[2]}T{[1]})|_{\lambda =\lambda _{3}}R_3$ (where $R_3=(f_3,g_3)^T$ is the solution of Eq. (2.2) at $\lambda =\lambda _{3}$ and $u=u[0]=0$) is the solution of Eq. (2.2) at $\lambda =\lambda _{3}$ and $u=u_{s}{[2]}$. The explicit expression of Eq. (3.4) is not given here because of its tedious formulas.

The three-soliton solution $u_{s}{[3]}$ represents the overtaking interaction among three bell-shaped bright solitons, whose dynamic features are shown in Fig. 3, and we find that the solitonic shapes as well as amplitudes have not changed after the interaction.

We remark that we can also obtain the higher-order soliton solutions of the new GNLS equation (2.1) by continuing the iteration process of the classical DT in Theorem 1.

Fig. 2

a Evolution of two-soliton solution $u_{s}{[2]}$ via Eq. (3.3) with parameters $\lambda _{1}=\frac{1}{4}+\frac{1}{4}i$, $\lambda _{2}=\frac{1}{2}+\frac{1}{2}i$, b corresponding density plot

Fig. 3

a Evolution of three-soliton solution $u_{s}{[3]}$ via Eq. (3.4) with parameters $\lambda _{1}=\frac{1}{4}+\frac{1}{4}i$, $\lambda _{2}=\frac{1}{2}+\frac{1}{2}i$, $\lambda _{3}=1+i$, b corresponding density plot

3.2 Multibreather solutions

In this subsection, we take the plane wave seed solution $u=u[0]=e^{i\theta }=e^{i(ax+bt)}$ of Eq. (2.1) with the dispersion condition $b =\frac{1}{a} (a\alpha \beta ^2+a^2\alpha +2a\alpha \beta +\alpha \beta ^2)$. Without loss of generality, we assume that $\alpha = 1$, $\beta = -1$, $a = -1$, that is $\theta =-(x+3t)$, then Eq. (2.2) is solved by

$$\begin{aligned} \begin{aligned}&R_{j}=(f_{j},g_{j})^T,\\&f_{j}=C1 e^{\frac{i}{2}(M+\theta )}-C2 e^{\frac{i}{2}(-M+\theta )},\\&g_{j}=C1 e^{-\frac{i}{2}(M+\theta )}+C2 e^{-\frac{i}{2}(-M+\theta )},\\ \end{aligned} \end{aligned}$$

(3.5)

with

$$\begin{aligned} \begin{aligned}&S = 4\lambda _{j}^4+1,\ \ M = \sqrt{S} (t+x-\frac{t}{2\lambda _{j}^2}),\\&C1 = \frac{2\lambda _{j}^2-\sqrt{S}-1}{2\lambda _{j}}, \ \ C2 = 1,\ \ j=1, 2, \ldots , n. \end{aligned} \end{aligned}$$

(1) When $n=1$ in the classical DT of Theorem 1, $R_{1}$ is the eigenfunction of Eq. (2.2) corresponding to $\lambda _{1}=\xi _{1}+\eta _{1}i$, and set $|\xi _{1}|=|\eta _{1}|$, so that $Im(S)=0$. Thus, the one-breather solution $u_{b}{[1]}$ is obtained as

$$\begin{aligned} u_{b}{[1]}=u[0]+\frac{f_{1}[0]g_{1}[0]^{*}(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}[0]|^{2}\lambda _{1}+|g_{1}[0]|^{2}\lambda ^{*}_{1})}, \end{aligned}$$

(3.6)

and $(f_{1}[0],g_{1}[0])^T=(f_1,g_1)^T$.

From Eq. (3.6), we can obtain several different one-breather solutions of Eq. (2.1) when taking different parameters, including the Akhmediev breather solution and the general breather solution.

Case 1 When $Re(S)>0$, that is $|\xi _{1}|=|\eta _{1}|<\frac{1}{2}$, we can obtain the Akhmediev breather solution of Eq. (2.1) if we take some appropriate parameters. For example, let $\lambda _{1}=\frac{2}{5}+\frac{2}{5}i$, then

$$\begin{aligned} u_{b-1}{[1]}=e^{i\theta }+\frac{\frac{i}{4}{{{e}}^{\frac{{{{3}}\sqrt{{{41}}} }}{{{{32}}}}{{t}}}} a_{1}a_{2}}{a_{3}}, \end{aligned}$$

(3.7)

where

$$\begin{aligned} \begin{aligned} a_{1}&= \left( {3\sqrt{{{41}}} i + {{41}}i - 3\sqrt{{{41}}} - 9} \right) {e^{i\left( {\frac{{3\sqrt{{{41}}} \left( {{{25it + 16t + 16x}}} \right) }}{{800}}{{ + }}\frac{\theta }{2}} \right) }} \\&\quad - 40{e^{ - i\left( {\frac{{3\sqrt{{{41}}} \left( {{{25it + 16t + 16x}}} \right) }}{{800}} - \frac{\theta }{2}} \right) }},\\ a_{2}&= \left( {3\sqrt{{{41}}} i + {{41}}i + 3\sqrt{{{41}}} + 9} \right) {e^{i\left( {\frac{{3\sqrt{{{41}}} \left( {{{ - 25it + 8t + 8x}}} \right) }}{{400}}{{ + }}\frac{\theta }{2}} \right) }} \\&\quad - 40{e^{ - i\left( {\frac{{3\sqrt{{{41}}} \left( {{{t + x}}} \right) }}{{50}} - \frac{\theta }{2}} \right) }},\\ a_{3}&= 5\left( {3\sqrt{{{41}}} i + {{9}}i - 3\sqrt{{{41}}} - {{41}}} \right) {e^{\frac{{3\sqrt{41} }}{8}t}} \\&\quad + 128i{e^{\frac{{3\sqrt{{{41}}} i}}{{400}}\left( {{{ - 25it + 16t + 16x}}} \right) }}\\&\quad - 8i\left( {3\sqrt{{{41}}} + 25} \right) {e^{\frac{{ - 3\sqrt{{{41}}} i}}{{400}}\left( {{{25it + 16t + 16x}}} \right) }} \\&\quad - 5\left( {3\sqrt{{{41}}} i + {{9}}i + 3\sqrt{{{41}}} {{ + 41}}} \right) . \end{aligned} \end{aligned}$$

The dynamic features of the Akhmediev breather solution in Eq. (3.7) are delineated in Fig. 4. And we can see that the Akhmediev breather solution is periodic in space and localized in time.

Case 2 When $Re(S)<0$, that is $|\xi _{1}|=|\eta _{1}|>\frac{1}{2}$, similarly, let $\lambda _{1}=\frac{11}{20}+\frac{11}{20}i$, then we get

$$\begin{aligned} u_{b-2}{[1]}=e^{i\theta }-\frac{ \frac{10i}{121}{{{e}}^{\frac{{\sqrt{{{4641}}} }}{{{{200}}}}{{(t+x)}}}}b_{1}b_{2}}{b_{3}}, \end{aligned}$$

(3.8)

where

$$\begin{aligned} \begin{aligned} b_{1}&= \left( {\sqrt{{{4641}}} i - {{221}}i + \sqrt{4641} - 21} \right) \\&\quad \times {e^{i\left( {\frac{{\sqrt{{{4641}}} \left( {{{ - 100t + 121it + 121ix}}} \right) }}{{24200}}{{ + }}\frac{\theta }{2}} \right) }} \\&\quad + 220{e^{ - i\left( {\frac{{\sqrt{{{4641}}} \left( {{{ - 100t + 121it + 121ix}}} \right) }}{{24200}} - \frac{\theta }{2}} \right) }},\\ b_{2}&= \left( {\sqrt{{{4641}}} i - {{221}}i - \sqrt{4641} + 21} \right) \\&\quad \times {e^{ - i\left( {\frac{{\sqrt{{{4641}}} \left( {{{50t + 121it + 121ix}}} \right) }}{{12100}} - \frac{\theta }{2}} \right) }} + 220{e^{i\left( {\frac{{\sqrt{4641} }}{{242}}t + \frac{\theta }{2}} \right) }},\\ b_{3}&= 11\left( {\sqrt{{{4641}}} i - {{21}}i - \sqrt{4641} + 221} \right) \\&\quad \times {e^{\frac{{\sqrt{4641} }}{{50}}\left( {t + x} \right) }} + 2000i{e^{\frac{{\sqrt{{{4641}}} }}{{12100}}\left( {{{100it + 121t + 121x}}} \right) }}\\&\quad + 20i\left( {\sqrt{{{4641}}} - 121} \right) {e^{\frac{{ - \sqrt{{{4641}}} }}{{12100}}\left( {{{100it - 121t - 121x}}} \right) }} \\ {}&\quad - 11\left( {\sqrt{{{4641}}} i - {{21}}i + \sqrt{4641} - 221} \right) . \end{aligned} \end{aligned}$$

Obviously, Eq. (3.8) is the general breather solution of Eq. (2.1), and it is periodic both in space and in time from Fig. 5.

Fig. 4

a Evolution of the Akhmediev breather solution $u_{b-1}{[1]}$ via Eq. (3.7) with parameter $\lambda _{1}=\frac{2}{5}+\frac{2}{5}i$, b corresponding density plot

Fig. 5

a Evolution of the general breather solution $u_{b-2}{[1]}$ via Eq. (3.8) with parameter $\lambda _{1}=\frac{11}{20}+\frac{11}{20}i$, b corresponding density plot

(2) When $n=2$, the two-breather solution $u_{b}{[2]}$ is also derived from the second step of classical DT in Eq. (2.11),

$$\begin{aligned} u_{b}{[2]}=u_{b}{[1]}+\frac{f_{2}{[1]}g_{2}[1]^{*}(\lambda ^{2}_{2} -\lambda ^{*2}_{2})}{|\lambda _{2}|^{2}(|f_{2}{[1]}|^{2}\lambda _{2}+|g_{2}{[1]}|^{2}\lambda ^{*}_{2})}, \end{aligned}$$

(3.9)

where $(f_{2}{[1]},g_{2}{[1]})^T$ is the solution of Eq. (2.2) at $\lambda =\lambda _{2}$ and $u_{b}{[1]}$. We can get distinct two-breather solutions of Eq. (2.1) while we take different parameters (see Figs. 6, 7, 8). Assuming that $\lambda _j=\xi _j+\eta _j$, $j=1,2$, and $|\xi _j|=|\eta _j|$, that is $Im(S|_{\lambda =\lambda _j})=0$.

Fig. 6

a Evolution of the first kind of two-breather solution $u_{b}{[2]}$ via Eq. (3.9) with parameters $\lambda _{1}=\frac{2}{5}+\frac{2}{5}i$, $\lambda _{2}=\frac{3}{5}+\frac{3}{5}i$, b corresponding density plot

Fig. 7

a Evolution of the second kind of two-breather solution $u_{b}{[2]}$ via Eq. (3.9) with parameters $\lambda _{1}=\frac{2}{5}+\frac{2}{5}i$, $\lambda _{2}=\frac{11}{25}+\frac{11}{25}i$, b corresponding density plot

Fig. 8

a Evolution of the third kind of two-breather solution $u_{b}{[2]}$ via Eq. (3.9) with parameters $\lambda _{1}=\frac{11}{20}+\frac{11}{20}i$, $\lambda _{2}=\frac{3}{5}+\frac{3}{5}i$, b corresponding density plot

When $Re(S|_{\lambda _{1}})>0$, and $Re(S|_{\lambda _{2}})<0$, the solution $u_{b}{[2]}$ represents the elastic interaction between two-breather solutions, in which one is a space-periodic breather solution and the other one is a periodic breather solution in both space and time (see Fig. 6).

When $Re(S|_{\lambda _{1}})>0$, and $Re(S|_{\lambda _{2}})>0$, the solution $u_{b}{[2]}$ represents the elastic interaction between two space-periodic breather solutions (see Fig. 7).

When $Re(S|_{\lambda _{1}})<0$, and $Re(S|_{\lambda _{2}})<0$, the solution $u_{b}{[2]}$ represents the elastic interaction between two-breather solutions, which are all periodic breather solutions both in space and in time (see Fig. 8).

It is obvious that the higher-order breather solutions of Eq. (2.1) can be obtained while we continue the iteration of the classical DT in Theorem 1.

3.3 Rogue wave solutions

In this subsection, we construct the rogue wave solutions of the new GNLS equation (2.1). This kind of solution only appears in some special region of time and space and then drowns into a fixed non-vanishing plane. In fact, the rogue wave solutions can be obtained by the limits of the eigenfunctions [41,42,43] or the limits of the breather solutions [44,45,46].

From Eq. (3.5), we can get a new eigenfunction of the Lax pair (2.2)

$$\begin{aligned} \begin{aligned}&R_1(\varepsilon )=(f_1,g_1)^T, \\&f_1=C1 e^{\frac{i}{2}(M+\theta )}-C2 e^{\frac{i}{2}(-M+\theta )},\\&g_1=C1 e^{-\frac{i}{2}(M+\theta )}+C2 e^{-\frac{i}{2}(-M+\theta )},\\&C1 = \frac{2\lambda ^2-\sqrt{S}-1}{2\lambda }, \ \ C2 = 1,\ \ S = 4\lambda ^4+1,\\&M = \sqrt{S} \left( t+x-\frac{t}{2\lambda ^2}+\sum _{k=1}^{n}s_{k}\varepsilon ^{2k}\right) , \end{aligned}\nonumber \\ \end{aligned}$$

(3.10)

where $\varepsilon$ is a small parameter, $s_{k}=m_{k}+n_{k}i$. If we fix $\lambda _1=\frac{1}{2}+\frac{1}{2}i$, and let $\lambda =\frac{1}{2}+\frac{1}{2}i+\varepsilon ^{2}$, then $R_1(\varepsilon )$ can be expanded at $\varepsilon =0$, so we have

$$\begin{aligned} R_1(\varepsilon )=R_1^{[0]}+R_1^{[1]}\varepsilon ^{2}+R_1^{[2]}\varepsilon ^{4}+R_1^{[3]}\varepsilon ^{6}+\cdots , \end{aligned}$$

(3.11)

where

$$\begin{aligned} R_1^{[0]}= & {} \begin{pmatrix} (i-1)e^{\frac{i\theta }{2}} \\ (i+1)e^{\frac{-i\theta }{2}} \end{pmatrix} , \end{aligned}$$

(3.12)

$$\begin{aligned} R_1^{[1]}= & {} \begin{pmatrix} P_1 e^{\frac{i\theta }{2}} \\ Q_1 e^{\frac{-i\theta }{2}} \end{pmatrix} , \end{aligned}$$

(3.13)

$$\begin{aligned} R_1^{[2]}= & {} \begin{pmatrix} - \frac{1}{{12}}P_1e^{\frac{i\theta }{2}} \\ \frac{1}{{12}}Q_1e^{-\frac{i\theta }{2}} \end{pmatrix} , \end{aligned}$$

(3.14)

$$\begin{aligned} R_1^{[3]}= & {} \begin{pmatrix} - \frac{1}{{180}}P_2e^{\frac{i\theta }{2}} \\ \frac{1}{{180}}Q_2e^{-\frac{i\theta }{2}} \end{pmatrix} , \end{aligned}$$

(3.15)

with

$$\begin{aligned} \begin{aligned} P_1=&\,2itx + i{x^2} + 2it - 2{t^2} - 2tx + 1 - i + 2t + 2x,\\ Q_1=&\,2i{t^2} + 2itx - 2it + 2tx + {x^2} + 1 - i - 2t - 2x,\\ P_2=&\, 24t - 12x - 12 - 12i + 4{t^4} - {x^4} - 18{x^2} - 84{t^2}\\ {}&- 24ix{m_1}- 12i{t^2}{x^2} - 24i{t^2}x - 24it{m_1} + 24it{n_1} \\ {}&- 4{x^3}+ 4i{t^4} - 16i{t^3} + 4i{x^3} - 36i{t^2}+ 12{t^2}{x^2} \\ {}&+ 48it + 12ix - 24i{n_1} - 72tx + 24t{n_1} + 24x{n_1} \\&+ 24t{m_1} - i{x^4}+ 16{t^3}x - 6i{x^2} - 24{t^2}x - 24{m_1} \\ {}&- 24t{x^2} - 8it{x^3}, \\ Q_2=&\, 16i{t^3}x + 12i{t^2}{x^2} - 72itx + 24it{m_1} + 24ix{n_1}\\ {}&+ 24t - 12x + 12 + 12I - 60i{t^2} - 30i{x^2} - 4{t^4} \\&+ {x^4}+ 18{x^2} + 60{t^2} - 4{x^3} - 24i{t^2}x + 24it{n_1} \\ {}&+ 4i{t^4} - i{x^4} - 16i{t^3} + 4i{x^3} + 48it + 12ix \\ {}&- 24i{n_1} + 48tx - 24t{n_1} - 24{m_1}+24x{m_1}+ 8t{x^3} \\&+ 12{t^2}{x^2} - 24{t^2}x - 24t{x^2} + 24t{m_1},\\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} P_3=&\, 360 - 1800t - {x^6} + 24{t^5} - 75{x^4} - 180{t^4} - 480{t^3} \\ {}&- 270{x^2} + 2340{t^2} - 360{m_2} + 8i{t^6} - 24i{t^5} \\ {}&- 40i{t^3}{x^3}- 540i{t^4} + 15i{x^4} + 960i{t^3} + 240i{x^3}\\ {}&- 540i{t^2} + 270i{x^2} - 180im_1^2 + 180in_1^2 + 360it \\ {}&+ 360ix + 180i{m_1} - 180i{n_1}- 360i{n_2} - 360it{m_2} \\ {}&- 1080it{n_1} - 180ix{m_1} - 180i{x^2}{n_1} - 360ix{m_2} \\ {}&- 540ix{n_1} + 60{t^4}{x^2} + 6i{x^5} - 30i{t^2}{x^4} - 6it{x^5} \\ {}&- 120i{t^4}x - 120i{t^3}{x^2} + 30it{x^4} - 720i{t^3}x \\ {}&+ 240i{t^3}{n_1} - 360tx - 60i{x^3}{m_1} - 60i{x^3}{n_1} \\ {}&+ 1440i{t^2}x - 360i{t^2}{m_1} - 360i{t^2}{n_1} + 720it{x^2} \\ {}&+ 180i{x^2}{m_1} + 360it{n_2} - 720itx + 360{t^2}{n_1}\\ {}&+ 360t{n_2} + 360x{n_2}+ 360t{m_2} - 30t{x^4} - 960{t^3}x \\ {}&+ 40{t^3}{x^3} - 6t{x^5} + 24{t^5}x + 60{x^3}{n_1} - 720tx{m_1}\\ {}&- 60{x^3}{m_1} + 360{m_1}{n_1} - 360i{t^2}x{m_1} - 180{m_1}\\ {}&- 360it{x^2}{m_1} - 720itx{n_1} - 120{t^3}{x^2} - 120{t^2}{x^3} \\ {}&- 360{t^2}{m_1}- 180{x^2}{n_1} + 240{t^3}{m_1} + 24i{t^5}x \\&- 900{t^2}{x^2} + 360{t^2}x{m_1} - 360t{x^3} - 180{x^2}{m_1} \\ {}&- 180i{t^2}{x^2} - 1080t{m_1} - 540x{m_1} + 180x{n_1} \\ {}&+ 360i{t^2}x{n_1} - 180{n_1} + 360t{x^2}{n_1} + 360{t^2}x{n_1} ,\\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} Q_3=&\, - 360 + 60i{t^4}{x^2} + 40i{t^3}{x^3} + 240i{t^3}{m_1}- 15{x^4}\\ {}&- 900i{t^2}{x^2} - 480it{x^3} + 60i{x^3}{n_1} + 24{t^5} - 90{x^2} \\ {}&- 180n_1^2 + 180m_1^2 - 1800t + 540{t^4} - 480{t^3} \\ {}&- 180{t^2} + 240i{x^3} - 360{m_2} + 6i{x^5} + 960i{t^3} \\ {}&+ 360it - 8{t^6} - 24i{t^5} + 360ix + 180i{m_1} \\&- 180i{n_1} - 360i{n_2} + 360it{n_2} + 24i{t^5}x - 6it{x^5}\\ {}&- 120i{t^4}x - 120i{t^3}{x^2} + 30it{x^4} - 720i{t^3}x \\ {}&- 180{m_1} - 60i{x^3}{m_1} + 1440i{t^2}x - 360i{t^2}{m_1} \\ {}&- 360i{t^2}{n_1} + 720it{x^2} + 180i{x^2}{m_1} - 24{t^5}x \\ {}&+ 360x{m_2} + 60{x^3}{n_1} + 360tx + 360i{t^2}x{n_1} \\ {}&- 720itx{n_1} + 1260i{t^2} + 60{x^3}{m_1} - 630i{x^2} \\ {}&- 60i{t^4} - 105i{x^4} + 360i{t^2}x{m_1} + 360it{x^2}{n_1} \\ {}&- 120{t^3}{x^2} - 30t{x^4} + 540{t^2}{x^2} + 120t{x^3}- i{x^6} \\ {}&- 360{t^2}{m_1} - 180{x^2}{m_1} - 180{x^2}{n_1} - 120{t^2}{x^3} \\ {}&+ 720t{m_1} + 1080t{n_1} + 900x{n_1} + 540x{m_1} \\ {}&- 180i{x^2}{n_1} - 1080it{m_1} - 180{n_1} + 360it{m_2} \\ {}&- 900ix{m_1} - 720tx{m_1}+ 540ix{n_1} + 360ix{n_2} \\ {}&+ 960{t^3}x + 720it{n_1}+ 360i{m_1}{n_1} + 360t{x^2}{m_1} \\ {}&+ 360{t^2}x{m_1} - 360{t^2}x{n_1} . \end{aligned} \end{aligned}$$

It is clear that $R_1^{[0]}$ is a special solution of Eq. (2.2) at $u=u[0]=e^{i\theta }$ and $\lambda =\frac{1}{2}+\frac{1}{2}i$.

(1) When $n=1$, substituting $u[0]=e^{i\theta }$, $\theta =-(3t+x)$ and $\lambda =\frac{1}{2}+\frac{1}{2}i$ into Eq. (2.15), we get a trivial solution

$$\begin{aligned} u{[1]}=-e^{i\theta }, \end{aligned}$$

(3.16)

for Eq. (2.1) and

$$\begin{aligned} \begin{aligned}&a_{11}{[0]}= -2, \ \ a_{22}{[0]}= -2, \\&b_{12}{[0]}= -2e^{i\theta },\ \ b_{21}{[0]}= 2e^{-i\theta },\\&{T{[1]}}|_{\lambda =\frac{1}{2}+\frac{1}{2}i} = \left( {\begin{array}{*{20}{c}} {1 - i}&{}{ - (1 + i){e^{i\theta }}}\\ {(1 + i){e^{ - i\theta }}}&{}{1 - i} \end{array}} \right) . \end{aligned} \end{aligned}$$

(2) When $n=2$, from Eqs. (2.16)–(2.18), we have

$$\begin{aligned} R_1{[1]}=\begin{pmatrix} f_{1}{[1]}\\ g_{1}{[1]} \end{pmatrix} =\begin{pmatrix} 4(it-i+t+x)e^{\frac{i\theta }{2}} \\ 4(it+ix-i-t)e^{\frac{-i\theta }{2}} \end{pmatrix}. \end{aligned}$$

(3.17)

$R_1{[1]}$ is the solution of Eq. (2.2) at $\lambda =\frac{1}{2}+\frac{1}{2}i$ and $u{[1]}=-e^{i\theta }$. Thus, we can obtain the first-order rogue wave solution of Eq. (2.1)

$$\begin{aligned} u_{1r}[2]=-\frac{4it+3ix+1-2i-2t^2-2tx-x^2+2t+x}{ix+2t^2+2tx+x^2-2t-x+1} e^{i\theta }. \end{aligned}$$

(3.18)

Figure 9 displays the evolution and density plots of $u_{1r}[2]$, which shows that the first-order rogue wave solution is localized in both space and time. Through simple calculations, we find that the first-order rogue wave solution reaches maximum amplitude $|u_{1r}[2]|=3$ at $(x,t)=(0,\frac{1}{2})$.

Fig. 9

a Evolution of the first-order rogue wave solution $u_{1r}[2]$ via Eq. (3.18) with parameter $\lambda =\frac{1}{2}+\frac{1}{2}i$, b corresponding density plot

(3) When $n=3$, by Eqs. (2.19)–(2.21), we have

$$\begin{aligned} \begin{aligned}&R_1{[2]}=\left( \begin{array}{l} f_1{[2]}\\ g_1{[2]} \end{array} \right) ,\\&f_1{[2]}= - \frac{{{{{F_{r1}}}}{{{e}}^{\frac{{i\theta }}{2}}}}}{{3\left( {ix + 2{t^2} + 2tx + {x^2} - 2t - x + 1} \right) }},\\&g_1{[2]}= - \frac{{{F_{r2}}{{{e}}^{\frac{{ - i\theta }}{2}}}}}{{3\left( {ix - 2{t^2} - 2tx - {x^2} + 2t + x - 1} \right) }}, \end{aligned} \end{aligned}$$

(3.19)

with

$$\begin{aligned} \begin{aligned} {F_{r1}}&= - 32{t^4} + 128{t^3} + 16{x^3} - 192{t^2} - 48{x^2} + 120t\\ {}&\quad + 72x + 8i{x^4} - 32i{x^3} + 24i{m_1} - 240tx + 24t{n_1} \\ {}&\quad + 8{x^4}+ 24x{n_1} - 24t{m_1} + 16t{x^3} - 32{t^3}x + 32i{t^4}\\ {}&\quad + 72it + 192{t^2}x + 96t{x^2} - 24{n_1} - 24i - 24it{n_1} \\ {}&\quad + 96i{t^2}{x^2} + 48it{x^3} - 24it{m_1} - 24ix{m_1} - 96i{t^2}x\\ {}&\quad + 96i{t^3}x-96it{x^2} + 48itx,\\ {F_{r2}}&= 24ix{n_1} + 8i{x^4} + 48x - 32{t^4} + 16it{x^3} + 24i-96it{x^2} \\ {}&\quad + 128{t^3}+ 16{x^3} - 32i{t^4} - 192{t^2} - 32i{x^3} + 48i{x^2} \\ {}&\quad - 72it - 72ix + 24i{m_1} - 144tx + 24t{n_1}+ 24t{m_1}\\ {}&\quad + 24x{m_1} - 48t{x^3} - 96{t^2}{x^2}+ 48itx - 96{t^3}x + 96t{x^2}\\&\quad - 8{x^4}- 24{n_1} - 24it{m_1} + 24it{n_1} - 32i{t^3}x - 96i{t^2}x\\ {}&\quad + 192{t^2}x+ 120t. \end{aligned} \end{aligned}$$

$R_1{[2]}$ is the solution of Eq. (2.2) at $\lambda =\frac{1}{2}+\frac{1}{2}i$ and $u_{1r}[2]$. Thus, we find the second-order rogue wave of the first kind when taking the parameters $m_{1}=0$, $n_{1}=0$ in Eq. (3.19) as follows:

$$\begin{aligned} u_{2r-1}[3]= & {} \frac{G_{r1}}{D_{r1} D_{r2}}e^{i\theta }, \\ D_{r2}= & {} ix + 2{t^2} + 2tx + {x^2} - 2t - x + 1,\\ D_{r1}= & {} 160{t^3}{x^5}+ 64{t^2}{x^6} - 448{t^6}x -\, 768{t^5}{x^2} - 800{t^4}{x^3} \\&+\, 306{t^2} + 117{x^2} + 320{t^5}{x^3} - 108{x^3} - 2112{t^3}{x^2} \\&-\, 544{t^3}{x^4} - 240{t^2}{x^5} - 64t{x^6}+ 48i{t^2}{x^3} + 96it{x^4}\\&+\, 256{t^6}{x^2} + 272{t^4}{x^4} + 144t{x^5} - 324t{x^4}+ 96i{t^3}x\\&+\, 1312{t^3}{x^3} + 576{t^2}{x^4} - 2040{t^4}x - 1128{t^2}{x^3}\\&+\,9 - 72it{x^2} - 54t - 27x + 448{t^6} + 20{x^6} - 816{t^5} \\&-\, 42{x^5} + 102{x^4} + 1032{t^4} - 720{t^3}32{t^8} + 16t{x^7} \\&-\, 288i{t^3}{x^3}- 128{t^7} + 1344{t^5}x + 1776{t^4}{x^2} \\&+\, 2064{t^3}x + 1584{t^2}{x^2} + 552t{x^3} -\, 1080{t^2}x \\&- 96i{t^5}x -\, 576t{x^2} + 306tx + 32i{t^6}x + 96i{t^5}{x^2} \\&+ 144i{t^4}{x^3} +\, 128i{t^3}{x^4} + 72i{t^2}{x^5} + 24it{x^6} \\&-\, 240i{t^4}{x^2}+ 144i{t^2}{x^2} +\, 128{t^7}x - 192i{t^2}{x^4} \\&- 72it{x^5} - 96i{t^3}{x^2} + 36i{x^5} -\, 24it{x^3} - 72i{t^2}x \\&- 48i{t^4}x -\, 12i{x^6}- 72itx + 4i{x^7} - \,36i{x^4} + 24i{x^3} \\&- 36i{x^2} + 27ix + 2{x^8} - 8{x^7}, \end{aligned}$$

$$\begin{aligned} {G_{r1}}= & {} 3920{t^6} + 544{x^6} - 5952{t^5} - 912{x^5} + 5412{t^4} \nonumber \\&+\, 909{x^4} - 3072{t^3} - 792{x^3} + 1008{t^2} + 306{x^2} \nonumber \\&+\, 1044itx- 64{t^{10}} - 320{t^9}x - 800{t^8}{x^2} + 320{t^9} \nonumber \\&-\, 1280{t^7}{x^3}- 1184{t^7} + 13680{t^5}x + 22368{t^4}{x^2}\nonumber \\&+\, 21104{t^3}{x^3}- 108x + 3876t{x^5} + 13632i{t^3}{x^4}\nonumber \\&-\, 1440{t^6}{x^4} - 1184{t^5}{x^5} - 720{t^4}{x^6} - 100{t^2}{x^8} \nonumber \\&+\, 11988{t^2}{x^4}- 20t{x^9} + 5100t{x^3}- 11656{t^3}{x^4}\nonumber \\&+\, 1440{t^8}x+ 3200{t^7}{x^2} + 4480{t^6}{x^3} + 4320{t^5}{x^4} \nonumber \\&+\, 2960{t^4}{x^5} + 1440{t^3}{x^6} + 480{t^2}{x^7}+ 11088{t^2}{x^2} \nonumber \\&+\, 100t{x^8} - 512{t^7}x - 64{t^6}{x^2} + 1216{t^5}{x^3}+ 272t{x^7} \nonumber \\&+\, 1856{t^3}{x^5} + 944{t^2}{x^6} + 2128{t^4}{x^4}- 5488{t^6}x\nonumber \\&-\, 11808{t^5}{x^2} - 14840{t^4}{x^3} - 5724{t^2}{x^5} - 1624t{x^6}\nonumber \\&-\, 16560{t^4}x - 20976{t^3}{x^2} - 14616{t^2}{x^3} - 5520t{x^4} \nonumber \\&+\, 1152tx - 144t + 11784{t^3}x - 5040{t^2}x - 3168t{x^2} \nonumber \\&-\, 2{x^{10}} + 10{x^9} + 34{x^8} - 206{x^7} + 384i{t^9} + 18i{x^9} \nonumber \\&-\, 9 + 36i- 1728i{t^8} - 84i{x^8} + 3840i{t^7} + 144i{x^7} \nonumber \\&-\, 126i{x^6} + 3360i{t^5} - 198i{x^5} - 672i{t^4} + 468i{x^4} \nonumber \\&-\, 864i{t^3} - 4896i{t^6}- 636i{x^3} + 792i{t^2} + 414i{x^2}\nonumber \\&-\, 288it - 180ix + 1824i{t^8}x + 4224i{t^7}{x^2} + 336i{t^3}x \nonumber \\&+\, 6144i{t^5}{x^4} + 4368i{t^4}{x^5} + 2208i{t^3}{x^6} + 768i{t^2}{x^7}\nonumber \\&+\, 168it{x^8} - 7296i{t^7}x - 14784i{t^6}{x^2} - 18432i{t^5}{x^3} \nonumber \\&-\, 15360i{t^4}{x^4} - 8736i{t^3}{x^5} - 3312i{t^2}{x^6} - 768it{x^7}\nonumber \\&+\, 13440i{t^6}x + 22080i{t^5}{x^2}- 1164it{x^5}- 320{t^3}{x^7}\nonumber \\&+\, 5472i{t^2}{x^5} 4560i{t^3}{x^2}+ 1296it{x^6} - 13584i{t^5}x \nonumber \\&-\, 16920i{t^4}{x^2} - 11952i{t^3}{x^3} - 4968i{t^2}{x^4} - 224{t^8} \nonumber \\&+\, 6456i{t^4}x + + 2088i{t^2}{x^2} + 936i{t^2}{x^3} - 504it{x^4}\nonumber \\&+\, 6144i{t^6}{x^3} + 1728it{x^3} - 2160i{t^2}x - 2016it{x^2}\nonumber \\&+ 21696i{t^4}{x^3} . \end{aligned}$$

(3.20)

We call this type of rogue wave as the fundamental pattern and show the structure of Eq. (3.20) in Fig. 10.

Similarly, let the parameters $m_{1}=200$, $n_{1}=0$ in Eq. (3.19), and then the second-order rogue wave of the second kind is obtained as

$$\begin{aligned} u_{2r-2}[3]= & {} \frac{G_{r2}}{D_{r2} D_{r3}}e^{i\theta }, \\ {D_{r3}}= & {} - 96i{t^3}{x^2}- 128{t^7} + 448{t^6} + 20{x^6} - 816{t^5}- 720{t^3}\\&-\, 48i{t^4}x- 1242{x^5} - 720054t - 363627x+32{t^8} \\&+\, 4902{x^4} + 1032{t^4} - 16440{t^4}x- 4908{x^3}- 24it{x^3} \\&+\, 367317{x^2}+ 1776{t^4}{x^2}+ 720306{t^2} + 1312{t^3}{x^3}\\&+\, 576{t^2}{x^4} + 1344{t^5}x - 28872itx- 28704i{t^3}x\\&-\, 72it{x^5}+ 128{t^7}x + 256{t^6}{x^2} + 320{t^5}{x^3} - 363627x \\&+\, 272{t^4}{x^4} + 160{t^3}{x^5} + 64{t^2}{x^6} + 48i{t^2}{x^3} - 64t{x^6}\\&-\, 448{t^6}x - 768{t^5}{x^2} - 352773ix- 800{t^4}{x^3} + 16t{x^7}\\&-\, 544{t^3}{x^4} - 240{t^2}{x^5} - 30912{t^3}{x^2} - 25128{t^2}{x^3}\\&-\, 9924t{x^4} + 44784{t^2}{x^2} + 24552t{x^3} - 29880{t^2}x\\&+\, 734706tx - 29376t{x^2} + 2{x^8} - 8{x^7} + 4i{x^7} - 12i{x^6} \\&+\, 36i{x^5} + 24i{x^3} - 14400i{t^4} - 28800i{t^2} + 28800i{t^3} \\&+\, 14400it - 14256i{t^2}{x^2} + 43128i{t^2}x + 14328it{x^2} \\&+\, 30864{t^3}x + 360009 - 3600i + 32i{t^6}x + 96i{t^5}{x^2}\\&+\, 144i{t^4}{x^3} + 128i{t^3}{x^4} + 72i{t^2}{x^5} + 24it{x^6} + 96it{x^4} \\&-\, 96i{t^5}x - 240i{t^4}{x^2} - 288i{t^3}{x^3} - 192i{t^2}{x^4} + 144t{x^5}\\&+\, 1164i{x^4} - 7236i{x^2} ,\nonumber \end{aligned}$$

$$\begin{aligned} {G_{r2}}= & {} - 64{t^{10}} + 320{t^9} - 224{t^8} - 1184{t^7} + 1396656t\nonumber \\&+\, 3920{t^6} - 5456{x^6} - 63552{t^5} - 74160{t^4}x \nonumber \\&+\, 691092x - 193632{t^4}{x^2} - 218896{t^3}{x^3} - 3312{x^5}\nonumber \\&-\, 1290588{t^4} - 339891{x^4} + 2704128{t^3} - 320{t^9}x\nonumber \\&-\, 2763792{t^2} - 1385694{x^2} + 1440{t^8}x + 3200{t^7}{x^2} \nonumber \\&+\, 4480{t^6}{x^3} + 4320{t^5}{x^4} + 2960{t^4}{x^5} + 1440{t^3}{x^6} \nonumber \\&+\, 25002i{x^5} + 655608{x^3} - 72720{t^5}x - 132012{t^2}{x^4} \nonumber \\&-\, 20t{x^9}- 41724t{x^5} + 480{t^2}{x^7} - 49356itx - 7326i{x^6} \nonumber \\&+\, 1216{t^5}{x^3} + 2128{t^4}{x^4} + 1856{t^3}{x^5} + 944{t^2}{x^6} \nonumber \\&+\, 10376t{x^6} + 23312{t^6}x - 800{t^8}{x^2} + 105160{t^4}{x^3}\nonumber \\&+\, 84344{t^3}{x^4} - 768it{x^7}+ 272t{x^7} + 74592{t^5}{x^2}\nonumber \\&-\, 64{t^6}{x^2} - 1280{t^7}{x^3} - 1440{t^6}{x^4} - 1184{t^5}{x^5} \nonumber \\&-\, 720{t^4}{x^6} - 320{t^3}{x^7} - 100{t^2}{x^8} - 20976{t^3}{x^2} \nonumber \\&+\, 144i{x^7} - 33696i{t^6} + 89760i{t^5} + 3420ix + 10{x^9}\nonumber \\&-\, 101472i{t^4} - 46332i{x^4} + 56736i{t^3} + 49764i{x^3} \nonumber \\&-\, 6408i{t^2} - 13986i{x^2} - 7488it + 199440i{t^2}x \nonumber \\&-\, 352809 + 1824i{t^8}x - 271152i{t^3}{x^3}- 18432i{t^5}{x^3}\nonumber \\&+\, 6144i{t^6}{x^3} + 6144i{t^5}{x^4} + 4368i{t^4}{x^5} + 2208i{t^3}{x^6}\nonumber \\&+\, 768i{t^2}{x^7}- 156168i{t^2}{x^4} - 14784i{t^6}{x^2}+ 3636i \nonumber \\&-\, 2609016{t^3}x - 15360i{t^4}{x^4} - 8736i{t^3}{x^5} + 168it{x^8}\nonumber \\&-\, 3312i{t^2}{x^6} + 13440i{t^6}x + 22080i{t^5}{x^2}+ 4224i{t^7}{x^2} \nonumber \\&+\, 21696i{t^4}{x^3} + 13632i{t^3}{x^4} + 5472i{t^2}{x^5} + 1296it{x^6} \nonumber \\&-\, 157584i{t^5}x - 276120i{t^4}{x^2} + 39876{t^2}{x^5} + 100t{x^8}\nonumber \\&-\, 51564it{x^5} + 366456i{t^4}x + 522960i{t^3}{x^2} + 994{x^7} \nonumber \\&+\, 150696it{x^4} - 374064i{t^3}x - 415512i{t^2}{x^2} - 512{t^7}x \nonumber \\&-\, 228672it{x^3} + 156384it{x^2} + 389736i{t^2}{x^3}+ 34{x^8}.\nonumber \\ \end{aligned}$$

(3.21)

This kind of rogue wave is called as the triangular structure, and we display the structure of Eq. (3.21) in Fig. 11.

Fig. 10

The fundamental pattern. a Evolution of the first kind of second-order rogue wave solution $u_{2r-1}[3]$ via Eq. (3.20) with parameters $\lambda =\frac{1}{2}+\frac{1}{2}i$, $m_{1}=0$, $n_{1}=0$, b corresponding density plot

Fig. 11

The triangular structure. a Evolution of the second kind of second-order rogue wave solution $u_{2r-2}[3]$ via Eq. (3.21) with parameters $\lambda =\frac{1}{2}+\frac{1}{2}i$, $m_{1}=200$, $n_{1}=0$, b corresponding density plot

Fig. 12

The fundamental pattern. a Evolution of third-order rogue wave solution $u_{3r}[4]$ via Eq. (3.22) with parameters $\lambda =\frac{1}{2}+\frac{1}{2}i$, $m_{1}=0$, $m_{2}=0$, $n_{1}=0$, $n_{2}=0$, b corresponding density plot

Fig. 13

The triangular structure. a Evolution of third-order rogue wave solution $u_{3r}[4]$ via Eq. (3.22) with parameters $\lambda =\frac{1}{2}+\frac{1}{2}i$, $m_{1}=400$, $m_{2}=0$, $n_{1}=0$, $n_{2}=0$, b corresponding density plot

Fig. 14

The ring structure. a Evolution of third-order rogue wave solution $u_{3r}[4]$ via Eq. (3.22) with parameters $\lambda =\frac{1}{2}+\frac{1}{2}i$, $m_{1}=0$, $m_{2}=400$, $n_{1}=0$, $n_{2}=0$, b corresponding density plot

(4) When $n=4$ in Eqs. (2.22) and (2.23), we can obtain the third-order rogue wave solution in the same way as the above (1)–(3),

$$\begin{aligned} u_{3r}[4]=u_{2r}[3]+\frac{f_{1}{[3]}g_{1}[3]^{*}(\lambda ^{2}_{1}-\lambda ^{*2}_{1})}{|\lambda _{1}|^{2}(|f_{1}{[3]}|^{2}\lambda _{1}+|g_{1}{[3]}|^{2}\lambda ^{*}_{1})}, \end{aligned}$$

(3.22)

where $R_1{[3]}=(f_{1}{[3]},g_{1}{[3]})^T$ is the solution of Eq. (2.2) at $u_{2r}[3]$ and $\lambda =\frac{1}{2}+\frac{1}{2}i$.

The dynamics of Eq. (3.22) is displayed in Figs. 12-14. We find that: when the parameters $m_1=0$, $n_1=0$, $m_2=0$, $n_2=0$, we get the first kind of third-order rogue wave which is the fundamental pattern (seen in Fig. 12); when the parameters $m_1=400$, $n_1=0$, $m_2=0$, $n_2=0$, we get the second kind of third-order rogue wave which is the triangular structure (seen in Fig. 13); what’s more, when the parameters $m_1=0$, $n_1=0$, $m_2=400$, $n_2=0$, we get the third kind of third-order rogue wave which is the ring structure (seen in Fig. 14). From Figs. 13 and 14, clearly, we see that the triangular structure and the ring structure all have six uniform peaks.

We remark that we can also construct the high-order rogue wave solutions of Eq. (2.1) if continuing the iteration of the generalized DT in Eqs. (2.18)–(2.20).

4 Conclusions

The nonlinear partial differential equations (NPDEs) have been the subject of extensive studies in various branches of nonlinear sciences. A class of analytical solutions for NPDEs is of fundamental importance because lots of mathematical–physical models are often described by such wave phenomena. Thus, the investigation of explicit solutions is becoming more and more attractive in nonlinear sciences. The integrable GNLS equation models the propagation of nonlinear light pulses in optical fibers when certain high-order nonlinear effects are taken into consideration [47, 48]. In this paper, we investigate the exact solutions (including soliton solutions, breather solutions, and rogue wave solutions) of a new GNLS equation based on its Lax pair by using the DT method. First of all, we construct the classical DT and the generalized DT of Eq. (2.1). Then, these exact solutions are obtained from the corresponding n-fold DT by assuming the suitable seed solution and depending on the parameter choices. Moreover, the dynamical features of these exact solutions are analyzed by their profile and density plots with the help of Maple software. Finally, we find that the higher-order solutions have rich and interesting dynamics and structures.