1 Introduction

Over the past years, the interaction of laser beams with turbulent atmosphere media has paid much attention owing to their wide applications in free-space optical communications (Navidpour et al. 2007), optical imaging systems (Hajjarian et al. 2010), and remote sensing (Korotkova and Gbur 2007). Therefore, the propagation properties of laser beams in atmospheric turbulence have been extensively studied by many authors (Belafhal et al. 2011; Lukin et al. 2012; Boufalah et al. 2016, 2018; Ez-zariy et al. 2016; Saad and Belafhal 2017; Zhang et al. 2019; Lin et al. 2020; Deng et al. 2020; Li and Gao 2020; Nossir et al. 2021). Recently, a lot of works have been focused on the investigation of the propagation of partially coherent beams traveling through turbulent environments due to their advantage of being less affected by the degradation induced by the turbulence (Wolf 2007; Korotkova 2004; Cai and He 2006; Gbur and Korotkova 2007; Cai et al. 2007; Yuan et al. 2009; Lu et al. 2007; Yang et al. 2008, 2009; Zhou and Chu 2009; Chib et al. 2020).

Generally, in the coherence theory, the cross-spectral density (CSD) function is used, in the space-frequency domain, or in the space–time domain to describe the correlation properties of partially coherent beams through the average fluctuations of the electric fields at two spatial points. The CSD function permits information concerning the field correlation at two points to be acquired during the propagation of the beam crossing a certain environment. On the other hand, the form of the planar correlation function for the optical field in the source plane is related to the intensity distribution of the far-field (Sahin and Korotkova 2012; Mei and Korotkova 2013). The analytical models for the correlation function are not very developed for Schell-model beams because to obtain a real correlation function a sufficient condition must be fulfilled. The correlation function of the planar source introduced so far are Gaussian Schell-model sources (Gori 1983), multi-Gaussian Schell-model sources (Sahin and Korotkova 2012), Bessel-Gaussian Schell-model sources, and Laguerre-Gaussian Schell-model sources (Mei and Korotkova 2013).

Based on the above-quoted correlation functions, the comportment of some Schell-model beams propagating through a turbulent environment has been examined by certain researchers (Jian 1990; Zhu et al. 2008, 2016; Cang et al. 2013a, 2013b; Zhou et al. 2020; Dong et al. 2020), however, we note that the case of QBGSMB has not been reported yet, to the best of our knowledge. Motivated by the work of Belafhal and Dalil-Essakali (Belafhal and Dalil-Essakali 2000) which concerns the propagation of the QBG beam through free space and the Fourier transform system, we introduce an optical Schell-model source for QBGSMB and investigate the evolution of the spectral density of this beam upon their propagation through a paraxial ABCD optical system in a turbulent atmosphere. It is well known that the QBG beam possesses both the usual Gaussian collinear geometry and fascinating non-Gaussian properties for certain values of its parameters. In order to have these features as well as the reduction of undesirable atmospheric effects, the use of the QBGSM beam is necessary. The rest parts of this manuscript are organized as follows: In Sect. 2, we introduce a mathematical model of the spectral degree of coherence for the QBGSMB source. The theoretical formula of the spectral density for QBGSMB propagating through a paraxial ABCD optical system in a turbulent atmosphere is performed in Sect. 3. The evolution of the spectral density of the diffracted beam, by varying the incident beam parameters and the turbulence strength, is exposed in Sect. 4. Finally, Sect. 5 concludes the paper.

2 The mathematical form of the spatial correlation function for QBGSMB

In this Section, we will give the expression of the spectral degree of coherence for the QBGSMB source. Let’s consider the CSD function that satisfies the nonnegative definiteness requirement, to be physically realizable. It can be expressed as follows (Gori and Santarsiero 2007)

$$ W^{0} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{r}}_{{\mathbf{2}}} } \right) = \int {p\left( {\mathbf{v}} \right)} H^{*} \left( {{\mathbf{r}}_{{\mathbf{1}}} ,{\mathbf{v}}} \right)H\left( {{\mathbf{r}}_{{\mathbf{2}}} ,{\mathbf{v}}} \right)d^{2} {\mathbf{v}}, $$
(1)

where \(p\left( {\mathbf{v}} \right)\) is a nonnegative Fourier transform function, \(H\left( {{\mathbf{r}},{\mathbf{v}}} \right)\) is an arbitrary kernel, \({\mathbf{r}}_{i} = \left( {x_{i} ,y_{i} } \right)\left( {i = 1,2} \right)\) are two-position vectors at \(z = 0\) and (*) designates the complex conjugate. Note that, the position vector \({\mathbf{r}}\) and the corresponding vector in Fourier space \({\mathbf{v}}\) are taken in the polar coordinate (\({\mathbf{r}}(r,\varphi )\) and \({\mathbf{v}}(v,\theta )\)). The aforementioned functions can be written under the form

$$ p\left( {\mathbf{v}} \right) = \left( { - i} \right)^{m} p\left( v \right)exp\left( {im\theta } \right), $$
(2)

where \(m\) is the azimuthal mode index, \(( - i)^{m}\) is a transform coefficient independent of the coordinate variables \(v\) and \(\theta\), \(p\left( v \right)\) is a nonnegative function,

and

$$ H\left( {{\mathbf{r}},{\mathbf{v}}} \right) = \tau \left( {\mathbf{r}} \right)\exp \left( {2\pi i{\mathbf{r}}\cdot {\mathbf{v}}} \right), $$
(3)

with \(\tau \left( {\mathbf{r}} \right)\) is a profile function. In the next step and for brevity, the function \(\tau \left( {\mathbf{r}} \right)\) is chosen as a Gaussian profile, \(\exp ( - \left| {\mathbf{r}} \right|^{2} /4\sigma_{s}^{2} )\) with \(\sigma_{s}\) is the source width.

On substituting Eqs. (2) and (3) into Eq. (1) and by using the following integral (Gradshteyn et al. 2007)

$$ \int\limits_{0}^{2\pi } {\exp \left[ {in\varphi + ix\cos \left( {\varphi - \theta } \right)} \right]} d\varphi = 2\pi \left( i \right)^{n} \exp \left( {in\theta } \right)J_{n} \left( x \right), $$
(4)

Equation (1) becomes

$$ W^{0} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = 2\pi \exp \left( {im\left| {\varphi_{12} } \right|} \right)\exp \left[ { - {{({\mathbf{r}}_{1}^{2} + {\mathbf{r}}_{2}^{2} )} \mathord{\left/ {\vphantom {{({\mathbf{r}}_{1}^{2} + {\mathbf{r}}_{2}^{2} )} {4\sigma_{s}^{2} }}} \right. \kern-\nulldelimiterspace} {4\sigma_{s}^{2} }}} \right]\int\limits_{0}^{\infty } {p\left( v \right)} J_{m} \left[ {2\pi v\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|} \right]vdv, $$
(5)

with \(\varphi_{12}\) is the phase coordinate of vector \({\mathbf{r}}_{1} - {\mathbf{r}}_{2}\) and \(J_{m} \left( . \right)\) is the m-order Bessel function of the first kind.

In the following, we will be interested in the case of the Bessel function of zero-order because the spectral density will be equal to zero in the input plane for \(m \ne 0\)\(\left( {m > 0} \right)\).

Hence, the CSD function can be rewritten as

$$ W^{0} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = 2\pi \exp \left[ { - {{({\mathbf{r}}_{1}^{2} + {\mathbf{r}}_{2}^{2} )} \mathord{\left/ {\vphantom {{({\mathbf{r}}_{1}^{2} + {\mathbf{r}}_{2}^{2} )} {4\sigma_{s}^{2} }}} \right. \kern-\nulldelimiterspace} {4\sigma_{s}^{2} }}} \right]\int\limits_{0}^{\infty } {p\left( v \right)} J_{0} \left[ {2\pi v\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|} \right]vdv. $$
(6)

Based on the work of Ref. (Mei and Korotkova 2013), on sets for the QBGSMB source the function \(p(v)\) as follows

$$ p\left( v \right) = \frac{{\sqrt {4 + a^{2} } }}{{4\pi^{3} \delta^{2} }}J_{0} \left( {\frac{a}{{\delta^{{\prime}{2}} }}v^{2} } \right), $$
(7)

where \(J_{0} \left( . \right)\) is a Bessel function with quadratic radial component of zero order.

By inserting Eq. (7) into Eq. (6), and applying the below identity (Gradshteyn et al. 2007)

$$ \int\limits_{0}^{\infty } {\exp \left( {{{ - \alpha x^{2} } \mathord{\left/ {\vphantom {{ - \alpha x^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \right)} J_{0} \left( {{{\beta x^{2} } \mathord{\left/ {\vphantom {{\beta x^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \right)J_{0} \left( {\gamma x} \right)xdx = \frac{2}{{\sqrt {\alpha^{2} + \beta^{2} } }}\exp \left( { - \frac{{\alpha \gamma^{2} }}{{\alpha^{2} + \beta^{2} }}} \right)J_{0} \left( { - \frac{{\beta \gamma^{2} }}{{\alpha^{2} + \beta^{2} }}} \right), $$
(8)

the CSD function of QBGSMB turns out to be

$$ W^{\left( 0 \right)} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = \exp \left[ { - \frac{{\left( {{\mathbf{r}}_{1}^{2} + {\mathbf{r}}_{2}^{2} } \right)}}{{4\sigma_{s}^{2} }}} \right]\exp \left[ { - \frac{1}{{2\delta^{2} }}\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|^{2} } \right]J_{0} \left[ {\frac{\mu }{{\delta^{2} }}\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|^{2} } \right], $$
(9)

where \(\delta^{2} = \frac{{\left( {4 + a^{2} } \right)}}{{4\pi^{2} \delta^{{\prime}{2}} }}\) denotes the coherence width and \(\mu = \frac{a}{4}\) describes the transverse wavenumber.

Therefore, the spectral degree of coherence at two points in the source plane for QBGSMB can be defined as

$$ \mu_{QBGSM}^{\left( 0 \right)} \left( {{\mathbf{r}}_{1} - {\mathbf{r}}{}_{2}} \right) = \exp \left[ { - \frac{1}{{2\delta^{2} }}\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|^{2} } \right]J_{0} \left[ {\frac{\mu }{{\delta^{2} }}\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|^{2} } \right]. $$
(10)

Equation (10) is the mathematical form of the QBGSMB source developed in this study. This equation is our first main result in the present study.

In Fig. 1, we illustrate the degree of coherence of the QBGSM source given by Eq. (10) versus \(\left| {r_{2} - r_{1} } \right|/\delta\) for various values of the transverse wavenumber \(\mu\). From this plot, we can observe that side lobes appear for large values of \(\mu\) and the spectral degree of coherence reduces to a fundamental Gaussian profile when the transverse wavenumber \(\mu\) tends to zero.

Fig. 1
figure 1

Degree of coherence of the QBGSMB source versus \({{\left| {r_{2} - r_{1} } \right|} \mathord{\left/ {\vphantom {{\left| {r_{2} - r_{1} } \right|} \delta }} \right. \kern-\nulldelimiterspace} \delta }\) for different values of \(\mu\)

Full size image

In the following Section, we derive the paraxial propagation formula of the cross-spectral density for QBGSMB traveling through a paraxial ABCD optical system in a turbulent atmosphere.

3 Average intensity of distribution QBGSMB in a turbulent atmosphere

The cross-spectral density from the source plane \((z = 0)\) to the output plane through a paraxial ABCD optical system in atmospheric turbulence can be expressed by utilizing the generalized Huygens-Fresnel diffraction integral in the paraxial approximation and the Rytov theory (Andrews and Phillips 2005; Noriega-Manez and Gutiérrez-Vega 2007)

$$ \begin{gathered} W\left( {{{\varvec{\uprho}}}_{1} ,{{\varvec{\uprho}}}_{2} ,z;\omega } \right) = \frac{1}{{\lambda^{2} B^{2} }}\iint {\iint {W^{\left( 0 \right)} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ;\omega } \right)}}\exp \left[ {{{ - ik({\mathbf{r}}_{2}^{2} - {\mathbf{r}}_{1}^{2} )} \mathord{\left/ {\vphantom {{ - ik({\mathbf{r}}_{2}^{2} - {\mathbf{r}}_{1}^{2} )} {2F_{0} }}} \right. \kern-\nulldelimiterspace} {2F_{0} }}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \frac{ik}{{2B}}\left[ {\left( {A{\mathbf{r}}_{1}^{2} - 2{\mathbf{r}}_{1} \cdot{{\varvec{\uprho}}}_{1} + D{{\varvec{\uprho}}}_{1}^{2} } \right) - \left( {A{\mathbf{r}}_{2}^{2} - 2{\mathbf{r}}_{2} \cdot {{\varvec{\uprho}}}_{2} + D{{\varvec{\uprho}}}_{2}^{2} } \right)} \right]} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\exp \left[ {\psi^{*} \left( {{\mathbf{r}}_{1} ,{{\varvec{\uprho}}}_{1} ,z;\omega } \right) + \psi \left( {{\mathbf{r}}_{2} ,{{\varvec{\uprho}}}_{2} ,z;\omega } \right)} \right]} \right\rangle_{m} d^{2} {\mathbf{r}}_{1} d^{2} {\mathbf{r}}_{2} , \hfill \\ \end{gathered} $$
(11)

where \({{\varvec{\uprho}}}_{1} = \left( {\rho_{1x} ,\rho_{1y} } \right)\) and \({{\varvec{\uprho}}}_{2} = \left( {\rho_{2x} ,\rho_{2y} } \right)\) are two-position vectors at the receiving plane, \(z\) is the propagation distance, \(d^{2} {\mathbf{r}}_{i} = dx_{i} dy_{i} ,\)\(\left( {i = 1,2} \right)\), \(k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }\) is the wavenumber with \(\lambda\) denotes the wavelength of the source radiation, \(A,\)\(B\) and \(D\) are the elements of the transfer matrix of the optical system, and \(F_{0}\) describes the wave-front radius of curvature of the initial beam.

The average intensity at a particular frequency \(\omega\) is obtained by setting \({{\varvec{\uprho}}}_{1} = {{\varvec{\uprho}}}_{2} = {{\varvec{\uprho}}}\) in Eq. (11), which leads to the following form

$$ \begin{gathered} S\left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{1}{{\lambda^{2} B^{2} }}\iint {\iint {W^{\left( 0 \right)} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ;\omega } \right)}}\exp \left[ {{{ - ik({\mathbf{r}}_{2}^{2} - {\mathbf{r}}_{1}^{2} )} \mathord{\left/ {\vphantom {{ - ik({\mathbf{r}}_{2}^{2} - {\mathbf{r}}_{1}^{2} )} {2F_{0} }}} \right. \kern-\nulldelimiterspace} {2F_{0} }}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \frac{ik}{{2B}}\left[ {\left( {A{\mathbf{r}}_{2}^{2} - A{\mathbf{r}}_{1}^{2} - 2{\mathbf{r}}_{2} \cdot{{\varvec{\uprho}}}_{2} + 2{\mathbf{r}}_{1} \cdot{{\varvec{\uprho}}}_{1} } \right)} \right]} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\exp \left[ {\psi^{*} \left( {{\mathbf{r}}_{1} ,{{\varvec{\uprho}}},z;\omega } \right) + \psi \left( {{\mathbf{r}}_{2} ,{{\varvec{\uprho}}},z;\omega } \right)} \right]} \right\rangle_{m} d^{2} {\mathbf{r}}_{1} d^{2} {\mathbf{r}}_{2} , \hfill \\ \end{gathered} $$
(12)

where \(\left\langle . \right\rangle_{m}\) is the ensemble average over the turbulent media; which describes the influence of the turbulence on the propagation of laser beam and can be expressed as

$$ \left\langle {\exp \left[ {\psi^{*} \left( {{\mathbf{r}}_{1} ,{{\varvec{\uprho}}},z;\omega } \right) + \psi \left( {{\mathbf{r}}_{2} ,{{\varvec{\uprho}}},z;\omega } \right)} \right]} \right\rangle_{m} = \exp \left[ { - \frac{{D_{w} \left( {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right)}}{2}} \right] = \exp \left( { - \frac{{\left| {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right|}}{{\sigma_{0} }}} \right)^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-\nulldelimiterspace} 3}}} , $$
(13)

with \(D_{w} \left( {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right)\) is referred to the generalized wave-structure function of the random phase in the Rytov’s representation and \(\sigma_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-\nulldelimiterspace} 5}}}\) is the coherence length of a spherical wave propagating in the turbulent environment, with \(C_{n}^{2}\) is the refractive index structure constant of the atmospheric turbulence.

By substituting Eqs. (9) and (13) into Eq. (12) and by introducing the variables of integration defined as \({\mathbf{s}}_{1} = {{\left( {{\mathbf{r}}_{1} + {\mathbf{r}}_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{r}}_{1} + {\mathbf{r}}_{2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) and \({\mathbf{s}}_{2} = {\mathbf{r}}_{2} - {\mathbf{r}}_{1}\), we obtain

$$ \begin{gathered} S\left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{1}{{\lambda^{2} B^{2} }}\iint {\iint {\exp \left[ {{{ - (4{\mathbf{s}}_{1}^{2} + {\mathbf{s}}_{2}^{2} )} \mathord{\left/ {\vphantom {{ - (4{\mathbf{s}}_{1}^{2} + {\mathbf{s}}_{2}^{2} )} {8\sigma_{s}^{2} }}} \right. \kern-\nulldelimiterspace} {8\sigma_{s}^{2} }}} \right]}}\exp \left[ {{{ - \left| {{\mathbf{s}}_{2} } \right|^{2} } \mathord{\left/ {\vphantom {{ - \left| {{\mathbf{s}}_{2} } \right|^{2} } {2\delta^{2} }}} \right. \kern-\nulldelimiterspace} {2\delta^{2} }}} \right]J_{0} \left[ {{{\mu \left| {{\mathbf{s}}_{2} } \right|^{2} } \mathord{\left/ {\vphantom {{\mu \left| {{\mathbf{s}}_{2} } \right|^{2} } {\delta^{2} }}} \right. \kern-\nulldelimiterspace} {\delta^{2} }}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( { - \frac{ik}{{F_{0} }}{\mathbf{s}}_{{\mathbf{1}}} {\mathbf{s}}_{{\mathbf{2}}} } \right)\exp \left( {\frac{ikA}{B}{\mathbf{s}}_{{\mathbf{1}}} {\mathbf{s}}_{{\mathbf{2}}} - \frac{{ik{{\varvec{\uprho}}}}}{B}{\mathbf{s}}_{{\mathbf{2}}} } \right)\exp \left[ { - \left( {\frac{{{\mathbf{s}}_{2} }}{{\sigma_{0} }}} \right)^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-\nulldelimiterspace} 3}}} } \right]d^{2} {\mathbf{s}}_{{\mathbf{1}}} d^{2} {\mathbf{s}}_{{\mathbf{2}}} . \hfill \\ \end{gathered} $$
(14)

To evaluate this last equation, we use the below integral formulae (Gradshteyn et al. 2007)

$$ \int\limits_{ - \infty }^{ + \infty } {\exp \left( { - p^{2} x^{2} + qx} \right)dx} = \frac{\sqrt \pi }{p}\exp \left( {\frac{{q^{2} }}{{4p^{2} }}} \right), $$
(15)

and

$$ \int\limits_{0}^{2\pi } {\exp \left[ { - ix\cos \left( {\theta - \varphi } \right)} \right]} d\theta = 2\pi J_{0} \left( x \right), $$
(16)

and after some rearrangements, Eq. (14) becomes

$$ S\left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{{4\pi^{2} \sigma_{s}^{2} }}{{\lambda^{2} B^{2} }}\int\limits_{0}^{ + \infty } {\exp \left( { - \eta {\mathbf{s}}_{{\mathbf{2}}}^{{\mathbf{2}}} } \right)\exp \left[ { - \left( {{{\left| {{\mathbf{s}}_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {{\mathbf{s}}_{2} } \right|} {\sigma_{0} }}} \right. \kern-\nulldelimiterspace} {\sigma_{0} }}} \right)^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-\nulldelimiterspace} 3}}} } \right]} J_{0} \left[ {\frac{\mu }{{\delta^{2} }}\left| {{\mathbf{s}}_{2} } \right|^{2} } \right]J_{0} \left( {\frac{{k\rho {\mathbf{s}}_{{\mathbf{2}}} }}{B}} \right){\mathbf{s}}_{{\mathbf{2}}} d{\mathbf{s}}_{{\mathbf{2}}} , $$
(17)

where

$$ \eta = \frac{1}{{8\sigma_{s}^{2} }} + \frac{1}{{2\delta^{2} }} + \frac{{k^{2} \sigma_{s}^{2} }}{{2B^{2} }}\left( {A - \frac{B}{{F_{0} }}} \right)^{2} . $$
(18)

To develop the above integral, we apply a Taylor-type limited expansion to the second exponential term quoted in Eq. (17). The exponential function can be written as (Wandzura 1981; Chu and Liu 2010)

$$ \exp \left[ { - \left( {{{\left| {{\mathbf{s}}_{2} } \right|} \mathord{\left/ {\vphantom {{\left| {{\mathbf{s}}_{2} } \right|} {\sigma_{0} }}} \right. \kern-\nulldelimiterspace} {\sigma_{0} }}} \right)^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-\nulldelimiterspace} 3}}} } \right] = \exp \left( { - \frac{{{\mathbf{s}}_{{\mathbf{2}}}^{{\mathbf{2}}} }}{{\sigma_{0}^{2} }}} \right) + \frac{{{\mathbf{s}}_{{\mathbf{2}}}^{{\mathbf{2}}} }}{{3\sigma_{0}^{2} }}\ln \left( {\frac{{{\mathbf{s}}_{{\mathbf{2}}} }}{{\sigma_{0} }}} \right)\exp \left( { - \frac{{{\mathbf{s}}_{{\mathbf{2}}}^{{\mathbf{2}}} }}{{\sigma_{0}^{2} }}} \right) + ... $$
(19)

Using the first-order Taylor-type developments, the spectral density takes the following form

$$ S_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{{4\pi^{2} \sigma_{s}^{2} }}{{\lambda^{2} B^{2} }}\left( {I_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) + \frac{{J_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right)}}{{3\sigma_{0}^{2} }}} \right), $$
(20)

where

$$ I_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \int\limits_{0}^{ + \infty } {\exp \left( { - \eta^{\prime}t^{2} } \right)} J_{0} \left( {\frac{\mu }{{\delta^{2} }}t^{2} } \right)J_{0} \left( {\beta t} \right)tdt, $$
(20a)

and

$$ J_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \int\limits_{0}^{ + \infty } {t{}^{3}\exp \left( { - \eta^{\prime}t^{2} } \right)} J_{0} \left( {\frac{\mu }{{\delta^{2} }}t^{2} } \right)J_{0} \left( {\beta t} \right)\ln \left( {\frac{t}{{\sigma_{0} }}} \right)dt, $$
(20b)

with

$$ \eta^{\prime} = \frac{1}{{8\sigma_{s}^{2} }} + \frac{1}{{2\delta^{2} }} + \frac{1}{{\sigma_{0}^{2} }} + \frac{{k^{2} \sigma_{s}^{2} }}{{2B^{2} }}\left( {A - \frac{B}{{F_{0} }}} \right)^{2} , $$
(20c)

and

$$ \beta = \frac{{k{{\varvec{\uprho}}}}}{B}. $$
(20d)

Recalling the following integral (Gradshteyn et al. 2007)

$$ \int\limits_{0}^{ + \infty } {t\exp \left( { - \gamma t^{2} } \right)} J_{2\nu } \left( {2at} \right)J_{\nu } \left( {bt^{2} } \right)dt = \frac{1}{{2\sqrt {\gamma^{2} + b^{2} } }}\exp \left( { - \frac{{a^{2} \gamma }}{{\gamma^{2} + b^{2} }}} \right)J_{\nu } \left( {\frac{{a^{2} b}}{{\gamma^{2} + b^{2} }}} \right), $$
(21)

the quantity \(I_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right)\) reduces to

$$ I_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{1}{{2\sqrt {\eta^{{\prime}{2}} + \frac{{\mu^{2} }}{{\delta^{4} }}} }}\exp \left[ { - {{\beta^{2} \delta^{4} \eta^{\prime}} \mathord{\left/ {\vphantom {{\beta^{2} \delta^{4} \eta^{\prime}} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]J_{0} \left[ {{{\beta^{2} \delta^{2} \mu } \mathord{\left/ {\vphantom {{\beta^{2} \delta^{2} \mu } {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]. $$
(22)

To perform Eq. (20b), we use the following identities (Gradshteyn et al. 2007)

$$ J_{0} \left( t \right) = \sum\limits_{m = 0}^{ + \infty } {\frac{{\left( {{{t^{2} } \mathord{\left/ {\vphantom {{t^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \right)^{m} }}{{\left( {m!} \right)^{2} }}} , $$
(23)

and

$$ \int\limits_{0}^{ + \infty } {t^{s} \exp \left( { - \gamma t^{2} } \right)\ln \left( {bt} \right)} dt = \frac{1}{{4\sqrt {\gamma^{{\left( {s + 1} \right)}} } }}\Gamma \left( {\frac{s + 1}{2}} \right)\left[ {\ln \left( {\frac{{b^{2} }}{\gamma }} \right) + \psi \left( {\frac{s + 1}{2}} \right)} \right], $$
(24)

with \(\psi \left( . \right)\) is the psi-function, hence, the quantity \(J_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right)\) can be written as

$$ J_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{1}{{4\eta^{{\prime}{2}} }}\sum\limits_{m,r = 0}^{ + \infty } {\Gamma \left( {2m + r + 2} \right)\frac{{\left( {{{ - \mu^{2} } \mathord{\left/ {\vphantom {{ - \mu^{2} } {4\eta^{\prime}\delta^{4} }}} \right. \kern-\nulldelimiterspace} {4\eta^{\prime}\delta^{4} }}} \right)^{m} }}{{\left( {m!} \right)^{2} }}\frac{{\left( {{{ - \beta^{2} } \mathord{\left/ {\vphantom {{ - \beta^{2} } {4\eta^{\prime}}}} \right. \kern-\nulldelimiterspace} {4\eta^{\prime}}}} \right)^{r} }}{{\left( {r!} \right)^{2} }}\left[ {\ln \left( {\frac{1}{{\eta^{\prime}\sigma_{0}^{2} }}} \right) + \psi \left( {2m + r + 2} \right)} \right]} . $$
(25)

Finally, the average intensity of QBGSMB traveling through the ABCD optical system in a turbulent atmosphere is expressed as

$$ \begin{gathered} S_{QBGSM} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{{2\pi^{2} \sigma_{s}^{2} }}{{\lambda^{2} B^{2} }}\left\{ {\frac{{\delta^{2} }}{{\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} }}\exp \left[ { - {{\beta^{2} \delta^{4} \eta^{\prime}} \mathord{\left/ {\vphantom {{\beta^{2} \delta^{4} \eta^{\prime}} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]J_{0} \left[ {{{\beta^{2} \delta^{2} \mu } \mathord{\left/ {\vphantom {{\beta^{2} \delta^{2} \mu } {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { + \frac{1}{{2\eta^{{\prime}{2}} }}\sum\limits_{m,r = 0}^{ + \infty } {\Gamma \left( {2m + r + 2} \right)\frac{{\left( {{{ - \mu^{2} } \mathord{\left/ {\vphantom {{ - \mu^{2} } {4\eta^{\prime}\delta^{4} }}} \right. \kern-\nulldelimiterspace} {4\eta^{\prime}\delta^{4} }}} \right)^{m} }}{{\left( {m!} \right)^{2} }}\frac{{\left( {{{ - \beta^{2} } \mathord{\left/ {\vphantom {{ - \beta^{2} } {4\eta^{\prime}}}} \right. \kern-\nulldelimiterspace} {4\eta^{\prime}}}} \right)^{r} }}{{\left( {r!} \right)^{2} }}\left[ {\ln \left( {{1 \mathord{\left/ {\vphantom {1 {\eta^{\prime}\sigma_{0}^{2} }}} \right. \kern-\nulldelimiterspace} {\eta^{\prime}\sigma_{0}^{2} }}} \right) + \psi \left( {2m + r + 2} \right)} \right]} } \right\}. \hfill \\ \end{gathered} $$
(26)

The average intensity for QBGSMB passing through the ABCD optical system in the absence of turbulence (free space) can be defined as

$$ S_{QBGSM}^{{\left( {FS} \right)}} \left( {{{\varvec{\uprho}}},z;\omega } \right) = \frac{{2\pi^{2} \sigma_{s}^{2} }}{{\lambda^{2} B^{2} }}\left\{ {\delta^{2} \left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \exp \left[ { - {{\beta^{2} \delta^{4} \eta^{\prime}} \mathord{\left/ {\vphantom {{\beta^{2} \delta^{4} \eta^{\prime}} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]J_{0} \left[ {{{\beta^{2} \delta^{2} \mu } \mathord{\left/ {\vphantom {{\beta^{2} \delta^{2} \mu } {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {4\left( {\eta^{{\prime}{2}} \delta^{4} + \mu^{2} } \right)}}} \right]} \right\}. $$
(27)

These two last equations are our second main result. In the next Section, we investigate the evolution of the average intensity of QBGSM beams after passing through a paraxial ABCD optical system in atmospheric turbulence. Therefore, we carry out the graphical representations utilizing the derived results cited by Eqs. (26) and (27).

4 Numerical results and analyses

The elements of the transfer matrix are taken as \(A = 1,\)\(B = z\) and \(D = 1\). In the simulation, the wave-front radius of curvature of the beam is considered infinite and the width of the source is fixed at \(\sigma_{s} = 5cm\).

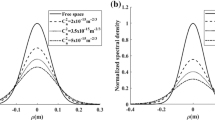
Figure 2 depicts the normalized intensity distribution of QBGSM beams versus \(\rho\) and in three-dimensional plots at various propagation distances with different turbulence strengths. The beams and source parameters in this plot are set as \(\delta = 3cm,\) \(\lambda = 1064nm\) and \(\mu = 0.6\). From these plots, it can be seen that the QBGSM beams keep their initial profile during propagation both in free space and in the turbulent atmosphere. Furthermore, the curves corresponding to the propagation of the QBGSM beams in free space (Fig. 2a) act as an asymptote for the other curves describing the evolution of the beam in a turbulent atmosphere. It is also shown that the lobe width of the diffracted beam widens at far-field and the brightness of the beam becomes weak for a strong turbulent atmosphere and large propagation distance.

Fig. 2
figure 2

Normalized intensity distribution and 3D plots of QBGSMB propagating in a turbulent atmosphere at several propagation distances with different strength turbulence: a Free space, b \(C_{n}^{2} = 3.10^{ - 15} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\), c \(C_{n}^{2} = 5.10^{ - 15} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and d \(C_{n}^{2} = 10^{ - 14} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\)

Full size image

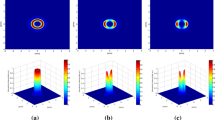
To show the influence of the wavelength on the behavior of the QBGSMB, we illustrate in Fig. 3 the normalized intensity distribution versus \(\rho\) for different values of \(\lambda\) and three values \(C_{n}^{2}\). The calculation parameters are taken as follows: \(z = 5km,\)\(\delta = 3cm\) and \(\mu = 0.6.\) We can see from this figure that the luminosity of the diffracted beam becomes less intense when the wavelength is large and the turbulent is weak (see Fig. 3a–b). The intensity of the QBGSMB follows the opposite evolution law versus the wavelength when the turbulence is strong (\(C_{n}^{2} = 10^{ - 14} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\)). As a result, the brightness of the diffracted beams increases with the increment of the wavelength. (Fig. 3c).

Fig. 3
figure 3

Normalized intensity distribution of the QBGSMB in the turbulent atmosphere for different wavelengths with: a \(C_{n}^{2} = 10^{ - 16} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\), b \(C_{n}^{2} = 10^{ - 15} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and c \(C_{n}^{2} = 10^{ - 14} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\)

Full size image

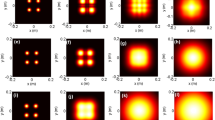
In Fig. 4 the normalized intensity distribution of the QBGSMB is represented as a function of \(\rho\) and in three-dimensional plots for three values of turbulence strength and with different coherence widths. The parameters used in the simulation are chosen as \(z = 5km\) and \(\lambda = 1064nm.\)

Fig. 4
figure 4

Normalized intensity distribution and 3D plots at the receiving plan for the QBGSMB for three values of the structure constant \(C_{n}^{2}\) with \(\mu = 0.6\) and \(\delta\) = : a \(1.5mm\) b \(2mm\), c \(3mm\) and d \(4mm\)

Full size image

As shown from Fig. 4, the QBGSMB has a peak intensity in the center surrounded by side lobes. Additionally, the number of the side lobes in the beam pattern of QBGSMB increases with the increase of the coherence width \(\delta\). Moreover, it is observed that the intensity reduces when the turbulence is strong. It can also be noted that the maximal intensity of the peaks rises when \(\delta\) is greater. Furthermore, by comparing Figs. 2d and 4c for \(C_{n}^{2} = 10^{ - 14} m^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\) and \(z = 5km\), we can observe that when the coherence width \(\delta\) is in the order of millimeters the beam profile contains the main lobe with secondary lobes but when the value of \(\delta\) increases taking for example \(\delta = 3cm\) the profile consists of only one lobe.

It is necessary to note that for \(\mu = 0\), the spectral density of QBGSMB expressed by Eq. (26) is reduced to the spectral density of Gauss-Schell model beam developed in Refs. (Mei et al. 2013; Chib and Dalil-Essakali 2022).

5 Conclusion

To summary, a mathematical form of the spectral degree of coherence for QBGSMB source is introduced in this manuscript. The analytical expression of the cross-spectral density for QBGSMB propagating through a paraxial ABCD optical system in a turbulent atmosphere is derived by using the extended Huygens-Fresnel integral formula and the Rytov theory. The numerical results revealed that the profile width of the diffracted QBGSMB widens and the intensity decreases when the turbulent atmosphere is strong and the propagation distance is large. It can be also observed that the intensity distribution of the beam increases with the increase of the wavelength for an atmosphere with strong turbulence while the beam loses its luminosity when the turbulent strength reduces. The obtained results can have a great deal of interest in many fields such as combination technology of laser beams, remote sensing, and free-space optical communications.