Spatiotemporal chirped solitary waves to the generalized (${\textbf {3}}+{\textbf {1}}$)-dimensional nonlinear Schrödinger equation with varying sources under different diffraction and potential functions

Abstract

We present analytical and numerical solutions for spatiotemporal chirped solitary waves in the generalized ($3+1$)-dimensional nonlinear Schrödinger equation with varying sources under different modulated diffraction and potential functions. Our analytical approach provides a general formula that enables us to generate various types of solitary waves by introducing specific functional forms into the designed diffraction and potential profiles. We investigate the compressed, breathing, and quasiperiodic solitary wave solutions, discussing their characteristics and physical applications in relevant fields. Additionally, we explore numerical solutions where parameters can be arbitrarily chosen, encompassing both snakelike and J-shaped solitary waves. The results demonstrate that transverse and longitudinal structures of these solitary waves can be effectively manipulated by appropriately tuning the diffraction, potential strength, and source term. Furthermore, we numerically investigate solution stability by adding initial white noise; our simulations show that propagation shapes of the solitary waves are preserved.

1 Introduction

The nonlinear Schrödinger equation (NLSE) is one of the most important models in the field of nonlinear science. It describes the behavior of wave packets in various physical systems, including optical fibers [1], Bose–Einstein condensations (BECs) [2], plasmas [3], and hydrodynamics [4]. The NLSE has been extensively studied over the years due to its importance in understanding complex phenomena such as solitons [5], periodic solitary waves [6], and localized waves [7, 8]. Researchers have used various analytical and numerical techniques to investigate the properties of solutions to this equation under different conditions [9,10,11,12,13]. Analytical solutions refer to mathematical expressions that provide an exact description of the NLSE, often involving special functions or series expansions. In contrast, numerical solutions rely on computational methods to approximate the NLSE using algorithms and simulations, making them useful for studying complex systems where analytical solutions may not be readily available. The NLSE in ($1+1$)-dimensions [$(1+1)$-D] is integrable through inverse scattering technique [14], while it is non-integrable in ($2+1$)-D. Nevertheless, there are still several exact analytical and numerical solutions for the NLSE available through various techniques [15, 16]. Moreover, the ($3+1$)-D NLSE has recently gained increasing interest in nonlinear optics due to its ability to support spatiotemporal solitons or light bullets—structures that remain localized along the coordinate axis while maintaining their shape during propagation in a nonlinear medium [17, 18]. For instance, the properties and stability of 3D spatiotemporal optical solitons in NLSE supported by full or low-dimensional optical lattices have been discussed in Ref. [19]. Analytical light bullet solutions to the generalized ($3+1$)-D NLSE with distributed coefficients have been found by F-expansion and balance principle method [20]. Three-dimensional rogue waves to the ($3+1$)-D inhomogeneous NLSE with variable coefficients and parabolic potential have been obtained by symmetry technique [21]. Analytical spatiotemporal soliton solutions to ($3+1$)-dimensional cubic-quintic NLSE with distributed coefficients have been presented in Ref. [22]. Various kinds of spatiotemporal solitons on cnoidal wave backgrounds in media with different distributed transverse diffraction and dispersion have been derived in Ref. [23]. Moreover, in Refs. [24, 25] the authors explore spatiotemporal localized modes and analytical light-bullet solutions of a ($3+1$)-D NLSE with inhomogeneous diffraction or dispersion and nonlinearity under the presence of harmonic and parity-time-symmetric potentials. Additionally, Refs. [26,27,28,29] investigate ($3+1$)-D analytical traveling wave and solitary solutions for varying diffraction and potential functions.

In addition to the aforementioned research, the investigation of dual-core fiber amplifiers is also highly prevalent [30,31,32]. The behavior of these amplifiers can be approximately described by employing the NLSE with a varying source. In ($1+1$)-D, the self-similar transformations have yielded several exact analytical solutions for the NLSE with varying sources [33,34,35]. The dynamics and nonlinear tunneling effect of snakelike self-similar solutions in grating dual-core waveguide amplifiers with different profiles have been investigated in Refs. [36,37,38,39]. Propagation characteristics of ultrashort self-similar periodic waves and similaritons in an inhomogeneous optical medium with varying sources and modulated coefficients have been studied in Ref. [40]. In ($3+1$)-D, exact asymptotic spatiotemporal optical self-similar solutions in a dual-core waveguide with an external source have been presented both analytically and numerically in Ref. [41]. Spatiotemporal optical solitons in the dual-core waveguide amplifiers with different modulated dispersions have been studied in Ref. [42]. Detailed discussions on various types of analytical light bullet solutions in dual-core media with dispersion-decreasing profiles can be found in Refs. [43, 44]. It should be noted that the NLSE with varying sources can also be found in BECs [45], where many types of exact nonautonomous matter-wave solutions were reported. A review of the spatiotemporal engineering of exact solutions generated through explicit transformations from various NLSE models is presented in Ref. [46].

In the aforementioned research on the ($3+1$)-D NLSE, few scholars have simultaneously considered the influence of external potentials and source terms on the equation. In fact, external potential and source term are indispensable factors in many physical systems in the real world. For example, in quantum mechanics, electrons are affected by external potentials when moving under electric or magnetic fields [47]; while in fields such as optical fiber communication, it is necessary to consider possible external influences during the propagation of light waves [48]. Therefore, for the ($3+1$)-D NLSE and other related equations, incorporating both external potential and source term is a highly important and challenging task. This can provide a more accurate description of real physical systems and offer more effective and reliable numerical simulation tools for relevant fields. Furthermore, most of the previous studies on the ($3+1$)-D NLSE have assumed that the diffraction coefficients are modulated equally in both transverse and longitudinal directions. However, in practical applications, diffraction may vary along different directions. Therefore, it is crucial to investigate the impact of diffraction coefficients under different transverse and longitudinal modulations on soliton propagation. This will help deepen our understanding of the complex dynamics and behaviors exhibited by nonlinear systems. Specifically, in terms of transverse modulation, we can adjust the diffraction coefficients by changing the intensity distribution of input beams or designing spatial filters [1]. This can effectively reduce or eliminate waveform distortions caused by diffraction and improve soliton transmission efficiency. On the other hand, longitudinal modulation involves controlling properties of the medium itself and external field strengths. For example, using current or temperature to modify refractive index distribution is a common method in optical fiber communication systems [49]. By selecting appropriate methods for longitudinal modulation and combining them with suitable feedback mechanisms, optical signals can be stably transmitted at expected speeds. In addition, it is of paramount importance to consider the different modulations of external potentials in both transverse and longitudinal directions within the context of BECs [2], as we are aware that external potentials play a crucial role in the formation and characteristics of BECs. In terms of transverse modulation, the behavior of the condensate system can be influenced by changing the interaction strength between particles through external potentials. For example, introducing periodic potential fields into an optical lattice can generate Bloch oscillations, thereby achieving transitions between superfluidity and normal solid states [50]. Additionally, local or nonlocal control methods can be employed to alter the coupling between particles within the system, thus affecting its dynamic behavior. As for longitudinal modulation, external potentials can control the characteristics of the condensate system by varying parameters such as particle number and temperature [51]. For instance, introducing radiation fields into a magneto-optical trap enables effective control over atomic numbers, while adjusting parameters like radiation field intensity and frequency allows fine-tuning of temperature distribution and coherence length within the condensate system.

Based on the above considerations, in this paper we will explore the analytical and numerical solutions of the generalized ($3+1$)-D NLSE with distributed coefficients and a varying source term under different transverse and longitudinal modulations for diffraction and potential functions. To our knowledge, this model has not been studied so far for obtaining spatiotemporal solutions. Compared with the results in Refs. [41,42,43,44], we pay more attention to the effects of different transverse and longitudinal modulations on the propagation of ($3+1$)-D spatiotemporal solutions. These studies are crucial and interesting, and they provide answers for manipulating soliton shapes in different directions. In Sect. 2, we propose the generalized ($3+1$)-D model and solution method to obtain spatiotemporal chirped solitary wave solutions. In Sect. 3, we provide a general formula that allows us to generate various types of analytical solitary waves by introducing the specific functional form into the designed diffraction and potential profiles. We then present some interesting solutions including compressed, breathing, and quasiperiodic solitary waves, discussing their characteristics and physical applications in relevant fields. In Sect. 4, we explore the numerical solutions for cases where parameters can be arbitrarily chosen and present two physically relevant examples demonstrating snakelike and J-shaped solitary waves. Furthermore, we numerically investigate the stability of these solutions. Section 5 concludes the main findings of this paper.

2 The ($3+1$)-D model and solution method

The generalized ($3+1$)-D NLSE with distributed coefficients and a varying source term under different transverse and longitudinal modulations for diffraction and potential functions can be written as:

$$\begin{aligned}&iu_t+\frac{1}{2}\left[ \beta _1(t)\left( u_{xx}+u_{yy}\right) +\beta _2(t)u_{zz}\right] \nonumber \\&\qquad + \frac{1}{2}\left[ f_1(t)\left( x^2+y^2\right) +f_2(t)z^2\right] u+\gamma (t)|u|^2u \nonumber \\&\quad =\frac{ig(t)}{2}u+s(t)\exp [i\phi (x,y,z,t)], \end{aligned}$$

(1)

where $u\equiv u(x,y,z,t)$ is the wave function to be solved. In BECs, x, y, and z are position coordinates, and t is time. The functions $\beta _1(t)$ and $\beta _2(t)$ represent the diffraction coefficients associated with distinct transverse coordinates x, y, and longitudinal coordinate z. $\gamma (t)$ is the nonlinearity coefficient, and g(t) is the gain or loss coefficient. $f_j(t)(j=1,2)$ denotes the strength of the harmonic potential, and $s(t)\exp [i\phi (x,y,z,t)]$ describes the transport of atoms from a reservoir to a waveguide in BECs [52]. In the context of nonlinear optics, t represents the propagation distance, $f_j(t)$ characterizes the type of the graded-index medium, and $s(t)\exp [i\phi (x,y,z,t)]$ is attributed to the built-in asymmetry of the dual-core optical fiber amplifiers [33, 36]. If $\beta _1(t)=\beta _2(t)=\beta (t)$ and $f_1(t)=f_2(t)=0$, Eq. (1) serves as the governing equation in [43, 44], where analytical bright light bullet solutions were explored by means of self-similar transformations. If $s(t)=0$, Eq. (1) serves as the governing equation in [53], where spatiotemporal breathers of 3D NLSE with different transverse diffractions were found.

We seek the solution to Eq. (1) in the following form

$$\begin{aligned} u(x,y,z,t)=p(t)\Phi (\Theta )\exp [i\phi (x,y,z,t)], \end{aligned}$$

(2)

where

$$\begin{aligned} \Theta&=k(t)x+l(t)y+m(t)z+h(t), \end{aligned}$$

(3)

$$\begin{aligned} \phi (x,y,z,t)&=c_1(t)(x^2+y^2)+c_2(t)z^2\nonumber \\&\quad +b_1(t)(x+y)+b_2(t)z+\phi _0(t). \end{aligned}$$

(4)

Here $p(t),k(t),l(t),m(t),h(t),c_1(t),c_2(t),b_1(t), b_2(t)$ and $\phi _0(t)$ are parameter functions to be determined. Substituting Eqs. (2)–(4) into Eq. (1), we can derive a set of equations:

$$\begin{aligned}&\frac{\textrm{d}k}{\textrm{d}t}+2c_1\beta _1 k=0, \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\textrm{d}l}{\textrm{d}t}+2c_1\beta _1 l=0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\textrm{d}m}{\textrm{d}t}+2c_2\beta _2 m=0, \end{aligned}$$

(7)

$$\begin{aligned}&\frac{\textrm{d}h}{\textrm{d}t}+\beta _1 b_1(k+l)+\beta _2 b_2m=0, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{\textrm{d}c_1}{\textrm{d}t}+2c_1^2\beta _1-\frac{f_1}{2} =0, \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\textrm{d}c_2}{\textrm{d}t}+2c_2^2\beta _2 -\frac{f_2}{2}=0, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\textrm{d}b_1}{\textrm{d}t}+2c_1\beta _1 b_1=0, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\textrm{d}b_2}{\textrm{d}t}+2c_2\beta _2 b_2=0, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\textrm{d}p}{\textrm{d}t}+(2c_1\beta _1+c_2\beta _2) p-\frac{gp}{2}=0, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\textrm{d}\phi _0}{\textrm{d}t}+b_1^2\beta _1+\frac{1}{2}b_2^2\beta _2+\mu [\beta _1(k^2+l^2)+\beta _2m^2]=0, \end{aligned}$$

(14)

$$\begin{aligned}&\gamma p^2-\sigma [\beta _1(k^2+l^2)+\beta _2m^2]=0, \end{aligned}$$

(15)

$$\begin{aligned}&s-s_0 p[\beta _1(k^2+l^2)+\beta _2m^2]=0. \end{aligned}$$

(16)

This holds true only if Eq. (1) can be transformed into the following ordinary differential equation

$$\begin{aligned} \frac{1}{2} \frac{d^2\Phi }{d\Theta ^2}+\mu \Phi + \sigma \Phi ^3-s_0=0, \end{aligned}$$

(17)

where $\mu$ is the eigenvalue, $s_0$ is the source amplitude, and $\sigma =\pm 1$ determines whether the nonlinearity exhibits self-focusing ($\sigma =1$) or self-defocusing ($\sigma =-1$).

Defining two auxiliary functions $\kappa _1=\exp (-2\int _0^t c_1\beta _1 \textrm{d}t)$ and $\kappa _2=\exp (-2\int _0^t c_2\beta _2 \textrm{d}t)$, we get

$$\begin{aligned} k(t)&=k_0\kappa _1,\quad l(t)=l_0\kappa _1,\quad m(t)=m_0\kappa _2,\nonumber \\ b_1(t)&=b_{10}\kappa _1, \quad b_2(t)=b_{20}\kappa _2, \end{aligned}$$

(18)

$$\begin{aligned} h(t)&=h_{0}-b_{10}(k_0+l_0)\int _0^t\beta _1\kappa _1^2 \textrm{d}t\nonumber \\&\quad -b_{20}m_0\int _0^t\beta _2\kappa _2^2 \textrm{d}t. \end{aligned}$$

(19)

Table 1 Explicit constraint conditions on the parameters $\sigma , \mu , s_0, P$, and Q for the bright and dark solutions

The amplitude can be determined by solving Eq. (13):

$$\begin{aligned} p(t)=p_0 \kappa _1\sqrt{\kappa _2}\exp \left( \frac{1}{2}\int _0^tg\textrm{d}t\right) , \end{aligned}$$

(20)

and the parameter $\phi _0(t)$ is given by

$$\begin{aligned} \phi _0(t)&=\phi _{10}-\left[ b_{10}^2+\mu \left( k_0^2+l_0^2\right) \right] \int _0^t\beta _1\kappa _1^2 \textrm{d}t\nonumber \\&\quad -\left( \frac{1}{2}b_{20}^2+\mu m_0^2\right) \int _0^t\beta _2\kappa _2^2 \textrm{d}t. \end{aligned}$$

(21)

The subscript “0” represents the initial value of a given function at $t=0$.

It is clear that both $\gamma (t)$ and s(t) can be effectively solved by utilizing Eqs. (15) and (16):

$$\begin{aligned} \gamma (t)&=\frac{\sigma }{p_0^2}\left[ \frac{\beta _1}{\kappa _2}\left( k_0^2+l_0^2\right) +\frac{\beta _2\kappa _2}{\kappa _1^2}m_0^2\right] \nonumber \\&\quad \times \exp \left( -\int _0^tg\textrm{d}t\right) , \end{aligned}$$

(22)

$$\begin{aligned} s(t)&=s_0p_0 \kappa _1\sqrt{\kappa _2}\left[ \beta _1\kappa _1^2(k_0^2+l_0^2) +\beta _2\kappa _2^2m_0^2\right] \nonumber \\&\quad \times \exp \left( \frac{1}{2}\int _0^tg\textrm{d}t\right) , \end{aligned}$$

(23)

which implies that $\gamma (t)$ and s(t) are not arbitrary but rather depend on $\beta (t)$ and g(t). Taking into account Eqs. (22) and (23), we can derive a constraint condition that must be satisfied by the coefficients of Eq. (1) using the present method:

$$\begin{aligned} s(t)=s_0p_0^3\sigma ^{-1}\kappa _1^3\kappa _2^{3/2}\gamma \exp \left( \frac{3}{2}\int _0^tg\textrm{d}t\right) . \end{aligned}$$

(24)

Equation (17) stands out as a particularly fascinating one due to its many exact solutions, ranging from the elegant simplicity of trigonometric function solutions to the more complex and nuanced elliptic function solutions [38, 54]. However, perhaps most intriguing are the soliton solutions—which can maintain their shape and speed even after colliding with other solitons or obstacles. For this purpose, we write the exact solution of ordinary differential equation (17) as:

$$\begin{aligned} \Phi (\Theta )=[P+QF^2(\Theta )]/[1+\delta F^2(\Theta )], \end{aligned}$$

(25)

where P, Q and $\delta$ are constants satisfying $P\delta -Q\not =0$, and the function F can be selected from Table 1.

It should be noted that there may be some restrictions on the value of $\delta$ as indicated in Table 1. When $F=\textrm{sech}$ (bright soliton), we choose $\delta \in (-1,-0.5)\cup (-0.5,0)$; when $F=\tanh$ (dark soliton), we choose $\delta \in (-1,0)$. These soliton solutions exhibit different profiles for different regions of source amplitude $\delta$. One can obtain U-shaped profile solutions as source amplitude $\delta \rightarrow 0$, and W-shaped profile solutions as source amplitude $\delta \rightarrow -1$.

The final solution for u then is

$$\begin{aligned} u(x,y,z,t)&=p_0 \kappa _1\sqrt{\kappa _2}\nonumber \\&\quad \times \exp \left( \frac{1}{2}\int _0^tg\textrm{d}t\right) \frac{P+QF^2(\Theta )}{1+\delta F^2(\Theta )}\nonumber \\&\quad \times \exp \{i[c_1(t)(x^2+y^2)+c_2(t)z^2\nonumber \\&\quad +b_1(t)(x+y)+b_2(t)z+\phi _0(t)]\}. \end{aligned}$$

(26)

3 Analytical spatiotemporal chirped solitary waves to Eq. (1) with different profiles

From Eqs. (18)–(23) one can see that the attainment of self-consistent solutions of the system is contingent upon successfully resolving $\kappa _1$ and $\kappa _2$, which depends on parameters $c_j(t)$ and $\beta _j(t)$. To solve this problem, one would have to solve Eqs. (9)–(10), which are known as the Riccati differential equations for $c_j(t)$. However, these two equations can only be solved analytically for specific choices of $\beta _j(t)$ and $f_j(t)$. In this section we consider four cases for the selection of $\beta _j(t)$ and $f_j(t)$:

Case 1. $\beta _j(t)=\beta _{j0}$ and $f_j(t)=f_{j0}$, corresponding to extended solitary waves.

Case 2. Either $\beta _j(t)$ or $f_j(t)$ is a function while the other is a constant, corresponding to compressed solitary waves.

Case 3. $\beta _j(t)=\beta _{j0}F(t)$ and $f_j(t)=f_{j0}F(t)$, corresponding to breathing solitary waves.

Case 4. $\beta _j(t)=\beta _{j0}F_j(t)$ and $f_j(t)=f_{j0}F_j(t)$, corresponding to quasiperiodic solitary waves.

In the above, $\beta _{j0}$ and $f_{j0}$ are constants, while F(t) and $F_j(t)$ are arbitrary functions. These type of solitary waves are very useful in nonlinear systems. For example, the compressed solitary waves can be applied to the design of soliton compressors associated with the generation of high-power ultrashort pulses. The breathing solitary waves can provide insights into how energy is transferred and distributed within a system and are also related to conservation laws and stability analysis. By studying these solitary waves, we can make a deeper understanding of wave propagation phenomena and their applications in optics and condensed matter physics.

In case 1, we obtain $c_j(t)=\frac{1}{2}\sqrt{\frac{f_{j0}}{\beta _{j0}}}\tanh (\sqrt{f_{j0}\beta _{j0}}t )$ and $\kappa _j(t)=\textrm{sech}\left( \sqrt{f_{j0}\beta _{j0}}t\right)$, which results in analytical extended solutions in the form of solitary waves. We will not go into details here. For the sake of clarity, in the subsequent discussion, we distinguish solitary waves into U-shaped and W-shaped profiles based on their distinct transverse and longitudinal modulations in the x, y, and z directions; similarly, we distinguish solitary waves as compressed, breathing, quasiperiodic, snakelike, and J-shaped profiles depending on their propagation dynamics with respect to t. It is worth noting that both U-shape and W-shape profiles are ubiquitous and can be observed in various scenarios.

3.1 Compressed solitary wave solutions

We now discuss case 2 where either $\beta _j(t)$ or $f_j(t)$ is a function while the other is a constant. As an example, we choose $\beta _j(t)=\beta _{j0}\exp (-\alpha t)$ and $f_j(t)=1$, where $\alpha \in {\mathcal {R}}$. Here we discuss the case for $\alpha >0$, corresponding to the dispersion-decreasing nonlinear media [55]. With this, we obtain

$$\begin{aligned} c_j(t)=-\frac{1}{2\sqrt{\beta _{j0}}}\frac{I_0\left[ 2\frac{\sqrt{\beta _{j0}}}{\alpha } \exp \left( -\frac{\alpha }{2}t\right) \right] }{I_1\left[ 2\frac{\sqrt{\beta _{j0}}}{\alpha }\exp \left( -\frac{\alpha }{2}t\right) \right] }, \end{aligned}$$

(27)

and

$$\begin{aligned} \kappa _j(t)=I_1^{-1}\left[ 2\frac{\sqrt{\beta _{j0}}}{\alpha }\exp \left( -\frac{\alpha }{2}t\right) \right] \exp \left( \frac{\alpha }{2}t\right) , \end{aligned}$$

(28)

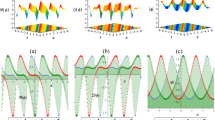
where $I_0$ and $I_1$ are the zero-order and first-order modified Bessel functions of the first kind, respectively. Then the expressions of other parameters and coefficients can be derived from Eqs. (18)–(23), and the analytical spatiotemporal solitary waves to Eq. (1) can be obtained by inserting these solved parameters into Eq. (26). The solitary waves and corresponding profiles of chirp $c_j(t)$, amplitude p(t), nonlinearity $\gamma (t)$, and source s(t) are depicted in Fig. 1. These solitary waves exhibit different transverse structures for different value region of source amplitude $s_0$. In our study, we have carefully selected four distinct $s_0$ values to investigate the fascinating properties of the solitary waves. The U-shaped bright solitary wave ($s_0=-8.4493$), as shown in Fig. 1e, is a remarkable phenomenon that exhibits a localized wave packet with an amplitude peak at its center. This type of solitary wave has been extensively studied in various fields such as optics and fluid dynamics due to its unique characteristics. The W-shaped bright solitary wave ($s_0=10.5173$, Fig. 1g) is another intriguing type of localized wave packet that possesses multiple peaks within its structure. The U-shaped dark solitary wave ($s_0=8.0659$, Fig. 1f) exhibits a dip in intensity at its center while maintaining positive background intensity levels around it; the W-shaped dark solitary wave ($s_0=0.0035$, Fig. 1h) displays an even more intricate structure with multiple dips and humps within its profile. It can be seen from the figure that the chirp function exhibits a monotonic decrease, while the amplitude p(t) shows a monotonic increase. For nonlinearity coefficient, when the solution is a bright solitary wave, it monotonically decreases to zero; when solved for a dark solitary wave, it monotonically increases to zero. Except for the s(t) corresponding to U-shaped bright solitary waves, which demonstrates a monotonic decrease, all other types of solitary waves’ associated s(t) exhibit a monotonic increase. Moreover, we find that the width of the solitary wave decreases as t increases while its amplitude increases, indicating a continuous compression process. This compression results in an increase in the solitary wave’s amplitude, making it more powerful than its original form, which may be useful in design of soliton compressors associated with the generation of high-power ultrashort pulses.

Fig. 1

Compressed solitary waves and system parameters in the case of $\beta _j(t)=\beta _{j0}\exp (-\alpha t)$ and $f_j(t)=1$. a Profiles of chirp functions $c_1(t)$ (blue solid line), $c_2(t)$ (red dashed line), and amplitude (green dash-dotted line) as functions of t. b Profiles of nonlinearity for bright solitary wave (blue solid line) and dark solitary wave (red dashed line). c and d Source s(t) vs t. These curves correspond to different types of solitary waves: U-shaped bright solitary wave (blue solid line,$s_0=-8.4493$), U-shaped dark solitary wave (red dashed line, $s_0=8.0659$), W-shaped bright solitary wave (green dashed-dotted line, $s_0=10.5173$), and W-shaped dark solitary wave (magenta solid line, $s_0=0.0035$). e–h Chirped solitary waves as functions of t: e U-shaped bright solitary wave, f U-shaped dark solitary wave, g W-shaped bright solitary wave, and h W-shaped dark solitary wave. The parameters are $p_0=\beta _{10}=1,\beta _{20}=3,b_{10}=b_{20}=1,\alpha =0.5,k_0=l_0=m_0=1,h_0=0,$ and $g=0$

It is worth noting that selecting $\beta _j(t)=1$ and $f_j(t)=f_{j0}\exp (-\alpha t)$ still results in a solitary solution expressed as Bessel functions, albeit an extended one. Moreover, alternative choices such as setting $\beta _j(t)=1$ and $f_j(t)=1+f_{j0}\cos (t)$ may lead to analytical solutions in terms of Mathieu functions to Eq. (1), which are also extended waves. We will not delve into it extensively here.

3.2 Breathing solitary wave solutions

More general situation is that both $\beta _j(t)$ and $f_j(t)$ are functions of t. We next provide a general formula that can generate various types of solitary waves and then proceed to discuss cases 3 and 4 separately. Assuming $\beta _j(t)=\beta _{j0}F_j(t)$ and $f_j(t)=f_{j0}F_j(t)$, we have

$$\begin{aligned} c_j(t)=\frac{1}{2}\sqrt{\frac{f_{j0}}{\beta _{j0}}}\tanh \left[ \sqrt{f_{j0}\beta _{j0}}\int F_j(t) \textrm{d}t\right] , \end{aligned}$$

(29)

then the auxiliary function

$$\begin{aligned} \kappa _j(t)=\textrm{sech}\left[ \sqrt{f_{j0}\beta _{j0}}\int F_j(t) \textrm{d}t\right] . \end{aligned}$$

(30)

Fig. 2

Breathing solitary waves and system coefficients in the case of $F(t)=\cos (\omega t)$. The setup is the same as in Fig. 1, except for $f_{10}=1,f_{20}=2,$ and $\omega =2$

According to formula (29), as long as we substitute the specific functional form of $F_j(t)$ into it, we can obtain the solution of $c_j(t)$, and then solve for $\kappa _j(t)$ from Eq. (30) and determine other parameters and coefficients in the system using Eqs. (18)–(23). Finally, by substituting these solutions into Eq. (26), we can obtain various types of analytical solitary waves. Therefore, we provide a general formula (29) that enables the generation of various types of solitary waves by inputting the specific functional form of $F_j(t)$ into it.

Let us consider case 3, where $\beta _j(t)$ and $f_j(t)$ have the same functional forms but with different amplitudes. This can be viewed as the special case when $F_j(t)=F(t)$ in formula (29). Two typical functional forms of F(t) are selected to produce some novel solitary wave solutions for Eq. (1): (i) $F(t)=\cos (\omega t)$, and (ii) $F(t)=J_n(\upsilon t)$, where $\omega ,\upsilon \in {\mathcal {R}}$, and $J_n$ is the n-order Bessel function of the first kind. The former case is usually relevant for periodic systems that involve dispersion or diffraction management in nonlinear media [56], and it holds significance for stabilizing the breathing solutions. The latter case, Bessel modulation, may be useful for stabilization of higher dimensional solitons in optical lattices [57].

When the system is modulated by the cosine function $F(t)=\cos (\omega t)$, we get $c_j(t)=\frac{1}{2}\sqrt{\frac{f_{j0}}{\beta _{j0}}}\tanh \left[ \frac{\sqrt{f_{j0}\beta _{j0}}}{\omega }\sin (\omega t)\right]$ and $\kappa _j(t)=\textrm{sech}\left[ \frac{\sqrt{f_{j0}\beta _{j0}}}{\omega }\sin (\omega t)\right] .$ Figure 2a–d show the profiles of chirp $c_j(t)$, amplitude p(t), nonlinearity $\gamma (t)$, and source s(t) vs t. These solitary waves again exhibit the aforementioned four types of structures in the distinct transverse and longitudinal directions for different ranges of source amplitude $s_0$, as shown in Fig. 2e–h. Besides, all the solutions display breathing structures with respect to t. This means that their properties repeat themselves after certain intervals of t. Such periodicity adds another layer of interest to their already fascinating behavior. In Fig. 2, we find that this breathing period is $\pi /\omega$. Additionally, the amplitude of solutions attains its maximum value $p_0$ at $t=n\pi /\omega$ and minimum value $p_0\textrm{sech}\left( \frac{1}{\omega }\right) ^{3/2}$ at $t=(2n+1)\pi /2\omega$, where $n=0,1,2,\ldots$. This breathing behavior can be attributed to the periodic variation of the chirp functions $c_j(t)$, which affects the amplitude and phase of solutions through their dependence on $\kappa _j(t),b_j(t)$, and $\phi _0(t)$. Therefore, our selection of these four $s_0$ values provides us with a comprehensive understanding of different types of solitary waves and their underlying physics in BECs and nonlinear optics.

Fig. 3

Quasibreathing solitary waves and system coefficients in the case of $F(t)=J_n(\upsilon t)$. The setup is the same as in Fig. 2, except for $b_{10}=b_{20}=0.5$ and $\upsilon =1$

Fig. 4

Quasiperiodic solitary waves and system coefficients in the case of $F_1(t)=\cos (\omega t)$ and $F_2(t)=J_1(\upsilon t)$. a Profiles of the chirp $c_1(t)$ (blue solid line) and $c_2(t)$ (red dashed line) as functions of t. b Amplitude of the solitary wave as a function of t. c Nonlinearity $\gamma (t)$, and d source s(t) (blue solid line for U-shaped, red dashed line for W-shaped) for the bright solution. Middle row: U-shaped solutions for e $|u(x,0,0,t)|^2$, f $|u(0,y,0,t)|^2$, and g $|u(0,0,z,t)|^2$. Bottom row: W-shaped solutions for h $|u(x,0,0,t)|^2$, i $|u(0,y,0,t)|^2$, and j $|u(0,0,z,t)|^2$. The parameters are $p_0=b_{10}=b_{20}=\upsilon =1,k_0=1,l_0=0.8,m_0=1,f_{10}=\beta _{10}=1,f_{20}=\beta _{20}=1.2,\omega =3,h_0=g=0$

Secondly, we consider the system with Bessel modulation $F(t)=J_n(\upsilon t)$. For simplicity, we restrict ourself to the order $n=1$. In this case, we have $c_j(t)=-\frac{1}{2}\sqrt{\frac{f_{j0}}{\beta _{j0}}}\tanh \left[ \frac{\sqrt{f_{j0}\beta _{j0}}}{\upsilon }J_0(\upsilon t)\right] ,$ which results in $\kappa _j(t)=\textrm{sech}\left[ \frac{\sqrt{f_{j0}\beta _{j0}}}{\upsilon }J_0(\upsilon t)\right] .$ Figure 3 shows the profiles of chirp $c_j(t)$, amplitude p(t), nonlinearity $\gamma (t)$, and source s(t), accompanied by the corresponding solitary wave solutions. From Fig. 3a we see that the chirp and amplitude first increase and then oscillate periodically, and the oscillation amplitude keeps decreasing. In addition, we observe that the nonlinearity $\gamma (t)$ and source s(t) exhibit periodic oscillations around the initial position, and the amplitude of these oscillations gradually diminishes, as shown in Fig. 3b–d. It can be seen from Fig. 3e–h that the solitary wave solutions oscillate quasiperiodically with respect to t, i.e., they are quasibreathing solutions. For a given real number n, $J_n(t)$ has an infinite number of real zeros, and there is a relation $\textrm{d}J_0(t)/\textrm{d}t=-J_1(t)$. Thus, the extreme points of $J_0(t)$ are the zeros of $J_1(t)$. Based on this property, we calculate that the amplitude of solutions attains its maximum value at about $t=(\nu -1/4)\pi$ and minimum value at about $t=(\nu +1/4)\pi$, where $\nu =0,1,2,\ldots$. Additionally, we also find that the global minimum amplitude in Fig. 3 is approximately 0.522. Furthermore, our findings indicate that an increase in n leads to a longer oscillation period and wider initial width for the solutions, while an increase in $\upsilon$ results in a shorter oscillation period and narrower initial width for the solutions. This suggests the possibility of controlling the oscillation period and initial width of the quasibreathing solutions.

3.3 Quasiperiodic solitary wave solutions

Finally, we consider case 4 where $F_1(t)$ and $F_2(t)$ have different functional forms, which will produce more general solitary waves. In this case, $f_1(t)$ and $\beta _1(t)$ in Eq. (9) can have different functional forms from $f_2(t)$ and $\beta _2(t)$ in Eq. (10). The implication arises that the modulation profiles of diffraction and external potential differ in the transverse and longitudinal directions. As an example, we choose $F_1(t)=\cos (\omega t)$ and $F_2(t)=J_1(\upsilon t)$. In this case we have $c_1(t)=\frac{1}{2}\sqrt{\frac{f_{10}}{\beta _{10}}}\tanh \left[ \frac{\sqrt{f_{10}\beta _{10}}}{\omega }\sin (\omega t)\right] , c_2(t)=-\frac{1}{2}\sqrt{\frac{f_{20}}{\beta _{20}}}\tanh \left[ \frac{\sqrt{f_{20}\beta _{20}}}{\upsilon }J_0(\upsilon t)\right] , \kappa _1(t)=\textrm{sech}\left[ \frac{\sqrt{f_{10}\beta _{10}}}{\omega }\sin (\omega t)\right]$ and $\kappa _2(t)=\textrm{sech}\left[ \frac{\sqrt{f_{20}\beta _{20}}}{\upsilon }J_0(\upsilon t)\right]$. This different modulation in transverse and longitudinal directions will lead to the amplitude

$$\begin{aligned} p(t)&=p_0\textrm{sech}\left[ \frac{\sqrt{f_{10}\beta _{10}}}{\omega }\sin (\omega t)\right] \nonumber \\&\quad \times \textrm{sech}\left[ \frac{\sqrt{f_{20}\beta _{20}}}{\upsilon }J_0(\upsilon t)\right] ^{1/2}\exp \left( \frac{1}{2}\int _0^tg\textrm{d}t\right) . \end{aligned}$$

(31)

In Fig. 4, we present the modulation profiles of system parameters and corresponding solitary waves for the bright solution. It can be observed that the chirp function $c_1(t)$ exhibits periodic variations, while the chirp function $c_2(t)$ first increases and then oscillates quasiperiodically. As shown in Fig. 4b, the amplitude of solution initially increases and then varies quasiperiodically with respect to t. For nonlinearity $\gamma (t)$ and source s(t), they all oscillate quasiperiodically with respect to t. The intensity distribution of the bright solution is presented in Fig. 4e–j. Figure 4e–g display the structures of U-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. Figure 4h–j display the structures of W-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. It is evident that these solitary waves evolve quasiperiodically with respect to t, owing to the combined modulations of cosine and Bessel functions. Notably, despite having the same amplitudes, the widths of these waves exhibit distinct evolutionary characteristics in the transverse and longitudinal directions due to the different modulation profiles of $F_1(t)$ and $F_2(t)$. For instance, the width of the waves increases from Fig. 4h–j, indicating a clear manifestation of this modulation.

Fig. 5

a Numerical simulations of solitary waves chosen from Fig. 2g at $y=1,z=2$ were conducted for the case of $F(t)=\cos (\omega t)$, except for $\beta _{10}=1,\beta _{20}=1.01,f_{10}=1$, and $f_{20}=1.02$. b Numerical simulations of solitary waves chosen from Fig. 3g at $y=1,z=2$ were conducted for the case of $F(t)=J_n(\upsilon t)$, except for $\beta _{10}=1,\beta _{20}=1.01,f_{10}=1$, and $f_{20}=1.02$. From left to right, $t=2, 6$, and 10. A 1% white noise is included in the initial data. c, d Are the 3D plots of (a) and (b), respectively. Only the dependence on x is shown for 3D case

The aforementioned examples illustrate that the solitary wave solutions can be acquired through the modulations of diffraction $\beta _j(t)$ and potential strength $f_j(t)$ via the function $F_j(t)$. Theoretically, there are infinite options of $F_j(t)$ available. Other novel solitary solutions and their properties can also be studied in the same way as described above.

The stability of the found solitary waves can be tested by numerical simulations using a split-step beam propagation method, since 3D solutions may be stabilized in some cases [20, 58,59,60]. We take the analytical solutions in the case of $F(t)=\cos (\omega t)$ and $F(t)=J_n(\upsilon t)$ as examples to run numerical experiments to Eq. (1), with initial field coming from Eq. (26). A 1% white noise is added to the initial data during the simulations. The numerical results are shown in Fig. 5, where we fixed $y=1,z=2$ to observe the evolution of solutions in $x-t$ coordinates. Figure 5a, b display the profiles of solitary waves at $t=2, 6$, and 10 in the case of $F(t)=\cos (\omega t)$ and $F(t)=J_n(\upsilon t)$, respectively. It should be noted that the evolution of the solutions in $y-z$ and $t-z$ coordinates can also be simulated by fixing the coordinates of the other two axes. To comprehensively observe the evolution of solitary waves, we present 3D plots depicting their evolutions in Fig. 5c, d. The numerical experiment was conducted up to $t=10$ in Fig. 5c and up to $t=20$ in Fig. 5d, with no obvious collapse phenomenon observed.

Fig. 6

Numerically found solitary waves and modulation profiles of system parameters in the case of $f_1(t)=0.1\cos (0.5t), f_2(t)=0.3\cos (0.5t), \beta _1(t)=0.1\sin (0.5t), \beta _2(t)=0.3\sin (0.5t)$. a Profiles of the chirp $c_1(t)$ (open circles) and $c_2(t)$ (squares) as functions of t. b Amplitude of the solitary wave as a function of t. c Nonlinearity $\gamma (t)$, and d source s(t) (squares for U-shaped, open circles for W-shaped) for the bright solution. Middle row: U-shaped solutions for e $|u(x,0,0,t)|^2$ with $k_0=l_0=m_0=1$, f $|u(0,y,0,t)|^2$ with $k_0=1,l_0=0.8,m_0=1$, and g $|u(0,0,z,t)|^2$ with $k_0=l_0=1,m_0=0.3$. Bottom row: W-shaped solutions for h $|u(x,0,0,t)|^2$ with $k_0=l_0=m_0=1$, i $|u(0,y,0,t)|^2$ with $k_0=1,l_0=0.8,m_0=1$, and j $|u(0,0,z,t)|^2$ with $k_0=l_0=1,m_0=0.3$. Here, $p_0=b_{10}=b_{20}=1,h_0=0,g=0.106$, the initial data for Eqs.(9) and (10) are $c_1(0)=c_2(0)=0$

4 Numerically found solitary wave solutions to Eq. (1)

In this section, we shall investigate the properties of spatiotemporal chirped solitary waves by allowing for arbitrary choices of the functional forms of $\beta _j(t)$ and $f_j(t)$. In this case, solving Eqs. (9) and (10) requires a meticulous numerical approach. We will consider two physically relevant examples by using the Runge–Kutta method to demonstrate some interesting solitary wave solutions for Eq. (1) in numerical forms.

4.1 Snakelike solitary wave solutions

The first example we consider pertains to the periodic variation of $f_j(t)$, a phenomenon commonly observed in BECs for time-dependent harmonic potentials. In this case, $\beta _j(t)$ is also chosen as a periodic function. In accordance with physical reality, we assume that they have the same oscillation frequency:

$$\begin{aligned}&f_1(t)=0.1\cos (0.5t),{} & {} f_2(t)=0.3\cos (0.5t),\nonumber \\&\beta _1(t)=0.1\sin (0.5t),{} & {} \beta _2(t)=0.3\sin (0.5t). \end{aligned}$$

(32)

Obviously, $f_j(t)$ and $\beta _j(t)$ do not have the same functional form, so we need to solve Eqs. (9) and (10) numerically. The numerical calculations were carried out based on the Runge–Kutta method, working with initial data $c_1(0)=c_2(0)=0$.

In Fig. 6, we present the numerically found solitary waves and modulation profiles of system parameters in this case for the bright solution. As can be seen from Fig. 6a, the chirp functions vary periodically with the increase of t. The situation with respect to amplitudes is somewhat complex. There exists a critical gain value, $g_c$, which results in three possible scenarios for the peak amplitude: (i) p(t) grows with periodic oscillation for increasing t $(g>g_c)$; (ii) p(t) decreases with periodic oscillation for increasing t $(g<g_c)$; (iii) p(t) exhibits approximately periodic oscillations for increasing t $(g=g_c)$. In cases (i) and (ii), the solitary waves display either compressing or spreading behavior while maintaining a linear chirp. In case (iii), one can obtain solitary waves with only periodically oscillating amplitudes, not going to extinction or infinity. Let us direct our attention to this particular set of solutions. To determine the value of $g_c$, we perform a curve fitting analysis of the $\kappa _1\sqrt{\kappa _2}$ term in Eq. (20), which represents an attenuation function of oscillating structures. The fitting results indicate that $\kappa _1\sqrt{\kappa _2}$ tends to $\exp (-0.053t)$, thus resulting in $g_c\approx 0.106$. Therefore, if we choose $g=0.106$ in this case, there are only periodic oscillations on p(t), as depicted in Fig. 6b. As for the nonlinearity and source, Fig. 6c, d, it is seen that they oscillate periodically with the oscillation amplitude decreasing over t. Meanwhile, Fig. 6e–j demonstrate the intensity profiles of the numerically found bright solutions, which demonstrate snakelike behaviors with respect to t. Figure 6e–g display the structures of U-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. Figure 6h–j display the structures of W-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. Due to the different amplitudes of oscillation between $\kappa _1$ and $\kappa _2$, the solitary waves exhibit distinct evolutionary properties in different coordinate directions. A very interesting phenomenon is that we can control the initial moving direction of the solutions by appropriately selecting $b_{10}$ and $b_{20}$. When both $b_{10}$ and $b_{20}$ are negative, the solitary waves initially propagate toward the left; when they are both positive, the solitary waves initially propagate toward the right. If $b_{10}$ and $b_{20}$ have opposite signs, the initial propagation direction of the solitary waves depends on their relative magnitudes.

Fig. 7

Numerically found solitary waves and modulation profiles of system parameters in the case of $f_1(t)=0.1\cos (0.5t), f_2(t)=0.3\cos (0.5t), \beta _1(t)=0.1\exp (-0.2t), \beta _2(t)=0.3\exp (-0.2t)$. a Profiles of the chirp $c_1(t)$ (open circles) and $c_2(t)$ (squares) as functions of t. b Amplitude of the solitary wave as a function of t. c Nonlinearity $\gamma (t)$, and d source s(t) (squares for U-shaped, open circles for W-shaped) for the bright solution. Middle row: U-shaped solutions for e $|u(x,0,0,t)|^2$ with $k_0=l_0=m_0=1$, f $|u(0,y,0,t)|^2$ with $k_0=1,l_0=0.8,m_0=1$, and g $|u(0,0,z,t)|^2$ with $k_0=l_0=1,m_0=0.3$. Bottom row: W-shaped solutions for h $|u(x,0,0,t)|^2$ with $k_0=l_0=m_0=1$, i $|u(0,y,0,t)|^2$ with $k_0=1,l_0=0.8,m_0=1$, and j $|u(0,0,z,t)|^2$ with $k_0=l_0=1,m_0=0.3$. Here, $p_0=b_{10}=b_{20}=1,h_0=0,g=0$, the initial data for Eqs. (9) and (10) are $c_1(0)=c_2(0)=0$

4.2 J-shaped solitary wave solutions

We will now shift our focus to the scenario in which $\beta _j(t)$ is modeled by an exponential function, while $f_j(t)$ remains expressed as per Eq. (32):

$$\begin{aligned}&f_1(t)=0.1\cos (0.5t),{} & {} f_2(t)=0.3\cos (0.5t),\nonumber \\&\beta _1(t)=0.1\exp (-0.2t),{} & {} \beta _2(t)=0.3\exp (-0.2t). \end{aligned}$$

(33)

In this case, Eqs. (9) and (10) were solved numerically with initial data $c_1(0)=c_2(0)=0$.

In Fig. 7, we present the numerically found solitary waves and modulation profiles of system parameters for the bright solution. It is seen that the chirp functions exhibit periodic variations with respect to t, as shown in Fig. 7a. There are three possible scenarios for the peak amplitude: (i) p(t) first decreases and then increases to infinity for $g>0$; (ii) p(t) decreases to zero for $g<0$; (iii) p(t) first decreases and then increases to a constant for $g=0$ (see Fig. 7b). Solitary waves in cases (i) and (ii) will either propagate infinitely or dissipate completely. As $t\rightarrow \infty$, one can obtain solitary waves with constant amplitudes in case (iii), which may be useful for the stabilization of waves in nonlinear media. For nonlinearity $\gamma (t)$, it monotonically decreases to zero when solved for a bright solution. As for the source s(t), Fig. 7d, when the solution takes a U-shaped profile, it exhibits monotonic increase toward zero; conversely, when the solution takes a W-shaped profile, it demonstrates monotonic decrease toward zero. The intensity distribution of the bright solution obtained through numerical calculation is presented in Fig. 7e–j. It is noteworthy that the trajectories of these solutions follow a “J” pattern with respect to t. Furthermore, we discover that the appropriate selection of values for $b_{10}$ and $b_{20}$ can effectively manipulate the orientation of the “J” shape. Specifically, when both $b_{10}$ and $b_{20}$ are negative, the “J” shape is oriented toward the right; when both are positive, it points to the left. When $b_{10}=-b_{20}$, the “J” shape disappears and a straight line is formed for bright solutions. Figure 7e–g display the structures of U-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. Figure 7h–j display the structures of W-shaped solitary waves in $x-t, y-t$, and $z-t$ coordinates, respectively. The parameters in the figure are chosen as $p_0=b_{10}=b_{20}=1,h_0=0,g=0$. Note that the solitary waves exhibit distinct evolutionary properties in different coordinate directions due to the different amplitudes of oscillation between $\kappa _1$ and $\kappa _2$.

We have presented only two physically relevant examples involving bright solutions. In fact, the same process applies to the dark solutions as well. Furthermore, numerical solutions of Eqs. (9) and (10) can be obtained for any given values of $\beta _j(t)$ and $f_j(t)$, thereby enabling the acquisition of spatiotemporal solitary wave solutions in numerical form for Eq. (1), encompassing both bright and dark scenarios. From Eqs. (18) and (20), it can be seen that the transverse structure of solitary waves can be regulated by manipulating $\kappa _1$, while the longitudinal structure can be controlled by adjusting $\kappa _2$; both factors significantly influence the amplitude of solitary waves. This is exactly how we want to manipulate the shape of solitary waves. The aforementioned conclusion is applicable to both analytical and numerical solutions. In addition, we have added an initial perturbation to the numerical solutions, such as white noise, and observed that the propagation shapes of the solitary waves are still preserved.

5 Conclusions

In conclusion, we have successfully obtained spatiotemporal chirped solitary waves in both analytical and numerical forms for the generalized ($3+1$)-D NLSE with varying sources under different modulated diffraction and potential functions. Concerning the analytical solutions, we have presented a general formula [Eq. (29)] that enables the generation of various types of solitary waves by introducing a specific functional form of $F_j(t)$. Some intriguing solutions, such as compressed, breathing, and quasiperiodic solitary waves, have been thoroughly investigated. The characteristic properties of these solitary solutions, including chirp, width, amplitude, periodicity, as well as their physical applications relevant to the field have been extensively discussed. Furthermore, we have conducted comprehensive numerical investigations on the properties of solitary waves with arbitrary choices of functional forms for $\beta _j(t)$ and $f_j(t)$. Two physically relevant examples were considered using the Runge–Kutta method to demonstrate fascinating trajectories of snakelike and J-shaped solitary waves. Additionally, it has been discovered that transverse and longitudinal structures of these solitary waves can be effectively manipulated by appropriately tuning the diffraction $\beta _j(t)$, potential strength $f_j(t)$, and source term s(t). We carefully selected four distinct values for $s_0$ to obtain bright and dark-type solitary waves with both U-shaped profiles and W-shaped profiles. In addition, an examination on stability was performed through numerical simulations by adding initial white noise which demonstrated that propagation shapes of solitary waves remain preserved.