1 Introduction

In recent years, Soliton solutions of nonlinear evolution equations plays an important part in the study of nonlinear complex physical phenomena and one of the most empowering and extremely active area of research investigation. Which appears in various fields of physical sciences such as solid state physics, plasma physics, relativity, optical fibers, biomechanics, and ecology. A search of direct approach for exact solutions of nonlinear equations has become more and more attractive in recent years because of the availability of computer symbolic systems like Maple or Mathematica.

Several methods including Auxiliary Equation (Kumar et al. 2008; Liu and Liu 2009), Variational Iteration (Mohyud-Din et al. 2011), Solitary wave ansatz (Zayed and Al-Nowehy 2016), Modified Simple Equation (Jawad et al. 2010; Zayed 2011; Zayed and Hoda Ibrahim 2012, 2013), Trigonometric function series (Zhang 2008), Jacobi elliptic function (Yan 2003), Sine–Cosine (Wazwaz 2004; Borhanifar et al. 2008, 2009, 2010; Filiz Taşcan 2009), first integral (Eslami et al. 2014; Mirzazadeh and Biswas 2014; Darvishi et al. 2016), exp (−φ(ξ))-expansion method (Khater 2016), Tanh (Wazwaz 2008a), Extended Tanh (Khater et al. 2017; Zahran and Khater 2016; Lü and Chen 2015; Shukri and Al-Khaled 2010), F-expansion (Yomba 2004, 2005; Wang and Li 2005a, b; Ren and Zhang 2006; Zhang et al. 2006; Abdou 2007), Exp-function (Wu and He 2006; Bekir and Boz 2008; Zhou et al. 2008; Borhanifar et al. 2009; Borhanifar and Kabir 2009; Guner and Atik 2016), \(\left( {\frac{{G^{\prime } }}{G}} \right)\)-expansion method (Wang et al. 2008; Zhang et al. 2008; Liu 2005), Trail Equation (Du 2010; Bulut 2013), Extended Trial Equation (Gurefe et al. 2013; Pandir 2014; Mirzazadeh et al. 2016) have been used to find appropriate solutions of nonlinear partial differential equations. Inspired and motivated by the ongoing research in this area, We apply Extended Trial Equation method on generalized ZK equation (gZK) (Wazwaz 2008b) and generalized ZK-BBM equation (Wazwaz 2005):

$$\frac{\partial u}{\partial t} + \alpha u^{n} \frac{\partial u}{\partial x} + \beta \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }} + \frac{{\partial^{3} u}}{{\partial y^{2} \partial x}}} \right) = 0,\quad n > 1,$$

and

$$\frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} - \alpha \frac{{\partial (u^{n} )}}{\partial x} + \beta \left( {\frac{{\partial^{3} u}}{{\partial x^{2} \partial t}} + \frac{{\partial^{3} u}}{{\partial y^{2} \partial x}}} \right) = 0,\quad n > 1,$$

where α and β are arbitrary constants. The ZK equation in two-dimension, was first derived for describing weakly nonlinear ion-acoustic waves in a polarized lossless plasma. While generalized ZK-BBM equation developed to the ZK Equation, imitative from standard BBM equation, its normally called generalized form of ZK-BBM equation. Moreover, in earlier literature the Extended Trial Equation method has not been applied to the above suggested equations. Wazwaz (2008b) studied generalized ZK equation by utilizing the Extended Tanh method. Wazwaz (2005) investigated generalized ZK-BBM equation via the Sine–Cosine method and Tanh method etc. The main merits of Extended Trial Equation method over the other techniques are that it gives more general solutions with a few constants and presents a wider applicability for handling nonlinear evolution equations (NLEEs) in a direct manner without any initial/boundary condition at the outset.

It is to be highlighted that, we use Extended Trial Equation method with complete discrimination system for polynomials in which balance number is not constant as we have in other methods. If the balance number is not constant then we get many solutions, but we suppose some of these solutions. By this approach, we obtain the analytical solutions of ZK and ZK-BBM equation with generalized evolution in mathematical physics, not use any specific value for \(\varvec{n}\) to obtain solutions. In this article, we not only discussed basic features of 1-soliton solution and singular soliton solution by analytically but also considered numerically in the form of graphs, and results are compared by substituting different values for \(\varvec{n}\), and obtained different new solutions numerically.

The paper is organized as follows: in Sect. 2, we give the numerical Scheme of the Extended Trial Equation method to obtain abundant exact solitary solutions. To demonstrate the technique, generalized ZK equation and generalized ZK-BBM equation are examined in Sect. 3. Furthermore, we finish up the paper in the last section

2 Extended Trial Equation method

The basic strategy of the technique can understand by the following strides:

  • Step I. We assume that the given nonlinear PDE

    $$H\left( {u,u_{t} , u_{x} , u_{y} ,u_{z} , u_{xx} ,u_{yy} u_{xt} , u_{tt} , \ldots } \right) = 0,$$
    (1)

    Utilizing the wave transformation

    $$u\left( {x_{1} , \ldots ,x_{N} ,t} \right) = u\left( \eta \right),\quad \eta = \lambda \left( {\sum\limits_{j = 1}^{N} {x_{j} - ct} } \right),$$

    where c ≠ 0 and λ ≠ 0. The wave transformation changes Eq. (1) into a nonlinear ODE.

    $$Q\left( {u,u^{\prime } , - \mu u^{\prime } ,u^{\prime \prime } , \mu^{2} u^{\prime \prime } , \ldots } \right) = 0,$$
    (2)

  • Step II. The solution of Eq. (1) has the following generalized form.

    $$u\left( \eta \right) = \sum\limits_{i = 0}^{\delta } {\tau_{i}\Gamma ^{i} } ,$$
    (3)

    where

    $$\left( {\Gamma^{\prime } } \right)^{2} =\Omega (\Gamma ) = \frac{{\upphi(\Gamma )}}{{\uppsi(\Gamma )}} = \frac{{\xi_{\theta } \Gamma^{\theta } + \cdots + \xi_{1} \Gamma + \xi_{0} }}{{\zeta_{\sigma } \Gamma^{\sigma } + \cdots + \zeta_{1} \Gamma + \zeta_{0} }},$$
    (4)

    By Eqs. (3) and (4), we have

    $$\left( {u^{\prime } } \right)^{2} = \frac{{\upphi(\Gamma )}}{{\uppsi(\Gamma )}}\left( {\sum\limits_{i = 0}^{\delta } {i\tau_{i} \Gamma^{i - 1} } } \right)^{2} ,$$
    (5)
    $$\left( {u^{\prime \prime } } \right) = \frac{{\upphi^{\prime } (\Gamma )\uppsi(\Gamma ) -\upphi(\Gamma )\uppsi^{\prime } (\Gamma )}}{{2\uppsi^{2} (\Gamma )}}\left( {\sum\limits_{i = 0}^{\delta } {i\tau_{i} \Gamma^{i - 1} } } \right) + \frac{{\upphi(\Gamma )}}{{\uppsi(\Gamma )}}\left( {\sum\limits_{i = 0}^{\delta } {i\left( {i - 1} \right)\tau_{i} \Gamma^{i - 2} } } \right).$$
    (6)

    In above equations, given \(\upphi(\Gamma )\) and \(\uppsi(\Gamma )\) are polynomials. Using Eqs. (5) and (6) into Eq. (2) yields a polynomial as:

    $$\chi \left( \Gamma \right) = {\varrho }_{s} \Gamma^{s} + \cdots + {\varrho }_{1} \Gamma + {\varrho }_{0} = 0.$$
    (7)

    We can determine a formula of \(\theta , \sigma\) and δ by using the balance principle technique and can find some estimations of \(\theta , \sigma\) and δ.

  • Step III. Setting each coefficient of polynomial \(\chi (\Gamma )\) to zero to derive system of algebraic equations:

    $${\varrho }_{i} = 0,\quad i = 0, \ldots ,s.$$
    (8)

    Now we will determine the values of \(\xi_{0} , \ldots ,\xi_{\theta } ,\quad \zeta_{0} , \ldots ,\zeta_{\sigma }\) and τ 0, …, τ δ , by simplification of the above system of equations.

  • Step IV. In the following step, we obtain elementary form of integral by reduction of Eq. (4), as follows

    $$\pm \left( {\eta - \eta_{0} } \right) = \int {\frac{d\Gamma }{{\sqrt {\Omega \left( \Gamma \right)} }}} = \int {\sqrt {\frac{{{\uppsi }(\Gamma )}}{{{\upphi }(\Gamma )}}} } d\Gamma$$
    (9)

    where η 0 is an arbitrary constant. We can classify the roots of \({\upphi }(\Gamma ),\) with the help of complete discrimination system for polynomials. We solve Eq. (9), by using Maple or Mathematica and acquire the solutions to Eq. (1).

3 Solution procedure

3.1 Generalized ZK equation

Generalized form of ZK equation (Wazwaz 2008b) read:

$$\frac{\partial u}{\partial t} + \alpha u^{n} \frac{\partial u}{\partial x} + \beta \left( {\frac{{\partial^{3} u}}{{\partial x^{3} }} + \frac{{\partial^{3} u}}{{\partial y^{2} \partial x}}} \right) = 0,\quad n > 1,$$
(10)

Now, we utilize the wave variable u(x, y, t) = u(η), η = x + y − ct, Eq. (10) in three independent variables is changing into the following ODE:

$$- cu\left( \eta \right) + \frac{\alpha }{n + 1}u\left( \eta \right)^{n + 1} + 2\beta \frac{{d^{2} u}}{{d\eta^{2 } }} = 0.$$
(11)

Obtained by integrating the resulting equation and considering each constant of integration to be zero. Now applying the following transformation

$$u = w^{{\frac{1}{n}}} ,$$
(12)

The transformation in Eq. (12) will transform Eq. (11) into the ODE

$$- cn^{2} \left( {n + 1} \right)w^{2} + \alpha n^{2} w^{3} - 2\beta \left( {n^{2} - 1} \right)\left( {w^{\prime } } \right)^{2} + 2\beta n\left( {n + 1} \right)ww^{\prime \prime } .$$
(13)

In Eq. (13), when substitute Eqs. (5), (6) and use balance principle technique, we get

$$\theta = 2 + \sigma + \delta ,$$
(14)

If we take into consideration \(\sigma = 0,\theta = 3\) and δ = 1, we can get solutions of Eq. (10), as follows

$$\left( {w^{\prime } } \right)^{2} = \frac{{\tau_{1}^{2} \left( {\xi_{3} \Gamma^{3} + \xi_{2} \Gamma^{2} + \xi_{1} \Gamma + \xi_{0} } \right)}}{{\zeta_{0} }},$$
(15)
$$w^{\prime \prime } = \frac{{\tau_{1} \left( {\xi_{1} + 2\xi_{2} \Gamma + 3\xi_{3} \Gamma^{2} } \right)}}{{2\zeta_{0} }},$$
(16)

where \(\zeta_{0} \ne 0\;{\text{and}}\;\xi_{3} \ne 0.\) Individually, solving the algebraic equation system (8) with the aid of Maple 2016, yields

$$\begin{aligned} \xi_{0} = & \frac{{\tau_{0}^{2} \left( {\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + 2\alpha n^{2} \zeta_{0} \tau_{0} } \right)}}{{\left( {n^{2} + 3n + 2} \right)\beta \tau_{1}^{2} }},\quad \xi_{1} = \frac{{2\left( {\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + \frac{3}{2}\alpha n^{2} \zeta_{0} \tau_{0} } \right)\tau_{0} }}{{\left( {n^{2} + 3n + 2} \right)\beta \tau_{1} }},\quad \xi_{3} = - \frac{{\alpha n^{2} \zeta_{0} \tau_{1} }}{{\left( {n^{2} + 3n + 2} \right)\beta }} \\ \quad c = & \frac{{2\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + 6\alpha n^{2} \zeta_{0} \tau_{0} }}{{n^{2} \zeta_{0} \left( {n^{2} + 3n + 2} \right)}},\quad \xi_{2} = \xi_{2,} \zeta_{0} = \zeta_{0} , \tau_{0} = \tau_{0} , \tau_{1} = \tau_{1} , \\ \end{aligned}$$
(17)

Substituting Eq. (17) into Eqs. (4) and (9), we have

$$\pm \left( {\eta - \eta_{0} } \right) = \sqrt A \int {\frac{d\Gamma }{{\sqrt {\Gamma^{3} + r_{2} \Gamma^{2} + r_{1} \Gamma + r_{0} } }}} ,$$
(18)

where

$$\begin{aligned} A = & - \frac{{\beta \left( {n^{2} + 3n + 2} \right)}}{{\alpha n^{2} \tau_{1} }},\quad r_{0} = - \frac{{\tau_{0}^{2} \left( {\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + 2\alpha n^{2} \zeta_{0} \tau_{0} } \right)}}{{\tau_{1}^{3} \alpha n^{2} \zeta_{0} }}, \\ r_{1} = & - \frac{{2\tau_{0} \left( {\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + \frac{3}{2}\alpha n^{2} \zeta_{0} \tau_{0} } \right)}}{{\tau_{1}^{2} \alpha n^{2} \zeta_{0} }},\quad r_{2} = - \frac{{\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} }}{{\alpha n^{2} \zeta_{0} \tau_{1} }}, \\ \end{aligned}$$

By integrating (18), we acquire the solutions to the (10) as:

$$\pm \left( {\eta - \eta_{0} } \right) = - 2\sqrt A \frac{1}{{\sqrt {\Gamma - \alpha_{1} } }},$$
(19)
$$\pm \left( {\eta - \eta_{0} } \right) = 2\sqrt {\frac{A}{{\alpha_{2} - \alpha_{1} }}} \arctan \sqrt {\frac{{\Gamma - \alpha_{2} }}{{\alpha_{2} - \alpha_{1} }}} ,\quad \alpha_{2} > \alpha_{1} ,$$
(20)
$$\pm \left( {\eta - \eta_{0} } \right) = \sqrt {\frac{A}{{\alpha_{1} - \alpha_{2} }}} \ln \left| {\frac{{\sqrt {\Gamma - \alpha_{2} } - \sqrt {\alpha_{1} - \alpha_{2} } }}{{\sqrt {\Gamma - \alpha_{2} } + \sqrt {\alpha_{1} - \alpha_{2} } }}} \right|,\quad \alpha_{1} > \alpha_{2}$$
(21)
$$\pm \left( {\eta - \eta_{0} } \right) = 2\sqrt {\frac{A}{{\alpha_{1} - \alpha_{3} }}} F\left( {\varphi ,l} \right),\quad \alpha_{1} > \alpha_{2} > \alpha_{3} ,$$
(22)

where

$$\begin{aligned} A = & - \frac{{\beta \left( {n^{2} + 3n + 2} \right)}}{{\alpha n^{2} \tau_{1} }},\quad F\left( {\varphi ,l} \right)\mathop \int \limits_{0}^{\varphi } \frac{d\omega }{{\sqrt {1 - {\text{l}}^{2} sin^{2} \omega } }}, \\ \omega = & \arcsin \sqrt {\frac{{\Gamma - \alpha_{3} }}{{\alpha_{2} - \alpha_{3} }},} \quad {\text{l}}^{2} = \frac{{\alpha_{2} - \alpha_{3} }}{{\alpha_{1} - \alpha_{3} }}. \\ \end{aligned}$$

Also \(\alpha_{1} , \alpha_{2} ,\alpha_{3}\) are solutions of the polynomial equation

$$\Gamma^{3} + r_{2} \Gamma^{2} + r_{1} \Gamma + r_{0} = 0$$
(23)

where \(r_{2} = \frac{{\xi_{2} }}{{\xi_{3} }},r_{1} = \frac{{\xi_{1} }}{{\xi_{3} }}\) and \(r_{0} = \frac{{\xi_{0} }}{{\xi_{3} }}\).

Substituting the solutions given in Eqs. (19)–(21) into (3) and (12), as follows

$$p = \frac{{2\beta \left( {n + 2} \right)\left( {n + 1} \right)\xi_{2} + 6\alpha n^{2} \zeta_{0} \tau_{0} }}{{n^{2} \zeta_{0} \left( {n^{2} + 3n + 2} \right)}},$$

Denoting \(\bar{\tau } = \tau_{0} + \tau_{1} \alpha_{1} ,\) and setting, respectively

$$u\left( {x, y,t} \right) = \left[ {\bar{\tau } + \frac{{4\tau_{1} A}}{{\left( {x + y - pt - \eta_{0} } \right)^{2} }}} \right]^{{\frac{1}{n}}} ,$$
(24)
$$u\left( {x,y,t} \right) = \left\{ {\bar{\tau } + \tau_{1} (\alpha_{2} - \alpha_{1} )\left[ {1 - { \tanh }^{2} \left( { \mp \frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} \left( {x + y - pt - \eta_{0} } \right)} \right)} \right]} \right\}^{{\frac{1}{n}}} ,$$
(25)
$$u\left( {x,y,t} \right) = \left\{ {\bar{\tau } + \tau_{1} (\alpha_{1} - \alpha_{2} ){\text{cosech}}^{2} \left( {\frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} \left( {x + y - pt} \right)} \right)} \right\}^{{\frac{1}{n}}} ,$$
(26)

If we take τ 0 = −τ 1 α 1, and η 0 = 0, for simplicity, then the solutions given in Eqs. (24)–(26) can be written in the following types:

  • Rational solution

    $$u\left( {x, y, t} \right) = \left[ {\frac{{2\sqrt {\tau_{1} A} }}{x + y - pt}} \right]^{{\frac{2}{n}}} ,$$
    (27)

  • 1-Soliton solution

    $$u\left( {x,y,t} \right) = \frac{{E_{1} }}{{cosh^{{\frac{2}{n}}} \left[ { \mp G(x + y - pt} \right]}},$$
    (28)

  • Singular soliton solution

    $$u\left( {x,y,t} \right) = \frac{{E_{2} }}{{sinh^{{\frac{2}{n}}} \left[ {G(x + y - pt} \right]}},$$
    (29)

    where

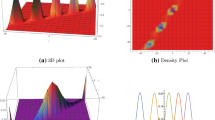
    $$E_{1} = \left[ {\tau_{1} (\alpha_{2} - \alpha_{1} )} \right]^{{\frac{1}{n}}} ,\quad E_{2} = \left[ {\tau_{1} (\alpha_{2} - \alpha_{1} )} \right]^{{\frac{1}{n}}} ,\quad G = \frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} .$$

    Here G is called the inverse width of the solitons, p the velocity. While amplitudes of the solitons represented by E 1 and E 2. Hence, we can say that the soliton occurs for τ 1 > 0 (Figs. 1, 2).

    Fig. 1
    figure 1

    Solution of Eq. (28) corresponding to the values \(n = 2,n = 3,n = 4\) from left to right with \(E_{1} = 4,B = 1,c = 1\)

    Full size image
    Fig. 2
    figure 2

    Solution of Eq. (29) corresponding to the values \(n = 2,n = 3,n = 4\) from left to right with \(E_{2} = 4,B = 1,c = 1\)

    Full size image

3.2 Generalized ZK-BBM equation

Generalized form of ZK-BBM equation (Wazwaz 2005) read:

$$\frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} - \alpha \frac{{\partial (u^{n} )}}{\partial x} + \beta \left( {\frac{{\partial^{3} u}}{{\partial x^{2} \partial t}} + \frac{{\partial^{3} u}}{{\partial y^{2} \partial x}}} \right) = 0,\quad n > 1,$$
(30)

Right now, we will make use of the travelling wave variable in (30)

$$u\left( {x,y, t} \right) = u\left( \eta \right),\quad \eta = x + y - ct,$$

We get the desired equation by integration the transformed ODE and setting each integration constant to zero.

$$\left( {1 - c} \right)u\left( \eta \right) - \alpha u\left( \eta \right)^{n} + \beta \left( {1 - c} \right)\frac{{d^{2} u}}{{d\eta^{2 } }} = 0.$$
(31)
$$u = w^{{\frac{1}{n - 1}}} ,$$
(32)

Equation (31) becomes

$$\left( {1 - c} \right)\left( {n - 1} \right)^{2} w^{2} + \alpha \left( {n - 1} \right)^{2} w^{3} + \beta \left( {1 - c} \right)\left( {2 - n} \right)\left( {w^{\prime } } \right)^{2} + \beta \left( {1 - c} \right)\left( {n - 1} \right)ww^{\prime \prime } .$$
(33)

In Eq. (33), when substitute Eqs. (5), (6) and use balance principle technique, we get

$$\theta = 2 + \sigma + \delta ,$$
(34)

If we consider \(\sigma = 0, \theta = 3\) and \(\delta = 1,\) then

$$\left( {w^{\prime } } \right)^{2} = \frac{{\tau_{1}^{2} \left( {\xi_{3} \Gamma^{3} + \xi_{2} \Gamma^{2} + \xi_{1} \Gamma + \xi_{0} } \right)}}{{\zeta_{0} }},$$
(35)
$$w^{\prime \prime } = \frac{{\tau_{1} \left( {\xi_{1} + 2\xi_{2} \Gamma + 3\xi_{3} \Gamma^{2} } \right)}}{{2\zeta_{0} }},$$
(36)

where \(\zeta_{0} \ne 0,\xi_{3} \ne 0\). Respectively, solving the algebraic equation system (8) using Maple 2016, we get

$$\begin{aligned} \xi_{0} & = - \frac{1}{3}\frac{{\tau_{0} \left( {\tau_{0} \left( {n - 1} \right)^{2} \zeta_{0} - \beta \tau_{1} \xi_{1} } \right)}}{{\beta \tau_{1}^{2} }},\quad \xi_{2} = \frac{{\tau_{0} \left( {n - 1} \right)^{2} \zeta_{0} + \beta \tau_{1} \xi_{1} }}{{\beta \tau_{0} }},\quad \xi_{3} = \frac{2}{3}\frac{{\left( {\tau_{0} \left( {n - 1} \right)^{2} \zeta_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)\tau_{1} }}{{\beta \tau_{0}^{2} }}, \\ c & = \frac{1}{2}\frac{{2\tau_{0} \left( {n - 1} \right)^{2} \left( {3\alpha \tau_{0} + n + 1} \right)\zeta_{0} + \beta \xi_{1} \tau_{1} \left( {n + 1} \right)}}{{\left( {n + 1} \right)\left( {\tau_{0} \left( {n - 1} \right)^{2} \zeta_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}},\quad \xi_{1} = \xi_{1,} \zeta_{0} = \zeta_{0} , \tau_{0} = \tau_{0} , \tau_{1} = \tau_{1} , \\ \end{aligned}$$
(37)

putting Eq. (37) into Eqs. (4) and (9), we have

$$\pm \left( {\eta - \eta_{0} } \right) = \sqrt A \int {\frac{d\Gamma }{{\sqrt {\Gamma^{3} + r_{2} \Gamma^{2} + r_{1} \Gamma + r_{0} } }}} ,$$
(38)

where

$$\begin{aligned} A = & \frac{3}{2}\frac{{\zeta_{0} \beta \tau_{0}^{2} }}{{\tau_{1} \left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}},\quad r_{0} = - \frac{1}{2}\frac{{\left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} - \beta \tau_{1} \xi_{1} } \right)\tau_{0}^{3} }}{{\tau_{1}^{3} \left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \frac{1}{2} \beta \tau_{1} \xi_{1} } \right)}},\quad r_{1} = \frac{1}{2}\frac{{\xi_{1} \beta \tau_{0}^{2} }}{{\tau_{1} \left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}}, \\ r_{2} = & \frac{3}{2}\frac{{\left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \beta \tau_{1} \xi_{1} } \right)\tau_{0} }}{{\tau_{1} \left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}}, \\ \end{aligned}$$

By integrating (38), we obtain the solutions to the Eq. (30) as follows

$$\pm \left( {\eta - \eta_{0} } \right) = - 2\sqrt A \frac{1}{{\sqrt {\Gamma - \alpha_{1} } }},$$
(39)
$$\pm \left( {\eta - \eta_{0} } \right) = 2\sqrt {\frac{A}{{\alpha_{2} - \alpha_{1} }}} \arctan \sqrt {\frac{{\Gamma - \alpha_{2} }}{{\alpha_{2} - \alpha_{1} }}} ,\quad \alpha_{2} > \alpha_{1} ,$$
(40)
$$\pm \left( {\eta - \eta_{0} } \right) = \sqrt {\frac{A}{{\alpha_{1} - \alpha_{2} }}} \ln \left| {\frac{{\sqrt {\Gamma - \alpha_{2} } - \sqrt {\alpha_{1} - \alpha_{2} } }}{{\sqrt {\Gamma - \alpha_{2} } + \sqrt {\alpha_{1} - \alpha_{2} } }}} \right|,\quad \alpha_{1} > \alpha_{2} ,$$
(41)
$$\pm \left( {\eta - \eta_{0} } \right) = 2\sqrt {\frac{A}{{\alpha_{1} - \alpha_{3} }}} F\left( {\varphi ,l} \right),\quad \alpha_{1} > \alpha_{2} > \alpha_{3} ,$$
(42)

where

$$\begin{aligned} A = & \frac{3}{2}\frac{{\zeta_{0} \beta \tau_{0}^{2} }}{{\tau_{1} \left( {\zeta_{0} \left( {n - 1} \right)^{2} \tau_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}},\quad F\left( {\varphi ,l} \right)\mathop \int \limits_{0}^{\varphi } \frac{d\omega }{{\sqrt {1 - {\text{l}}^{2} sin^{2} \omega } }}, \\ \omega = & \arcsin \sqrt {\frac{{\Gamma - \alpha_{3} }}{{\alpha_{2} - \alpha_{3} }}} ,\quad {\text{l}}^{2} = \frac{{\alpha_{2} - \alpha_{3} }}{{\alpha_{1} - \alpha_{3} }}, \\ \end{aligned}$$

Also \(\alpha_{1} , \alpha_{2} ,\alpha_{3}\) are solutions of the polynomial equation

$$\Gamma^{3} + r_{2} \Gamma^{2} + r_{1} \Gamma + r_{0} = 0,$$
(43)

where \(r_{2} = \frac{{\xi_{2} }}{{\xi_{3} }}, r_{1} = \frac{{\xi_{1} }}{{\xi_{3} }}\) and \(r_{0} = \frac{{\xi_{0} }}{{\xi_{3} }}\).

Substituting the solutions (39)–(41) into Eq. (3) and Eq. (32).Denoting \(\bar{\tau } = \tau_{0} + \tau_{1} \alpha_{1} ,\) and setting

$$m = \frac{1}{2}\frac{{2\tau_{0} \left( {n - 1} \right)^{2} \left( {3\alpha \tau_{0} + n + 1} \right)\zeta_{0} + \beta \xi_{1} \tau_{1} \left( {n + 1} \right)}}{{\left( {n + 1} \right)\left( {\tau_{0} \left( {n - 1} \right)^{2} \zeta_{0} + \frac{1}{2}\beta \tau_{1} \xi_{1} } \right)}},$$

We find, respectively

$$u\left( {x,y,t} \right) = \left[ {\bar{\tau } + \frac{{4\tau_{1} A}}{{\left( {x + y - mt - \eta_{0} } \right)^{2} }}} \right]^{{\frac{1}{n - 1}}} ,$$
(44)
$$u\left( {x,y,t} \right) = \left\{ {\bar{\tau } + \tau_{1} (\alpha_{2} - \alpha_{1} )\left[ {1 - { \tanh }^{2} \left( { \mp \frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} \left( {x + y - mt - \eta_{0} } \right)} \right)} \right]} \right\}^{{\frac{1}{n - 1}}} ,$$
(45)
$$u\left( {x,y,t} \right) = \left\{ {\bar{\tau } + \tau_{1} (\alpha_{1} - \alpha_{2} ){\text{cosech}}^{2} \left( {\frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} \left( {x + y - mt} \right)} \right)} \right\}^{{\frac{1}{n - 1}}} ,$$
(46)

If we take τ 0 = −τ 1 α 1, that is \(\bar{\tau } = 0\),then the solutions given in Eqs. (44)–(46) can be written in the following types:

  • Rational solution

    $$u\left( {x,y,t} \right) = \left[ {\frac{{2\sqrt {\tau_{1} A} }}{x + y - mt}} \right]^{{\frac{2}{n - 1}}} ,$$
    (47)

  • 1-Soliton solution

    $$u\left( {x,y,t} \right) = \frac{{E_{1} }}{{cosh^{{\frac{2}{n - 1}}} \left[ { \mp G(x + y - mt} \right]}},$$
    (48)

  • Singular soliton solution

    $$u\left( {x,y,t} \right) = \frac{{E_{2} }}{{sinh^{{\frac{2}{n - 1}}} \left[ {G(x + y - mt} \right]}},$$
    (49)

    where

    $$E_{1} = \left[ {\tau_{1} (\alpha_{2} - \alpha_{1} )} \right]^{{\frac{1}{n - 1}}} ,\quad E_{2} = \left[ {\tau_{1} (\alpha_{2} - \alpha_{1} )} \right]^{{\frac{1}{n - 1}}} ,\quad G = \frac{1}{2}\sqrt {\frac{{\alpha_{1} - \alpha_{2} }}{A}} .$$

    Here G is called the inverse width of the solitons, m the velocity. While amplitudes of the solitons represented by E 1 and E 2. Hence, we can say that the soliton occurs for τ 1 > 0 (Figs. 3, 4).

    Fig. 3
    figure 3

    Solution of Eq. (48) corresponding to the values \(n = 2,n = 3\) and n = 4 from left to right with \(E_{1} = 4,B = 1,c = 1\)

    Full size image
    Fig. 4
    figure 4

    Solution of Eq. (49) corresponding to the values \(n = 2,n = 3\) and \(n = 4\) from left to right with \(E_{2} = 4,B = 1,c = 1\)

    Full size image

4 Conclusions

In this work, we obtained more general wave solutions of generalized ZK equation and generalized ZK-BBM equation by using the Extended Trial Equation method. Through this technique some renowned equations were tackled. The overall performance of the Extended Trial Equation methods reliable and effective. Furthermore, our obtained results are in more general form. With the support of Maple 2016, we have guaranteed the correctness of the obtained results by substituting them back into the nonlinear partial differential equations. The solutions acquired in this article might have significant impact on future researchers.