1 Introduction

The growth of the amount of information exchange across Internet in open network has caused people’s concern for the information security when the data are subjected for transmission over all network system. Nowadays, optical chaotic communications have been demonstrated to have the potential for the secure communication, and have drawn considerable attention due to chaotic signal’s advantages such as sensitive to initial values, noise-like, unpredictable, as well as the broad bandwidth, large transmission capability and high level of privacy. With these characteristics, the chaotic system has various applications in some fields, e. g., secure communication (Aliabadi et al. 2022; Fadil et al. 2022; Cai et al. 2021), optical radar (Pappu and Flores 2019; Feng et al. 2022) and random bit generation (Zhao et al. 2018), etc. Pecora and Carroll realized the synchronization of chaotic systems in 1990 (Pecora and Carroll 1990), later, optical chaos communications using chaotically emitting semiconductor lasers were first proposed 24 years ago. In this method, utilizing the intrinsic nonlinear interaction between the light field and the gain material of the semiconductor laser, and combining delayed feedback which can either be optical or electrical, complex chaotic dynamics is induced (Gao et al. 2022; Colet and Roy 1994; Liu et al. 2021).

Recently, optical chaos synchronization has been applied for communication systems over a wide range of bandwidth (Li et al. 2022a, b; Bouchez et al. 2019). Synchronization schemes in semiconductor laser systems include optical-feedback, optical injection and optoelectronic feedback (Wang et al. 2021; Kamaha et al. 2022; Tseng et al. 2021), etc. Chaotic optical communications based on chaos synchronization have also been considered (Xiang et al. 2022; Zhao et al. 2019). Nevertheless, when applying chaotic synchronization scheme for secure communication, the synchronization between transmitter and receiver may not be very easy to establish because the chaotic signal is sensitive to noise and parameters mismatch (Cheng et al. 2018). In order to overcoming these disadvantages, people have proposed a non-synchronized scheme of chaotic secure communication. E.g., Ryabov proposed a way based on the notion of an inverse system and chaotic masking in 1999 and proved that in ideal situation the information signal can be restored by solving the inversed differential equations by adding information signal directly into chaotic dynamic system in transmitter (Ryabov et al. 1999). In 2011, Wang suggested a hyperchaotic asynchronous communication system based on 6-order cellular neural network, which doesn’t depend on synchronization and manage to improve the security of the communication system by dividing the range of chaotic signal (Wang et al. 2012). Liu designed an asynchronous communication system based on dynamic delay and state variables switching, which demonstrated that by switching time delay and state variables, the BER performance of Wang’s scheme can be improved. All of these approaches use electrical circuits to generate chaotic signals. Comparing to the electrical chaotic signal, optical chaotic signal has larger bandwidth, higher complexity of chaos signal, and easy to implement. Therefore, optical chaotic signal is more suitable for secure communication (Dong et al. 2021; Tang et al. 2021).

The aims of this paper are to investigate and design a non-synchronized way of secure communication through an optical chaotic system, and the scheme uses the original chaotic signal and two own delayed chaotic signals (which correspond to delay one time unit and two time units respectively) to encrypt the sending data. Concretely, we first compute and obtain the difference between the maximum and minimum which are the sums of the absolute values of chaotic signals at adjacent three moments, and divide it to 8 segments by setting 9 different threshold values. Then we use different segment to control a digital signal processor (DSP) to generate a new chaotic series in the basis of original chaotic signal. As we know, there is always noise in the physical channels, but the model proposed by Wang only works well in ideal noise-free channel (Wang et al. 2012), otherwise, there is a big chance that the receiver will recover wrong messages. The model proposed by Liu can deal with it, but it only works well under some circumstances, because it relies on proportionally adjusting the amplitudes of the state variables (Liu et al. 2011). Inspired by the movement, we use (6, 3) linear block code (LBC) and majority decoding to improve the bit error rate (BER) performance of our scheme. After the optic signal is converted to electric signal through a photoelectric detector (PD), a bias current is added to the electric signal to make it has both positive and negative level. After the new chaotic series is multiplied by bipolar information signal, the encryption of message is realized. In addition, we calculate the largest Lyapunov exponent (LLE), permutation entropy (PE), Lempel-Ziv complexity (LZC) of the output of SL to verify that the chaos generated by our system has a high complexity under the appropriate parameter conditions of our optic chaotic laser system.

The non-synchronized communication system uses the characteristics of the chaotic system itself to achieve the encryption and decryption of the information. Typically, the key space of a secure communication system based on semiconductor laser is limited due to a narrow range of the parameter of a semiconductor laser. Thus, eavesdroppers can easily reconstruct the chaotic system by enumeration method or neural networks. To avoid this, we propose a scheme that can enlarge the key space of the security system through the previous method, namely, in eight small segments, each segment corresponds to different encryption and decryption algorithm. Therefore, if an eavesdropper has no clue to obtain the whole set of secret keys, one cannot recover information correctly.

The rest of this paper is organized as follow: In Sect. 2, the block diagram of the scheme is introduced, and the rate equations based on Lang-Kobayashi theory are presented in detail. Section 3 describes the algorithms of encryption and decryption of message. In Sect. 4, we investigate the complexity of the optic chaos system by computing LLE, PE and LZC, and simulate and achieve the encryption and decryption of message, as well as analyze the BER performance. Finally, an overview conclusion is drawn in Sect. 5.

2 System model

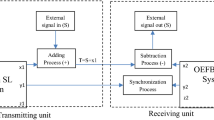
The schematic of the block diagram of the proposed scheme is presented in Fig. 1. In the scheme, at transmitting end, a PD is used to convert the optical signal into electric signal, and a bias current is added to the electric signal so that the chaotic signal has both positive and negative level. Then, the signal is divided into 3 parts: the first part is directly sent to an encoder; the second and third parts are delayed one and two sampling time units through two delay lines, and then they are sent to encoder, respectively. The sum of absolute chaos values at adjacent three moments can exist a certain scope, and it is divided to 8 segments by setting 9 different threshold values, and in the encoder the 8 segments control a DSP to generate new chaos series in the basis of original chaotic signal. The “signal processing 1” module is used to map the original information to LBC; “the signal processing 2” module is used to convert single polar to bipolar code. The bipolar signal and the new chaos series are sent to multiplier, in which two signals are performed a multiply operation to achieve modulation. Then, after using a code converter changes the bipolar to single polar codes, an electro-optic modulator converts the modulated electric signal to optic signal generated by a continuous wave (CW) laser. The optic signal is launched into fiber to transmit to receiver. In receiving end, after the received optical signal is converted to electric signal, a code converter changes the single polar codes to bipolar codes. Then the signal is also split into three parts: the first part is directly sent into comparer; the second part and third part are delayed one and two sampling time units through two delay lines and they are sent a comparer. The comparer calculates their sum with a certain scope, and it is divided into 8 segments through the 9 threshold values. For each segment we use different demodulator to perform the corresponding decryption. Finally, the output of the demodulator is sent to “signal processing 3” module to correct error bits, thus the original message is recovered.

Fig. 1
figure 1

The structure diagram of our scheme

Full size image

The optic chaotic system used for encryption is illustrated in Fig. 2. Beam splitter 1 (BS1) divides the output of semiconductor laser (SL) into two parts. One part is used as chaos signal in our system, and the other one is split into two parts through BS2. One part of the outputs of BS2 is fed into a photodetector (PD), where it is converted into electrical signal that is amplified by an amplifier. The converted electrical signal modulates the other the optical chaotic signal from BS2 in the phase modulator (PM). The modulated signal is reflected by a mirror and passes through the PM again, and then fed back to SL. Thus, our scheme applies phase-modulated optical feedback to generate the complex chaotic series. Basing on well-known Lang-Kobayashi (LK) equation, we obtain the following dynamical equations (Dong et al. 2021; Tang et al. 2021):

$$\frac{dE}{{dt}} = \frac{1}{2}(1 + i\alpha )G(N,\left\| E \right\|^{2} )E + k_{f} E(t - \tau_{1} )e^{{ - i\omega \tau_{f} }} e^{i\varphi } + \sqrt {2\beta N(t)} \zeta (t)$$
(1)
$$\frac{dN}{{dt}} = \frac{I}{e} - \gamma_{e} N - [G(N,\left\| E \right\|^{2} ) + \gamma ]\left\| E \right\|^{2}$$
(2)
$$G(N,\left\| E \right\|^{2} ) = \frac{{g(N - N_{0} )}}{{1 + s\left\| E \right\|^{2} }} - \gamma$$
(3)
$$\varphi (t) = G_{A} \frac{{\pi Sh\omega \left\| {E(t - \tau_{1} )} \right\|^{2} }}{{4\varepsilon n^{2} V_{\pi } }}$$
(4)
Fig. 2
figure 2

The structure diagram of optic chaotic lasers. SL semiconductor laser; BS beam splitter; ISO isolator; PD Photodetector; RF radio frequency amplifier; PM phase modulator; M mirror

Full size image

In the rate equations, E is the complex amplitude of the optical field of SL. N is the carrier number of MSL and SSL. G(N, ||E||2) represents the gain function. The internal parameters of SL are as follows: α is the linewidth enhancement factor. kf and τf are the feedback strength and feedback delay of SL from the mirror. φ(t) and τ1 represents electro-optic phase feedback and its’ delay of SSL. S represents the conversion efficiency of PD. h represents Planck constant. ε represents vacuum dielectric constant. n represents Refractive index of the semiconductor medium. \(V_{\pi }\) represents the half-wave voltage. The light wavelength is 1550 nm. The bias current is I = (3.6∙Ith) in SL. N0 is the transparent carrier number. g(N − N0) represents the differential gain. s represents the saturation coefficient. γe is the photon decay rate. γ is the carrier decay rate. I is the bias current of SL. β is the spontaneous emission rate. ζs(t) is the Gaussian white noise term. The parameters in our simulation are shown in Table 1.

Table 1 Chaotic laser parameters
Full size table

3 Encryption and decryption of message

3.1 Using chaotic series for generating keys to construct new chaotic series

Next the chaotic signal produced by SL is presented by E(t). After passing through a photodetector (PD), the optical chaotic signal is converted to electrical chaotic signal x0(t), Here the sampling time interval is ∆t, so t becomes a discrete n∆t (\(n = 0,1,2, \ldots\)), and x0(t) becomes x0(n). Then a bias current is added to the electric signal x0(n) so that the new chaotic signal x0′(n) has both positive and negative level. Then x0′(n) will be split into three parts. One of them is sent to encoder directly, the second and third part are delayed one ∆t and two sampling time 2∆t through two delay lines, and then they are sent to encoder, respectively. In our simulation ∆t = 1 ns.

After receiving three parts of x0′(n), the encoder performs the following operations for chaotic series to generate secret keys:

  • Step 1: We use the encoder to normalize the electrical signal by Eq. (5), where M represents the normalized constant.

    $$x_{1} (n) = \frac{{x_{0}^{\prime } (n)}}{M}$$
    (5)

  • Step 2: We use encoder to determine the value of D1 and D9 through Eq. (6).

    $$\left\{ \begin{array}{l} \min (\left| {x_{1} (n)} \right| + \left| {x_{1} (n + 1)} \right| + \left| {x_{1} (n + 2)} \right|) = D_{1} \hfill \\ \max (\left| {x_{1} (n)} \right| + \left| {x_{1} (n + 1)} \right| + \left| {x_{1} (n + 2)} \right|) = D_{9} \hfill \\ \end{array} \right.$$
    (6)

  • Step 3: We set seven arbitrary values D2, D3, D4, D5, D6, D7, D8 in an interval [D1, D9]. These values can be considered as secret keys. Therefore, the domain [D1, D9] is divided by D2, D3, D4, D5, D6, D7, D8 into 8 segments.

Let U = |x1(n)| + |x1(n + 1)| + |x1(n + 2)|. Basing on these keys, we use the flowing rule to generate the new chaotic sequence x(n), as shown in Eq. (7). Then these keys are negotiated through a secret channel between emitting and receiving end.

$$\left\{ \begin{array}{l} x(n) = - \left| {x_{1} (n)} \right|, \, x(n + 1) = - \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = - \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{1} ,D_{2} ) \hfill \\ x(n) = - \left| {x_{1} (n)} \right|, \, x(n + 1) = - \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{2} ,D_{3} ) \hfill \\ x(n) = - \left| {x_{1} (n)} \right|, \, x(n + 1) = \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{3} ,D_{4} ) \hfill \\ x(n) = - \left| {x_{1} (n)} \right|, \, x(n + 1) = \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = - \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{4} ,D_{5} ) \hfill \\ x(n) = \left| {x_{1} (n)} \right|, \, x(n + 1) = \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = - \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{5} ,D_{6} ) \hfill \\ x(n) = \left| {x_{1} (n)} \right|, \, x(n + 1) = \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{6} ,D_{7} ) \hfill \\ x(n) = \left| {x_{1} (n)} \right|, \, x(n + 1) = - \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{7} ,D_{8} ) \hfill \\ x(n) = \left| {x_{1} (n)} \right|, \, x(n + 1) = - \left| {x_{1} (n + 1)} \right|, \, x(n + 2) = - \left| {x_{1} (n + 2)} \right|,\;\;if\;\;U \in [D_{8} ,D_{9} ] \hfill \\ \end{array} \right.$$
(7)

3.2 Coding message by using (6, 3) LBC

By using (6, 3) LBC, every three bits from original signal is encoded to a codeword. Suppose the codeword is a1a2a3a4a5a6, where a1a2a3 information bits are and a4a5a6 are parity-check bits. Besides, S1, S2 and S3 are used to represent three syndromes. The relationships between syndromes and error bit position are shown in Table 2. We notice that as long as a syndrome is 1 or two syndromes equal to 1, there is a bit error in the codeword, otherwise, there is no bit error in the codeword.

Table 2 The relationship syndromes and the error bit position in the codeword
Full size table

We also notice that only when the single error bit position is a1, a2 or a4, the syndrome S1 = 1. Only when the single error bit position is a1, a3 or a5, the syndrome S2 = 1. Only when the single error bit position is a2, a3 or a6, the syndrome S3 = 1. Therefore, the relationship between syndromes and codeword can be described by Eq. (8), which is an odd supervision relationship:

$$\left\{ \begin{array}{l} S_{1} = a_{1} \oplus a_{2} \oplus a_{4} \hfill \\ S_{2} = a_{1} \oplus a_{3} \oplus a_{5} \hfill \\ S_{3} = a_{2} \oplus a_{3} \oplus a_{6} \hfill \\ \end{array} \right.$$
(8)

Using Eq. (8), we can get the relationship between parity-check bits and data bits, as shown in Eq. (9):

$$\left\{ \begin{array}{l} a_{4} = a_{1} \oplus a_{2} \hfill \\ a_{5} = a_{1} \oplus a_{3} \hfill \\ a_{6} = a_{2} \oplus a_{3} \hfill \\ \end{array} \right.$$
(9)

Therefore, as long as the data bits are given, the corresponding parity-check bits are also fixed. The coding rules are shown in Table 3.

Table 3 Coding rules for (6, 3) LBC
Full size table

We use the following steps to perform the encoding for the original signal:

  • Step 1: We use every three bits from original series to construct a row of matrix A1.

  • Step 2: We use (6, 3) LBC to encode each row of A1 to get matrix A2.

  • Step 3: Each row in A2 is repeated five times to get matrix A3.

  • Step 4: These parallel row vectors in A3 are converted into a cascade vector in turn, and then the signal is changed to bipolar signal by Eq. (10).

    $$s_{1} (n) = 2s(n) - 1$$
    (10)

Here we use an example to illustrate the above process, as displayed in Fig. 3.

Fig. 3
figure 3

Illustration of the (6, 3) LBC encoding

Full size image

The reasons why we choose (6, 3) LBC are as follow. Firstly, LBC is easy to be implemented in our model. Secondly, according to Eq. (9), three new chaotic values in a segment implies that the choice of (6, 3) LBC is a better scheme, so we don’t use (7, 4) LBC to code it in our scheme. More importantly, (6, 3) LBC can correct one wrong bit, and cannot decrease too much encoding efficiency. We know that the code efficiency of (6, 3) LBC is 50%, and it is less than that of (7, 4) LBC. However, if we choose (7, 4) LBC, the encryption for generating new x(n) and decryption for recovering are far more complex than the now model. Therefore, (6, 3) LBC is a compromise between code efficiency and scheme complexity.

3.3 Encryption of message and optical channel

We assume that

$$l(n) = s_{1} (n)x(n)$$
(11)

here l(n) is the transmitted signal. Hence, a new chaotic sequence x(n) multiplies by signal s2(n), the message modulation or encryption is achieved. As we know, negative signal cannot be transmitted inside fiber, therefore, transmitted signal l(n) is sent into a code converter to transfer single polar code l1(n). Then we use an electro-optical modulator to modulate electrical signal l1(n) into optical signal l2(n).

During long distance propagation, the waveform of transmitted signal will be distorted due to the group velocity dispersion (GVD) and the nonlinearity inside fiber. The propagation of slowly varying envelope can be governed by nonlinear Schrödinger equation (NLSE) shown by Eq. (12).

$$j\frac{\partial E}{{\partial Z}} = - \frac{j}{2}\alpha_{1} E + \frac{1}{2}\beta_{2} \frac{{\partial^{2} E}}{{\partial T^{2} }} - \gamma_{1} \left| E \right|^{2} E$$
(12)

where E represents the slowly varying amplitude of the electric field. Z represents the direction of propagation. T represents the time. α1 represents loss coefficient. β2 represents GVD coefficient and γ1 represents nonlinear coefficient. Therefore, In order to reduce the distortion, a dispersion compensating fiber (DCF) is used to compensate in the fiber.

3.4 Recovery of message

After receiving the transmission signal l3(n), we use a PD to convert optical signal to electrical signal. Then we use a code converter to recover the bipolar signal l′(n). l′(n) will be spitted to three parts. One of them is directly sent to the comparator, and the other two parts are delayed one sampling time unit and two units to send to comparator, and the obtained signals are l′(n + 1) and l′(n + 2), respectively. After receiving l′(n), l′(n + 1) and l′(n + 2), and according to the rules in Eq. (13), we use the comparator for choosing a certain demodulator to recover message.

$$\left\{ \begin{array}{l} {\text{use}}\;{\text{Demodulator}}1,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in (0,D2) \hfill \\ {\text{use}}\;{\text{Demodulator}}2,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D2,D3) \hfill \\ {\text{use}}\;{\text{Demodulator}}3,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D3,D4) \hfill \\ {\text{use}}\;{\text{Demodulator}}4,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D4,D5) \hfill \\ {\text{use}}\;{\text{Demodulator}}5,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D5,D6) \hfill \\ {\text{use}}\;{\text{Demodulator}}6,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D6,D7) \hfill \\ {\text{use}}\;{\text{Demodulator}}7,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D7,D8) \hfill \\ {\text{use}}\;{\text{Demodulator}}8,\;\;if\;\left| {l^{\prime}(n)} \right| + \left| {l^{\prime}(n + 1)} \right| + \left| {l^{\prime}(n + 2)} \right| \in [D8, + \infty ) \hfill \\ \end{array} \right.$$
(13)

Next, we describe the step of the decryption of message:

  • Step 1: After receiving the signal from the comparator, demodulators use the following algorithms shown in Table 4 to recover the signal r(n).

  • Step 2: After obtaining the r(n), we divide each six bits from r(n) as a group, then use each group as a row of matrix B.

  • Step 3: We use majority decoding to recover message. For a column in a matrix B, if there are more “1” rather than “0” the column of matrix B will correspond to a “1” element in a new vector C. Otherwise, the element in C will be “0”.

  • Step 4: Using Table 2, we correct bit error in vector C. Then using the vector C to construct a new matrix C′.

  • Step 5: The parallel rows in matrix C′ is converted into a cascade vector in turn to recover the original message r(n).

Table 4 The algorithm of demodulators for different cases
Full size table

For example, r(n) = 101101101001001001111101101101. These operations are shown in Fig. 4.

Fig. 4
figure 4

Process from matrix B to vector C′

Full size image

4 Results and discussion

4.1 Analysis chaotic feature of optical chaos

In order to verify the effect of nonlinear dynamics and complexity of our system, we will analyze the performance of attractors of SL output and compute the LLE, LZC and PE. By calculating the amplitudes of local extrema of the intensity chaos time series in different optical feedback strength, we plot the bifurcation diagram which shows the path of SL entering chaos, as shown in Fig. 5. Obviously, the dynamics of SL can be clearly understood through the bifurcation diagram. From the Fig. 5, we notice that when the feedback strength kf is about less than 6 ns−1, the output of SL is stable; when kf approximately ranges from 7 and 11 ns−1, the SL undergoes a bifurcation and enters the two-period state, and then with further increase of kf, the SL will completely enter into chaotic state.

Fig. 5
figure 5

Bifurcation diagram of photo number versus the feedback strength

Full size image

Then we fix feedback strength kf = 20 ns−1 and plot the chaotic attractor diagram of the intensity in phase space [Real(E), Imag(E)], as shown in Fig. 6a. We notice that the motion trajectory of chaos is locally unstable, but the whole is confined to a finite space. Furthermore, the mapping with one-to-many means that chaotic dynamics is too complicated to exactly forecast. Simultaneously, we also plot the curves diagram of LLE versus the bias current, as displayed in Fig. 6b. We can conclude that the increase of the bias current leads to an oscillating increase of LLE, furthermore, the LLE is always greater than 0. The fact means that the output of SL exhibits very obvious chaotic characteristics.

Fig. 6
figure 6

Illustration of chaotic dynamics. a Chaos attractors of SL output. b LLE versus bias current

Full size image

In order to generate signal with high complexity, it is worth optimizing the value of bias current as well as feedback strength. We know that PE and LZC are frequently used to measure the complexity of time series (Boaretto et al. 2021; Li et al. 2022a, b). Therefore, we use pseudo-color plot of PE and LZC to find the optimum values of bias current and feedback strength. We notice that when bias current and feedback strength are set respectively at 3.6 Ith mA and 20 ns−1 (marked in Fig. 7), the LZC and PE value are at a high level.

Fig. 7
figure 7

Complexity versus bias current and feedback strength. a The value of LZC. b The value of PE

Full size image

4.2 Using dispersion compensation

In optical channel, we assume that an addition Gaussian white noise N(n) is introduced, and the transmitted signal can be described by Eq. (14).

$$l_{3} (n) = l_{2} (n) + N(n)$$
(14)

Some parameters in our experiments are as follows: the original signal s(n) = 00001100110110101011 0101010100000011001101101010110101010100, M = 1 × 108, D1 = 0.0073, D9 = 0.1200. We set D2 = 0.0214, D3 = 0.0355, D4 = 0.0486, D5 = 0.0637, D6 = 0.0778, D7 = 0.0918, D8 = 0.1059. After the propagation over a SMF with distance L1 = 50 km, the signal is launched into a DCF with a length L2 ≪ L1, which satisfies the condition β21L1 + β22L2 = 0. For SMF, we assume the loss coefficient α = 0.16 dB/km, dispersion coefficient β21 = − 20 ps2/km, nonlinear coefficient γ = 1.47 × 10–3/W km. For DCF, we assume loss coefficient α1 = 3α, dispersion coefficient β22 = 200 ps2/km, nonlinear coefficient γ1 = 6 × 10–3/W km. We use split-step Fourier method to solve nonlinear Schrödinger equation.

The effect of dispersion in SMF and its compensation are shown in Fig. 8a–c. Figure 8a presents the waveform of the original chaotic carrier, and in Fig. 8b, after traveling over L1 distance in SMF, the chaotic carrier undergoes distort, and then it is launched into DCF in which the chaotic carrier goes back closer to its original state, as shown in Fig. 8c. In general, the similarity of signal is measured by the cross-correlation coefficient (XCF), hence we plot Fig. 8d to describe the cross-correlative degree between the chaotic signal along DCF and the initial signal, and find that only the dispersion induced in SMF is completely compensated by DCF, the chaotic carrier goes back to its initial waveform. The reason of dispersion compensation is that our model doesn’t depend on chaotic synchronization but the sum of the chaos value at adjacent three moments, so a slight change of waveform can cause serious bit error.

Fig. 8
figure 8

Illustration dispersion effect in SMF and its compensation. a The waveform of the original chaotic carrier. b The distortion of chaotic carrier after traveling over a certain distance in SMF, c the chaotic waveform after compensation. d Cross-correlation coefficient between original signal and the chaotic signal along DCF

Full size image

4.3 Recovery of message

Next, we use the proposed scheme to decrypt the transmitted message. Figure 9a shows the original chaotic signal x0(n), which is transferred into chaotic sequence x(n) of Fig. 9b after encrypting by Eq. (7). In receiving end, the procedure to decrypt the message starts by compensating dispersion of DCF. The received optical chaos is converted into the electrical signal in which a bias is added. At last, we obtain the received message l′(n) similar to that in Eq. (11), as shown in Fig. 9c. Clearly, the encoded message l′(n) is very different in waveform with original chaotic signal x0(n). In term of the previous decrypting rule, the sum of three adjacent |l′(n)| allows one to choose the proper demodulator, in which the data can be recovered by using Table 4. Then we use (6, 3) LBC and majority decoding principle to obtain the recovered message, which is shown by blue line in Fig. 9d, and the original message is shown by the red line. From this figure we can find that the original message has been successfully recovered.

Fig. 9
figure 9

Illustration of the decryption. a Waveform of signal x0′(n). b Waveform of the first encrypting signal x(n). c The received signal l′(n). d Waveform of original message s(n) and recovered message r(n)

Full size image

4.4 Performance analysis of system

For a communication system, it is worth discussing the aspects of communication quality. Usually the bit error rate (BER) is a physical quantity to measure the communication quality, here we will analyze the influence of signal noise rate (SNR) and dispersion compensation on the BER.

Firstly, we analyze the effect of SNR. In order to have a better result, the original signal that we use in this simulation is 100000 binary bits, which subject to uniform distribution. We plot the curve of the BER as function of the SNR. As seen in Fig. 10, the increase of SNR leads to the improvement of the system performance. When the SNR is 20 dB, the corresponding BER is low to ~ 1.9 × 10–4. The fact means that the chaotic asynchronous communication scheme is more sensitive to noise. The reason is that the sum of three adjacent |l′(n)| easily exceeds the original set domain orange in Eq. (13) due to the presence of the noise. For example, in absence of noise, the sum of three adjacent |l′(n)| is in the set interval range: |l′(n)| + |l′(n + 1)| + |l′(n + 2)| ∈ [D2, D3). Thus, the l′(n) should be correctly sent the Demodulator 2; however, in presence of the noise, it is possible: |l′(n)| + |l′(n + 1)| + |l′(n + 2)| ∈ [D3, D4), thus, l′(n) is mistakenly sent to Demodulator 3. As a result, the original message cannot be are recovered without error.

Fig. 10
figure 10

BER as function of the SNR

Full size image

Secondly, we analyze the effect of dispersion on the BER. In order to find out whether the dispersion in SMF will affect the BER, we fix the SNR to 20 dB, and obtain the relation plot of BER as the function of transmission distance, as shown in Fig. 11a. We notice that if the signal only transmits about 8 km in SMF, the BER is up to 0.5. Therefore, the dispersion must be compensated. Here we use 5 km long DCF to the dispersion of 50 km long SMF, and draw the relation curve of the BER versus the length of DCF, as shown in Fig. 11b. We notice that if the dispersion is not completely compensated, the BER of the system can be closed to 0.5 even more than 0.5. In our scheme, after dispersion is accurately compensated, the BER can be low to ~ 1.9 × 10–4, and the corresponding waveform of the l2(n) in Fig. 8c is very similar to the original waveform. Moreover, in Fig. 8d the XCF close to 1 means that two waveforms are highly consistent.

Fig. 11
figure 11

Illustration of BER performance. a BER as function of the length of SMF. b BER as function of the length of DCF

Full size image

5 Conclusions

In conclusions, an asynchronous optical chaotic communication system, combining (6, 3) LBC with majority decoding, is proposed. In this scheme, the SL with phase-modulated optical feedback is applied for generating the chaotic carrier with high complexity. After the optical chaotic signal is changed into the electric signal with positive and negative level, the interval of the maximum and minimum, corresponding to the sum of the absolute values at adjacent three moments, is divided into eight different segments, and which is used as the key for generating a new chaotic sequence. Consequently, the enlarged key space can enhance the security of system. This is because even if the eavesdroppers correctly guess the internal parameters of lasers (due to the small range of variety) and obtain feedback delay by analyzing the auto correlation of transmitted signal. As long as they have no clue to obtain the domain of eight segments, they still cannot recover information correctly. In order to reduce the impact of noise on our system, we introduce (6, 3) LBC to encode the message, which multiplied by the chaotic carrier enables the modulation of the message. The distortion of waveform induced by the dispersion of SMF is compensated by DCF. At receiving end, a reverse process with majority decoding is used to demodulate the original message.

We have demonstrated that the optical chaotic carrier possesses high complexity by calculating LZC and PE. The simulation results still reveal that the introduced (6, 3) LBC and majority decoding significantly improve the performance of BER of in a channel with noise, and the compensation of dispersion in SMF by using DCF greatly reduces the distortion and improves the performance of BER, moreover our system can realize secure communication between transmitter and receiver without chaotic synchronization, and the scheme allows one to negotiate these keys through a secret channel. The proposed scheme is promising due to its enlarged key space.