1 Introduction

Nowadays, due to the continuous demand for designing energy efficient and high-performance engineering systems and devices, the usage of optimization methods is of high importance. Regarding flow systems, in specific, Computational Fluid Dynamics (CFD) combined with optimization algorithms come in handy for designing new models with higher performance measured by an appropriate objective function. The choice of the objective function together with the set of design variables, according to a shape parameterization scheme, is the first step. The optimization intends to find the optimal value-set of the design variables that minimizes the objective function.

To find the optimal value-set of design variables, an efficient approach is to use gradient-based optimization methods, after computing the gradient of the objective function, to improve the existing geometry at each optimization cycle. These methods have good convergence properties and are cost-effective, with the risk of occasionally being trapped into local minima and, of course, the extra burden to compute gradients. In the literature, there are many techniques on how to compute the gradient e.g. finite differences, complex variable method (Martins et al. 2003), automatic/direct differentiation (Rall 1981); among them, the adjoint method (Pironneau 1984; Jameson 1988) is the most cost-efficient as the cost is independent from the number of design variables. This method allows the use of a rich parameterization, leading to a rich design space, being beneficial for the optimization.

There are two main approaches for the adjoint method (discrete and continuous) depending on whether the differentiation or discretization comes first; this paper relies upon the continuous adjoint method in which the system of equations is first differentiated to derive the adjoint to‘x the fluid flow differential equations; these are then discretized and numerically solved. The continuous adjoint method is well formulated in the literature for the single-fluid compressible and incompressible Navier-Stokes equations, including also the differentiation of various turbulence models and integrated into shape and topology optimization frameworks that can successfully optimize even complex geometries as demonstrated by Jameson (1988), Anderson and Venkatakrishnan (1999), Papoutsis-Kiachagias and Giannakoglou (2014) and the papers cited there.

In cases involving two or more fluids, a multiphase model considers the interactions between them. There is a variety of models on how to cope with the existence of more than one fluids in the same computational domain (Hirt and Nichols 1981; Brennen 2005; Ishii and Hibiki 2011; Drew 1983; Manninen 1996). The most suitable model depends mostly on the nature of the fluids (miscible or immiscible), the way they interact (formation or not of a discrete interface) and their concentrations inside the fluid domain (if one of the phases could be considered dispersed, formulations that treat the dispersed phase as particles might be needed).

This paper is dealing with cases with (two) miscible fluids and uses a Eulerian description for the simulation of flows inside static mixing devices. These are motionless structures (also called mixers) used for the continuous blending of fluids inside a pipeline and are met in a wide range of different applications, from wastewater treatment to chemical processes and medical applications. Their role is to secure high mixing for liquids traveling through a pipeline by enforcing flow recirculation through several baffles (or blades) placed inside the pipeline. It is essential, especially for chemical engineering applications, to have a uniform flow at the exit of the pipeline. It is also important to have the smallest possible total pressure losses in order to reduce energy consumption. There are several papers dealing with the optimization of static mixing devices for improving mixture uniformity (Regner et al. 2006; Byrde and Sawley 1999; Hanada et al. 2016) and/or total pressure drop (Hirschberg et al. 2009; Song and Han 2005), though none of them uses the adjoint method, at least to the author’s knowledge. In detail, Regner et al. (2006) makes a parametric study comparing the efficiency of two commercial static mixer geometries in different flow regimes. Similarly, Byrde and Sawley (1999) derived correlation graphs between the twist angles of the blades of a mixer and the total pressure losses and mixing efficiency. Hanada et al. (2016) presents a parametric study in which, by changing the pitch and diameter of the components of a time-difference-type mixer, a configuration that achieves up to \(40\%\) reduction in total pressure drop between the branch paths was found. Finally, Song and Han (2005) proposed a correlation between geometry and total pressure drop inside a Kenics type static mixer, by also investigating its efficiency for different Reynolds numbers, whereas Hirschberg et al. (2009) validated the improvement in total pressure losses for a modified Sulzer SMX mixer.

In this paper, a method for optimizing static mixing devices, through the development of a continuous adjoint to a two-phase flow model that allows the computation of gradients of the mixing device geometry is proposed. A two-phase model is used for a laminar steady-state flow of two incompressible fluids, assuming a Fickian diffusion between them. The optimization focuses on finding optimal shape configurations for the baffles inside the mixing device by also respecting a set of manufacturing constraints. The objective function(s) gradients over the surface of the baffles, combined with a shape deformation tool, are parts of a gradient-based optimization framework used to optimize a static mixing device. The optimization problem is formulated with two objective functions, namely mixture uniformity (\(F_U\)) and total pressure losses (\(F_P\)), combined into a single one using weights; optimization runs with different combinations of weights lead to the Pareto front of optimal solutions.

2 Two-phase model description

The two-phase flow model conservation includes the continuity, the momentum and a phase transport equation for the mixture, assuming a laminar flow and steady-state conditions (Ishii and Hibiki 2011; Manninen 1996).

$$\begin{aligned} R^{p}= & {} -\frac{\partial (\rho v_i )}{\partial x_i}=0 \end{aligned}$$
(1)
$$\begin{aligned} R^{v}_{i}= & {} \rho v_j \frac{\partial v_i}{\partial x_j} - \frac{\partial (\mu \epsilon _{ij})}{\partial x_j} + \frac{\partial p}{\partial x_i}=0 \quad i=1,2,3 \end{aligned}$$
(2)
$$\begin{aligned} R^{a}= & {} v_i\frac{\partial \alpha }{\partial x_i} - \frac{\partial }{\partial x_j}\left( D \frac{\partial a}{\partial x_j} \right) = 0 \end{aligned}$$
(3)

where \(v_i\) are the velocity components, p is the static pressure, \(\rho\) is the density, \(\mu\) is the dynamic viscosity and \(\epsilon _{ij} = \frac{\partial v_i}{\partial x_j} +\frac{\partial v_j}{\partial x_i}\) is the strain tensor of the mixture. \(\alpha\) is the volume fraction of the mixture and D is the mass diffusivity coefficient. Equation 3 is equivalent to Fick’s law of diffusivity. D depends on the fluid characteristics, such as the temperature, the viscosity and the size of the fluid molecules. Diffusivity coefficients of one substance into the other are commonly determined experimentally and presented in reference tables (Cussler 2009), from which a representative value is chosen based on the densities and viscosities of the two fluids. Throughout this paper, repeated indices imply summation according to Einstein’s convention.

For the closure of the above system, the mixture density and viscosity are linear combinations of \(\rho _i\) and \(\mu _i\) which are the constant density and viscosity values for each of the two fluids, based on the volume fraction \(\alpha\),

$$\begin{aligned} \rho&= \alpha \rho _1 + (1-\alpha )\rho _2 \end{aligned}$$
(4)
$$\begin{aligned} \mu&= \alpha \mu _1 + (1-\alpha )\mu _2 \end{aligned}$$
(5)

Note that, even if both fluids are assumed to be incompressible, this does not mean that the mixture has a constant density: in fact, there is a non-uniform spatial distribution of density depending on the local values of the volume fraction. This does not allow to neglect \(\frac{\partial \rho }{\partial x_i}\) in the above equations as standard incompressible flow solvers do; the same is valid for the spatial derivatives of \(\mu\).

The static mixing device comprises of walls, inlets and outlets. Dirichlet conditions for \(v_i\) and \(\alpha\) together with zero Neumann conditions for p are imposed at the inlet(s). For the solid walls, Dirichlet conditions for \(v_i\) together with zero Neumann conditions for p and \(\alpha\) are imposed. In addition, zero Neumann conditions for \(v_i\) and \(\alpha\) together with a Dirichlet condition for p are imposed at the outlet(s).

3 Continuous adjoint method

The gradient of the objective function with respect to (w.r.t.) the design variables \(b_n = [b_1, b_2, \ldots , b_N]\) controlling the shape is computed by the continuous adjoint method. The objective functions are expressed in a generic form as surface integrals (Papoutsis-Kiachagias and Giannakoglou 2014),

$$\begin{aligned} F = \int _{S_I} F_{S_{I,i}} n_i dS + \int _{S_O} F_{S_{O,i}} n_i dS \end{aligned}$$
(6)

where \(S_I\) is the inlet and \(S_O\) the outlet boundary of the flow domain \(\varOmega\). The first objective function this paper is dealing with, is the volume-averaged mixture uniformity at the outlet, written as

$$\begin{aligned} F_U = \frac{1}{2}\int _{S_O} v_i n_i (\alpha - \bar{\alpha })^2 dS \end{aligned}$$
(7)

where \(n_i\) is the unit outward normal vector to the boundary and \(\bar{\alpha }\) is the mean value of \(\alpha\) at the outlet,

$$\begin{aligned} \bar{\alpha } = \frac{1}{\vert S_O\vert }\int _{S_O} \alpha dS \end{aligned}$$
(8)

For a steady state simulation, \(\bar{\alpha }\) depends on the inlet mass-flow of the two phases. Accordingly, for the (volume-averaged) total pressure losses, the corresponding objective function is

$$\begin{aligned} F_P = -\frac{1}{2}\int _{S_{I,O}} v_i n_i \left( p + \frac{1}{2}\rho v_j^2\right) dS \end{aligned}$$
(9)

Both \(F_U\) and \(F_P\) should be minimized. To do so, the two objectives are combined into a single one as follows

$$\begin{aligned} \begin{aligned} F = w_1 F_U + w_2 F_P \\ \end{aligned} \end{aligned}$$
(10)

where \(w_1\) and \(w_2\) are user-defined weights.

For the differentiation of the objective function, the total variation \(\delta\) on any quantity \(\varPhi\) is given by (Papoutsis-Kiachagias and Giannakoglou 2014)

$$\begin{aligned} {\delta \varPhi } = \frac{\partial \varPhi }{\partial b_n}{\delta b_n} + \frac{\partial \varPhi }{\partial x_k} {\delta x_k} \end{aligned}$$
(11)

so as to get

$$\begin{aligned} \frac{\delta F}{\delta b_n} = \int _{S_I\cup S_O} \frac{\partial F_{S,i}}{\partial b_n} n_i dS + \int _{S_I\cup S_O} \frac{\partial F_{S,i}}{\partial x_k} \frac{\delta x_k}{\delta b_n} n_i dS + \int _{S_I\cup S_O} F_{S,i}\frac{\delta }{\delta b_n}(n_i dS) \end{aligned}$$
(12)

The augmented objective function \(F_{aug}\) is defined as

$$\begin{aligned} F_{aug} = F + \int _{\varOmega } q R^p d\varOmega + \int _{\varOmega } u_i R_i^v d\varOmega + \int _{\varOmega } \phi R^a d\varOmega \end{aligned}$$
(13)

where \(q, u_i, \phi\) are the adjoint pressure, velocities and phase fraction accordingly. \(F_{aug}\) is then differentiated w.r.t. the design variables \(b_n\)

$$\begin{aligned} \begin{aligned} \frac{ \delta F_{aug} }{\delta b_n}&= \frac{\delta F}{\delta b_n} + \int _{\varOmega } q \frac{\partial R^p}{\partial b_n} d\varOmega + \int _{\varOmega } u_i \frac{\partial R_i^v}{\partial b_n} d\varOmega + \int _{\varOmega } \phi \frac{\partial R^a }{\partial b_n} d\varOmega \\&\quad + \int _{S} (q R^p + u_i R_i^v + \phi R^a) \frac{\partial x_j}{\partial b_n}n_jdS \end{aligned} \end{aligned}$$
(14)

where S is the boundary of the domain \(\varOmega\) formed by inlet (\(S_I\)), outlet (\(S_O\)) and parameterized (\(S_{W_P}\)) solid walls. The last term in Eq. 14 is the Leibniz term which is herein neglected under the assumption that the residuals of the field equations are asymptotically zero along the domain boundary. Nevertheless, as demonstrated by Kavvadias et al. (2015), this term can be important especially in cases with coarse computational meshes.

The application of the Green–Gauss theorem to the volume integrals of Eq. 14 gives the following in a term-by-term basis. The first volume integral becomes

$$\begin{aligned} \begin{aligned} \int _{\varOmega } q \frac{\partial R^p}{\partial b_n} d\varOmega&= \int _{\varOmega } \rho _\varDelta \, v_i \frac{\partial q}{\partial x_i} \frac{\partial \alpha }{\partial b_n} d\varOmega + \int _{\varOmega } \rho \frac{\partial q}{\partial x_i} \frac{\partial v_i}{\partial b_n}d\varOmega \\&\quad - \int _{S} q\rho \frac{\partial v_i}{\partial b_n} n_i dS - \int _{S} q \rho _\varDelta \, v_i n_i \frac{\partial \alpha }{\partial b_n} dS \end{aligned} \end{aligned}$$
(15)

where \(\rho _\varDelta = \rho _1 - \rho _2\) represent the density difference between the two phases. The second volume integral can be written as

$$\begin{aligned} \begin{aligned} \int _{\varOmega } u_i \frac{\partial R_i^v}{\partial b_n} d\varOmega&= \int _{\varOmega } u_iv_j \frac{\partial v_i}{\partial x_j} \rho _\varDelta \frac{\partial a}{\partial b_n}d\varOmega +\int _{\varOmega } \rho u_j \frac{\partial v_j}{\partial x_i} \frac{\partial v_i}{\partial b_n}d\varOmega \\&\quad - \int _{\varOmega } \frac{\partial ( \rho u_i v_j )}{\partial x_j} \frac{\partial v_i}{\partial b_n} d\varOmega \\&\quad + \int _{S} \rho u_i v_j n_j \frac{\partial v_i}{\partial b_n} dS - \int _{\varOmega } \frac{\partial u_i}{\partial x_i} \frac{\partial p}{\partial b_n} d\varOmega + \int _{S} u_in_i \frac{\partial p}{\partial b_n} dS\\&\quad + \int _{\varOmega } \mu _\varDelta \, \frac{\partial u_i}{\partial x_j} \epsilon _{ij} \frac{\partial a}{\partial b_n}d\varOmega - \int _{S} \mu _\varDelta \, u_i \epsilon _{ij} n_j \frac{\partial a}{\partial b_n} dS\\&\quad - \int _{\varOmega } \frac{\partial (\mu \epsilon _{ij}^{\alpha })}{\partial x_j} \frac{\partial v_i}{\partial b_n} d\varOmega + \int _{S} \mu \epsilon _{ij}^{\alpha } n_j \frac{\partial v_i}{\partial b_n} dS - \int _{S} n_j u_i \mu \frac{\partial \epsilon _{ij}}{\partial b_n} dS \end{aligned} \end{aligned}$$
(16)

where \(\epsilon _{ij}^{\alpha } = \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i}\) is the adjoint strain tensor and \(\mu _\varDelta = \mu _1 - \mu _2\) is the dynamic viscosity difference between the two phases. The third volume integral can be written as

$$\begin{aligned} \begin{aligned} \int _{\varOmega } \phi \frac{\partial R^a }{\partial b_n} d\varOmega&= \int _{\varOmega } \phi \frac{\partial \alpha }{\partial x_i} \frac{\partial v_i}{\partial b_n}d\varOmega - \int _{\varOmega } \frac{\partial (\phi v_i)}{\partial x_i} \frac{\partial \alpha }{\partial b_n}d\varOmega \\&\quad - \int _\varOmega \frac{\partial }{\partial x_j}\left( D \frac{\partial \phi }{\partial x_j}\right) \frac{\partial \alpha }{\partial b_n}d\varOmega \\&\quad + \int _S \phi v_in_i\frac{\partial \alpha }{\partial b_n}dS - \int _S n_j \phi D \frac{\partial }{\partial x_j}\left( \frac{\partial \alpha }{\partial b_n}\right) dS + \int _S D \frac{\partial \phi }{\partial x_j}n_j\frac{\partial \alpha }{\partial b_n}dS \end{aligned} \end{aligned}$$
(17)

In order to avoid the computation of the partial derivatives of the flow variables \(v_i, p\) and \(\alpha\) w.r.t. \(b_n\) involved in the field integrals, their multipliers in Eq. 14 are set to zero giving rise to the system of the field adjoint equations

$$\begin{aligned} R^q= & {} -\frac{\partial u_i}{\partial x_i} \end{aligned}$$
(18a)
$$\begin{aligned} R^{u_i} &= \rho u_j \frac{\partial v_j}{\partial x_i} - \frac{\partial (\rho u_i v_j)}{\partial x_j} - \frac{\partial (\mu \epsilon _{ij}^{\alpha })}{\partial x_j} \nonumber \\&+ \rho \frac{\partial q}{\partial x_i} + \phi \frac{\partial \alpha }{\partial x_i} = 0 \quad i=1,2,3 \end{aligned}$$
(18b)
$$\begin{aligned} R^{\phi }= & {} -\frac{\partial (\phi v_i)}{\partial x_i} - \frac{\partial }{\partial x_j}\left( D \frac{\partial \phi }{\partial x_j}\right) + \left( u_iv_j \frac{\partial v_i}{\partial x_j} + v_i \frac{\partial q}{\partial x_i} \right) \rho _\varDelta \nonumber \\&\quad +\,\, \mu _\varDelta \, \frac{\partial u_i}{\partial x_j} \epsilon _{ij} = 0 \end{aligned}$$
(18c)

After satisfying the adjoint equations, the remaining terms in the gradient expression are

$$\begin{aligned} \begin{aligned} \frac{\delta F_{aug}}{\delta b_n}&= \int _S \left( \phi v_i n_i + D\frac{\partial \phi }{\partial x_j}n_j - q\rho _\varDelta \, v_in_i - u_i \mu _\varDelta \, \epsilon _{ij}n_j + \frac{\partial F_{S_j}}{\partial \alpha }n_j\right) \frac{\partial \alpha }{\partial b_n}dS\\&\quad + \int _S \left( -q\rho n_i + \rho u_i v_j n_j + \mu \epsilon ^{\alpha }_{ij}n_j + \frac{\partial F_{S_j}}{\partial v_i}n_j \right) \frac{\partial v_i}{\partial b_n} dS\\&\quad - \int _S u_in_j\mu \frac{\partial \epsilon _{ij}}{\partial b_n}dS + \int _S \left( u_i n_i + \frac{\partial F_{S_i}}{\partial p}n_i \right) \frac{\partial p}{\partial b_n} dS\\&\quad - \int _S \phi D \frac{\partial }{\partial b_n}\left( \frac{\partial \alpha }{\partial x_j}\right) n_jdS \end{aligned} \end{aligned}$$
(19)

From Eq. 19, the adjoint boundary conditions are derived together with the expression of the sensitivity derivatives.

3.1 Adjoint boundary conditions

During the optimization, only the parameterized boundaries (\(S_{W_P}\)) are changing whereas the rest (\(S_I, S_O\)) remain fixed.

For the inlet (\(S_I\)), \({\delta \alpha }/{\delta b_n} = {\partial \alpha }/{\partial b_n} =0\) and \({\delta v_i}/{\delta b_n} = {\partial u_i}/{\partial b_n} =0\) . Thus, the first two integrals in Eq. 19 are eliminated. The elimination of the third and fourth integral under the assumption of a uniform velocity distribution at the inlet imposes the following two conditions

$$\begin{aligned} u_n = -\frac{\partial F_{S_{I,i}}}{\partial p}n_i ,\quad u_t^I = u_t^{II} = 0 \end{aligned}$$
(20)

where \(u_n\) is the normal to the boundary adjoint velocity component and \(u_t^I\) and \(u_t^{II}\) are two tangential components forming a local Frenet trihedron with \(u_n\). Finally, the elimination of the last integral in Eq. 19 imposes a zero Dirichlet condition for \(\phi\) at the inlet.

For the outlet (\(S_O\)), \(\delta p/\delta b_n = \partial p/\partial b_n = 0\). So the fourth integral in Eq. 19 vanishes. Also, assuming a uniform velocity profile distribution at the outlet, the third integral vanishes as well. The rest of the terms in the first and second integrals are set to zero, resulting to the adjoint boundary conditions for \(\phi\) and \(u_i\) at the outlet.

Finally, for the parameterized walls (\(S_{W_P}\)), the first, third and fourth integrals in Eq. 19 vanish by setting

$$\begin{aligned} \frac{\partial \phi }{\partial x_i}n_i = - \frac{\partial F_{S_{W,i}}}{\partial \alpha }n_i, \quad u_n = -\frac{\partial F_{S_{W,i}}}{\partial p}n_i, \quad u_t^I = u_t^{II} = 0 \end{aligned}$$
(21)

Since wall integrals are excluded from the objective functions (Eqs.  7, 9), it holds that

$$\begin{aligned} \frac{\partial F_{S_{W,i}}}{\partial p} = \frac{\partial F_{S_{W,i}}}{\partial \alpha } = 0 \end{aligned}$$

leading to a zero-Dirichlet and zero-Neumann conditions for \(u_i\) and \(\phi\), respectively.

For the second integral in Eq. 19, because of the zero-Dirichlet conditions for the primal velocity components, \(\delta v_i/\delta b_n = 0\), the partial derivatives of the velocities w.r.t. \(b_n\) read

$$\begin{aligned} \frac{\partial v_i}{\partial b_n} = -\frac{\partial v_i}{\partial x_j} \frac{\delta x_j}{\delta b_n} \end{aligned}$$
(22)

Assuming that the tangential component of \({\delta x_j}/{\delta b_n}\) does not have an impact on surface deformation, only its normal component is kept resulting in

$$\begin{aligned} \frac{\partial v_i}{\partial b_n} = -\frac{\partial v_i}{\partial x_j}n_j\frac{\delta x_k}{\delta b_n}n_k \end{aligned}$$
(23)

Before deriving the final sensitivities expression, a brief analysis has to be made for the term \(\int _S \phi D \frac{\partial }{\partial b_n}\left( \frac{\partial \alpha }{\partial x_j}\right) n_jdS\). Using (Papoutsis-Kiachagias and Giannakoglou 2014)

$$\begin{aligned} \frac{\delta }{\delta b_n} \left( \frac{\partial \alpha }{\partial x_j}\right) = \frac{\partial }{\partial x_j} \left( \frac{\delta \alpha }{\delta b_n}\right) - \frac{\partial \alpha }{\partial x_k}\frac{\partial }{\partial x_j}\left( \frac{\delta x_k}{\delta b_n}\right) \end{aligned}$$
(24)

the above term becomes

$$\begin{aligned} \begin{aligned}&\int _{S_{W_P}} \phi D \frac{\delta }{\delta b_n}\left( \frac{\partial \alpha }{\partial x_j} n_j \right) dS - \int _{S_{W_P}} \phi D \frac{\delta n_j}{\delta b_n}\frac{\partial \alpha }{\partial x_j} dS \\&\quad - \int _{S_{W_P}} \phi D \frac{\partial ^2 \alpha }{\partial x_k \partial x_j} \frac{\delta x_k}{\delta b_n} dS \end{aligned} \end{aligned}$$
(25)

The first integral in Eq. 25 can be neglected because of the zero-Neumann condition for \(\alpha\). The other two integrals contribute to the final sensitivity derivatives expression.

3.2 Sensitivity derivatives expression

After satisfying the adjoint field equations and their boundary conditions, the resulting terms in Eq. 19 stand for the sensitivity derivatives,

$$\begin{aligned} \begin{aligned} \frac{\delta F}{\delta b_n}&= - \int _{S_{W_p}} \left( -q\rho n_i + \mu \epsilon ^{a}_{ij}n_j + \frac{\partial F_{S_j}}{\partial v_i}n_j \right) \frac{\partial v_i}{\partial x_j}n_j\frac{\delta x_k}{\delta b_n}x_k dS\\&\quad + \int _{S_{W_p}} \phi D \frac{\delta n_j}{\delta b_n}\frac{\partial \alpha }{\partial x_j} dS + \int _{S_{W_p}} \phi D \frac{\partial ^2 \alpha }{\partial x_k \partial x_j} \frac{\delta x_k}{\delta b_n}n_j dS \end{aligned} \end{aligned}$$
(26)

4 Optimization of a static mixing device

The developed method and software is applied to the shape optimization of a static mixing device. Figure 1 shows such a device which has two inlets and one outlet. It is equipped with seven baffles, evenly distributed in the axial direction, which force the flow to recirculate increasing, thus, the mixing procedure. The initial positions of the baffles across the mixer are demonstrated in Fig. 2. The material properties of the two fluids are listed in Table 1.

Fig. 1
figure 1

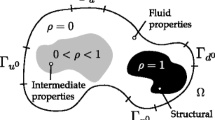
Static mixer geometry. The colored zones are associated with the application presented in Sect. 4.2

Full size image
Fig. 2
figure 2

Locations and geometry of the baffles in the initial geometry of the static mixer device

Full size image
Table 1 Properties of the two fluids
Full size table

The duct has a length of 0.6 m and an inner radius of 0.1 m which is equal to the radius of the baffles. The mean Reynolds number of the flow is based on the mean values of viscosity and the mixture mass flow rate and is \({\sim }\,450\). The computational mesh is unstructured and consists of 200 K cells with higher resolution refinement around the baffles in order to accurately capture the flow separation and recirculation. These meshes have been tested to produce solutions which are insensitive to further refinement (studies not included in the paper). Figure 3 shows velocity streamlines in the initial geometry, colored by the velocity magnitude. In order to facilitate the weight selection process, one can define

$$\begin{aligned} w_1 = \frac{\bar{w}_1}{F_U^0}, \quad w_2 = \frac{\bar{w}_2}{F_P^0} \end{aligned}$$
(27)

where \(F_P^0\) and \(F_U^0\) are the values of the mixture uniformity and total pressure losses of the initial static mixer geometry, respectively.

Fig. 3
figure 3

Velocity streamlines in the initial geometry

Full size image

Two different optimization problems are solved and for each a different parameterization approach is considered. The first one considers that the axial positions of the baffles are fixed and seeks the optimal shape for each baffle that minimizes F for the given set of \(\bar{w}_1\) and \(\bar{w}_2\). The second one seeks the optimal positional angle of each baffle, by keeping the same longitudinal distance between them. This means that each baffle is allowed to rotate around an axis with a fixed center of rotation. In both optimization runs, the baffles are retained planar, with a constant thickness for manufacturing reasons. The way geometry is parameterized and constraints are satisfied in each approach is explained below in detail. The first one is referred to as “in-plane” whereas the second one as “positional angle” optimization.

4.1 In-plane optimization

For the in-plane optimization, only the baffles’ shapes are subject to deformation while the duct’s boundaries remain fixed. The goal is to re-design the profile of each baffle separately by retaining its flatness and thickness. In more detail, only the sensitivities along the top part of each baffle are taken into account and by doing this, the baffle is not allowed to change in the longitudinal direction and thus it remains in the same plane. The first thing is to define a parameterization to translate sensitivity derivatives into shape deformation. A node-based parameterization which considers the normal displacements of the surface nodes as design variables, is followed. This approach offers the richest design space possible (for the given spatial discretization) but any numerical noise in the adjoint derivatives, combined with the fact that each surface node is being perturbed independently from its neighbors, can create wiggles and irregularities. To cope with this problem, an implicit smoothing technique together with a mesh regularization method are used, which allow smooth deformations while maintaining high mesh quality as demonstrated by Alexias and de Villiers (2019).

By solving the adjoint system of equations and computing the gradient of the objective function (Eq. 26), the sensitivity map is generated. Figure 4 demonstrates an example of the surface sensitivities on the top part of one of the baffles, for \(F_U\), in the initial geometry. Figure 5 shows an example of changing the profile of the top part of one of the baffles during the optimization. It has to be noted that the periphery of the baffle remains attached to the rest of the duct and that the edge points of the top part of the baffle have a fixed position.

Fig. 4
figure 4

In-plane optimization. Sensitivity map obtained from the sensitivity expression. Red color indicates that the surface should be pushed in whereas blue that it must be pulled out, to reduce the objective function. (Color figure online)

Full size image
Fig. 5
figure 5

In-plane optimization. Example of the modification of the profile of an arbitrarily selected baffle. Initial flat-lined profile (top) and the outcome of the optimization (bottom)

Full size image

Six value-sets of weights, Table 2, are tried and, for each optimization problem a limited memory BFGS method (Nocedal 2006) is used.

Table 2 Value-sets of the weights of the objective function
Full size table

By running these six optimizations, a Pareto front is computed as shown in Fig. 6. A higher weight for \(F_U\) (higher \(\bar{w}_1\) values) results in a massive drop in this objective function. For instance, using \(\bar{w}_1 = 1\) and \(\bar{w}_2 = 0\), \(F_U\) has reduced by \(~96\%\). The unexpected result is that, even if the weight of the \(F_P\) objective is zero, this experiences a drop by 8%. On the other side, the opposite optimization run with \(\bar{w}_1 = 0\) and \(\bar{w}_2 = 1\) gives a huge drop in \(F_P\) (around 60%) but for a higher \(F_U\) value. To have a complete overview of the effect baffles have on the flow, an additional simulation is performed for the static mixer after removing all the baffles. The computed values of \(F_P\) and \(F_U\) are demonstrated in Fig. 6 together with the rest of the Pareto points. Removing all the baffles results in the smallest \(F_P\) value (compared to all other Pareto points) and the weakest mixing, as there is no mechanism to enhance it.

Fig. 6
figure 6

In-plane optimization. Pareto front of optimal solutions (asterisks) together with the convergence history of each optimization for the different sets of weights

Full size image
Fig. 7
figure 7

In plane optimization. Optimal baffle shapes for each set of weights colored by the final displacement vector from its original position

Full size image
Fig. 8
figure 8

In-plane optimization. Final distribution of the phase fraction on the outlet for each Pareto point

Full size image

Figure 7 shows the optimal baffle shapes for each set of weights. As it can be noticed, in case the \(F_P\) weight is higher, the optimization tends to reduce the area of the baffles in order to reduce the losses caused by flow recirculation. Figure 8 shows the final distribution of the phase fraction at the outlet for each Pareto point.

In case the uniformity objective is given priority, using for instance \(\bar{w}_1=0.9\) and \(\bar{w}_2 = 0.1\) (see Fig. 9, which comparing streamlines in the initial and optimal geometries; streamlines are coloured with the value of the phase fraction) the flow vorticity vector after the optimization is redirected and the resulting vortical flow increases the mixing between the two fluids. The vortical flow can also be seen in Fig. 10, where the velocity components that are tangent to the plane are plotted.

In all optimization runs, the primal and adjoint systems of equations are converged to a relative residual of \(10^{-7}\). Indicatively, the convergence history of the primal and adjoint set of equations, for the first optimization cycle, with a value set of \(\bar{w}_1 = \bar{w}_2 = 0.5\) is demonstrated in Fig. 11.

Fig. 9
figure 9

In-plane Optimization. Velocity streamlines colored with the phase fraction value (\(\alpha\)) before (top) and after (bottom) the optimization

Full size image
Fig. 10
figure 10

In-plane Optimization. Projected velocity vectors that indicate the generation of a more intense vortical flow in the optimized geometry (bottom figure). The vortical flow has an impact on the mixing of the two fluids

Full size image
Fig. 11
figure 11

In-plane Optimization. Convergence history of primal (left) and adjoint (right) equations for the first iteration of the optimization run with a selected value-set of \(\bar{w}_1 = \bar{w}_2 = 0.5\)

Full size image

4.2 Positional angle optimization

In this optimization run the goal is to find the optimal angle to place each baffle in order to minimize F (Eq. 10), for each set of \(\bar{w}_1\) and \(\bar{w}_2\). The outcome of this run, compared to the previous one, has an important advantage from the manufacturing point of view because there is no need to re-design the shape of the baffles. In fact, the baffles retain their shapes and their axial positions and only the positional angle varies. The mixer is aligned with the z-axis; the design variables are the positional angles around this axis for each baffle. To calculate these angles at each optimization step, the “torque” of the sensitivities around the z-axis for each baffle is calculated through

$$\begin{aligned} \tau _{b_i} = \sum _{j} (\mathbf {r}_j \times G_j \mathbf {n}_j )\cdot \mathbf {z} \end{aligned}$$
(28)

where \(\mathbf {r}_j\) is a vector pointing from the origin of rotation to the center of each boundary. \(G_j\) is the gradient computed from Eq. 26, \(\mathbf {n}_j\) is the surface normal of each face.

Then, the “torque” of each baffle is translated into a change of the positional angle around the z-axis through

$$\begin{aligned} \delta \bar{\theta }_b = H^{-1} \cdot \bar{\tau }_b \end{aligned}$$
(29)

where \(H^{-1}\) is the inverse Hessian matrix approximated by the limited memory BFGS method.

The difficulty with this run is that one cannot change the positional angle of the baffle without redesigning the CAD model of the mixer or without using an advanced morphing method [e.g. Biancolini (2017)], which could allow the baffle to slide along wall. In this paper, to cope with this problem, the mesh is divided into eight different regions, differently colored in Fig. 1, with each baffle belonging solely to one region. Consecutive mesh regions are communicating by interpolating each discrete field \(v_i\), p, a over their interfaces. The same is done also for the adjoint variables \(u_i\), q and \(\phi\) To do this effectively, a Galerkin projection method is used as demonstrated by Farrell and Maddison (2010). This has the advantage of minimizing the \(L_2\) norm of the interpolation error and guarantees mass conservativeness in the general case of unstructured meshes. By doing this and since all regions are cylindrical, they can be displaced in the peripheral direction independently from each other. This means that, after having computed \(\tau _{b_i}\) for each baffle, each mesh region can be rotated by \(\delta \theta _{b_i}\).

For this optimization run, the same set of weights as in Table 2 is used. Thus, the Pareto front is generated and presented in Fig. 12 in logarithmic scale for the x-axis for better illustration. The same figure also depicts the Pareto points computed from the in-plane optimization, together with the initial design point and the solution obtained for the geometry without baffles. By comparing the corresponding Pareto points based on their weights for the two different approaches (in-plane and positional angle), it can be noticed that those points computed by the latter have a much bigger reduction in \(F_U\) compared to the former. This happens because the peripheral displacement of the baffles creates a more effective mixing mechanism, through the continuous change of the flow vorticity vector. In contrast, the reduction of \(F_P\) is a bit smaller compared to the in-plane (though there is still a substantial reduction) as the primary mechanism to reduce \(F_P\), which is to reduce the height of the baffles, is not allowed. Finally combining both sets of Pareto points, the final set of non-dominated solutions can be computed, Fig. 12. All the points of the positional angle optimization are non-dominated solutions. On the other hand, for the in-plane optimization, the three points with the lowest total pressure losses belong to the set of non-dominated solutions. It is important to notice that the design that does not include baffles is also a non-dominated solution as it is the design with the highest \(F_P\) reduction.

Figure 13 shows the final position of the baffles for the two extreme Pareto solutions resulting from the positional angle optimization. For the case targeting only \(F_P\) (the weight of \(F_U\) is zero), the baffles tend to be placed on the same side of the duct rather than alternate, in order to reduce total pressure losses. The final/optimal positional angles for the two extreme Pareto solutions are illustrated in Fig. 14.

Fig. 12
figure 12

Pareto front of optimal solutions for all optimization runs. The initial and the design without baffles are also included in the plot. The combined Pareto front of non-dominated solutions is demonstrated

Full size image
Fig. 13
figure 13

Positional Angle Optimization. Final positions of the baffles for the two extreme Pareto solutions. Top: positions when optimizing only for \(F_P\); bottom: positions when optimizing only for \(F_U\)

Full size image
Fig. 14
figure 14

Positional angle optimization. Optimal values of the positional angles for the two extreme Pareto solutions

Full size image

5 Conclusions

In this paper, the continuous adjoint method for a two-phase model for laminar flows of miscible fluids was developed. The derivation of the adjoint equations was presented, and a multi-objective optimization problem was formulated aiming at maximizing the mixture uniformity and minimizing total pressure losses inside a static mixing device.

The optimization runs produced optimal results while generating flat baffles shapes with the same thickness. By using the in-plane optimization, a Pareto front of optimal solutions was generated. The two extremes are associated with different baffle shapes pointing out the primary mechanism to improve mixing uniformity and total pressure losses, respectively. Namely, by creating “wavy” baffle profiles improved the mixing performance whereas by reducing the area of the baffles the total pressure losses are reduced.

On the other hand, the positional angle optimization has led to greater reductions in the mixture uniformity for the same sets of weights, compared to the in-plane optimization, which means that rearranging the baffles in different angles is a much more effective mechanism to improve mixing performance. However, this approach is lagging on the effectiveness of reducing the total pressure losses compared to the in-plane optimization. This is mostly because shrinking (or, even, removing completely) the baffles leads to a drastic reduction in the total pressure losses of the static mixer.

The combination of in-plane and positional angle optimizations into a single work-flow is expected to provide better results as it will share the advantages of both approaches. It is expected to exploit a greater number of shape variations, alleviating the inherent limitation of the two approaches. This work is in progress.