1 Introduction

Thin-walled structures have a high ratio between load carrying capabilities and mass and play a primary role in lightweight design. In order to improve the structural efficiency, i.e. stiffness and mass ratio, a rigorous optimization approach is required.

Multi Objective Optimization (MOO) can be effectively applied to structural design (Miettinen 1998; Mastinu et al. 2006; Haftka and Gurdal 2002; Banichuk 1990) with particular reference to mass minimization while maximizing the structural stiffness (or, equivalently, minimizing the compliance of the structure). In such problems, mass and compliance are considered objective functions (to be minimized). The design variables are the geometrical dimensions of the structural members. Constraints on safety (i.e. admissible stress), elastic stability and maximum available room have to be satisfied.

The solution of the optimization process in the Pareto-optimal framework is composed by a set of optimal solutions (the so-called Pareto-optimal set). Those solutions represent the best compromise in terms of both minimum mass and compliance. The designer can then choose the final structure configuration among these optimal solutions (Papalambros and Wilde 2000).

In Kasperska et al. (2007) and Ostwald and Rodak (2013) multi-objective optimization theory was employed for mass and deflection minimization of structural members in bending. Optimized profiles of thin-walled open cross sections were obtained by means of numerical methods. Shape optimization of bars under torsion was addressed by Wang Wang (2013). The shape and rounding of the corners of polygonal bars was optimized by means of numerical methods with the aim to maximize the torsional stiffness for a prescribed target of mass. The topology of the cross section of thin-walled beams under torsion was optimized in Kim and Kim (2002). A multi-objective optimization approach was followed for maximizing the torsional stiffness and minimizing the distortion of the thin-walled cross section. The optimal solution was derived numerically by a weighted sum method. Gobbi and Mastinu (2001) presented a method for the optimal design of composite material tubular helical springs. In the paper, Multi-Objective Programming (MOP) was adopted. Both theoretical studies and experimental activities were conducted.

The solution of (simple) multi-objective optimization problems can be derived analytically for a number of engineering problems [see for example Mastinu et al. (2006), Gobbi et al. (2014, 2017), Ballo et al. (2017) or the four-bars plane truss problem in Askar and Tiwari (2011)]. When available, analytical formulae can be very useful for designers since they provide a broader view of the problem and may guide the designers at the conceptual design stage.

Referring to beams, analytical formulae for designing optimal beams under torsion or bending are presented in several papers. In Ashby (2011), a set of design formulae for beams of arbitrary cross section under torsion or bending is provided to compare different materials and shapes. In Gobbi et al. (2017) and Previati et al. (2017), with reference to the bending of a cantilever of arbitrary shape and material, it was demonstrated that the Pareto-optimal set for any beam subject to bending is given by two connected regions, the first one is given by the elastic stability while the second one by the available room constraint. A more in depth analysis on optimal design of specific cross sections of uniformly bent beams was performed in Gobbi et al. (2014), Mastinu et al. (2017) and Ballo et al. (2017) where analytical solutions for the Pareto-optimal sets are provided both in the design variables and objective functions domains.

In this paper, the optimal design of a thin-walled tube under torsion is discussed. A rigorous multi-objective optimization approach is followed. The mass of the tube is minimized together with its compliance. Analytical formulae providing the cross section dimensions of the optimized tube are derived. These formulae may be a useful tool for designers, who can choose an optimized cross section without any further iteration.

The paper is structured as follows. Firstly the basic principles related to the analytical derivation of the Pareto-optimal set of a general multi-objective optimization problem are recalled. Then, the mathematical formulation of the optimization problem of a thin-walled tube under torsion is presented and analytically solved. The analytical expressions of the Pareto-optimal set in the design variables domain (tube diameter and wall thickness) and in the objective functions domain (mass and compliance) are given. On the basis of the derived analytical formulae, a comparison of optimized tubes made from different materials is performed. Finally, a practical example showing the application of the analytical expressions is presented and discussed.

2 The Fritz John condition for Pareto-optimality

In this section, a brief description of the optimality conditions of a multi-objective optimization problem is provided. For the sake of space, the description is limited to the particular case in which the number of design variables is the same of the number of objective functions, all the mathematical passages are reported in “Appendix”; the reader can refer to Gobbi et al. (2014) for a thorough insight into the method.

Let us consider a general constrained multi-objective minimisation problem:

$$\begin{aligned} \begin{array}{l} min\;\;\;{\mathbf {F}}({\mathbf {x}})={\mathbf {F}}(f_1{}({\mathbf {x}}),f_2{}({\mathbf {x}},\ldots ,f_k{}({\mathbf {x}}))\\ s.t.\;\;\; {\mathbf {G}}({\mathbf {x}})=(g_{1}({\mathbf {x}}),g_{2}({\mathbf {x}}),\ldots ,g_{w}({\mathbf {x}}))\le {\mathbf {0}},\;\;\; {\mathbf {x}}\in {\mathbf {R}}^{n} \end{array} \end{aligned}$$
(1)

where F is the vector of the k objective functions, x is the vector of the n design variables and G is the vector of the w constraint functions.

Fritz John necessary condition (Miettinen 1998; Mastinu et al. 2006). Let the objective function and the constraint vector of Eq. 1 be continuously differentiable at a decision vector \({\mathbf {x}}^*\in { S }\). A necessary condition for \({\mathbf {x}}^*\) to be Pareto-optimal is that there exist vectors \(\varvec{\lambda } \in {\mathbf R} ^{k} \ge {\mathbf 0}\) and \(\varvec{\mu } \in {\mathbf R} ^{w} \ge {\mathbf 0}\)\((\varvec{\lambda },\varvec{\mu } \ne ({\mathbf 0},{\mathbf 0} ))\) such that

$$\begin{aligned} \begin{array}{l} \sum \limits _{i=1}^{k}{\mathbf {\lambda }}_{i}\nabla f_{i}({\mathbf x} ^{*})+\sum \limits _{j=1}^{w}{\mathbf {\mu }}_{j}\nabla g_{j}({\mathbf x} ^{*}) = {\mathbf 0} \\ \mu _{j}g_{j}({\mathbf x} ^{*}) = {\mathbf 0} \end{array} \end{aligned}$$
(2)

If the number of design variables n equals the number of objective functions k, the Pareto-optimal solution \({\mathbf {x}}^{*}\) of problem 1 is given by the solution of Eq. 3

$$\begin{aligned} \left( \coprod _{j=1}^wg_{j}\right) \cdot det(\nabla {\mathbf {F}})=0 \end{aligned}$$
(3)

where the term \(\nabla {\mathbf {F}} = [\begin{array}{llll} \nabla f_{1}&\nabla f_{2}&\ldots&\nabla f_{k}]_{n\times k}\end{array}\) (a square matrix being \(n=k\)) contains the gradient of the objective functions.

Equation 3 states that the solution of the problem is given by the active constraints and/or the solution of the unconstrained problem.

3 Equations for a thin-walled tube under torsion

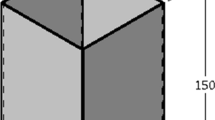
The torsion of a thin-walled circular tube is shown in Fig. 1.

Fig. 1
figure 1

Thin-walled circular tube subject to torsion

Full size image

The tube has length l, external diameter d, wall thickness t and is subject to a torsional moment M. The design problem refers to mass and compliance minimization. For the sake of generality, mass and compliance are divided by the tube length, the objective functions of the problem are therefore the mass per unit of length m and the compliance per unit of length c of the tube.

The design parameters are the tube diameter d and its thickness t, that will be referred to as design variables hereafter.

The analytical expressions of the objective functions read

$$\begin{aligned} m= & {} \dfrac{m_t}{l}=\pi \rho dt \end{aligned}$$
(4)
$$\begin{aligned} c= & {} \dfrac{\theta }{l}=\dfrac{4M}{\varGamma \pi d^3t} \end{aligned}$$
(5)

where \(\rho\) is the density of the material and \(\varGamma\) is the shear modulus, while \(m_t\) and \(\theta\) are the overall mass of the tube and the relative rotation of the two end sections of the tube (Fig. 1) respectively. The design variables d and t are limited by maximum and minimum attainable values (Papalambros and Wilde 2000)

$$\begin{aligned} d_{min}\le & {} d\le d_{max} \end{aligned}$$
(6)
$$\begin{aligned} t_{min}\le & {} t\le t_{max} \end{aligned}$$
(7)

The upper bound of the diameter \(d_{max}\) can be interpreted as a constraint on the available room, while the lower bound on the wall thickness \(t_{min}\) as a technological constraint. The other bounds \(d_{min}\) and \(t_{max}\) can assume, theoretically, any value. In practice, the thin-walled condition \(\dfrac{t}{d}\le \dfrac{1}{20}\) (and therefore the validity of the mathematical model employed) should always be checked after a solution is obtained.

The structural safety is related to the maximum stress occurring in the tube, that introduces a constraint in the optimization problem

$$\begin{aligned} \tau _{max}\le \dfrac{\tau _y}{\eta } \end{aligned}$$
(8)

The left-hand side of Eq. 8 represents the maximum shear stress acting in the cross section, that can be expressed as (Young and Budynas 1989)

$$\begin{aligned} \tau _{max}=\dfrac{2M}{\pi d^2t} \end{aligned}$$
(9)

The right-hand side of Eq. 8 represents the admissible shear stress, given by the yielding shear stress of the material \(\tau _y\) divided by the safety coefficient \(\eta\).

When thin-walled cross sections are employed, the structure gets more exposed to failure by local buckling. Local buckling phenomena depend on many parameters (cross section geometry, material, etc...) but mainly on the wall thickness. To avoid buckling failure, an additional constraint on the maximum admissible torsional moment is introduced

$$\begin{aligned} M\le \dfrac{M_{cr}}{\eta } \end{aligned}$$
(10)

where \(M_{cr}\) is the critical buckling moment and \(\eta\) the safety coefficient.

The critical moment \(M_{cr}\) depends on the material properties and on the geometry of the cross section. Many analytical expressions of this quantity can be found in the literature. The first work on the topic was conducted by Schwerin (1924). Other expressions of the critical torsional moment of a thin-walled tube can be found in Young and Budynas (1989) or in Donnell’s (1935) and Lundquist’s (1934) works.

For sake of simplicity, in this analysis, Lundquist’s relation has been considered.

$$\begin{aligned} M_{cr}=\pi \dfrac{d^2}{2}tK_sE\left( \dfrac{d}{2t}\right) ^{\alpha } \end{aligned}$$
(11)

where E is the material elastic modulus, \(\alpha\) is a constant equal to \(-\,1.35\) and \(K_s\) can be related to the geometry of the tube as (Crate et al. 1944)

$$\begin{aligned} K_s=B\left( \dfrac{2l}{d}\right) ^{\beta } \end{aligned}$$
(12)

with B and \(\beta\) numerical constants equal to 1.27 and \(-\,0.46\) respectively.

4 Optimal design of a thin-walled tube subject to torsion

In this section the optimal design problem of the tube is formulated by following a multi-objective optimization (MOO Miettinen 1998; Mastinu et al. 2006) approach.

The problem is formulated as follows.

Find

$$\begin{aligned} \begin{array}{l} min\begin{bmatrix} c(t,d)=\dfrac{4M}{\pi \varGamma td^{3}}\\ m(t,d)=\pi \rho t d \end{bmatrix} ~~~such ~that\\ \\ \tau _{max}=\dfrac{2M}{\pi d^2t}\le \dfrac{\tau _y}{\eta }\\ M\le \dfrac{M_{cr}}{\eta }=\pi \dfrac{d^2}{2\eta }tK_sE\left( \dfrac{d}{2t}\right) ^{\alpha }\\ K_s=B\left( \dfrac{2l}{d}\right) ^{\beta }\\ \\ t_{min} \le t \le t_{max}\\ d_{min}\le d \le d_{max} \end{array} \end{aligned}$$
(13)

The solution of problem (13) can be obtained by applying the theory described in Sect. 2. Being the number of design variables equal to the number of objective functions Eq. 3 applies. The solution is therefore given either by the solution of the unconstrained problem or by the active constraint(s).

The buckling constraint provides the following relation:

$$\begin{aligned} d\ge \left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^{\frac{1}{2+\alpha -\beta }}t^{\frac{\alpha -1}{2+\alpha -\beta }} \end{aligned}$$
(14)

while the stress constraint gives

$$\begin{aligned} d\ge \sqrt{\dfrac{2M\eta }{\pi t \tau _y}} \end{aligned}$$
(15)

Let us consider the unconstrained problem which reads

$$\begin{aligned} \begin{array}{l} min\begin{bmatrix} c(t,d)=\dfrac{4M}{\pi \varGamma td^{3}}\\ m(t,d)=\pi \rho t d \end{bmatrix} \end{array} \end{aligned}$$
(16)

The solution of the unconstrained problem in Eq. 16 is given by Eq. 17.

$$\begin{aligned} det\left( \begin{bmatrix}\frac{\partial c}{\partial d}&\frac{\partial m}{\partial d}\\ \frac{\partial c}{\partial t}&\frac{\partial m}{\partial t}\end{bmatrix}\right) =det\left( \begin{bmatrix}-\,\frac{12M}{\pi \varGamma d^{4}t}&\pi \rho t\\ -\,\frac{-4M}{\pi \varGamma d^{3}t^{2}}&\pi \rho d\end{bmatrix}\right) =0 \end{aligned}$$
(17)

which leads to

$$\begin{aligned} -\,\dfrac{8M\rho }{\varGamma d^3t}=0 \end{aligned}$$
(18)

Equation 18 has solution for \(d^3t\rightarrow \infty\). Such solution, not belonging to the set of the finite positive numbers has no physical meaning and has to be discarded (Papalambros and Wilde 2000).

The Pareto optimal set is therefore given by the combination of active constraints (Eq. 3). By applying Eq. 3 the following result is obtained

$$\begin{aligned} \begin{aligned}&-\,\left( d-\left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^{\frac{1}{2+\alpha -\beta }}t^{\frac{\alpha -1}{2+\alpha -\beta }}\right) \left( d-\sqrt{\dfrac{2M\eta }{\pi t\tau _y}}\right) \cdot \\&\left( d-d_{max}\right) \left( t-t_{max}\right) \left( d-d_{min}\right) \left( t-t_{min}\right) \dfrac{8M\rho }{\varGamma d^3t} = 0 \end{aligned} \end{aligned}$$
(19)

Equation 3 gives a necessary condition for the Pareto-optimal solutions of the problem. The Pareto-optimal solution is, in general, a subset of the solution given by Eq. 19.

In order to extract Pareto-optimal solutions the intersections among the active constraints have to be studied. Depending on the relative values of the parameters, different scenarios are possible. These scenarios are analysed in the following section.

5 Sizing of thin-walled tubes with constraints on available room, on minimum thickness, on buckling and admissible stress


Figures 2 and 3 show the number of possible scenarios in the design variables domain. The grey area represents the feasible set of solutions (i.e. solutions that satisfy the design constraints), while the black lines are the Pareto-optimal solutions.

Fig. 2
figure 2

Possible scenarios in the design variables domain. The gray area is the set of feasible solutions, the black lines are the Pareto-optimal sets. Intersection points are marked with diamond, square and circle

Full size image
Fig. 3
figure 3

Possible scenarios in the objective functions domain. The grey area is the set of feasible solutions, the black lines are the Pareto-optimal sets. Intersection points are marked with diamond, square and circle

Full size image

Case ①

The lower bounds \(d_{min}\) and \(t_{min}\) of the design variables prevent both static and buckling failures. Buckling and stress constraints are not active.

By inspecting the expressions of the objective functions in Eq. 13, one can observe that the compliance objective function is monotonically decreasing with d and t, while the mass objective function is monotonically increasing with d and t. This means that the Pareto-optimal solution (i.e. the set of solutions that minimize the mass and compliance at the same time) lies on the borders of the design domain and is given either by the combination \(d=d_{max}\) and \(t=t_{min}\) or \(d=d_{min}\) and \(t=t_{max}\).

By substituting \(d=d_{min}\) and \(d=d_{max}\) in the objective functions, the respective expression in the objective functions domain (i.e. the m, c domain) can be computed

$$\begin{aligned}&m\left( c\right) \bigg |_{d=d_{min}}=\dfrac{4M\rho }{\varGamma d_{min}^2c} \end{aligned}$$
(20)
$$\begin{aligned}&m\left( c\right) \bigg |_{d=d_{max}}=\dfrac{4M\rho }{\varGamma d_{max}^2c} \end{aligned}$$
(21)

By comparing Eqs. 20 and 21, the solution for \(d=d_{max}\) (Eq. 21) is always lower than Eq. 20 and therefore \(t=t_{min}\) and \(d=d_{max}\) are subsets of the Pareto-optimal set (see Figs. 2, 3).


The expression of Pareto-optimal solutions for Case ① are reported in Table 1 in the design variables and objective functions domain.

Table 1 Case ① of Figs. 2 and 3
Full size table

Case ②


This is the most general case since both the buckling constraint and stress constraint are active and part of the Pareto-optimal set.

From Case ① we have demonstrated that solutions \(t=t_{min}\) and \(d=d_{max}\) are Pareto-optimal. If a sufficiently large design space is considered, the solutions \(t=t_{min}\) can violate the constraints on buckling and admissible stress. The intersection point \(P_{buck,stress}\) between the buckling and stress constraint reads

$$\begin{aligned} \hat{t}=\left( \dfrac{\left( \pi BE\right) ^2\left( 2l\right) ^{2\beta }}{2^{\alpha +\beta }\left( M\eta \right) ^{\beta -\alpha }\left( \pi \tau _y\right) ^{2+\alpha -\beta }}\right) ^{\frac{1}{3\alpha -\beta }} \end{aligned}$$
(22)

for \(t\ge \hat{t}\) the stress equation is more binding than the buckling equation. This means that for \(t\le \hat{t}\) the buckling constraint is active, then the active constraint switches from the buckling equation to the admissible stress.

By substituting the stress constraint of Eq. 15 (where the \(\ge\) is replaced by \(=\)) in the objective functions expressions, a relation between m and c when the stress constraint is active can be obtained and reads

$$\begin{aligned} m\left( c\right) \bigg |_{\tau =\dfrac{\tau _y}{\eta }}=\dfrac{\varGamma M\eta ^2\rho }{\tau _y^2}c \end{aligned}$$
(23)

which is a straight line (monotonically increasing) in the objective functions domain and therefore does not belong to the Pareto-optimal set.

With the same procedure the buckling constraint in the objective functions domain can be derived and reads

$$\begin{aligned} m\left( c\right) \bigg |_{buck.}=\rho \pi \left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^\frac{1}{2+\alpha -\beta }\left( \dfrac{4M}{\varGamma \pi \left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^\frac{3}{2+\alpha -\beta }}\right) ^\frac{2\alpha -\beta +1}{4\alpha -\beta -1}\dfrac{1}{c^\frac{2\alpha -\beta +1}{4\alpha -\beta -1}} \end{aligned}$$
(24)

which is monotonically decreasing in the objective functions domain and therefore belongs to the Pareto-optimal set.


The expression of Pareto-optimal solutions for Case ② are reported in Table 2 in the design variables and objective functions domain.

Table 2 Case ② of Figs. 2 and 3
Full size table

Case ③


The minimum attainable diameter d is defined by the admissible stress.

The Pareto optimal set is given by the solutions \(t=t_{min}\) and \(d=d_{max}\). The stress constraint, as demonstrated in Case ②, does not belong to the Pareto optimal set and it defines the solution with the lowest mass as shown in Fig. 3.


The expression of Pareto-optimal solutions for Case ③ are reported in Table 3 in the design variables and objective functions domain.

Table 3 Case ③ of Figs. 2 and 3
Full size table

Case ④


The solution is defined by the maximum diameter \(d=d_{max}\), the stress constraint is limiting t from below and defines the point with the minimum mass as shown in in Fig. 3.


The expression of Pareto-optimal solutions for Case ④ are reported in Table 4 in the design variables and objective functions domain.

Table 4 Case ④ of Figs. 2 and 3
Full size table

Case ⑤


The minimum diameter d, corresponding to minimum mass is defined by the admissible stress and buckling, as shown in Figs. 2 and 3.


The full analytical expressions of the Pareto optimal sets, both in the design variable domain and in the objective function domain, are reported in Table 5.

Table 5 Case ⑤ of Figs. 2 and 3
Full size table

Case ⑥


In this case, we see from Fig. 2 that no solution within the bounds \(t_{min} \le t \le t_{max}\) and \(d_{min}\le d \le d_{max}\) is feasible since buckling and stress constraints are not satisfied.

6 Comparison of tubes made from different materials

In this section a comparison between optimized tubes made from two different materials (material A and B) is performed. The comparison is made referring to Pareto-optimal solutions (Mastinu et al. 2006). Considering Fig. 2, the Pareto-optimal sets can be divided into a number of subsets, depending on the considered case, namely

  • \(d=d_{max}\) (subsets 1 in Fig. 2)

  • \(t=t_{min}\) (subsets 2 in Fig. 2)

  • active constraint on buckling (subsets 3 in Fig. 2)

In the following, the single subsets will be compared for two thin-walled tubes made from different materials.

6.1 Comparison referring to Pareto-optimal subset 1, \(d=d_{max}\)

If the Pareto-optimal subsets 1 of Fig. 2 are considered, the optimized tubes have \(d=d_{max}\) for any value of t. This case represents the maximum exploitation of the available room.

The Pareto-optimal subset 1 in the objective functions domain reads

$$\begin{aligned} m=\frac{4\rho M}{\varGamma d^{2}_{max}c} \end{aligned}$$
(25)

If two tubes made from different materials (let’s say material A and material B) are considered, the ratio between the mass per unit of length at a given stiffness of the two tubes can be written as

$$\begin{aligned} \dfrac{m_A}{m_B}=\dfrac{\rho _AE_B}{\rho _BE_A} \end{aligned}$$
(26)

where \(\varGamma\) has been replaced by E through the relation \(\varGamma =\dfrac{E}{2\left( 1+\nu \right) }\)

If we assume aluminum for material A and steel for material B \((\rho _A=2800\,\hbox {kg}/\hbox {m}^3, \rho _B=7800~\hbox {kg}/\hbox {m}^3,E_A=70\,\hbox {GPa},E_B=210\,\hbox {GPa},\nu _A=\nu _B=0.3)\) Eq. 26 returns 1.077, meaning that when all the available room is exploited (i.e. \(d=d_{max}\)) steel allows to design a tube with about \(7.7 \%\) less mass than the aluminum counterpart.

6.2 Comparison referring to Pareto-optimal subset 2, \(t=t_{min}\)

This case can be interpreted as a technological constraint that limits the minimum manufacturing thickness of the tube. This constraint may depend on the material and technological manufacturing process.

The Pareto-optimal subset 2 in the objective functions domain reads

$$\begin{aligned} m=\rho \root 3 \of {\frac{4\pi ^2M t_{min}^2}{\varGamma c}} \end{aligned}$$
(27)

By considering the two materials A and B the ratio \(\dfrac{m_A}{m_B}\) has the following expression

$$\begin{aligned} \dfrac{m_A}{m_B}=\dfrac{\rho _A}{\rho _B}\root 3 \of {\dfrac{E_B}{E_A}} \end{aligned}$$
(28)

If we consider again aluminum for material A and steel for material B Eq. 28 returns 0.52, thus making the mass of aluminum tube about one half of the steel one for the same compliance c.

6.3 Comparison referring to Pareto-optimal subset 3, active constraint on buckling

In this case the minimum allowable thickness is determined by the constraint on buckling which is active. The expression of the Pareto-optimal subset 3 in the objective functions domain is

$$\begin{aligned} m=\rho \pi \left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^\frac{1}{2+\alpha -\beta }\left( \dfrac{4M}{\varGamma \pi \left( \dfrac{2^{\alpha +1}M\eta }{\pi BE\left( 2l\right) ^\beta }\right) ^\frac{3}{2+\alpha -\beta }}\right) ^\frac{2\alpha -\beta +1}{4\alpha -\beta -1}c^{-\frac{2\alpha -\beta +1}{4\alpha -\beta -1}} \end{aligned}$$
(29)

Again by considering the relation between \(\varGamma\) and E, the ratio \(\dfrac{m_A}{m_B}\) reads

$$\begin{aligned} \dfrac{m_A}{m_B}=\dfrac{\rho _A}{\rho _B}\left( \dfrac{E_B}{E_A}\right) ^{0.545} \end{aligned}$$
(30)

Substituting the values of aluminum (material A) and steel (material B) Eq. 30 gives 0.65. Therefore it turns out that, when the buckling constraint is active, the aluminum tube is about \(35\%\) lighter for a prescribed compliance.

7 Optimal design of a race car driveshaft

In this section, a practical example of an application of the derived formulae is presented. The problem analysed refers to the optimal design of the main driveshaft of a high-performance race car. The component is highlighted in the scheme of Fig. 4 and has the role of transmitting the drive torque M from the engine to the drive axle.

Fig. 4
figure 4

General schematics of the driveline of a two wheel drive vehicle

Full size image

The shaft has a tubular shape, the design variables to be optimized are the tube diameter and its wall thickness, whereas the design objectives are:

  • minimization of the overall mass of the shaft

  • minimization of the deflection of the shaft when subject to the applied load

The driveshaft is subjected to the following constraints. The available room for the driveshaft limits the massimum diameter to 90 mm (\(d_{max}=90\,\hbox {mm}\)) and constraints on structural safety and elastic stability have to be satisfied to avoid failures when the maximum drive torque is applied. The maximum torque M on the driveshaft is 3600 Nm, obtained by multiplying the maximum engine torque (800 Nm) by the first gear (4.5). Additionally, a safety factor of 2.5 is considered in the design process to account for overloads on the driveline and durability requirements.

A C45 quenched and tempered steel is assumed as reference material for the shaft.

All the parameters that are necessary for the optimization are listed in Table 6.

Table 6 Design of the main driveshaft of a race car—input data
Full size table

By substituting the numerical values of Table 6 in the analytical expressions obtained in Sect. 5, one realizes that Case ④ applies. The Pareto-optimal solution is therefore given by the constraint \(d=d_{max}\), the solution with the minimum attainable mass is defined by the intersection between the stress constraint and \(d=d_{max}\); the relative analytical expressions are reported in Table 4.

Figure 5 shows the set of feasible solutions both in terms of design variables (i.e. tube diameter and wall thickness) and objective functions (mass and compliance per unit of length). The (Pareto) optimal solutions are identified by the black line in the graphs of Fig. 5, the designer has to select his final design among this set of solutions. The solution with the lowest attainable mass is identified by the black dot of Fig. 5 and is given by the intersection point of the stress constraint with the constraint \(d=d_{max}\). Such a solution is characterized by an outer diameter of 90 mm and a wall thickness of 2.71 mm, with a mass per unit of length of 5.98 \(\dfrac{\hbox {kg}}{\hbox {m}}\); this solution exhibits also the highest deflection (0.0293 \(\dfrac{\hbox {rad}}{\hbox {m}}\)) when subject to the torsional moment.

On the other hand, the solution with the lowest compliance (marked with a diamond in Fig. 5) is given by a tube with the maximum admissible diameter (90 mm) and the maximum admissible wall thickness (5 mm); regarding the objective functions, this solution is the stiffest (with a deflection of 0.0132 \(\dfrac{\hbox {rad}}{\hbox {m}}\)) but the heaviest one (13.23 \(\dfrac{\hbox {kg}}{\hbox {m}}\)).

The driveshaft currently mounted on the car is also highlighted in the graphs of Fig. 5 and has an outer diameter of 90 mm with and a wall thickness of 3 mm. As evidenced from Fig. 5, the currently adopted solution lies on the Pareto front, showing that the proposed approach for the design of thin walled tubes under torsion is in accordance with practical designs obtained by experienced specialists.

Fig. 5
figure 5

Optimal design of the driveshaft of a race car—Pareto-optimal solution (black line) both in the design variables domain (left) and objective functions domain (right)

Full size image

8 Conclusion

In the paper, the analytical multi-objective optimization for the lightweight design of a thin-walled tube subject to torsion has been dealt with. Tube mass and compliance have been minimized at the same time. Constraints on safety (i.e. admissible stress), elastic stability (buckling), available room (maximum diameter) and manufacturing constraints (minimum thickness) have been considered.

Analytical formulae of the Pareto-optimal set have been obtained for the considered design problem. The analytical expressions are derived both in the design variables (tube diameter and wall thickness) and in the objective functions (mass and compliance of the tube) domain. A comparison of optimized designs made from different materials has been included.

It has been demonstrated that

  • the Pareto-optimal set of the thin-walled tube under torsion is given by the combination of the buckling limit, minimum thickness and maximum diameter.

  • apart from the solution having maximum thickness and maximum diameter, all the other designs with \(t=t_{max}\) are non-optimal and have to be discarded

  • the stress constraint is not part of the Pareto-optimal set, actually it has a role only in the definition of the minimum attainable mass.

The comparative lightweight design of tubes made from different materials showed that aluminium alloy allows an effective lightweight construction, but when the available room is saturated and proper stiffness is requested, steel allows to obtain a lighter structure by \(8\%\).

A simple engineering problem related to the design of the main driveshaft of a race car has been solved by employing the obtained analytical expressions, showing the practical use of the method and its effectiveness in the definition of early-stage optimal design solutions. From a direct comparison with the currently adopted driveshaft, it has been shown that the proposed method is in accordance with the solution obtained by experienced specialists.