1 Introduction

Motivated by industrial demands, computer-aided design optimization has been extensively improved and applied to various real-world applications so far. Magnucki and Szyc (1996) tackled the optimal design problem of non-circular cylindrical shells under uniform internal pressure and determined the optimum shapes of steel and aluminum shells. Later, Vu (2010) performed the minimum weight design for toroidal pressure vessels subjected to internal pressure using differential evolution and particle swarm optimization techniques and reported promising material savings. Different structural and mechanical applications of optimization can also be found in Zheng et al. (2009), Lellep and Paltsepp (2010), Arora and Wang (2005), Saka (2007). In the case of industrial thick-walled pressure tubes, it is sometimes advantageous to use multi-layer tubes with different materials—instead of using a single-layer tube—to achieve more economical or lightweight solutions. Obviously, design of a multi-layer assembly entails taking into account the effect of the involved design variables, such as thickness of layers or material type, on the optimality of final designs. Thanks to modern computational technologies, today it is a common practice to employ efficient optimization techniques capable of locating promising solutions for engineering optimization problems with different design variables.

It is also generally known that in the course of design optimization, structural response calculations under different loading conditions should be performed for evaluating the feasibility of the generated designs. The stress analysis of thick-walled pressure tubes under different loading and boundary conditions has been carried out in many studies. The analysis of pressurized single-layer thick-walled tube was treated in purely elastic stress state (Timoshenko and Goodier 1970; Ugural and Fenster 1987; Boresi et al. 1993), fully plastic stress state (Boresi et al. 1993; Mendelson 1986; Nadai 1931), and elastic–plastic stress state (Parker 2001; Perry and Aboudi 2003) in the past. On the other hand, pressurized tightly and shrink-fitted multi-layer as well as functionally graded cylindrical pressure tubes were investigated by many researchers. Among them, Eraslan and Akis studied the tightly fitted concentric thick-walled pressure tubes in the elastic (Akis and Eraslan 2005) and partially plastic (Eraslan and Akış 2004) states. They also reported the results of stress and deformation analyses of such assemblies under cyclic loading of pressure (Eraslan and Akis 2015; Eraslan et al. 2016). Besides, thick-walled pressure tubes composed of functionally graded materials (FGM) were also investigated by many researchers in the elastic, partially plastic and elastic–plastic stress states (Horgan and Chan 1999; Tutuncu and Ozturk 2001; Jabbari et al. 2002; Ma et al. 2003; Eraslan and Akış 2005; Eraslan and Akis 2006; Chen and Lin 2008; Xin et al. 2014, 2016). In addition to these, the response of two-layer shrink-fitted composite tubes under internal or external radial pressure was investigated by Eraslan and Akis (2005). They obtained analytical expressions for the limiting pressures causing plastic flow in terms of material properties and tube dimensions. In a similar work by Qiu and Zhou (2016), the analyses of two- and three-layer shrink-fitted composite tubes were performed analytically and then verified using the finite element method.

Besides all the foregoing studies, research on optimization of pressurized shrink-fitted multi-layer thick-walled tubes has been conducted by several researchers with different methods and constraints than those used in the past. Jahed et al. (2006) studied the optimum design of a three-layer pressure vessel under the effects of autofrettage and shrink fit for maximum fatigue life expectancy. Other studies on the optimization of shrink-fitted multi-layer tubes with different methods can be found in Yuan et al. (2010, 2011), Miraje and Patil (2011), Majumder et al. (2014), Sharifi et al. (2012, 2014). Among them, Sharifi et al. (2012) used an analytical method to minimize the weight of shrink-fitted multi-layer cylinders with similar material properties considering Tresca criterion. They reported that the maximum shear stress decreases with the increase in the number of tube layers. In another related study by the same authors (Sharifi et al. 2014), an analytical optimization method was proposed for the optimum design of shrink-fitted multi-layer cylinders with different material layers where the maximum shear stress of each layer is minimized.

The optimization of internally pressurized tightly fitted multi-layer tubes has been recently addressed by the authors in Kazemzadeh Azad and Akış (2016). The aim of this paper is to study the optimization of shrink-fitted composite tubes under either internal or both internal and external pressure. The geometry considered here consists of axially constrained concentric two- and three-layer shrink-fitted tubes. The shrink-fitting process for a two-layer tube system consists of heating the outer tube so that its inner radius is enlarged slightly more that the outer radius of the inner tube. The difference between the outer radius of the inner tube and the inner radius of the outer tube is called interference. Due to the interference, the composite tube system becomes prestressed after assembling. The method for the fabrication of the three-layer systems is similar to that of the two-layer assemblies, for which the outer layer is heated to fit to the previously shrink-fitted two-layer assembly. In this work, it is assumed that the installation of tubes is performed simultaneously. Under plane strain assumption and within a small elastic deformation range, the analytical expressions of stresses and displacement for pressurized two- and three-layer shrink-fitted composite tubes are provided, which are valid for both internal and internal and external pressure cases, to calculate the response of the system. Furthermore, von Mises criterion, which complies better with experimental observations, is used in the analysis stage to determine the onset of yielding in the composite tube assemblies.

In this paper, in order to investigate the effect of shrink-fitting, first, optimal material selection and thickness optimization of tightly fitted assemblies are performed without shrink-fitting. Next, using the same algorithm and under the same loading and boundary conditions, the assemblies are optimally designed where shrink-fitting parameters are considered for weight and cost minimization. The obtained results for multi-layer composite tubes with and without shrink-fitting show that more economical or lightweight assemblies can be designed if shrink-fitting parameters are treated as additional design variables. In addition, it is observed that considering the shrink-fitting design variables in the course of optimization is more advantageous for the test instances with a higher ratio of internal pressure to external pressure. The main outcomes of this study can be outlined as (i) treating the shrink-fitting parameters as additional design variables for optimization of multi-layer composite tubes, (ii) numerical evolutionary optimization of shrink-fitted multi-layer assemblies based on von Mises criterion, and (iii) quantifying the weight/cost efficiency of multi-layer composite tubes with and without shrink-fitting under either internal or both internal and external pressure.

In the next section, the analytical solutions for response calculations of axially constrained two- and three-layer shrink-fitted tubes under both internal and external pressure are provided. In section three, the optimization problem is stated, and related mathematical formulations are presented. Section four outlines the main steps for implementation of the employed optimization algorithm. Section five covers shrink-fitting for optimal design of two- and three-layer assemblies. The last section provides the concluding remarks.

2 Analysis of Shrink-Fitted Multi-Layer Composite Tubes

In this section, the main steps of the analytical solutions for structural response calculations are presented for axially constrained two- and three-layer shrink-fitted tubes subjected to both internal and external pressure. In the derivations, cylindrical polar coordinates (r, θ, z) are considered and a state of plane strain (ɛz = 0), as well as small deformations are presumed. For a single-layer tube with axially constrained ends, the stress and displacement expressions are as follows (Eraslan and Akis 2005):

$$\sigma_{r} (r) = \frac{E}{1 + \nu }\left[ { - \frac{{C_{1} }}{{r^{2} }} + \frac{{C_{2} }}{1 - 2\nu }} \right]$$
(1)
$$\sigma_{\theta } (r) = \frac{E}{1 + \nu }\left[ {\frac{{C_{1} }}{{r^{2} }} + \frac{{C_{2} }}{1 - 2\nu }} \right]$$
(2)
$$\sigma_{z} (r) = \frac{{2\nu EC_{2} }}{(1 + \nu )(1 - 2\nu )}$$
(3)
$$u(r) = \frac{{C_{1} }}{r} + C_{2} r$$
(4)

where σi denotes the stress components in radial, circumferential, and axial directions, u is the radial displacement, E is the modulus of elasticity, ν denotes the Poisson’s ratio, and C1 and C2 are arbitrary integration constants.

2.1 Shrink-Fitted Two-Layer Composite Tubes

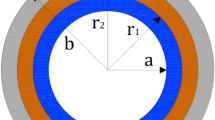
For the shrink-fitted two-layer tubes, the same stress and displacement expressions given in Eqs. (1–4) are valid and these expressions contain four unknown integration constants: C1, C2 for the inner tube, and C3, C4 for the outer tube. In the derivations, the subscripts 1 and 2 are used to denote material properties (E and ν) of the inner and outer tubes, respectively. In addition, superscripts I and II denote the inner and outer tubes. The boundary conditions for the shrink-fitted two-layer tubes under both internal and external pressure are \(\sigma_{r}^{I} (a) = - P_{\text{int}}\) and σ II r (b) = − Pext. Here, a is the inner radius and b is the outer radius of the tube assembly (see Fig. 1). In addition, at the interface of the tubes (r = r1) the radial stress must be continuous which gives σ I r (r1) = σ II r (r1). Finally, the shrink fit requirement at the interface is uI(r1) + i = uII(r1). Here, i is the interference between the two tubes. Application of these conditions results in

$$C_{1} = - \frac{{a^{2} r_{1} M_{1} \left[ {P_{\text{ext}} r_{1} b^{2} E_{1} M_{3} (1 + M_{4} ) - P_{\text{int}} r_{1} \left( {b^{2} M_{5} + r_{1}^{2} M_{6} } \right) + iE_{1} E_{2} \left( {b^{2} - r{}_{1}^{2} } \right)} \right]}}{{E_{1} E_{2} M_{1} \left( {b^{2} - r{}_{1}^{2} } \right)\left( {a^{2} + r{}_{1}^{2} M_{2} } \right) + E_{1}^{2} M_{3} \left( {r{}_{1}^{2} - a^{2} } \right)\left( {b^{2} + r{}_{1}^{2} M_{4} } \right)}}$$
(5)
$$C_{2} = - \frac{{M_{1} M_{2} \left[ {P_{\text{ext}} r_{1}^{2} b^{2} E_{1} M_{3} (1 + M_{4} ) + P_{\text{int}} a^{2} \left( {b^{2} M_{7} - r_{1}^{2} M_{8} } \right) + ir_{1} E_{1} E_{2} \left( {b^{2} - r{}_{1}^{2} } \right)} \right]}}{{E_{1} E_{2} M_{1} \left( {b^{2} - r{}_{1}^{2} } \right)\left( {a^{2} + r{}_{1}^{2} M_{2} } \right) + E_{1}^{2} M_{3} \left( {r{}_{1}^{2} - a^{2} } \right)\left( {b^{2} + r{}_{1}^{2} M_{4} } \right)}}$$
(6)
$$C_{3} = - \frac{{b^{2} r_{1} M_{3} \left[ {P_{\text{ext}} r_{1} \left( {a^{2} M_{8} - r_{1}^{2} M_{6} } \right) - P_{\text{int}} a^{2} r_{1} E_{2} M_{1} (1 + M_{2} ) - iE_{1} E_{2} \left( {r{}_{1}^{2} - a^{2} } \right)} \right]}}{{E_{1} E_{2} M_{3} \left( {r{}_{1}^{2} - a^{2} } \right)\left( {b^{2} + r{}_{1}^{2} M_{4} } \right) + E_{2}^{2} M_{1} \left( {b^{2} - r{}_{1}^{2} } \right)\left( {a^{2} + r{}_{1}^{2} M_{2} } \right)}}$$
(7)
$$C_{4} = - \frac{{M_{3} M_{4} \left[ {P_{\text{ext}} b^{2} \left( {a^{2} M_{7} + r_{1}^{2} M_{5} } \right) - P_{\text{int}} a^{2} r_{1}^{2} E_{2} M_{1} (1 + M_{2} ) - ir_{1} E_{1} E_{2} \left( {r{}_{1}^{2} - a^{2} } \right)} \right]}}{{E_{1} E_{2} M_{3} \left( {r{}_{1}^{2} - a^{2} } \right)\left( {b^{2} + r{}_{1}^{2} M_{4} } \right) + E_{2}^{2} M_{1} \left( {b^{2} - r{}_{1}^{2} } \right)\left( {a^{2} + r{}_{1}^{2} M_{2} } \right)}}$$
(8)

where

$$\begin{array}{*{20}l} {M_{1} = 1 + \nu_{1} ,} \hfill & {M_{2} = 1 - 2\nu_{1} ,} \hfill \\ {M_{3} = 1 + \nu_{2} ,} \hfill & {M_{4} = 1 - 2\nu_{2} ,} \hfill \\ {M_{5} = E_{2} M_{1} M_{2} + E_{1} M_{3} ,} \hfill & {M_{6} = E_{1} M_{3} M_{4} - E_{2} M_{1} M_{2} ,} \hfill \\ {M_{7} = E_{2} M_{1} - E_{1} M_{3} ,} \hfill & {M_{8} = E_{2} M_{1} + E_{1} M_{3} M_{4} } \hfill \\ \end{array}$$
(9)
Fig. 1
figure 1

Cross section of multi-layer tube under internal and external pressure

Full size image

Here, E1 and E2 are the modulus of elasticity of the inner and outer tubes, respectively. Similarly, ν1 and ν2 are the Poisson’s ratio of the two tube layers. It should be noted that for i = 0 the analytical solutions yield the results of a tightly fitted tube. It is also trivial that for Pext = 0 the assembly will be under internal pressure only.

2.2 Shrink-Fitted Three-Layer Composite Tubes

For the three-layer shrink-fitted tubes, the analytical expressions given in Eqs. (1–4) contain six integration constants: C1, C2 for the inner tube, C3, C4 for the middle tube, and C5, C6 for the outer tube. In the derivations, the superscripts I, II, and III denote the inner, middle, and outer tubes. The boundary conditions for the shrink-fitted three-layer tubes under both internal and external pressure are \(\sigma_{r}^{I} (a) = - P_{\text{int}}\) and σ III r (b) = − Pext. In addition, at the interfaces of the tubes (r = r1 and r = r2) the radial stress must be continuous which gives σ I r (r1) = σ II r (r1) and σ II r (r2) = σ III r (r2). Finally, the shrink fit requirements at the two interfaces are uI(r1) + i1 = uII(r1) and uII(r2) + i2 = uIII(r2). Here, i1 and i2 are the interferences between the inner and middle tubes and middle and outer tubes, respectively. Application of these conditions results in

$$C_{1} = \frac{{N_{27} P_{\text{ext}} + N_{28} P_{\text{int}} + N_{29} i_{1} + N_{30} i_{2} }}{{E_{1} \left( {N_{26} r_{2}^{2} + N_{20} N_{22} r_{2}^{4} - b^{2} N_{19} N_{21} r_{1}^{2} } \right)}}$$
(10)
$$C_{2} = \frac{{N_{31} P_{\text{ext}} + N_{32} P_{\text{int}} + N_{33} i_{1} + N_{34} i_{2} }}{{E_{1} \left( {N_{26} r_{2}^{2} + N_{20} N_{22} r_{2}^{4} - b^{2} N_{19} N_{21} r_{1}^{2} } \right)}}$$
(11)
$$C_{3} = \frac{{N_{35} P_{\text{ext}} + N_{36} P_{\text{int}} + N_{37} i_{1} + N_{38} i_{2} }}{{b^{2} \left( {N_{19} N_{21} r_{1}^{2} + N_{15} N_{22} r_{2}^{2} } \right) - r_{2}^{2} \left( {a^{2} N_{13} N_{14} r_{1}^{2} + N_{14} N_{16} r_{1}^{4} + N_{20} N_{22} r_{2}^{2} } \right)}}$$
(12)
$$C_{4} = \frac{{N_{39} P_{\text{ext}} + N_{40} P_{\text{int}} + N_{41} i_{1} + N_{42} i_{2} }}{{b^{2} \left( {N_{19} N_{21} r_{1}^{2} + N_{15} N_{22} r_{2}^{2} } \right) - r_{2}^{2} \left( {a^{2} N_{13} N_{14} r_{1}^{2} + N_{14} N_{16} r_{1}^{4} + N_{20} N_{22} r_{2}^{2} } \right)}}$$
(13)
$$C_{5} = \frac{{N_{43} P_{\text{ext}} + N_{44} P_{\text{int}} + N_{45} i_{1} + N_{46} i_{2} }}{{E_{3} \left[ {b^{2} \left( {N_{19} N_{21} r_{1}^{2} + N_{15} N_{22} r_{2}^{2} } \right) - N_{51} r_{2}^{2} } \right]}}$$
(14)
$$C_{6} = \frac{{N_{47} P_{\text{ext}} + N_{48} P_{\text{int}} + N_{49} i_{1} + N_{50} i_{2} }}{{E_{3} \left[ {b^{2} \left( {N_{19} N_{21} r_{1}^{2} + N_{15} N_{22} r_{2}^{2} } \right) - N_{51} r_{2}^{2} } \right]}}$$
(15)

where

$$\begin{array}{*{20}l} {N_{1} = 1 + \nu_{1} ,} \hfill & {N_{2} = 1 - 2\nu_{1} ,} \hfill \\ {N_{3} = 1 + \nu_{2} ,} \hfill & {N_{4} = 1 - 2\nu_{2} ,} \hfill \\ {N_{5} = 1 + \nu_{3} ,} \hfill & {N_{6} = 1 - 2\nu_{3} ,} \hfill \\ {N_{7} = (r_{1} - r_{2} )(r_{1} + r_{2} ),} \hfill & {N_{8} = N_{4} r_{1}^{2} + r_{2}^{2} ,} \hfill \\ {N_{9} = r_{1}^{2} + N_{4} r_{2}^{2} ,} \hfill & {N_{10} = E_{2} N_{5} N_{6} N_{7} + E_{3} N_{3} N_{9} ,} \hfill \\ {N_{11} = E_{2} N_{5} N_{7} - E_{3} N_{3} N_{9} ,} \hfill & {N_{12} = (1 + N_{4} )(1 + N_{6} ),} \hfill \\ {N_{13} = E_{2} N_{1} + E_{1} N_{3} N_{4} ,} \hfill & {N_{14} = E_{3} N_{3} + E_{2} N_{5} N_{6} ,} \hfill \\ {N_{15} = E_{3} N_{3} N_{4} + E_{2} N_{5} ,} \hfill & {N_{16} = E_{2} N_{1} N_{2} - E_{1} N_{3} N_{4} ,} \hfill \\ {N_{17} = E_{2} N_{1} N_{2} + E_{1} N_{3} ,} \hfill & {N_{18} = E_{2} N_{1} - E_{1} N_{3} ,} \hfill \\ {N_{19} = E_{3} N_{3} - E_{2} N_{5} ,} \hfill & {N_{20} = E_{3} N_{3} N_{4} - E_{2} N_{5} N_{6} ,} \hfill \\ {N_{21} = a^{2} N_{13} + r_{1}^{2} N_{16} ,} \hfill & {N_{22} = a^{2} N_{18} + r_{1}^{2} N_{17} ,} \hfill \\ {N_{23} = N_{13} N_{14} r_{1}^{2} - b^{2} N_{15} N_{18} ,} \hfill & {N_{24} = E_{2} N_{1} N_{2} N_{11} + E_{1} E_{3} N_{3}^{2} N_{4} N_{7} - E_{1} E_{2} N_{3} N_{5} N_{8} ,} \hfill \\ {N_{25} = E_{1} E_{3} N_{3}^{2} N_{4} N_{7} + E_{1} E_{2} N_{3} N_{5} N_{6} N_{8} - E_{2} N_{1} N_{2} N_{10} ,} \hfill & {} \hfill \\ {N_{26} = a^{2} N_{23} - b^{2} N_{15} N_{17} r_{1}^{2} + N_{14} N_{16} r_{1}^{4} ,} \hfill & {N_{27} = a^{2} b^{2} E_{1} E_{2} N_{1} N_{3} N_{5} N_{12} r_{1}^{2} r_{2}^{2} ,} \hfill \\ {N_{28} = a^{2} N_{1} r_{1}^{2} \left( {b^{2} N_{24} - N_{25} r_{2}^{2} } \right)} \hfill & {N_{29} = - a^{2} E_{1} E_{2} N_{1} r_{1} \left( {b^{2} N_{11} + r_{2}^{2} N_{10} } \right),} \hfill \\ {N_{30} = a^{2} E_{1} E_{2} E_{3} N_{1} N_{3} (1 + N_{4} )\left( {b^{2} - r_{2}^{2} } \right)r_{1}^{2} r_{2} ,} \hfill & {N_{31} = b^{2} E_{1} E_{2} N_{1} N_{2} N_{3} N_{5} N_{12} r_{1}^{2} r_{2}^{2} ,} \hfill \\ {N_{32} = a^{2} N_{1} N_{2} \left[ {b^{2} \left( {N_{13} N_{19} r_{1}^{2} + N_{15} N_{18} r_{2}^{2} } \right) - r_{2}^{2} \left( {N_{13} N_{14} r_{1}^{2} + N_{18} N_{20} r_{2}^{2} } \right)} \right],} \hfill & {} \hfill \\ {N_{33} = - E_{1} E_{2} N_{1} N_{2} r_{1} \left( {b^{2} N_{11} + r_{2}^{2} N_{10} } \right),} \hfill & {N_{34} = E_{1} E_{2} E_{3} N_{1} N_{2} N_{3} (1 + N_{4} )r_{1}^{2} r_{2} \left( {b^{2} - r_{2}^{2} } \right),} \hfill \\ {N_{35} = - b^{2} N_{3} N_{5} N_{21} (1 + N_{6} )r_{1}^{2} r_{2}^{2} ,} \hfill & {N_{36} = a^{2} N_{1} (1 + N_{2} )N_{3} r_{1}^{2} r_{2}^{2} \left( {b^{2} N_{15} - N_{20} r_{2}^{2} } \right),} \hfill \\ {N_{37} = E_{1} N_{3} \left( {a^{2} - r_{1}^{2} } \right)r_{1} r_{2}^{2} \left( {N_{20} r_{2}^{2} - b^{2} N_{15} } \right),} \hfill & {N_{38} = E_{3} N_{3} N_{21} r_{1}^{2} r_{2} \left( {r_{2}^{2} - b^{2} } \right),} \hfill \\ {N_{39} = - b^{2} N_{3} N_{4} N_{5} N_{22} (1 + N_{6} )r_{2}^{2} ,} \hfill & {N_{40} = a^{2} N_{1} (1 + N_{2} )N_{3} N_{4} r_{1}^{2} \left( {N_{14} r_{2}^{2} - b^{2} N_{19} } \right),} \hfill \\ {N_{41} = E_{1} N_{3} N_{4} \left( {a^{2} - r_{1}^{2} } \right)r_{1} \left( {b^{2} N_{19} - N_{14} r_{2}^{2} } \right),} \hfill & {N_{42} = E_{3} N_{3} N_{4} N_{22} r_{2} \left( {r_{2}^{2} - b^{2} } \right),} \hfill \\ {N_{43} = - b^{2} N_{5} r_{2}^{2} \left[ \begin{aligned} a^{2} \left( {E_{2} N_{1} N_{10} + E_{1} E_{3} N_{3}^{2} N_{4} N_{7} + E_{1} E_{2} N_{3} N_{5} N_{6} N_{8} } \right) \hfill \\ + r_{1}^{2} \left( {E_{2} N_{1} N_{2} N_{10} - E_{1} E_{3} N_{3}^{2} N_{4} N_{7} - E_{1} E_{2} N_{3} N_{5} N_{6} N_{8} } \right) \hfill \\ \end{aligned} \right],} \hfill & {} \hfill \\ {N_{44} = a^{2} b^{2} E_{2} E_{3} N_{1} (1 + N_{2} )N_{3} (1 + N_{4} )N_{5} r_{1}^{2} r_{2}^{2} ,} \hfill & {} \hfill \\ {N_{45} = b^{2} E_{1} E_{2} E_{3} N_{3} (1 + N_{4} )N_{5} r_{1} r_{2}^{2} \left( {r_{1}^{2} - a^{2} } \right),} \hfill & {} \hfill \\ {N_{46} = - b^{2} E_{2} E_{3} N_{5} r_{2} [a^{2} (E_{2} N_{1} N_{7} + E_{1} N_{3} N_{8} ) + r_{1}^{2} (E_{2} N_{1} N_{2} N_{7} - E_{1} N_{3} N_{8} ) ],} \hfill & {} \hfill \\ {N_{47} = - b^{2} N_{5} N_{6} \left[ {N_{16} N_{19} r_{1}^{4} + N_{15} N_{17} r_{1}^{2} r_{2}^{2} + a^{2} \left( {N_{13} N_{19} r_{1}^{2} + N_{15} N_{18} r_{2}^{2} } \right)} \right],} \hfill & {} \hfill \\ {N_{48} = a^{2} E_{2} E_{3} N_{1} (1 + N_{2} )N_{3} (1 + N_{4} )N_{5} N_{6} r_{1}^{2} r_{2}^{2} ,} \hfill & {} \hfill \\ {N_{49} = E_{1} E_{2} E_{3} N_{3} (1 + N_{4} )N_{5} N_{6} r_{1} \left( {r_{1}^{2} - a^{2} } \right)r_{2}^{2} ,} \hfill & {} \hfill \\ {N_{50} = - E_{2} E_{3} N_{5} N_{6} r_{2} [a^{2} (E_{2} N_{1} N_{7} + E_{1} N_{3} N_{8} ) - r_{1}^{2} (E_{1} N_{3} N_{8} - E_{2} N_{1} N_{2} N_{7} ) ],} \hfill & {} \hfill \\ {N_{51} = a^{2} N_{13} N_{14} r_{1}^{2} + N_{14} N_{16} r_{1}^{4} + N_{20} N_{22} r_{2}^{2} } \hfill & {} \hfill \\ \end{array}$$
(16)

2.3 The von Mises Yield Criterion

For the shrink-fitted two-layer tubes under internal and/or external pressure, the inner surfaces of the tubes are critical and the plastic flow may begin in the inner tube at r = a or in the outer tube at r = r1 (Eraslan and Akis 2005). Similarly, for pressurized (internally and/or externally) three-layer shrink-fitted tubes, the yielding may commence at the inner surfaces of the tubes (i.e., at r = a, r = r1 or r = r2). In order to detect the onset of the yielding in the assemblies, von Mises yield criterion is used in this study. For the plane strain assumption, von Mises yield stress σY is expressed as:

$$\sigma_{Y} = \sqrt {\frac{1}{2}[(\sigma_{r} - \sigma_{\theta } )^{2} + (\sigma_{r} - \sigma_{z} )^{2} + (\sigma_{\theta } - \sigma_{z} )^{2} ]}$$
(17)

The plastic flow begins as soon as the yield stress σY becomes greater than the uniaxial yield limit σ0 of the material. In order to determine commencement of the yielding at the layers of the assemblies, the following non-dimensional yield variable is introduced based on von Mises yield stress:

$$\phi = \sqrt {\frac{1}{2}[(\bar{\sigma }_{r} - \bar{\sigma }_{\theta } )^{2} + (\bar{\sigma }_{r} - \bar{\sigma }_{z} )^{2} + (\bar{\sigma }_{\theta } - \bar{\sigma }_{z} )^{2} ]}$$
(18)

Here, \(\bar{\sigma }_{i}\) are the non-dimensional stress components defined by

$$\bar{\sigma }_{i} = \frac{{\sigma_{i} }}{{\sigma_{0} }}$$
(19)

It should be noted that for the values of ϕ < 1, the assembly is in elastic stress state and for ϕ = 1, the yielding starts at that location.

3 Optimization Problem Formulation

This section presents the mathematical formulation of the tackled design optimization problem. The minimum weight design problem of a pressurized multi-layer composite tube with nl material layers and nv number of design variables, including thickness, material, and shrink-fitting variables, can be stated as follows:

$${\text{Find}}\quad {\mathbf{X}}^{\text{T}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{nv} } \right]$$
(20)

such that X minimizes the weight W(X) objective function:

$$W(X) = \sum\limits_{i = 1}^{nl} {\rho_{i} } A_{i}$$
(21)

where W(X) is the weight per unit length of the tube. Here, ρi and Ai are unit weight and cross-sectional area of the i-th material layer, respectively. In the case of cost optimization of multi-layer composite assemblies, the following cost objective function is to be minimized:

$$C(X) = \sum\limits_{i = 1}^{nl} {c_{i} \rho_{i} } A_{i}$$
(22)

where C(X) is the cost per unit length of the tube. Here, ρi, ci, and Ai are unit weight, cost per unit weight, and cross-sectional area of the i-th material layer, respectively. In this study, both the minimum weight and cost design of multi-layer tubes are subjected to the following strength constraint.

$$\phi_{\,i} - 1 \le 0$$
(23)

In Eq. (23), ϕi is non-dimensional stress variable at the inner surface of the i-th layer defined by Eq. (18). In the course of optimization, weight and cost objective function values of the feasible designs that satisfy the problem constraint are directly computed using Eqs. (21) and (22), respectively. However, infeasible designs that violate the problem constraint are penalized based on an external penalty function method, and their objective function values are calculated using the following equation:

$$f_{p} (X) = f(X)\left[ {1 + K\left( {\sum\limits_{i} {g_{i} } } \right)} \right]$$
(24)

In Eq. (24), f(X) is the considered weight or cost objective function, fp(X) is the penalized objective function, gi is the i-th problem constraint, and K is the penalty coefficient. In the present study, the numerical evolutionary algorithm developed by Kazemzadeh Azad and Akış (2016) is employed for design optimization of multi-layer assemblies. The main steps for implementation of the optimization algorithm are outlined in the following section.

4 Optimization Algorithm

Considering the sound reputation of evolutionary algorithms, as numerical optimization methods in practical design optimization applications, a reformulation of the big bang-big crunch algorithm (Erol and Eksin 2006) recently proposed by Kazemzadeh Azad and Akış (2016) is employed for optimal design of multi-layer assemblies. The advantages of evolutionary algorithms can be attributed to their ease of understanding and implementation, independency on gradient information of objective function, global search features, and capability of handling discrete design variables involved in the optimum design problem of multi-layer assemblies. The main steps to implement the optimization algorithm are as follows:

  • Step 1. Initial population Generate an initial population by randomly spreading candidate solutions (individuals) over the solution space (first big bang) in a uniform manner.

  • Step 2. Evaluation Evaluate all the candidate solutions in the generated population. To this end, the objective function values of the feasible candidate solutions that satisfy all the design constraints are calculated from Eqs. (21) or (22). However, infeasible candidate solutions are penalized and their objective function values are computed using Eq. (24). The fitness scores of the candidate solutions are then obtained through taking the inverse of their objective function values. The fitness scores are considered as the mass values of the candidate solutions.

  • Step 3. Big crunch phase Find the center of mass by taking the weighted average based on the coordinates (solution variables) and the mass values of candidate solutions or choose the best candidate solution among all as their center of mass (the latter approach is used in this study).

  • Step 4. Big bang phase Generate new candidate solutions using normal distribution (big bang phase). In case of a continuous optimization instance, the following equation can be employed at each iteration to generate new solutions around the mass center:

    $$x_{i}^{\text{new}} = x_{i}^{c} + \alpha \cdot N(0,1)_{i} \frac{{\left( {x_{i}^{\hbox{max} } - x_{i}^{\hbox{min} } } \right)}}{k}$$
    (25)

    Here, x c i is the value of i-th continuous solution variable in the best candidate solution, x min i and x max i are the lower and upper bounds on the value of i-th solution variable, respectively, N(0, 1)i is a random number produced using a standard normal distribution with mean (μ) zero and standard deviation (σ) equal to one, k is the iteration number, and α is a constant.

  • Step 5. Elitism Keep the current best candidate solution in a separate place or as a member of the population.

  • Step 6. Termination Return to Step 2 until a termination criterion is met, which can be considered as a maximum number of iterations or no improvement of the best solution found over a predetermined number of iterations.

In order to improve the performance of the BB-BC algorithm in discrete design optimization problems, a third power reformulation of Eq. (25) is proposed by Hasançebi and Kazemzadeh Azad (2014). In the present study, the following formulation based on Hasançebi and Kazemzadeh Azad (2014) is employed in lieu of Eq. (25):

$$x_{i}^{\text{new}} = x_{i}^{c} + \alpha \cdot N(0,1)_{i}^{3} \frac{{\left( {x_{i}^{\hbox{max} } - x_{i}^{\hbox{min} } } \right)}}{k}$$
(26)

Here, in order to satisfy the fabrication requirements thickness of each layer is rounded to the nearest available value during the optimization process. For the sake of clarity, flowchart of the optimization algorithm is outlined in Fig. 2.

Fig. 2
figure 2

Flowchart of the optimization algorithm

Full size image

5 Shrink-Fitting for Optimal Design

This section presents the numerical experiments performed to investigate the effect of shrink-fitting on the design optimization of multi-layer composite tubes subjected to internal and external pressure. Using a numerical evolutionary optimization algorithm, weight and cost minimization of multi-layer composite tubes are carried out using a set of available steel and aluminum alloys presented in Table 1. This set of steel and aluminum alloys has been formerly used in Kazemzadeh Azad and Akış (2016) for design optimization of internally pressurized tightly fitted multi-layer composite tubes with axially constrained ends. It should be noted that for all the test examples, thickness of each layer is selected from multiplies of 0.002 m.

Table 1 Material properties and costs of the available steel and aluminum alloys
Full size table

In order to investigate the effect of shrink-fitting, first, optimal material selection and thickness optimization of tightly fitted assemblies are carried out (without shrink-fitting). Next, under the same loading and boundary conditions the assemblies are optimally designed where shrink-fitting parameters are also considered as design variables for weight and cost minimization. For the optimization algorithm, the maximum number of iterations is taken as 1000, and a population of 50 individuals is employed. It is worth mentioning that due to the stochastic nature of the optimization technique, for each case the algorithm is executed 50 times and the best solution obtained is reported as the final design.

Minimum cost design of internally pressurized one-, two-, and three-layer tubes is performed with and without shrink-fitting, and the results are depicted in Fig. 3 for two different inner radius values of the tube assembly, i.e., 0.2 and 0.4 m. It is worth mentioning that in this work the shrink-fitting process is not included in the cost computations. It is apparent from the figure that the results of two- and three-layer assemblies with shrink-fitting are better than those of assemblies fabricated without shrink-fitting.

Fig. 3
figure 3

Comparison of cost optimization results for internally pressurized tubes with and without shrink-fitting: aa = 0.2; and ba = 0.4 m

Full size image

Detailed cost optimization results for internally pressurized tubes with and without shrink-fitting are given in Tables 2 and 3 for one-, two- and three-layer tubes. As can be seen from the results, shrink-fitting provides alternative cost-efficient solutions for two- and three-layer assemblies. For instance, under an internal pressure of Pint = 140 MPa it can be seen from Table 2 that the algorithm finds the best solution with a design cost of 1851.2 $/m using the shrink-fitted three-layer assembly. For this test case, the second best solution with a cost of 1959.9 $/m belongs to the shrink-fitted two-layer assembly. More expensive designs are achieved as 2454.4, 2501.6 and 2764.4 $/m for three-, two-, and one-layer assemblies, respectively. It is also observed that in this test case although optimal materials selected for two- and three-layer assemblies without shrink-fitting are different for each layer (e.g., AL-5, AL-4, and AL-3 selected for three-layer assembly), in the case of shrink-fitted designs the algorithm finds promising solutions using only one material, namely AL-5 for all the layers. These alternative solutions provided by shrink-fitting, which reduce the number of required material type for fabrication, can be very beneficial, especially in mass production of these assemblies. It can also be observed that in almost all the investigated cases von Mises yield variable ϕ is close to 1 at critical points of the tube layers.

Table 2 Cost optimization results for internally pressurized tubes with and without shrink-fitting (Pint = 100, 120, 140 MPa)
Full size table
Table 3 Cost optimization results for internally pressurized tubes with and without shrink-fitting (Pint = 160, 180, 200 MPa)
Full size table

Cost optimization of internally and externally pressurized tubes is carried out with and without shrink-fitting, and the results are shown in Fig. 4. The corresponding detailed cost optimization results are also presented in Tables 4 and 5. Based on the numerical results, it can be deduced that generally the shrink-fitting process is more advantageous for the test examples with a higher ratio of internal pressure to external pressure. For instance, as given in Table 4 under Pint/Pext = 100/200 MPa, the best solution using the shrink-fitted three-layer assembly is 1391.6 $/m which is only slightly better than the result obtained for the three-layer assembly without shrink-fitting, i.e., 1393.3 $/m. Similarly, in this test case it is seen that shrink-fitting does not improve the solution of the two-layer assembly which is 1398.8 $/m. On the other hand, as tabulated in Table 5, for an internal pressure of 200 MPa and external pressure of 100 MPa (i.e., Pint/Pext = 200/100 MPa), the best solution using the shrink-fitted three-layer assembly is achieved as 1133.1 $/m, which is considerably better that the result of three-layer tube without shrink-fitting, namely 1290.8 $/m. Similarly, here the shrink-fitting improves the solution of the two-layer assembly and produces a final design with a cost of 1181.9 $/m which is much better than that of the corresponding tube without shrink-fitting (1306.9 $/m).

Fig. 4
figure 4

Comparison of cost optimization results for internally and externally pressurized tubes with and without shrink-fitting: aa = 0.2; and ba = 0.4 m

Full size image
Table 4 Cost optimization results for internally and externally pressurized tubes with and without shrink-fitting (Pint < Pext)
Full size table
Table 5 Cost optimization results for internally and externally pressurized tubes with and without shrink-fitting (Pext < Pint)
Full size table

Sometimes the objective of optimization is to reduce the final weight of the assembly while satisfying the predetermined design constraints. Here, minimum weight design of internally pressurized one-, two-, and three-layer tubes is performed with and without shrink-fitting and the results are shown in Fig. 5 for two different inner radius values of the tube assembly, i.e., 0.2 and 0.4 m. Furthermore, detailed weight optimization results for internally pressurized tubes with and without shrink-fitting are tabulated in Tables 6 and 7. As can be seen from Table 6, the design weights obtained for two- and three-layer assemblies with shrink-fitting are lighter compared to those of assembles fabricated without shrink-fitting. For example, under an internal pressure of Pint = 140 MPa it can be seen from Table 6 that the algorithm locates the best solution with a design weight of 336.6 kg/m using the shrink-fitted three-layer assembly. For this test instance, the second best solution with a cost of 356.4 kg/m belongs to the shrink-fitted two-layer assembly. Other heavier designs are achieved as 419.8, 427.5 and 486.1 kg/m for three-, two-, and one-layer assemblies, respectively.

Fig. 5
figure 5

Comparison of weight optimization results for internally pressurized tubes with and without shrink-fitting: aa = 0.2; and ba = 0.4 m

Full size image
Table 6 Weight optimization results for internally pressurized tubes with and without shrink-fitting (Pint = 100, 120, 140 MPa)
Full size table
Table 7 Weight optimization results for internally pressurized tubes with and without shrink-fitting (Pint = 160, 180, 200 MPa)
Full size table

Weight optimization of internally and externally pressurized tubes is carried out with and without shrink-fitting, and the results are shown in Fig. 6. The corresponding detailed weight optimization results are also given in Tables 8 and 9. The numerical results of weight optimization indicate that, similar to the cost optimization results, generally the shrink-fitting process becomes more advantageous for the test instances with a higher ratio of internal pressure to external pressure. For example, as given in Table 8 under Pint/Pext = 100/200 MPa, the solution obtained using the shrink-fitted three-layer assembly is 264.8 kg/m which is only slightly better than the result obtained for the three-layer assembly without shrink-fitting, namely 265.4 kg/m. Similarly, in this test case it is seen that solution obtained using the shrink-fitted two-layer assembly is 263.4 kg/m which is only slightly better than the result obtained for the two-layer assembly without shrink-fitting, i.e., 265.8 kg/m. On the other hand, as given in Table 9, for an internal pressure of 200 MPa and external pressure of 100 MPa (i.e., Pint/Pext = 200/100 MPa), the best solution using the shrink-fitted three-layer assembly is achieved as 206 kg/m which is considerably better that the result of three-layer tube without shrink-fitting, namely 246.7 kg/m. Similarly, here the shrink-fitting improves the solution of the two-layer assembly and produces a final design with a weight of 214.9 kg/m which is much better than that of the corresponding tube without shrink-fitting, namely 250.1 kg/m. Typical cost and weight optimization histories for two- and three-layer composite tubes with and without shrink-fitting are plotted in Figs. 7, 8, 9, and 10.

Fig. 6
figure 6

Comparison of weight optimization results for internally and externally pressurized tubes with and without shrink-fitting: aa = 0.2; and ba = 0.4 m

Full size image
Table 8 Weight optimization results for internally and externally pressurized tubes with and without shrink-fitting (Pint < Pext)
Full size table
Table 9 Weight optimization results for internally and externally pressurized tubes with and without shrink-fitting (Pext < Pint)
Full size table
Fig. 7
figure 7

Cost optimization histories of internally pressurized tubes with and without shrink-fitting: a two-layer, and b three-layer tube with a = 0.2 m, and Pint = 160 MPa

Full size image
Fig. 8
figure 8

Cost optimization histories of internally and externally pressurized tubes with and without shrink-fitting: a two-layer, and b three-layer tube with a = 0.2 m, Pint = 200, and Pext = 100 MPa

Full size image
Fig. 9
figure 9

Weight optimization histories of internally pressurized tubes with and without shrink-fitting: a two-layer, and b three-layer tube with a = 0.2 m and Pint = 160 MPa

Full size image
Fig. 10
figure 10

Weight optimization histories of internally and externally pressurized tubes with and without shrink-fitting: a two-layer, and b three-layer tube with a = 0.2 m, Pint = 200, and Pext = 100 MPa

Full size image

Figure 11 presents the variations of non-dimensional stress variable ϕ in radial direction for shrink-fitted two- and three-layer composite tubes in a typical cost optimization case under Pint = 200 and Pext = 100 MPa. It is apparent from the figure that the obtained designs satisfy the design constraint of the optimization problem with promising values which are very close to ϕ = 1 at the critical points of the assembly. It is worth mentioning that further research is indeed required for optimization of multi-layer composite assemblies under different loading conditions as well as developing more realistic cost objective functions by taking into account all the fabrication, installation, and maintenance costs of the assemblies.

Fig. 11
figure 11

Variations of non-dimensional stress variable in radial direction for typical shrink-fitted a two-layer, and b three-layer tubes in cost optimization under Pint = 200 and Pext = 100 MPa

Full size image

6 Concluding Remarks

In the present work, the effect of shrink-fitting on the optimum design of multi-layer composite tubes subjected to internal and external pressure is investigated. The main steps for structural response calculations are provided based on analytical solutions for axially constrained two- and three-layer shrink-fitted tubes under both internal and external pressure. A recently developed numerical evolutionary optimization algorithm is employed to minimize the weight and cost of pressurized multi-layer composite tubes. In order to investigate the effect of shrink-fitting, first, optimal material selection and thickness optimization of tightly fitted assemblies are carried out without shrink-fitting. Next, under the same loading and boundary conditions the assemblies are optimally designed where shrink-fitting parameters are also considered as design variables for weight and cost minimization. The numerical results obtained for multi-layer composite tubes with and without shrink-fitting indicate that more economical or lightweight assemblies can be achieved if shrink-fitting parameters are treated as additional design optimization variables. Furthermore, in light of the numerical results obtained, it can be deduced that in the test cases with a higher ratio of internal pressure to external pressure, the use of shrink-fitting for optimum design becomes more advantageous.