The generalized quadrature method for a class of highly oscillatory Volterra integral equations

Abstract

A generalized quadrature method is studied for Volterra integral equations with highly oscillatory kernels. According to the kernel, a two-point quadrature rule is constructed by Lagrange’s identity at first. The error of the quadrature formula is presented as well. Then, it is employed to discretize the highly oscillatory equation without the need to compute moment. For the convergence, the asymptotic order as well as the classical order of the quadrature method for equation is analyzed. It is shown that the method has asymptotic order two and converges with order two as step length decreases. Some numerical examples are conducted to test its efficiency.

1 Introduction

Volterra integral equations (VIEs) are important in many fields and they have been studied extensively. To get the approximate solution, a plenty of numerical methods have been devised [1, 10, 15, 17]. However, they may be inefficient for equations with special structures. Therefore, it is necessary to construct new methods. This paper concerns highly oscillatory VIEs

$$ y(t)=g(t)+{{\int}^{t}_{0}}K_{\omega}(t,s)y(s)ds,\quad t\in I:=[0,T], $$

(1)

where K_ω(t,s) is the oscillatory kernel function which usually takes Bessel function or trigonometric function. Such equations can be seen in [2, 3, 19, 21]. For the properties of solutions, we refer to [2, 3, 24] where the boundedness of the solutions and its derivatives have been discussed. Traditional methods will suffer from a disaster if the kernel is highly oscillatory, i.e., the frequency ω ≫ 1. To overcome the difficulty, some quadrature methods for discretizing the highly oscillatory integrals in the VIE have been devised, such as Filon method [11, 25], exponential fitting (EF) method [12] and Levin method [13]. Applying them to the oscillatory equations results in some efficient numerical methods. It is worth noticing that there is a class of method whose error behaves as O(ω^−α) for ω ≫ 1, where α can be any positive number. These methods are said to have asymptotic order α. For highly oscillatory VIEs, such methods are desired because they can provide more accurate results for large ω at low cost.

In 2013, Xiang and Brunner [21] constructed Filon method, piecewise constant and linear collocation method for (1) with weakly singular and highly oscillatory Bessel kernels. They obtained that the direct Filon method has an asymptotic order and it will be higher if g(0) = 0. The asymptotic order of the piecewise ones was derived as well. In addition, they proved that the piecewise ones also converge with respect to step length, i.e., they have a classical order. Since the successful application of Filon method, it has been employed to solve other kinds of oscillatory equations [9]. What is more, the Filon method is combined with some normal methods to deal with highly oscillatory problems [18, 23, 27]. While most of the researches mainly pay their attention to the asymptotic order. Recently, Zhao et al. [24] proposed a collocation method combined with the Filon method for (1) with trigonometric kernels. The asymptotic order as well as the classical order has been analyzed in detail. It should be noticed that these methods dependent heavily on the computation of moment. As for the EF method, it has been adapted for VIEs with oscillatory or periodic solutions. In [4,5,6], the numerical results were obtained by discretizing the equation with EF quadrature formula. In 2020, Zhao and Huang [26] took EF collocation methods to get the solution. These convergence results only reflect the influence of the step length. For the application of Levin method, Li et al. [14] employed it to solve the Fredholm oscillatory integral equation and tested its performance numerically without convergence analysis.

This work will go a further step on the quadrature method for highly oscillatory VIEs. Not only the asymptotic order, but also the classical order is concerned. In detail, this paper studies a quadrature method for VIE

$$ y(t)=g(t)+{{\int}^{t}_{0}}K(t,s)\cos (\omega p(s))y(s)ds,\quad t\in I:=[0,T], $$

(2)

where g(t), p(t) and K(t,s) are given continuous functions on I and D := {(t,s) : 0 ≤ s ≤ t ≤ T} respectively and y(t) is unknown. Moreover, we assume $p^{\prime }(t) \neq 0$ for t ∈ I. For ω ≫ 1, the VIE is highly oscillatory. To discretize the integrals in VIE (2) efficiently, we consider the generalized quadrature method proposed in [7]. Since the oscillatory function ${\cos \limits } (\omega p(s))$ satisfies a differential equation, a two-point quadrature formula could be constructed by Lagrange’s identity without the need to compute moment. Then the generalized quadrature formula is applied to VIE (2) to get the numerical solution. The quadrature method is proved to have asymptotic order 2 no matter g(0) = 0 or not. What is more, it converges with classical order 2 as step length decreases as well. To verify the sharpness of the analysis, some examples are given in the numerical part.

The rest of the paper is arranged as follows. In Section 2, a two-point quadrature rule is constructed. In Section 3, the quadrature method is employed to solve VIE (2). The convergence analysis is conducted in this part as well. Section 4 gives some numerical examples to see the performance. At last, some conclusions are obtained.

2 The generalized quadrature formula

For $Q(f;a,b):={{\int \limits }^{b}_{a}}f(s){\cos \limits } (\omega p(s))ds$, we want to construct a two-point quadrature formula in the following form

$$ {{\int}^{b}_{a}}f(s)\cos (\omega p(s))ds\approx \hat{Q}(f;a,b):=w_{1}f(a) + w_{2}f(b), $$

(3)

where the weights w₁ and w₂ are to be determined.

Notice that $\phi (s):={\cos \limits } (\omega p(s))$ satisfies the differential equation

$$ (\mathscr{L}\phi)(s):= \left( \frac{\phi^{\prime}(s)}{\omega p^{\prime}(s)}\right)'+\omega p^{\prime}(s)\phi(s)\equiv 0. $$

According to [7], its adjoint operator is defined by

$$(\mathscr{M}\psi)(s):= (\mathscr{L}\psi)(s)=\left( \frac{\psi^{\prime}(s)}{\omega p^{\prime}(s)}\right)'+\omega p^{\prime}(s)\psi(s).$$

Then, in the theory of linear differential equation, the Lagrange’s identity

$$\psi(s)(\mathscr{L}\phi)(s)-\phi(s)(\mathscr{M}\psi)(s)= \left( Z(\phi(s),\psi(s))\right)'$$

reduces to

$$ \phi(s)(\mathscr{M}\psi)(s)= -\left( Z(\phi(s),\psi(s))\right)' $$

(4)

with

$$Z(\phi(s),\psi(s)):=\frac{\phi^{\prime}(s)\psi(s)-\psi^{\prime}(s)\phi(s)}{\omega p^{\prime}(s)}.$$

Since $p^{\prime }(s)$ appears in the denominator, we need $p^{\prime }(s)\neq 0$ for s ∈ [a,b].

With the help of (4), the integral Q(f;a,b) has a closed form for $f(s)=({\mathscr{M}}\psi )(s)$, i.e.,

$$ {{\int}^{b}_{a}}\phi(s)(\mathscr{M}\psi)(s)ds=-Z(\phi(s),\psi(s))\Big|^{b}_{a}. $$

(5)

To obtain w_i, let formula (3) hold exactly for $f(s)=({\mathscr{M}}\psi _{i})(s)$ with ψ_i(s) = s^i− 1(i = 1,2), i.e.,

$$ \begin{array}{ll} Q((\mathscr{M}\psi_{1})(s);a,b)&=\hat{Q}((\mathscr{M}\psi_{1})(s);a,b),\\ Q((\mathscr{M}\psi_{2})(s);a,b)&=\hat{Q}((\mathscr{M}\psi_{2})(s);a,b). \end{array} $$

(6)

That is to say that the following equations hold

$$ \begin{array}{ll} {{\int}^{b}_{a}}(\mathscr{M}\psi_{1})(s)\cos (\omega p(s))ds&=w_{1}(\mathscr{M}\psi_{1})(a) + w_{2}(\mathscr{M}\psi_{1})(b)\\ &=-Z(\cos (\omega p(s)),\psi_{1}(s))\Big|^{b}_{a},\\ {{\int}^{b}_{a}}(\mathscr{M}\psi_{2})(s)\cos (\omega p(s))ds&=w_{1}(\mathscr{M}\psi_{2})(a) + w_{2}(\mathscr{M}\psi_{2})(b)\\ &=-Z(\cos (\omega p(s)),\psi_{2}(s))\Big|^{b}_{a}. \end{array} $$

Thus, we have

$$ \begin{array}{ll} \left( \begin{array}{cc} (\mathscr{M}\psi_{1})(a)& \quad (\mathscr{M}\psi_{1})(b)\\ (\mathscr{M}\psi_{2})(a)& \quad (\mathscr{M}\psi_{2})(b) \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2} \end{array} \right)= \left( \begin{array}{c} -Z(\phi(s),\psi_{1}(s))\big|^{b}_{a}\\ -Z(\phi(s),\psi_{2}(s))\big|^{b}_{a} \end{array} \right). \end{array} $$

If $A := \left | {\begin {array}{cc} ({\mathscr{M}}\psi _{1})(a)&\quad ({\mathscr{M}}\psi _{1})(b)\\ ({\mathscr{M}}\psi _{2})(a)&\quad ({\mathscr{M}}\psi _{2})(b) \end {array}} \right |\neq 0$, the weights w₁ and w₂ will be given by

$$ w_{1}=\frac{A_{1}}{A},\quad w_{2}=\frac{A_{2}}{A}, $$

(7)

where

$$A_{1} := \left| {\begin{array}{cc} -Z(\phi(s),\psi_{1}(s))\big|^{b}_{a}& \quad (\mathscr{M}\psi_{1})(b)\\ -Z(\phi(s),\psi_{2}(s))\big|^{b}_{a}& \quad (\mathscr{M}\psi_{2})(b) \end{array}} \right|$$

and

$$A_{2} := \left| {\begin{array}{cc} (\mathscr{M}\psi_{1})(a)&\quad -Z(\phi(s),\psi_{1}(s))\big|^{b}_{a}\\ (\mathscr{M}\psi_{2})(a)&\quad -Z(\phi(s),\psi_{2}(s))\big|^{b}_{a} \end{array}} \right|.$$

The readers are referred to [8, 22] for the theoretical aspects of the generalized quadrature method.

We are now in a position to estimate the weights. For the elements $-Z(\phi (s),\psi _{i}(s))\big |^{b}_{a}$ in A_i, the mean value theorem gives

$$ -Z(\phi(s),\psi_{i}(s))\big|^{b}_{a} = -\frac{d}{ds}Z(\phi(s),\psi_{i}(s))\big|_{s=\xi_{i}}(b-a)\\ $$

with ξ_i ∈ (a,b) if p(s) ∈ C²([a,b]). Since $({\mathscr{M}}\psi _{1})(s)=\omega p^{\prime }(s)$, $({\mathscr{M}}\psi _{2})(s)=-\frac {p^{\prime \prime }(s)}{\omega p^{\prime }(s)^{2}}+\omega p^{\prime }(s)s$ and

$$ \begin{array}{ll} Z(\cos (\omega p(s)),\psi_{1}(s))&=-\sin (\omega p(s)),\\ Z(\cos (\omega p(s)),\psi_{2}(s))&=-s\sin (\omega p(s))-\frac{\cos (\omega p(s))}{\omega p^{\prime}(s)}, \end{array} $$

according to (7), we have

$$ \begin{array}{ll} w_{1} = (b-a)&\left[ \frac{\frac{p^{\prime}(b)p^{\prime\prime}(\xi_{2})\cos (\omega p(\xi_{2}))}{p^{\prime}(\xi_{2})^{2}}-\frac{p^{\prime}(\xi_{1})p^{\prime\prime}(b)\cos (\omega p(\xi_{1}))}{p^{\prime}(b)^{2}}}{\frac{p^{\prime}(b)p^{\prime\prime}(a)}{p^{\prime}(a)^{2}}-\frac{p^{\prime}(a)p^{\prime\prime}(b)}{p^{\prime}(b)^{2}}-\omega^{2}p^{\prime}(b)p^{\prime}(a)(a-b)}\right.\\ &\left.-\frac{\omega^{2}p^{\prime}(b)\left( p^{\prime}(\xi_{2})\xi_{2}\cos (\omega p(\xi_{2}))-p^{\prime}(\xi_{1})b\cos (\omega p(\xi_{1}))\right)}{\frac{p^{\prime}(b)p^{\prime\prime}(a)}{p^{\prime}(a)^{2}}-\frac{p^{\prime}(a)p^{\prime\prime}(b)}{p^{\prime}(b)^{2}}-\omega^{2}p^{\prime}(b)p^{\prime}(a)(a-b)}\right],\\ w_{2}= (b-a)&\left[\frac{\frac{p^{\prime\prime}(a)p^{\prime}(\xi_{1})\cos (\omega p(\xi_{1}))}{p^{\prime}(a)^{2}}-\frac{p^{\prime}(a)p^{\prime\prime}(\xi_{2})\cos (\omega p(\xi_{2}))}{p^{\prime}(\xi_{2})^{2}}}{\frac{p^{\prime}(b)p^{\prime\prime}(a)}{p^{\prime}(a)^{2}}-\frac{p^{\prime}(a)p^{\prime\prime}(b)}{p^{\prime}(b)^{2}}-\omega^{2}p^{\prime}(b)p^{\prime}(a)(a-b)}\right.\\ &\left.-\frac{\omega^{2}p^{\prime}(a)(p^{\prime}(\xi_{1})a\cos (\omega p(\xi_{1}))-p^{\prime}(\xi_{2})\xi_{2}\cos (\omega p(\xi_{2})))}{\frac{p^{\prime}(b)p^{\prime\prime}(a)}{p^{\prime}(a)^{2}}-\frac{p^{\prime}(a)p^{\prime\prime}(b)}{p^{\prime}(b)^{2}}-\omega^{2}p^{\prime}(b)p^{\prime}(a)(a-b)}\right]. \end{array} $$

Then, considering p(s) ∈ C²([a,b]), we have

$$ \left|w_{i}\right|\leq {C_{1}}(b-a). $$

(8)

For the error of the quadrature formula (3) with (7), we have the following analysis. Denote $\hat {f}(s)=k_{1}({\mathscr{M}}\psi _{1})(s)+k_{2}({\mathscr{M}}\psi _{2})(s)$ where k₁ and k₂ are such that

$$ \hat{f}(a)=f(a), \quad \hat{f}(b)=f(b). $$

(9)

Therefore, we have

$$ \begin{array}{ll} \hat{Q}(f;a,b)&=w_{1}f(a) + w_{2}f(b)=w_{1}\hat{f}(a)+ w_{2}\hat{f}(b). \end{array} $$

(10)

Taking the expression of $\hat {f}(s)$ into (10) and rearranging it leads to

$$ \begin{array}{@{}rcl@{}} \hat{Q}(f;a,b)&=&k_{1}\left( w_{1}(\mathscr{M}\psi_{1})(a)+w_{2}(\mathscr{M}\psi_{1})(b)\right)\\ &&+k_{2}\left( w_{1}(\mathscr{M}\psi_{2})(a)+w_{2}(\mathscr{M}\psi_{2})(b)\right)\\ &=&k_{1}\hat{Q}\left( (\mathscr{M}\psi_{1})(s);a,b\right)+k_{2}\hat{Q}\left( (\mathscr{M}\psi_{2})(s);a,b\right). \end{array} $$

Paying attention to equality (6), there is

$$ \begin{array}{@{}rcl@{}} \hat{Q}(f;a,b)&=&k_{1}Q\left( (\mathscr{M}\psi_{1})(s);a,b\right)+k_{2}Q\left( (\mathscr{M}\psi_{2})(s);a,b\right)\\ &=&Q\left( k_{1}(\mathscr{M}\psi_{1})(s)+k_{2}(\mathscr{M}\psi_{2})(s);a,b\right)\\ &=&Q(\hat{f};a,b). \end{array} $$

Then, the quadrature error has the form

$$ E(f) = \left|Q(f;a,b) - \hat{Q}(f;a,b)\right| = \left|Q(f;a,b)-\!Q(\hat{f};a,b)\right| = \left|Q(f-\hat{f};a,b)\right|.\\ $$

Let $F(s):=f(s)-\hat {f}(s)$. Then, we have F(a) = F(b) = 0 according to condition (9). By Lemma 2.1 in [20], there is

$$F(s)=\frac{F^{\prime\prime}(\zeta_{1})}{2}(s-a)(s-b)$$

with ζ₁ ∈ [a,b]. As a result, the error could be estimated as

$$ \begin{array}{l} E(f)=\left|Q(F;a,b)\right|{\leq{\int}^{b}_{a}} \left|F(s)\right|ds\leq {\frac{||F^{\prime\prime}(s)||_{\infty}}{2}(b-a)^{3}:=C_{2}(b-a)^{3}}. \end{array} $$

(11)

Estimate (11) gives the influence of interval length on the error and it may provide a better prediction for small integral interval length. However, it does not reflect the superiority of the quadrature formula (3). Next, we aim to analyze the influence of the frequency ω in detail.

For ${{\int \limits }_{a}^{b}}{\sin \limits } (\omega p(s))ds$, integration by parts yields

$$ \begin{array}{@{}rcl@{}} \left|{{\int}_{a}^{b}}\sin(\omega p(s))ds\right|&=&\frac{1}{\omega}\left|\frac{\cos(\omega p(s))}{p^{\prime}(s)}\Big|^{b}_{a}-{{\int}_{a}^{b}}\cos (\omega p(s))\left( \frac{1}{p^{\prime}(s)}\right)'ds\right|\\ &\leq& \frac{1}{\omega}\left( \left|\frac{1}{p^{\prime}(b)}\right|+\left|\frac{1}{p^{\prime}(a)}\right|+{{\int}_{a}^{b}}\left|\left( \frac{1}{p^{\prime}(s)}\right)'\right|ds\right)\\ &:=&C_{3}\frac{1}{\omega}. \end{array} $$

(12)

Therefore, we have

$$ \begin{array}{@{}rcl@{}} &&{{\int}_{a}^{b}}F(s)\cos(\omega p(s))ds=\frac{1}{\omega}{{\int}_{a}^{b}}\left( \frac{F(s)}{p^{\prime}(s)}\right)'\sin (\omega p(s))ds\\ &&=\frac{1}{\omega}{{\int}_{a}^{b}}\left( \frac{F(s)}{p^{\prime}(s)}\right)'d{{\int}^{s}_{a}}\sin (\omega p(\tau))d\tau\\ &&=\frac{1}{\omega}\left( \left( \frac{F(s)}{p^{\prime}(s)}\right)'\Big|_{s=b}{{\int}^{b}_{a}}\sin (\omega p(\tau))d\tau-{{\int}_{a}^{b}}\left( \frac{F(s)}{p^{\prime}(s)}\right)^{\prime\prime}{{\int}^{s}_{a}}\sin (\omega p(\tau))d\tau ds\right),\\ \end{array} $$

where F(a) = F(b) = 0 has been employed. Taking advantage of (12), there is

$$ \left|{{\int}_{a}^{b}}F(s)\cos(\omega p(s))ds\right|\leq \frac{C_{3}}{\omega^{2}}\left( \left|\left( \frac{F(s)}{p^{\prime}(s)}\right)'\Big|_{s=b}\right|+{{\int}_{a}^{b}}\left|\left( \frac{F(s)}{p^{\prime}(s)}\right)^{\prime\prime}\right|ds\right).\\ $$

(13)

Noticing that $\frac {F(s)}{p^{\prime }(s)}$ has zero points a and b, there is ζ₂ ∈ [a,b] making $\left (\frac {F(s)}{p^{\prime }(s)}\right )'\Big |_{s=\zeta _{2}}=0$ by Rolle’s mean value theorem. Then Lemma 2.1 in [20] tells

$$\left( \frac{F(s)}{p^{\prime}(s)}\right)'=\left( \frac{F(s)}{p^{\prime}(s)}\right)^{\prime\prime}\Big|_{s=\zeta_{3}}\left( s-\zeta_{2}\right) $$

for ζ₃ ∈ [a,b] if p(s) ∈ C³([a,b]). Taking s = b leads estimate (13) to

$$ \left|{{\int}_{a}^{b}}F(s)\cos(\omega p(s))ds\right|\leq C_{3}\left|\left|\left( \frac{F(s)}{p^{\prime}(s)}\right)^{\prime\prime}\right|\right|_{\infty}\frac{b-a}{\omega^{2}}:=C_{4}\left( \frac{b-a}{\omega^{2}}\right).\\ $$

(14)

This is in accordance with the result in [22]. We summarize the estimate (11) and (14) in Theorem 2.1.

Theorem 2.1

Assume that f(s) ∈ C²([a,b]), $p^{\prime }(s)\neq 0$ and f^(j)(s)(j = 0,1,2) is uniformly bounded for ω. The error by the generalized quadrature method $\hat {Q}(f;a,b)$ approximating Q(f;a,b) is given by

$$ E(f):=\left|Q(f;a,b)-\hat{Q}(f;a,b)\right|\leq \min \left\{C_{2}(b-a)^{3},C_{4}\frac{b-a}{\omega^{2}}\right\} $$

(15)

with $C_{2}=\frac {||F^{\prime \prime }(s)||_{\infty }}{2}$ and $C_{4}=(|\frac {1}{p^{\prime }(b)}|+|\frac {1}{p^{\prime }(a)}|+{{\int \limits }_{a}^{b}}|(\frac {1}{p^{\prime }(s)})'|ds)||(\frac {F(s)}{p^{\prime }(s)})^{\prime \prime }||_{\infty }$.

As indicated by Theorem 2.1, generalized quadrature could provide a satisfactory result when ω is large. And the accuracy will increase as ω increases.

3 The method and its convergence

3.1 The quadrature method for the equation

Firstly, we discretize the interval I with uniform mesh which is simple but not necessary

$$I_{h} := \left\{t_{n}:=nh,n=0,...,N,h \geq 0, Nh=T\right\}. $$

Then, VIE (2) at t = t_n can be written as

$$ y(t_{n})=g(t_{n})+\sum\limits_{i=0}^{n-1}{\int}^{t_{i+1}}_{t_{i}}K(t_{n},s)\cos (\omega p(s))y(s)ds. $$

(16)

Replacing the integrals on the right by the quadrature formula (3) and disregarding the quadrature errors obtains

$$ \begin{array}{@{}rcl@{}} y_{n}&=&g(t_{n})+\sum\limits_{i=0}^{n-1}\left( w_{1}^{(i)}K(t_{n},t_{i})y_{i}+w_{2}^{(i)}K(t_{n},t_{i+1})y_{i+1}\right)\\ &=&g(t_{n})+w_{1}^{(0)}K(t_{n},t_{0})y_{0}+\sum\limits_{i=1}^{n-1}\left( w_{1}^{(i)}+w_{2}^{(i-1)}\right)K(t_{n},t_{i})y_{i}\\ &&+w_{2}^{(n-1)}K(t_{n},t_{n})y_{n} \end{array} $$

(17)

where y_n is the approximation for y(t_n) and $w_{j}^{(i)}$ are the weights defined in (7) with a and b replaced by t_i and t_i+ 1 respectively, i.e.,

$$w_{1}^{(i)}=\frac{A_{1}^{(i)}}{A^{(i)}},\quad w_{2}^{(i)}=\frac{A_{2}^{(i)}}{A^{(i)}}$$

with

$$ \begin{array}{@{}rcl@{}} F^{(i)}&=& \left( t_{i+1}\sin(\omega p(t_{i+1}))+\frac{\cos (\omega p(t_{i+1}))}{\omega p^{\prime}(t_{i+1})}\right)-\left( t_{i}\sin(\omega p(t_{i}))+\frac{\cos (\omega p(t_{i}))}{\omega p^{\prime}(t_{i})}\right),\\ A^{(i)}&=&\frac{p^{\prime}(t_{i+1})p^{\prime\prime}(t_{i})}{p^{\prime}(t_{i})^{2}}-\frac{p^{\prime}(t_{i})p^{\prime\prime}(t_{i+1})}{p^{\prime}(t_{i+1})^{2}}+\omega^{2}hp^{\prime}(t_{i+1})p^{\prime}(t_{i}),\\ A_{1}^{(i)}&=&\left( -\frac{p^{\prime\prime}(t_{i+1})}{\omega p^{\prime}(t_{i+1})^{2}}+\omega p^{\prime}(t_{i+1})t_{i+1}\right)\left( \sin(\omega p(t_{i+1}))\right.\\ &&\left.-\sin(\omega p(t_{i}))\right)-\omega p^{\prime}(t_{i+1})F^{(i)},\\ A_{2}^{(i)}&=&\left( \frac{p^{\prime\prime}(t_{i})}{\omega p^{\prime}(t_{i})^{2}}-\omega p^{\prime}(t_{i})t_{i}\right)\left( \sin(\omega p(t_{i+1}))-\sin(\omega p(t_{i}))\right)+\omega p^{\prime}(t_{i})F^{(i)}.\\ \end{array} $$

When n = 1, the symbol ${\sum }_{i=1}^{n-1}$ in (17) means that this term does not exist.

According to (8) and p(t) ∈ C²(I), the weights meet $|w_{j}^{(i)}|\leq C_{5}h$. Since K(t,s) is continuous, there exists an $\bar {h}>0$ small enough such that

$$|w_{2}^{(n-1)}K(t_{n},t_{n})|\leq C_{5}h\hat{K}<1$$

for $h<\bar {h}$ with $\hat {K}:={\max \limits } |K(t,s)|$. Therefore, for n > 0 and $h<\bar {h}$, we have

$$ y_{n}=\frac{1}{1-w_{2}^{(n-1)}K(t_{n},t_{n})}\left( g(t_{n})+w_{1}^{(0)}K(t_{n},t_{0})y_{0}+\sum\limits_{i=1}^{n-1}\left( w_{1}^{(i)}+w_{2}^{(i-1)}\right)K(t_{n},t_{i})y_{i}\right).\\ $$

(18)

While for n = 0, we have y₀ = g(0) by letting t = 0 in (2).

3.2 The convergence

Theorem 3.1

Assume g(t) ∈ C²(I), p(t) ∈ C³(I), $p^{\prime }(t)\neq 0$ and K(t,s) ∈ C²(D). y_n is the numerical solution defined by (18). Let e_n := y(t_n) − y_n. Then, we can conclude that

$$ |e_{n}|=|y(t_{n})-y_{n}|\leq C\min \left\{h^{2},\frac{1}{\omega^{2}}\right\} $$

if y^(j)(t) (j = 0,1,2) is uniformly bounded for ω.

Remark 1

It can be seen that the quadrature method has asymptotic order 2 for ω ≫ 1 which means that the numerical solution will become more accurate as the increase of ω. In addition, the method also converges with order 2 as the decrease of step length in the final.

Proof

Subtracting (17) from (16) leads to

$$ \begin{array}{@{}rcl@{}} e_{n}&=&y(t_{n})-y_{n}\\ &=&\sum\limits_{i=0}^{n-1}{\int}^{t_{i+1}}_{t_{i}}K(t_{n},s)\cos (\omega p(s))y(s)ds-\sum\limits_{i=0}^{n-1}\left( w_{1}^{(i)}K(t_{n},t_{i})y_{i}+w_{2}^{(i)}K(t_{n},t_{i+1})y_{i+1}\right)\\ &=&\sum\limits_{i=0}^{n-1}\left( w_{1}^{(i)}K(t_{n},t_{i})e_{i}+w_{2}^{(i)}K(t_{n},t_{i+1})e_{i+1}\right)+R_{n}\\ &=&w_{1}^{(0)}K(t_{n},t_{0})e_{0}+\sum\limits_{i=1}^{n-1}\left( w_{1}^{(i)}+w_{2}^{(i-1)}\right)K(t_{n},t_{i})e_{i}+w_{2}^{(n-1)}K(t_{n},t_{n})e_{n}+R_{n}, \end{array} $$

(19)

with

$$ \begin{array}{@{}rcl@{}} R_{n}&=&\sum\limits_{i=0}^{n-1}{\int}^{t_{i+1}}_{t_{i}}K(t_{n},s)\cos (\omega p(s))y(s)ds\\ &&-\sum\limits_{i=0}^{n-1}\left( w_{1}^{(i)}K(t_{n},t_{i})y(t_{i})+w_{2}^{(i)}K(t_{n},t_{i+1})y(t_{i+1})\right)\\ &=&\sum\limits_{i=0}^{n-1}\left (Q(K(t_{n},s)y(s);t_{i},t_{i+1})-\hat{Q}(K(t_{n},s)y(s);t_{i},t_{i+1})\right). \end{array} $$

Obviously, e₀ = y(t₀) − y₀ = 0. Therefore, (19) gives

$$ \left|e_{n}\right|\leq \sum\limits_{i=1}^{n-1}2C_{5}h\hat{K}\left|e_{i}\right|+C_{5}h\hat{K}\left|e_{n}\right|+\left|R_{n}\right| $$

recalling the estimate of $w_{j}^{(i)}$ and $\hat {K}={\max \limits } |K(t,s)|$. Then we have, for suitable h,

$$ |e_{n}|\leq\frac{2C_{5}h\hat{K}}{1-C_{5} h\hat{K}}\sum\limits_{i=1}^{n-1}|e_{i}|+\frac{1}{1-C_{5} h\hat{K}}|R_{n}|. $$

The Gronwall inequality [1] implies that

$$ |e_{n}|\leq\frac{1}{1-C_{5} h\hat{K}}|R_{n}|\exp\left( \frac{2C_{5}\hat{K}}{1-C_{5} h\hat{K}}T\right). $$

(20)

For the estimate of |R_n|, we give the following procedure. Since g(t),p(t) ∈ C²(I) and K(t,s) ∈ C²(D), we conclude that y(t) ∈ C²(I) by Theorem 2.1.3 in [1]. Then, Theorem 2.1 tells

$$ \left|Q(K(t_{n},s)y(s);t_{i},t_{i+1})-\hat{Q}(K(t_{n},s)y(s);t_{i},t_{i+1})\right|\leq C_{6}\min \left\{h^{3},\frac{h}{\omega^{2}}\right\} $$

if y^(j)(s) (j = 0,1,2) is uniformly bounded for ω. Therefore, R_n has the estimate

$$ \begin{array}{@{}rcl@{}} \left|R_{n}\right|&\leq& \sum\limits_{i=0}^{n-1}\left|Q(K(t_{n},s)y(s);t_{i},t_{i+1})-\hat{Q}(K(t_{n},s)y(s);t_{i},t_{i+1})\right|\\ &\leq& C_{6}\min \left\{h^{2},\frac{1}{\omega^{2}}\right\}. \end{array} $$

Applying it to the estimate (20) implies

$$ |e_{n}|\leq C\min \left\{h^{2},\frac{1}{\omega^{2}}\right\} $$

which completes the proof. □

4 Numerical examples

The generalized quadrature method (GQ) is applied to some examples in this part to confirm its efficiency. We want to verify that the asymptotic order is 2 for ω ≫ 1 and the method converges with order 2 as h → 0. The errors with different N and ω are presented in tables. To see the classical order directly, we plot the pictures according to the first rows of the tables with ω = 100. In addition, the absolute errors scaled by ω², i.e., absolute errors multiplied by ω², are presented to show the asymptotic order with N = 2. If the scaled errors are bounded, the asymptotic order 2 could be verified by the definition.

Example 1

Consider the highly oscillatory VIE

$$y(t)=g(t)+{{\int}^{t}_{0}}e^{s}\cos (\omega s)y(s)ds,\quad t\in I:=[0,1], $$

with g(t) such that the exact solution is $y(t)=\cos \limits (t)$.

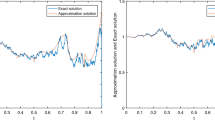
In Example 1, the oscillator p(s) = s takes a simple form and K(t,s) = e^s. The solution $y(t)=\cos \limits (t)$ satisfies Theorem 2.1. The numerical errors of the generalized quadrature method are presented in Table 1 and Fig. 1.

Table 1 $\max \limits _{1\leq n\leq N} |e_{n}|$ of the quadrature method for Example

Fig. 1

The classical order with ω = 100 and asymptotic order with N = 2 for Example 1

In Table 1, the errors decrease as h tends to 0 which means that the method is convergent. The classical order 2 could be seen from the left picture of Fig. 1. One may observe that the absolute errors in the table change slightly at first with ω = 400. This is not surprising because the term ω^− 2 dominates in the stage. The boundedness of the scaled errors in the right picture of Fig. 1 indicates that the asymptotic order is 2.

To show the superiority, we compare the generalized quadrature(GQ) method developed here with the trapezoid quadrature (TQ) method in [16]. The results are listed in Table 2. We can see that both of the methods converge with respect to step length. But the GQ method provides more accurate numerical results.

Table 2 Comparison of GQ and TQ with ω = 20 for Example

Example 2

Consider the highly oscillatory VIE

$$ y(t)=g(t)+{{\int}^{t}_{0}}\sin(s)\cos (\omega e^{-s})y(s)ds,\quad t\in I:=[0,1], $$

with g(t) such that the exact solution is y(t) = e^−t.

Here, the oscillator p(s) = e^−s and $p^{\prime }(s)= -e^{-s}\neq 0$. The numerical results are reported in Table 3 and Fig. 2.

Table 3 $\max \limits _{1\leq n\leq N} |e_{n}|$ of the quadrature method for Example 2

Fig. 2

The classical order with ω = 100 and asymptotic order with N = 2 for Example 2

According to the data in Table 3, we can infer the convergence of the method and its order could be seen by Fig. 2. The asymptotic order could be obtained from Fig. 2 as well. The same as Example 1, the numerical results are in accordance with Theorem 3.1.

Example 3

Consider VIE

$$ y(t)=g(t)+{{\int}^{t}_{0}}\cos (\omega s)y(s)ds,\quad t\in I:=[0,1], $$

with g(t) such that $y(t)=t+\frac {\cos \limits (\omega t)}{\omega ^{2}}$ which is oscillatory.

This example is conducted to show our method for VIE with oscillatory solution. It is clear that y^(j) (j = 0,1,2) is uniformly bounded. The corresponding errors in Table 4 and Fig. 3 are in good agreement with the analysis. These results imply that the method is also feasible for some VIEs with highly oscillatory solutions.

Table 4 $\max \limits _{1\leq n\leq N} |e_{n}|$ of the quadrature method for Example 3

Fig. 3

The classical order with ω = 100 and asymptotic order with N = 2 for Example 3

5 Conclusion

This paper proposed and analyzed a quadrature method for VIEs with oscillatory kernel. Our method does not need to compute the moment. The convergence rate with respect to frequency shows that the asymptotic order is two. As the decrease of step length, we also proved that the two-point quadrature method converges with classical order two. The numerical test in the last part verified its efficiency.