1. INTRODUCTION

Integral equations with oscillatory kernels have numerous applications in many fields of sciences and engineering like electrostatics, mechanics, fluid mechanics [1, 2], and many others. Among these, the Volterra integral equations (VIEs) with convolution type kernels are the most important (see, for example, [3–5] and references therein). For accurate computations of highly oscillatory integrals of convolution type, many methods have been developed over the years. In many cases, exact analytical solutions of such type integral equations with highly oscillatory kernels cannot be obtained in a closed form. Consequently, numerical methods may be a good alternative for efficient computation of such type of models (see, for example, [6, 7]). Some of the best numerical methods developed very recently can be found in [8–10]. The most important feature of such problems is the oscillation parameter \(\omega\gg 1\), which occurs in the kernel of integral equations and thus becomes extremely oscillatory. In that case, most of the standard collocation methods may face difficulty when applied to solving integral equations with large oscillations [8, 11–14].

First-kind Volterra integral equations of more general form that have been studied numerically in the past can be found in [6, 15–17]. The specially developed methods, where an integral is approximated, contain a large oscillation parameter. The computations of such integrals by quadrature methods are always difficult and require high costs [18, 19]. The Filon-type approximate methods have been proved to be the best for approximating integral equations with highly oscillatory kernels [11, 20–22]. More research is still needed to fully explore the oscillatory behavior of such oscillatory integral equations theoretically and numerically. In this study, the main objective is to approximate VIEs with highly oscillatory kernels of convolution type by a transform based method. The VIEs with highly oscillatory kernels considered in this study are defined by

$$\int\limits_{0}^{t} \kappa(x,t)e^{i \omega g(x,t)} F(x,y(x)) dx=f(t), ~~ t \in [0,T], $$
(0.1)

where \(\omega\) is the oscillation parameter, \(\kappa(x,t)\) and \(g(x,t)\) is the difference kernel and oscillator, respectively, \(f(t)\) is some smooth function, and \(F\) is an unknown nonlinear function. So, we replace the unknown nonlinear function by another unknown linear function and solve the new linear VIE with highly oscillatory kernels.

2. ANALYSIS OF THE METHOD FOR VOLTERRA INTEGRAL EQUATIONS

Suppose that \(y(t)\) is a function of the variable \(t\), for which the Laplace transform exists:

$$\mathscr{L}[y(t)]= \hat{y}(s)=\int\limits_{0}^{\infty} e^{-s t} y(t) dt,$$

and consequently its inverse Laplace transform also exists:

$$y(t) = \frac{1}{2\pi \iota} \int\limits_{c- \iota \infty}^{c+ \iota \infty} e^{s t}\hat{y}(s) ds.$$

A convolution type VIE can often be easily handled with the pair of Laplace transforms [23,24]. Let \(y(t)\) be the solution of VIE (0.1). Then its inverse transform \(\hat{y}\) is an extension in the space \(Z\) of a subset of the complex plane and is given by

$$\hat{y}: \mathcal{C} \backslash \Sigma_{\theta} \rightarrow Z, $$
(1.1)

where

$$\Sigma_{\theta} = \{s \in \mathcal{C} : | \arg(-s) | \leq \theta \},~~ 0< \theta < \frac{\pi}{2}, $$
(1.2)

and outside of this sector \(\Sigma_{\theta}\), the function \(\hat{y}(s)\) holds the condition

$$\ \|\hat{y}(s)\|= O(1/|s|). $$

Consequently, there exists a constant \(C_\theta >0\) such that

$$\|\hat{y}(s)\| \leq \frac{C_\theta}{|s|}, ~~s \in \mathcal{C} \backslash \Sigma_{\theta}. $$
(1.3)

So, the inversion Laplace transform formula is reduced to the form

$$y(t)=\frac{1}{2\pi \iota} \int\limits_{\Theta} e^{t s} \hat{y}(s)~ds, ~~t >0, $$
(1.4)

where the contour \(\Theta\) joins the limits \(c-\iota \infty\) and \(c+\iota \infty\). The parametric representation of the path \(\Theta\) is defined as \(\sigma:(a,b) \rightarrow \mathcal{C}\). So, \(y(t)\) is given by

$$y(t)= \frac{1}{2\pi \iota} \int\limits_{a}^{b} e^{t \sigma(x)} \hat{y}(\sigma(x)) \sigma^{\prime}(x)~dx, ~~ t>0. $$
(1.5)

The above integral is approximated by the classical technique [25,26], involving the equal width rule. So, for a given \(N \geq1\), \(h>0\), \(x_k = kh\), \(-N:k:N\), the solution \(y(t)\) of VIE (0.1) at any \(t > 0\) can be computed by the following numerical scheme:

$$y_N(t)= \frac{h}{2\pi \iota} \sum\limits_{k=-N}^{N} e^{t \sigma(x_k)} \hat{y}(\sigma(x_k)) \sigma^{\prime}(x_k), ~~ t>0. $$
(1.6)

For the computation of the inverse \(\hat{y}\) for the interval \((-\infty,+\infty)\), Talbot’s algorithm using the interval \((-\pi,\pi)\) and the modification using the interval \((a,b)\), are very helpful for finding the error estimates by the trapezoidal rule:

$$\int\limits_{-\infty}^{+\infty} q(x)~dx \simeq h \sum\limits_{k=-N}^{N} q(hk),~~ N \geq 1, ~~h>0. $$
(1.7)

We use (1.2) when selecting \(\theta\). Then for \(d>0\), \(\alpha\) can be chosen so that the following inequalities are satisfied:

$$d < \min\{ \pi/2-\alpha, \alpha \}~~ \mbox{and}~~ d+\alpha +\theta < \pi/2. $$
(1.8)

For the mapping \(\zeta(w)=-\sin(\alpha+\iota w)\), \(w= x+\iota Y\), it is easy to show that the transformation \(\zeta\) converted the horizontal path \(\mathrm{ Im}\, {w} = Y\), where \(-d < Y < d,\) into the left branch of the hyperbola in the following equation:

$$\left( \frac{ \mathrm{ Re}\,s}{\sin(\alpha-Y)} \right)^2 - \left( \frac{ \mathrm{ Im}\, s}{\cos(\alpha-Y)} \right)^2 =1.$$

Therefore, \(\zeta\) converted the stripe \(S_d\) to the left branches when \(Y = \pm d\). Let \(\lambda >0\), then we have the mapping

$$s=\sigma(w)= \lambda (1+\zeta(w)). $$
(1.9)

Consequently, \(\Theta\) is obtained in its parametric form and we can compute the following:

$$y(t) = \int\limits_{-\infty}^{+\infty} Q_t (x)~dx,~~ t>0,$$

where the mapping \(Q_t : S_d \rightarrow X\), \(t>0\), is defined by

$$Q_t(w)= \frac{1}{2\pi \iota} \exp(t\sigma(w))\hat{y}(\sigma(w))\sigma^{\prime}(w).$$

The main advantage of numerical scheme (1.6) is its non-oscillatory nature, which can be computed very easily and accurately. Another advantage is that the approximate solution \(u(t)\) at different times and its transform \(\hat{y}\) when \(- N:k:N\) can be computed very efficiently in parallel. Once the optimal parameters are chosen for the selected path \(\sigma\), we can maintain a uniform error over the time interval \([t_0,\wedge t_0]\) with moderate \(\ \wedge \geq 1\), for any time \(t \in (t_0, T)\), where \(T=\wedge t_0\), \(t_0 \geq 0 \) [27].

2. NUMERICAL EXAMPLES AND APPLICATION

Fig. 1
figure 1

Numerical solution of Problem 1: actual and estimated errors against \(N\) and \(\omega\) and comparison of exact and numerical solution.

Full size image
Fig. 2
figure 2

Numerical solution of Problem 2: actual and estimated errors against \(N\) and \(\omega\) and comparison of exact and numerical solution.

Full size image
Fig. 3
figure 3

Numerical solution of Problem 3: actual and estimated errors against \(N\) and \(\omega\), and comparison of exact and numerical solution.

Full size image

The constructed numerical scheme is applied both for linear and nonlinear Volterra integral equations (0.1) with highly oscillatory kernels. The method has been tested in terms of error versus quadrature nodes and error versus oscillation parameters and was also compared with other methods. The above hyperbolic contour has been derived in the following form:

$$\sigma(x_k)= \eta + \lambda (1-\sin(\alpha-\iota x_k)). $$
(2.1)

For the best accuracy of all computations, the following optimized shape parameters, corresponding to the hyperbolic path defined above, can be used: \(\eta=2\), \(\alpha= 0.3812\), \(\lambda=\frac{\delta r_b N}{\varepsilon T}\), \(x_k=hk\), with \(\delta =0.1\), \(r_b=2\pi r\), \(r=0.3431\), \(x_k=hk\), \(\varepsilon=\cosh^{-1}(\frac{1}{\delta \tau \sin(\alpha)})\), \(h=\varepsilon/N\), \(\tau=t_0/T\), \(t_0=0.1\), \(T=5\).

Theorem 1 [28]. The unique solution of a first-kind VIE with the linear operator

$$\int\limits_{0}^{t} \kappa(t-x) e^{i\omega(t-x)}y(x) dx=f(t), ~~ t\in [0,T], $$
(2.2)

is given by

$$y(t)=f^{\prime}(t)+\int\limits_{0}^{t}r_1(t-x)e^{i\omega(t-x)} f^{\prime}(x)dx -i\omega\left( f(t)+\int\limits_{0}^{t}r_1(t-x)e^{i\omega(t-x)}f(x)dx \right), $$
(2.3)

where \(r_1(t-x)=\kappa^{\prime}(t-x)\) and it is assumed that \(\kappa(0)=1\).

Problem 1. We consider VIE (0.1) for the following functional:

$$\int\limits_{0}^{t} (1+t-x)e^{i \omega (t-x)} y(x) dx=t,~~ t \in [0,T], $$
(2.4)

where the exact solution can be obtained from (2.3):

$$y(t)=1-\frac{1}{(i \omega-1)^2}-\frac{(i \omega)^2 t}{(i \omega-1)}+\frac{e^{i (\omega-1)t}}{(i \omega-1)^2}. $$
(2.5)

The numerical solution of VIE (2.4) for various values of parameters involved is obtained by the present numerical scheme and shown in Fig. 1. The actual error and error estimate \(e^{\frac{-c N}{\ln N}}\) of the numerical scheme with \(c=1\) are in good agreement when \(5 < N< 10^2\). Figure 1 also shows the actual error versus the parameter \(\omega\); one can see high accuracy with \(1< \omega <10\), a sudden drop in the accuracy, then a gradual increase in the accuracy for \(10 < \omega < 10^5\), and then a gradual decrease in the accuracy when \(\omega > 10^5\). Figure 1 also indicates that for highly oscillatory kernels, the solution is non-oscillatory.

Problem 2. We consider VIE (0.1) in the following form:

$$\int\limits_{0}^{t} e^{i \omega (t-x)} \ln(y(x)) dx = \sinh{t}, ~~ t \in [0,T]. $$
(2.6)

Let \(v(x)=\ln(y(x))\). We perform the Laplace transform and get the solution

$$v(t)=\left(e^{-t}(i w+1)/2-e^{t}(iw+1)/2\right). $$
(2.7)

The exact solution of the problem is defined by

$$y(t)=\exp\left(v(t)\right)=\exp\left(e^{-t}(i w+1)/2-e^{t}(iw+1)/2\right). $$
(2.8)

We have solved this problem by the present method for various values of quadrature nodes along the hyperbolic contour and oscillation parameter. The results are shown in Fig. 2. Figure 2 presents a comparison of the actual error and the error estimate \(e^{\frac{-c N}{\ln N}}\) for \(c=1\) of the numerical scheme for various quadrature nodes; the actual and estimated errors are in good agreement when \(1<N < 10^2\). It is worth noting that the solution in this case is oscillatory and the accuracy decreases with increase in the oscillation parameter \(\omega\).

Problem 3. In this problem, we consider the following VIE integral equation:

$$\int\limits_{0}^{t} cos(t-x) e^{i \omega (t-x)} y^2(x) dx= f(t), ~~ t \in [0,T]. $$
(2.9)

Let \(\ v(x)=y^{2}(x)\). Performing the Laplace transform, we get the solution

$$v(t)={g_1(t)+g_2(t)-g_3(t)-g_4(t)}. $$
(2.10)

The exact solution of this problem is defined by

$$y(t)=\sqrt{v(t)}=\sqrt{g_1(t)+g_2(t)-g_3(t)-g_4(t)}, $$
(2.11)
$$g_1(t)= \sin{t}+t \cos{t}-i \omega t \sin{t}, \quad g_2(t)=\frac{2i\omega e^{i\omega t}}{(-\omega^2+1)^2},$$
$$g_3(t)=\frac{-2\omega^2\sin(t)+2i\omega\cos(t)}{(-\omega^2+1)^2}, \quad g_4(t)= \frac{t \cos(t)-\sin(t)+i\omega t \sin(t)}{(-\omega^2+1)}.$$

The problem is solved for various quadrature nodes \(N\) with the varying oscillation parameter \(\omega\); the results are shown in Fig. 3. The solution of this problem is non-oscillatory; it can be seen in Fig. 3, where the accuracy increases with growth of the oscillation parameter. The actual error and error estimates are well comparable in a certain range of quadrature nodes.

Problem 4. In the last problem we consider the following linear integral equation with highly oscillatory kernels:

$$y(t)+\int\limits_{0}^{t} \frac{e^{i\omega(t-x)}}{{(t-x)^{\alpha}}}y(x)dx=e^{t}, $$
(2.12)

where \(\omega\) is the oscillation parameter, \(0 < \alpha < 1\), and the exact solution is given by

$$y(t)=e^{t}+\int\limits_{0}^{t}r(t-x)e^{x}dx, $$
(2.13)

where the function \(r(x)\) is defined by

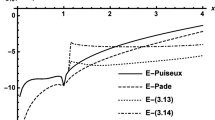
$$r(x)=e^{i\omega x}\sum\limits_{n=1}^{\infty}\frac{(-\Gamma(1-\alpha)x^{1-\alpha})^n}{x\Gamma(n(1-\alpha))}. $$
(2.14)

This particular problem is selected for comparison of the results of the present numerical scheme with the results of other methods. The numerical and exact solutions of this problem at different times are shown in Table 1. Values for various other quadrature nodes \(N\) and increasing values of the oscillation parameter \(\omega\) are shown in Table 2. In comparison, the present numerical method performed better than the method discussed in [29].

Table 1. Approximate solution of Problem 4 at \(\alpha =0.5\) and \(\omega=10^4\) by present method
Full size table
Table 2. Approximate solution of Problem 4 at \(\alpha =0.5\), \(\omega=10^4\), and \(t=0.91\) and error = \(|y_{ap}-y_{ex}|\) by present method
Full size table

3. CONCLUSIONS

Solving linear and nonlinear Volttera integral equations with highly oscillatory kernels is a challenging task due to the presence of oscillation parameter in the VIE kernels, particularly so when these VIEs have oscillatory solutions. The numerical algorithms developed over the years for computing the inverse Laplace transform are mostly less accurate and ill-conditioned (see, for example, [31,31] and the references therein). However, the present numerical method, which is based on computing the inverse Laplace transform formula numerically, performed well. We applied the numerical scheme for linear and some nonlinear VIEs with highly oscillatory kernels and obtained results of very high order accuracy. The actual error and the error bound of the numerical scheme are in very good agreement over a range of quadrature nodes. The present numerical scheme is a very good alternative for similar types of VIEs with highly oscillatory kernels.