A class of new Magnus-type methods for semi-linear non-commutative Itô stochastic differential equations

Abstract

In this paper, a class of new Magnus-type methods is proposed for non-commutative Itô stochastic differential equations (SDEs) with semi-linear drift term and semi-linear diffusion terms, based on Magnus expansion for non-commutative linear SDEs. We construct a Magnus-type Euler method, a Magnus-type Milstein method and a Magnus-type Derivative-free method, and give the mean-square convergence analysis of these methods. Numerical tests are carried out to present the efficiency of the proposed methods compared with the corresponding underlying methods and the specific performance of the simulation Itô integral algorithms is investigated.

1 Introduction

It is now generally accepted that stochastic differential equations (SDEs) can describe some problems more accurately than deterministic differential equations. For example, input data may be uncertain or systems may be subject to internal or external random fluctuations. It is often difficult to obtain explicit expressions of exact solutions for SDEs and so numerical methods become an important tool to provide good approximations.

In this paper, our main focus is the numerical approximations of the semilinear Itô SDEs

$$ \quad \mathrm{d} y=(A_{0} y+g_{0}(y)) \mathrm{d} t+\sum\limits_{i=1}^{m}\left( A_{i} y+g_{i}(y)\right) \mathrm{d} W_{i}(t), \quad y(0)=y_{0} \in \mathbb{R}^{\mathrm{d}}, $$

(1)

where W_j(t), j = 1,…,m, are independent Wiener processes on a complete probability space $({\varOmega }, \mathcal {F}, \mathbb {P})$ with a filtration $\left \{\mathcal {F}_{t}\right \}_{t>0}$ satisfying the usual conditions. Here g_j: $\mathbb {R}^{d} \rightarrow \mathbb {R}^{d}$, j = 1,…,m, are nonlinear functions of y and $A_{j} \in \mathbb {R}^{d \times d}$, j = 0,…,m, are constant matrices. The random initial value satisfies $\mathbb {E}\left \|y_{0}\right \|^{2}<\infty$ and $\mathbb {E}$ is the expectation.

Numerical integrators for (1) in the sense of Itô and Stratonovich are thoroughly studied in [1] based on the stochastic Runge–Kutta Lawson methods under the following commutative conditions

$$ \left[A_{l}, A_{k}\right]=A_{l} A_{k}-A_{k} A_{l}=0 \quad { \mathrm{for~ all} } \quad l, k=0,1, \ldots, m, $$

(2)

where [A,B] = AB − BA is called the Lie-product or matrix commutator of A and B. Under this commutative condition, Euler and Milstein versions of exponential methods are investigated in [2], and the strong convergence analysis of these two methods is given. Their numerical results show that these exponential methods are more effective than the corresponding underlying methods. Under similar commutative conditions, Yang, Burrage and Ding [3] investigate (1) in the sense of Stratonovich and construct structure-preserving stochastic exponential Runge–Kutta methods to the case of time independent matrix A₀ = A(t), A_k = 0, k = 1,…,m. There is also some interesting work on the exact solution and the corresponding numerical solution under the commutative condition where A₀ is a constant matrix and A_k = 0, k = 1,…,m. For example, an exponential Euler method is constructed for the stiff problem and it is applied to solve an ion channel model in [4]. A class of weak second-order exponential Runge–Kutta methods is investigated for non-commutative SDEs in [5].

It is worth noting that when the commutative condition is not established, even the solution of the linear system cannot be expressed explicitly. We know that Magnus gave the deterministic Magnus expansion [6] in 1954, which expresses the solution as an exponential infinite matrix series. This topic has been further studied in [7,8,9]. In recent years, the Magnus-type expansion for SDEs has attracted an increasing number of researchers. The Magnus expansion for linear autonomous Stratonovich SDEs was derived by Burrage and Burrage [10]. They compare the truncated Magnus expansion with stochastic Runge–Kutta methods with the same convergence order and concluded that the Magnus expansion enjoys a considerably smaller error coefficient. The authors of [11] consider the Magnus expansion for the linear and nonlinear Stratonovich SDEs and the convergence analysis is given based on binary rooted trees. In [12] a new explicit Magnus expansion is applied to solve a class of Stratonovich SDEs and the authors show that the Magnus expansion can preserve the positivity of the solution. A new version of Magnus expansion for linear Itô SDEs is derived in [13] and the authors have analyzed the convergence of the Magnus expansion and applied it to solve semi-discrete stochastic partial differential equations (SPDEs). In [14], for SPDEs driven by multiplicative noise, the authors first use the finite element method to discretize space, and then construct a Magnus-type method in the time direction.

We have to say that when the commutative condition is not established, the corresponding theoretical results on exponential numerical methods for the corresponding semi-linear problem are sparse. This is the motivation for us to consider a new class of Magnus-type integrators for the semi-linear problem (1).

The structure of this paper is organized as follows. In Section 2, we will give a brief review of the use of the Magnus formula in both linear non-autonomous ordinary differential equations (ODEs) and linear SDEs. In Section 3, we will derive a new class of Magnus-type integrators for the semi-linear problem (1) by the application of the Magnus expansion for linear non-commutative SDEs. In Section 4, we will give the results of the mean-square convergence analysis of the Magnus-type methods proposed in Section 3. In Section 5, we will compare three algorithms for simulating iterated Itô integrals and some details of numerical implementation will be presented on low-dimensional SDEs and a high-dimensional SDE obtained from a discretized SPDE, which illustrate the efficacy of Magnus-type methods.

2 Magnus formula

In this section we will briefly review the Magnus formula in both a linear deterministic setting and a linear stochastic setting.

2.1 Magnus formula for linear non-autonomous ODEs

Consider the non-autonomous linear initial value problem

$$ Y^{\prime}(t)=A(t) Y(t), t \geq 0, \quad Y(0)=Y_{0} \in \mathbb{R}^{\mathrm{d}\times\mathrm{d}}. $$

(3)

This problem is investigated in [6] where the d × d matrix A(t) is non-commutative. The solution is given in the form

$$ Y(t)=\exp\left( {{\varOmega}\left( 0,t\right)}\right) Y_{0}, $$

(4)

where ${\varOmega }\left (0,t\right )$ is the combination of integrals and nested Lie brackets of A, i.e.,

$$ \begin{array}{ll} {\varOmega}(0,t)=& {{\int}_{0}^{t}} A\left( s_{1}\right) \mathrm{d} s_{1}+\frac{1}{2} {{\int}_{0}^{t}}\left[A\left( s_{1}\right), {\int}_{0}^{s_{1}} A\left( s_{2}\right) \mathrm{d} s_{2}\right] \mathrm{d} s_{1} \\ &+\frac{1}{4} {{\int}_{0}^{t}}\left[A\left( s_{1}\right), {\int}_{0}^{s_{1}}\left[A\left( s_{2}\right), {\int}_{0}^{s_{2}} A\left( s_{3}\right) \mathrm{d} s_{3}\right] \mathrm{d} s_{2}\right] \mathrm{d} s_{1}+\cdots. \end{array} $$

For this problem, the Magnus expansion has received some attention in the past few decades, see [15].

2.2 Magnus formula for linear SDEs

We consider autonomous linear SDE given by

$$ \mathrm{d} Y(t)=\sum\limits_{j=0}^{m} A_{j} Y(t) \mathrm{d} W_{j}(t), \quad Y(0)=I \in \mathbb{R}^{\mathrm{d}\times\mathrm{d}}, $$

(5)

where W₀(t) = t. The d ×d matrices A_j are constant and I is the identity d ×d-matrix. When the commutative condition (2) is satisfied, the exact solution of (5) can be expressed explicitly by

$$ Y(t)=\exp \left( \left( A_{0}-\gamma^{\ast} \sum\limits_{i=1}^{m} {A_{i}^{2}}\right)t+\sum\limits_{i=1}^{m} A_{i}W_{i}(t)\right), $$

where $\gamma ^{\ast }=\frac {1}{2}$. When the commutative condition is not established, the solution of (5) cannot be expressed explicitly. The solution to (5) is given in the form $Y(t)=\exp ({\varOmega }(0,t))I$ by Kamm and his coauthors [13] in the Itô setting. Here we apply the relationship between Itô and Stratonovich integrals [17] to obtain the expansion of the Itô case through Ω(0,t) given by Burrage and Burrage [10] in the Stratonovich setting,

$$ \begin{array}{ll} {\varOmega}(0,t) =& \sum\limits_{j=0}^{m} \hat{A}_{j} {{\int}_{0}^{t}}\mathrm{d}W_{j}\\ &+\frac{1}{2} \sum\limits_{i=0}^{m} \sum\limits_{j=i+1}^{m}\left[\hat{A}_{i}, \hat{A}_{j}\right]\left( {{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{j}\mathrm{d}W_{i}-{{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{i}\mathrm{d}W_{j}\right) \\ &+\sum\limits_{i=0}^{m} \sum\limits_{k=0}^{m} \sum\limits_{j=k+1}^{m}\left[\hat{A}_{i},\left[\hat{A}_{j}, \hat{A}_{k}\right]\right]\left\{\frac{1}{3}\left( \left( {{\int}_{0}^{t}}{{\int}_{0}^{s}}{\int}_{0}^{s_{1}}\mathrm{d}W_{k}\mathrm{d}W_{j}\mathrm{d}W_{i}\right.\right.\right. \\ &+\left.\left.\left.\gamma^{\ast} I_{(j=i\neq 0)}{{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{k}\mathrm{d}W_{0}\right)\right.\right. \left.-\left( {{\int}_{0}^{t}}{{\int}_{0}^{s}}{\int}_{0}^{s_{1}}\mathrm{d}W_{j}\mathrm{d}W_{k}\mathrm{d}W_{i}\right.\right. \\ &+\left.\left.\gamma^{\ast} I_{(k=i\neq 0)}{{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{j}\mathrm{d}W_{0}\right)\right)\\ &+\left.\frac{1}{12}{{\int}_{0}^{t}}\mathrm{d}W_{i}\left( {{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{j}\mathrm{d}W_{k}-{{\int}_{0}^{t}}{{\int}_{0}^{s}}\mathrm{d}W_{k}\mathrm{d}W_{j}\right)\right\}+\cdots, \end{array} $$

(6)

where $\hat {A}_{0}=A_{0}-\gamma ^{\ast }{\sum }_{j=1}^{m}{A_{j}^{2}}$ and $\hat {A}_{j}=A_{j},~j\geq 1$. In the rest of this paper, we denote the iterated Itô integral as

$$ I_{i j}\left( t_{n}, t_{n}+h\right)={\int}_{t_{n}}^{t_{n+h}} {\int}_{t_{n}}^{s} \mathrm{d} W_{i}(s_{1}) \mathrm{d} W_{j}(s),~i,j\geq1. $$

(7)

The relationship between Itô and Stratonovich integrals [17] is

$$ \begin{aligned} J_{\alpha}=& I_{\alpha}, & & l(\alpha)=0 \text { or } 1, \\ J_{\alpha}=& I_{\alpha}+\frac{1}{2} I_{\left\{j_{1}=j_{2} \neq 0\right\}} I_{0}, & & l(\alpha)=2, \\ J_{\alpha}=& I_{\alpha}+\frac{1}{2}\left( I_{\left\{j_{1}=j_{2} \neq 0\right\}} I_{\left( 0, j_{3}\right)}+I_{\left\{j_{2}=j_{3} \neq 0\right\}} I_{\left( j_{1}, 0\right)}\right), & & l(\alpha)=3, \end{aligned} $$

where l(α) is the length of the index α and I_A is the indicator function, i.e., I_A = 1 if A is true, otherwise I_A = 0. The expansion (6) can also be obtained through the expansion rules in [13] and the convergence of the Magnus expansion for (5) is given by the following lemma.

Lemma 1

[13] LetA₀,A₁,…,A_m be constant matrices. For T > 0 let $Y=\left (Y({t})\right )_{t \in [0, T]}$ be the solution to (5) in the Itô case. There exists a strictly positive stopping time τ ≤ T such that:

• (i) Y (t) has a real logarithm ${\varOmega }(0,t) \in \mathbb {R}^{\mathrm {d\times d}}$ up to time τ, i.e.,

  $$ Y({t})=e^{{\varOmega}(0,t)}, \quad 0 \leq t<\tau; $$

• (ii) the following representation holds $\mathbb {P}$-almost surely:

  $$ {\varOmega}(0,t)={\sum}_{n=0}^{\infty} {\varOmega}^{[n]}(0,t), \quad 0 \leq t<\tau, $$

  where Ω^[n](0,t) is the n th term in the stochastic Magnus expansion (6);

• (iii) there exists a positive constant C, only dependent on $\left \|A_{0}\right \|, \ldots ,~\left \|A_{m}\right \|,~T$ and d, such that

  $$ \mathbb{P}(\tau \leq t) \leq C t, \quad t \in[0, T]. $$

3 A class of new Magnus-type methods for semi-linear SDEs

We shall now derive Magnus-type methods of mean-square order 1/2 and 1.0 for semi-linear SDEs (1). Throughout this paper, consider a partition t₀ = 0 < t₁ < ⋯ < t_N = T of the interval [0,T] with constant step size h = t_j − t_j− 1, j = 1,⋯ ,N, and let y_n be the approximation of exact solution. To make sure of the existence of the unique solution of (1), we first give the following important result.

Theorem 1

[16] There exists a constant L > 0 such that the global Lipschitz condition holds: for $y,~z\in \mathbb {R}^{d},$

$$ |g_{0}(y)-g_{0}(z)| +\sum\limits_{i=1}^{m} |g_{i}(y)-g_{i}(z)|\leq L|y-z|. $$

Then there exists a unique solution y(t) to (1).

Here we only require the Lipschitz condition as the linear growth condition

$$ |g_{0}(y)|^{2}+\sum\limits_{i=1}^{m}\left|g_{i}(y)\right|^{2} \leq L\left( 1+|y|^{2}\right) ~\text{for}~y \in \mathbb{R}^{d},$$

is automatically satisfied from the Lipschitz condition in the autonomous case, see [18].

For the semi-linear Itô SDEs (1), we assume that the exact solution has the form

$$ y(t)=Y(t)\tilde{y}(t), $$

(8)

where Y (t) is the solution of the linear equation (5), and $\tilde {y}(t)$ is to be determined. Using the Itô chain rule to y(t), we have

$$ \begin{aligned} \mathrm{d}y = (\mathrm{d}Y)\tilde{y}+Y\mathrm{d}\tilde{y}+dY\mathrm{d}\tilde{y} =\sum\limits_{j=0}^{m}A_{j}Y\tilde{y}\mathrm{d}W_{j}+ Y\mathrm{d}\tilde{y}+\mathrm{d}Y\mathrm{d}\tilde{y}. \end{aligned} $$

(9)

Comparing this with (1) shows that (8) is a solution of (1) if and only if

$$ \begin{array}{@{}rcl@{}} Y\mathrm{d}\tilde{y} &=&g_{0}(y)\mathrm{d}t-\mathrm{d}Y\mathrm{d}\tilde{y}+\sum\limits_{j=1}^{m}g_{j}(y)\mathrm{d}W_{j}. \end{array} $$

So, $\mathrm {d}\tilde {y}$ has the form

$$ \begin{array}{@{}rcl@{}} \mathrm{d}\tilde{y}&=&\exp(-{\varOmega}(0,t))(g_{0}(y)\mathrm{d}t-\mathrm{d}Y\mathrm{d}\tilde{y})+\sum\limits_{j=1}^{m}\exp(-{\varOmega}(0,t))g_{j}(y\mathrm{)d}W_{j}. \end{array} $$

Since

$$ \begin{array}{@{}rcl@{}} \mathrm{d}Y\mathrm{d}\tilde{y}&=&\sum\limits_{j=1}^{m}A_{j}g_{j}(y)\mathrm{d}t, \end{array} $$

then we get

$$ \begin{aligned} y(t)=&\exp({\varOmega}(0,t))(y(0)+{{\int}_{0}^{t}}\exp(-{\varOmega}(0,s))\tilde{g}_{0}(y(s))\mathrm{d} s\\ &+\sum\limits_{j=1}^{m}{{\int}_{0}^{t}}\exp(-{\varOmega}(0,s))g_{j}(y(s)) \mathrm{d} W_{j}(s)), \end{aligned} $$

(10)

where $\tilde {g}_{0}=g_{0}-{\sum }_{j=1}^{m}A_{j}g_{j}$.

It needs to be said that this transformation is also applicable to the case where the A_j(t) depend on time t, that is, the non-autonomous case, but this paper focuses on the case of (1). Numerical methods will be derived by using this form. Different approximations to the integrals in the above equation will yield different numerical schemes, and we will consider Magnus-type Euler (ME) and Magnus-type Milstein (MM) methods.

3.1 Magnus-type Euler method

If the integrals in (10) are approximated as follows

$$ \begin{aligned} &\exp({\varOmega}(t_{n},t_{n+1})){\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}(t_{n},s))g_{j}(y) \mathrm{d} W_{j}(s)\\ \approx&~ \exp({\varOmega}^{[1]}(t_{n},t_{n+1}))g_{j}(y_{n}){\varDelta} W_{jn},~j=1,\ldots,m, \end{aligned} $$

where ${{\varOmega }}^{[1]}(t_{n},t_{n+1})= {\sum }_{j=0}^{m} {\hat {A}}_{j} {\int \limits }_{t_{n}}^{t_{n+1}}\mathrm {d}W_{j},$ ΔW_jn = W_j(t_n+ 1) − W_j(t_n), j ≥ 1, ΔW_0n = t_n+ 1 − t_n, the following ME method is obtained,

$$ y_{n+1}=\exp({\varOmega}^{[1]}(t_{n},t_{n+1}))\left( y_{n}+\tilde{g}_{0}(y_{n})h+\sum\limits_{j=1}^{m}g_{j}(y_{n}){\varDelta} W_{jn}\right). $$

(11)

In particular, when g_j = 0, j ≥ 1, and if

$$\exp({{\varOmega}}^{[2]}(t_{n},t_{n+1}))= \sum\limits_{j=0}^{m} \hat{A}_{j} {\int}_{t_{n}}^{t_{n+1}}\mathrm{d}W_{j}+\frac{1}{2} \sum\limits_{i=1}^{m} \sum\limits_{j=i+1}^{m}\left[\hat{A}_{i}, \hat{A}_{j}\right]\left( I_{ji}-I_{ij}\right) $$

is selected instead of $\exp ({{\varOmega }}^{[1]}(t_{n},t_{n+1}))$, the resulting numerical scheme is mean-square 1 order convergent, which is actually a special case of the MM methods that we will give below. Next, we choose a higher order approximation for the diffusion terms, and then we obtain the MM method.

3.2 Magnus-type Milstein method

Note that $\hat {Y}(t)=\exp \left (-{\varOmega }\left (t_{n}, t\right )\right )$ is the solution of the following linear Itô SDE,

$$ \mathrm{d} \hat{Y}(t)=\left( -A_{0}+\sum\limits_{j=1}^{m} {A_{j}^{2}}\right) \hat{Y}(t) \mathrm{d} t-\sum\limits_{j=1}^{m} A_{j} \hat{Y}(t) \mathrm{d} W_{j}(t), \quad \hat{Y}\left( t_{n}\right)=I. $$

(12)

Applying the Itô–Taylor theorem to the stochastic integral

$$ \begin{aligned} &{\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}(0,s))g_{j}(y) \mathrm{d} W_{j}(s)\\ =&{\int}_{t_{n}}^{t_{n+1}}\left( g_{j}(y_{n})+{\int}_{t_{n}}^{s}\left( (\mathrm{d}\hat{Y})g_{j}(y)+\hat{Y}\mathrm{d}g_{j}(y)+\mathrm{d}\hat{Y}\mathrm{d}g_{j}(y)\right)\right)\mathrm{d} W_{j}(s)\\ =&{\int}_{t_{n}}^{t_{n+1}}\left( g_{j}(y_{n})+{\int}_{t_{n}}^{s}\left( (-A_{0}+\sum\limits_{l=1}^{m}{A_{l}^{2}})\hat{Y}g_{j}(y)\mathrm{d}t-\sum\limits_{l=1}^{m}A_{l}\hat{Y}g_{j}(y)\mathrm{d}W_{l}(s_{1})\right.\right.\\ &\left.\left.+\hat{Y}g_{j}^{\prime}(y)\left( (A_{0}y+g_{0}(y))\mathrm{d}t+\sum\limits_{l=1}^{m}(A_{i}y+g_{i}(y))\mathrm{d}W_{l}(s_{1})\right)\right.\right.\\ &\left.\left.+\frac{1}{2}\hat{Y}\sum\limits_{l=1}^{m}g_{j}^{\prime\prime}(A_{l}y+g_{l}(y),A_{l}y+g_{l}(y))\mathrm{d}t+\mathrm{d}\hat{Y}\mathrm{d}g_{j}(y)\right)\right)\mathrm{d}W_{j}(s)\\ =&{\int}_{t_{n}}^{t_{n+1}}\left( g_{j}(y_{n}) + {\int}_{t_{n}}^{s}\!\left( \sum\limits_{l=1}^{m}(\!-A_{l}g_{j}(y_{n}) + g_{j}^{\prime}(y_{n})(A_{l}y_{n} + g_{l}(y_{n}))\right)\mathrm{d}W_{l}(s_{1})\right)\mathrm{d}W_{j}(s)\\ &+h.o.t. \end{aligned} $$

Then we obtain the MM scheme

$$ \begin{aligned} y_{n+1}=&\exp({\varOmega}^{[2]}(t_{n},t_{n+1}))\left( y_{n}+\tilde{g}_{0}(y_{n})h+\sum\limits_{j=1}^{m}g_{j}(y_{n}){\varDelta} W_{jn}\right.\\ &\left.+\sum\limits_{j,l=1}^{m}\mathbf{H}_{j,l}\left( y_{n}\right)I_{lj}\right), \end{aligned} $$

(13)

where

$$\mathbf{H}_{j l}(y_{n})={g}_{j}^{\prime}(y_{n})\left( A_{l} y_{n}+{g}_{l}(y_{n})\right)-A_{l} {g}_{j}(y_{n}).$$

As a particular example, we apply the MM method to solve the damped nonlinear Kubo oscillator (21) in Section 5 with m = 2, ω₀ = ω₁ = ω₂ = 1, β₀ = − 1, β₁ = − 1/2, β₂ = 0 and α = 0. It is

$$ y_{n+1}=\exp({\varOmega}^{[2]}(t_{n},t_{n+1}))\left( y_{n}+\tilde{g}_{0}(y_{n})h+\sum\limits_{j=1}^{2}g_{j}(y_{n}){\varDelta} W_{jn}+\sum\limits_{j,l=1}^{2}\mathbf{H}_{j, l}\left( y_{n}\right) I_{lj}\right), $$

where

$$\begin{aligned} \tilde{g}_{0}(y_{n})&=g_{0}(y_{n})-\left( \begin{array}{cc} 0 &-1 \\ 1& -1/2 \end{array} \right)g_{1}(y_{n})-\left( \begin{array}{cc} 0 &-1 \\ 1& 0 \end{array} \right)g_{2}(y_{n}),\\ H_{11}(y_{n})&=g_{1}^{\prime}(y_{n})\left( \left( \begin{array}{cc} 0 &-1 \\ 1& -1/2 \end{array} \right)y_{n}+g_{1}(y_{n})\right)-\left( \begin{array}{cc} 0 &-1 \\ 1& -1/2 \end{array} \right)g_{1}(y_{n}),\\ H_{12}(y_{n})&=g_{1}^{\prime}(y_{n})\left( \left( \begin{array}{cc} 0 &-1 \\ 1& 0 \end{array} \right)y_{n}+g_{2}(y_{n})\right)-\left( \begin{array}{cc} 0 &-1 \\ 1& 0 \end{array} \right)g_{1}(y_{n}),\\ H_{21}(y_{n})&=g_{2}^{\prime}(y_{n})\left( \left( \begin{array}{cc} 0 &-1 \\ 1& -1 \end{array} \right)y_{n}+g_{1}(y_{n})\right)-\left( \begin{array}{cc} 0 &-1 \\ 1& -1 \end{array} \right)g_{2}(y_{n}),\\ H_{22}(y_{n})&=g_{2}^{\prime}(y_{n})\left( \left( \begin{array}{cc} 0 &-1 \\ 1& 0 \end{array} \right)y_{n}+g_{2}(y_{n})\right)-\left( \begin{array}{cc} 0 &-1 \\ 1& 0 \end{array} \right)g_{2}(y_{n}). \end{aligned}$$

As seen above, the disadvantage of the MM method is that a large number of derivatives and matrix operations need to be calculated for each step as the number of the nonlinear noise terms increases, which greatly reduces the efficiency of the method. From this point, it is natural to think of a Magnus-type Derivative-free (MDF) method, that is, use finite differences instead of these derivatives.

3.3 Magnus-type Derivative-free method

The MDF method can be derived from the MM method by replacing these derivatives with finite differences,

$$ {g}_{j}^{\prime}(y_{n})(A_{l} y_{n}+{g}_{l}(y_{n}))\approx \frac{g_{j}(Y_{l})-g_{j}(y_{n})}{\sqrt{h}}, $$

where

$$Y_{l} =y_{n}+hg_{0}(y_{n})+\sqrt{h}(A_{l}y_{n}+g_{l}(y_{n})),~l=1,2,\ldots,m.$$

We obtain the MDF method

$$ \begin{aligned} y_{n+1} &=\exp({\varOmega}^{[2]}(t_{n},t_{n+1}))\left( y_{n}+\tilde{g}_{0}(y_{n})h+{\sum}_{j=1}^{m}g_{j}(y_{n}){\varDelta} W_{jn}\right. \\&\left.+{\sum}_{j,l=1}^{m}\hat{\mathbf{H}}_{jl}\frac{I_{lj}}{\sqrt{h}}\right), \end{aligned} $$

(14)

where $\hat {\mathbf {H}}_{jl}=g_{j}(Y_{l})-g_{j}(y_{n})+(\exp (-A_{l}\sqrt {h})-I)g_{j} (y_{n}).$

4 Convergence analysis

In this section we will give the mean-square convergence results for both the ME method and the MM method. From [19], we review the following fundamental convergence theorem of one-step numerical methods.

Lemma 2

Suppose that the one-step approximation y_t+h has order of accuracy p₁ for the mathematical expectation of the deviation and order of accuracy p₂ for the mean-square deviation; more precisely, for arbitrary t₀ ≤ t ≤ T − h, $y(t)=y\in \mathbb {R}^{d}$ the following inequalities hold:

$$ \begin{aligned} |\mathbb{E}(y(t+h)-y_{t+h})|&\leq K\sqrt{1+|y|^{2}}h^{p_{1}},\\ (\mathbb{E}|(y(t+h)-y_{t+h})|^{2})^{1/2}&\leq K\sqrt{1+|y|^2}h^{p_{2}}, \end{aligned} $$

with p₂ ≥ 1/2, p₁ ≥ p₂ + 1/2, i.e., the approximation is consistent in the mean order p₁ and in the mean-square order p₂. Then for any N and k = 0,1,...,N the following inequality holds:

$$\left[\mathbb{E}\left|y\left( t_{k}\right)-y_{k}\right|^{2}\right]^{1 /2} \leq K\left( 1+\mathbb{E}\left|y_{0}\right|^{2}\right)^{1 /2} h^{p_{2}-1/2},$$

i.e., the method is convergent of order p₂ − 1/2 in the sense of mean-square.

The following theorems show the convergence results of the Magnus-type method. We suppose that the coefficients of (1) satisfy the linear growth condition and the global Lipschitz condition. We also assume uniformly bounded derivatives up to order 2 for the MM method and MDF method. Let y(t_n + h) be the exact evaluation of (1) at t_n+ 1 starting from y(t_n) = y_n. We will estimate the p₁, p₂ for the Magnus-type method satisfying

$$ \begin{aligned} \left|\mathbb{E}\left( y\left( t_{n}+h\right)-y_{n+1}\right)\right| &=O\left( h^{p_{1}}\right), \\ \left( \mathbb{E}\left|y\left( t_{n}+h\right)-y_{n+1}\right|^{2}\right)^{\frac{1}{2}} &=O\left( h^{p_{2}}\right). \end{aligned} $$

Theorem 2

Let y_n be an approximation to the solution of (1) using the ME method. Then for any N and k = 0,1,...,N the following inequality holds:

$$\left[\mathbb{E}\left|y\left( t_{k}\right)-y_{k}\right|^{2}\right]^{1 /2} \leq K\left( 1+\mathbb{E}\left|y_{0}\right|^{2}\right)^{1 /2} h^{1/2},$$

i.e., the ME method is convergent of order 1/2 in the sense of mean-square.

Proof

For the ME method, it can be readily shown that

$$ \begin{aligned} y\left( t_{n}+h\right)-y_{n+1}=P_{1}+P_{2}+P_{3}, \end{aligned} $$

where

$$ \begin{aligned} P_{1}=&\left( \exp({\varOmega}(t_{n},t_{n+1}))-\exp({\varOmega}^{[1]}(t_{n},t_{n+1}))\right)y_{n},\\ P_{2}=&\exp({\varOmega}(t_{n},t_{n+1})){\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}({t_{n},s}))\tilde{g}_{0}(y(s))\mathrm{d}s\\ &-\exp({\varOmega}^{[1]}(t_{n},t_{n+1})){\int}_{t_{n}}^{t_{n+1}}\tilde{g}_{0}(y(t_{n}))\mathrm{d}s,\\ P_{3}=&\exp({\varOmega}(t_{n},t_{n+1}))\sum\limits_{j=1}^{m}{\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}({t_{n},s}))g_{j}(y(s))\mathrm{d}W_{j}(s)\\ &-\exp({\varOmega}^{[1]}(t_{n},t_{n+1}))\sum\limits_{j=1}^{m}{\int}_{t_{n}}^{t_{n+1}}g_{j}(y(t_{n}))\mathrm{d}W_{j}(s). \end{aligned} $$

For term P₁, since $\exp ({\varOmega }(t_{n},t_{n+1}))y_{n}$ is the solution of (5), we can easily find

$$ \begin{aligned} |\mathbb{E}(P_{1})|=O\left( h^{2}\right),~(\mathbb{E}|P_{1}|^{2})^{1/2}=O\left( {h}\right). \end{aligned} $$

(15)

For P₂, adding and subtracting $\exp ({\varOmega }(t_{n},t_{n+1})){\int \limits }_{t_{n}}^{t_{n+1}}\tilde {g}_{0}(y_{n})\mathrm {d}s$ give

$$ \begin{aligned} P_{2}&=\exp({\varOmega}(t_{n},t_{n+1})){\int}_{t_{n}}^{t_{n+1}}\left( \exp(-{\varOmega}({t_{n},s}))\tilde{g}_{0}(y(s))-\tilde{g}_{0}(y_{n})\right)\mathrm{d}s\\ &~~+ \left( \exp({\varOmega}(t_{n},t_{n+1}))-\exp({\varOmega}^{[1]}(t_{n},t_{n+1}))\right){\int}_{t_{n}}^{t_{n+1}}\tilde{g}_{0}(y(t_{n}))\mathrm{d}s\\ &=P_{21}+P_{22}. \end{aligned} $$

Utilizing (1) and (12),

$$\begin{aligned} &\exp \left( -{\varOmega}\left( t_{n}, s\right)\right) \tilde{g}_{0}(y(s))\\ =& \tilde{g}_{0}\left( y_{n}\right)+{\int}_{t_{n}}^{s}\left( -A_{0}+\sum\limits_{j=1}^{m} {A_{j}^{2}}\right) Y\left( s_{1}\right) \tilde{g}_{0}\left( y\left( s_{1}\right)\right) \mathrm{d} s_{1} \\ &-{\int}_{t_{n}}^{s}\sum\limits_{j=1}^{m} A_{j} Y\left( s_{1}\right) \tilde{g}_{0}\left( y\left( s_{1}\right)\right) \mathrm{d} W_{j}\left( s_{1}\right)+{\int}_{t_{n}}^{s} Y\left( s_{1}\right) \mathrm{d} \tilde{g}_{0}(y\left( s_{1}\right)) \\ &+{\int}_{t_{n}}^{s}\sum\limits_{j=1}^{m} A_{j} Y\left( s_{1}\right)\left( A_{j} y\left( s_{1}\right)+g_{j}\left( y\left( s_{1}\right)\right)\right) \mathrm{d} s_{1}, \end{aligned}$$

we can easily find

$$ \begin{aligned} |\mathbb{E}(P_{21})|&=O\left( h^{2}\right),~(\mathbb{E}|P_{21}|^{2})^{1/2}=O\left( {h^{3/2}}\right),\\ |\mathbb{E}(P_{22})|&=O\left( h^{3}\right),~(\mathbb{E}|P_{22}|^{2})^{1/2}=O\left( {h^{2}}\right). \end{aligned} $$

(16)

For P₃, adding and subtracting $\exp ({\varOmega }({t_{n},t_{n+1}})){\int \limits }_{t_{n}}^{t_{n+1}}{g}_{j}(y_{n})\mathrm {d}W_{j}(s)$ gives

$$ \begin{aligned} P_{3}=&\exp({\varOmega}({t_{n},t_{n+1}}))\sum\limits_{j=1}^{m}{\int}_{t_{n}}^{t_{n+1}}\left( \exp(-{\varOmega}({t_{n},s}))g_{j}(y(s))-g_{j}(y_{n})\right)\mathrm{d}W_{j}(s)\\ &+\left( \exp({\varOmega}({t_{n},t_{n+1}}))-\exp({\varOmega}^{[1]}({t_{n},t_{n+1}}))\right)\sum\limits_{j=1}^{m}{\int}_{t_{n}}^{t_{n+1}}g_{j}(y(t_{n}))\mathrm{d}W_{j}(s). \end{aligned} $$

Similar to term P₂, we can get

$$ \begin{aligned} |\mathbb{E}(P_{3})|=O\left( h^{2}\right),~(\mathbb{E}|P_{3}|^{2})^{1/2}=O\left( {h}\right). \end{aligned} $$

(17)

With (15), (16) and (17), we have p₁ = 2, p₂ = 1. From Lemma 2, we know that the ME method is of mean-square order 0.5. □

For the MM methods, we can obtain the following convergence results.

Theorem 3

Let y_n be an approximation to the solution of (1) using the MM method. Then for any N and k = 0,1,...,N the following inequality holds:

$$\left[\mathbb{E}\left|y\left( t_{k}\right)-y_{k}\right|^{2}\right]^{1 /2} \leq K\left( 1+\mathbb{E}\left|y_{0}\right|^{2}\right)^{1 /2} h,$$

i.e., the MM method is convergent of order 1 in the sense of mean-square.

Proof

For the MM method, through direct calculation, we find

$$ \begin{aligned} y\left( t_{n}+h\right)-y_{n+1}=P_{1}+P_{2}+P_{3}, \end{aligned} $$

where

$$ \begin{aligned} P_{1}=&\left( \exp({\varOmega}({t_{n},t_{n+1}}))-\exp({\varOmega}^{[2]}({t_{n},t_{n+1}}))\right)y_{n},\\ P_{2}=&\exp({\varOmega}({t_{n},t_{n+1}})){\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}({t_{n},s}))\tilde{g}_{0}(y(s))\mathrm{d}s\\ &-\exp({\varOmega}^{[2]}({t_{n},t_{n+1}})){\int}_{t_{n}}^{t_{n+1}}\tilde{g}_{0}(y(t_{n}))\mathrm{d}s,\\ P_{3}=&\left.\exp({\varOmega}({t_{n},t_{n+1}}))\sum\limits_{j=1}^{m}{\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}({t_{n},s}))g_{j}(y(s))\mathrm{d}W_{j}(s) \right.\\ &-\left.\exp({\varOmega}^{[2]}({t_{n},t_{n+1}}))\sum\limits_{j=1}^{m}\left( {\int}_{t_{n}}^{t_{n+1}}g_{j}(y(t_{n}))\mathrm{d}W_{j}(s)\right.\right.\\ &+\left.\left.\sum\limits_{l=1}^{m}\mathbf{H}_{j, l}\left( y_{n}\right) {\int}_{t_{n}}^{t_{n+1}}{\int}_{t_{n}}^{s}dW_{l}(s_{1})dW_{j}(s)\right) \right.. \end{aligned} $$

For term P₁, since $\exp ({\varOmega }({t_{n},t_{n+1}}))y_{n}$ is the solution of (5), we can easily see through an Itô-Taylor expansion

$$ \begin{aligned} |\mathbb{E}(P_{1})|=O\left( h^{2}\right),~(\mathbb{E}|P_{1}|^{2})^{1/2}=O\left( {h^{3/2}}\right). \end{aligned} $$

(18)

For P₂, adding and subtracting $\exp ({\varOmega }({t_{n},t_{n+1}})){\int \limits }_{t_{n}}^{t_{n+1}}\tilde {g}_{0}(y_{n})\mathrm {d}s,$ we have

$$ \begin{aligned} P_{2}=&\exp({\varOmega}({t_{n},t_{n+1}})){\int}_{t_{n}}^{t_{n+1}}\left( \exp(-{\varOmega}({t_{n},s}))\tilde{g}_{0}(y(s))-\tilde{g}_{0}(y_{n})\right)\mathrm{d}s\\ &+ \left( \exp({\varOmega}({t_{n},t_{n+1}}))-\exp({\varOmega}^{[2]}({t_{n},t_{n+1}}))\right){\int}_{t_{n}}^{t_{n+1}}\tilde{g}_{0}(y(t_{n}))\mathrm{d}s\\ =&P_{21}+P_{22}, \end{aligned} $$

and

$$ \begin{aligned} |\mathbb{E}(P_{21})|=O\left( h^{2}\right),~(\mathbb{E}|P_{21}|^{2})^{1/2}=O\left( {h^{3/2}}\right),\\ |\mathbb{E}(P_{22})|=O\left( h^{3}\right),~(\mathbb{E}|P_{22}|^{2})^{1/2}=O\left( {h^{5/2}}\right). \end{aligned} $$

(19)

For term P₃, since

$$ \begin{aligned} &\exp({\varOmega}({t_{n},t_{n+1}})){\int}_{t_{n}}^{t_{n+1}}\exp(-{\varOmega}({t_{n},s}))g_{j}(y(s))dW_{j}(s) \\ =&\exp({\varOmega}({t_{n},t_{n+1}}))\left( {\int}_{t_{n}}^{t_{n+1}}g_{j}(y_{n})dW_{j}(s)+{\int}_{t_{n}}^{t_{n+1}}{\int}_{t_{n}}^{s}\left( g_{j}^{\prime}(y_{n})\left( A_{l}y_{n}+g_{l}(y_{n})\right)\right.\right.\\ &\left.\left.-A_{l}g_{j}(y_{n}) \right)dW_{l}(s_{1})dW_{j}(s)+R_{1j}\right), \end{aligned} $$

where

$$ \begin{aligned} |\mathbb{E}(R_{1j})|=O\left( h^{2}\right),~(\mathbb{E}|R_{1j}|^{2})^{1/2}=O\left( {h^{3/2}}\right), \end{aligned} $$

we have

$$ \begin{aligned} P_{3}=&\left( \exp({\varOmega}({t_{n},t_{n+1}}))-\exp({\varOmega}^{[2]}({t_{n},t_{n+1}}))\right)\sum\limits_{j=1}^{m}\left( {\int}_{t_{n}}^{t_{n+1}}g_{j}(y(t_{n}))\mathrm{d}W_{j}(s)\right.\\ &\left.+\sum\limits_{l=1}^{m}\mathbf{H}_{j, l}\left( y_{n}\right) {\int}_{t_{n}}^{t_{n+1}}{\int}_{t_{n}}^{s}dW_{l}(s_{1})dW_{j}(s)\right)+\sum\limits_{j=1}^{m}\exp({\varOmega}({t_{n},t_{n+1}}))R_{1j}, \end{aligned} $$

which gives

$$ \begin{aligned} |\mathbb{E}(P_{3})|=O\left( h^{2}\right),~(\mathbb{E}|P_{3}|^{2})^{1/2}=O\left( h^{3/2}\right). \end{aligned} $$

(20)

From (18), (19) and (20), p₁ = 2, p₂ = 3/2. Hence by Lemma 2, we see that the MM method is of mean-square order 1. □

The following theorem describes the convergence of the MDF method. The proof is analogous to that of Theorem 3 and we omit it.

Theorem 4

Let y_n be an approximation to the solution of (1) using the MDF method. Then for any N and k = 0,1,...,N the following inequality holds:

$$\left[\mathbb{E}\left|y\left( t_{k}\right)-y_{k}\right|^{2}\right]^{1 /2} \leq K\left( 1+\mathbb{E}\left|y_{0}\right|^{2}\right)^{1 /2} h.$$

Thus the MDF method is convergent of order 1 in the sense of mean-square.

5 Implementation and numerical tests

Using the Milstein or MM method to generate numerical approximations, the iterated integrals (7) are included in the numerical scheme. For i = j, there is such a relationship $I_{i i}\left (t_{n}, t_{n}+h\right )=\frac {1}{2}(({\varDelta } W_{in})^{2}-h)$. For i≠j, this issue has been fully described in [20, 21] and [22] by Kuznetsov and Wiktorsson from a different perspective, respectively. Both of them expand the iterated integrals (7) into infinite series, and then truncate the infinite series to approximate the iterated integrals. A brief overview is given in the Appendix.

To compare the convergence rate of the truncated series, for different step sizes and m = 2, we respectively give the minimum truncated terms indices q_w, q_t, q_p of the Wiktorsson’s algorithm, Kuznetsov’s algorithm with the orthonormal system of trigonometric functions and Legendre polynomials in Table 1. We can see that Wiktorsson’s algorithm requires smaller truncated indices to achieve the mean square error $O\left (h^{3}\right )$, especially for a smaller step size h, which also means that Wiktorsson’s algorithm needs to simulate fewer random variables.

Table 1 The minimum q_w, q_t, q_p that needs to be selected for different time steps

In order to show the specific performance of the three algorithms, for the integral I₂₁, choosing h = 2^− 6, the mean $(\mathbb {E}(I_{21})=0)$ and standard deviation $((\mathbb {E}(I_{21})^{2})^{1/2}=h/\sqrt {2}\approx 0.01105)$ are calculated in Table 2 with 2000 samples. Their mean and standard deviation are almost in the same range. At the same time, the numerical tests in the next will also show that using Kuznetsov and Wiktorsson algorithms in practical implementation can give almost the same simulation results for different step size.

Table 2 Iterated Itô integral I₂₁ with truncating the first 3, 5, 7, 11 terms of the infinite series, respectively

For the rest of this section, the performances of the introduced Magnus-type methods are presented and then compared with classical stochastic methods, namely the Euler–Maruyama method and the Milstein method. For convenience, let M (W) denote the mean-square order 1.0 Milstein method, where the iterated Itô integrals are simulated by Wiktorsson’s algorithm. Let M (K_t) and M (K_p) denote the mean-square order 1.0 Milstein method, where the iterated Itô integrals are simulated by Kuznetsov’s algorithm with the orthonormal system of trigonometric functions and Legendre polynomials, respectively. This shorthand notation also applies to the MM method and the MDF method.

To present the performance of Wiktorsson’s and Kuznetsov’s algorithms for the iterated Itô integrals, we will compare the number of random variables required by Wiktorsson’s and Kuznetsov’s algorithms in each iteration as a measure of computational effort. The exponential function needs to be calculated during the implementation of the numerical algorithm, which is not the subject of this article, so we compare the time required by Wiktorsson’s and Kuznetsov’s algorithms to generate random variables as a measure of the efficiency. In all numerical simulations, we choose the minimum truncation number.

5.1 Damped nonlinear Kubo oscillator

As a first numerical test, we consider the damped nonlinear Kubo oscillator

$$ \mathrm{d} y(t)=\sum\limits_{j=0}^{m}\left[\omega_{j}\left( \begin{array}{cc} 0 & -1 \\ 1 & \beta_{j} \end{array}\right) y(t)+\left( \begin{array}{cc} 0 & -g_{j}(y(t)) \\ g_{j}(y(t)) & 0 \end{array}\right)y(t)\right] \mathrm{d} W_{j}(t) $$

(21)

with $g_{j}: \mathbb {R}^{2} \rightarrow \mathbb {R}$, where t ∈ [0,T] and $\omega _{j},~\beta _{j}\in \mathbb {R}$. This problem is investigated in [24] with β_j = 0. We also let m = 2 and

$$g_{0}(y(t))=\frac{1}{5}\left( y_{1}+y_{2}\right)^{5}, g_{1}(y(t))=0, g_{2}(y(t))=\frac{1}{3}\left( y_{1}+y_{2}\right)^{3}.$$

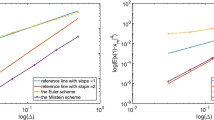
Since we do not know the exact solution of (21), the reference solution is produced by the Milstein method with a small step h = 2^− 19. Set the parameters ω₀ = 2, ω₁ = 0.5, ω₂ = 0.2,β₀ = − 0.5, β₁ = − 0.2, β₂ = − 0.1 and initial value y₀ = (1,1). The mean-square convergence order of ME method, MM method and MDF method is presented in Fig. 1. Here, the mean-square error

$$||\text{ERROR}||_{L2}=\sqrt{\frac{\displaystyle\sum\limits_{j=1}^{2000}|y_{N}-y(T)|^{2}}{2000}}$$

is calculated at the time T = 1 for a set of increasing time steps h = 2ⁱ, i = − 11, …, − 2. As some of the lines are on the top of each other, we use separate figures to show the performance of Wiktorsson’s and Kuznetsov’s algorithms in Fig. 1. From Fig. 1a, we can see that the Magnus-type methods enjoy considerably smaller error coefficient compared to the Euler–Maruyama method and the Milstein method and the performance of the three simulations of the iterated Itô integral is similar. It can be seen from Fig. 2a that when the step size is large (i.e., the error is large), Wiktorsson’s and Kuznetsov’s algorithms perform similarly in terms of calculation time. As the step size becomes smaller (i.e., the error becomes smaller), Wiktorsson’s algorithm performs better, as it can be seen in (b) that the number of random variables that need to be simulated at each step of Wiktorsson’s algorithm is less. In addition, Kuznetsov’s algorithm with polynomial functions is slightly better than Kuznetsov’s algorithm with trigonometric functions in terms of calculation time and the number of random variables that need to be simulated at each step. The increment for different steps is given by

$$\begin{aligned} I_{i,j,t_{n}, t_{n}+p h}=&{\int}_{t_{n}}^{t_{n+ph}} {\int}_{t_{n}}^{s} \mathrm{d} W_{i}(s_{1}) \mathrm{d} W_{j}(s)\\ \approx& I_{i, j, t_{n}, t_{n}+p h}^{q}\\ =&\sum\limits_{k=0}^{p-1}\left[I_{i, j, t_{n}+k h, t_{n}+(k+1) h}^{q}+{\varDelta} W_{j, n+k}I_{k \geq 1} \sum\limits_{l=0}^{k-1} {\varDelta} W_{i, n+l}\right]. \end{aligned}$$

Fig. 1

a The convergence rate of the ME method, MM method and MDF method for solving (21) with $g_{0}(y(t))=\frac {1}{5}\left (y_{1}+y_{2}\right )^{5}$, g₁(y(t)) = 0 and $g_{2}(y(t))=\frac {1}{3}\left (y_{1}+y_{2}\right )^{3}$. b Kuznetsov’s algorithms with the orthonormal system of trigonometric functions. c Kuznetsov’s algorithms with the orthonormal system of Legendre polynomials. d Wiktorsson’s algorithm

Fig. 2

Comparison of Wiktorsson’s and Kuznetsov’s algorithm in average computing time and number of random variables at each step for (21) with a set of increasing time steps h = 2ⁱ, i = − 11, …, − 2. a Average computing time. b Number of random variables at each step

5.2 SDE with linear non-commutative noise

We consider the following SDE [2] in $\mathbb {R}^{4},$ with

$$ \mathrm{d}y=(r A_{0} y+\mathbf{F}(y)) \mathrm{d} t+G(y) \mathrm{d} \mathbf{W}(t), $$

(22)

where r = 4, $\quad \mathbf {F}(y)=(F_{1},F_{2},F_{3},F_{4}), \quad F_{j}=\frac {y_{j}}{1+\left |y_{j}\right |},~j=1,~2,~3,~4,$ and initial value y(0) = y₀. dW(t) = (dW₁(t),dW₂(t),dW₃(t),dW₄(t)). Here A₀ takes the form

$$A_{0}=\left( \begin{array}{cccc} -2 & 1 & 0 & 0 \\ 1 & -2 & 1 & 0 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & -2 \end{array}\right),$$

which usually comes from a discrete Laplacian operator. Consider the following non-commutative noise

$$ G(y)=\left( \begin{array}{cccc} \beta y_{1} & 0 & 0&0 \\ 0 & \beta y_{2}-\alpha y_{1} & 0 & 0 \\ 0 & 0 & \beta y_{3}-\alpha y_{2} & 0 \\ 0 & 0 & 0 & \beta y_{4}-\alpha y_{3} \end{array}\right).$$

Then, we have

$$\begin{small} \begin{aligned} A_{1}=\left( \begin{array}{cccc} \beta & 0 & 0&0 \\ 0 &0 & 0 & 0 \\ 0 & 0 & 0& 0 \\ 0 & 0 & 0 & 0 \end{array}\right),A_{2}=\left( \begin{array}{cccc} 0 & 0 & 0&0 \\ -\alpha &\beta & 0 & 0 \\ 0 & 0 & 0& 0 \\ 0 & 0 & 0 & 0 \end{array}\right),A_{3}=\left( \begin{array}{cccc} 0 & 0 & 0&0 \\ 0& 0 & 0 & 0 \\ 0 & -\alpha &\beta& 0 \\ 0 & 0 & 0 & 0 \end{array}\right),A_{4}=\left( \begin{array}{cccc} 0 & 0 & 0&0 \\ 0& 0 & 0 & 0 \\ 0 & 0 &0& 0 \\ 0 & 0 & -\alpha & \beta \end{array}\right). \end{aligned}\end{small}$$

Simulations with α = 0.5, β = 1 and y₀ = (1,1,1,1)^⊤ are carried out until the time T = 1 with a set of increasing time steps h = 2ⁱ, i = − 11, …, − 3. The mean-square convergence order of the ME method and the MM method is presented in Fig. 3. In each case 2000 samples are generated as before. Here, the reference solution is produced by the Milstein method with the step h = 2^− 16. Figure 3 compares the cases for r = 4, α = 0.8, β = 1 in (a) and compares the cases for r = 4, α = 2, β = 0.1 in (b). We see that the case r = 4, α = 0.8, β = 1 enjoys a smaller error than the mildly stiff case r = 4, α = 2, β = 0.1. Figure 4a shows that Wiktorsson’s and Kuznetsov’s algorithms perform similarly in terms of calculation time. This is because the truncation index of Wiktorsson’s algorithm is related to m, so when m and the step size are both large, Kuznetsov’s algorithm is a sensible choice. In addition, Kuznetsov’s algorithm with polynomial functions is also slightly better than Kuznetsov’s algorithm with trigonometric functions in terms of calculation time and the number of random variables that need to be simulated at each step for m = 4. As the step size decreases, Wiktorsson’s algorithm has obvious advantages in the number of random variables at each step.

Fig. 3

The convergence rate of the ME method and the MM method for solving (22) with m = 4 in a r = 4, α = 0.8, β = 1 and in b r = 4, α = 2, β = 0.1

Fig. 4

Comparison of the algorithms in computing time and number of random variables at each step with a set of increasing time steps h = 2ⁱ, i = − 11, …, − 3. Here r = 4, α = 0.8 and β = 1. a Average computing time. b Number of random variables at each step

5.3 Stochastic Manakov equation

In order to confirm the performance of the methods for high-dimensional SDEs, we consider the stochastic Manakov system

$$ \begin{aligned} &\mathrm{i} \mathrm{d} u+\left( {\partial_{x}^{2}} u +|u|^{2} u \right)\mathrm{d} t+\mathrm{i} \sqrt{\gamma} \sum\limits_{k=1}^{3} \sigma_{k} \partial_{x} u \circ \mathrm{d} W_{k}=0,\\ u(0,x)=&\left( \cos(\pi/8)~ \sin(\pi/8)\right)\text{sech}(x),~x\in[-a,a]\\ u(t,-a)=&u(t,a)=0, ~t\in[0,T], \end{aligned} $$

(23)

where $u=u(t, x)=\left (u_{1}, u_{2}\right )\in \mathbb {C}^{2}$ with $t \geqslant 0$ and $x \in \mathbb {R}$. The symbol ∘ means that the stochastic integrals are established in the sense of Stratonovich and $\gamma \geqslant 0$ is the noise intensity. Here $|u|^{2}u=\left (\left |u_{1}\right |^{2}+\left |u_{2}\right |^{2}\right )u$ is the nonlinear term, and σ₁,σ₂ and σ₃ are the Pauli matrices taking the form

$$ \sigma_{1}=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left( \begin{array}{cc} 0 & -\mathrm{i} \\ \mathrm{i} & 0 \end{array}\right), \quad \text { and } \quad \sigma_{3}=\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right). $$

The stochastic Manakov system (23) is usually used to describe pulse propagation in randomly birefringent optical fibers. The existence and uniqueness of the solution have been obtained in [25]. The equivalent Itô form is

$$ d u(t)=\left( C_{\gamma} \frac{\partial^{2} u(t)}{\partial x^{2}}+\mathrm{i} |u|^{2} u\right) d t-\sqrt{\gamma} \sum\limits_{k=1}^{3} \sigma_{k} \frac{\partial u(t)}{\partial x} d W_{k}(t), $$

(24)

where $C_{\gamma }=\mathrm {i}+\frac {3 \gamma }{2}$. Applying the central finite-difference scheme to discretize the space interval by N + 2 uniform points

$$\partial_{x} u_{t}\left( x_{i}\right) \approx \frac{u_{t, i+1}-u_{t, i-1}}{2{\varDelta} x} ~\text{or}~\frac{u_{t, i}-u_{t, i-1}}{{\varDelta} x} , \quad\! \partial_{x x} u_{t}\left( x_{i}\right) \approx \frac{u_{t, i+1}-2 u_{t, i}+u_{t, i-1}}{{\varDelta} x^{2}},$$

we get the non-commutative SDE

$$ \begin{aligned} \mathrm{d} y(t)=&(C_{\gamma}A_{0} y(t)+\boldsymbol{f}(y(t))) \mathrm{d} t-\sqrt{\gamma} \sum\limits_{k=1}^{3} \sigma_{k}A_{k}{y}(t) \mathrm{d} W_{k}(t), \end{aligned} $$

(25)

with

$$\\ y(0)=\left[\cos(\frac{\pi}{8})\text{sech}(x_{1})\cdots\cos(\frac{\pi}{8})\text{sech}(x_{N}) ~\sin(\frac{\pi}{8})\text{sech}(x_{1})\cdots\sin(\frac{\pi}{8})\text{sech}(x_{N})\right]_,^{\top}$$

where

$$y(t) \underset{=}{\text { def }}\left[u\left( t, x_{1}\right)~ u\left( t, x_{2}\right)~ \cdots~ u\left( t, x_{N}\right)\right]^{\top},$$

$$f(y) \underset{=}{\text { def }}i\left[y_{1}|y_{1}|^{2}~ y_{2}|y_{2}|^{2}~ \cdots~ y_{N}|y_{N}|^{2}\right]^{\top},$$

and the matrices A₀, A₁, A₂ and A₃ are defined by

$$A_{0} \underset{=}{\text { def }}N^{2}\left[\begin{array}{ccccc} -2 & 1 & & & 0 \\ 1 & -2 & 1 & & \\ & {\ddots} & {\ddots} & {\ddots} & \\ & & 1 & -2 & 1 \\ 0 & & & 1 & -2 \end{array}\right],~A_{k} \underset{=}{\text { def }}N\left[\begin{array}{ccccc} 1 & 0 & & & 0 \\ -1 & 1 & 0 & & \\ & {\ddots} & {\ddots} & {\ddots} & \\ & & -1 & 1 & 0 \\ 0 & & & -1 & 1 \end{array}\right],k=1,~2,~3.$$

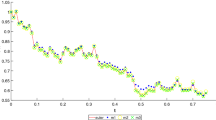
First, we set a = 20, h = 0.001 and Δx = 2/5 to simulate (23) with the MM method on the time interval [0,3]. The evolution of $\left |u_{1}\right |^{2}$ and $\left |u_{2}\right |^{2}$ is given in Fig. 5. We can see that the results of the MM method show the energy exchange due to stochastic noise and nonlinearity. These results are similar to the structure-preserving method in [26].

Fig. 5

Space-time evolution of the intensity of the first component (left) and the second component (right)

Then, simulations with a = 50 and Δx = 2/5 are carried out until the time T = 1/2 with a set of increasing time steps h = 2ⁱ, i = − 13, …, − 7. The mean-square convergence order of the ME method and the MM method is presented in Fig. 6. In each case 500 samples are generated. Here, the reference solution is produced by the Milstein method with the step h = 2^− 16. In Fig. 7, (a) shows that Wiktorsson’s and Kuznetsov’s algorithms perform similarly in terms of calculation time. Wiktorsson’s algorithms is better than Kuznetsov’s algorithms in terms of calculation time and the number of random variables that need to be simulated in each step. This is because as the step size decreases, the number of noise terms m has less impact on the truncation index of Wiktorsson’s algorithm. In addition, as the step size decreases, the difference between Kuznetsov’s algorithm with polynomial functions and Kuznetsov’s algorithm with trigonometric functions is not significant.

Fig. 6

The convergence rate of the ME and the MM method with a = 50 and Δx = 2/5, T = 1/2 and a set of increasing time steps h = 2ⁱ, i = − 13, …, − 7

Fig. 7

Comparison of the algorithms in computing time and number of random variables at each step with a set of increasing time steps h = 2ⁱ, i = − 13, …, − 7. Here a = 50, Δx = 2/5 and T = 1/2. a Average computing time. b Number of random variables at each step

Remark 1

Here we use the built-in expmdemo2 function in Matlab to calculate $\exp ({\varOmega }^{[1]}(t_{n},t_{n+1}))$ and $\exp ({\varOmega }^{[2]}(t_{n},t_{n+1}))$ using a Taylor series. For such high-dimensional problems, each path requires considerable computational time. Although the calculation of exponential function is not the subject of this article, the application of efficient techniques (such as Krylov subspace methods) will have a significant impact on the Magnus-type methods to address very high-dimensional semilinear SDEs.

Remark 2

In the high-dimensional problem (25), we choose mildly stiff matrices A₀ as opposed to the nonlinear term. When the stiffness is very strong, our methods require a small step size. For this type of stiff high-dimensional complex-valued SDEs, the combination of the SROCK methods [27, 28] and the Magnus method will be an interesting work that we will consider in future work.

Remark 3

With the specific performance in the above three test examples, we see that for the simulation of iterated Itô integrals, when the step size is large and the number of noise terms is large, Kuznetsov’s algorithm with polynomial functions is superior, and when the step size is smaller, Wiktorsson’s algorithm is better.

6 Conclusion

We have derived Magnus-type methods, based on Magnus expansion for non-commutative linear SDEs, for noncommutative Itô stochastic differential equations with semi-linear drift term and semi-linear diffusion terms. By truncating the Magnus series, the ME method, the MM method and the MDF method have been constructed. We have investigated the mean-square convergence of these methods and shown the same mean-square convergent order as the corresponding method, that is, the ME method is order 0.5, and the MM and MDF method is order 1.0. Then, we have compared two types of algorithms for simulating iterated Itô integrals. Numerical tests have been carried out to present the efficiency of the proposed methods for low-dimensional SDEs and a high-dimensional SDE from discretized SPDE.

Finally, we should make the following remarks. We can apply our methods to non-autonomous semi-linear SDEs, where we only need to truncate the non-autonomous Magnus expansion. However, the linear stability analysis of numerical methods for high-dimensional stochastic differential equations with non-commutative noises is quite complicated, especially for complex coefficient matrices. The mean-square stability analysis of Magnus-type methods for such problems is a motivation for future work. In addition, weak convergence Magnus methods will be a good choice to avoid simulating iterated stochastic integrals.

Appendix

1.1 A.1 The expansion of iterated Itô stochastic integrals based on the generalized multiple Fourier series

Let $\left \{\phi _{j}(x)\right \}_{j=0}^{\infty }$ be an orthonormal basis of the space $L_{2}\left (\left [t_{n}, t_{n+1}\right ]\right ).$ If the trigonometric series

$$ \phi_{j}(s)=\frac{1}{\sqrt{h}}\left\{\begin{array}{cc} 1, & j=0, \\ \sqrt{2} \sin \frac{2 \pi r\left( s-t_{n}\right)}{h}, & j=2 r-1, \\ \sqrt{2} \cos \frac{2 \pi r\left( s-t_{n}\right)}{h}, & j=2 r, \end{array}\right. $$

where r = 1, 2,…, are selected as an orthonormal basis, for the iterated Itô integral (7), using the expansion theorem in [20], the following representations are obtained,

$$ \begin{aligned} I_{ij}(t_{n}, t_{n}+h)=&\frac{1}{2}h\left[\zeta_{0}^{\left( j\right)} \zeta_{0}^{\left( i\right)}+\frac{1}{\pi} \sum\limits_{r=1}^{\infty} \frac{1}{r}\left\{\zeta_{2 r}^{\left( j\right)} \zeta_{2 r-1}^{\left( i\right)}-\zeta_{2 r-1}^{\left( j\right)} \zeta_{2 r}^{\left( i\right)}\right.\right.\\ &+\left.\left.\sqrt{2}\left( \zeta_{2 r-1}^{\left( j\right)} \zeta_{0}^{\left( i\right)}-\zeta_{0}^{\left( j\right)} \zeta_{2 r-1}^{\left( i\right)}\right)\right\}\right],~i\neq j, \end{aligned} $$

(A.1)

where $\zeta _{0}^{(i)} \underset {=}{\text { def }} W_{i}(h)/\sqrt {h}$ and $\zeta _{j}^{(i)} \underset {=}{\text { def }} {{\int \limits }_{t}^{T}} \phi _{j}(s) d W_{i}(s)$, i = 1,…,m. The expansion (A.1) coincides with Kloeden, Platen and Wright’s (1992) algorithm [23] based on Kahunen–Loève expansion and it converges to the iterated Itô integral (7) in the mean-square sense.

If orthonormal Legendre polynomials are selected as an orthonormal basis,

$$ \left\{\phi_{j}(s)\right\}_{j=0}^{\infty}, \phi_{j}(s)=\sqrt{\frac{2 j+1}{h}} P_{j}\left( \left( s-\frac{h}{2}\right) \frac{2}{h}\right) $$

the expansion is

$$ \begin{aligned} I_{ij}(t_{n}, t_{n}+h)=\frac{h}{2}\left[\zeta_{0}^{\left( i\right)} \zeta_{0}^{\left( j\right)}+\sum\limits_{r=1}^{\infty} \frac{1}{\sqrt{4 r^{2}-1}}\left\{\zeta_{r-1}^{\left( i\right)} \zeta_{r}^{\left( j\right)}-\zeta_{r}^{\left( i\right)} \zeta_{r-1}^{\left( j\right)}\right\}\right]. \end{aligned} $$

(A.2)

As the expansions (A.1) and (A.2) are infinite series, we need to truncate them for practical simulation. During the implementation of the Milstein and MM methods, the mean-square error of the approximated iterated integrals should not be larger than h³, which is to ensure mean-square convergence of 1.

Truncating the infinite series (A.1) and (A.2) to q terms, we have $I_{i j}^{q}$. From the truncated mean-square error in [21], we obtain the mean-square error for truncating (A.1)

$$ \begin{aligned} \mathrm{E}\left\{\left( I_{i j}\left( t_{n}, t_{n}+h\right)-I_{i j}^{q}\left( t_{n}, t_{n}+h\right)\right)^{2}\right\}\leq \frac{3 h^{2}}{2 \pi^{2} q}. \end{aligned} $$

Here we need 3h²/(2π²q) ≤ h³, so we should choose

$$ q_{t} \geq\left\lceil\frac{3}{2 \pi^{2} h}\right\rceil. $$

Truncating the expansion (A.1) to q, we get the mean-square error

$$ \begin{aligned} \mathrm{E}\left\{\left( I_{i j}\left( t_{n}, t_{n}+h\right)-I_{i j}^{q}\left( t_{n}, t_{n}+h\right)\right)^{2}\right\}\leq -\frac{h^{2}}{8} \ln \left|1-\frac{2}{2 q+1}\right|. \end{aligned} $$

Here we need the mean-square error less than h³, so we should choose

$$ q_{p} \geq\left\lceil\left( \frac{2}{1-e^{-8 h}}-1\right) / 2\right\rceil. $$

Since q_p ≈ 1/(8h), the truncated indices of A.1 and (A.2) both are O(1/h), and it can be calculated that the convergence speed of (A.1) is about q_t/q_p ≈ 1.22 times that of (A.2). This means that the approximation based on the multiple Legendre Fourier series is slightly more efficient than that based on the multiple trigonometric Fourier series.

1.2 A.2 Wiktorsson’s algorithm

If I(h) and A(h) are matrices with elements $I_{i j}\left (t_{n}, t_{n}+h\right )$, A_ii = 0 and

$$ A_{i j}(h)=\frac{h}{2\pi} {\sum}_{r=1}^{\infty} \frac{1}{r}\left\{\zeta_{2 r}^{(j)} \zeta_{2 r-1}^{(i)}-\zeta_{2 r-1}^{(j)} \zeta_{2 r}^{(i)}+\sqrt{2}\left( \zeta_{2 r-1}^{(j)} \zeta_{0}^{(i)}-\zeta_{0}^{(j)} \zeta_{2 r-1}^{(i)}\right)\right\},i\neq j $$

respectively, the approximation based on the multiple trigonometric Fourier series can be written in matrix form

$$ \begin{aligned} & \mathbf{I}(h)=\frac{{\varDelta} \mathbf{W}(h) {\varDelta} \mathbf{W}(h)^{\top}-h I_{m}}{2}+\mathbf{A}(h), \\ &\mathbf{A}(h)=\frac{h}{2 \pi} {\sum}_{k=1}^{\infty} \frac{1}{k}\left\{\mathbf{X}_{k}\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right)^{\top}-\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right) \mathbf{X}_{k}^{\top}\right\}, \end{aligned} $$

(A.3)

where ${\varDelta } \mathbf {W}(h) \sim N\left (0, h I_{m}\right ), \mathbf {X}_{k} \sim N\left (0_{m}, I_{m}\right )$ and $\mathbf {Y}_{k} \sim N\left (0_{m}, I_{m}\right ), k=$1, 2,…,q are all independent. As the Lévy stochastic area has the relationship I_ij − I_ji = 2A_ij, we only need to simulate I_ij for i < j or i > j in the simulation.

Wiktorsson’s algorithm is based on approximation of the tail-sum distribution of (A.3)

$$\varepsilon_{q}=\frac{h}{2 \pi} {\sum}_{k=q+1}^{\infty} \frac{1}{k}\left\{\mathbf{X}_{k}\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right)^{\top}-\left( \mathbf{Y}_{k}+\sqrt{2 / h} {\varDelta} \mathbf{W}(h)\right) \mathbf{X}_{k}^{\top}\right\}, $$

which improves the rate of convergence. Let vec $\left (\mathbf {I}(h)^{T}\right )$ be column vectors of (A.3), and the following is the procedure of Wiktorsson’s algorithm [22]:

• 1. First simulate ${\varDelta } \mathbf {W}(h) \sim N\left (0_{m}, \sqrt {h} I_{m}\right )$.

• 2. Simulate the truncated first q terms

  $$ \tilde{A}^{(q)}(h)=\frac{h}{2 \pi} {\sum}_{k=1}^{q} \frac{1}{k} K_{m}\left( P_{m}-I_{m^{2}}\right)\left\{\left( \mathbf{Y}_{k}+\sqrt{\frac{2}{h}} {\varDelta} \mathbf{W}(h)\right) \otimes \mathbf{X}_{k}\right\} $$

  where $\mathbf {X}_{k} \sim N\left (0_{m}, I_{m}\right )$ and $\mathbf {Y}_{k} \sim N\left (0_{m}, I_{m}\right )$

• 3. Then simulate $\mathbf {G}_{q} \sim N\left (0_{M}, I_{M}\right )$ and add the approximation of tail-sum distribution:

  $$ \widetilde{A}^{(q)^{\prime}}(h)=\widetilde{A}^{(q)}(h)+\frac{h}{2 \pi} a_{q}^{1 / 2} \sqrt{{\Sigma}_{\infty}} \mathbf{G}_{q} $$

  where $a_{q}={\sum }_{k=q+1}^{\infty } 1 / k^{2}$

• 4. Finally obtain the approximation vec $\left (\mathbf {I}(h)^{T}\right )^{(q)^{\prime }}$ of vec $\left (\mathbf {I}(h)^{T}\right )$

  $$ \operatorname{vec}\left( \mathbf{I}(h)^{T}\right)^{(q)^{\prime}}=\frac{{\varDelta} \mathbf{W}(h) \otimes {\varDelta} \mathbf{W}(h)-\operatorname{vec}\left( h I_{m^{2}}\right)}{2}+\left( I_{m^{2}}-P_{m}\right) {K_{m}^{T}} \widetilde{A}^{(q)^{\prime}}(h) $$

  Here P_m is the m² × m² permutation matrix and for the specific expression of matrices P_m please refer to [22].

The mean-square error of Wiktorsson’s algorithm [22] is

$$ \underset{i, j}{\max} E\left\{\left( I_{i j}(h)-I_{i j}^{(q)^{\prime}}(h)\right)^{2}\right\} \leq \frac{5 h^{2}}{24 \pi^{2} q^{2}} m^{2}(m-1). $$

Here we also need the mean-square error less than h³, so we should choose truncated indices as

$$ q_{w} \geq\left\lceil\frac{\sqrt{5 m^{2}(m-1) /\left( 24 \pi^{2}\right)}}{\sqrt{ h}}\right\rceil, $$

and the truncated indices q_w is $O(1/\sqrt {h})$ that is much better than O(1/h).